Abstract
Patients with repaired tetralogy of Fallot (TOF) account for the majority of cases with late onset right ventricle failure. Comparing TOF patients with healthy people may provide information to address this challenge. Cardiac magnetic resonance (CMR) data were obtained from 16 TOF patients (patient group, PG) and 6 healthy volunteers (healthy group, HG). At begin-of-ejection, better patient group (n=5, BPG) stress was very close to HG stress (54.7±38.4 kPa vs. 51.2±55.7 kPa, p=0.6889) while worse patient group (n=11, WPG) stress was 84% higher than HG stress (p=0.0418). Stress may be used as an indicator to differentiate BPG patients from WPG patients, with further validations.
Keywords: Heart modeling, cardiac mechanics, normal ventricle, right ventricle, tetralogy of Fallot
1 Introduction
With the recent development of modelling and imaging technology, computational mechanical analysis and computer-aided procedures have become more widely used in cardiac function analysis and patient-specific surgical design, replacing traditional empirical and often risky experimentation to examine the efficiency and suitability of various reconstructive cardiac procedures [McCulloch, Waldman, Rogers et al. (1992); Hunter, Pullan and Smaill (2003); Pfeiffer, Tangney and Omens (2014); Fan, Yao, Yang et al. (2016)].
Tetralogy of Fallot (TOF) is a congenital heart defect which involves four anatomical abnormalities of the heart: pulmonary infundibular stenosis, overriding aorta, ventricular septal defect and right ventricular (RV) hypertrophy. With the introduction of TOF repair surgery, survival of TOF patients has increased substantially starting from the 80s. One recent report showed that long-term survival rate for repaired TOF patients decreased significantly after the first two decades of the initial repair [Nollert, Fischlein, Bouterwek et al. (1997)]. Pulmonary valve replacement (PVR) is one traditional surgical approach for repaired TOF patients with failing RV. Although the current PVR surgical approaches are meant to address pulmonary regurgitation issue, many patients do not experience an improvement in RV function and some show a decline after PVR [del Nido (2006); Geva, Gauvreau, Powell et al. (2010); McKenzie, Khan, Dietzman et al. (2014); Tweddell, Simpson, Li et al. (2012)].
In our previous publications [Tang, Yang, Geva et al. (2008); (2010)], computational RV/LV models were used in the comparison between regular PVR surgeries and PVR surgeries with RV remodeling, and PVR surgeries with RV remodeling were found to result in reduced stress/strain conditions in the patch area which may lead to improved recovery of RV function. In [Tang, Yang, Geva et al. (2011)], RV/LV models with different patch materials were constructed to evaluate the effect of patch materials on RV function. RV/LV models with contracting band were built to investigate the impact of band material stiffness variations, band length and active contraction [Yang, Tang, Geva et al. (2013)]. More recently, [Tang, Del Nido, Yang et al. (2016)] introduced RV/LV models with different zero-load diastole and systole geometries to reflect zero-stress sarcomere length changes in active contraction. These results indicated that computational models were powerful in the investigation of PVR surgeries.
In this study, CMR-based computational RV/LV models were constructed for 6 healthy volunteers and 16 TOF patients. The purposes of this study are: a) use RV/LV models to obtain RV morphological and mechanical parameters (circumferential and longitudinal curvatures, RV stress and strain) for healthy people which are lacking in the current literature; b) identify the differences in morphological and mechanical stress/strain characteristics between TOF patients and healthy people and see if these will help to differentiate better-outcome TOF patients from worse outcome TOF patients.
2 Data acquisition, models and methods
2.1 Data acquisition
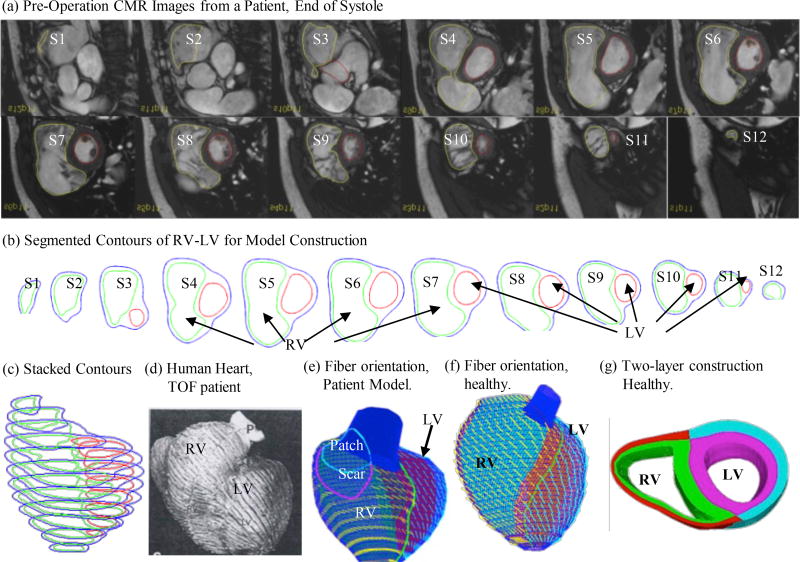
This study was approved by the Boston Children’s Hospital Committee on Clinical Investigation. CMR data were obtained from 22 people (9 male, 13 female; median age, 36.6 years; 16 with TOF, 6 healthy) previously enrolled in our RV surgical remodeling trial with written consent obtained [Geva, Gauvreau, Powell et al. (2010)]. For the 16 TOF patients, CMR data before and 6 months after PVR were available for model construction and analysis. Based on their RV ejection fraction (EF) changes, the patients were categorized into two groups, the Better-Outcome Patient Group (BPG, n=5) which had positive RV EF changes (RV EF change: 3.94±2.20) and Worse-Outcome Patient Group (WPG, n=11) which had negative RV EF changes (RV EF change: −8.88±5.30, p-value: 0.00015). Demographic information, RV volumes, pressure conditions, and RV EF for the participants are summarized in Table 1. CMR acquisition procedures have been previously described [Tang, Yang, Geva et al. (2014)]. Each CMR data set consists of 30 time steps per cardiac cycle, and each time step data has 9–14 slices covering ventricles in ventricular short axis from base to apex. Three-dimensional RV/LV geometry and computational meshes were constructed following the procedures described in [Tang, Yang, Geva et al. (2011)]. Figure 1 shows selected CMR images from a TOF patient before the PVR surgery with segmented contours and re-constructed 3D RV/LV geometries. Our two-layer model construction and fiber orientation information were also provided [Hunter, Pullan and Smaill (2003); Sanchez-Quintana, Anderson and Ho (1996)].
Table 1.
Demographic and CMR data for healthy volunteers and TOF patients
| Patient | Sex | Age (y) |
Begin- Filling Pressure |
Begin- Ejection Pressure |
RV EDV (cm3) |
RV ESV (cm3) |
RV EF (%) |
ΔEF (%) |
|---|---|---|---|---|---|---|---|---|
| Healthy Group (HG) | ||||||||
|
| ||||||||
| H1 | F | 46.7 | 3.6 | 22 | 128.4 | 46.9 | 63 | - |
| H2 | M | 23.6 | 5 | 27.9 | 226.6 | 105.4 | 53 | - |
| H3 | M | 20.8 | 4.5 | 24 | 231.7 | 107.0 | 54 | - |
| H4 | M | 19.4 | 3.9 | 23.8 | 213.5 | 94.2 | 56 | - |
| H5 | M | 17.7 | 4.2 | 24.3 | 233.7 | 105.5 | 55 | - |
| H6 | M | 6.7 | 4.3 | 24.8 | 67.6 | 28.2 | 58 | - |
|
| ||||||||
| Mean ± SD | 22.5 ±13.2 | 4.25 ±0.48 | 24.5 ±1.93 | 183.6 ±69.4 | 81.2 ±34.6 | 56.5 ±3.62 | - | |
|
| ||||||||
| Better-Outcome Patient Group (BPG) | ||||||||
|
| ||||||||
| P1 | M | 22.5 | 21.6 | 31.4 | 406.9 | 254.5 | 37.5 | 1.4 |
| P2 | F | 42.0 | 10 | 45 | 323.3 | 177.8 | 45.0 | 4.0 |
| P3 | F | 14.3 | 3 | 29 | 204.0 | 104.3 | 48.8 | 5.6 |
| P4 | F | 15.3 | 2 | 15 | 193.7 | 105.1 | 45.7 | 6.6 |
| P5 | M | 17.0 | 3 | 27 | 188.3 | 108.3 | 42.5 | 2.0 |
|
| ||||||||
| Mean ± SD | 22.2 ±11.5 | 7.92 ±8.29 | 29.5 ±10.7 | 263.2 ±97.7 | 150.0 ±66.2 | 43.9 ±4.22 | 3.92 ±2.24 | |
|
| ||||||||
| Worse-Outcome Patient Group (WPG) | ||||||||
|
| ||||||||
| P6 | F | 38.5 | 6 | 28 | 328.8 | 196.0 | 40.4 | −3.4 |
| P7 | M | 47.7 | 2 | 31 | 408.8 | 254.8 | 37.7 | −2.6 |
| P8 | M | 50.0 | 3 | 33 | 364.6 | 239.5 | 34.3 | −2.9 |
| P9 | F | 56.9 | 5 | 41 | 385.1 | 184.6 | 52.1 | −18.0 |
| P10 | M | 11.6 | 10 | 36 | 204.2 | 121.3 | 40.6 | −8.4 |
| P11 | M | 43.5 | 17 | 65 | 665.1 | 464.0 | 30.2 | −15.2 |
| P12 | M | 54.1 | 4 | 63 | 334.8 | 170.8 | 49.0 | −7.0 |
| P13 | F | 49.5 | 12 | 52 | 277.2 | 151.3 | 45.4 | −5.0 |
| P14 | M | 17.8 | 2 | 30 | 365.0 | 178.0 | 51.2 | −9.5 |
| P15 | F | 44.6 | 11 | 50 | 299.0 | 186.0 | 37.8 | −12.3 |
| P16 | F | 45.3 | 9 | 49 | 571.1 | 371.3 | 35.0 | −13.4 |
|
| ||||||||
| Mean ± SD | 41.8 ±14.4 | 7.36 ±4.82 | 43.5 ±13.2 | 382.2 ±131 | 228.9 ±102 | 41.2 ±7.27 | −8.88 ±5.29 | |
Figure 1.
Model construction process using CMR image slices from a TOF patient. (a) Pre-operative CMR images of a TOF patient; (b) segmented contours; (c) stacked contours; (d) fiber orientation from a human heart; (e–f) fiber orientation from RV/LV models of a TOF patient and a healthy volunteer; (g) two-layer construction.
Abbreviations: F: Female; M: male; EDV: end-diastolic volume; ESV: end-systolic volume; EF: ejection fraction.
2.2 The active anisotropic RV/LV models
The ventricular material was assumed to be hyperelastic, anisotropic, nearly-incompressible and homogeneous. Right Ventricular Outflow Tract (RVOT) material, patch and scar were assumed to be hyper-elastic, isotropic, nearly-incompressible and homogeneous. The governing equations for the structure models are:
| (1) |
| (2) |
Here σ is the stress tensor, ε is Green’s strain tensor, u is the displacement, and ρ is material density. The normal stress on the outer RV/LV surface was set to zero, and was set to the imposed RV/LV pressure conditions on the inner RV/LV surfaces:
| (3) |
The Mooney-Rivlin model was used to describe the nonlinear anisotropic and isotropic material properties. The strain energy function for the isotropic modified Mooney-Rivlin model (for patch, scar tissue and RVOT material) was given by [Tang, Yang, del Nido et al. (2011, 2015)]:
| (4) |
| (5) |
where I1 and I2 are the first and second strain invariants, C = [Cij]= XTX is the right Cauchy–Green deformation tensor, X=[Xij] = [∂x i/∂aj], (xi) is current position, (ai) is original position), and ci and Di are material parameters chosen to match experimental measurements [Tang, Yang, del Nido et al. (2015)]. The strain energy function for the anisotropic modified Mooney-Rivlin model was used for the ventricle tissue [Tang, Yang, del Nido et al. (2011); (2015)]:
| (6) |
where I4 = Cij(nf)i(nf)j, Cij is the Cauchy-Green deformation tensor, nf is the fiber direction, K1 and K2 are material constants. The anisotropic strain-energy function with respect to the local fiber direction was given below [McCulloch, Waldman, Rogers et al. (1992)].
| (7) |
| (8) |
where Eff is fiber strain, Ecc is cross-fiber in-plane strain, Err is radial strain, and Ecr, Efr and Efc are the shear components in their respective coordinate planes, C, b1, b2, and b3 are parameters to be chosen to fit experimental data. It should be noted that Equations (7)–(8) were used because it is desirable to use local coordinate system to identify material parameters which are independent of fiber directions.
Biaxial mechanical testing of human myocardium was performed in Billiar’s lab and results were reported in our previous paper [Tang, Yang, del Nido et al. (2015)]. Active contraction and relaxation were modeled by material stiffening and softening. In our material model, parameter values c1, D1 and C in equations (6) and (7) were adjusted at every CMR time step to match CMR-measured RV volume data for each patient. Fiber orientation was set the same way as in our previous papers (see Figure 1) [Hunter, Pullan and Smaill (2003); Sanchez-Quintana, Anderson and Ho (1996)].
2.3 Geometry-fitting mesh generation
Ventricles have complex irregular geometries which are challenging for mesh generation. A geometry-fitting mesh generation technique was developed to generate mesh for our models. Figure 1 (g) gives an illustration of RV/LV geometry between two slices. In each slice, “points” (ADINA mesh generation terms) were first defined based on the results of MRI segmentation. Then, “lines” were defined to divide the slice into geometry-fitting areas (called “surfaces” in ADINA). The neighboring slices were stacked to form “volumes”. Using this technique, the 3D RV/LV domain was divided into many small “volumes” to curve-fit the irregular ventricular geometry with patch and scar as inclusions. Finally, meshes were generated in each small volume. 3D surfaces, volumes and computational mesh were made under ADINA computing environment. Mesh analysis was performed by decreasing mesh size by 10% (in each dimension) until solution differences were less than 2%. The mesh was then chosen for our simulations.
2.4 Pre-shrink process
Numerical simulation needs to start from an initial condition where the initial ventricular geometry, pressure and stress/strain conditions of a working heart were provided. Since stress is hard to measure in vivo, our numerical simulations started from zero-load ventricular geometries with zero pressure and zero stress/strain distributions. Under in vivo condition, the ventricles were pressurized and the zero-load ventricular geometries were not known. In our model construction process, a pre-shrink process was applied to the in vivo begin-filling ventricular geometries to generate the starting shape (zero-load ventricular geometries) for the computational simulation. The initial shrinkage for the inner ventricular surface was 2–3% which was adjusted iteratively so that when begin-filling pressure was applied, the ventricles would match their in vivo morphology as much as possible. The ventricular out surface shrinkage was determined by volume conservation law so that the total ventricular wall volume was conserved. Without this pre-shrink process, the pressurized ventricle volume would be greater than its in vivo volume due to the initial expansion when pressure was applied.
2.5 Solution methods and morphological and stress/strain data for analysis
The RV/LV computational models (n=22) were constructed and solved by ADINA (ADINA R&D, Watertown, Mass) using finite elements and the New-Raphson iteration method. CMR-measured RV volume and pressure data were used to adjust model parameters so that model-predicted RV volume matched CMR-measure data.
Each ventricle model had 9–14 CMR slices. Every slice was divided into 4 quarters, each with equal inner wall circumferential length. Ventricular wall thickness (WT), circumferential curvature (C-cur), longitudinal curvature (L-cur), maximal principle stress (Stress-P1) and maximal principle strain (Strain-P1) were calculated at all nodal points (100 points per slice, 25 points per quarter). Their average values over the 25 points in each quarter provided the quarter values of these parameters which were collected for analysis. The formulas used for calculation of circumferential curvature (κc) at each point was
| (9) |
The formulas used for calculation of longitudinal curvature (κ) at each point was
| (10) |
Details can be found from [Tang, Yang, del Nido et al. (2015)].
2.6 Statistical analysis
The mean and standard deviation values of RV volumes, WT, C-cur, L-cur, Stress-P1 and Strain-P1 were summarized by Table 2. Unpaired Student t test was used to compare mean RV volumes between different groups. Due to the small size of data, the quarter mean values were used in the analysis of RV wall thickness, curvatures, Stress-P1 and Strain-P1. Similar to what we did in [Tang, Yang, del Nido et al. (2015)], the Linear Mixed-Effect Model was used to take care of data dependence structure and make comparisons between different outcome groups.
Table 2.
Summary of mean geometric and stress/strain parameter values at begin of ejection
| WT (cm) |
C-cur (1/cm) |
L-cur (1/cm) |
RV EDV (cm3) |
Stress-P1 (kPa) |
Strain-P1 | |
|---|---|---|---|---|---|---|
| HG | ||||||
|
| ||||||
| H1 | 0.35 | 1.15 | 0.87 | 125.2 | 70.2 | 0.63 |
| H2 | 0.68 | 0.68 | 0.56 | 227.1 | 51.6 | 0.58 |
| H3 | 0.64 | 0.77 | 0.68 | 226.7 | 36.3 | 0.40 |
| H4 | 0.51 | 0.62 | 0.61 | 213.1 | 56.0 | 0.39 |
| H5 | 0.57 | 0.57 | 1.27 | 232.6 | 45.9 | 0.57 |
| H6 | 0.31 | 0.90 | 1.11 | 66.37 | 48.0 | 0.51 |
|
| ||||||
| Mean ± SD | 0.51 ±0.15 | 0.81 ±0.19 | 0.85 ±0.29 | 183.6 ±69.4 | 51.3 ±11.4 | 0.51 ±0.10 |
|
| ||||||
| BPG | ||||||
|
| ||||||
| P1 | 0.39 | 0.47 | 1.24 | 406.9 | 56.9 | 0.29 |
| P2 | 0.47 | 0.43 | 0.96 | 323.3 | 82.4 | 0.44 |
| P3 | 0.48 | 0.50 | 1.20 | 204.0 | 61.9 | 0.48 |
| P4 | 0.42 | 0.53 | 1.84 | 193.7 | 33.5 | 0.46 |
| P5 | 0.51 | 0.53 | 1.85 | 188.3 | 42.0 | 0.40 |
|
| ||||||
| Mean ± SD | 0.45 ±0.05 | 0.49 ±0.04 | 1.42 ±0.40 | 263.2 ±97.7 | 55.3 ±18.9 | 0.41 ±0.08 |
|
| ||||||
| WPG | ||||||
|
| ||||||
| P6 | 0.34 | 0.39 | 0.77 | 328.8 | 65.3 | 0.43 |
| P7 | 0.65 | 0.37 | 1.01 | 408.8 | 41.0 | 0.33 |
| P8 | 0.49 | 0.54 | 1.54 | 364.6 | 64.1 | 0.36 |
| P9 | 0.48 | 0.42 | 0.91 | 385.1 | 172.1 | 0.66 |
| P10 | 0.41 | 1.34 | 1.32 | 204.2 | 82.9 | 0.49 |
| P11 | 0.80 | 0.36 | 0.59 | 665.1 | 82.4 | 0.23 |
| P12 | 0.71 | 0.44 | 0.72 | 334.8 | 83.1 | 0.42 |
| P13 | 0.45 | 0.46 | 0.97 | 277.2 | 191.7 | 0.66 |
| P14 | 0.43 | 0.65 | 1.60 | 365.0 | 65.4 | 0.44 |
| P15 | 0.46 | 0.44 | 1.23 | 299.0 | 154.3 | 0.51 |
| P16 | 0.59 | 0.33 | 1.25 | 571.1 | 76.2 | 0.34 |
|
| ||||||
| Mean ± SD | 0.53 ±0.14 | 0.52 ±0.29 | 1.08 ±0.33 | 382.2 ±131.1 | 98.0 ±50.1 | 0.44 ±0.13 |
Abbreviations: WT: wall thickness; C-cur: circumferential curvature; L-cur: longitudinal curvature
3 Results
3.1 Comparison of geometrical parameters: TOF patients have noticeable differences in RV volume, L-cur and C-cur from healthy group
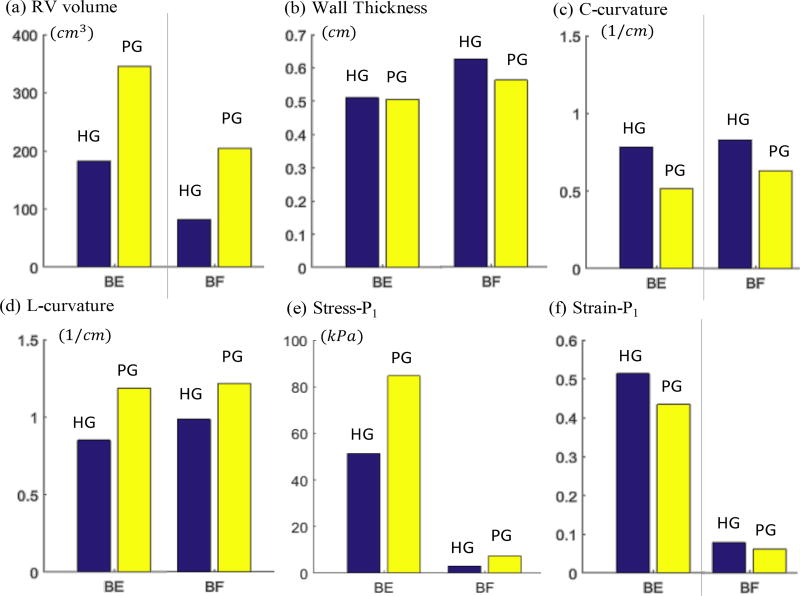
Table 2 summarized the average values of the geometrical and mechanical parameters from HG, BPG and WPG. These values were used in our group comparisons. Table 3 summarized and compared the average values of geometrical parameters (RV volume, wall thickness, L-cur and C-cur) between healthy group (HG) and patient group (PG = BPG + WPG). Bar plots of the average values are given in Figure 2 showing group differences. At the beginning of ejection, average Stress-P1 of PG was 60.5% higher than that from HG (82.2±79.4 kPa vs. 51.2±55.7 kPa, p=0.1031). At the beginning of filling, mean Stress-P1 of PG was 143.7% higher than that from HG (7.31±8.49 kPa vs. 3.00±2.30 kPa, p=0.0831). The high percentage should be discounted because the overall stress values were small. At begin of ejection, average Strain-P1 from HG was 18% higher than that from PG. Noticing that average Strain-P1 values from both HG and PG at begin-filling were about the same, higher strain from HG means that healthy ventricles had better contractibility, consistent with our expectations. RV volume was the parameter with the most noticeable difference between HG and PG. At the beginning of ejection, average PG RV volume was 87.9% higher than that from HG (344.9±131.3 cm3 vs. 183.6±69.4 cm3, p=0.0102). At the beginning of filling, average RV volume of PG was 151.5% higher than that from HG (204.2±97.9 cm3 vs. 81.2±34.6 cm3, p=0.0076). The high percentage difference at begin-filling was due to the fact that RV of PG contracted much less that HG.
Table 3.
Comparison of RV volumes, geometric parameters, and stress/strain values between healthy group (HG) and patient group (PG=BPG+WPG) at begin of ejection and begin of filling.
| Begin of Ejection | Begin of Filling | |||||
|---|---|---|---|---|---|---|
| PG | HG | P value | PG | HG | P value | |
| RV volume(cm3) | 344.9±131.3 | 183.6±69.4 | 0.0102 | 204.2±97.9 | 81.2±34.6 | 0.0076 |
| WT (cm) | 0.51±0.24 | 0.51±0.30 | 0.9315 | 0.57±0.27 | 0.64±0.32 | 0.3616 |
| C-cur (1/cm) | 0.52±1.21 | 0.81±1.05 | 0.0237 | 0.64±1.23 | 0.83±0.51 | 0.1519 |
| L-cur (1/cm) | 1.19±1.21 | 0.86±0.71 | 0.0756 | 1.22±1.22 | 0.99±0.66 | 0.2585 |
| Stress-P1 (kPa) | 82.2±79.4 | 51.2±55.7 | 0.1031 | 7.31±8.49 | 3.00±2.30 | 0.0831 |
| Strain-P1 | 0.43±0.19 | 0.51±0.17 | 0.1486 | 0.06±0.07 | 0.07±0.06 | 0.5376 |
Values are expressed as mean±standard deviation.
Abbreviations are the same as in Table 2.
Figure 2.
Bar plots comparing RV volume, WT, C-cur, L-cur, Stress-P1 and Strain-P1 values from Healthy Group (HG) and Patient Group (HG) at Begin-Ejection (BE) and Begin-Filling (BF).
C-cur and L-cur also showed large differences between HG and PG. At begin of ejection, mean PG C-cur was 35.8% lower than mean HG C-cur, and mean PG L-cur was 38.4% higher than mean HG L-cur. At begin of filling, average C-cur of PG was 22.9% lower than that from HG, and average L-cur of PG was 23.2% higher than that from HG. It is worth noting that the ratio of L-cur over C-cur for PG at begin-ejection is 2.29, compared to 1.06 for HG. At begin of filling, the ratio of L-cur over C-cur for PG is 1.90, compared to 1.19 for HG. RV WT did not show much difference between HG and PG.
3.2 HG may help differentiate BPG from WPG
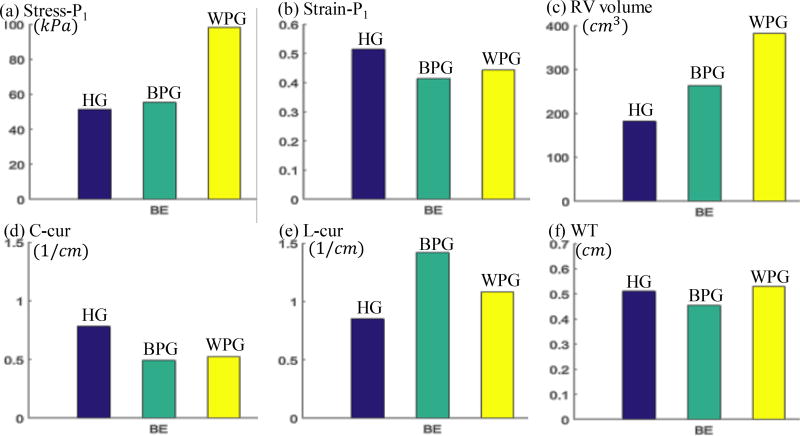
Table 4 summarized and compared geometrical and mechanical parameter values of BPG and WPG to HG. Figure 3 gave the bar plots of average Stress-P1, StrainP1, RV volume, C-cur, L-cur and WT at begin-ejection, showing the differences among the three groups. Table 4 and Figure 3 showed that differences in wall thickness, C-cur and Strain-P1 between BPG and WPG may not be very useful in differentiating BPG patients from WPG patients. Stress-P1 from BPG was found to be closer to that from HG, compared to Stress-P1 of WPG. At the beginning of ejection, mean Stress-P1 of BPG was only 6.8% higher than that from HG (54.7±38.4 kPa vs. 51.2±55.7 kPa, p=0.6889), and the difference was not significant; while average Stress-P1 of WPG was 84.1% higher than that of HG (94.3±89.2 kPa vs. 51.2±55.7 kPa, p=0.0418), and the difference was significant.
Table 4.
Comparison of geometric and stress/strain mean values between healthy group (HG) and patient groups (better-outcome patient group (BPG), worse-outcome patient group (WPG)).
| Begin of Ejection | Begin of Filling | |||||
|---|---|---|---|---|---|---|
| BPG | HG | P value | BPG | HG | P value | |
| RV volume 3) (cm3) | 263.2±97.7 | 183.6±69.4 | 0.1482 | 150.0±66.2 | 81.2±34.6 | 0.0534 |
| WT (cm) | 0.45±0.20 | 0.52±0.30 | 0.4441 | 0.50±0.21 | 0.64±0.32 | 0.1099 |
| C-cur (1/cm) | 0.49±0.26 | 0.81±1.05 | 0.0094 | 0.63±0.34 | 0.83±0.51 | 0.0082 |
| L-cur (1/cm) | 1.42±1.40 | 0.86±0.71 | 0.0263 | 1.58±1.56 | 0.99±0.66 | 0.0420 |
| Stress-P1 (kPa) | 54.7±38.4 | 51.2±55.7 | 0.6889 | 3.76±4.17 | 3.00±2.30 | 0.5968 |
| Strain-P1 | 0.41±0.18 | 0.51±0.17 | 0.1042 | 0.03±0.02 | 0.07±0.06 | 0.1047 |
|
| ||||||
| WPG | HG | P value | WPG | HG | P value | |
| RV volume (cm3) | 382.1±131.1 | 183.6±69.4 | 0.0038 | 228±102.4 | 81.2±34.6 | 0.0041 |
| WT (cm) | 0.53±0.26 | 0.52±0.30 | 0.8150 | 0.60±0.29 | 0.64±0.32 | 0.6508 |
| C-cur (1/cm) | 0.54±1.45 | 0.81±1.05 | 0.0709 | 0.64±1.46 | 0.83±0.51 | 0.2427 |
| L-cur (1/cm) | 1.09±1.11 | 0.86±0.71 | 0.2006 | 1.07±1.00 | 0.99±0.66 | 0.6194 |
| Stress-P1 (kPa) | 94.3±89.2 | 51.2±55.7 | 0.0418 | 8.87±9.39 | 3.00±2.30 | 0.0290 |
| Strain-P1 | 0.43±0.20 | 0.51±0.17 | 0.2603 | 0.08±0.07 | 0.07±0.06 | 0.9860 |
Figure 3.
Bar plots comparing average Stress-P1, Strain-P1, RV volume, C-cur, L-cur and WT values from Healthy Group (HG), Better-outcome Patient Group (BPG) and Worse-outcome Patient Group (WPG) at Begin-Ejection (BE). Blue: HG; Green: BPG; Yellow: WPG.
At the beginning of filling, average Stress-P1 of BPG was 25% higher than that from HG (3.76±4.17 kPa vs. 3.00±2.30 kPa, p=0.5968), while average Stress-P1 of WPG was 195.7% higher than that of HG (8.87±9.39 kPa vs. 3.00±2.30 kPa, p=0.0290). The results suggested that comparing patient’s RV stress values with healthy RV stress values may help identify patients with possible better outcome.
Similarly, BPG RV volumes at Begin-Ejection were closer to HG RV volumes (263 cm3 vs. 184 cm3, 43% higher) compared to WPG volumes (382 cm3 vs. 184 cm3, 107% higher). BPG L-curvature was much greater than HG L-curvature at Begin-Ejection (1.42 vs. 0.86 1/cm, 65% higher) than WPG L-cur over HG (1.09 vs. 0.861/cm, 27% higher). Based on these results, RV volume and L-cur could be useful in identifying better-outcome patients.
4 Discussion
4.1 Modeling techniques for models based on in vivo data with complex geometry
It should be emphasized that the pre-shrink and mesh generation techniques presented in this paper are of general interest for models based on in vivo geometry and of complex structures. In vivo data of organs such as ventricles and arteries are under pressure and internal stress conditions. Most mechanical models require zero-stress geometry as their starting point for stress/strain calculations. Our pre-shrink pressure presented in this paper is a way to obtain the zero-load ventricle geometry as our model starting geometry. Without the shrinking process, as soon as pressure is added to the ventricle, the ventricle will be inflated and its volume will be greater than its in vivo size. This is a major difference between models based on in vivo data and models based on ex vivo data.
4.2 Motivation to construct models of healthy people
TOF patients have mixed results after PVR. It has remained challenging for the surgeons and clinicians to differentiate patients with better outcome from those with worse outcome. This work aims to determine if information from healthy people could be helpful in meeting that challenge. At the same time, general mechanical stress/strain and morphological information for healthy people will be good contributions since such data are still lacking in the current literature. It should be explained that our purpose is not only looking for differences between TOF patients and healthy people. We were also trying to find methods and indicators which could help us to separate BPG from WPG by using HG information. As the main result of this paper, it was found that BPG Stress-P1 and HG Stress-P1 were close to each other. In fact, they were not statistically different. This indicates RV stress could be a biomarker to be used for possible prediction of post-PVR outcome. RV volume and longitudinal curvature could serve the same purpose in a similar way.
4.3 Limitations
One limitation of this study is the small sample size which results in limited statistical power. The reason for the small sample size is the extensive amount of time required for constructing each computational model. Currently, it would take a trained modeling technician 2 weeks to generate one 3D patient-specific model. Thus, improving the model-building technique to make the process less labor-intensive and more clinically applicable will be a major effort for our future work.
Other limitations include: a) fluid-structure interactions can be added to obtain blood flow velocity and shear stress which can be also included in the investigation of predictors for good recovery after PRV; b) patient-specific and location-specific measurements of tissue mechanical properties (such as MRI with tagging) will be very desirable for improved accuracy of our models; c) inclusion of patient-specific fiber orientations; d) inclusion of pulmonary valve mechanics in the current model will be an important addition.
5 Conclusion
Our results indicated that RV stress from the better-outcome patient group was close to stress from the healthy group, and stress could be used as a potential indicator to differentiate BPG patients from WPG patients, with further validations.
Acknowledgments
This research was supported in part by National Heart, Lung and Blood Institute grants R01 HL089269 (PI del Nido, Tang, Geva), R01 HL63095 (PI del Nido) and 5P50HL074734 (PI: Geva). Tang’s research was also supported in part by National Sciences Foundation of China grants 11672001, 81571691.
References
- Del Nido PJ. Surgical Management of Right Ventricular Dysfunction Late after Repair of Tetralogy of Fallot: Right Ventricular Remodeling Surgery. Semin Thorac Cardiovasc Surg Pediatr Card Surg Annu. 2006;9:29–34. doi: 10.1053/j.pcsu.2006.02.007. [DOI] [PubMed] [Google Scholar]
- Fan L, Yao J, Yang C, Xu D, Tang D. Modeling Active Contraction and Relaxation of Left Ventricle Using Different Zero-load Diastole and Systole Geometries for Better Material Parameter Estimation and Stress/Strain Calculations. MCB: Molecular & Cellular Biomechanics. 2016;13(1):44–68. doi: 10.3970/mcb.2016.013.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Geva T, Gauvreau K, Powell AJ, Cecchin F, Rhodes J, et al. Randomized trial of pulmonary valve replacement with and without right ventricular remodeling surgery. Circulation. 2010;122(11 Suppl):S201–208. doi: 10.1161/CIRCULATIONAHA.110.951178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hunter PJ, Pullan AJ, Smaill BH. Modeling total heart function. Annual Review of Biomedical Engineering. 2003;5:147–177. doi: 10.1146/annurev.bioeng.5.040202.121537. [DOI] [PubMed] [Google Scholar]
- McCulloch AD, Waldman L, Rogers J, Guccione JM. Large-scale finite element analysis of the beating heart. Critical Reviews in Biomedical Engineering. 1992;20:427–449. [PubMed] [Google Scholar]
- McKenzie ED, Khan MS, Dietzman TW, Guzm an-Pruneda FA, Samayoa AX, et al. Surgical pulmonary valve replacement: a benchmark for outcomes comparisons. Journal of Thoracic and Cardiovascular Surgery. 2014;148:1450–1453. doi: 10.1016/j.jtcvs.2014.02.060. [DOI] [PubMed] [Google Scholar]
- Nollert G, Fischlein T, Bouterwek S, Bohmer C, Klinner W, et al. Longterm survival in patients with repair of tetralogy of Fallot: 36-year follow-up of 490 survivors of the first year after surgical repair. Journal of The American College of Cardiology. 1997;30:1374–1383. doi: 10.1016/s0735-1097(97)00318-5. [DOI] [PubMed] [Google Scholar]
- Pfeiffer RE, Tangney RJ, Omens HJ, McCulloch AD. Biomechanics of cardiac electromechanical coupling and mechanoelectric feedback. Journal of Biomechanical Engineering. 2014;136:021007. doi: 10.1115/1.4026221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez-Quintana D, Anderson R, Ho SY. Ventricular myoarchitecture in tetralogy of Fallot. Heart. 1996;76:280–286. doi: 10.1136/hrt.76.3.280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang D, Del Nido PJ, Yang C, Zuo H, Huang X, et al. Patient-Specific MRI-Based Right Ventricle Models Using Different Zero-Load Diastole and Systole Geometries for Better Cardiac Stress and Strain Calculations and Pulmonary Valve Replacement Surgical Outcome Predictions. PLoS One 2016. 2016 Sep 14;11(9):e0162986. doi: 10.1371/journal.pone. 0162986.eCollection 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang D, Yang C, del Nido PJ, Zuo H, Rathod RH, et al. Mechanical stress is associated with right ventricular response to pulmonary valve replacement in patients with repaired tetralogy of Fallot mechanical stress. Journal of Thoracic and Cardiovascular Surgery. 2015;151:687–694. doi: 10.1016/j.jtcvs.2015.09.106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang D, Yang C, Geva T, del Nido PJ. Image-based patient-specific ventricle models with fluid-structure interaction for cardiac function assessment and surgical design optimization. Progress in Pediatric Cardiologyi. 2010;30:51–62. doi: 10.1016/j.ppedcard.2010.09.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang D, Yang C, Geva T, del Nido PJ. Patient-specific MRI-based 3D FSI RV/LV/Patch models for pulmonary valve replacement surgery and patch optimization. Journal of Biomechanical Engineering. 2008;130:041010. doi: 10.1115/1.2913339. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang D, Yang C, Geva T, del Nido PJ. Right ventricular local longitudinal curvature as a marker and predictor for pulmonary valve replacement surgery outcome: an initial study based on preoperative and postoperative cardiac magnetic resonance data from patients with repaired tetralogy of Fallot. Journal of Thoracic and Cardiovascular Surgery. 2014;147:537–538. doi: 10.1016/j.jtcvs.2013.08.054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tang D, Yang C, Geva T, Gaudette G, del Nido PJ. Multi-physics MRI-based two-layer fluid-structure interaction anisotropic models of human right and left ventricles with different patch materials: cardiac function assessment and mechanical stress analysis. Computers & Structures. 2011;89:1059–1068. doi: 10.1016/j.compstruc.2010.12.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tweddell JS, Simpson P, Li SH, Dunham-Ingle J, Bartz PJ, et al. Timing and technique of pulmonary valve replacement in the patient with tetralogy of Fallot. Journal of Thoracic and Cardiovascular Surgery. 2012;15:27–33. doi: 10.1053/j.pcsu.2012.01.007. [DOI] [PubMed] [Google Scholar]
- Yang C, Tang D, Geva T, Rathod R, Yamauchi H, et al. Using contracting band to improve right ventricle ejection fraction for patients with repaired tetralogy of Fallot: a modeling study using patient-specific CMR-based 2-layer anisotropic models of human right and left ventricles. Journal of Thoracic and Cardiovascular Surgery. 2013;145:285–293. doi: 10.1016/j.jtcvs.2012.03.009. [DOI] [PMC free article] [PubMed] [Google Scholar]