Genome-Scale Modeling of NADPH-Driven β-Lapachone Sensitization in Head and Neck Squamous Cell Carcinoma

Abstract

Aims: The purpose of this study was to investigate differential nicotinamide adenine dinucleotide phosphate, reduced (NADPH) production between radiation-sensitive and -resistant head and neck squamous cell carcinoma (HNSCC) cell lines and whether these differences are predictive of sensitivity to the chemotherapeutic β-lapachone.

Results: We have developed a novel human genome-scale metabolic modeling platform that combines transcriptomic, kinetic, thermodynamic, and metabolite concentration data. Upon incorporation of this information into cell line-specific models, we observed that the radiation-resistant HNSCC model redistributed flux through several major NADPH-producing reactions. Upon RNA interference of canonical NADPH-producing genes, the metabolic network can further reroute flux through alternate NADPH biosynthesis pathways in a cell line-specific manner. Model predictions of perturbations in cellular NADPH production after gene knockdown match well with experimentally verified effects of β-lapachone treatment on NADPH/NADP⁺ ratio and cell viability. This computational approach accurately predicts HNSCC-specific oxidoreductase genes that differentially affect cell viability between radiation-responsive and radiation-resistant cancer cells upon β-lapachone treatment.

Innovation: Quantitative genome-scale metabolic models that incorporate multiple levels of biological data are applied to provide accurate predictions of responses to a NADPH-dependent redox cycling chemotherapeutic drug under a variety of perturbations.

Conclusion: Our modeling approach suggests differences in metabolism and β-lapachone redox cycling that underlie phenotypic differences in radiation-sensitive and -resistant cancer cells. This approach can be extended to investigate the synergistic action of NAD(P)H: quinone oxidoreductase 1 bioactivatable drugs and radiation therapy. Antioxid. Redox Signal. 29, 937–952.

Introduction

NADPH is a ubiquitous metabolite implicated in over 700 reactions in human metabolism. For a subset of these reactions, nicotinamide adenine dinucleotide phosphate, reduced (NADPH) and NADH are interchangeable as cofactors, although with different thermodynamic favorability. Despite the loose usage of NAD(P)H to indiscriminately describe the nicotinamide pool used in two-electron transfer, there are distinct differences in function. The largely anabolic couple [NADPH]/[NADP⁺] (∼100:1) is maintained out of equilibrium in cellular environments with [NADH]/[NAD⁺] (1:10–1:1000), which is primarily used in catabolic processes (45). NADPH/NADP⁺ has a half-cell potential on the order of −400 mV (48) and plays an essential role in limiting oxidative stress caused by reactive oxygen species (ROS); NADPH is a shared substrate for glutathione reductase (GSR) and thioredoxin reductase, linking antioxidant defense and thiol-based signaling.

Innovation.

We have developed a human genome-scale metabolic model incorporating quantitative transcriptomic, kinetic, thermodynamic, and metabolite concentration data to investigate nicotinamide adenine dinucleotide phosphate, reduced (NADPH) production in radiation-sensitive and -resistant matched cell line models of head and neck squamous cell carcinoma. Model estimations of NADPH production in an oxidoreductase-targeted RNAi screen supported experimental assays of cell viability and NADPH/NADP⁺ ratio after β-lapachone treatment, allowing us to accurately predict β-lapachone sensitization in a cell line-specific manner. Moreover, we demonstrate the feasibility of this approach for investigating synergy between NAD(P)H: quinone oxidoreductase 1 bioactivatable drugs and ionizing radiation in cancer treatment through the common demands on the NADPH/NADP⁺ redox couple.

A feature of NADPH utilization is the phenomenon of redox cycling, in which two coupled reduction and oxidation reactions can perpetuate a sustained directional cyclic flux of a quinone substrate between quinone and semiquinone (reduced) forms due to an ample source of electrons. Noted as early as 1968 in Escherichia coli metabolism of streptonigrin (53), NADPH-dependent redox cycling has been attributed to acetaminophen hepatotoxicity and cardiac lethality of anthracyclines via cytochrome P450 reductase (30). Systems biology modeling of this latter mechanism identified the role of NADPH availability in modulating the doxorubicin concentration-dependent switch in ROS formation (23). Model-predicted control via glucose-6-phosphate dehydrogenase (G6PD) was experimentally tested through inhibition of the enzyme and confirmed to alter cell line-specific changes in drug sensitivity.

A distinct but related mechanism of drug redox cycling is observed through NAD(P)H: quinine oxidoreductase 1 (NQO1) bioactivatable compounds. Drugs such as β-lapachone and deoxynyboquinone rely upon two-electron transfer via NQO1 to catalyze interconversion between quinone, hydroquinone, and semiquinone forms, expending one NADPH molecule per quinone oxidation to generate two molecules of superoxide (Fig. 1) (42); they are the only known quinones to cycle through this mechanism. Tumor cells, which typically express higher ratios of NQO1 to catalase (CAT) than nonmalignant tissue, are known to redox cycle in a futile manner to generate 120 moles of superoxide in 2 min for every mole of β-lapachone (27). Cellular superoxide dismutase (SOD) enzymes convert superoxide to the relatively more stable hydrogen peroxide (H₂O₂). Elevated H₂O₂ (>300 μM) leads to extensive base damage, single-strand DNA lesions, and eventually double-strand lesions of DNA (27). Furthermore, the high rate of NADPH consumption contributes to depletion of the nicotinamide pool by subsequent poly(ADP-ribose)polymerase-1 (PARP1) hyperactivation, with cell death proceeding through caspase-independent programmed necrosis (4, 5, 27, 33).

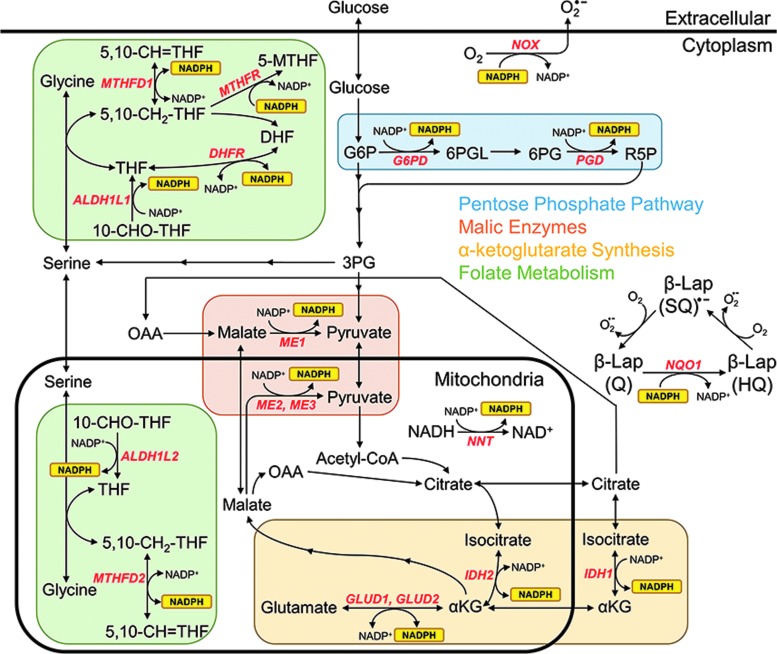
FIG. 1.

Major NADPH biogenesis pathways and reactions. Interconnection of well-studied biochemical reactions that convert oxidized NADP⁺ to reduced NADPH, labeled with their associated enzymes and grouped into biochemical pathways (colored boxes). Also shown is the NADPH-consuming futile redox cycle of β-lapachone, which interconverts between hydroquinone (HQ), semiquinone (SQ), and quinone (Q) forms, as well as select NADPH consumption reactions. αKG, alpha-ketoglutarate; 3PG, 3-phosphoglucerate; 5,10-CH=THF, 5,10-methenyltetrahydrofolate; 5,10-CH₂-THF, 5,10-methylenetetrahydrofolate; 5-MTHF, 5-methyltetrahydrofolate; 6PG, 6-phosphogluconate; 6PGL, 6-phosphogluconolactone; ALDH, aldehyde dehydrogenase; DHF, dihydrofolate; DHFR, dihydrofolate reductase; G6P, glucose-6-phosphate; G6PD, glucose-6-phosphate dehydrogenase; GLUD, glutamate dehydrogenase; IDH, isocitrate dehydrogenase; ME, malic enzyme; MTHFD, methylenetetrahydrofolate dehydrogenase; NADPH, nicotinamide adenine dinucleotide phosphate, reduced, NADP⁺, nicotinamide adenine dinucleotide phosphate, oxidized; NNT, nicotinamide nucleotide transhydrogenase; NOX, NADPH oxidase; OAA, oxaloacetate; R5P, ribulose 5-phosphate; THF, tetrahydrofolate.

NADPH is also oxidized to NADP⁺ by ribonucleotide reductase to maintain dNTP pools for DNA repair and cell survival following ionizing radiation (18). A synergistic effect is reported when combining sublethal doses of β-lapachone with radiation therapy in NQO1⁺ human prostate and head and neck cancers (7, 8, 34), as well as in non-small cell lung cancers (Boothman, pers. comm.). Increased consumption of NAD⁺ and ATP, enhanced DNA double-strand breaks, and prolongation of γ-H2AX were attributed, in the combined therapy, to result in head and neck squamous cell carcinoma (HNSCC) tumor regression. The competition for NADPH as a substrate for futile redox cycling, reduction of antioxidant defense systems (thioredoxin and glutaredoxin), PARP activity, and as a cofactor for dNTP synthesis upon radiation and chemotherapeutic insult in high NQO1/CAT tumor cells results in selective cytotoxicity (34).

Collectively, this evidence suggests that metabolic flux through NADPH biogenesis pathways in different cancer types may have significant implications in the success of both chemotherapy and radiation treatment. Because NADPH is involved in such a large number of reactions and pathways throughout the cellular metabolic network (Fig. 1), it has not been traditionally considered in design of therapeutic strategies for selectively targeting tumor cells. Recent bioinformatic analyses, however, have indicated that genetic or pharmacological suppression of intracellular [NADPH] through the NAMPT or glutamine biosynthesis pathway can confer enhanced sensitivity to β-lapachone by reduced antioxidant defenses and increased ROS, thereby lowering the in vivo dose needed for selective tumor cytotoxicity (11, 12, 37). This result suggests that strategically targeting biosynthesis pathways concomitant with NQO1-bioactivated futile redox cycling for therapeutic design may be advantageous. Computational systems biology approaches are required to more systematically consider the genes that contribute to whole-cell NADPH supply and demand across the entire metabolome. Flux balance analysis (FBA) is a metabolic modeling methodology that—when provided with information about the cell type of interest and its environment—can predict steady-state flux values through an entire metabolic network with thousands of reactions within seconds. While originally developed in the context of biotechnology applications to optimize growth of E. coli and yeast in industrial bioreactors, the predictive power and computationally inexpensive nature of FBA have led to its use in a variety of different biomedical areas, including drug target identification (14, 25) and human disease modeling (49, 51, 56, 57). Many recent FBA algorithms, such as GIMME (3), iMAT (47), and MADE (28), leverage transcriptomic data to obtain cell-type-specific flux distributions; however, these algorithms completely delete reactions with low gene expression from the model, which does not necessarily reflect underlying cellular physiology (6). In addition, many genome-scale FBA models fail to include kinetic and thermodynamic constraints, which greatly affect metabolic networks and their potential flux distributions (26).

To evaluate the role of global NADPH production on cancer cell phenotype and improve upon existing FBA models, we have developed a human genome-scale metabolic model that incorporates quantitative transcriptomic, kinetic, thermodynamic, and metabolite concentration constraints. These constraints have the potential to greatly improve the accuracy and cell-type specificity of predicted flux distributions associated with redox metabolism. The goal of our model development was to compare intrinsic metabolic changes in matched head and neck cancer cell lines that may yield phenotypic differences in sensitivity to NAD(P)H: quinone oxidoreductase 1 (NQO1)-dependent drugs such as the chemotherapeutic compound β-lapachone that relies on redox cycling, ROS production, and nicotinamide depletion for its cytotoxic effects.

Results

Construction of genome-scale metabolic models for matched HNSCC cell lines

The cell lines under investigation are a parental line (SCC-61) and a radiation-resistant line selected after successive survival after ionizing radiation (rSCC-61); these cell lines have been extensively characterized for metabolic, transcriptomic, proteomic, and epigenetic changes (2, 15, 36). We hypothesized that β-lapachone sensitivity of gene silencing in SCC-61 and rSCC-61 cells could be predicted by FBA models of NADPH production. To test this hypothesis, a key component of our model framework is the use of a novel objective function that optimized the yield of NADP⁺ → NADPH conversion while maintaining sufficient ATP production to obtain biologically viable results; this is a departure from prior FBA models of cancers that solely optimize biomass or ATP production.

Our model comprises three main components (Fig. 2A). The first component is the core metabolic network, which is based on the Recon 2 genome-scale human metabolic network with 5063 metabolites and 7440 reactions (49). The core network represents the collection of all known human metabolites and associated reactions and is the starting point to create cell-type-specific models. We have made additional changes to the Recon 2 metabolic network to address missing or inaccurate redox-based reaction information (see the Materials and Methods section). The second component of the model is the incorporation of an upper bound v_max to every reaction flux within the network. This upper bound was set as the product of the turnover number k_cat (units of s⁻¹) and abundance [E] (units of mmol/gDW) of the enzyme that catalyzes each particular reaction; this product is equivalent to the Michaelis–Menten constant V_max. If a reaction within the model is not enzyme-catalyzed, an arbitrarily large upper bound is given. Turnover numbers for every enzyme in the Recon 2 model were obtained from the BRENDA database (http://brenda-enzymes.org/) (46) (Supplementary Fig. S1; Supplementary Data are available online at www.liebertpub.com/ars), and enzyme abundance values for cell types of interest were obtained using proteomic and transcriptomic data from multiple sources. The last component of the model is the incorporation of thermodynamic constraints on each reaction (26). If the ΔG of any reaction could not achieve a value <0, then thermodynamically it cannot carry a net flux, and therefore the upper flux bound v_max was set to zero. Standard reaction free energies used to calculate ΔG were obtained from the Virtual Metabolic Human database (40, 49). Metabolite concentrations used include experimentally verified cellular metabolite concentration ranges, components of cell culture media to simulate the extracellular environment, and measured concentration values specific to the cell types of interest. The incorporation of enzyme abundances and metabolite concentrations allows for the creation of cell-type-specific models, and incorporation of enzyme turnover numbers and reaction standard free energies further improves the biological accuracy of model predictions.

FIG. 2.

Construction of genome-scale metabolic model. (A) Incorporation of disparate sources of biological information into the mathematical modeling framework. (B) Correlation between experimental proteomic and experimental gene expression values (as ratios of rSCC-61 to SCC-61) corresponding to the same NCBI gene ID. (C) Correlation between experimental proteomic and model proteomic values. Estimation of model proteomic values from experimental gene expression data (see the Materials and Methods section for details) conserves most of the original correlation between experimental proteomic and gene expression values shown in (B). (D) Net conversion of NADP⁺ to NADPH, expressed as a ratio of rSCC-61/SCC-61. Values obtained from the model with and without utilizing metabolite concentration data (Q) and reaction standard free energy values (ΔG^O) are shown. The dotted line corresponds to the experimentally measured ratio of NADPH/NADP⁺ concentration between rSCC-61 and SCC-61 cells.

Models specific to SCC-61 and rSCC-61 cell types were constructed to better understand their differences in NADPH production. Because proteome-wide enzyme abundance values for these two cell types were not available, these values were estimated from SCC-61 and rSCC-61 gene expression data by extrapolating onto proteomic values measured in CAL-27 head and neck cancer cells; missing values where no proteomic data was available were imputed (see the Materials and Methods section for more information). This methodology conserves most of the correlation between experimental gene expression data (used to estimate enzyme abundance) and the small amount of experimental proteomic data available for SCC-61 and rSCC-61 cells (Fig. 2B, C).

To determine whether the incorporation of thermodynamic constraints is necessary to achieve accurate model predictions, the net conversion of NADP⁺ to NADPH was compared in both cell types, with and without standard free energy values (ΔG^o) and experimentally measured metabolite values (Q) included in the model (Fig. 2D). Only when both data sets were included was the conversion of NADP⁺ to NADPH greater in rSCC-61 cells than in SCC-61 cells. In this case, the ratio of net conversions (rSCC-61/SCC-61 = 1.40) was very close to the experimentally measured ratio of NADPH/NADP⁺ concentration between rSCC-61 cells and SCC-61 cells (rSCC-61/SCC-61 = 1.56) (36).

Predicted NADPH production across the HNSCC metabolome

The flux distributions of major NADPH-producing reactions shown in Figure 1 were calculated in both SCC-61 and rSCC-61 cell types (Fig. 3A). Flux values span multiple orders of magnitude and most predicted values are within one order of magnitude of experimentally measured flux values determined using ¹³C-tracers in other cell types (41). Even though the upper flux bound on the glutamate dehydrogenase GLUD1/GLUD2 reaction is higher in SCC-61 cells than rSCC-61 cells (due to greater gene expression), the observed flux values through this reaction in rSCC-61 cells are significantly greater. While rSCC-61 cells exhibit a flux distribution constrained relatively close to the upper flux bound, SCC-61 cell flux deviates greatly from the GLUD1/GLUD2 upper bound. This result highlights the importance of developing genome-scale models for accurate prediction of metabolic phenotypes instead of simply comparing individual gene or protein expression values. While a large difference in flux through the GLUD1/GLUD2 reaction was found between SCC-61 and rSCC-61 cell types, most reactions did not display substantial differences in flux distribution. One exception is nicotinamide nucleotide transhydrogenase (NNT), which shows significantly greater flux in rSCC-61 cells than SCC-61 and was previously found to be a potential prognostic marker in HNSCC (16). However, because NNT flux values are several orders of magnitude lower than flux values through other NADPH-producing reactions, differences in NNT flux between SCC-61 and rSCC-61 cell types may not be biologically significant. Note that no nonzero solutions for the malic enzyme ME2/ME3 reaction were obtained in SCC-61 cells; this artifact is likely due to the unrestricted flux of malate and pyruvate across the mitochondrial membrane to the cytoplasm, along with the ability of ME1 to catalyze the same reaction as ME2/ME3 in the cytoplasm.

FIG. 3.

Model-generated flux distributions and impact on total cellular NADPH production of major NADPH biogenesis reactions. (A) Box plot showing the flux distributions in both SCC-61 and rSCC-61 cells of major NADPH biogenesis reactions shown in Figure 1. Note that no nonzero solutions for the ME2/ME3 reaction were obtained in SCC-61 cells (see text). Boxes represent the following percentiles: 2.5th, 25th, 50th, 75th, and 97.5th. Dots represent the upper flux bound for each reaction (v_max = k_cat[E]). (B) Effect of 75% simulated gene knockdown on net conversion of NADP⁺ to NADPH in both SCC-61 and rSCC-61 cells, expressed as a percentage of net conversion before knockdown.

To determine whether the calculated flux through NADPH-producing reactions correlates with the importance of the corresponding gene's expression toward total cellular NADPH production, the maximum net NADP⁺ → NADPH flux in both SCC-61 and rSCC-61 cell types was calculated after 75% simulated gene knockdown (Fig. 3B). Surprisingly, even though the GLUD1/GLUD2 reaction had the largest calculated flux values among all reactions in both cell types, knockdown of these genes caused very little change in total cellular NADPH production. However, some gene perturbations had a substantial impact on NADPH production, differentially impacting rSCC-61 cells (isocitrate dehydrogenase IDH1, G6PD, ME2) or SCC-61 cells (IDH2). These differences between reaction flux distributions and impact of gene knockdown suggest that the NADPH-producing reactions with the largest flux are not necessarily the most important toward global NADPH production. Instead, metabolic flux can be diverted to other parts of the metabolic network to maintain NADPH production in these cases.

To determine whether our model predictions on HNSCC cell lines are consistent with HNSCC patient tumor samples, we compared results between 116 radiation-sensitive and 16 radiation-resistant HPV-negative HNSCC patients using transcriptomic data from The Cancer Genome Atlas (TCGA) (9). Supplementary Figure S2 shows that total cellular NADP⁺ → NADPH conversion in radiation-resistant tumors (0.82 ± 0.07 mmol/gDW/h) is slightly greater than in radiation-sensitive tumors (0.79 ± 0.05 mmol/gDW/h). In addition, we observe that simulated 75% IDH1 knockdown causes a greater percentage decrease in total cellular NADP⁺ → NADPH conversion in radiation-resistant tumors (knockdown [KD]/wild-type [WT] = 82.2% ± 5.5%) than in radiation-sensitive tumors (KD/WT = 86.2% ± 6.3%; p = 0.017). These results follow the same trends as the comparison between SCC-61 and rSCC-61 cell lines: rSCC-61 cells demonstrated increased total cellular NADP⁺ → NADPH conversion as well as a greater percentage decrease after IDH1 knockdown. Interestingly, while SCC-61 values lie near the median of the radiation-sensitive tumor distributions, rSCC-61 values represent an extreme case compared with the radiation-resistant tumor distributions. This may indicate that the rSCC-61 cell line represents an exaggerated phenotypic case of radiation-resistant HNSCC tumors, possibly due to repeated rounds of radiation treatment and selection used to generate this cell line (2). Overall, these findings demonstrate that our model predictions of NADPH production in SCC-61 and rSCC-61 cell lines are consistent with predictions in radiation-sensitive and -resistant HNSCC patient tumors.

Simulated silencing of IDH1 highlights alternative NADPH production pathways in SCC-61 cells

As shown in Figure 3, simulated knockdown of a gene involved in NADPH production does not necessarily impact the total cellular production of NADPH. Instead, the cell can reroute flux toward other pathways to achieve the goal of maximizing NADPH production. To further investigate this rerouting of flux, the flux distributions of SCC-61 and rSCC-61 cells after simulated 75% knockdown of five canonical NADPH-producing genes from Figure 3, as well as methylenetetrahydrofolate reductase (MTHFR), were calculated (Fig. 4 and Supplementary Fig. S3). The condition generating the most interesting insight in flux redistribution was the simulated silencing of IDH1, which increased flux through GLUD1/GLUD2 toward its v_max value in the SCC-61 line and decreased flux through GLUD1/GLUD2 in the rSCC-61 cell line. A likely explanation of this differential effect is that both IDH1 and GLUD1/GLUD2 reactions produce α-ketoglutarate. Because the objective function is to maximize conversion of NADP⁺ to NADPH, the preferred direction of both of these reactions is to produce α-ketoglutarate and NADPH. Due to other model constraints on α-ketoglutarate consumption, there is a limit to how much combined flux can occur through IDH1 and GLUD1/GLUD2. Therefore, reduction in protein levels of IDH1 affords the opportunity of cells to maintain NADPH production by rerouting flux through GLUD1/GLUD2. However, whereas SCC-61 cells normally operate far from the maximum GLUD1/GLUD2 flux bound and can therefore increase this flux, rSCC-61 cells cannot increase GLUD1/GLUD2 flux due to other constraints on the genome-wide metabolic network. A similar result is obtained with simulated G6PD silencing, accounting for the greater impact of G6PD knockdown on NADPH production in rSCC-61 cells than SCC-61 cells (Supplementary Fig. S3).

FIG. 4.

Alternative NADPH production pathways after knockdown of IDH1. Flux distributions of simulated wild-type and 75% IDH1 knockdown SCC-61 and rSCC-61 cells. Boxes represent the following percentiles: 2.5th, 25th, 50th, 75th, and 97.5th. Dots represent the upper flux bound for each reaction (v_max = k_cat[E]), taking into account the lowered IDH1 flux bound in IDH1 knockdown cells.

β-Lapachone effects on NADPH production flux are consistent with differential sensitivity of HNSCC cell lines

Through its redox cycling mechanism with NQO1, β-lapachone treatment results in a net conversion of NADPH to NADP⁺, thus lowering the NADPH/NADP⁺ concentration ratio. Subsequent hyperactivation of PARP1 by DNA damage and elevated pools of NAD⁺ confers loss of NAD⁺ in exposed cells. With cell line-specific models of NADPH production established for SCC-61 and rSCC-61 that account for experimentally observed differences in NADPH/NADP⁺, we next asked if these phenotypes correspond to differences in each line's ability to redox cycle β-lapachone. To determine what effect siRNA knockdown of canonical NADPH-producing genes as well as MTHFR has on changes in NADPH/NADP⁺ due to redox cycling, we measured relative changes in [NADPH] and [NADP⁺] in each knockdown in the presence of 3 μM β-lapachone for 2 h. To quantify the effect of β-lapachone on NADPH/NADP⁺, a β-lapachone effect parameter was developed:

This effect parameter ranges in value [0,1], where a value of 0 signifies that β-lapachone has no effect on the NADPH/NADP⁺ ratio, and a value of 1 signifies that β-lapachone completely eliminates cellular stores of NADPH. A β-lapachone effect ratio is used to compare the β-lapachone effects between rSCC-61 and SCC-61 cells:

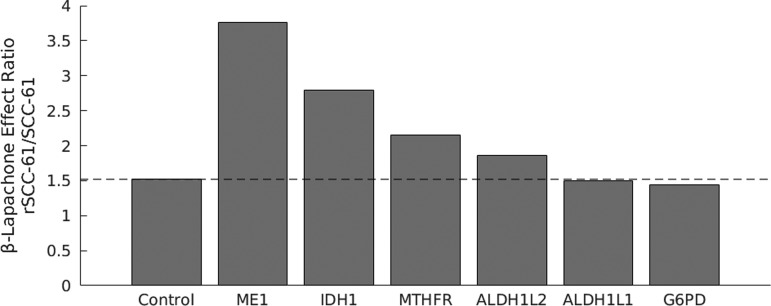
As expected, the effect ratio for Drosophila siRNA control cells is >1 since β-lapachone is known to have a greater effect on rSCC-61 cells than SCC-61 cells (Fig. 5). ME1, IDH1, and MTHFR knockdowns display substantial increases in effect ratio over control cells, indicating that these knockdowns have a greater negative impact on NADPH/NADP⁺ ratio in rSCC-61 cells than SCC-61 cells. The G6PD siRNA resulted in a minimal change from control for both cell lines. This finding is consistent with reports of quinone-based chemotherapeutic tolerance for G6PD-deficient individuals (31, 32).

FIG. 5.

β-Lapachone effect ratio in wild-type and siRNA gene knockdown cells. Equations [1] and [2] used to calculate β-lapachone effect ratio. NADPH/NADP⁺ ratios were measured both with and without 2 h of exposure of 3 μM β-lapachone. The dotted line represents the effect ratio for Drosophila control siRNA-transfected cells.

Simulated and experimental RNA interference yields cell line-specific changes in β-lapachone sensitivity

Because NQO1-driven quinone redox cycling is a major driver of PARP1 hyperactivation and programmed necrosis, we hypothesized that large changes in the abundance of major NADPH-producing enzymes would directly impact cell viability in the presence of β-lapachone. The rSCC-61 cells have NQO1 mRNA that is over twofold higher than SCC-61 cells. Correspondingly, the measured β-lapachone IC₅₀ of rSCC-61 cells by 7-day clonogenic assay is 3 μM, while SCC-61 cells show no sensitivity to the drug (data not shown). Twenty-four-hour cell viability measurements also indicated sensitivity to 3 μM β-lapachone that is abrogated in the presence of 50 μM dicoumarol, suggesting that the differences in viability are due to NQO1-mediated redox cycling (Supplementary Figs. S4 and S5). To investigate whether our genome-wide estimates of NADPH production can be used to predict modulation of β-lapachone sensitivity in SCC-61 and rSCC-61 cells, model simulations were run in conjunction with an experimental siRNA screen of 338 oxidoreductase genes, 229 of which are found in Recon 2 (Fig. 6A). RNA interference was simulated by individually knocking down gene expression of all 229 genes by 75% and determining the fraction of total cellular NADPH production after knockdown compared with before. Model knockdown of 80 genes caused a greater decrease in NADPH production in rSCC-61 cells than SCC-61 cells, compared with 56 gene knockdowns causing a greater decrease in SCC-61 cells than rSCC-61 cells (Fig. 6B, C). Experimental knockdown of 59 genes decreased cell viability in rSCC-61 cells, while knockdown of only 10 genes in SCC-61 cells decreased viability in the presence of β-lapachone (Fig. 6D, E). In addition, experimental knockdown of 181 genes had a more negative impact on cell viability upon β-lapachone exposure in rSCC-61 cells than SCC-61 cells, compared with 48 gene knockdowns having a more negative impact in SCC-61 cells than rSCC-61 cells. This corroboration between model and experimental results suggests that the SCC-61 metabolic network's response to β-lapachone is more robust than in rSCC-61 cells, likely due to SCC-61's ability to reroute NADPH-producing flux through alternative metabolic pathways.

FIG. 6.

Model NADPH production predicts experimental siRNA knockdown cell viability after β-lapachone treatment. (A) Heat map showing cell viability of all 338 gene knockdowns after 24 h of treatment with 3 μM β-lapachone in three replicate experiments. Cell viability values are normalized to those from Drosophila control siRNA-transfected cells, and the log2 of normalized values was taken (values >0 signify increased cell viability after knockdown, values <0 signify decreased cell viability after knockdown). Genes are ordered from highest to lowest rSCC-61/SCC-61 cell viability ratio. (B, C) Model-predicted effect of gene knockdown on net conversion of NADP⁺ to NADPH, expressed as a fraction of net conversion before knockdown. (B) SCC-61 and rSCC-61 results separately. (C) The ratio of rSCC-61/SCC-61 (values <1 signify gene knockdowns that lower NADPH production more in rSCC-61 cells, values >1 signify gene knockdowns that lower NADPH production more in SCC-61 cells). (D, E) Experimental effect of gene knockdown on cell viability after β-lapachone treatment; the average value of three replicate experiments was taken, and the result expressed as a fraction of Drosophila control siRNA-transfected cells. (D) SCC-61 and rSCC-61 results separately; the dotted line represents division between genes that decrease versus increase cell viability after knockdown. (E) The ratio of rSCC-61/SCC-61 (values <1 signify gene knockdowns that lower cell viability more, or raise cell viability less, in rSCC-61 cells; values >1 signify gene knockdowns that lower cell viability more, or raise cell viability less, in SCC-61 cells). (F) Comparison of model and experimental results for canonical NADPH-producing genes (left) and discovered HNSCC-specific genes of interest (right). CAT, catalase; GSR, glutathione reductase; HNSCC, head and neck squamous cell carcinoma.

Six of the eighteen genes from Figure 1 were included in the siRNA panel; among these six genes, five displayed the same rSCC-61/SCC-61 relationship (>1 or <1) when comparing model NADPH production and experimental cell viability (Fig. 6F). Aldehyde dehydrogenase ALDH1L1 and ALDH1L2, which had the third and second largest rSCC/SCC cell viability ratio among all 229 genes, also had the eighth and 12th largest rSCC/SCC NADPH production ratio. This result demonstrates the model's capability to predict β-lapachone sensitivity from cellular NADPH production for canonical NADPH-producing genes.

In addition, there was strong agreement between model and experimental results for genes not identified as major contributors to NADPH production, but nonetheless implicitly involved in metabolic differences between the two cell lines. The emergence of CYP4F3 as a gene affecting both model NADPH production and experimental β-lapachone sensitivity may stem from the tissue-specific expression of this monooxygenase in the trachea and esophagus as well as its reliance on NADPH as a cofactor for arachidonic acid utilization (17). The strong effect of NADH-cytochrome b5 reductase (CYB5R1) levels on 24-h drug response (smallest experimentally determined rSCC-61/SCC-61 cell viability ratio) further confirms that rerouting of NADPH flux to enhance fatty acid synthesis serves as a critical metabolic difference between the cell lines as reported by Mims et al. (36), with knockdown in rSCC-61 cells increasing drug sensitivity (0.60 ± 0.28 cell viability ratio compared with control siRNA) while knockdown in SCC-61 cells protecting against chemotherapy (1.77 ± 0.42 cell viability ratio compared with control siRNA).

Surprisingly, silencing of CAT showed this differential trend as well to a lesser degree. CAT is typically associated with low expression in tumor cells that are β-lapachone sensitive (13, 27), and the ratio of NQO1/CAT is critical for tumor-specific selectivity; thus, we expected that reduction of CAT would enhance redox cycling and reduce cell viability in both cell lines. Slightly reduced cell viability was observed in the CAT-silenced rSCC-61 cells along with slightly enhanced viability in the CAT-silenced SCC-61 cells, resulting in a pronounced rSCC-61/SCC-61 ratio of 0.53 and placing this perturbation in the top 10% of differentially affected genes. To explore this observation further, we evaluated the flux distributions of CAT and SOD1 to determine if concomitant changes in superoxide disproportionation could be the source of cell line-specific responses. We found no correlation in either cell line model between SOD1 and CAT flux values (SCC-61: R² = 0.09, rSCC-61: R² = 0.02); however, we did note that SOD1 flux values in the rSCC-61 model were constrained within a narrow range at a much higher flux than in SCC-61 cells (0.73 ± 0.08 mmol/gDW/h vs. 0.13 ±0.11 mmol/gDW/h). Thus, rSCC-61 cells may be selected to a regime in which there is little to no margin for adjusting H₂O₂ production when H₂O₂ clearance becomes limited. GSR is another redox enzyme predicted to yield differential β-lapachone sensitivity by cell line-specific models and validated by experimental results. GSR provides a key couple between NAPDH/NADP⁺ and GSH/GSSG in the cytosol to sustain ROS clearance through the glutathione/glutaredoxin antioxidant pathway. Glutathione S-transferase conjugates GSH adducts to β-lapachone hydroquinone for drug efflux from cells (44); our results are consistent with GSR modulation limiting reduced glutathione for this process and thus sustaining intracellular drug levels for enhanced redox cycling.

Carbonyl reductase (CBR1), highly expressed in the oral mucosa (1, 50), also demonstrated pronounced differences between the cell lines. Because CBR1 is a two-electron reductase capable of reducing quinones (52), the increased sensitivity of rSCC-61 cells to β-lapachone with reduced CBR1 levels suggests a competing role of CBR1 in the β-lapachone redox cycling mechanism. Finally, not all perturbations resulted in more β-lapachone sensitivity and greater reduction of viability in the rSCC-61 cells. For example, ALDH3A1 is implicated in the enzymatic detoxification of aldehydes specifically in the gastrointestinal tract. Consistent with other ALDHs examined in this study (ALDH1L1 and ALDH1L2), silencing of this NAD(P)⁺-consuming enzyme resulted in an rSCC-61/SCC-61 ratio >1.

Discussion

Because of the NADPH involvement throughout the human metabolic network, genome-scale metabolic modeling is an ideal tool to investigate NADPH production between radiation-sensitive and radiation-resistant HNSCC phenotypes. Genome-wide metabolic models for NCI-60 cancer cell lines are being rapidly developed (20, 56, 58); however, models for head and neck cancer cell lines that are not represented in the NCI-60 list are lacking. To establish HNSCC-specific models, we have developed a human genome-scale metabolic modeling platform that incorporates quantitative transcriptomic, kinetic, thermodynamic, and metabolite concentration data to create cell-type-specific models of radiation-sensitive (SCC-61) and radiation-resistant (rSCC-61) HNSCC cell lines (Fig. 2A). While model predictions are in close proximity to experimental measurements when both concentration and thermodynamic data are used, unsatisfactory predictions result when one or both data sources are not included, demonstrating the necessity of integrating disparate biological data types into the metabolic model to achieve valid results (Fig. 2D).

Although many efforts have been made to study cancer metabolism using genome-scale FBA models [e.g., Nilsson and Nielsen (39)], very few have focused the modeling on NADPH production. Fan et al. recently developed FBA models to identify metabolic reactions that contribute to the cellular NADPH pool in immortalized baby mouse kidney epithelial cells, highlighting the role of folate metabolism in NADPH maintenance (22). Although experimentally measured metabolite uptake and excretion rates were incorporated as model constraints, most of the model reactions in this prior study were not constrained by cell-type-specific information. A common practice used in FBA models is treating gene expression data as binary (reaction on or off) to achieve cell-type-specific results. Proteomic data better represent gradations in enzyme levels than gene expression data, and setting reaction upper bounds relative to quantitative proteomic values is more accurate biologically than completely removing reactions from the model that fall under some arbitrary threshold. For our model construction, we leveraged the transcriptional similarities and differences between the matched SCC-61/rSCC-61 cell lines and the CAL-27 head and neck cancer cell line to estimate proteomic values for SCC-61 and rSCC-61 cells. This approach maintains known proteomic–transcriptomic correlations where this information was available and provides accurate predictions of NADPH production (Fig. 2B–D).

β-Lapachone is a chemotherapeutic drug that has tremendous promise in increasing the radiation sensitivity of cancer cells through an NADPH-consuming futile redox cycle and depletion of cellular NADPH stores. Since antioxidative and DNA repair mechanisms in radiation-resistant tumors rely on sufficient NADPH supply, combining radiation therapy with β-lapachone treatment may be an effective strategy for cancer patients who previously have not responded to radiation. Because of the interconnection between β-lapachone's mechanism of action and cellular NADPH levels, our hypothesis was that the relative β-lapachone sensitivity tested with the siRNA screen of oxidoreductase genes on radiation-susceptible and radiation-resistant cells could be predicted by the impact of gene knockdown on total cellular NADPH. To test this hypothesis, we combined our novel genome-scale metabolic modeling platform with the cellular objective function of maximizing conversion from NADP⁺ to NADPH while maintaining sufficient ATP production to obtain biologically viable results; this differs from the classical cancer objective functions of maximizing biomass or ATP production. We justify our choice of a novel objective function by noting the generation of the rSCC-61 cell line: SCC-61 cells were subjected in vitro to repeated rounds of ionizing radiation (2 Gy for a cumulative total of 16 Gy) to select radiation-resistant cells; thus, the cells optimized to repair double-stranded DNA breaks through the use of NADPH were more likely to survive. The interconnectedness of NADH, NAD⁺, NADPH, and NADP⁺ in maintenance of the global nicotinamide pool warrants future exploration in the use of alternative objective functions, such as optimization of NAD⁺ in the radioresistant phenotype. For example, in all NQO1⁺ cancer cells examined to date (pancreatic, breast, prostate, NSCLC, and others), NAD⁺ loss correlates well with loss of survival monitored by short-term or long-term assays. Because the two cell lines are so extensively characterized for epigenetic, transcriptomic, proteomic, and metabolomic changes occurring with gain of a radiation resistance phenotype, they serve as a useful system for testing the underlying hypothesis that cumulative alterations across the genome that yield changes in NADPH production to facilitate radiation-induced DNA damage repair will also enhance NADPH-dependent redox cycling for increased β-lapachone sensitivity. Synergy between ionizing radiation therapy and β-lapachone treatment has been established in head and neck cancer (34); our flux balance models suggest specific mechanisms that result in this effect.

We first found through our modeling that different NADPH-producing reactions contribute to the total cellular NADPH pool on varying flux scales (Fig. 3A). Unlike a prior FBA model that strongly implicated the 10-formyl-tetrahydrofolate pathway and malic enzyme in NADPH production for HEK293 cells (22), reactions in the α-ketoglutarate production and pentose phosphate pathways appear to contribute more to the NADPH pool for head and neck cancer cells. In addition, whereas most reaction flux distributions did not differ much between SCC-61 and rSCC-61 cells, flux values through the GLUD1/GLUD2 reaction were greatly increased in rSCC-61 cells compared with SCC-61. Even though some reactions produce more NADPH than others, the amount of NADPH production did not appear to correlate with the effect of simulated gene knockdown on total cellular NADPH (Fig. 3B). For example, knockdown of GLUD1 or GLUD2 in the models had very little effect on total NADPH production in SCC-61 and rSCC-61 cells. In contrast, knockdown of IDH1, G6PD, and ME2 differentially impacted NADPH production in rSCC-61 cells, and knockdown of IDH2 differentially impacted SCC-61 cells. Collectively, these results suggest that the metabolic network can reroute NADPH-producing flux to other pathways in a cell-type-specific manner to achieve the goal of maximizing NADPH production. This was verified with the differential effect of IDH1 knockdown on rerouting flux through GLUD1/GLUD2 between SCC-61 and rSCC-61 cells (Fig. 4).

Although our modeling approach represents a vast improvement over past human genome-scale metabolic models, it still lacks some detail regarding redox-based reactions. Given the dramatic changes in flux distributions upon simulated IDH silencing, inclusion of oncometabolite-generating reactions, such as recently reported for IDH mutations in HNSCC (38), would be informative for prediction of quinone drug redox cycling. Another limiting factor in genome-scale metabolic modeling is the lack of proteomic, kinetic, thermodynamic, and concentration parameters for all reactions and metabolites within human metabolism. The FBA modeling platform is constraint based, meaning that more accurate predictions are obtained through the incorporation of more constraints on cellular function (Fig. 2D). With greater availability of biological parameters to include within genome-scale models, more constraints can be imposed on cellular function to improve the predictive power of genome-scale models. This necessitates collaborative efforts to document experimentally verified parameter values on a genome scale. Furthermore, a limitation of FBA modeling is the steady-state assumption required for calculation of metabolic flux values. Many of the oxidoreductase enzymes under discussion in this study are regulated by the redox-sensing transcription factor, Nrf2. In particular, NQO1 contains an antioxidant response element sequence in the promoter region and, due to its high induction, is often used as a positive control for Nrf2-regulated gene activation (19). A feature of β-lapachone cytotoxicity is that the generation of intracellular ROS by futile quinone cycling can trigger Nrf2, thereby increasing NQO1 levels and augmenting the initial drug mechanism of action. We did not observe changes in NQO1 levels in either cell line during a period of 8 h post-β-lapachone exposure (data not shown); however, other enzyme expression changes during this time frame may alter metabolic flux values from our baseline analysis. Nonetheless, the snapshot of genome-wide metabolism determined by our systems approach highlights the importance of basal NADPH flux distributions in the predictive value for NQO1 bioactivated chemotherapeutic compounds.

In conclusion, this systems biology analysis on a matched model of HNSCC radiation response provides insight on how small variations in cell line transcriptomics and proteomics can cumulatively yield dramatic changes in metabolism and large phenotypic changes to a therapeutic treatment. Our modeling efforts demonstrate that depending on the distribution of flux, perturbations in metabolic enzymes can have opposite effects on the NADPH/NADP⁺ redox couple, the degree of futile redox cycling of a chemotherapeutic, and ultimately the sensitivity of cell viability to the drug. This modeling approach allows for continued investigations on synergy of redox-based chemotherapies and radiation therapy. Ultimately, with additional development in the field of FBA methods, personalized transcriptomic data can be mined for genome-scale models to improve our understanding of cancer and facilitate clinical decision-making for patients.

Materials and Methods

Flux balance analysis

A metabolic network can be represented by a stoichiometric matrix S of size m × r, where m and r are the number of metabolites and reactions in the network, respectively. Entry S_ij is equal to the stoichiometric coefficient of metabolite i in reaction j (S_ij < 0 for reactants, >0 for products, and = 0 if metabolite i is not involved in reaction j). The relationship between reaction flux and metabolite concentrations in the network can be written as follows:

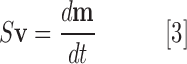where v is an r × 1 vector of reaction flux and m is an m × 1 vector of metabolite concentrations. In FBA, we assume the steady state (metabolite concentrations do not change with time), changing Equation [3] to the following:

Each reaction flux v_j is also constrained by lower and upper bounds:

The solutions to Equations [4] and [5] that maximize a particular objective function f(v) are chosen. Thus, the FBA problem can be represented as a linear programming problem:

Redox-based changes to Recon 2 network

Recon 2.04 was used as the core metabolic network to build our SCC-61 and rSCC-61 models (21, 49). To address missing and inaccurate redox-based reaction information within the Recon 2 metabolic network, we have made the following changes (for the reactions below, c = cytoplasm, e = extracellular, n = nucleus, and r = endoplasmic reticulum):

• 1.We split the RECON-labeled reaction “FTHFDH” (NADPH-producing reaction originally catalyzed by ALDH1L1 and ALDH1L2) into two separate cytosolic and mitochondrial reactions. The cytosolic reaction is catalyzed by ALDH1L1, and the mitochondrial reaction is catalyzed by ALDH1L2.
• Originally:

  
• Updated:

  

  
• 2.We removed gene MTHFR from reaction MTHFD (NADPH-producing reaction originally catalyzed by MTHFR and MTHFD1). MTHFR catalyzes the reaction converting 5,10-methylenetetrahydrofolate to 5-methyltetrahydrofolate, which is already included in the Recon 2 network.
• Originally:

  
• Updated:

  
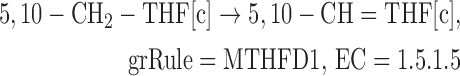
• 3.We added reactions catalyzed by isoforms of NADPH oxidase.

• Originally: None

• Updated:

  

  

  

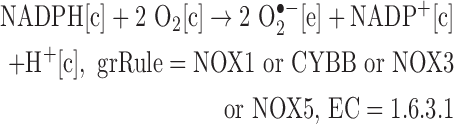
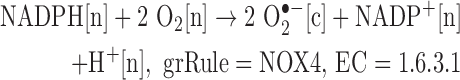
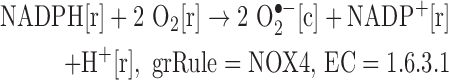
• Note: The SOD-catalyzed reaction is already in Recon 2, allowing for the production of H₂O₂ from superoxide.

Objective function

Because FBA models produce a steady-state solution, there cannot be net consumption or production of any metabolites in the model. However, adding an artificial demand reaction allows for net metabolite consumption or production through existing model reactions. To maximize the flux through existing Recon 2 reactions that convert NADP⁺ into NADPH within the cytoplasm and mitochondria, a new reaction is added with the following stoichiometry:

where c = cytoplasm and m = mitochondria. Maximizing this reaction as the objective function in turn maximizes the net conversion of NADP⁺ + H⁺ into NADPH through all other existing model reactions. This allows for the calculation of net NADP⁺ → NADPH flux (equal to the flux through the maximized objective function), as well as the flux through all Recon 2 reactions that convert NADP⁺ into NADPH.

However, the sole maximization of NADP⁺ → NADPH flux may result in biologically nonviable solutions since it does not take into consideration the production of energy sources such as ATP that are necessary for cell survival. To ensure that biologically viable outcomes are obtained, we first maximize cellular ATP production through the following objective function:

where c = cytoplasm and m = mitochondria. After calculating the maximum cellular ATP production, we set the lower bound of this reaction to 50% of the maximum value. This creates an ATP demand where only solutions that result in at least 50% of maximal ATP production are considered. While imposing this ATP demand, we then maximize cellular conversion of NADP⁺ to NADPH through the objective function given above.

Thermodynamic constraints

To include thermodynamic constraints within the FBA model, all reversible reactions (reactions that can carry a net flux in either the forward or reverse direction) within the model had to be broken down into two separate reactions—one which only runs in the original forward direction, and one which only runs in the original reverse direction. All reactions within the model now only have a forward direction. This allows us to set all v_min,j values to zero.

Two additional sets of equations were added to include thermodynamic constraints within the FBA model. The first is of the following form:

where b_j is a boolean variable representing the thermodynamic status of reaction j. If reaction j is thermodynamically feasible, then b_j = 1, and v_j ≤ v_max,j (Eq. [5] with v_min,j = 0). If reaction j cannot carry a net flux due to thermodynamic constraints, then b_j = 0, and v_j ≤ 0 (since v_min,j = 0, this means that v_j must equal zero).

To determine the value of b_j, another set of equations is included of the following form:

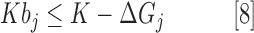where ΔG_j is the change in Gibbs free energy of reaction j and K is an arbitrarily large constant that must be set greater than the largest ΔG_j value in the model. A chemical reaction j can carry a net flux if ΔG_j <0. If ΔG_j < 0, then K − ΔG_j > K, and Equation [8] will hold whether b_j = 0 or b_j = 1. Any thermodynamically feasible reaction that may contribute to the maximization of our objective function will choose to have b_j = 1, if possible, to carry a nonzero flux. However, if ΔG_j > 0, K − ΔG_j < K, and Equation [8] will only hold if b_j = 0. Therefore, this reaction cannot carry a nonzero flux.

The ΔG_j of nontransport reactions can be calculated as follows:

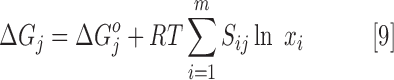where ΔG_j^O is the standard change in Gibbs free energy of the reaction, R is the gas constant, T is the temperature, S_ij is the stoichiometric coefficient of metabolite i in reaction j, and x_i is the concentration of metabolite i. For reactions involving transport of metabolites between cellular compartments, ΔG_j is calculated as follows:

where c_i is the charge of metabolite i, S_trans,ij is the transport stoichiometric coefficient of metabolite i in reaction j (representing how many molecules of the metabolite are being transported between compartments), F is the Faraday constant, and V is the potential of the membrane separating the transport metabolites. V is estimated using the Goldman-Hodgkin-Katz voltage equation:

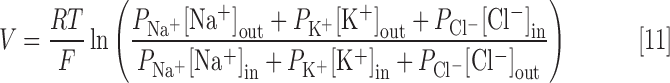where P_Na+, P_K+, and P_Cl− are the relative permeabilities of Na⁺, K⁺, and Cl⁻ across the membrane (assigned to 1, 5, and 80, respectively).

Estimated ΔG_j^O values for many reactions in the Recon 2 model were available from the Virtual Metabolic Human database (40, 49). For any reaction where ΔG_j^O was not available, the value ΔG_j^O = −999,999 was used so that reactions with no available thermodynamic data were not made thermodynamically infeasible.

Gurobi 6.5 optimization software was used to solve the mixed-integer linear programming problem represented by Equations [6]–[8].

Proteomic and kinetic constraints

For reactions in the Recon 2 model with an associated enzyme commission (EC) number and gene-reaction rule, the upper bound on the reaction flux was set to be as follows:

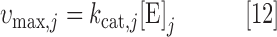where k_cat,j is the turnover number (1/h) and [E]_j is the total abundance (mmol/gDW) of the enzyme catalyzing reaction j. This is equivalent to the formula for V_max in Michaelis–Menten kinetics. Reactions that are missing either an EC number or gene-reaction rule (either because the reaction is not enzyme catalyzed or due to missing information) were unconstrained by assigning an artificially high v_max,j = 999,999.

Cell line proteomic and transcriptomic data

To estimate protein expression values for SCC-61 and rSCC-61 cell lines, gene expression data for these cells (15) were compared with gene expression data for CAL-27 cells measured using the same Illumina HumanHT-12 v4 Expression BeadChip platform (24). Data from three samples each of SCC-61, rSCC-61, and CAL-27 were log2 transformed and normalized using z-score normalization. ComBat was then used to remove batch effects between the SCC-61/rSCC-61 data and CAL-27 data (29). For each Illumina probe, the mean expression value for each cell line was calculated. The fold change comparing SCC-61 with CAL-27 as well as comparing rSCC-61 with CAL-27 was calculated for each probe. The fold changes for all Illumina probes for a particular gene were averaged. Protein expression values in ppm units were calculated for SCC-61 and rSCC-61 by multiplying CAL-27 expression values from the ProteomicsDB database by the SCC-61/CAL-27 and rSCC-61/CAL-27 fold changes, respectively (54). The rSCC-61 and SCC-61 protein concentration values estimated in this manner were then compared with stable isotope labeling of amino acids in cell culture (SILAC) proteomic data acquired by mass spectrometry (2). The experimentally obtained values provide independent confirmation of the relative rSCC-61/SCC-61 values on 8.7% coverage of the proteome needed for the FBA models.

Missing protein expression values were imputed by performing k-nearest neighbors between data from all available tissues and cell lines from the GeneCards database, as well as CAL-27, SCC-61, and rSCC-61 cell lines (43). A custom k-nearest neighbor script was written to assign greater weight to neighboring genes that have more available data that can be compared between samples. The distance metric d_ij between genes i and j is calculated using the following equation:

where d_Euclidean,ij is the Euclidean distance between two genes (only for samples where both genes have values available), n_ij is the number of samples where both genes have values available, and α is a constant with value ≥0.5. The larger the value of α, the greater the weight that is given to neighboring genes that have more available data comparable between samples (weight_ij ∼ 1/d_ij). The k-nearest neighbor script also employs a parameter, minsamples, which is the minimum number of samples n_ij that gene neighbors must both have to be valid neighbors. Multiple rounds of k-nearest neighbors are run until no more missing values are imputed. Afterward, values that are still missing are imputed with the mean value of all genes for a particular sample. Parameter values used in this article are k = 100, minsamples = 3, and α = 1.5.

Proteomic data were converted from units of ppm to mmol/gDW through the following conversion:

where N_a is Avogadro's number, n_aa is the average number of amino acids per protein, m_aa is the average molecular mass of an amino acid in Daltons, g_Da is the number of grams per Dalton, and f_dw is the fraction of the cell's dry weight that is protein. Parameter values used in this article are n_aa = 300, m_aa = 100, and f_dw = 0.5.

Proteomic data for every gene were used to calculate enzyme concentration values [E]_j using each reaction's gene-reaction rule, which is an and/or statement stating which genes must be expressed for the enzyme catalyzing the particular reaction to be produced. For every cell type analyzed, gene names were replaced with their respective proteomic value (units of mmol/gDW), X or Y statements were replaced with X + Y, and X and Y statements were replaced with min(X,Y).

TCGA patient clinical and transcriptomic data

Clinical and transcriptomic data from TCGA were retrieved using the Firebrowse API (10). Only HNSCC patients who were HPV negative, had a radiation response classification available, and had transcriptomic data available from the primary tumor site were considered in the analysis. Patients with either complete or partial response to radiation therapy were classified as radiation sensitive, and patients with either stable or radiographic progressive disease after radiation therapy were classified as radiation resistant.

Missing transcriptomic data were imputed using the impute.knn function in the R Bioconductor. After log2 transformation and z-score normalization, ComBat was performed with CAL-27 transcriptomic data so that gene expression values could be directly compared (29); CAL-27 values for Illumina probes corresponding to the same gene were averaged before ComBat was performed. The fold change comparing each TCGA patient with CAL-27 was calculated for each gene. Protein expression values in ppm units were calculated for each TCGA patient by multiplying CAL-27 expression values from the ProteomicsDB database by the patient/CAL-27 fold change (54). Protein expression data were subsequently handled analogous to SCC-61 and rSCC-61 proteomic data described above.

Kinetic data

Turnover number data for enzymes within the Recon 2 model were obtained from the BRENDA database API (46). Supplementary Figure S1 provides an outline of the steps used to get turnover numbers for all reactions with EC numbers available, starting from most accurate to least accurate. When multiple k_cat values were available for the correct enzyme and substrate, the mean of these values was used. To ensure the physiological accuracy of kinetic parameters used in the model, only BRENDA k_cat values measured at a pH between 7 and 8 were selected, and no k_cat values taken from recombinant or mutated enzymes were used.

Metabolite concentration data

Supplementary Table S1 provides the fixed compartmental metabolite concentrations used in the model. Metabolite concentration ranges from Park et al. (41) were incorporated, giving preference to values available in mammalian immortalized baby mouse kidney epithelium (iBMK) cells over yeast cells and yeast cells over E. coli cells (Supplementary Table S2). Human metabolite concentration ranges from The Human Metabolome Database (HMDB) for α-ketoglutarate and pyruvate were used instead of mammalian iBMK cell values to make the IDH1 and ME1 Recon 2 reactions thermodynamically feasible (55). Supplementary Table S3 shows the extracellular metabolite concentrations used to model Dulbecco's Modified Eagle Medium/Nutrient Mixture F-12 (DMEM/F-12) media (ThermoFisher Scientific; 11320033). Supplementary Table S4 shows the experimentally measured cell-type-specific metabolite values and ranges used in SCC-61 and rSCC-61 models (36). All other metabolite concentrations in the model were allowed to range from e⁻¹⁵ to e⁻² M.

Random sampling

Reaction flux distributions for SCC-61 and rSCC-61 cell types were obtained by performing random sampling of the solution space for Equation [6] with all thermodynamically infeasible reactions removed from the model. optReduceModel and optGpSampler were used to perform random sampling, and only solutions that achieved at least 95% of the maximum objective function value were kept (35).

Modeling gene knockdown

siRNA gene perturbations were modeled by decreasing the protein expression of individual genes by 75% (predicted percent knockdown using N-TER Nanoparticle siRNA Transfection System provided by the manufacturer is ≥70%). These decreased protein expression values were used to calculate enzyme concentration values [E]_j using each reaction's gene-reaction rule, as detailed above.

siRNA screen

SCC-61 and rSCC-61 cells were maintained in DMEM/F12 medium that was supplemented with 10% fetal bovine serum (Sigma-Aldrich; F4135) at 37°C and 5% CO₂. For siRNA experiments, cells were plated on 96-well plates at seeding densities of 4 × 10³ cells per well. White, opaque-bottom 96-well plates were used for the cell viability and NADPH luminescent assays. Twenty-four hours after plating, cells were transfected using the N-TER Nanoparticle siRNA Transfection System (Sigma-Aldrich; N2913) and the MISSION siRNA Oxidoreductase Gene Panel (Sigma-Aldrich; SI12100). Drosophila sequences were used for transfection controls, as provided by the manufacturer. Three siRNA sequences for each of 338 gene targets in the library were pooled, and wells were each treated with a final siRNA concentration of 40 nM. All transfections and controls were performed in triplicate. Serum-containing transfection medium was used.

Cell viability assay

Twenty-four hours after transfection, β-lapachone diluted in serum-containing media was added to each well at a final concentration of 3 μM (ID50 of rSCC-61 cells). After 24 h of β-lapachone exposure, the CellTiter-Glo Luminescent Cell Viability Assay was performed (Promega; G7572) according to the manufacturer. Luminescence readings were performed using a Bio-Tek Synergy 4 hybrid microplate reader.

NADPH assay

Plates with transfected cells were split into control and treatment plates. Twenty-four hours after transfection, β-lapachone diluted in serum-containing media was added to the treatment plates at a final concentration of 3 μM. An equal volume of media was added to the control plates. After 2 h of β-lapachone exposure, the NADP/NADPH-Glo assay (Promega; G9081) was performed on both control and treatment plates according to the manufacturer. Luminescence readings were performed using a Bio-Tek Synergy 4 hybrid microplate reader.

Abbreviations Used

αKG

alpha-ketoglutarate

3PG

3-phosphoglycerate

5,10-CH

THF = 5,10-methenyltetrahydrofolate

5,10-CH₂-THF

5,10-methylenetetrahydrofolate

5-MTHF

5-methyltetrahydrofolate

6PG

6-phosphogluconate

6PGL

6-phosphogluconolactone

10-formyl-THF

10-formyltetrahydrofolate

ALDH

aldehyde dehydrogenase

CAT

catalase

CBR

carbonyl reductase

DHF

dihydrofolate

DHFR

dihydrofolate reductase

EC

enzyme commission

FBA

flux balance analysis

G6P

glucose-6-phosphate

G6PD

glucose-6-phosphate dehydrogenase

GLUD

glutamate dehydrogenase

GSH

glutathione

GSR

glutathione reductase

GSSG

glutathione disulfide

H₂O₂

hydrogen peroxide

HNSCC

head and neck squamous cell carcinoma

HPV

human papillomavirus

IDH

isocitrate dehydrogenase

ME

malic enzyme

MTHFD

methylenetetrahydrofolate dehydrogenase

MTHFR

methylenetetrahydrofolate reductase

NADPH

nicotinamide adenine dinucleotide phosphate, reduced

NADP⁺

nicotinamide adenine dinucleotide phosphate, oxidized

NAMPT

nicotinamide phosphoribosyltransferase

NNT

nicotinamide nucleotide transhydrogenase

NOX

NADPH oxidase

Nrf2

nuclear factor (erythroid-derived 2)-like 2

NQO1

NAD(P)H: quinone oxidoreductase 1

OAA

oxaloacetate

PARP

poly(ADP-ribose)polymerase

PGD

phosphogluconate dehydrogenase

R5P

ribulose 5-phosphate

ROS

reactive oxygen species

SOD

superoxide dismutase

TCGA

The Cancer Genome Atlas

THF

tetrahydrofolate

Acknowledgments

The authors gratefully acknowledge support for this work from the Whitaker Foundation and the NIH 5T32GM105490 training grant fellowship to J.E.L.

Author Disclosure Statement

No competing financial interests exist.