Abstract
The matching law constitutes a quantitative description of choice behavior that is often observed in foraging tasks. According to the matching law, organisms distribute their behavior across available response alternatives in the same proportion that reinforcers are distributed across those alternatives. Recently a few biophysically plausible neural network models have been proposed to explain the matching behavior observed in the experiments. Here we study systematically the learning dynamics of these networks while performing a matching task on the concurrent variable interval (VI) schedule. We found that the model neural network can operate in one of three qualitatively different regimes depending on the parameters that characterize the synaptic dynamics and the reward schedule: (1) a matching behavior regime, in which the probability of choosing an option is roughly proportional to the baiting fractional probability of that option; (2) a perseverative regime, in which the network tends to make always the same decision; and (3) a tristable regime, in which the network can either perseverate or choose the two targets randomly approximately with the same probability. Different parameters of the synaptic dynamics lead to different types of deviations from the matching law, some of which have been observed experimentally. We show that the performance of the network depends on the number of stable states of each synapse and that bistable synapses perform close to optimal when the proper learning rate is chosen. Because our model provides a link between synaptic dynamics and qualitatively different behaviors, this work provides us with insight into the effects of neuromodulators on adaptive behaviors and psychiatric disorders.
1. Introduction
One of the most extensively studied foraging behaviors is known as matching behavior, where animals allocate their responses among the reward sites proportional to the relative abundance of reward at each site (Herrnstein, 1961; Herrnstein, Rachlin, & Laibson, 1997). This type of foraging behavior has been observed across a wide range of species, including pigeons, rats, monkeys, and humans (Herrnstein, 1961; Herrnstein et al., 1997; Gallistel, 1994; Gallistel, Mark, King, & Latham, 2001; Sugrue, Corrado, & Newsome, 2004; Corrado, Sugrue, Seung, & Newsome, 2005; Lau & Glimcher, 2005, 2008; Rutledge et al., 2009). Although the matching law is widely observed, it is still unclear under which conditions the subjects follow it.
Several theoretical works explain the matching behavior observed in experiments (Sugrue et al., 2004; Lau & Glimcher, 2005) with different models (see Soltani, Lee, & Wang, 2006; Loewenstein & Seung, 2006; Loewenstein, 2008, 2010; Neiman & Loewenstein, 2013; Sakai & Fukai, 2008a, 2008b; Simen & Cohen, 2009; Katahira, Okanoya, & Okada, 2012). Here we systematically studied the dynamics of an extended version of the neural network model proposed in Soltani et al. (2006). The model network reproduces the matching behavior observed in experiments in which monkeys are trained to choose between two visual targets that are rewarded with different probabilities. We found that the same model can operate in qualitatively different regimes. The richness of the behavior may explain why matching is observed only under certain circumstances, and it can give interesting indications on how alterations of the network parameter due to neurological disorders may affect matching behavior. The model is based on the decision-making network introduced in Wang (2002). Two populations of recurrently connected excitatory neurons, which represent two decisions, compete through a population of inhibitory neurons. The network exhibits a winner-take-all behavior as only one of the two excitatory populations can win the competition. This decision model can be complemented with dynamic synapses to reproduce the matching behavior observed in experiments. The synapses that weight the inputs to the two decision populations are continuously updated depending on the outcome of the choice of the subject. Eventually the distribution of the synapses encodes some estimate of the probability that a choice will be rewarded (Rosenthal, Fusi, & Hochstein, 2001; Soltani & Wang, 2006; Fusi, Asaad, Miller, & Wang, 2007).
The model has been shown to reproduce several interesting features of the matching behavior observed in recent experiments (Sugrue et al., 2004; Lau & Glimcher, 2005). However, the analysis of the dynamics was usually restricted to the minimal models that could generate the behavior observed in specific experiments. Here we extend the model of Soltani and Wang (2006) by considering more general synapses with multiple states and a different updating rule. Our model has a rich behavior that we studied systematically with a mean field approach. We analytically derived the Dynamical Regimes in Neural Network Models of Matching Behavior 3095 probability of choosing a target, which depends in a complicated way on the reward and choice history. This probability can approximate the matching law, but it can also converge to different stable solutions that represent other dynamical regimes. Moreover, we considered a more general graded synaptic model with m states and hard boundaries. This allows us to predict the effects on the behavior that some neuromodulators may have when they change the amplitude of the synaptic modifications (the synaptic changes are proportional to 1/m). We finally studied how the learning rates can affect the performance of the network when it executes a dynamical foraging task, in which the probability of reward changes with a certain frequency. Fast synapses are obviously good at adapting to new environments but poor at generating accurate estimates of the probability of reward. Slow synapses are poor at adapting and good at integrating reward and choice history. As the number of synaptic states increases, the synapses become slower, and although the integration time increases, the performance can deteriorate even when the obvious negative effects of slow transients are not considered. As a consequence, the optimal harvesting performance can be achieved with synapses with a relatively small number of stable states.
2. Methods and Description of the Model
2.1. The Task.
On each trial, the subject selects a left (L) or a right (R) target. The selection leads to an outcome that depends on the reward schedule. In our study, we considered the discretized concurrent variable interval (VI) schedule. Each target is in either a baited or empty state. If the subject then selects a baited target, it receives a reward, and the state of the chosen target returns to empty. Otherwise the subject does not receive any reward. In this case, if the other target is baited, it remains baited until the subject selects it. Before the beginning of each trial, each target is baited with some probability (rL for the left target, rR for the right target). The state of target (baited or empty) is not known to the subject. The VI reward schedule is designed to encourage the subject to “explore” and sample the target that is baited with a lower probability. The optimal strategy in a stationary environment is to follow the matching law (Sakai & Fukai, 2008a).
2.2. The Decision-Making Neural Circuit.
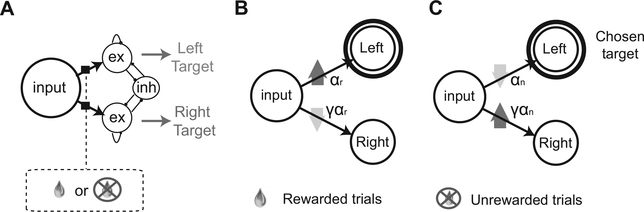
The neural circuit that operates the selection is basically the decision-making network proposed in Wang (2002), Soltani and Wang (2006), and Fusi et al. (2007) and illustrated in Figure 1. An input, activated at the beginning of each trial, is weighted and then injected into two populations of excitatory neurons that represent the two choices. These populations excite themselves through recurrent connections and compete through a mutual inhibition mediated by a population of inhibitory cells. The synaptic couplings are chosen so that there are only two stable patterns of activity in the presence of the external input. These two patterns correspond to the two possible decisions (selecting the left or the right target). Because the neurons also receive a background noisy input, the decision is probabilistic. The probability of choosing the left target PL depends on the difference between the synaptic input currents IL — IR to the two decision populations, and it is well fitted by a sigmoid (Soltani & Wang, 2006),
| (2.1) |
where T is a parameter called temperature that depends on the amplitude of the noise.
Figure 1:
Model description. (A) Decision-making network. Each circle represents a population of neurons. As the targets appear, the input population is activated in the same way on each trial. The input is fed through plastic synapses into two excitatory populations representing the two possible choices. These two populations compete through an inhibitory population and work as a winner-take-all network. The plastic synapses are modified depending on the activity of the pre- and, postsynaptic neurons and on the outcome of the choice (reward or no reward). (B) Learning rule in rewarded trials in which the population representing the left target is activated. The synapses to the chosen target are potentiated with a learning rate αr, and those to the other target are depressed with a learning rate γα7.. (C) Same as in panel B but in unrewarded trials. The synapses to the chosen target are depressed αn, and those to the other target are potentiated γαη.
2.3. The Plastic Synapses.
The afferent currents IL and IR are proportional to the average synaptic weights that connect the population of neurons representing the input and the two decision populations. The decision bias can be changed by modifying the efficacy of these synapses (Soltani & Wang, 2006; Fusi et al., 2007). The current to a neuron that belongs to the Dynamical Regimes in Neural Network Models of Matching Behavior 3097 decision of selecting the left target can be written as
| (2.2) |
where the νj’s are the firing rates of the N neurons in the input population. We now focus on the left target, but analogous expressions can be written for the population representing the right target. Assuming that the input population is uniform νj = ν, we can simplify the expression of the current,
| (2.3) |
where (w)L is the average synaptic weight to the left population. Here we can assume νΝ = 1 without any loss of generality, as the choice probability PL depends on only the ratio between the difference of currents and the temperature, and hence we can reabsorb the constant νN in the temperature (T/νN → T).
We assume that each synaptic weight can vary between 0 and 1. The synapses can be potentiated or depressed by a fixed amount ᐃw = ±1/(m — 1), where m is the total number of stable synaptic states (Fusi & Abbott, 2007). Bistable synapses correspond to the case in which m = 2.
At the end of each trial, the synapses are modified stochastically depending on the activity of the pre-and postsynaptic neurons and on the outcome—whether the subject receives a reward. (See Figures 1B and 1C.) The synapses connecting the input population (always active once the targets are on the screen) to the decision population corresponding to the chosen target (active at the end of the trial) are potentiated (w → w + ᐃ w) stochastically with probability αr in case of reward; they are depressed (w → w — △ w) stochastically with probability αn in case of no reward. Conversely, the synapses between the population input and the decision population of the unchosen target are depressed with probability γαn in case of reward and potentiated with probability γαn in case of no reward. Synaptic modifications that would bring the synapse outside the boundaries are ignored (hard bounds). The probabilities of modification determine the learning rate. The scheme of synaptic modifications is similar to the one proposed in Soltani and Wang (2006) and Fusi et al. (2007), and it biases the choice toward the rewarded target by increasing (decreasing) the probability of choosing a target that has been rewarded (not rewarded).
2.4. Mean Field Analysis.
The average synaptic current to a decision population (say, left) can be rewritten as
| (2.4) |
where the sum extends over all the discrete values of the synapses. The synaptic efficacies are , and is the fraction of synapses between the input and the left decision population whose synaptic efficacy is equal to w(k). The synaptic strength distribution changes every time the synapses are updated according to the following equation,
| (2.5) |
where t indicates time expressed in number of trials and the ZL is the following matrix:
| (2.6) |
where and are, respectively, the average potentiation and depression rate, which depend on the learning rules and the reward schedule. On the VI reward schedule, they can be written as
| (2.7) |
where bL (t) is a binary variable that is 1 when the left target is baited on trial t. Unfortunately this quantity depends in a complicated way on the reward and the choice history. However, when the baiting probabilities are stationary and PL (t) changes slowly enough to be replaced by its average over a certain number of trials, then the expected value of bL (t) () can be approximated by (Sakai & Fukai, 2008a)
| (2.8) |
Notice that is usually defined as the return. More generally, the return from a choice X is the total reward that has been harvested on that choice divided by the number of choices for X. In contrast, the income from choice X is the total reward that has been harvested on that choice divided by the total number of choices. Using our notation, the income from the left target is . We discuss below how these quantities are encoded by the statistics of the synaptic weights. Under the approximation , the stochastic process for updating the synapses becomes a Markov process, and Z is its transition matrix. This Markov process is homogeneous, as Z has lost its dependence on t. The distribution of the synapses relaxes to equilibrium, whose properties can be fully characterized. Indeed, the Markov process has a unique equilibrium distribution given by Fusi and Abbott (2007):
| (2.9) |
where and are stationary potentiation and depression rates determined by equations 2.7 and 2.8. Notice that both and depend on the behavior of the subject, which is determined by the probability of choosing one of the targets (e.g., ). This probability depends in turn on the full distribution of the synapses , as they determine the total synaptic currents to the two-choice population. This means that the distribution and the choice probability should be determined self-consistently by finding a solution that satisfies simultaneously equations 2.1, 2.4, 2.7, 2.8, and 2.9. Not surprisingly, the distribution of the synapses that converge to the population representing the choice of the left target becomes a function of the return from left target when γ = 0, as already shown in Soltani and Wang (2006). Indeed, from equation 2.9, the synaptic distribution is a function of the ratio between potentiation and depression rate qL/qr, which, using equation 2.7, can be rewritten as
| (2.10) |
where, as we noted above, is the return from target L. This is expected, as in the case of γ = 0 the synapses to the population of neurons representing left are updated only when the left target is chosen. When γ > 0, the synaptic distribution also becomes a function of PL and pR, and hence it may encode the income from the two targets. Note also that equation 2.10 shows that the dependence of the equilibrium synaptic distribution on αr and αn is always through the dependence on term αr/αn. This is true for any value of γ (see equations 2.7 and 2.9), and it greatly simplifies the analysis of the dynamical regimes of the network as the independent variables are only αr/αn and γ. We now need to find a self-consistent solution for PL. In general, it is not possible to find a closed expression for the VI schedule; however, when the noise is small (i.e., in the limit of T → 0), it is possible to derive analytical expressions. In the matching regime, the difference between the synaptic currents (I = IL — Ir) should be comparable to the temperature T, so that I/T is not too large or too small, cases that lead to trivial solutions (PL = 0or 1). This implies that as T → 0, the difference between the synaptic current should also decrease at the same rate (I = IL — IR = κ T → 0).
We now consider two solvable cases. The first is when there is no interaction between synaptic populations during learning (γ = 0). From equations 2.7 and 2.8, we can rewrite IL — IR = κT as
| (2.11) |
In the limit of T → 0, this reduces to
| (2.12) |
Thus for T → 0, the choice probability approaches what is determined by the matching law (Herrnstein, 1961):
| (2.13) |
Note that this is consistent with our finding that the synaptic distribution becomes a function of the return when γ = 0. In a realistic situation, the noise is finite (T > 0), leading to a deviation from the matching law (undermatching), which is often observed in experiments (Herrnstein et al., 1997; Sugrue et al., 2004; Lau & Glimcher, 2005).
In the case γ = 1, we can obtain the asymptotic slope of the choice probability PL as a function of the fractional baiting rate. When the reward rate is small, rL + rR ≪ 1, we can linearize the potentiation and depression rate as
| (2.14) |
and
| (2.15) |
The first term in equation 2.14, rL, represents the average rate of obtaining reward from left. The second term, , represents the average rate of not obtaining reward when right is selected (Soltani & Wang, 2006). Following a procedure similar to the one used in the case γ = 0, we obtain
| (2.16) |
where . Equation 2.16 shows that the asymptotic slope is given by at γ = 1.
3. Results
The results of the analysis described in section 2 can be summarized as follows. First, depending on the parameters of the synaptic dynamics and the overall reward rate, the model neural circuit can operate in three qualitatively different regimes: the widely studied matching regime; a persevera-tive regime, where the animal repeatedly chooses the same target regardless of the reward history; and a tristable regime, where the animal can either perseverate by choosing repeatedly only one target or it selects randomly one of the two targets with approximately the same probability. Second, in the matching regime, slow plastic synapses lead to more accurate estimates but take longer to adapt to environmental changes. This is a speed-accuracy trade-off shared by all realistic models. Third, neural circuits with graded synapses with hard bounds have a harvesting performance comparable to the simpler bistable synapses.
3.1. The Three Qualitatively Different Behavioral Regimes.
3.1.1. The Matching Regime.
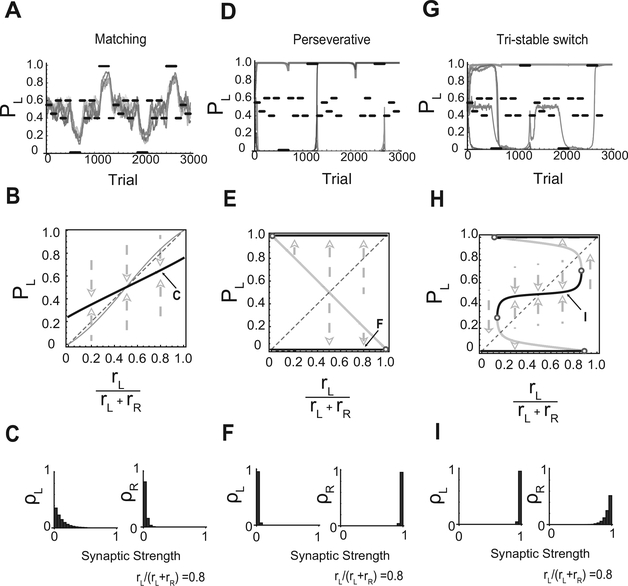
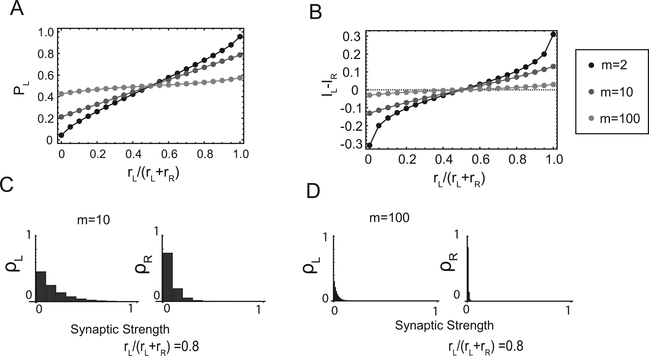
Previous studies have shown that the matching behavior observed in experiments can be obtained with the model circuit that we studied (Soltani & Wang, 2006). A simulation of the network model exhibiting matching behavior is shown in Figure 2A. We show in Figure 2B that this type of matching behavior is actually stable in the sense that for any initial condition of the synaptic weights, the model circuit converges to the matching behavior after a sufficient number of trials. More specifically, for a given fractional baiting probability (on the x-axis), the equilibrium choice probability PL (on the y-axis) is on the solid black line. This line is “attractive” in the sense that the combined learning and neural dynamics converge to the point of the solid black line that corresponds to the baiting ratio for any initial condition. In Figure 2B, the matching law, equation 2.13, corresponds to the thin gray line. The neural circuit can only approximate the matching law. We say that the circuit operates in a matching regime or that it exhibits matching behavior whenever there is only one stable point for rL = rR (at PL = 0.5). The stable solutions of the matching regime are various approximations of the matching law.
Figure 2:
The three regimes. (A-C) Matching regime. (A) Simulated dynamics of the choice probability PL. The probability of baiting left is set to different values in different blocks of trials (solid black lines). The thick solid line represents PL in different runs of simulations with the same parameters. In this regime, PL tends to follow the changes in the baiting probability. (B) Equilibrium PL versus the fractional baiting probability rL/(rL + rR ). The thick solid line represents the stable equilibrium PL, which in this regime it is approximately linear. The thin solid line represents the matching law. (C) The equilibrium distribution of the synaptic weights to the two-choice populations in the matching regime at the point indicated by C in panel B. (D-F) Same as in panels A-C but for the perseverative regime. (D) Now the simulated network tends to always choose the same target regardless the baiting probability. The chosen target depends on the initial conditions. Occasionally, for strongly biased baiting probabilities, the network switches target (see the vertical lines). (E) Now there are two stable equilibrium values for PL (top and bottom solid horizontal lines). The thin solid line in the middle represents unstable fixed points of PL and separates the two basins of attractions. (F) The distributions of the synapses are now skewed in opposite directions for the two populations of synapses. (G-I) Same as in panels A-C but for the tristable regime. (G) PL is most of the time close to one of the three stable points (0, 0.5, 1). (H) For an extended range around a fractional baiting probability of 0.5, there are three stable and two unstable points. (I) The distribution of the synapses for the stable point around PL = 0.5. The distributions for the other two stable points are similar to those of the perseverative regime. Parameters: (A) m = 2, T = 0.1, , γ = 1, rR + rL = 0.35; (B) m = 50, T = 0.1, , γ = 0.1, rR + rL = 1; (C) m = 50, T = 0.1, , γ = 1, rR + rL = 1.
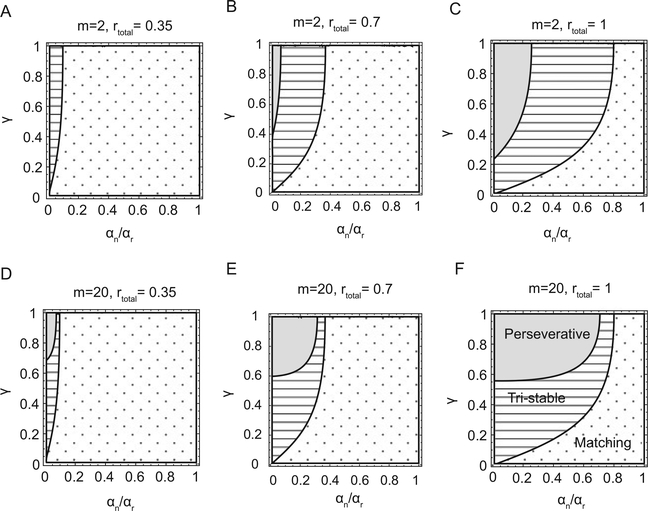
The stability of the matching regime depends on the parameters of both the reward schedule and the neural circuit. In particular we show in Figure 3 that matching behavior is stable when the overall baiting rate (i.e., the sum of the baiting probabilities) is small, the noise is small (T ≪ 1), and the synaptic modifications prevalently affect the connections to the chosen action (γ ≪ 1).
Figure 3:
How the parameters of the neural circuit and the experimental protocol determine the behavioral regime. Each plot shows for what values of αn/αr (x-axis) and γ (y-axis) the network exhibits the three behavioral regimes (gray region = perseverative; striped = tristable; dotted = matching). Different plots correspond to different values of the number of synaptic states m and the overall reward affluence rtotal = rL + rR. The behavior of the network is shown for rtotal = 0.35 (A, D). The value used in experiments in which the matching behavior is observed (Sugrue et al., 2004; Corrado et al., 2005). As rtotal increases, the region with the matching behavior gradually shrinks. (B, E) rtotal = 0.7. (C, F) rtotal = 1. Notice that the border separating the striped from the dotted region does not depend on m.
In the limit case of γ → 0 and T → 0, it is possible to derive analytically the choice probability PL:
| (3.1) |
where rL and rR are the baiting rates for the L and R targets, respectively. This expression indicates that in this limit, the model approaches the matching law. A matching behavior that deviates from matching law can still be obtained when γ and T are small enough. It is also instructive to consider the choice probability when the learning rate is the same for chosen and unchosen targets (γ = 1) in the limit T → 0:
| (3.2) |
where . This shows that the asymptotic slope of PL against is given by when γ = 1. When αr = αn, the model still exhibits matching behavior if the overall baiting rate is small rL + rR < 1/2, but the slope of the choice probability versus the baiting probability ratio is smaller than 1 (undermatching). This is consistent with the experimental observation that when the overall baiting rate is small rL + rR < 1 /2, undermatching is observed (Sugrue et al., 2004). Undermatching has already been studied in other models (Loewenstein, Prelec, & Seung, 2009; Katahira et al., 2012).
In Figure 2C, we show the equilibrium distributions of the efficacies of the synapses to the two target populations in the case of a model synapse with 20 states. Both distributions are highly biased toward the depressed states. This is due to the fact that synaptic depression dominates for both the left and the right target populations when the overall baiting probability and γ are small. One of the two distributions is more skewed than the other (left), reflecting the fact that one target is more baited than the other. Note that one could also encode the differences between the baiting probabilities by having two distributions biased toward the opposite ends—one toward the depressed and the other toward the potentiated states. However, this solution would require some tuning in the case of small temperatures, as the difference between the currents to the left and to the right populations should be restricted to vary in a very limited range to have matching behavior (see Fusi et al., 2007). In the case of larger values of γ, the distributions can be skewed in opposite directions, but the imbalance between the potentiating and the depressing events is always very small.
3.2. Perseveration.
Consider now the limit situation in which following reward, the synaptic populations to both targets are modified (γ > 0), and in the case of no reward, the synapses remain unchanged. If the model network initially selects the left target, it will keep selecting left indefinitely, as the synapses to the left population can only be strengthened. This is true whether left is the most baited target or not. This extreme case illustrates the behavior of the network in the perseverative regime (see Figures 2D and 2E), in which there is a strong tendency to select repeatedly only one target. Formally, we define the perseverative regime as the one in which there are three fixed points of the learning/neural dynamics when the two choices are baited with equal probability (rL = rR). The fixed point in the middle is unstable, whereas the other two are stable (see Figure 2E) and correspond to the repeated selection of one of the two targets (p = 0, PL = 1). If the temperature is large enough and the fractional baiting probability is biased toward 0 or 1, then there is some finite probability that the neural circuit switches from one choice to the other (see Figure 2D).
This perseverative behavior has previously been studied in matching penny games. In these tasks, simulated neural networks that are similar to the model studied here exhibit perseveration when the random choice behavior, the optimal strategy, becomes unstable (Soltani et al., 2006). This type of behavior is observed in some experiments in the early stages of learning or when the baiting rate is high (Lee, Conroy, McGreevy, & Barraclough, 2004).
3.3. Tristability.
In addition to the two regimes already described, we found another qualitatively different behavioral regime that we named the tristable regime. In this regime (see Figures 2G and 2H), the model either selects the targets with approximately the same probability () or it perseverates at selecting only one target (PL = 0or PL = 1). This behavior can be interpreted as matching with a coarsely grained estimation of the reward rates. The perseverative behavior is observed when the choice probability is initially close to either 0 or 1 (Pl ~ 0 or Pl ~ 1 ), that is, in all cases in which there is a strong initial bias toward one target or the other. It is also observed when the baiting rate is analogously biased (when , or ).
Formally, the tristable regime is characterized by five fixed points at rL = rR. The two at PL = 0 or PL = 1 are stable and correspond to perseverative behavior. The one in the middle (at PL = 0.5) is also stable and corresponds to stochastic behavior in which the subject selects the two choices with equal probability. The other two fixed points are unstable.
Figure 3 shows that the tristable regime is obtained in a region of the γ-αn/αr plane that separates the perseverative from the matching regime. As one decreases αn/αr, the neural circuit switches from the matching regime to the tristable regime and then to the perseverative regime. Interestingly, the boundary separating the tristable from the matching regime does not depend on the number of synaptic states. This is explained by the fact that the transition into the tristable regime is characterized by the appearance of two perseverative states. For these states, the distributions of the synaptic efficacies depend on the drift determined by the imbalance between potentiation and depression. This drift is positive for one population (the chosen target) and negative for the other (see Figure 2F). These types of distributions have a very weak dependence on the number of synaptic states (Fusi & Abbott, 2007). Moreover, it is important to notice that these distributions with opposing drifts can be obtained only if γ is sufficiently large.
3.4. The Speed-Accuracy Trade-Off.
For the VI schedule, the optimal strategy that maximizes the harvesting performance (i.e., total reward accumulate over multiple trials) relies on the ability of the subject to estimate the probability of obtaining a reward.
The accuracy of the estimate depends on the learning rate: slow synapses can integrate evidence on longer time windows, and hence are better in terms of accuracy than fast synapses. However, this is true only in a stationary environment. If the environment changes, then slow synapses are disadvantaged because they take longer to adapt to new situations.
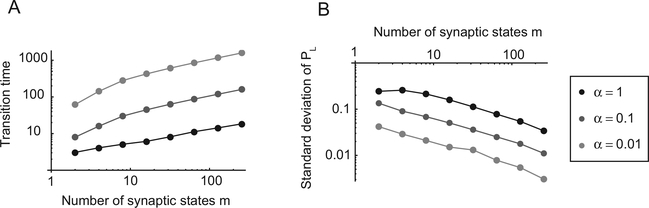
For our synaptic model, the learning rate is determined by αr, αn, γ and the number of synaptic states, m. Slow learning (small αr, αn, γ, or large m) means a more accurate estimate at the expense of the adaptation time. This behavior is illustrated in Figure 4, where we plotted the adaptation time and the accuracy of the probability estimate as a function of m and the learning rates. These quantities are measured in a simulation in which a network operating in the matching regime starts working in an environment in which the fractional baiting probability for the left target is rL/(rL + rR) = 0.1. Then at time zero, rL/(rL + rR) changes to 0.9 and the network adapts to the new environment. The adaptation time τ is the number of trials it takes to reach PL = 0.5, and the standard deviation of PL is estimated at equilibrium. The adaptation time scales approximately like , where αR = αL = α an γ = 0. The amplitude of the fluctuations scales as 1/τ.
Figure 4:
Speed and accuracy as a function of m, the number of synaptic states, and of a, the learning rate (αn = αr = α, γ = 0). (A) Time τ required to converge to an estimate of the baiting probability versus m. Different curves correspond to different values of α. τ(α,Μ) is approximately . (B) Standard deviation of PL versus m for different values of α. As m increases, the fluctuations decrease approximately as , and the accuracy of the estimate increases. The initial fractional baiting probability is , and at time zero, it changes to . τ is estimated as the time it takes to reach PL = 0.5, and the standard deviation of PL is estimated at equilibrium. The other parameters are T = 0.05 and rL + rR = 0.35.
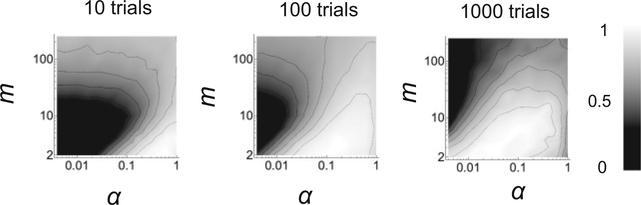
The optimal learning rates in general will depend on the temporal statistics of the changes in the environment. Figure 5 shows the average performance of the neural circuit on VI schedule as a function of m and α for different lengths of the blocks in which the baiting probability is kept constant. The shorter the blocks are, the more volatile is the environment. The performance is estimated by measuring the harvesting efficiency, defined as the average number of rewards per trial divided by the total reward rate. As expected, the peak performance shifts toward circuits with slower learning dynamics as the environment becomes more stable.
Figure 5:
Optimal learning rates and number of synaptic states for environments with different volatility. The baiting probabilities change at different rates in the three plots (from left to right, the number of trials per block is s = 10, 100,1000). Each plot shows the overall performance of the simulated network (gray/scale) as a function of the learning rate α (αr = αn = α) and the number of synaptic states m. The performance is the harvesting efficiency, which is defined as the average number of received rewards per trial, divided by the total reward rate. The optimal parameter region is always achieved for a relatively small number of synaptic states (m < 10), even in the case of stable environments (right). T = 0.05, γ = 0 and rL + rR = 0.35.
Interestingly, Figure 5 shows that the optimal number of synaptic states m is always close to 2. This means that increasing the complexity of the synapse by increasing the number of synaptic states does not significantly improve the harvesting performance. Eventually, for large enough m, the performance actually decreases. When m increases above optimal, the estimate continues to become more accurate because the fluctuations decrease. However, two other effects disrupt the performance. The first one is more obvious and is due to longer adaptation times; the second one is more subtle and is explained in Figure 6. As m increases, the distribution of the synaptic weights becomes more localized around one of the boundaries. This decreases the difference between the total synaptic current IL to the left population and the total synaptic current IR to the right population. As a consequence, the matching behavior shows a more prominent undermatching (PL becomes closer to 0.5 for every fractional baiting probability). This deviation from the optimal behavior leads to a decrease in the performance. When the environment is volatile, the disruptive effects of longer adaptation times dominate the decrease in the performance. However, in stable environments, undermatching is the main cause of performance degradation.
Figure 6:
Increasing the number of synaptic states decreases performance. (A) The deviation from the matching law increases as the number of synaptic states m increases and it causes a decrease of the harvesting performance. (B) As m increases, the difference IL — IR between the total synaptic currents injected in the choice populations decreases. (C, D) This decrease is due to fact that the equilibrium distribution of the two synaptic populations is biased toward the same side. The synaptic current difference is due to the skewness of the distribution. As m increases, the equilibrium distribution becomes progressively more localized around one of the two synaptic bounds, making the difference between IL and IR progressively smaller. This leads to an increased deviation from the matching law (A), which deteriorates the performance.
It is important to notice that a and m both affect the adaptation time in a similar way; however, the effects on the equilibrium distribution are significantly different. In addition, in the case in which the subject has only to estimate probabilities (e.g., on the concurrent variable rate schedule), an increase in m may lead to strong overmatching, and hence it is qualitatively different from the VI schedule (see Ostojic & Fusi, 2013).
4. Discussion
We analyzed a model of a decision-making neural circuit that exhibits matching behavior. The analysis has been performed in a matching task with a discrete variable interval (VI) schedule in which the two targets are baited with some probability. We found that the same neural circuit has three qualitatively different behaviors depending on the parameters of the synaptic dynamics and the parameters of the reward schedule. It is already known that matching behavior can be observed only under restricted conditions. For example, the total baiting rate should be sufficiently small (typically rL + rR ~ 0.35). For larger rates, our model predicts that the subject either perseverates or randomly chooses the two targets with equal probability.
Our analysis can also predict the effects of drugs that affect the learning rates (αr,αn, γ) or change how strongly the synapses are modified at every update (when the synapse has m states, the synaptic modification is proportional to 1/m). For example, dopaminergic drugs used to treat Parkinson’s disease increase the learning rate from positive outcomes (our αr) (Rutledge et al., 2009). Patients who are treated with these drugs exhibit a lower tendency to perseverate, which, in our language, would correspond to a transition from the tristable regime to the matching regime. A detailed analysis of the data would be required to establish whether the observed perseveration is compatible with the behavior of our network in the tristable regime. If that will be confirmed, then it will be possible to understand what parameter changes cause the perseveration in the untreated patients. This will probably require studying an extension of the model proposed here in which γ is different for positive and negative outcomes, but the formalism will be the same.
Our models also showed, not surprisingly, that learning rates can significantly affect performance. It is well known that optimal learning rates vary depending on the volatility of the environment (Behrens, Woolrich, Walton, & Rushworth, 2007; Nassar et al., 2012; Nassar, Wilson, Heasly, & Gold, 2010). In our analysis, we assumed for simplicity that the learning rates are fixed, but it is likely that they actually change dynamically to adapt more rapidly to new environments. There could be biophysical mechanisms to modify the learning rates in individual synapses (Fusi, Drew, & Abbott, 2005; Clopath, Ziegler, Vasilaki, Busing, & Gerstner, 2008) or system-level changes in which different brain areas operate concurrently on different timescales (Roxin & Fusi, 2013). All of these mechanisms will be investigated in future studies.
The number of synaptic states also affects the performance. Our analysis shows that the optimal performance is always achieved for a relatively small number of synaptic states. This result seems to contradict previous studies on memory, which show that synaptic complexity can greatly extend memory lifetimes without sacrificing the amount of information stored per memory (Fusi et al., 2005). However, we need to consider that the multistate synapses that we analyzed are relatively simple not representative of all types of complex synapses. On the contrary, the analyzed multistate synapses are not among the most efficient for solving a memory problem (Fusi & Abbott, 2007). In addition, we are considering a problem in which memory is an essential component as it is needed to estimate probabilities; however, our problem is inherently different from the typical benchmarks used to assess memory capacity. In these benchmarks, memories are random and uncorrelated, and hence they are presented for storage only once. Then typically the memory strength decays as the synaptic distribution relaxes to equilibrium. In contrast, in a probability estimation problem, the equilibrium distribution contains information about the quantity to be estimated. As a consequence, the speed of convergence to equilibrium is not the limiting factor for the performance. Instead the fluctuations around equilibrium can strongly affect the ability to estimate probabilities (Ostojic & Fusi, 2013).
Acknowledgments
We thank Yonatan Loewenstein for valuable discussions. The work has been supported by the Gatsby Foundation, the Swartz Foundation, and the Kavli Foundation.
Contributor Information
Kiyohito Iigaya, Center for Theoretical Neuroscience, Department of Neuroscience, Columbia University Medical Center, New York, NY 10032, and Department of Physics, Columbia University, New York, NY 10027, U.S.A, ki2151@columbia.edu.
Stefano Fusi, Center for Theoretical Neuroscience, Department ofNeuroscience, Columbia University Medical Center, New York, NY 10032, U.S.A. sf2237@columbia.edu.
References
- Behrens TE, Woolrich MW, Walton ME, & Rushworth MF (2007). Learning the value of information in an uncertain world. Nat. Neurosci, 10(9), 1214–1221. [DOI] [PubMed] [Google Scholar]
- Clopath C, Ziegler L, Vasilaki E, Busing L, & Gerstner W (2008). Tag-trigger-consolidation: A model of early and late long-term-potentiation and depression. PLoS Comput. Biol, 4(12), e1000248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Corrado GS,Sugrue LP,Seung HS, & Newsome WT (2005). Linear-nonlinear-Poisson models of primate choice dynamics. J. Exp. Anal. Behav, 84(3), 581–617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fusi S, and Abbott LF (2007). Limits on the memory storage capacity of bounded synapses. Nat. Neurosci, 10, 485–493. [DOI] [PubMed] [Google Scholar]
- Fusi S, Asaad WF, Miller EK, & Wang XJ (2007). A neural circuit model of flexible sensorimotor mapping: Learning and forgetting on multiple timescales. Neuron, 54, 319–333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fusi S, Drew PJ, & Abbott LF (2005). Cascade models of synaptically stored memories. Neuron, 45(4), 599–611. [DOI] [PubMed] [Google Scholar]
- Gallistel CR (1994). Foraging for brain stimulation: Toward a neurobiology of computation. Cognition, 50, 151–170. [DOI] [PubMed] [Google Scholar]
- Gallistel CR, Mark TA, King AP, & Latham PE (2001). The rat approximates an ideal detector of changes in rates of reward: Implications for the law of effect. J. Exp. Psychol. Anim. Behav. Process, 27, 354–372. [DOI] [PubMed] [Google Scholar]
- Herrnstein RJ (1961). Relative and absolute strength of response as a function of frequency of reinforcement. J. Exp. Anal. Behav, 4, 267–272. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrnstein RJ (1997). In Rachlin H & Laibson DI (Eds.), The matching law: Papers in psychology and economics. Cambridge, MA: Harvard University Press. [Google Scholar]
- Katahira K, Okanoya K, & Okada M (2012). Statistical mechanics of reward- modulated learning in decision-making networks. Neural Comput., 24(5), 1230–1270. [DOI] [PubMed] [Google Scholar]
- Lau B, & Glimcher P W. (2005). Dynamic response-by-response models of matching behavior in rhesus monkeys. J. Exp. Anal. Behav, 84(3), 555–579. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lau B, & Glimcher PW (2008). Value representations in the primate striatum during matching behavior. Neuron, 58(3), 451–463. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee D, Conroy ML, McGreevy BP, & Barraclough DJ (2004). Reinforcement learning and decision making in monkeys during a competitive game. Brain Res. Cogn. Brain Res, 22(1), 45–58. [DOI] [PubMed] [Google Scholar]
- Loewenstein Y (2008). Robustness of learning that is based on covariance-driven synaptic plasticity. PLoS Comput. Biol, 4(3), e1000007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loewenstein Y (2010). Synaptic theory of replicator-like melioration. Front. Comput. Neurosci, 4, 17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Loewenstein Y, Prelec D, & Seung HS (2009). Operant matching as a Nash equilibrium of an intertemporal game. Neural Comput, 21, 2755–2773. [DOI] [PubMed] [Google Scholar]
- Loewenstein Y, & Seung HS (2006). Operant matching is a generic outcome of synaptic plasticity based on the covariance between reward and neural activity. Proc. Natl. Acad. Sci. U.S.A, 103, 15224–15229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nassar MR,Rumsey KM, Wilson RC,Parikh K,Heasly B, &Gold JI (2012). Rational regulation of learning dynamics by pupil-linked arousal systems. Nat. Neurosci, 15(7), 1040–1046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nassar MR, Wilson RC, Heasly B, & Gold JI (2010). An approximately Bayesian delta-rule model explains the dynamics of belief updating in a changing environment. J. Neurosci, 30(37), 12366–12378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neiman T, & Loewenstein Y (2013). Covariance-based synaptic plasticity in an attractor network model accounts for fast adaptation in free operant learning. J. Neurosci, 33(4), 1521–1534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ostojic S, & Fusi S (2013). Synaptic encoding of temporal contiguity. Front. Comput. Neurosci, 7, 32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenthal O, Fusi S, & Hochstein S (2001). Forming classes by stimulus frequency: Behavior and theory. Proc. Natl. Acad. Sci. U.S.A, 98, 4265–4270. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Roxin A, & Fusi S (2013). Efficient partitioning of memory systems and its importance for memory consolidation. Plos Computational Biology, 9(7), e1003146. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rutledge RB, Lazzaro SC, Lau B, Myers CE, Gluck MA, & Glimcher PM (2009). Dopaminergic drugs modulate learning rates and perseveration in Parkinson’s patients in a dynamic foraging task. J. Neurosci, 29, 15104–15114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sakai Y, & Fukai T (2008a). The actor-critic learning is behind the matching law: Matching versus optimal behaviors. Neural Comput., 20(1), 227–251. [DOI] [PubMed] [Google Scholar]
- Sakai Y, & Fukai T (2008b). When does reward maximization lead to matching law? PLoS ONE, 3, e3795. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Simen P, & Cohen JD (2009). Explicit melioration by a neural diffusion model. Brain Res., 1299, 95–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soltani A, Lee D, & Wang X-J (2006). Neural mechanism for stochastic behaviour during a competitive game. Neural Networks, 19(8), 1075–1090. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soltani A, & Wang X-J (2006). A biophysically based neural model of matching law behavior: Melioration by stochastic synapses. J. Neurosci, 26(14), 3731–3744. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sugrue LP, Corrado GS, & Newsome WT (2004). Matching behavior and the representation of value in the parietal cortex. Science, 304(5678), 1782–1787. [DOI] [PubMed] [Google Scholar]
- Wang X-J (2002). Probabilistic decision making by slow reverberation in cortical circuits. Neuron, 36(5), 955–968. [DOI] [PubMed] [Google Scholar]