Frequency-Encoded Multicolor Fluorescence Imaging with Single-Photon-Counting Color-Blind Detection

Abstract

Standard fluorescence microscopy relies on filter-based detection of emitted photons after fluorophore excitation at the appropriate wavelength. Although of enormous utility to the biological community, the implementation of approaches for simultaneous multicolor fluorescence imaging is commonly challenged by the large spectral overlap between different fluorophores. Here, we describe an alternative multicolor fluorescence imaging methodology that exclusively relies on the absorption spectra of the fluorophores instead of their fluorescence emissions. The method is based on multiplexing optical excitation signals in the frequency domain and using single color-blind detection. Because the spectral information is fully encoded during excitation, the method requires minimal spectral filtering on detection. This enables the simultaneous identification of multiple color channels in a single measurement with only one color-blind detector. We demonstrate simultaneous three-color confocal imaging of individual molecules and of four-target imaging on cells with excellent discrimination. Moreover, we have implemented a non-negative matrix factorization algorithm for spectral unmixing to extend the number of color targets that can be discriminated in a single measurement. Using this algorithm, we resolve six spectrally and spatially overlapping fluorophores on fixed cells using four excitation wavelengths. The methodology is fully compatible with live imaging of biological samples and can be easily extended to other imaging modalities, including super-resolution microscopy, making simultaneous multicolor imaging more accessible to the biological research community.

Introduction

Fluorescence microscopy is one of the most powerful tools employed in basic life sciences because it allows the detection of different molecular components in fixed and living cells with high specificity and ultimate sensitivity. With the advent of super-resolution microscopy (1, 2, 3, 4) and the rapid development of improved fluorescent probes (5, 6, 7, 8), the possibility of visualizing complex cellular structures at the nanoscale is now within reach (9). Understanding the structure and dynamics of macromolecular complexes generally requires the labeling of different species of biomolecules with a variety of fluorophores and analysis of their spatial distributions and temporal behaviors. Single-molecule sensitivity, short acquisition times, and minimal spectral cross talk are all critical requirements in quantitative biology to simultaneously visualize multiple labeled targets at relevant temporal and spatial scales.

The last few years have witnessed remarkable advances toward the implementation of multicolor fluorescence imaging, aiming to improve spectral discrimination in a wide variety of configurations that seek to address improved spatial and temporal resolution. Simultaneous excitation and detection of multiple colors can be performed by a combination of different lasers and detectors via filter-based isolation of the fluorescence signals. However, in practice, the large spectral overlap of fluorophores limits simultaneous multicolor imaging to three or four different targets (10, 11). To reduce spectral cross talk, standard multicolor methods, including most commercial systems, commonly rely on temporal separation, i.e., different excitation wavelengths are switched on, one at the time, and the sample is imaged sequentially (12, 13, 14). Unfortunately, this approach poses restrictions to live-cell-imaging applications because the total image acquisition time is increased.

To increase the number of target molecules that can be simultaneously imaged, more innovative methods take advantage of the photophysical properties of fluorescent probes, such as their excited-state lifetimes (15) and/or emission spectra (15, 16, 17). The combination of spectral and lifetime information significantly extends the number of targets that can be simultaneously imaged, but it comes at the expense of a highly complex experimental setup while requiring precise a priori knowledge of the photophysical properties of each fluorophore as well as high photon-count rates that are incompatible with single-molecule and live-cell imaging (15). Hyperspectral imaging is another method that overcomes the challenge of spectral overlap by spectrally dispersing the fluorescence signal that is sent to a charge-coupled device camera or multichannel detector (18, 19). Linear unmixing algorithms are then used to retrieve the fluorescence contribution of each fluorophore to a given spatial position on the image (19, 20). Because the full spectra are recorded at each point of the image, this method requires long integration times, although individual multicolor images of six different targets have been recently recorded below 10 s, either under confocal or lattice light sheet illumination (21).

Within the field of fluorescence-based biosensing and DNA sequencing, several strategies have been also developed to extend the number of different targets that can be detected in a cost-efficient manner (22, 23, 24, 25). From these methods, frequency-encoded multiplexed excitation with color-blind detection has been developed and successfully applied for detection of multiple targets, each target labeled with an individual fluorophore (22, 23, 24). In this implementation, different excitation lasers are modulated at distinct frequencies, exciting the fluorophores to varying degrees according to their absorption cross section at each given excitation wavelength (23, 24, 25). The total fluorescence emission is collected simultaneously on a single detector in a color-blind fashion, and it is then demodulated using Fourier analysis to retrieve the magnitude of the individual fluorophore signals. Besides the advantage of utilizing fewer optical components than standard detection systems, the method benefits from an increased signal/noise ratio because it avoids the use of spectral filters and instead relies on the inherent filtering during demodulation, as the frequency of interest can be isolated from other frequencies that might be present in the frequency domain. However, the discrimination sensitivity of the method requires spatial separation of the different color targets, which is achieved by means of capillary electrophoresis (22, 23). More recently, the concept of frequency-encoded multicolor excitation has been extended to fluorescence-lifetime confocal imaging, albeit incorporating multiple detectors (26). The methodology significantly improves fluorescence-lifetime spectral multiplexing capability and speed by modulating multiple laser lines using a fast frequency-sweeping Fourier transform interferometer (26). Nevertheless, it requires high laser stability and synchronization electronics as well as the use of multiple detectors, one for each of the spectral bands to be detected.

Here, we report on the implementation of frequency-encoded excitation multiplexing together with color-blind detection for simultaneous multicolor scanning confocal imaging. In contrast to the earlier implementations of this approach for DNA sequencing and protein detection (22, 23), our method does not require spatial separation of the target molecules. This enables simultaneous multicolor cell imaging of spatially and spectrally overlapping targets. We demonstrate that our fully color-blind configuration provides excellent discrimination of different fluorescent targets with single-molecule detection sensitivity using integration times that are comparable to those used for one-color, single-molecule imaging. Addition of a second detector provides multidimensional single-molecule data in which spatial coordinates, intensity, polarization, and spectral discrimination are obtained in a single measurement. Finally, we describe a non-negative matrix-factorization-based spectral unmixing algorithm to extend the number of targets that can be discriminated in a single measurement. Using this approach, we demonstrate four-color imaging on fixed cells and determine the quantitative distributions of up to six spatially overlapping targeted organelles in fixed cells simultaneously using only four excitation sources.

Materials and Methods

Nanobeads and single-molecule sample preparation

Four colors of 20-nm-diameter nanobeads were purchased from Invitrogen (Carlsbad, CA): yellow-green (F8787), Nile red (F8784), crimson (F8782), and dark red (F8783). These stock solutions were combined to have a final concentration (0.25 nM per color) appropriate for confocal imaging. The final solution was mixed with a polyvinyl alcohol (PVA) solution to obtain a final PVA concentration of 1% v/v, and samples were prepared by spinning 50 μL of the nanosphere-PVA solution on a #1 (0.15 mm) cover glass at 6000 rotations per minute for 60 s.

For multicolor single-molecule imaging experiments, we used carbocyanine dyes purchased from Molecular Probes (Eugene, OR): 3,3'-Dioctadecyloxacarbocyanine (DiO) (excitation wavelength (λexc) = 488 nm), 1,1'-Dioctadecyl-3,3,3',3'-Tetramethylindocarbocyanine (DiI) (λexc = 561 nm), and 1,1'-Dioctadecyl-3,3,3',3'-Tetramethylindodicarbocyanine (DiD) (λexc = 640 nm). Stock solutions of these fluorophores were diluted and mixed to prepare a solution with a final concentration (0.3 nM per color) suitable for confocal imaging. The mixed solution was combined with a polymethylmethacrylate solution to a final concentration of 1% v/v polymethylmethacrylate, then spin-coated onto cover glasses using the same procedure as for the nanobead samples. All samples were stored in the dark and under ambient atmosphere until imaged.

Cell-imaging sample preparation

The following primary antibodies (final concentration; epitope/reference and supplier) were used: rabbit anti-Tom20 antibody to label mitochondria (0.4 μg/mL; FL-145 from Santa Cruz, Dallas, TX) and mouse anti-HDAC-1 (histone deacetylase) to label the nucleus (1:6400; 10E2 from Cell Signaling, Danvers, MA). Fluorescent probes Lysotracker Red DND-99, Alexa Fluor 660 phalloidin, and BODIPY 500/510 C₁, C₁₂ (4,4-difluoro-5-methyl-4-bora-3a,4a-diaza-s-indacene-3-dodecanoic acid) were obtained from Thermo Fisher Scientific (Waltham, MA). Oleic acid (O1383) and fatty-acid-free bovine serum albumin (BSA) (A8806) were obtained from Sigma-Aldrich (St. Louis, MO). Secondary antibody Alexa Fluor 647 donkey anti-mouse was obtained from Invitrogen, whereas Alexa Fluor 532 donkey anti-rabbit and Cy3/Alexa Fluor 647 donkey anti-mouse were labeled in house. All secondary antibodies were used at 2 μg/mL final concentrations. The in-house labeling reaction was performed by incubating a mixture containing the secondary antibody (from Jackson ImmunoResearch, West Grove, PA), NaHCO₃, and the dyes as N-hydroxysuccinimide-ester derivatives (Alexa Fluor 532/647 carboxylic acid succinimidyl ester, purchased from Invitrogen; Cy3 monoreactive dye pack, purchased from GE HealthCare, Chicago, IL) for 40 min at room temperature diluted in dimethyl sulfoxide. Finally, purification of labeled antibodies was performed using NAP5 Columns (GE HealthCare). The ratio of dyes per antibody was measured to be 1 for Alexa Fluor 532 and Alexa Fluor 647-labeled antibodies and 3.4 and 0.8 for Cy3 and Alexa Fluor 647, respectively, in the doubly labeled antibody.

HeLa cells stably expressing the targeting motif of the Golgi-complex-resident enzyme mannosidase II fused to enhanced green fluorescent protein (eGFP) (HeLa-MannII-GFP) were provided by V. Malhotra (Centre for Genomic Regulation, Barcelona, Spain) and described previously (27, 28). HeLa-MannII-GFP cells were cultured in complete medium (Dulbecco’s modified Eagle’s medium (Gibco, Gaithersburg, MD) containing 10% fetal bovine serum (Gibco)) in a humidified incubator at 37°C and 5% CO₂. HeLa-MannII-GFP cells were seeded on a 35-mm glass-bottomed dish with 20-mm microwell #1 cover (Cellvis, Mountain View, CA) 24 h before fixation. To induce lipid droplet formation, HeLa-MannII-GFP cells were incubated in complete medium containing 400 μM oleic acid (complexed with 0.3% BSA) for 4 h in a humidified incubator. These cells were routinely tested for mycoplasma contamination.

Oleic-acid-treated HeLa-MannII-GFP cells were washed four times with complete medium and incubated with 0.2 μg/mL of BODIPY 500/510 in complete medium for 10 min, after which the cells were washed four times and incubated with 100 nM Lysotracker Red DND-99 in complete medium for 30 min. The cells were then sequentially fixed with 4% paraformaldehyde in phosphate-buffered saline (PBS) for 15 min at room temperature, permeabilized with 0.2% Triton X-100 in PBS for 15 min, and blocked in 4% BSA in PBS for 30 min before immunostaining. For immunostaining, blocked cells were incubated for 1 h at room temperature with primary antibodies against HDAC-1 (to label the nucleus) and Tom20 (to label mitochondria) diluted in 1% BSA in PBS. Anti-rabbit Alexa 532 (for Tom20) and anti-mouse Alexa 647 or anti-mouse Cy3/Alexa 647 secondary antibodies (for HDAC-1) were diluted in 1% BSA in PBS, and cells were incubated with this solution for 1 h at room temperature covered from light. Actin staining was performed by incubating cells with 1 unit/mL of Alexa Fluor 660 phalloidin for 20 min. The cells were finally washed and kept in PBS.

Implementation of the multicolor confocal setup

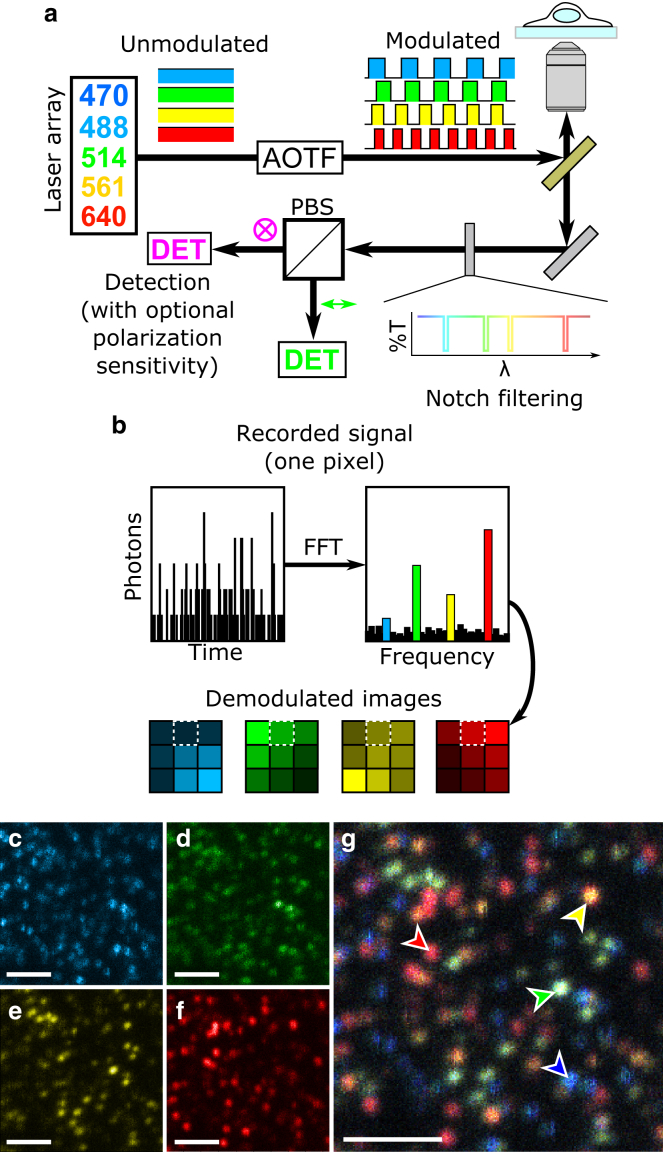
A detailed schematic of the experimental setup is shown in Fig. S1. To provide maximal flexibility for multicolor experiments, we constructed an array of lasers spanning the visible spectrum: 2-ps pulsed lasers at 470 and 640 nm operated in continuous wave mode (LDH-D-C-470 and LDH-D-C-640, respectively; Picoquant, Berlin, Germany); a multiline argon-krypton laser (Model 3060; Spectra-Physics, Santa Clara, CA); and a continuous-wave diode-pumped solid-state laser at 561 nm (ventus 561; Laser Quantum, Stockport, United Kingdom). The outputs of these lasers are combined on appropriate dichroic mirrors and launched collinearly into an acousto-optic tunable filter (AOTF) (AOTFnC-Vis-TN; AA Optoelectronics, Orsay, France). The AOTF driver (MDS4C-B66-22-80.153; AA Optoelectronics) has four independent channels, each containing a direct digital synthesizer feeding an analog amplifier that can be used to select a laser wavelength and control its diffracted power over 30 dB of dynamic range. Both of these parameters are controlled via a proprietary software interface on a host computer and sent to the AOTF driver via a universal serial bus connection. Intensity modulation of each channel is achieved via high-speed digital blanking inputs, which are driven separately by a LabVIEW-controlled data-acquisition card (PCI-6602; National Instruments, Austin, TX) using custom software. We typically operate the AOTF at modulation frequencies between 10 and 20 kHz.

The AOTF requires linearly polarized input beams, and the first diffracted order of the output is likewise linearly polarized. We use an achromatic quarter-wave plate (AQWP05M-600; Thorlabs, Newton, NJ) to generate circularly polarized light that is directed toward the microscope (Axiovert 135TV; Zeiss, Jena, Germany), reflected by a dual-band dichroic mirror (FF500/646-Di01-25x36; Semrock, Rochester, NY), and focused onto the sample with a 60×, 1.45-NA (numerical aperture) oil-immersion objective (PLAPON 60XOTIRFM; Olympus, Tokyo, Japan). The sample is mounted on a three-axis translational piezo stage and is raster-scanned to produce an image.

Fluorescence generated by the sample is collected by the focusing objective, spatially filtered through a 30-μm confocal pinhole, and directed through a set of narrow-band notch filters that are specifically selected for the wavelengths used in each experiment. After the excitation light is rejected by the notch filters, the remaining fluorescence is focused onto a low-dark-count single-photon avalanche detector (SPAD) (SPCM-AQR-16; PerkinElmer, Waltham, MA). The SPAD is operated in photon-counting mode, wherein each detected photon generates a digital pulse on the SPAD output. These pulses are recorded by a digital data acquisition card (PCI-6602; National Instruments) in 10-μs bins for the duration of the pixel dwell time, typically on the order of a few milliseconds. The time-resolved photon stream is demodulated in custom software (LabVIEW 2011; National Instruments) on a pixel-by-pixel basis, and the amplitudes of the signals at each modulation frequency are demultiplexed and plotted in real time. The fast Fourier transform (FFT) yields symmetric signals at positive and negative frequencies, so we record the doubled amplitude at each positive frequency as an effective photon count rate. The results that are saved by the acquisition software include one image per modulator. The demodulation is not phase sensitive, and so only the modulation frequencies are needed; the actual modulation waveforms do not need to be measured by the demodulation routine. The indirect synchronization between these two systems greatly simplifies the acquisition hardware and software. In our system, both the modulation software and demodulation/scanning software operate on the same LabVIEW-equipped computer and communicate the modulation frequencies via global variables, but the demodulation software is blind to the modulation waveforms.

Image processing and data analysis

Single-molecule intensity and degree-of-linear-polarization (DOLP) analysis was performed using a custom-written routine in MATLAB (The MathWorks, Natick, MA). Histograms shown in Fig. 3, f–h were obtained by measuring the average number of counts of each individual fluorescent spot (background subtracted). The DOLP histograms shown in Fig. 4, f–h were obtained for each fluorescent spot using the relation

$$\mathit{\Delta }P=\frac{I_V-I_H}{I_V+I_H},$$ (1)

where I_V and I_H correspond to the average number of photon counts per spot detected on the vertical and horizontal SPAD detectors, respectively.

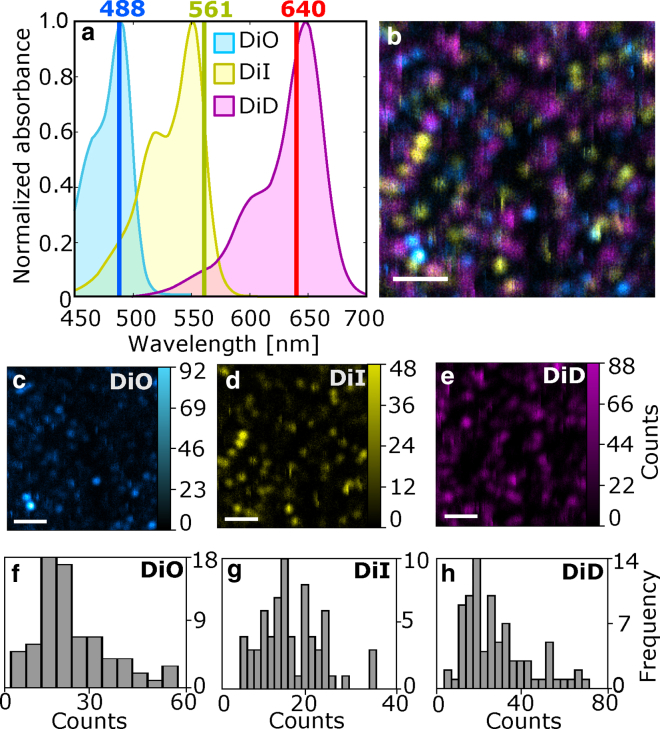
Figure 3.

(a) Absorption spectra of the different carbocyanine dyes used for three-color single-molecule imaging. The vertical lines indicate the different excitation wavelengths. (b) A composite overlay of the three individual channels to render the multicolor single-molecule image is shown. Arrows highlight discrete photobleaching events on three spectrally different molecules. (c–e) Individual channels for DiO (c), DiI (d), and DiD (e) are shown. Intensity scales correspond to the number of photons detected within 5-ms pixel integration time. Scale bars, 2 μm. (f–h) Histograms of the average counts/pixel measured for the individual molecules shown in (c)–(e), respectively, are displayed. To see this figure in color, go online.

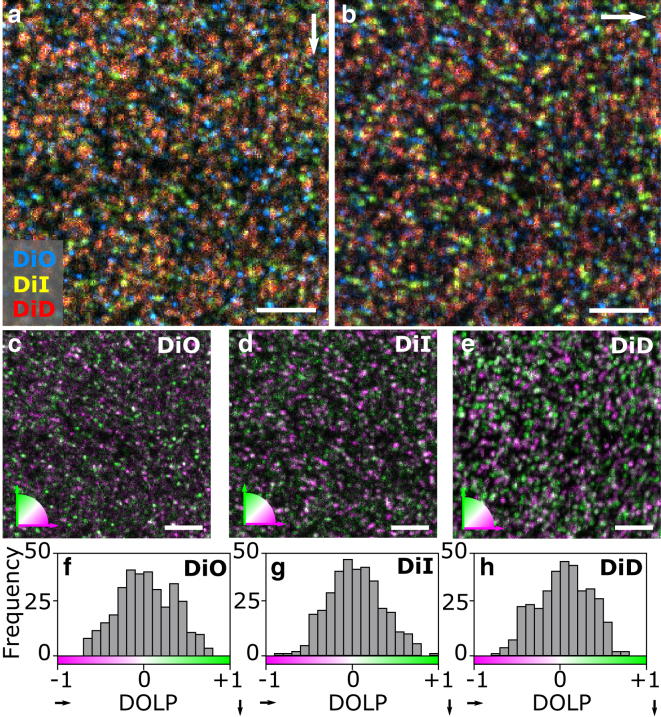
Figure 4.

(a and b) Three-color, polarization-resolved single-molecule images for vertical (a) and horizontal (b) detection SPADs. The colors in the images correspond to the different Di molecules used in the experiments. (c–e) Polarization-resolved images of DiO (c), DiI (d), and DiD (e) molecules, pseudo-color-coded according to the in-plane orientation of the emission dipole, are shown, with green being vertical and magenta horizontal in the images. Molecules oriented at ±45° appear white. Images recorded simultaneously at 488, 561, and 640 nm with a 2-ms pixel dwell time. Scale bars, 5 μm. (f–h) Respective DOLP histograms for each of the three colors are shown. To see this figure in color, go online.

Data processing of the confocal images shown in Figs. 5 and 6 was performed primarily in custom-written Python software with a graphic interface (29, 30, 31). Within this software, the user is able to plot the raw data in various forms, including integrated intensity per pixel, the intensities of the individual color channels, and a false-color overlay of all spectral channels. The spectral unmixing routine can be accessed through menus.

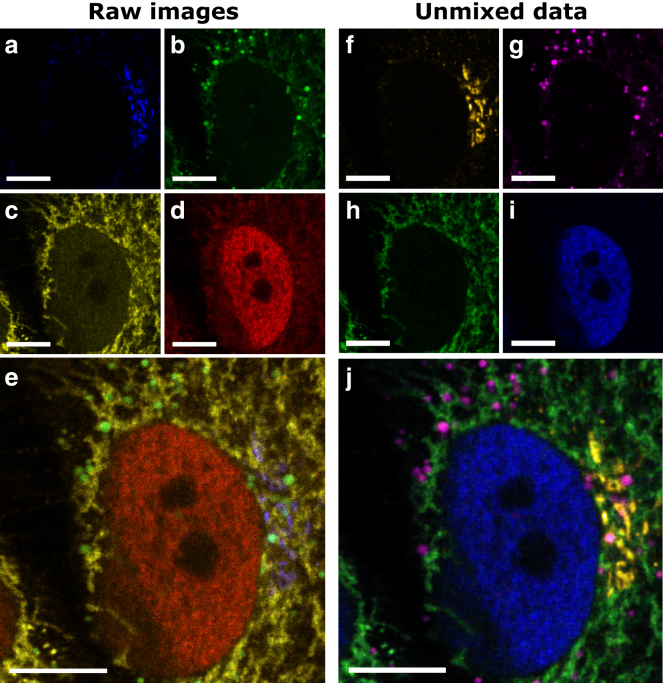
Figure 5.

(a–e) Representative excitation-wavelength demodulated raw confocal images of a HeLa cell with Golgi complex labeled with eGFP, lipid droplets labeled with BODIPY 500/510, mitochondria labeled with Alexa 532, and nucleus labeled with Alexa 647, excited at 470 nm (a), 514 nm (b), 561 nm (c), and 640 nm (d). The brightest pixels in each image contain 161, 171, 97, and 55 photons, respectively, recorded with a 1-ms pixel dwell time. (e) A composite overlay of (a)–(d) is shown. (f–i) Spectrally unmixed images obtained via a modified NMF show the quantitative distributions of the Golgi complex (f), lipid droplets (g), mitochondria (h), and nucleus (i). (j) A composite overlay of (f)–(i) is shown. To see this figure in color, go online.

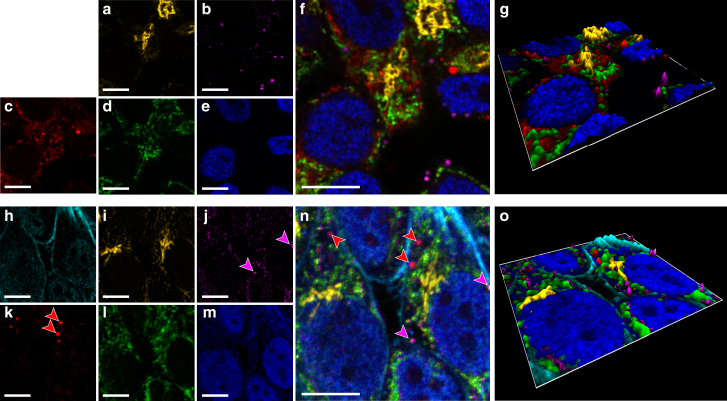
Figure 6.

Simultaneous multicolor excitation-multiplexed microscopy of up to six different cellular structures in HeLa cells using four excitation lasers at 470, 514, 561, and 640 nm. (a–g) Spectrally unmixed data from a five-color sample are shown, with Golgi complex (a), lipid droplets (b), lysosomes (c), mitochondria (d), and nucleus (e), with composite overlay (f) and volumetric (g) images. (h–o) Spectrally unmixed data from a six-color sample, adding actin (h) to the existing components, are shown: Golgi complex (i), lipid droplets (j), lysosomes (k), mitochondria (l), and nucleus (m), with composite overlay (n) and volumetric (o) images. The magenta and red arrows in (j), (k), and (n) identify distinct lipid droplets and lysosomes, respectively. Scale bars, 10 μm. All images were acquired with 1-ms pixel dwell times, covering 512 × 512 pixels. To see this figure in color, go online.

The raw demodulated images are preprocessed with a narrow band-stop filter, a shot-noise-background subtraction, and a one-pixel-radius Gaussian mean filter to reduce noise. Spectral unmixing analysis was performed via a non-negative matrix factorization (NMF) (32, 33, 34, 35). The three-dimensional data set S_l(x, y, λ) is flattened into a two-dimensional m × n matrix S, which contains m samples (pixels) and n features (lasers). The NMF iteratively attempts to find two matrices W (m × p) and H (p × n), where p is the number of components (fluorophores), such that the matrix product $\mathit{WH}\cong \mathit{S}$. Although NMF implementations generally attempt to reduce the dimensionality of the problem by choosing p < min(m, n), we have found that by slightly modifying the minimization strategy and selecting p > n, we can effectively unmix an underdetermined data set.

The NMF implementation that we use is based heavily on the Python scikit-learn nmf package (36). We have modified the nmf to minimize the objective function

$${\Vert \mathit{S}-\mathit{WH}\Vert }_2^2+{\alpha }_{L1,W}\Vert \mathit{W}\Vert +{\alpha }_{L1,H}\Vert \mathit{H}\Vert +{\alpha }_{L2,W}{\Vert \mathit{W}\Vert }_2^2+{\alpha }_{L2,H}{\Vert \mathit{H}\Vert }_2^2$$ (2)

via a coordinate descent, where

$$\Vert \mathit{A}\Vert ={\sum }_{\mathit{i,j}}\left|A_{ij}\right|$$ (3)

is the L1-norm and

$${\Vert \mathit{A}\Vert }_2^2=\frac{1}{2}{\sum }_{\mathit{i,j}}{A}_{ij}^2$$ (4)

is the Frobenius norm. The first term in the objective function represents the error of the total matrix product, whereas the other four terms consist of regularization terms that influence the degree of sparseness in the resulting spectral and spatial matrices. The regularization coefficients α_N,M are free parameters that are used to optimize the behavior of the NMF algorithm, and no set of coefficients exists that is universally valid. We have empirically determined that values of α_L1,W = 0.002, α_L1,H = 0.001, α_L2,W = 1.0, and α_L2,H = 0.002 are sufficient to unmix the overwhelming majority of our data sets. Small modifications of up to a factor of two may be required to optimize the unmixing for the underdetermined data sets.

Validation of the unmixed data sets was performed as follows. First, we performed normalized cross correlations of each pair of unmixed spatial matrices to reveal whether there was significant overlap between the individual components (these values are also calculated by the unmixing software). In the case of the four-target sample in which the number of fluorophores is equal to the number of lasers (i.e., determined data set), the cross-correlation values resulted close to zero, indicating successful unmixing. For the undetermined data set (i.e., for the five- and six-target samples with four excitation lasers), the cross-correlation values in some of the pairs of spatial matrices were larger than zero. High cross-correlation values, close to 1, indicated that the unmixing had erroneously combined multiple different organelles into a pair of components, which could be visually verified. Therefore, we implemented in the software the possibility of setting a threshold based on the cross correlation. This threshold value depends on the degree of spatial and spectral overlap between the different labeled structures. In the most favorable scenario, in which there is no spatial overlap between the different targets, the cross-correlation values are close to zero, and therefore a low threshold can be used. However, in conditions of severe spatial and spectral overlap (such as the ones shown in Figs. 5 and 6), the threshold value can be increased to tolerate a certain degree of cross talk and accepting (or not) the results of the unmixing. Based on our images, we found that a threshold of 0.7 (on a scale of −1 to +1) would allow unmixing of six colors with an acceptable level of cross talk, i.e., identifying at least 60% of the signal in the correct channel. Second, we visually compared the results of the unmixing algorithm to those of the composite overlay images of the raw data from which the distributions of each organelle were estimated. If both visual inspection and cross correlations were satisfactory, the unmixing was judged to be successful.

Figs. 5 and 6 in the text were further processed in ImageJ to improve contrast by adjusting only the threshold for maximal pixel value. The low-intensity threshold was not adjusted so that image intensities are scaled linearly without artificially suppressing background features and noise in the data.

Results and Discussion

Frequency-encoded multiplexed wavelength excitation scheme with color-blind detection

In contrast to standard fluorescence detection, in which color discrimination is achieved based on spectral filtering of the emitted fluorescence, our method exclusively relies on the absorption properties of the fluorophores. Indeed, we take advantage of the fact that fluorescence emission is directly proportional to the absorption cross section of the fluorophore at a given excitation wavelength and to the local excitation intensity. Thus, for our implementation, we encoded wavelength-dependent frequency modulations on the excitation path. The frequency modulations shift the spectroscopic wavelength axis into a frequency-domain measurement, eliminating the need to filter the corresponding fluorescence emissions, so that measurements can be performed in a color-blind fashion with the use of a single detector. The schematic of our excitation and detection configuration is shown in Fig. 1 a (detailed in Fig. S1). On the excitation side, the intensities of the excitation lasers are independently modulated at unique frequencies. We use an AOTF to modulate up to four lasers simultaneously. The AOTF can provide intensity modulation frequencies from direct current to ∼200 kHz to each channel with 100% modulation depth, limited by beam size and the acoustic propagation speed within the AOTF crystal. The choice and range of the modulation frequencies depend on the experimental conditions and can be selected by the AOTF. For the experiments described here aiming at single-molecule detection sensitivity, the image acquisition time is ultimately limited by the photon-emission rate of individual molecules. To minimize photobleaching, one commonly uses low excitation powers, which concomitantly require long integration times (i.e., milliseconds). Therefore, we typically operate at modulation frequencies between 10 and 19 kHz separated by at least 2 kHz to resolve them individually in the frequency domain without significant cross talk. These frequencies are lower than the data-acquisition rate (100 kHz) and higher than the pixel-update rate (between 500 and 1000 Hz, required for single-molecule imaging). For applications for which single-molecule detection sensitivity is not a requirement, much higher modulation frequencies can be used—up to 200 kHz—essentially limited by the AOTF, such that much faster imaging rates can be readily obtained.

Figure 1.

(a) Schematics of the frequency-encoded multicolor confocal fluorescence setup with color-blind detection. Up to four modulated wavelengths excite the sample at a time using an AOTF. Fluorescence generated by the sample is collected by the same microscope objective as used for excitation and relayed directly to the detector through a set of notch filters. An optional polarizing beam splitter and second detector can be placed on the detection side to enable polarization sensitive measurements. (b) The fluorescence incident on the detector is converted into a digital data stream, and an FFT is performed on a pixel-by-pixel basis to convert the photon data stream into the frequency domain, where the amplitudes of the signal at each modulation frequency are measured and plotted as pixel intensities in individual images for each excitation source. (c–g) Representative demodulated confocal images of a sample containing four colors of spectrally overlapping fluorescent nanospheres are shown (absorption spectra shown in Fig. S2), recorded at (c) 470 nm, (d) 514 nm, (e) 561 nm, and (f) 640 nm. (g) A composite overlay of the individual images is shown, with arrows highlighting individual nanospheres of each color. Images were acquired simultaneously with a 2-ms pixel dwell time, maximal values of 72, 60, 119, and 108 photons in a pixel, respectively. Scale bars, 2 μm. To see this figure in color, go online.

The collinear modulated laser beams are launched into a standard scanning confocal microscope and focused to a diffraction-limited spot using a 1.45-NA oil-immersion objective. Fluorophores within the illuminated region will radiate light proportionally to the product of the local excitation intensity and their absorption cross sections at each excitation wavelength. The fluorescence generated by the sample is collected by the same objective, spatially filtered through a 30-μm confocal pinhole, and directed through a set of notch filters chosen specifically to reject the excitation wavelengths; no further spectral filtering was performed, yielding absolute maximal signal throughput to the detector. The fluorescence is then directed toward a fast, sensitive detector. We used a low-noise SPAD to achieve single-molecule sensitivity with pixel-integration times on the order of a millisecond for confocal measurements. A polarizing beam-splitter cube can be installed to direct part of the fluorescence to a second SPAD detector, enabling polarization-resolved multicolor measurements with an arbitrary number of excitation wavelengths and fluorescent species at the single-molecule level with a single pair of detectors.

An FFT converts the digital time-resolved photon stream from the SPAD into an analog-frequency domain signal on a pixel-by-pixel basis. The frequency-domain amplitudes are demultiplexed and plotted in real time to generate excitation maps for each wavelength as the sample is raster-scanned across the excitation spot (Fig. 1 b). As the FFT yields symmetric signals at positive and negative frequencies, we record the doubled amplitude at each positive frequency as an effective photon-count rate. The phase component of the FFT is not important, and so we run this demodulation independently and asynchronously of the laser modulation, simplifying the experimental scheme considerably.

To validate our multicolor-excitation multiplexing technique, we first imaged a sample containing a spin-coated layer of 20-nm polymer beads, each bead labeled with one of four different fluorophores: yellow-green, Nile red, crimson, or dark red (individual absorption spectra shown in Fig. S2). The concentration of the nanobeads was adjusted so that they could be individually resolved by our diffraction-limited confocal microscope. The sample was simultaneously illuminated with four different frequency-modulated wavelengths of light. A single imaging measurement (2-ms pixel dwell time) was performed using one SPAD. Each demodulated excitation channel is independently displayed in Fig. 1, c–f. The resulting excitation images show significant cross-excitation between all four excitation wavelengths resulting from the absorption spectra overlap of the four fluorophores. Based on the spectral information contained in each demodulated excitation channel, the composite four-color image (Fig. 1 g) allows for clear qualitative distinction between the various species of nanobeads (highlighted by arrows).

Detection sensitivity and multicolor performance

To determine the sensitivity limits amid signal/noise ratios, we first employed Monte Carlo simulations across a variety of experimental parameters, including modulation frequencies, pixel dwell times, and photon-count expectation values. Known parameters, such as detector dark counts, were fixed in advance. For each set of parameters, we performed 1000 independent simulations corresponding to the equivalent of 1000 pixels in an image with identical fluorophore concentrations.

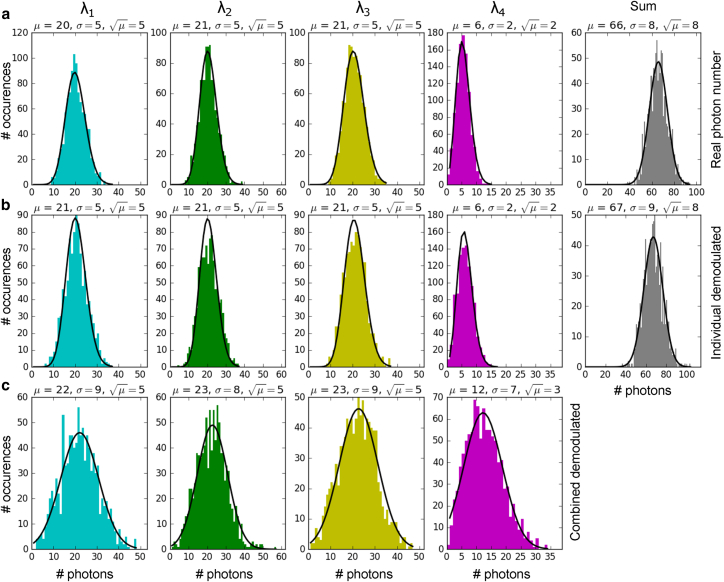
In the first step of the simulations, we generated a photon data stream for each color having a mean expectation value μ and standard deviation σ according to Poisson statistics. These data were individually multiplied by square-wave modulations at four unique frequencies (10–19 kHz, representing our experimental conditions). The sum of photons detected for each run was histogrammed for each color and shown as an example in Fig. 2 a for one set of simulated conditions. The first four histograms represent each color (from left to right), whereas the rightmost histogram corresponds to the sum of all four colors. The parameters listed for each plot are the mean (μ), fitted standard deviation (σ), and predicted standard deviation (√μ) based on the mean photon number according to Poisson (for μ < 20) or Gaussian (for μ ≥ 20) statistics. The equivalence of the predicted and fitted standard deviations indicates that the simulations are shot-noise limited as expected, with no interaction between the various colors. Fig. 2 b shows the results after applying an FFT on each color of the raw data stream and extracting the amplitude of the signal at the modulation frequency assigned to that color. The strong agreement between the raw data (Fig. 2 a) and demodulated data (Fig. 2 b) indicates that the demodulation procedure by itself does not change either the signal or noise characteristics of the measurement.

Figure 2.

Simulations of signal and noise at the shot-noise detection threshold. (a) The real photon number simulated at each excitation wavelength (λ₁–λ₄, from left to right) and total number of photons (sum, rightmost plot) are shown. This particular simulation considers around 20 photons/pixel for excitations at λ₁–λ₃ and 6 photons at λ₄. (b) Individual demodulated data after applying FFT for the different excitation wavelengths and total number of photons are shown. (c) Combined demodulated data for the different excitation wavelengths are shown, containing all the raw photon data stream plus noise data stream. To see this figure in color, go online.

We further performed simulations in which all the raw individual photon data streams are summed with a “noise” data stream, converted in the frequency domain, and demultiplexed to yield the combined demodulated photon number per color (Fig. 2 c), which is equivalent to experimental data. In these conditions, the fitted standard deviation σ is always larger than the predicted standard deviation √μ. These σ-values come very close to those obtained for the summed of the raw (Fig. 2 a) and demodulated (Fig. 2 b) data, indicating that the dominant noise source in these measurements is shot noise generated by the entire photon stream. This has two major implications. First, the ability to resolve a signal is determined by the ratio of the amplitude of that signal to the shot noise of the ensemble measurement. Although this slightly decreases the signal/noise ratio as compared to individual detection (i.e., colors 1–3 in Fig. 2), our simulations indicate that ∼20 photons per color per pixel are sufficient to resolve multiple colors simultaneously. Using integration times/pixel between 2 to 5 ms, these values would correspond to 4–10 kcounts/s, which are characteristic in single-molecule-detection experiments (37, 38, 39), suggesting that our method should have the sensitivity for multicolor single-molecule imaging. Second, but most critically, a weak signal can be overwhelmed by the shot noise generated by a strong signal. This is illustrated in Fig. 2 for color 4, in which the signal in this channel is lower than the shot noise of the ensemble and thus cannot be reliably detected.

Acquisition of simultaneous multidimensional single-molecule confocal imaging

The simulations described above indicate that our method should have the required sensitivity to simultaneously detect and resolve multiple colors of single molecules. To demonstrate this capability, we prepared a sample containing three different lipophilic probes from the carbocyanine family (DiO, DiI, and DiD) with absorption spectra closely matching our laser wavelengths (Fig. 3 a). Fluorescence detection was performed using a single SPAD detector with an imaging integration time of 5 ms/pixel. Individual molecules could be readily distinguished according to their excitation wavelength, exhibiting blinking and discrete photobleaching, both characteristics of single-molecule detection (Fig. 3, b–e). Although the frequency-multiplexing approach increases the overall shot noise per channel, the lack of additional band-pass filtering on the detection side effectively increases the total number of detected photons per channel. As a result, individual molecules in all three colors are easily discriminated above the background with counts rates between one and nine kcounts/s per molecule (Fig. 3, f–h), whereas the overall background is below 400 counts/s. Importantly, these images were obtained in a single measurement using similar integration times as those used for single-color, single-molecule confocal imaging (37, 38, 39).

As single molecules have discrete dipole moments, we further used a polarizing beam-splitter cube and a second SPAD in the detection arm of the setup to enable simultaneous polarization-resolved, multicolor single-molecule imaging. In this way, we distinguished individual molecules according to both their excitation wavelength and dipolar in-plane orientation (Fig. 4, a and b). Moreover, given the relatively low cross excitation of the different dyes, we could separate the three color channels with minimal misidentification and generate composite single-molecule images containing in-plane orientation information (Fig. 4, c–e). The high signal/background ratios obtained for the three color sets of individual molecules allowed us to calculate the DOLP for each molecule using Eq. 1. As expected from a random spatial distribution of molecules, the DOLP histograms for each color (Fig. 4, f–h) show the occurrence of all possible in-plane orientations with a peak at the center of each distribution, mainly resulting from polarization scrambling from the high NA objective and contribution from out-of-plane-oriented molecules (38, 39, 40). These results thus demonstrate the simultaneous acquisition of six different images containing multidimensional information—spatial, spectral, intensity, and polarization contrast—at the single-molecule level with modest count rates and acquisition times similar to single-color detection by using only two detectors.

Simultaneous multitarget confocal imaging on fixed cells and spectral unmixing

To further establish the utility of our multicolor multiplex-excitation and color-blind detection method for simultaneous multitarget cell imaging, we labeled different intracellular structures on fixed cells using fluorophores with overlapping absorption spectra (spectra provided in Fig. S3). We used a HeLa cell line stably expressing eGFP-MannII, a Golgi complex protein, and labeled lipid droplets, mitochondria, and the nucleus with BODIPY 500/510, Alexa 532, and Alexa 647, respectively. Cells were simultaneously illuminated with four lasers (470, 514, 561, and 640 nm) modulated at frequencies ranging from 10 to 19 kHz and imaged in confocal mode. As anticipated, the raw excitation maps show substantial spectral cross talk between adjacent color channels, resulting from the large overlap in absorption spectra (Fig. 5, a–d, composite overlay in Fig. 5 e) so that only organelles that do not spatially overlap can be discerned.

To unequivocally determine the spectra and spatial distributions of the different fluorescent species from the demodulated raw images, we first performed excitation-based linear unmixing using a custom algorithm written in Python. For data that contain L lasers exciting F fluorophores, the (demodulated) fluorescence S_l generated by each laser at a given pixel can be represented by

$$S_l\left(x,y,\lambda \right)=\sum _{f=1}^F{\alpha }_{lf}\left(\lambda \right)I_l\left(x,y,\lambda \right)C_f\left(x,y\right),$$ (5)

where α_lf is the excitation cross-section of fluorophore f by laser l, I_l is the local intensity of laser l, and C_f is the local concentration of dye f. The laser intensity term is written with a spatial dependence to account for variations in time. The terms α_lfI_l correspond to the effective excitation spectra of the individual fluorophores at a given pixel so that

$$\sum _{l=1}^L{\alpha }_{lf}{I}_l=1.$$ (6)

To assign the relative spectral contributions at each pixel without the need of prior reference excitation spectra of individual fluorophores, we further developed a user-friendly spectral unmixing algorithm that utilizes an NMF (31) (see Materials and Methods). In brief, this algorithm iteratively optimizes the spectral and spatial matrices H and W, respectively, whose matrix product WH yields the closest approximation to the recorded data set S. Crucially, in contrast to earlier spectral unmixing methods (36, 41), our NMF implementation can operate on underdetermined data sets, in which the number of fluorophores exceeds the number of independent excitation and detection channels.

Application of the NMF spectral unmixing algorithm to our raw demodulated data yielded clear distribution maps of each organelle (Fig. 5, f–i, composite overlay in Fig. 5 j) with intensities that are proportional to the concentration of the fluorophore at each pixel. Table 1 shows the resulting effective excitation spectra α_lfI_l as retrieved with the NMF unmixing algorithm for each of the targeted organelles, which can be compared to the absorption spectra of each fluorophore (Fig. S3). In the cases of the Golgi complex and the nucleus, their identification is unambiguous. The unmixing for the other two organelles, i.e., lipid droplets and mitochondria, is somewhat lower (above 50%) and results from differences between the intensity of one organelle with respect to the others (i.e., weak lipid droplet signal) or severe spatial overlap (i.e., mitochondria). Despite these constraints, the different α_lfI_l values per channel allow clear discrimination between the different organelles.

Table 1.

Normalized Effective Excitation Spectra Retrieved by the Unmixing Algorithm, i.e., α_lfI_l Components from Unmixing for the Four-Target Sample, at the Four Different Excitation Wavelengths

	470 nm	514 nm	561 nm	640 nm
Golgi	0.89	0.00	0.00	0.11
Lipid droplets	0.10	0.60	0.21	0.11
Mitochondria	0.10	0.18	0.53	0.20
Nucleus	0.05	0.03	0.12	0.81

The sums of the rows corresponding to each organelle may not exactly equal 1.0 due to rounding. Golgi complex was labeled with eGFP, lipid droplets labeled with BODIPY 500/510, mitochondria labeled with Alexa 532, and nucleus labeled with Alexa 647.

To further establish the performance of the technique, we used the four modulated lasers to image cells labeled with five different fluorophores. We added Lysotracker Red DND-99, a lysosome-specific reporter, to the existing set of labels shown in Fig. 5. These measurements constituted an underdetermined data set, which is mathematically and computationally difficult to unmix. Despite this challenge, our NMF algorithm determined the locations of all five organelles with very high fidelity even in regions where multiple organelles spatially overlap (Fig. 6, a–g). Finally, to extend the palette of colors and generate a six-target sample, we replaced the nuclear protein label by combinatorial labeling using two different fluorophores (4:1 stoichiometric ratio of Cy3 and Alexa 647) and additionally stained the actin cytoskeleton with Alexa 660 phalloidin. We used the same four wavelength excitation lasers so that each laser excited all the fluorophores to varying degrees. This data set represents a near-worst-case scenario: it is strongly underdetermined, containing two more fluorophores than excitation channels; signal levels across the sample and within each channel are highly variable; all of the fluorophores have overlapping excitation spectra; and the variations in sparsity among the labeled organelles are distinctly heterogeneous. Strikingly, the unmixing algorithm recovered the distributions of all six cellular structures with high reliability (Fig. 6, h–o).

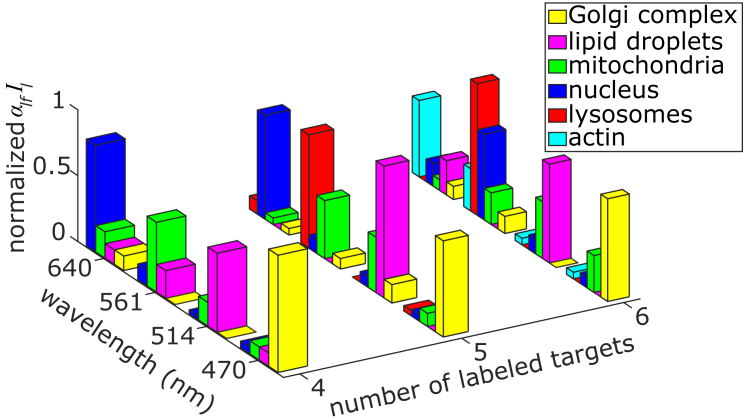
The effective excitation spectra α_lfI_l as retrieved with the NMF unmixing algorithm for each of the targeted organelles on the different images are summarized in Fig. 7 (absorption spectra of each fluorophore are given in Fig. S3 for each set of samples). For all the labeled organelles, the reliability to unequivocally identify distinct spatially overlapping organelles is above 60%, and it can reach up to 100% identification in the most favorable scenario of spatial separation. These values are remarkably high considering that our NMF unmixing algorithm makes no assumptions about the spatial location of the fluorophores, nor does it rely on prior excitation spectra for calibration. The main parameter affecting the identification of a given channel is the large intensity differences between a given organelle with respect to the others (as already discussed in the simulations shown in Fig. 2). This is, for instance, the case for the lipid droplet channel, which has a much lower intensity as compared to the mitochondrial channel (see the case of four and six labeled targets in Fig. 7). Obviously, this drawback is alleviated if the two signals are spatially separated, as it occurs in the case of the five labeled targets, in which identification of the lipid droplet channel is 100% (see also Fig. 6, b and d). Overall, these results thus demonstrate the capability of this method to resolve the distributions of up to six spectrally and spatially overlapping fluorophores in a single measurement by the use of four excitation wavelengths and only one color-blind detector.

Figure 7.

Normalized effective excitation spectra retrieved by the unmixing algorithm, i.e., α_lfI_l components from unmixing in Figs. 5 and 6, for the four-, five-, or six-color labeled samples, at the four different excitation wavelengths. The different organelles were labeled with the following dyes: Golgi complex labeled with eGFP, lipid droplets labeled with BODIPY 500/510, mitochondria labeled with Alexa 532, nucleus labeled with Alexa 647 (for the four- and five-target sample), and lysosomes labeled with Lysotracker Red DND-99. For the six-color labeled sample, the nucleus was labeled with a mixed Cy3/Alexa 647 (4:1), and actin was labeled with Alexa 660 phalloidin. The absorption spectra for all the different dyes and samples are summarized in Fig. S3. Note that the data for the four-color labeled sample corresponds to the same data shown in Table 1. To see this figure in color, go online.

Conclusions

We have presented a technology that enables the simultaneous acquisition of multicolor fluorescence images by encoding multiple excitation signals in the frequency domain and performing detection using a single color-blind detector. We demonstrate the sensitivity of the technique by detecting individual fluorescent molecules in multiple colors without compromising integration times or imaging contrast. Further implementation of an unmixing algorithm allowed us to readily discriminate multiple labeled organelles on fixed cells with high fidelity regardless of their spatial overlap. We have implemented our method on a confocal imaging system, but it can be easily extended to other fluorescent imaging configurations, including super-resolution single-molecule localization methods.

It is important to mention that our NMF unmixing algorithm does not require individual fluorophore emission spectra as input information or prior information on the spatial distribution of the labels. Moreover, the algorithm can operate on underdetermined data sets, in which the number of fluorophores exceeds the number of independent excitation and detection channels. These added performances constitute significant improvements over earlier NMF implementations for multicolor fluorescence applications (41). The degree of successful unmixing will ultimately depend on the intensity differences between the different labeled structures and their spatial overlap. We have demonstrated here unmixing of six spectrally and spatially overlapping colors above 60% using four wavelength excitations and nearly 100% unmixing in the case of signals that are spatially separated.

The general requirement for successful spectral unmixing, particularly in samples containing more targets than excitation lasers, is that the fluorophore excitation spectra are sufficiently distinct, i.e., the dyes can be differentially excited at each given wavelength (even if there is significant overlap in the absorption spectra). With samples containing up to four targets, we generally selected fluorophores that closely matched the excitation laser wavelengths, but in principle, any combination of fluorophores that are differentially excited by all of the laser wavelengths could be used. For instance, the four-color sample shown in Fig. 5 contains three overlapping blue-green fluorophores (see Fig. S3). Despite its similarity to BODIPY 500/510, the Alexa Fluor 532 could be marginally excited by the 561-nm laser and therefore be spectrally resolved. The challenge of selecting six fluorescent targets for imaging with four lasers was resolved by selecting four fluorophores with relatively narrow absorption spectra and peaks close to our excitation laser wavelengths (eGFP, Alexa 532, Lysotracker Red, and Alexa 647) and then adding two more targets (BODIPY 500/510 and Alexa 660) with broad excitation spectra that would label spatially distinct organelles. We empirically determined that Alexa 647 and Alexa 660 could not be readily unmixed despite being on spatially nonoverlapping organelles, and so we generated a dual-color secondary antibody containing both Cy3B and Alexa 647 to be a spectrally distinct target relative to Alexa 660. With this approach, we created a functional six-target labeling scheme, wherein organelles with broad absorption spectra (lipid droplets and the nucleus) would be spatially distinct from overlapping organelles with narrow absorption spectra, easing the unmixing process.

We note that our experimental configuration has been optimized for achieving single-molecule detection sensitivity, which necessarily requires long integration times. Therefore, we implemented our approach under a sample-scanned confocal microscope and ran the AOTF at relatively low frequency modulations (10–19 kHz). In applications in which there is a high labeling density and single-molecule detection sensitivity is not a requirement, the acquisition rate, and thus imaging speed, can be increased by using laser-scanning Galvano mirrors. In these conditions, the modulation frequencies could be increased up to 200 kHz by means of the AOTF or even higher by replacing the AOTF with individual acoustic optic modulators in each laser. This opens the door to simultaneous multicolor live-cell imaging.

The fundamental limit of sensitivity in a given channel is determined by noise, which in our measurements is shot noise. Although a small amount of shot noise becomes redistributed through the frequency domain, our simulations show that for all but the weakest signals, this excess noise is negligible. This minor drawback is largely compensated for by the color-blind detection scheme, in which the full stream of photons is detected without further filtering, which is a major advantage in the case of multicolor single-molecule applications for which photon budget becomes the bottleneck. As added value, our implementation is less technically complex than an equivalent time-domain microscope, which requires direct synchronization between the modulation and acquisition modules. With single-molecule sensitivity, inexpensive and widely available optical and electronic components, and direct applicability in multicolor live-cell imaging, we anticipate that this method will become a workhorse in microscopy labs.

Data and source code availability

Raw data and all of the software source code used to generate the results reported in this article are available upon reasonable request to the corresponding author.

Author Contributions

E.T.G. implemented the method and the NMF algorithm. M.S.-P. performed research. K.J.E.B. and F.C. contributed with sample preparation and cell labeling. E.T.G. and M.F.G.-P. designed the research. M.F.G.-P. wrote the manuscript.

Editor: Katharina Gaus.