A Spatially Explicit Model Shows How Titin Stiffness Modulates Muscle Mechanics and Energetics

Abstract

In striated muscle, the giant protein titin spans the entire length of a half-sarcomere and extends from the backbone of the thick filament, reversibly attaches to the thin filaments, and anchors to the dense protein network of the z-disk capping the end of the half-sarcomere. However, little is known about the relationship between the basic mechanical properties of titin and muscle contractility. Here, we build upon our previous multi-filament, spatially explicit computational model of the half-sarcomere by incorporating the nonlinear mechanics of titin filaments in the I-band. We vary parameters of the nonlinearity to understand the effects of titin stiffness on contraction dynamics and efficiency. We do so by simulating isometric contraction for a range of sarcomere lengths (SLs; 1.6–3.25 µm). Intermediate values of titin stiffness accurately reproduce the passive force–SL relation for skeletal muscle. The maximum force–SL relation is not affected by titin for SL≤2.5 µm. However, as titin stiffness increases, maximum force for the four thick filament system at SL = 3.0 µm significantly decreases from 103.2 ± 2 to 58.8 ± 1 pN. Additionally, by monitoring ATP consumption, we measure contraction efficiency as a function of titin stiffness. We find that at SL = 3.0 µm, efficiency significantly decreases from 13.9 ± 0.4 to 7.0 ± 0.3 pN/ATP when increasing titin stiffness, with little or no effect below 2.5 µm. Taken together, our results suggest that, despite an increase in the fraction of motors bound to actin along the descending limb when titin is stiffer, the force-generating capacity of the motors is reduced. These results suggest that titin stiffness has the potential to affect contractile efficiency.

Introduction

Across all animal taxa, striated muscles show markedly different properties that reflect a stunningly diverse array of functions, from the slow, energy-saving molluscan catch muscles (Kendrick-Jones et al. 1970), to exceedingly rapid stretch-activated asynchronous flight muscles (Hu et al. 2016), to vertebrate cardiac muscle regulating systemic blood supply on a beat-to-beat basis (Gordon et al. 2000). Many of the functional differences between various muscles types are associated with their cellular and subcellular ultrastructure, and the immense diversity of muscle geometry observed in biology presents exciting opportunities to relate basic biophysics of muscle to function (Hoyle 1983).

At the subcellular level, striated muscle contraction occurs through complex molecular interactions in dense, highly organized, repeating protein networks known as the sarcomere. The sarcomere is comprised of interdigitating thick (myosin) and thin (actin) myofilaments that are each decorated with various regulatory proteins. The giant protein titin is considered the third myofilament (Granzier and Labeit 2005), as it spans the entire length of the half-sarcomere (from the Z-disk to the M-line). The A-band region of titin interacts primarily with the myosin filament, whereas the I-band region reversibly interacts with the actin filament and acts as an elastic link between the myosin filament and the Z-disk. Consequently, the I-band region of titin is responsible for the majority of the passive mechanical properties of muscle (Granzier and Irving 1995).

However, the elasticity of the I-band region of titin varies from muscle to muscle, and can be modified in vivo to adjust the mechanical properties of the muscle. The I-band region of titin has multiple serially linked domains, each with unique elasticity (Linke and Granzier 1998; Linke et al. 1998), giving the whole filament complex and nonlinear mechanical properties. Additionally, different striated muscle types express different titin isoforms and therefore have different mechanical properties (Linke and Hamdani 2014). Human cardiac muscle, for example, expresses multiple titin isoforms, including a cardiac-specific isoform (the so-called N2B isoform), which has a molecular mass of ∼3 MDa (Linke and Hamdani 2014). This isoform is notably shorter (and therefore stiffer) than other isoforms expressed in human cardiac and skeletal muscle, which can be upward of ∼3.8 MDa, thereby contributing to the stiffer properties of cardiac muscle compared with skeletal muscle. Furthermore, various post-translational modifications of the I-band region of titin can affect its mechanical properties, such as calcium-mediated stiffening (Labeit et al. 2003) and phosphorylation of different spring elements in the I-band region [see Linke and Hamdani (2014) and references therein].

A current question in muscle physiology is: to what extent do the mechanical properties of titin influence the mechanics and energetics of active muscle contraction? This has been a central issue in a number of recent studies [Lindstedt and Nishikawa (2017) and references therein (Granzier and Labeit 2005; Prado et al. 2005; Tonino et al. 2017)]. Answering this question has remained elusive due to inherent difficulties of studying titin in situ. For one, it is difficult to discern titin-based contributions to the total sarcomere elasticity from other elastic elements within the sarcomere (e.g., cross-bridges, myosin binding protein C) or outside of the sarcomere (e.g., dystrophin, desmin). Secondly, modulating the stiffness of titin in situ is extremely difficult, and requires either precise control over post-translational modifications (e.g., PKA-mediated phosphorylation), or genetically engineered animal models with truncated or elongated titin isoforms that may display problematic secondary effects as a result of the mutated titin.

Early theoretical models of the sarcomere attempted to complement experimental analyses and uncover the effects of myofilament compliance on muscle contractility (Schoenberg et al. 1974; Ford et al. 1977). Historically, Huxley and Simmons (1971) used theoretical models to investigate the compliance of the contractile apparatus in relation to force generation and responses to rapid force transients (Ford et al. 1981, 1985), but did not consider titin as an elastic element in the sarcomere. Moreover, more recent computational models have shown that the kinetics and magnitude of muscle force generation depend on the mechanics of the myofilaments, cross-bridges, and the geometry of the myofilament lattice (Daniel et al. 1998; Chase et al. 2004; Tanner et al. 2007, 2008, 2012; Williams et al. 2010, 2013; Fenwick et al. 2017), which was unaccounted for in early mathematical models of the sarcomere.

Here we modify previously developed, spatially explicit, multi-filament computational models of the half-sarcomere (Williams et al. 2010, 2012, 2013), to incorporate the mechanical influence of titin (Powers and Williams 2018). Modeling titin as a nonlinear I-band spring, we are able to broadly investigate in silico the role titin stiffness in modulating the mechanics and energetics of contracting muscle.

Methods

Model description

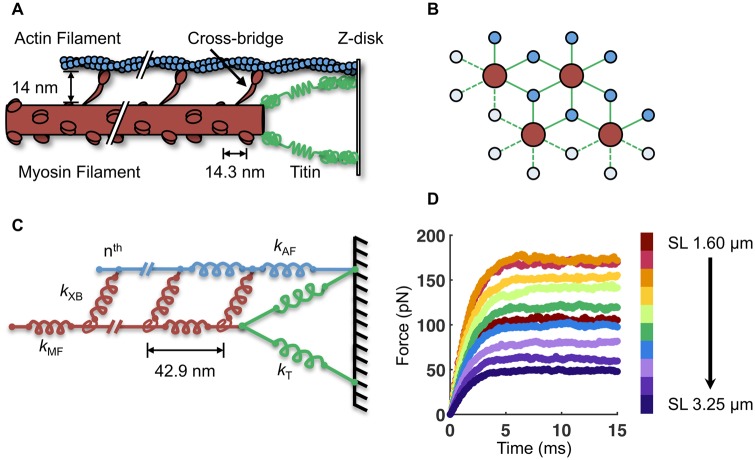
Many aspects of the computational model used in this work have been described previously (Williams et al. 2010, 2012, 2013). Briefly, the model consists of four myosin filaments and eight actin filaments arranged in a double-hexagonal lattice in three dimensions (Figs. 1A, B). Periodic (toroidal) boundary conditions were employed to simulate a semi-infinite lattice. Each cross-bridge is modeled as a two-spring system consisting of a torsional and a linear element (Williams et al. 2010). Myosin and actin filaments consist of linear springs serially linked between each node of cross-bridge crowns (Fig. 1C). The stiffness of the springs for the myosin and actin filaments is 2020 and 1743 pN/nm, respectively (Daniel et al. 1998), and the lattice spacing (i.e., radial face-to-face distance between the myosin and actin filaments) is set to 14 nm.

Fig. 1.

Description of the half-sarcomere model. A) A simplified schematic of the half-sarcomere, with the myosin filament in red, the actin filament in blue, and the I-band region of titin in green. B) The myosin and actin filaments are arranged in 3D with double-hexagonal symmetry. Four myosin and eight actin filaments are modeled with periodic boundary conditions to simulate a semi-infinite lattice. C) The half-sarcomere is modeled as an array of springs of different stiffness (k) for the myosin filament (MF), actin filament (AF), titin (T), and n cross-bridges (XB). Each myosin filament contains 60 crowns of three myosin motors (180 cross-bridges per myosin filament). D) By simulating 15 ms of isometric contraction, the steady-state force for each SL is measured. The average force of 50 independent runs with b = 7.5 μm⁻¹ is shown here.

The simulation is based on a three-state model for attachment, force generation, and detachment of cross-bridges (Daniel et al. 1998; Williams et al. 2013). These state transitions determine not only the local forces borne by each cross-bridge, they also determine the ATP utilization rate associated with the number of times each cross-bridge detaches from the thin filament and hydrolyzes a subsequent ATP for subsequent binding and force generation. Thus, the model provides predictions of both the mechanics and energetics of isometric contractions, and it is worth noting that all of the underlying mechanical, geometric, and kinetic parameters can readily be modified to simulate various muscle types with different cross-bridge kinetics.

We build upon our previous spatially explicit model (Williams et al. 2013) by including nonlinear springs in the I-band to model titin. Six titin springs are added to each of the four myosin filaments, each of which span the length of the I-band and anchor to the Z-line at the actin filament-Z-line junction. Thus, each titin spring makes an angle, θ, with the myosin filament that is equal to the arctangent of the ratio of the filament lattice spacing (radial myosin-to-actin filament distance) and the length of the I-band.

Similar to other models (Campbell 2009; Campbell et al. 2011), the total force exerted by each titin spring (F_T) is modeled as an exponential dependence on length change of titin (ΔL):

$$F_{\mathrm{T}}=a·{\mathrm{e}}^{(b·\Delta L)}.$$ (1)

where a and b are tunable parameters. For the “no titin” case, a was set to 0 pN, whereas for all other cases, a was arbitrarily fixed at 260 pN. The parameter b was varied across a range of 4–10 µm⁻¹. Using this value of a and range of b resulted in passive force–SL relations that span the range of published estimates for single titin molecules (Linke et al. 1998). The axial and radial components of F_T were taken as F_T·cos(θ) and F_T·sin(θ), respectively.

Simulation details

With the above geometric and mechanical properties established, the two key parameters we explore in this model are the influence of both sarcomere length (SL) and the titin stiffness parameter b. Each simulation trajectory represents a 15 ms isometric contraction (simulated time with 0.1 ms time-steps), which was sufficient time for isometric force to reach a steady state (Fig. 1D). For all parameter specifications, we average 50 independent trials.

As in previous iterations of the model (Williams et al. 2013), which followed from a long history of spatially explicit models of the sarcomere, beginning with Daniel et al. (1998), the simulation is initiated by defining a SL, lattice spacing, and titin stiffness, none of which change during contraction. As there is not any thin filament regulation in the current model (we do not consider Ca²⁺ regulation such as has been done by Tanner et al. 2012), the thin filament is completely activated upon initiation of the simulation. A stochastic perturbation is then given to the myosin motor positions and their state transition (i.e., unbound, weakly bound, or strongly bound) is then determined using Monte Carlo methods. After each time-step, we use an iterative optimization method to balance axial forces at all internal nodes (dots on the lattice proteins in Fig. 1C) of the spring system comprising the myofilaments (using an improvement over the optimization method in Williams et al. 2013) such that the net force is only experienced at the M-line of each myosin filament. [See the Supplementary Material in Williams et al. (2013) for more details.]

Results

We investigated a range of SLs from 1.5 µm to 3.25 µm for three different values of titin stiffness, and one case without titin. For the “no titin” case, the force of titin (F_T) was set to zero [by setting a = 0 in Equation (1)]. For all other cases, a was set to 260 pN, and b was set to 4, 7.5, or 10 µm⁻¹. The relationship between predicted passive force and SL (Fig. 2A) shows that increasing values of b result in stiffer titin and therefore steeper passive force–SL relations (the force for the “no titin” case is necessarily 0 at all SL values; see also Supplementary Fig. S1 in the supplement for the full range of passive tension values for b = 7.5 µm⁻¹ and 10 µm⁻¹.) The passive force–SL relation for b = 4 µm⁻¹ is in good quantitative agreement with previously published experimental data on isolated skeletal muscle myofibrils from rat psoas (Linke et al. 1998), shown in Supplementary Fig. S2 in the Supplementary Material.

Fig. 2.

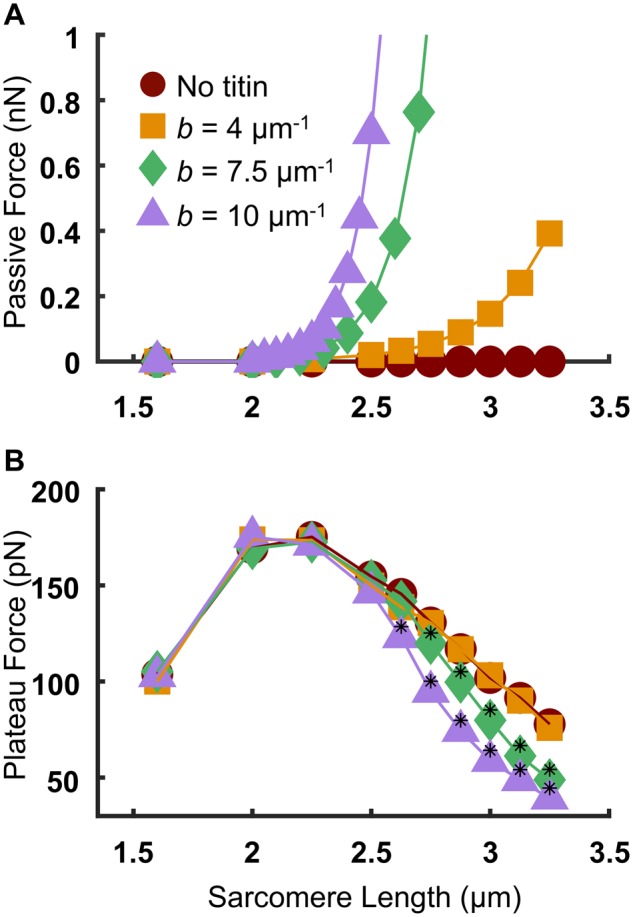
Effects of titin stiffness on the passive and active force–SL relations. A) Passive force–SL relation (average of 50 independent runs). B) Active force–SL relation (with the passive component subtracted). Black asterisks indicate a statistically significant difference from both the “no titin” case and the b = 4 μm⁻¹ case (P < 0.05 using a one-way ANOVA with a Tukey’s post hoc test of significance).

We then investigated the effects of titin stiffness on the active force–SL relation by simulating isometric contraction and subtracting the passive force values from the steady-state force for each condition (Fig. 2B). The force–SL relation for the “no titin” condition (filled red circles) is nearly superimposed with the b = 4 µm⁻¹ condition. However, for the b = 7.5 µm⁻¹ and 10 µm⁻¹ conditions (filled green diamonds and purple triangles, respectively), the descending limb of the active force–SL relation is significantly and progressively reduced compared with the “no titin” and b = 4 µm⁻¹ cases. Since the descending limb of the force–SL relation of the “no titin” depends only on the extent of myofilament overlap (Gordon et al. 1966), the similarity of the active force–SL relation between the “no titin” case and the b = 4 µm⁻¹ case (Fig. 2B) suggests minimal effects of compliant realignment of binding sites upon introducing moderately stiff titin into the system.

To better understand the cause for the reduction of steady-state force along the descending limb with increasing titin stiffness, we investigated the effects of titin stiffness on the force-generating capacity of the cross-bridges. ATP utilization rates of the half-sarcomere were calculated by monitoring the number of times any one cross-bridge in the system underwent a transition from a strongly bound state to an unbound state. This was monitored for each cross-bridge and summed over all cross-bridges in the half-sarcomere, for 5 ms of simulation time during the plateau region of isometric tetanic force, and averaged from 50 independent trajectories for each condition (SL and titin stiffness). Figure 3A shows that the SL-dependence of ATP utilization rate is nearly identical for the “no titin” case (red circles) and the b = 4 µm⁻¹ case (orange squares). However, for very stiff titin (b = 7.5 and 10 µm⁻¹), the ATP utilization rate during the plateau of isometric tetanus is significantly increased compared with the “no titin” case for SL > 2.7 µm. Despite these changes in ATP consumption, we did not observe any significant SL-dependent or titin-dependent changes in the rate of force development (Supplementary Fig. S3).

Fig. 3.

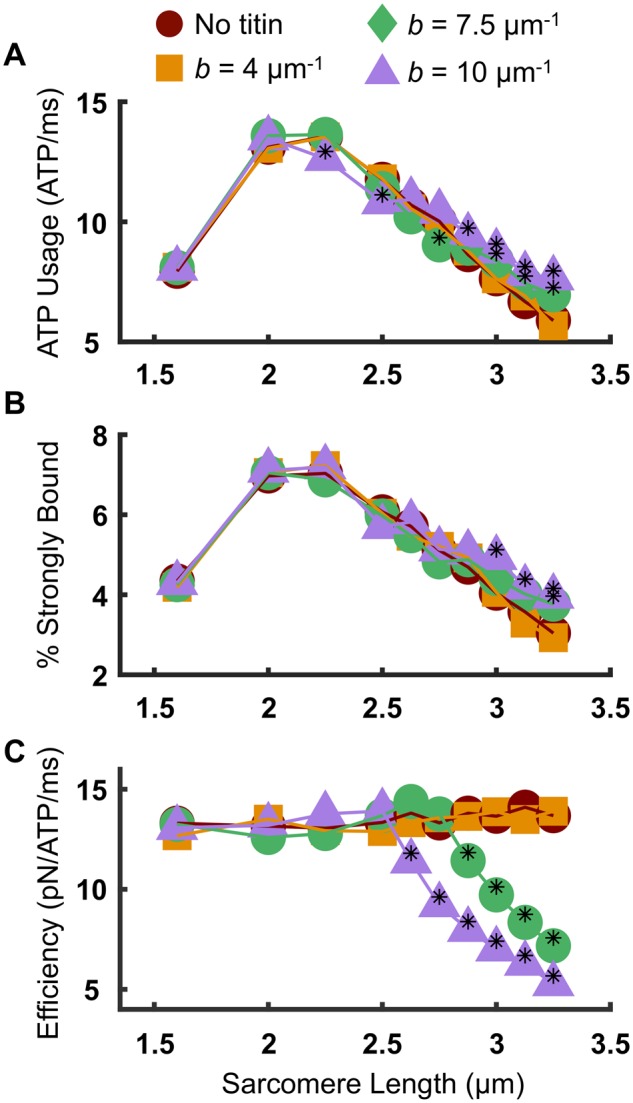
Effects of titin stiffness on cross-bridge mechanics and energetics. A) ATP usage was quantified by monitoring the number of transitions of each cross-bridge from a strongly bound state to an unbound state. Values reported here reflect the average of the entire cross-bridge ensemble during the plateau of isometric contraction. Stiff titin increases the amount of ATP at long SL compared with the “no titin” case. B) Stiff titin does not affect the % of cross-bridges in the strongly bound state at the plateau of force generation, until SL=3 μm, at which point there are significantly more motors bound for b = 10 μm⁻¹ compared with the “no titin” case and the b = 4 μm⁻¹ case. C) Despite the increase in strongly bound crossbridges, there is a significant reduction in contraction efficiency as measured by the force per ATP during a period of the plateau of isometric contraction. Black asterisks indicate a statistically significant difference from both the “no titin” case and the b = 4 μm⁻¹ case (P < 0.05 using a one-way ANOVA with a Tukey’s post hoc test of significance).

Importantly, the fraction of strongly bound cross-bridges for the same 5 ms of the plateau region of contraction is not different when comparing the “no titin” case to the b = 4 and 7.5 µm⁻¹ case over the SL range (Fig. 3B). However, for b = 10 µm⁻¹ and SL ≥ 3.0 µm, there are significantly more motors in the strongly bound state compared to the “no titin” and the b = 4 µm⁻¹ cases. This result was somewhat surprising given the significantly reduced force along the descending limb of the active force–SL relation for the b = 10 µm⁻¹ case (Fig. 2B). We attribute this to potentially two factors: (i) titin-induced myosin filament strain bringing more motors overlapped with the actin filament at long SL in the stiff titin case compared with more compliant titin at the same SL (Supplementary Fig. S4), and (ii) more compliant realignment of binding sites (Daniel et al. 1998) at long SL with stiff titin compared with more compliant titin.

Finally, by relating the force generated to the amount of ATP used over 5 ms during the plateau of isometric tetanus, the contraction efficiency (as measured by the ratio of force to ATPase rate) in the half-sarcomere was determined for each case. Figure 3C shows that, similar to the active force (Fig. 2B), the contraction efficiency significantly decreases for SL >∼2.7 µm for stiff titin compared with the b = 4 µm⁻¹ and “no titin” cases.

Discussion and conclusion

This paper presents the first spatially explicit and multi-filament model of the half-sarcomere that relates the effects of increased titin stiffness to the mechanics and energetics of muscle contraction. We found that increased titin stiffness leads to reduced active force along the descending limb of the active force–SL relation (Fig. 2B). That force reduction corresponds with lower levels of contractile efficiencies in the SL range above about 2.7 µm (Fig. 3C). Moreover, both the reduced force and lower efficiency arose despite a significant increase in strongly bound cross-bridges for the same SL range (Fig. 3B).

Taken together, our results suggest that despite more motors bound to actin along the descending limb when titin is stiffer, the force-generating capacity of the motors is reduced as titin stiffness increases. We speculate that there is likely an elastic energy limit in the myosin filament above which cross-bridges become less efficient in producing force in the isometric condition. That is, our model predicts that increased titin stiffness limits the energy transfer from cross-bridges to the M-line by imposing significant strain in the myosin filament backbone. It is this titin-induced myosin filament strain that cross-bridges must have sufficient energy to deform in order to produce active force in the isometric condition.

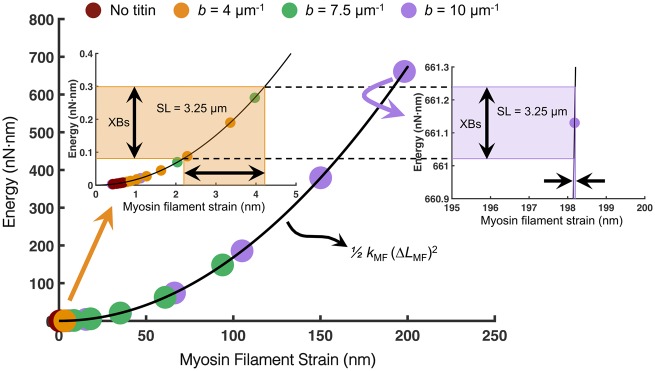
Relying on the notion that energy (not force) is conserved, Fig. 4 illustrates this point by depicting the elastic potential energy versus strain relation of the myosin filament. The elastic energy stored in each myosin filament was calculated using the effective stiffness of the entire myosin filament (k_MF) and the amount of strain (ΔL_MF) at the steady-state force for each SL. For compliant titin (b = 4 µm⁻¹), the amount of titin-based myosin filament strain (and therefore the amount of elastic energy stored in the myosin filament) at long SL (>3 µm) is on the same order of magnitude as the collective energy delivered by the cross-bridges during tetanic contraction at that SL (left inset of Fig. 4). However, for very stiff titin (b = 10 µm⁻¹) at the same SL, the amount of titin-based strain imposed in the myosin filament results in orders-of-magnitude increases in elastic energy stored in the myosin filament backbone (right inset of Fig. 4). Consequently, since the collective amount of cross-bridge energy able to be produced during contraction and transferred to the myosin filament is constant for a given SL, there is very little additional myosin filament strain (and therefore, force) delivered by the cross-bridges when titin has already delivered significant elastic potential energy to the myosin filament prior to activation at long SL. Thus, there is a point in our model (albeit outside the range of physiological titin stiffness and SL) where titin delivers enough elastic energy to the myosin filament backbone to render the added energy delivered by the cross-bridges insignificant.

Fig. 4.

With stiffer titin and longer SL, cross-bridges produce less myosin filament strain thereby reducing force output and contraction efficiency. The elastic potential energy was calculated (using the equation in the inset) for the myosin filament based on the amount of myosin filament strain imposed by the cross-bridges (XBs) under isometric maximum tension or by titin prior to activation. Each circle on the curve represents the amount of titin-based strain for each SL and titin stiffness. For more compliant titin (b = 4 μm⁻¹), the amount of titin-based strain at SL 3.25 μm is on the same order of magnitude as that delivered by the XBs (left inset). However, for very stiff titin (b = 10 μm⁻¹), the same amount of elastic energy delivered to the myosin filament from the XBs results in <1 nm of strain. As titin delivers more strain to the myosin filament, the XBs become less effective in generating force.

The inclusion of titin in this model provides a platform for many future investigations into the role of titin elasticity in regulating muscle function. Future iterations of the model will explore biophysical phenomena known to exist in the sarcomere. For example, it is known that there are significant geometrical dynamics (e.g., changes in SL and lattice spacing) during contraction, and these dynamics are not included in the current work. To investigate such lattice dynamics would require fairly extensive changes in the model architecture, but would represent an interesting avenue for future work, particularly given subtle lattice spacing changes that may arise during contraction (George et al. 2013). Additionally, recent experimental evidence has emerged demonstrating that both skeletal (Linari et al. 2015) and cardiac muscle (Reconditi et al. 2017) exhibit a mechanosensing-based (strain-dependent) mechanism of myosin filament activation in which titin may play a key role (Ait-Mou et al. 2016; Fusi et al. 2016; Marcucci et al. 2017). It is also known that titin interacts in the I-band with actin, which may change where it is structurally anchored (Schappacher-Tilp et al. 2015; Herzog et al. 2016). It has also been suggested that the I-band region of titin has calcium-dependent stiffness such that it may become stiffer upon activation [Rassier et al. (2015) and references therein], which can also be investigated with this model in the future.

Other models also predict that there may be appreciable and important torsional dynamics in the actin filaments during contraction that may influence the effective stiffness of titin if titin is strongly interacting with actin in the I-band (Nishikawa et al. 2012; Lindstedt and Nishikawa 2017). We suspect that interaction with axial tension and cross-bridge force generation would be similar to our results. That said, our current model lacks these types of molecular interactions, and therefore may miss interesting and important cooperative mechanisms occurring between titin, myosin, and actin.

Additionally, little is understood about how the mechanics of titin and the sarcomere determine whole muscle function, and a classic metric of whole muscle performance is the work done during cyclical length changes [a.k.a. work loop (Josephson 1985)]. Our model is well-poised to study the effects of titin stiffness on the ability of sarcomeres to produce positive, zero, or negative work, and assess how titin influences a whole muscle’s ability to behave as a motor, spring, brake, or strut [for a review, see Dickinson et al. (2000)]. Based on a recent experimental results (Hessel and Nishikawa 2017), it is likely that increasing titin stiffness results in a reduction in negative work production, and we intend to investigate this via future iterations of the model presented here.

It is interesting to note the similarities between the “no titin” case and the b = 4 µm⁻¹ case in the results we present here. We anticipate that this case will take on a more prominent role in future studies in which additional lattice dynamics and thick filament mechanosensing-based myosin activation are included.

Lastly, there is an emerging theme in the experimental literature in which titin is considered a major player in muscle function in general (Hessel and Nishikawa 2017; Tonino et al. 2017) as well as in muscular disorders (Hinson et al. 2015). With titin-truncating mutations being one of the leading causes of dilated cardiomyopathy (Schafer et al. 2016), a deadly genetic cardiac disorder without current treatment options other than cardiac transplantation, there is a pressing need to understand how titin affects muscle contractility. In fact, recent work using a transgenic murine model with truncated (and stiffer) titin leads to reduced myosin filament lengths, and produces similar trends in decreased force along the descending limb of the force–SL relation as presented here (Tonino et al. 2017). The model we describe here presents an exciting new approach to specifically probe the mechanical properties of titin and examine the effects on contractility in silico. This ability represents a powerful new technique to predict how certain myopathy-associated titin mutations may drive pathological behavior in vivo.

Funding

This work was supported by grants ARO W911NF-14-1-0396 awarded to T.L.D., NIH HL128368 awarded to M.R., NIH T32-HL007312 awarded to J.D.P., The Washington Research Foundation Endowed Professorship awarded to M.R., and the Joan and Richard Komen Endowed Chair to T.L.D.