Abstract
In traditional watershed delineation and topographic modeling, surface depressions are generally treated as spurious features and simply removed from a digital elevation model (DEM) to enforce flow continuity of water across the topographic surface to the watershed outlets. In reality, however, many depressions in the DEM are actual wetland landscape features with seasonal to permanent inundation patterning characterized by nested hierarchical structures and dynamic filling-spilling-merging surface-water hydrological processes. Differentiating and appropriately processing such ecohydrologically meaningful features remains a major technical terrain-processing challenge, particularly as highresolution spatial data are increasingly used to support modeling and geographic analysis needs. The objectives of this study were to delineate hierarchical wetland catchments and model their hydrologic connectivity using high-resolution lidar data and aerial imagery. The graph-theory-based contour tree method was used to delineate the hierarchical wetland catchments and characterize their geometric and topological properties. Potential hydrologic connectivity between wetlands and streams were simulated using the least-cost-path algorithm. The resulting flow network delineated potential flow paths connecting wetland depressions to each other or to the river network on scales finer than those available through the National Hydrography Dataset. The results demonstrated that our proposed framework is promising for improving overland flow simulation and hydrologic connectivity analysis.
1. Introduction
The prairie pothole region (PPR) of North America extends from the north-central United States (US) to southcentral Canada, encompassing a vast area of approximately 720 000 km2. The landscape of the PPR is dotted with millions of wetland depressions formed by the glacial retreat that happened during the Pleistocene epoch (Winter, 1989). The PPR is considered as one of the largest and most productive wetland areas in the world, which serves as a primary breeding habitat for much of North America’s waterfowl population (Keddy, 2010; Steen et al., 2014; Rover and Mushet, 2015). The wetland depressions, commonly known as potholes, possess important hydrological and ecological functions, such as providing critical habitat for many migrating and breeding waterbirds (Minke, 2009), acting as nutrient sinks (Oslund et al., 2010), and storing surface water that can attenuate peak runoff during a flood event (Huang et al., 2011b). The potholes range in size from a relatively small area of less than 100 m2 to as large as 30 000 m2, with an estimated median size of 1600 m2 (Zhang et al., 2009; Huang et al., 2011a). Most potholes have a water depth of less than 1 m with varying water permanency, ranging from temporary to permanent (Sloan, 1972). Due to their small size and shallow depth, these wetlands are highly sensitive to climate variability and are vulnerable to ecological, hydrological, and anthropogenic changes. Wetland depressions have been extensively drained and filled due to agricultural expansion, which is considered the greatest source of wetland loss in the PPR (Johnston, 2013). In a report to the US Congress on the status of wetland resources, Dahl (1990) estimated that the conterminous US lost more than 50 % of its original wetland acreage over a period of 200 years between the 1780s and the 1980s. More recently, Dahl (2014) reported that the total wetland area in the PPR declined by approximately 300 km2 between 1997 and 2009. This represents an average annual net loss of 25 km2. Regarding the number of depressions, it was estimated that the wetland depressions declined by over 107 000, or 4 %, between 1997 and 2009 (Dahl, 2014).
The extensive wetland drainage and removal have increased precipitation runoff into regional river basins, an occurrence which is partially responsible for the increasing frequency and intensity of flooding events in the PPR (Miller and Nudds, 1996; Bengtson and Padmanabhan, 1999; Tod- hunter and Rundquist, 2004). Concerns over flooding along rivers in the PPR have stimulated the development of hydrologic models to simulate the effects of depression storage on peak river flows (Hubbard and Linder, 1986; Gleason et al., 2007; Gleason et al., 2008; Huang et al., 2011b). Since most of these prairie wetlands do not have surface outlets or well- defined surface water connections, they are generally considered as geographically isolated wetlands (GIWs) or upland- embedded wetlands (Tiner, 2003; Mushet et al., 2015; Cohen et al., 2016; Lane and D’Amico, 2016). Recently, the US Environmental Protection Agency conducted a comprehensive review of over 1350 peer-reviewed papers with the aim of synthesizing existing scientific understanding of how wetlands and streams affect the physical, chemical, and biological integrity of downstream waters (US EPA, 2015). The report concludes that additional research focused on the frequency, magnitude, timing, duration, and rate of fluxes from GIWs to downstream waters is needed to better identify wetlands with hydrological connections or functions that substantially affect other waters and maintain the long-term sustainability and resiliency of valued water resources.
In addition to the comprehensive review by the US EPA (2015), a number of recent studies focusing on the hydrologic connectivity of prairie wetlands have been reported in the literature. For example, Chu (2015) proposed a modeling framework to delineate prairie wetlands and characterize their dynamic hydro-topographic properties in a small North Dakota research area (2.55 km2) using a 10 m resolution digital elevation model (DEM). Vanderhoof et al. (2016) examined the effects of wetland expansion and contraction on surface water connectivity in the PPR using time-series Landsat imagery. Ameli and Creed (2017) developed a physically based hydrologic model to characterize surface and groundwater hydrologic connectivity of prairie wetlands. These reported studies represent some of the latest research developments on hydrologic connectivity in the PPR. To our knowledge, little work has been done to delineate potential flow paths between wetlands and stream networks and use flow paths to characterize hydrologic connectivity in the PPR. In addition, previous remote-sensing-based work on the hydrology of prairie wetlands mainly focused on mapping wetland inundation areas (e.g., Huang et al., 2014; Vanderhoof et al., 2017) or wetland depressions (e.g., Mc-Cauley and Anteau, 2014; Wu and Lane, 2016); few studies have treated wetlands and catchments as integrated hydrological units. Therefore, there is a call for treating prairie wetlands and catchments as highly integrated hydrological units because the existence of prairie wetlands depends on lateral inputs of runoff water from their catchments in addition to direct precipitation (Hayashi et al., 2016). Furthermore, hydrologic models for the PPR were commonly developed using coarse-resolution DEMs, such as the 30 m National Elevation Dataset (see Chu, 2015; Evenson et al., 2015, 2016). High-resolution light detection and ranging (lidar) data have rarely been used in broad-scale (e.g., basin- or subbasin-scale) studies to delineate wetland catchments and model wetland connectivity in the PPR.
In this paper, we present a semi-automated framework for delineating nested hierarchical wetland depressions and their corresponding catchments as well as simulating wetland connectivity using high-resolution lidar data. Our goal was to demonstrate a method to characterize fill-spill wetland hydrology and map potential hydrological connections between wetlands and stream networks. The hierarchical structure of wetland depressions and catchments was identified and quantified using a localized contour tree method (Wu et al., 2015). The potential hydrologic connectivity between wetlands and streams was characterized using the least-cost-path algorithm. We also utilized high-resolution lidar intensity data to delineate wetland inundation areas, which were compared against the National Wetlands Inventory (NWI) to demonstrate the hydrological dynamics of prairie wetlands. Our ultimate goal is to build on our proposed framework to improve overland flow simulation and hydrologic connectivity analysis, which subsequently may improve the understanding of wetland hydrological dynamics at watershed scales.
2. Study area and datasets
2.1. Study area
The work focused on the Pipestem River subbasin in the prairie pothole region of North Dakota (Fig. 1). The subbasin is an 8-digit hydrologic unit code (no. 10160002) with a total area of approximately 2770 km2, covering four counties in North Dakota (see Fig. 1). The climate of the subbasin is characterized by long, cold, dry winters and short, mild, variably wet summers (Winter and Rosenberry, 1995). Average annual precipitation is approximately 440 mm, with substantial seasonal and annual variations (Huang et al., 2011a). The land cover of the Pipestem subbasin is dominated by cultivated crops (44.1 %), herbaceous vegetation (25.9 %), and hay or pasture (13.1 %), with a substantial amount of open water (7.1 %) and emergent herbaceous wetlands (5.6 %; Jin et al., 2013). The Cottonwood Lake area (see the blue rectangle in Fig. 1), a long-term field research site established by the US Geological Survey (USGS) and the US Fish and Wildlife Service (USFWS) in 1977 for wetland ecosystem monitoring, has been a very active area of research for several decades (e.g., Sloan, 1972; Winter and Rosenberry, 1995; Huang et al., 2011a; Mushet and Euliss, 2012; Hayashi et al., 2016).
Figure 1.
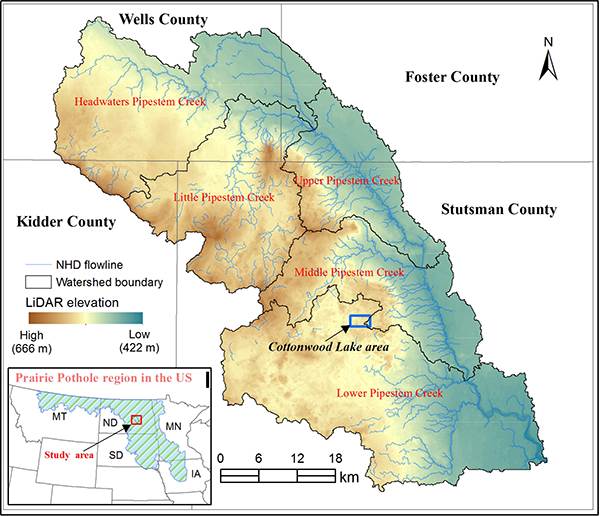
Location of the Pipestem subbasin within the prairie pothole region of North Dakota.
2.2. Lidar data
The lidar elevation data for the Pipestem subbasin were collected in late October 2011 and distributed through the North Dakota GIS Hub Data Portal (https://gis.nd.gov/, accessed 30 December 2016). The bare-earth DEMs derived from lidar point clouds are freely available as 1 m resolution image tiles (2 km × 2 km). The vertical accuracy of the lidar DEM is 15.0 cm. We created a seamless lidar DEM (see Fig. 1) for the Pipestem subbasin by mosaicking 786 DEM tiles and used it for all subsequent data analyses (approximately 22.66 GB). The elevation of the subbasin ranges from 422 to 666 m, with relatively high-elevation areas in the west and low-elevation areas in the east.
The lidar intensity data for the Pipestem subbasin were also collected at 1 m resolution coincident with the lidar elevation data collection. In general, the return signal intensities of water areas are relatively weak due to water absorption of the near-infrared spectrum (Lang and McCarty, 2009; McCauley and Anteau, 2014). As a result, water bodies typically appear as dark features, whereas nonwater areas appear as relatively bright features in the lidar intensity image. Thresholding techniques have been commonly used to distinguish water pixels from nonwater pixels (Huang et al., 2011b, 2014; Wu and Lane, 2016). In this study, the lidar intensity data were primarily used to extract standing- water areas (i.e., inundation areas) while the lidar DEMs were used to derive nested wetland depressions and their corresponding catchments above the standing-water surface. It is worth noting that October 2011 was an extremely wet period, with a Palmer Hydrological Drought Index (PHDI) of 7.84. The PHDI typically falls within the range between −4 (extreme drought) and +4 (extremely wet; Huang et al., 2011a). Consequently, small individual wetland depressions nested within larger inundated wetland complexes might not be detectable from the resulting lidar DEM.
2.3. Ancillary data
In addition to the lidar datasets, we used three ancillary datasets, including the 1 m resolution aerial imagery from the National Agriculture Imagery Program (NAIP) of the US Department of Agriculture (USDA), the National Wetlands Inventory from the USFWS, and the National Hydrography Dataset (NHD) from the USGS.
The NAIP imagery products were also acquired from the North Dakota GIS Hub Data Portal. The default spectral resolution of the NAIP imagery in North Dakota is natural color (red, green, and blue, or RGB). Beginning in 2007, however, the state data have been delivered with four bands of data: RGB and near infrared. We downloaded and processed 6 years of NAIP imagery for the Pipestem subbasin, including 2003, 2004, 2006, 2009, 2012, and 2014. A small portion of the study area with the NAIP imagery is shown in Fig. 2. This time-series NAIP imagery clearly demonstrates the dynamic nature of prairie pothole wetlands under various dry and wet conditions. In particular, the extremely wet year of 2014 resulted in many individual wetlands coalescing and forming larger wetland complexes (see the yellow arrows in Fig. 2). It should be noted that all the NAIP imagery was collected during the summer growing season of agricultural crops. Since no coincident aerial photographs were collected during the lidar data acquisition campaign in 2011, this NAIP imagery can serve as a valuable data source for validating the lidar-derived wetlands catchments and hydrological pathways in this study.
Figure 2.

Examples of the National Agriculture Imagery Program (NAIP) aerial imagery in the prairie pothole region of North Dakota illustrate the dynamic nature of prairie pothole wetlands under various dry and wet conditions. The yellow arrows highlight locations where filling-spilling-merging dynamics occurred (imagery location: 47° 1′23.519″ N, 99°8′34.454″ W).
The NWI data for our study area were downloaded fromhttps://www.fws.gov/wetlands/ (accessed 30 December 2016). The wetland inventory data in this region were created by manually interpreting aerial photographs acquired in the 1980s, with additional support from soil surveys and field checking (Cowardin et al., 1979; Huang et al., 2011b; Wu and Lane, 2016). Tiner (1997) reported that the target mapping unit, the size class of the smallest group of NWI wetlands that can be consistently mapped, was between 1000 and 4000 m2 in the prairie pothole region. It should be noted that the target mapping unit is not the minimum wetland size of the NWI. In fact, there are a considerable amount of NWI wetland polygons smaller than the target mapping unit (1000 m2). In this study, we focused on the prairie wetlands that are greater than 500 m2. Therefore, 5644 small NWI wetland polygons (< 500 m2) were eliminated from further analysis. In total, there were 32 016 NWI wetland polygons (≥ 500 m2) across the Pipestem subbasin (Table 1). The total size of these NWI wetlands was approximately 279.5 km2, covering 10.1 % of the Pipestem subbasin. The areal composition of NWI wetlands consisted of freshwater emergent wetlands (86.5 %), lakes (7.5 %), freshwater ponds (5.3 %), freshwater forested/shrub wetland (0.4 %), and riverine systems (0.3%). The median size of wetlands (≥ 500 m2) in our study area was 1.8 × 103 m2. Although the NWI is the only spatially comprehensive wetland inventory for our study area, it is now considerably out of date, as it was developed 30 years ago and it does not reflect the wetland temporal change (Johnston, 2013). The wetland extent and type for many wetland patches have changed since its original delineation (e.g., Fig. 2). Nevertheless, NWI does provide valuable information about wetland locations (Tiner, 1997; Huang et al., 2011b). Furthermore, the NWI definition of wetlands requires only one of three wetland indicators (soils, hydrology, or plants) whereas regulatory delineation requires all three - 33 Code of Federal Regulations 328.3(b). In our study, the NWI polygons were primarily used to compare with the wetland depressions delineated from the lidar DEM.
Table 1.
Summary statistics of the National Wetlands Inventory (NWI) for the Pipestem subbasin, North Dakota.
| Wetland type | Count | Min. (103 m2) |
Max. (106 m2) |
Median (103 m2) |
Sum(106 m2) | Percentage (%) |
|---|---|---|---|---|---|---|
| Freshwater emergent | 31,046 | 0.50 | 3.1 | 1.8 | 241.7 | 86.5 |
| Freshwater forested/shrub | 108 | 0.55 | 0.34 | 2.6 | 1.18 | 0.4 |
| Freshwater pond | 760 | 0.53 | 0.72 | 1.8 | 14.7 | 5.3 |
| Lake | 50 | 3.7 | 9.4 | 188.6 | 21.1 | 7.5 |
| Riverine | 52 | 0.63 | 0.43 | 4.0 | 0.81 | 0.3 |
| Total (all polygons) | 32,016 | 0.50 | 9.4 | 1.8 | 279.5 | 100.0 |
The high-resolution NHD data were downloaded from http://nhd.usgs.gov (accessed 30 December 2016). There were 1840 polyline features in the NHD flowline layer for the Pipestem subbasin, with a total length of 1.4 × 103km and an average length of 762 m. The NHD flowlines overlaid on top of the lidar DEM are shown in Fig. 1. It is worth noting that the majority of the NHD flowline features were found in the low-elevation areas in the east. The high-elevation areas in the west, where most NWI wetland polygons are located, have very few NHD flowlines, except for the Little Pipestem Creek. This suggests that a large number of temporary and seasonal flow paths were not captured in the NHD dataset, perhaps due to the fact that the NHD does not try to systematically measure stream lines < 1.6 km (Stanislawski, 2009; Lane and D’Amico, 2016). In this study, the NHD flowlines were used to compare the lidar-derived potential flow paths using our proposed methodology.
3. Methodology
3.1. Outline
Our methodology for delineating nested wetland catchments and flow paths is a semi-automated approach consisting of several key steps: (a) extraction of hierarchical wetland depressions using the localized contour tree method (Wu et al., 2015), (b) delineation of nested wetland catchments, (c) calculation of potential water storage, and (d) derivation of potential flow paths using the least-cost-path search algorithm. The lidar DEM was used to delineate hierarchical wetland depressions and nested wetland catchments. The lidar intensity imagery was used to extract wetland inundation areas. The potential water storage of each individual wetland depression was calculated as the volume between the standing water surface and the maximum water boundary, where water might overspill into downstream wetlands or waters. The potential flow paths representing surface water connectivity were derived according to the potential water storage and simulated rainfall intensity. The flowchart in Fig. 3 shows the detailed procedures of the methodology for delineating wetland catchments and potential flow paths.
Figure 3.
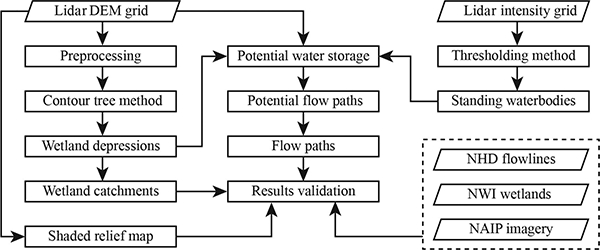
Flowchart of the methodology for delineating wetland catchments and flow paths.
3.2. Extraction of hierarchical wetland depressions
The fill-and-spill hydrology of prairie wetland depressions has received considerable attention in recent years (Shaw et al., 2012, 2013; Golden et al., 2014; Chu, 2015; Hayashi et al., 2016; Wu and Lane, 2016). It is generally acknowledged that the fill-and-spill mechanism of wetland depressions results in intermittent hydrologic connectivity between wetlands in the PPR. In this study, wetland depressions were categorized into two groups based on their hierarchical structure: simple depressions and composite depressions. A simple depression is a depression that does not have any other depressions embedded in it, whereas a composite depression is composed of two or more simple depressions (Wu and Lane, 2016). As shown in Fig. 4a, for example, depressions A-E are all simple depressions. As water level gradually increases in these simple depressions, they will eventually begin to spill and merge to form composite depressions. For instance, the two adjoining simple depressions A and B can form a composite depression F (see Fig. 4b). Continuously, composite depression F and simple depression C can further coalesce to form an even larger composite depression G. Similarly, the two adjoining simple depressions D and E can coalesce to form a composite depression H.
Figure 4.
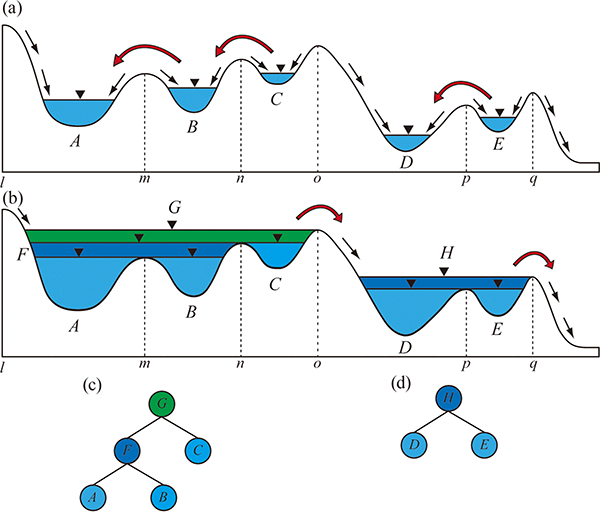
Illustration of the filling-merging-spilling dynamics of wetland depressions: (a) first-level depressions, (b) nested hierarchical structure of depressions under fully filled condition, (c) corresponding contour tree representation of the composite wetland depression (left) in (a), and (d) corresponding contour tree representation of the composite wetland depression (right) in (a). Different color of nodes in the tree represents different portions of the composite depression in (a): light blue (first-level), dark blue (second-level), and green (third-level).
It is worth noting that the flow direction of surface waters resulting from the fill-and-spill mechanism between adjoining wetland depressions can be bidirectional, depending on the antecedent water level and potential water storage capability of the depressions. Most previous studies simply assumed that water always flows unidirectionally from an upper water body to a lower one. This assumption, however, does not apply when two adjoining depressions share the same spilling elevation or when there is a groundwater hydraulic head preventing the flow from one to another. For example, in Fig. 4a, the water flow direction resulting from fill-and-spill between depressions A and B can be bidirectional. If depression B fills up more quickly than depression A, then water will flow from depression B to depression A through the spilling point, and vice versa. A depression with a high elevation of antecedent water level does not necessarily spill to an adjoining depression with a lower elevation of antecedent water level. The key factors affecting the initialization of spilling process leading to flow direction are the depression ponding time and catchment precipitation conditions. If the rain or runoff comes from the east and that is where depression B is, then it might fill more quickly than if the runoff comes from the west where depression A is. Whichever wetland depression takes less time to fill up will spill to the adjoining depression and eventually coalesce to form a larger composite depression. If no adjoining depression with the same spilling elevation is available, the upstream wetland depression will directly spill to downstream wetlands or streams. For example, the largest fully filled composite depression G will spill to the simple depression D or the composite depression H, if available.
To identify and delineate the nested hierarchical structure of potential wetland depressions, we utilized the localized contour tree method proposed by Wu et al. (2015). The concept of the contour tree was initially proposed to extract key topographic features (e.g., peaks, pits, ravines, and ridges) from contour maps (Kweon and Kanade, 1994). The contour tree is a tree-shaped data structure that can represent the nesting of contour lines on a continuous topographic surface. Wu et al. (2015) improved and implemented the contour tree algorithm, making it a locally adaptive version. In other words, the localized contour tree algorithm builds a series of trees rather than a single global contour tree for the entire area. Each localized contour tree represents one disjointed depression (simple or composite), and the number of trees represents the total number of disjointed depressions for the entire area. When a disjointed depression is fully flooded, the water in it will spill to the downstream wetlands or waters through overland flow. For example, Fig. 4c and d show the corresponding contour tree graphs for the composite depressions in Fig. 4b. Once the composition G is fully filled, water will spill into simple depression D or composite depression H.
3.3. Delineation of nested wetland catchments
After the identification and extraction of hierarchical wetland depressions from the contour maps, various hydrologically relevant terrain attributes can be derived based on the DEM, including flow direction, flow accumulation, catchment boundary, flow path, flow length, etc. The calculation of flow direction is essential in hydrological analysis because it frequently serves as the first step to derive other hydrologically important terrain attributes. On a topographic surface represented in a DEM, flow direction is the direction of flow from each grid cell to its steepest downslope neighbor. One of the widely used flow direction algorithms is the eight-direction flow model known as the D8 algorithm (O’Callaghan and Mark, 1984), which is available in most GIS software packages. Flow accumulation is computed based on flow direction. Each cell value in the flow accumulation raster represents the number of upslope cells that flow into it. In general, cells with high flow accumulation values correspond to areas of concentrated flow (e.g. stream channels), while cells with a flow accumulation value of zero correspond to the pattern of ridges (Zhu, 2016). Therefore, flow accumulation provides a basis for identifying ridgelines and delineating catchment boundaries.
A catchment is the upslope area that drains water to a common outlet. It is also known as the watershed, drainage basin, or contributing area. Catchment boundaries can be delineated from a DEM by identifying ridgelines between catchments based on a specific set of catchment outlets (i.e., spilling points). In traditional hydrological modeling, topographic depressions are commonly treated as spurious features and simply removed to create a hydrologically correct DEM, which enforces water to flow continuously across the landscape to the catchment outlets (e.g., stream gauges, dams). In the PPR, however, most topographic depressions in the DEM are real features that represent wetland depressions, which are rarely under fully filled condition (see Hayashi et al., 2016; Lane and D’Amico, 2016; Vanderhoof et al., 2016). As illustrated above, we used the localized contour tree algorithm to delineate the hierarchical wetland depressions, which were used as the source locations for delineating wetland catchments. Each wetland depression (simple or composite) has a corresponding wetland catchment. As shown in Fig. 4b, the corresponding wetland catchment of each wetland depression is bounded by the vertical lines surrounding that depression. For example, the wetland catchment of simple depression A is Catchmentlm, and the wetland catchment of simple depression B is Catchmentmn. Similarly, the wetland catchment of composite depression F is Catchmentln, which is an aggregated area of Catchmentlm and Catchmentmn, resulting from the coalescence of simple depressions A and B.
3.4. Calculation of potential water storage and ponding time
The potential water storage capacity (V, m3) of each wetland depression was computed through statistical analysis of the grid cells that fall within the depression (Wu and Lane, 2016):
| (1) |
where C is the spilling elevation (m), i.e., the elevation of the grid cell where water spills out of the depression; Zi is the elevation of the grid cell i (m); R is the spatial resolution (m); and n is the total number of grid cells that fall within the depression.
The ponding time of a depression was calculated as follows:
| (2) |
where V is the potential water storage capacity of the depression (m3), Ac is the catchment area of the corresponding depression (m2), and I is the rainfall intensity (mmh−1). For the sake of simplicity, we made two assumptions. First, we assumed that the rainfall was temporally and spatially consistent and uniformly distributed throughout the landscape (e.g., 50mmh−1) and all surfaces were impervious. Second, we assumed no soil infiltration. Note that assuming no infiltration is a reasonable assumption for the prairie pothole landscape (Shaw et al., 2013; Hayashi et al., 2016). However, this assumption might be problematic in other landscapes with more heterogeneity in infiltration capacity.
The proportion of wetland depression area (Aw) to catchment area (Ac) was calculated by the following:
| (3) |
The wetland depression area (Aw) refers to the maximum ponding extent of the depression. The proportion (Pwc) can serve as a good indicator for percent inundation of the study area under extremely wet conditions (e.g., Vanderhoof et al., 2016).
3.5. Derivation of surface-water flow paths
Based on the computed ponding time of each depression under a specific rainfall intensity, the most probable sequence of the overland flow path was constructed. The depression with the least ponding time will first fill and then start to overspill down-gradient. In hydrology, the path which water takes to travel from the spilling point to the downstream surface outlet or channel is commonly known as the flow path. The distance it takes for water to travel is known as flow length. In this study, we adopted and adapted the least-cost-path search algorithm (Wang and Liu, 2006; Metz et al., 2011; Stein et al., 2011) to derive the potential flow paths. The least-cost- path algorithm requires two input datasets: the DEM and the depression polygons. Given the fact that topographic depressions in high-resolution lidar DEM are frequently a combination of artifacts and actual landscape features (Lindsay and Creed, 2006), the user can set a minimum size threshold for depressions to be treated as actual landscape features. In other words, depressions with a size smaller than the threshold will be treated as artifacts, and thus removed from the DEM. This results in a partially filled DEM in which depressions smaller than the chosen threshold are filled to enforce hydrologic flow while larger depressions are kept for further analysis. Based on the partially filled DEM, flow direction for each grid cell can be calculated using the D8 flow direction algorithm (O’Callaghan and Mark, 1984). The least-cost path minimizes the cumulative cost (i.e., elevation) along its length. Flow paths are computed by tracing down-gradient, from higher to lower cells, following assigned flow directions. With the simulated overland flow path, flow length can be calculated, which is defined as the distance between the spilling point of an upslope wetland and the inlet of a downs- lope wetland or stream. In our study, hydrologic connectivity refers to the water movement between wetland and wetland and between wetland and stream via hydrologic pathways of surface water.
3.6. Wetland hydrology analyst
To facilitate automated delineation of wetland catchments and flow paths, we implemented the proposed framework as an ArcGIS toolbox - Wetland Hydrology Analyst, which is freely available for download at https://GISTools.github.io/ (accessed 30 December 2016). The core algorithms of the toolbox were implemented using the Python programming language. The toolbox consists of three tools: wetland depression tool, wetland catchment tool, and flow path tool. The wetland depression tool asks the user to select a DEM grid, and then executes the localized contour tree algorithm with user-defined parameters (e.g., base contour elevation, contour interval, minimum depression size, minimum ponding depth) automatically to delineate hierarchical wetland depressions. The depressional wetland polygons can be stored as ESRI Shapefiles or a Feature Dataset in a Geodatabase. Various morphometric properties (e.g., width, length, size, perimeter, maximum depth, mean depth, volume, elongatedness, compactness) are computed and included in the attribute table of the wetland polygon layers. The wetland catchment tool uses the DEM grid and the wetland polygon layers resulted from the wetland depression tool as input, as well as exports wetland catchment layers in both vector and raster format. The flow path tool can be used to derive potential overland flow paths of surface water based on the DEM grid and the wetland polygon layers.
3.7. Wetland inundation mapping
The lidar intensity image was primarily used to map inundation areas. Before inundation mapping, we applied a median filter to smooth the lidar intensity image. The median filter is considered as an edge-preserving filter that can effectively remove data noise while preserving boundaries between image objects (Wu et al., 2014). Subsequently, a simple thresholding method was used to separate inundated and noninundated classes. Similar thresholding techniques have been used in previous studies to extract water areas from lidar intensity imagery (Lang and McCarty, 2009; Huang et al., 2011b). By examining typical inundation areas and the histogram of the lidar intensity imagery used in our study, we chose an intensity threshold value of 20. Grid cells with an intensity value between 0 and 20 were classified as an inundated class while grid cells with an intensity value greater than 20 were classified as a noninundated class, which resulted in a binary image. In the binary image, each region composed of inundated pixels that were spatially connected (8-neighbor) was referred to as a potential inundation object. The “boundary clean” and “region group” functions in Ar- cGIS Spatial Analyst were then used to clean ragged edges of the potential inundation objects and assign a unique number to each object. It should be noted that water and live trees might both appear as dark features in the lidar intensity imagery and have similar intensity values, although trees are not particularly common in this region. As a result, some trees were misclassified as inundation objects. To correct the mis- classifications and obtain reliable inundation objects, we further refined the potential inundation objects using additional criteria with the aid of the lidar DEM. First, we assumed that each inundation object must occur within a topographic depression in order to retain water. In other words, all inundation objects must intersect with depression objects derived using the “sink” function in ArcGIS Spatial Analyst. Secondly, given the relatively flat and level surface of inundated regions, the standard deviation of pixel elevations within the same inundation object should be very small. By examining the standard deviation of pixel elevations of some typical inundation objects and tree objects, we chose a threshold of 0.25 m, which is slightly larger than the vertical accuracy of the lidar data (0.15 m). This step can be achieved using the “zonal statistics as table” in ArcGIS Spatial Analyst. Thirdly, we only focused on wetlands greater than 500 m2. Therefore, inundation objects with areas smaller than 500 m2 were eliminated from further analysis.
4. Results
4.1. Inundation mapping results
Using the above procedures, we identified 15 784 inundation objects (i.e., depressions > 500 m2 with water as determined through lidar-based analyses), which were then compared against the NWI wetland polygons in our study area. We have made the inundation map publicly available at https:// GISTools.github.io/ (accessed 30 December 2016). The identified inundation objects encompassed an area of approximately 278.5 km2, accounting for 10.1% of the Pipestem subbasin. Using the empirical area-to-volume equation developed for this region of the PPR (see Gleason et al., 2007; Wu and Lane, 2016), we estimated that the 15 784 inundated depressions stored approximately 448.5 million m3 of water. The histogram of inundation polygons is shown in Fig. 5a. The median size of the inundation polygons identified using the lidar intensity data was 1.8 × 103 m2, which was slightly larger than the reported median size of NWI polygons (Table 2). Contrary to expectations, 18 957 out of 32016 NWI wetland polygons did not intersect with the inundation objects. In other words, 59.2 % of the NWI wetland polygons mapped in the 1980s did not contain visible waterbodies during the lidar collection period. The total area of these “dried” NWI wetlands was 43.6 km2, accounting for 15.6% of the original NWI wetland areas (279.5 km2). The histogram of the “dried” NWI wetlands is shown in Fig. 5b. It is worth noting that most of these “dried” NWI wetlands were relatively small, with a median size of 1.2 × 103 m2 (Table 2). The lidar intensity data were acquired in late October 2011, an extremely wet month according to the Palmer Hydrological Drought Index (Fig. 6). During this wet season, most wetlands would be expected to have abundant standing water. If no standing water could be detected in a wetland patch during this extremely wet period, it is possible that some of these small wetlands might have dried out during the previous weeks to months. It is possible that land use change surrounding the “dried” wetlands (e.g., row-cropping replacing pasture lands) may have affected their hydrology (Wright and Wimberly, 2013); water diversion via drainage or ditches could also be responsible for the lack of inundation, though we did not explore either of these potential drivers of change in this study. However, it is also likely that some of the “dried” wetland might become wet again in the spring, following snowmelt. The “dried” NWI wetlands could also be attributed to the source of error in the original NWI data, which have a minimum mapping unit (i.e., the minimum size of wetland that can be consistently mapped) of 0.1 ha for the PPR (Tiner, 1997). Figure 5b shows that 37 % of the “dried” NWI polygons are smaller than the minimum mapping unit (1000 m2). This implies that these small “dried” NWI polygons could be due to the NWI mapping error. Figure 7 illustrates the difference in shape and extent between the lidar- derived wetland inundation maps and the NWI wetland polygons. The areas of disagreement (discrepancy) can be partly explained by the different image acquisition dates. As mentioned earlier, the NWI maps for Pipestem subbasin of the PPR were created in the early 1980s while the lidar data were acquired in 2011. Clearly, most small NWI wetlands (see yellow-outline polygons in Fig. 7) appeared to not have visible standing water. Conversely, large NWI wetlands exhibited expansion and coalesced to form even larger wetland complexes (see blue-outline polygons in Fig. 7).
Figure 5.
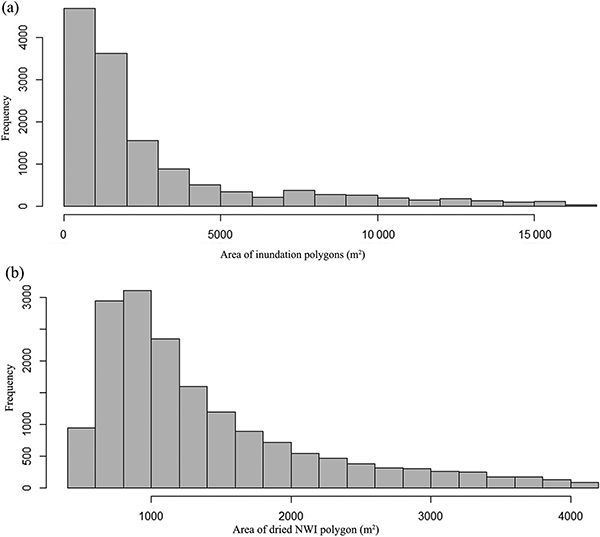
Histograms of inundation and NWI wetland polygons. (a) Inundation objects derived from lidar intensity data; (b) dried NWI wetland polygons not intersecting inundation objects.
Table 2.
Summary statistics of NWI wetland polygons and inundation polygons derived from lidar intensity data.
| Type | Count | Min. (103 m2) |
Max. (106 m2) |
Mean (103 m2) |
Median (103 m2) |
Sum (106 m2) |
|---|---|---|---|---|---|---|
| NWI polygons | 32016 | 0.50 | 9.4 | 8.7 | 1.8 | 279.5 |
| Inundation polygons | 15 784 | 0.50 | 7.3 | 17.7 | 1.8 | 278.5 |
| Dried NWI polygons | 18 957 | 0.50 | 0.11 | 2.3 | 1.2 | 43.6 |
Figure 6.
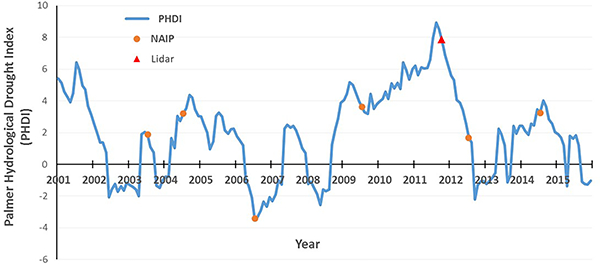
Palmer Hydrological Drought Index (PHDI) of the Pipestem subbasin (2001–2015).
Figure 7.
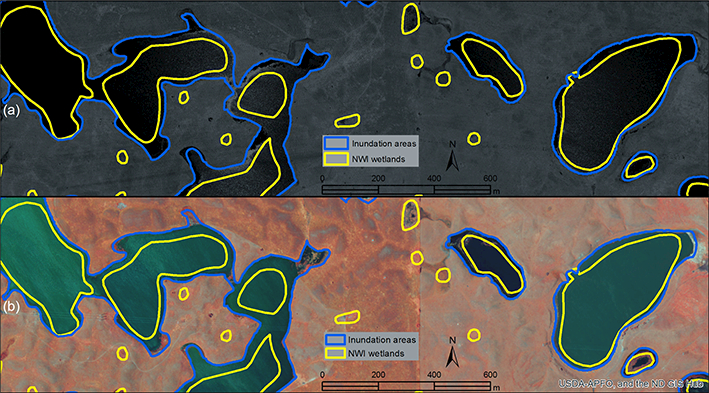
Comparison between inundation areas (derived from lidar intensity data) and NWI wetland polygons (image location: 47°334.474” N, 99°953.9” W). (a) Inundation areas and NWI wetlands overlaid on lidar intensity image; (b) inundation areas and NWI wetlands overlaid on color infrared aerial photograph (2009).
4.2. Nested wetland depressions and catchments
We applied the localized contour method on the lidar-derived DEM and identified 33 241 wetland depressions. It should be noted that the ‘wetland depression’ refers to the maximum potential ponding extent of the depression. The inundated wetland depressions identified in the prior section can be seen as a subset of these depressions with water in them. The total area of the identified wetland depressions was approximately 0.55 × 109m2 (Table 3), accounting for 20% of the entire study area. This histogram of the wetland depressions is shown in Fig. 8a. The median size of wetland depressions was 2.6 × 103 m2, which is larger than that of the NWI wetland polygons as well as the inundation polygons (see Table 2). Using Eq. (1), we estimated that the potential water storage capacity of the Pipestem subbasin resulting from these wetland depressions is 782.8 million m3, which is 1.75 times as large as the estimated existing water storage (448.5 million m3) for the 15 784 inundated wetlands mentioned above. As noted by Hayashi et al. (2016), wetlands and catchments are highly correlated and should be considered as integrated hydrological units. The water input of each wetland largely depends on runoff from the upland areas within the catchment. Using the method described in Sect. 3.3, we delineated the associated wetland catchments for each of the 33 241 wetland depressions. The histogram of the delineated wetland catchments is shown in Fig. 8b. The median size of wetland catchments was 26 × 103 m2, which is approximately 10 times larger than that of the wetland depressions (Table 3).
Table 3.
Summary statistics of 33 241 wetland depressions and catchments derived from lidar DEM.
| Type | Min. | Max. | Mean | Median | Sum |
|---|---|---|---|---|---|
| Depression area (m2) | 1.0 × 103 | 20.0 × 106 | 16.6 × 103 | 2.6 × 103 | 0.55 × 109 |
| Catchment area (m2) | 1.8 × 103 | 57.9 × 106 | 82.7 × 103 | 26 × 103 | 2.77 × 109 |
| Depression volume (m3 ) | 1 | 153 ×106 | 23.4 × 103 | 0.42 × 103 | 0.78 × 109 |
| Proportion of depression area to catchment area (%) | 0.04 | 83.72 | 16.59 | 14.31 | 20.06 |
Figure 8.
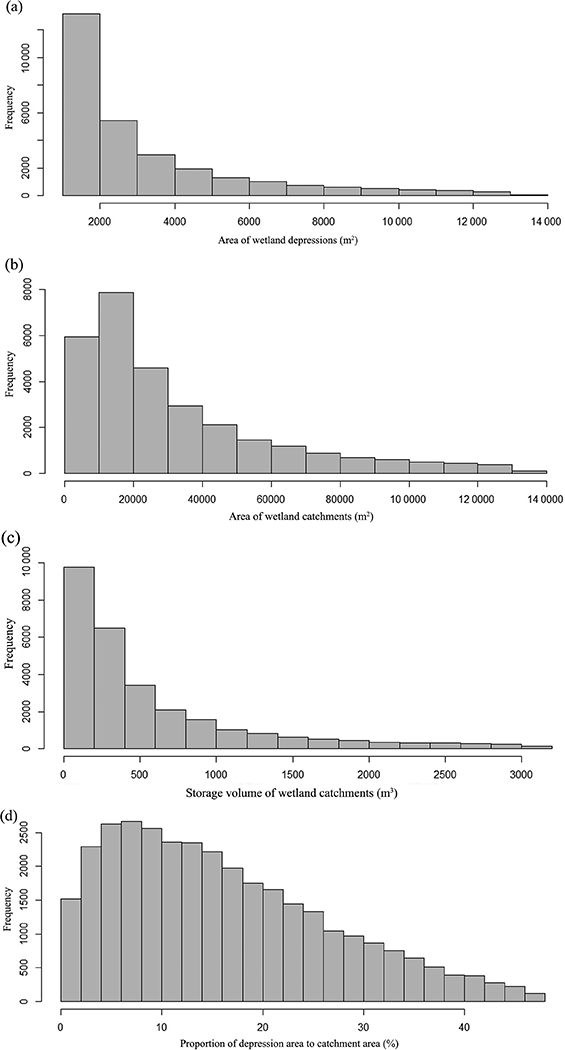
Histogram of wetland depressions and catchments. (a) Wetland depressions, (b) wetland catchments, (c) potential storage capacity, and (d) proportion of depression area to catchment area.
Using Eq. (3), we calculated the proportion of depression area to catchment area (Aw/Ac) for each wetland depression. It was found that the proportion ranged from 0.04 to 83.72 %, with a median of 14.31 % (Table 3). Our findings are in general agreement with previous studies; for instance, Hayashi et al. (1998) reported an average proportion (Aw/Ac) of 9 % for 12 prairie wetlands in the Canadian portion of the PPR. Similarly, Watmough and Schmoll (2007) analyzed 13 wetlands in the Cottonwood Lake Area during the high-stage period and reported an average proportion (Aw/Ac) of 18 %. It should be noted that the average proportion of wetland area to catchment area (Aw/Ac) reported in the above studies were calculated on the basis of a limited number of wetlands. On the contrary, our results were computed from more than 30000 wetland depressions and catchments, which provides a statistically reliable result for the study area due to a much larger sample size.
4.3. Potential flow paths and connectivity lengths
Based on the lidar DEM and wetland depression polygon layer, we derived the potential flow path network for our study area using the least-cost-path algorithm. We have made the interactive map of modeled hydrologic connectivity in the Pipestem subbasin publicly available at https: //GISTools.github.io#wetland-connectivity (accessed 30 December 2016). A number of data layers derived from our study are available on the map, such as the inundation polygons, wetland depressions, wetland catchments, and potential flow paths. NWI polygons, NHD flowlines, lidar intensity image, lidar shaded relief, and time-series aerial photographs are also available for comparison and visualization of results. A small proportion of the map is shown in Fig. 9. Clearly, the derived potential flow paths not only captured the permanent surface water flow paths (see the thick blue NHD flowline in Fig. 9), but also the potential intermittent and infrequent flow paths that have not been mapped previously. By examining the potential flow paths overlaid on the color infrared aerial photograph (Fig. 9b), we can see that the majority of potential flow paths appeared to be collocated with vegetated areas. This indicates that flow paths are likely located in high soil moisture areas that are directly or indirectly related to surface water or groundwater connectivity. It should be reiterated that the derived flow paths are only potential flow paths. Water may not have flowed along a fraction of them to date.
Figure 9.

Examples of lidar-derived wetland depressions and flow paths in the Pipestem subbasin (image location: 47° 132.679” N, 98°59r48.82” W). (a) Wetland depressions and flow paths overlaid on lidar shaded relief map; (b) NWI polygons, wetland depressions, and flow paths overlaid on color infrared aerial photograph (2012).
In total, there are 1840 NHD flowlines in the Pipestem subbasin. The mean and median length of NHD flowlines are 762 and 316 m, respectively (Table 4). However, the potential flow lengths derived from our study, which connected not only stream segments but also wetlands to wetlands, revealed much shorter flow paths than the NHD flowlines. This finding is within our expectation. The histogram of the derived potential flow lengths is shown in Fig. 10. The median potential flow length is 83 m, which is approximately 1 /4 of the median NHD flowlines. The median elevation difference between an upstream wetland and a downstream wetland connected through the potential flow path is 0.89 m.
Table 4.
Summary statistics of wetland depression ponding depth, NHD flowlines, flow path length, and elevation difference. n/a = not applicable.
| Type | Count | Min. (m) | Max. (m) | Mean (m) | Median (m) | Sum (m) |
|---|---|---|---|---|---|---|
| Ponding depth | 33 241 | 0.01 | 7.6 | 0.23 | 0.16 | n/a |
| NHD flowlines | 1840 | 3.9 | 15.5 × 103 | 762 | 317 | 1.4 × 106 |
| Flow path length | 41 449 | 1.5 | 4.7 × 103 | 138 | 83 | 5.0 × 106 |
| Elevation difference | 41 449 | 0.01 | 70.9 | 2.1 | 0.89 | n/a |
Figure 10.
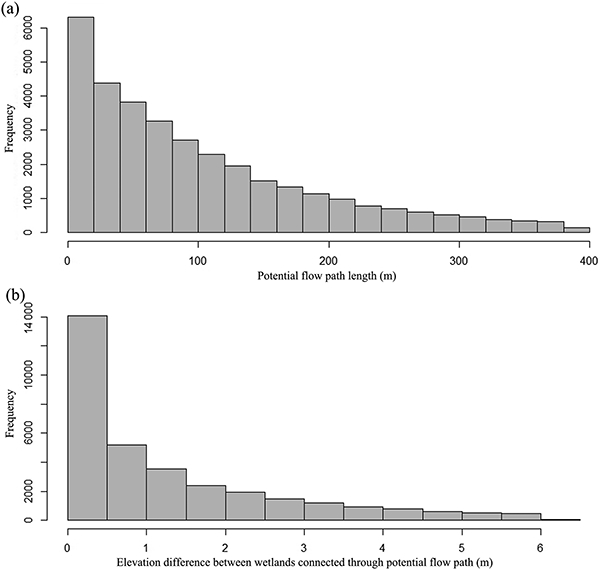
Histogram of potential wetland connectivity. (a) Potential flow path lengths; (b) elevation differences between wetlands connected through potential flow paths.
5. Discussion
The lidar data we used in this study were collected in late October 2011, which was an extremely wet period according to the Palmer Hydrological Drought Index (see Fig. 6). Most wetlands exhibited high water levels and large water extents, which can be evidenced from the lidar intensity image in Fig. 7 and the aerial photograph in Fig. 9. It can be clearly seen that most wetlands, particularly those larger ones, appeared to have larger water extents compared to the NWI polygons. A substantial number of inundated NWI wetlands were found to coalesce with adjoining lidar- based wetland depressions and form larger wetland complexes. Lidar data acquired during high water levels are desirable for studying maximum water extents of prairie wetlands. However, the use of wet-period lidar data alone is not ideal for studying the fill-and-spill hydrology of prairie wetlands. Since lidar sensors working in the near-infrared spectrum typically could not penetrate water, it is impractical to derive bathymetry of the wetland depressions. As a result, the delineation and characterization of individual wetland depressions nested within larger inundated wetland complexes were not possible. Bathymetric lidar systems with a green laser onboard offer a promising solution for acquiring wetland basin morphometry due to the higher penetration capability of the green laser (Wang and Philpot, 2007). In addition, the derivation of antecedent water depth and volume of wetland depressions is difficult, which can only be estimated using empirical equations based on the statistical relationship between depression area and depression volume (Hayashi and Van der Kamp, 2000; Gleason et al., 2007). As noted earlier, the volume of water in the 15 784 inundated wetlands was estimated to be 448.5 million m3. Ideally, using multiple lidar datasets acquired in both dry and deluge conditions in conjunction with time-series aerial photographs would be essential for studying the fill-and-spill mechanism of prairie wetlands. In this case, we could use the dry-period lidar data to delineate and characterize the morphology of individual wetland depressions before the fill-and-spill processes occur. Furthermore, we can derive the potential flow paths and project the coalescing of wetland depressions after the fill-and-spill processes initiate. The wet-period lidar data and time-series aerial photographs can serve as validation datasets to evaluate the fill-and-spill patterns.
It is also worth noting that the proposed methodology in this study was designed to reflect the topography and hydrologic connectivity between wetlands in the prairie pothole region. We have made assumptions to simplify the complex prairie hydrology. Physically based hydrological models (e.g., Brunner and Simmons, 2012; Ameli and Creed, 2017) have not yet been integrated into our framework. However, fill-and-spill is a complex and spatially distributed hydrological process highly affected by many factors, such as surface topography, surface roughness, soil infiltration, soil properties, depression storage, precipitation, evapotranspiration, snowmelt runoff, and groundwater exchange (Tromp-van Meerveld and McDonnell, 2006a, b; Evenson et al., 2015; Zhao and Wu, 2015; Evenson et al., 2016; Hayashi et al., 2016). Nevertheless, our study presents the first attempt to use lidar data for deriving nested wetland catchments and simulating flow paths in the broad- scale Pipestem subbasin in the PPR. Previous studies utilizing high-resolution digital elevation data (e.g., lidar, Interferometric Synthetic Aperture Radar - IfSAR) for studying prairie wetlands were mostly confined to small-scale areas (e.g., plot scale, small-watershed scale) with a limited number of wetlands, whereas broad-scale studies using physically based hydrological models have rarely used lidar data to delineate and characterize individual wetland depressions or catchments. The connectivity between surface and subsurface waters and the associated hydrologic and ecological functions are spatially variable and temporally dynamic (Blume and van Meerveld, 2015). Coupled surface- subsurface flow models with hydrologic, biogeochemical, ecologic, and geographic perspectives have yet to be developed for broad-scale studies in the PPR (Golden et al., 2014; Amado et al., 2016). Further efforts are still needed to improve the understanding of the integrated surface-water and groundwater processes of prairie wetlands.
6. Conclusions
Accurate delineation and characterization of wetland depressions and catchments are essential to understanding and correctly analyzing the hydrology of many landscapes, including the prairie pothole region. In this study, we delineated the inundation areas while reducing the confounding factor of live trees by using the lidar-derived DEM in conjunction with the coincident lidar intensity imagery. In addition, we developed a semi-automated framework for identifying nested hierarchical wetland depressions and delineating their corresponding catchments using the localized contour tree method. Furthermore, we quantified the potential hydrologic connectivity between wetlands and streams based on the overland flow networks derived using the least-cost- path algorithm on lidar data. Although the results presented in this study are specific to the Pipestem subbasin, the proposed framework can be easily adopted and adapted to other wetland regions where lidar data are available. The new tools that we developed and have made freely available to the scientific community for identifying potential hydrologic connectivity between wetlands and stream networks can better inform regulatory decisions and enhance the ability to better manage wetlands under various planning scenarios. The resulting flow network delineated potential flow paths connecting wetland depressions to each other or to the river network on scales finer than those available through the National Hydrography Dataset. The results demonstrated that our proposed framework is promising for improving overland flow modeling and hydrologic connectivity analysis (Golden et al., 2017).
Broad-scale prairie wetland hydrology has been difficult to study with traditional remote sensing methods using multi- spectral satellite data due to the limited spatial resolution and the interference of tree canopy (Klemas, 2011; Gallant, 2015). Lidar-derived DEMs can be used to map potential hydrologic flow pathways, which regulate the ability of wetlands to provide ecosystem services (Lang and McCarty, 2009). This study is an initial step towards the development of a spatially distributed hydrologic model to fully describe the hydrologic processes in broad-scale prairie wetlands. Additional field work and the integration of physically based models of surface and subsurface processes would benefit the study. Importantly, the results capture temporary and ephemeral hydrologic connections and provide essential information for wetland scientists and decision-makers to more effectively plan for current and future management of prairie wetlands.
Acknowledgements.
The authors would like to thank Rose Kwok, Daniel Auerbach, Jan Seibert, and two anonymous journal reviewers for providing insightful comments which improved the quality of the paper. This paper has been reviewed in accordance with the US Environmental Protection Agency’s peer and administrative review policies and approved for publication. Mention of trade names or commercial products does not constitute endorsement or recommendation for use. Statements in this publication reflect the authors’ professional views and opinions and should not be construed as representing any determination or policy of the US Environmental Protection Agency.
Footnotes
Competing interests. The authors declare that they have no conflict of interest.
Code and data availability. The data and ArcGIS toolbox developed for this paper are available for download at https://GISTools.github.io/.
References
- Amado AA, Politano M, Schilling K, and Weber L: Investigating Hydrologic Connectivity of a Drained Prairie Pothole Region Wetland Complex using a Fully Integrated, Physically- Based Model, Wetlands, https://doi.org/10.1007/s13157-016- 0800-5, in press, 2016. [Google Scholar]
- Ameli AA and Creed IF: Quantifying hydrologic connectivity of wetlands to surface water systems, Hydrol. Earth Syst. Sci, 21,1791–1808, 10.5194/hess-21-1791-2017, 2017. [DOI] [Google Scholar]
- Bengtson ML and Padmanabhan G: A hydrologic model for assessing the influence of wetlands on flood hydrographs in the Red River Basin: Development and application, North Dakota Water Resources Research Institute, North Dakota State University, North Dakota, 1999. [Google Scholar]
- Blume T and van Meerveld HJ: From hillslope to stream: methods to investigate subsurface connectivity, Wiley Interdis- cipl. Rev.: Water, 2,177–198, 10.1002/wat2.1071, 2015. [DOI] [Google Scholar]
- Brunner P and Simmons CT: HydroGeoSphere: A Fully Integrated, Physically Based Hydrological Model, Ground Water, 50, 170–176, 10.1111/j.1745-6584.2011.00882.x, 2012. [DOI] [Google Scholar]
- Chu X: Delineation of Pothole-Dominated Wetlands and Modeling of Their Threshold Behaviors, J. Hydrol. Eng, 22, D5015003, 10.1061/(ASCE)HE.1943-5584.0001224, 2015. [DOI] [Google Scholar]
- Cohen MJ, Creed IF, Alexander L, Basu NB, Calhoun AJ, Craft C, D’Amico E, DeKeyser E, Fowler L, and Golden HE: Do geographically isolated wetlands influence landscape functions?, P. Natl. Acad. Sci. USA, 113, 1978–1986, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cowardin LM, Carter V, Golet FC, and LaRoe ET: Classification of wetlands and deepwater habitats of the United States, US Department of the Interior, Fish and Wildlife Service, Washington, D.C., 1979. [Google Scholar]
- Dahl TE: Wetlands losses in the United States, 1780’s to 1980’s Report to the Congress, US Department of the Interior, Fish and Wildlife Service, Washington, D.C., 1990. [Google Scholar]
- Dahl TE: Status and trends of prairie wetlands in the United States 1997 to 2009, US Department of the Interior, Fish and Wildlife Service, Ecological Services, Washington, D.C., 2014. [Google Scholar]
- Evenson GR, Golden HE, Lane CR, and D’Amico E: Geographically isolated wetlands and watershed hydrology: A modified model analysis, J. Hydrol, 529, 240–256, 10.1016/jjhydrol.2015.07.039, 2015. [DOI] [Google Scholar]
- Evenson GR, Golden HE, Lane CR, and D’Amico E: An improved representation of geographically isolated wetlands in a watershed-scale hydrologic model, Hydrol. Process, 30, 4168–4184, 10.1002/hyp.10930, 2016. [DOI] [Google Scholar]
- Gallant A:The Challenges of Remote Monitoring of Wetlands, Remote Sensing, 7, 10938–10950, 10.3390/rs70810938, 2015. [DOI] [Google Scholar]
- Gleason RA, Tangen BA, Laubhan MK, Kermes KE, and Euliss NH Jr.: Estimating water storage capacity of existing and potentially restorable wetland depressions in a subbasin of the Red River of the North, US Geological Survey Open-File Report 2007–1159, US Geological Survey, Reston, Virginia, 36 pp., 2007. [Google Scholar]
- Gleason RA, Laubhan MK, Tangen BA, and Kermes KE: Ecosystem services derived from wetland conservation practices in the United States Prairie Pothole Region with an emphasis on the US Department of Agriculture Conservation Reserve and Wetlands Reserve Programs, US Geological Survey, Reston, Virginia, 2008. [Google Scholar]
- Golden HE, Lane CR, Amatya DM, Bandilla KW, Kiperwas HR, Knightes CD, and Ssegane H : Hydrologic connectivity between geographically isolated wetlands and surface water systems: A review of select modeling methods, Environ. Model. Softw, 53, 190–206, 10.1016/j.envsoft.2013.12.004, 2014. [DOI] [Google Scholar]
- Golden HE, Creed I, Ali G, Basu N, Neff B, Rains M, McLaughlin D, Alexander L, Ameli A, Christensen J, Evenson G, Jones C, Lane C, and Lang M: Scientific tools for integrating geographically isolated wetlands into land management decisions, Front. Ecol. Environ, 10.1002/fee.1504, in press, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hayashi M and Van der Kamp G: Simple equations to represent the volume-area-depth relations of shallow wetlands in small topographic depressions, J. Hydrol, 237, 74–85, 2000. [Google Scholar]
- Hayashi M, van der Kamp G, and Rudolph DL: Water and solute transfer between a prairie wetland and adjacent uplands, 1. Water balance, J. Hydrol, 207, 42–55, 10.1016/S0022-1694(98)00098-5, 1998. [DOI] [Google Scholar]
- Hayashi M, van der Kamp G, and Rosenberry DO: Hydrology of Prairie Wetlands: Understanding the Integrated Surface- Water and Groundwater Processes, Wetlands, 36, 237–254, 10.1007/s13157-016-0797-9, 2016. [DOI] [Google Scholar]
- Huang C, Peng Y, Lang M, Yeo IY, and McCarty G: Wetland inundation mapping and change monitoring using Landsat and airborne LiDAR data, Remote Sens. Environ, 141, 231–242, 2014. [Google Scholar]
- Huang S, Dahal D, Young C, Chander G, and Liu S: Integration of Palmer Drought Severity Index and remote sensing data to simulate wetland water surface from 1910 to 2009 in Cottonwood Lake area, North Dakota, Remote Sens. Environ, 115, 3377–3389, 2011a. [Google Scholar]
- Huang S, Young C, Feng M, Heidemann K, Cushing M, Mushet DM, and Liu S: Demonstration of a conceptual model for using LiDAR to improve the estimation of floodwater mitigation potential of Prairie Pothole Region wetlands, J. Hydrol, 405, 417–426, 2011b. [Google Scholar]
- Hubbard DE and Linder RL: Spring runoff retention in prairie pothole wetlands, J. Soil Water Conserv, 41, 122–125, 1986. [Google Scholar]
- Jin S, Yang L, Danielson P, Homer C, Fry J, and Xian G: A comprehensive change detection method for updating the national land cover database to circa 2011, Remote Sens. Environ, 132, 159–175, 2013. [Google Scholar]
- Johnston CA: Wetland losses due to row crop expansion in the dakota prairie pothole region, Wetlands, 33, 175–182, 10.1007/s13157-012-0365-x, 2013. [DOI] [Google Scholar]
- Keddy PA: Wetland ecology: principles and conservation, Cambridge University Press, Cambridge, 2010. [Google Scholar]
- Klemas V: Remote sensing of wetlands: case studies comparing practical techniques, J. Coast. Res, 27, 418–427, 2011. [Google Scholar]
- Kweon IS and Kanade T: Extracting topographic terrain features from elevation maps, CVGIP: Image Understanding, 59, 171–182, 10.1006/ciun.1994.10, 1994. [DOI] [Google Scholar]
- Lane CR and D’Amico E: Identification of Putative Geographically Isolated Wetlands of the Conterminous United States, J. Am. Water Resour. Ass, 52, 705–722, 10.1111/1752-1688.12421, 2016. [DOI] [Google Scholar]
- Lang M and McCarty G: Lidar intensity for improved detection of inundation below the forest canopy, Wetlands, 29,1166–1178, 10.1672/08-197.1, 2009. [DOI] [Google Scholar]
- Lindsay JB and Creed IF: Distinguishing actual and artefact depressions in digital elevation data, Comput. Geosci, 32,1192–1204, 10.1016/j.cageo.2005.11.002, 2006. [DOI] [Google Scholar]
- McCauley L and Anteau M: Generating Nested Wetland Catchments with Readily-Available Digital Elevation Data May Improve Evaluations of Land-Use Change on Wetlands, Wetlands, 34, 1123–1132, https://doi.org/10.1007/s13157-014-0571- 9, 2014. [Google Scholar]
- Metz M, Mitasova H, and Harmon RS: Efficient extraction of drainage networks from massive, radar-based elevation models with least cost path search, Hydrol. Earth Syst. Sci, 15, 667–678, 10.5194/hess-15-667-2011, 2011. [DOI] [Google Scholar]
- Miller MW and Nudds TD: Prairie landscape change and flooding in the Mississippi River Valley, Conserv. Biol, 10, 847–853, 1996. [Google Scholar]
- Minke AGN: Estimating water storage of prairie pothole wetlands, University of Saskatchewan, Saskatchewan, 2009. [Google Scholar]
- Mushet DM and Euliss NH: The Cottonwood Lake study area, a long-term wetland ecosystem monitoring site, US Geological Survey 2327–6932, US Geological Survey, Reston, Virginia, 2012. [Google Scholar]
- Mushet DM, Calhoun AJ, Alexander LC, Cohen MJ, DeKeyser ES, Fowler L, Lane CR, Lang MW, Rains MC, and Walls SC: Geographically isolated wetlands: rethinking a misnomer, Wetlands, 35, 423–431, 2015. [Google Scholar]
- O’Callaghan JF and Mark DM: The extraction of drainage networks from digital elevation data, Comput. Vis. Graph. Image Process, 28, 323–344, 1984. [Google Scholar]
- Oslund FT, Johnson RR, and Hertel DR: Assessing Wetland Changes in the Prairie Pothole Region of Minnesota From 1980 to 2007, J. Fish Wildlife Manage, 1, 131–135, 10.3996/122009-JFWM-027, 2010. [DOI] [Google Scholar]
- Rover J and Mushet DM: 16 Mapping Wetlands and Surface Water in the Prairie Pothole Region of North America, Remote Sens. Wetlands: Appl. Adv, 347, 347–368, 2015. [Google Scholar]
- Shaw DA, Vanderkamp G, Conly FM, Pietroniro A, and Martz L: The fill-spill hydrology of Prairie wetland complexes during drought and deluge, Hydrol. Process, 26, 3147–3156, 2012. [Google Scholar]
- Shaw DA, Pietroniro A, and Martz L: Topographic analysis for the prairie pothole region of Western Canada, Hydrol. Process, 27,3105–3114, 2013. [Google Scholar]
- Sloan CE: Ground-water hydrology of prairie potholes in North Dakota, Professional Paper 585-C, US Government Printing Office, Washington, D.C., USA, 1972. [Google Scholar]
- Stanislawski LV: Feature pruning by upstream drainage area to support automated generalization of the United States National Hydrography Dataset, Comput. Environ. Urb. Syst, 33, 325–333, 10.1016/j.compenvurbsys.2009.07.004, 2009. [DOI] [Google Scholar]
- Steen V, Skagen SK, and Noon BR: Vulnerability of Breeding Waterbirds to Climate Change in the Prairie Pothole Region, U.S.A, PLoS ONE, 9, e96747, 10.1371/journal.pone.0096747, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stein A, Pebesma E, Heuvelink G, Melles SJ, Jones NE, Schmidt B, and Rayfield B: Spatial Statistics 2011: Mapping Global ChangeA least-cost path approach to stream delineation using lakes as patches and a digital elevation model as the cost surface, Proced. Environ. Sci, 7, 240–245, 10.1016/j.proenv.2011.07.042, 2011. [DOI] [Google Scholar]
- Tiner RW: NWI maps: what they tell us, Natl. Wetlands Newslett, 19, 7–12, 1997. [Google Scholar]
- Tiner RW: Geographically isolated wetlands of the United States, Wetlands, 23, 494–516, https://doi.org/10.1672/0277- 5212(2003)023[0494:GIW0TU]2.0.C0;2, 2003. [Google Scholar]
- Todhunter PE and Rundquist BC: Terminal lake flooding and wetland expansion in Nelson County, North Dakota, Phys. Ge- ogr, 25, 68–85, 2004. [Google Scholar]
- Tromp-van Meerveld HJ and McDonnell JJ: Threshold relations in subsurface stormflow: 2. The fill and spill hypothesis, Water Resour. Res, 42, W02411, 10.1029/2004WR003800, 2006a. [DOI] [Google Scholar]
- Tromp-van Meerveld HJ and McDonnell JJ: Threshold relations in subsurface stormflow: 1. A 147-storm analysis of the Panola hillslope, Water Resour. Res, 42, W02410, 10.1029/2004WR003778, 2006b. [DOI] [Google Scholar]
- US EPA: Connectivity and effects of streams and wetlands on downstream waters: A review and synthesis of the scientific evidence, US Environmental Protection Agency, Washington, D.C., 2015. [Google Scholar]
- Vanderhoof M, Alexander L, and Todd MJ: Temporal and spatial patterns of wetland extent influence variability of surface water connectivity in the Prairie Pothole Region, United States, Landscape Ecol., 31, 805–824, https://doi.org/10.1007/s10980- 015-0290-5, 2016. [Google Scholar]
- Vanderhoof M, Distler H, Mendiola D, and Lang M: Integrating Radarsat-2, Lidar, and Worldview-3 Imagery to Maximize Detection of Forested Inundation Extent in the Delmarva Peninsula, USA, Remote Sensing, 9, 105, 10.3390/rs9020105, 2017. [DOI] [Google Scholar]
- Wang C-K and Philpot WD: Using airborne bathymetric lidar to detect bottom type variation in shallow waters, Remote Sens. Environ, 106, 123–135, 2007. [Google Scholar]
- Wang L and Liu H: An efficient method for identifying and filling surface depressions in digital elevation models for hydrologic analysis and modelling, Int. J. Geogr. Inform. Sci, 20, 193–213, 2006. [Google Scholar]
- Watmough MD and Schmoll MJ: Environment Canada’s Prairie & Northern Region Habitat Monitoring Program, Phase II: Recent Habitat Trends in the Prairie Habitat Joint Venture, Canadian Wildlife Service, Edmonton, Alberta, 2007. [Google Scholar]
- Winter TC: Hydrologic studies of wetlands in the northern prairie, in: Northern Prairie Wetlands, edited by: Van Der Valk AG, Iowa-State University Press, Ames, IA, 1989. [Google Scholar]
- Winter TC and Rosenberry DO: The interaction of ground water with prairie pothole wetlands in the Cottonwood Lake area, east-central North Dakota, 1979–1990, Wetlands, 15, 193–211, 1995. [Google Scholar]
- Wright CK and Wimberly MC: Recent land use change in the Western Corn Belt threatens grasslands and wetlands, P. Natl. Acad. Sci. USA, 110, 4134–4139, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Q and Lane CR: Delineation and Quantification of Wetland Depressions in the Prairie Pothole Region of North Dakota, Wetlands, 36, 215–227, 10.1007/s13157-015-0731-6, 2016. [DOI] [Google Scholar]
- Wu Q, Lane C, and Liu H: An Effective Method for Detecting Potential Woodland Vernal Pools Using High-Resolution LiDAR Data and Aerial Imagery, Remote Sensing, 6, 11444–11467, 10.3390/rs61111444, 2014. [DOI] [Google Scholar]
- Wu Q, Liu H, Wang S, Yu B, Beck R, and Hinkel K: A localized contour tree method for deriving geometric and topological properties of complex surface depressions based on high- resolution topographical data, Int. J. Geogr. Inform. Sci, 29, 2041–2060, 10.1080/13658816.2015.1038719, 2015. [DOI] [Google Scholar]
- Zhang B, Schwartz FW, and Liu G: Systematics in the size structure of prairie pothole lakes through drought and deluge, Water Resour. Res, 45, W04421, 10.1029/2008WR006878, 2009. [DOI] [Google Scholar]
- Zhao L and Wu F: Simulation of Runoff Hydrograph on Soil Surfaces with Different Microtopography Using a Travel Time Method at the Plot Scale, PloS one, 10, e0130794, 10.1371/journal.pone.0130794, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X: GIS for Environmental Applications: A Practical Approach, Routledge, New York, 2016. [Google Scholar]


