The Impact of Dialect Density on the Growth of Language and Reading in African American Children

Abstract

Purpose

The goal of the current study was to examine the impact of dialect density on the growth of oral language and reading skills in a sample of African American English (AAE)-speaking children reared in urban communities.

Method

Eight hundred thirty-five African American children in first through fifth grades participated. Using an accelerated cohort design, univariate and bivariate growth models were employed to examine dialect density, oral language and reading, and the relationships between these variables.

Results

For the univariate models, results indicated that (a) dialect density decreased over time by approximately 5% per year beyond first grade, (b) language skills improved approximately 0.5 SD per year, and (c) reading comprehension increased significantly from first to second grade and slowed 23% per year in second through fifth grades. Results from the bivariate models revealed that (a) dialect density and language ability are negatively associated, although dialect density did not affect change in language over time, and (b) higher dialect density is related to slower growth in reading.

Conclusions

Findings from this investigation provide converging evidence for accounts in the extant literature particularly supporting a negative relationship between dialect density and oral language and between dialect density and reading while also contributing novel longitudinal evidence that suggests that changes in dialect use over time may be driven by oral language skills and that reading and dialect have a reciprocal relationship.

African American English (AAE) is a major dialect of American English that has been studied widely across disciplines and language domains. AAE impacts primarily the morphosyntactic (e.g., deletion of copula and auxiliary forms of BE; deletion of third-person singular “s”) and phonological (e.g., deletion of final consonant sounds; substitution of f/Θ in word final position) structures of American English, although its impact on semantics and pragmatics has also been examined (Stockman, 2010; Stockman, Karasinski, & Guillory, 2008; Stockman & Vaughn-Cooke, 1984, 1986). Within the field of speech-language pathology, the impact of AAE on assessment and diagnosis of speech and language impairments has been the primary focus. These studies, focused on difference versus disorder (Campbell, Dollaghan, & Needleman, 1997; Craig & Washington, 2002; Newkirk-Turner, Oetting, & Stockman, 2014; Seymour, Bland-Stewart, & Green, 1998; Stockman, Guillory, Seibert, & Boultd, 2013) and disorder within difference (Oetting, Gregory, & Riviere, 2016), have highlighted a significant overlap between the features of AAE and the linguistic characteristics of language impairment in mainstream American English (MAE) speakers. Accordingly, the extant literature includes many studies focused on distinguishing the cultural linguistic differences of AAE speakers from the language disorders of MAE speakers (Garrity & Oetting, 2010; Ivy & Masterson, 2011; Kohler et al., 2007; Oetting et al., 2010; Seymour et al., 1998; Stockman, 2010) as well as studies focused on improving diagnostic accuracy of language impairments within AAE speakers, which includes not only eliminating false positives but also avoiding false negatives (Craig & Washington, 2000; Oetting & McDonald, 2001; Washington & Craig, 2004).

In addition to its documented impact on oral language, AAE has been examined for its potential influence on the development of reading skills. The preponderance of the evidence suggests that reading is impacted by the presence of AAE (Connor & Craig, 2006; Terry, 2006, 2014; Terry, Connor, Johnson, Stuckey, & Tani, 2016; Terry, Connor, Thomas-Tate, & Love, 2010). In some cases, African American (AA) children who use the most dialect have been found to struggle with reading across a variety of skill areas, including decoding, development of phonological awareness, and reading comprehension (Charity, Scarborough, & Griffin, 2004; Craig, Thompson, Washington, & Potter, 2004; Terry et al., 2016), whereas other studies have demonstrated strengths in early reading and language skills in the presence of substantial use of AAE (Connor & Craig, 2006; Craig & Washington, 1994).

The degree to which a child uses a dialectal or diglossic form of a major language has been identified as an important variable impacting language and reading skill development across languages, most notably Arabic (Aram et al., 2013; Saiegh-Haddad, 2005), Greek-Cypriot (Ioannidou, 2009; Triga & Kakopsitou, 2010), and Australian Aboriginal English (Bennet & Lancaster, 2013; Scull, 2016). Quantification of the degree of dialect use within a speaker's oral productions is referred to as “dialect density.” Oetting and McDonald (2002) identified three different methods across studies used to measure dialect density. What all three measurement methods share is that they are focused on the number of dialect features present in a child's oral language sample at either the word or utterance level and the percentage, or proportion, of dialect used in the overall language sample. These methods are highly correlated with each other (Horton & Apel, 2014; Oetting & McDonald, 2002). Dialect density has become a standard metric used in investigations focused on AAE in children. The result has been a growing body of evidence for AAE speakers that acknowledges the importance of considering dialect density when examining any language-influenced skill area, including oral language (Craig et al., 2004; Thompson, Craig, & Washington, 2004; Washington, Craig, & Kushmaul, 1998), reading (Charity et al., 2004; Connor & Craig, 2006; Terry, 2014; Terry et al., 2010), and writing (Ivy & Masterson, 2011). These studies have demonstrated overwhelmingly that the degree to which an AA child utilizes dialect is related to overall language or literacy performance.

A crucial complexity and limitation of prior research is that all three of these constructs (dialect, language, and literacy) may change over time and their relations may be complex. The absence of longitudinal research in this line of inquiry has limited our understanding of the changes that occur in dialect density over time and how these changes impact oral language and reading skills. The purpose of this investigation was to examine dialect density in relation to reading and oral language in a large sample of AA children growing up in urban poverty. The overarching research question driving this investigation is “How does dialect density impact the growth of language and reading skill development in AA children?” To answer this question, we examine the longitudinal nature of each of three constructs for this population: dialect, language, and reading.

Dialect Density and Oral Language

Studies of oral language and AAE dialect in young children and youth have had three broad goals in educational and clinical contexts: (a) to document the developmental nature of AAE, including the use of specific morphological, syntactic, and phonological dialect forms and their impact in various discourse contexts (Craig & Washington, 2002; Horton & Apel, 2014; Mills, 2015; Mills, Watkins, Washington, Nippold, & Schneider, 2013; Moyle, Heilmann, & Finneran, 2014; Thompson et al., 2004); (b) to examine the impact of AAE on educational skills, in particular, reading, spelling, and writing (Ivy & Masterson, 2011; Kohler et al., 2007; Thompson et al., 2004); and (c) to differentiate language difference from language disorder in clinical speech and language contexts (Garrity & Oetting, 2010; Newkirk-Turner et al., 2014; Oetting et al., 2010). These studies have been influential in shaping our current thinking about dialect and its impact, in that they have confirmed its developmental nature and documented differences in the use of dialect across ages in cross-sectional samples of dialect users.

The density with which AAE is produced changes dramatically as children get older and are exposed to MAE through schooling. Decreased dialect density has been reported for many AAE-speaking children with increasing age and schooling, in both oral and written language (Craig et al., 2004; Ivy & Masterson, 2011; Thompson et al., 2004). For example, in a cross-sectional study of the oral language performance of 400 preschool through fifth grade children, Craig and Washington (2004) examined systematic changes in dialect use by grade. Participants varied by socioeconomic status and urban versus suburban community of residence. The findings revealed no significant changes in dialect use from preschool to kindergarten. However, there was a decline in dialect density in first grade that remained stable across subsequent grades. Importantly, children who did not shift, or decrease their dialect density, performed lower on measures of reading and vocabulary. Nonshifters were more likely to be from urban than suburban communities. Connor and Craig (2006) examined the language and emergent literacy skills of a small sample (N = 63) of AA preschoolers using hierarchical linear modeling. Participants' vocabulary, oral narrative, and sentence imitation skills were assessed in the fall and spring of the preschool year. In addition, letter–word identification and rhyming were examined. Results indicated that children who used AAE at high and low densities significantly outperformed their peers whose dialect density was characterized as moderate but that this relation decreased in a nonlinear, quadratic way. The authors interpreted these outcomes, based on the quadratic trend, as support of prolific use of AAE as a sign of linguistic strength among preschool-aged AAE speakers that positively influenced their performance on both language and reading measures. Interestingly, only vocabulary at the time of school entry was influenced by dialect density. The authors also reported clear evidence of “style shifting” among these young children. Specifically, their preschool-aged participants decreased the use of AAE in literacy and language contexts where Standard Classroom English was expected, demonstrating evidence of early dialect shifting ability. Ivy and Masterson (2011) examined the use of AAE in the spoken and written language of 15 AA third graders and 15 eighth graders. The goal of their study was to characterize the developmental shift in the use of AAE in spoken and written language for older versus younger children as well as to characterize differences across oral and written contexts. Third graders showed no significant difference in the use of AAE in oral and written contexts. Eighth graders, on the other hand, showed decreased use of AAE in their written language samples compared with third graders, but not in their spoken narratives. The authors estimated that approximately 67% of the participants shifted their use of dialect with increasing grade. Furthermore, their data suggested that this shift, especially in writing, will occur after third grade. Taken together, these studies provide a mixed picture of the impact of dialect density on the development of oral language skills as well as the ages at which children demonstrate changes in their overall dialect use. Specifically, they suggest that changes in the use of dialect occur across grades (based on differences between grades) and that these changes may impact use and development of language skills in either positive or negative ways.

With rare exception, these investigations of AAE density and oral language are cross-sectional. Although these studies have been important for contributing to our knowledge about the impact of dialect density in toddlers and preschoolers (Craig & Washington, 1994, 2002; Horton-Ikard, Weismer, & Edwards, 2005; Newkirk-Turner et al., 2014; Stockman et al., 2013), young school-aged children (Cleveland & Oetting, 2013; Craig et al., 2004; Garrity & Oetting, 2010; Pruitt & Oetting, 2009; Terry, 2006), and older children (Horton-Ikard & Miller, 2004), the cross-sectional nature of these investigations has not been maximally informative for understanding the complexity and changes in the growth of dialect density as they relate to changes in the growth of related skills such as language and reading or, conversely, how changes in the growth of language and reading potentially might impact changes in the use and growth of AAE. The exception to this trend of cross-sectional studies of AAE is Craig, Kolenic, and Hensel (2014) who examined changes in dialect use across three time points for AA children in kindergarten through third grade. The focus of this investigation was to document dialect “shifting” across these early grades as well as to examine how metalinguistic and cognitive factors influenced this shift. Findings showed that the use of AAE decreased significantly at each grade level in selected contexts (narrative production) but showed little difference by grade in others (picture description). This is consistent with previous cross-sectional studies focused on contextual differences in the use of AAE (Connor & Craig, 2006; Thompson et al., 2004). Importantly, not all children demonstrated shifts in dialect use across these early grades, continuing to produce dialect at comparable levels across the three time points. Furthermore, shifting was determined to be significantly influenced by other variables including executive function and cognition. However, only the presence of a significant relationship between these skills and dialect was established. No information regarding the growth of these important skills as they relate to dialect was offered. Whereas it is important to acknowledge these complex relationships, it is also critical that we move toward trying to develop a better understanding of how AAE itself changes over time as well as specifically how AAE impacts the growth of important developmental and educational skills. The current investigation contributes important information concerning dialect use, as well as its changes and influences, using a longitudinal design, from first through fifth grade to examine the contribution of dialect to the growth of early language and reading skills.

Dialect Density and Reading

The use of AAE in educational contexts has focused primarily on language-based academic skills, including reading, spelling, and writing. National reading data document the significant difficulty with reading development experienced by AA children (Morgan, Farkas, & Wu, 2011; National Assessment of Education Progress [NAEP], 2015). The 2016 NAEP results indicated that only 17% of AA fourth graders were able to read at a proficient level (NAEP, 2015). The specific role of AAE in overall reading performance, however, is likely complex and not well understood.

Compared with oral language, the findings from studies examining the relationship between reading and dialect have been somewhat more consistent. Kohler et al. (2007) examined the impact of AAE dialect on phonemic awareness and nonword spelling tasks in 80 AA first and third graders. Findings were that phonologically based dialect density measures did not explain differences in phonological processing performance and that children with a higher dialect density produced more nonword spelling errors; these errors were influenced by AAE phonological patterns. Charity et al. (2004) investigated the role of familiarity with school English on early reading achievement for a sample of 217 low-income, urban AA children. Findings suggested that familiarity with Standard Classroom English was associated with better reading achievement. Importantly, familiarity with classroom English varied widely across their low-socioeconomic-status sample. In a more recent investigation, Gatlin and Wanzek (2015) performed a meta-analysis focused on the relationship between use of dialect and literacy skills. Results showed a consistent, negative, and moderate relationship between dialect and overall literacy performance and for dialect and reading specifically. For writing, the relationship was also negative but was smaller. Importantly, not all participants in the studies included were speakers of AAE but could be speakers of other nonmainstream dialects of English. These outcomes are similar to the work of Terry and colleagues (Terry, 2006, 2014; Terry et al., 2016, 2010) whose studies document significant, negative relationships between dialect and development of reading skills, although they do not focus specifically on AAE. Overall, the negative relationship between substantial use of AAE/dialects and reading achievement has been consistently reported. An exception to these consistent negative findings is Connor and Craig (2006) who reported positive relationships between high dialect use and emergent literacy skills in young AAE speakers. These findings mirror those of Craig and Washington (1994) who reported that, at the time of school entry, AA children who are high dialect users demonstrate strong early syntactic development. The positive outcomes of Connor and Craig and those of Craig and Washington suggest that, for very young children entering school, substantial use of AAE may be a sign of strong early language skills but that children's later reading skills may be negatively impacted by the presence of AAE.

This Study

The purpose of this investigation was to address the question, “How does dialect density impact the growth of language and reading skill development in AA children?” Previous investigations of language and reading have demonstrated mixed results for the reported relationship between AAE and oral language and between AAE and reading. In most cases, the impact of AAE is reportedly mediated by the density with which it is produced. Children who are high dialect users generally show poorer outcomes in oral and written language and reading achievement than do their peers who use lower amounts of AAE (Charity et al., 2004; Gatlin & Wanzek, 2015; Ivy & Masterson, 2011). The complexity of these relationships has not been fully explored, as most of these studies have utilized cross-sectional designs.

In the current study, the relationships between dialect density, general oral language skills, and reading were examined in a large sample of AA children (n = 835) enrolled in first through fifth grades in a large urban, metropolitan area. Participants were administered a battery of language, reading, and cognitive assessments. Data were sampled using a 5-year longitudinal design in which each child was tested across 2 years of the project using an accelerated cohort design. The following research questions were posed:

1. What is the nature of change in dialect density in AA children in first through fifth grades?

2. How does dialect density relate to the change in language and reading in these children?

Method

Participants

Participants were enrolled in a larger project focused on language, literacy, and dialectal variation. The larger project included 890 AA boys and girls in first through fifth grades from a major urban school district in the Southeastern United States. Fifty-five of these children were enrolled in special education services based on their school records and were excluded from analysis in the current project. Accordingly, the current analytic sample included 835 children.

Table 1 presents participant characteristics. Participants ranged in age from 5.8 to 12.5 years (M = 8.3 years, SD = 1.3 years). The sample had nonverbal intelligence within normal limits (M = 97.36, SD = 14.83) as measured by the Kaufman Brief Intelligence Test–Second Edition (Kaufman & Kaufman, 2004). Approximately half of the participants were boys (48%). Participants were enrolled in schools in very-low-income communities and attended traditional public elementary schools. In these high-poverty schools, 87%–100% of children qualified for participation in the National School Lunch program, which provides free or reduced priced meals to low-income students.

Table 1.

Demographic characteristics of students by cohort.

Cohort	Sample size in each grade					Women (%)	Age		KBIT
	1	2	3	4	5		M	SD	M	SD
1-1	131	76	—	—	—	50	6.83	0.41	95.49	14.44
1-2	—	126	85	—	—	60	7.88	0.49	96.51	15.17
1-3	—	—	123	76	—	48	8.86	0.47	96.40	15.23
1-4	—	—	—	112	65	52	9.97	0.60	95.19	13.58
2-1	123	52	—	—	—	55	6.86	0.48	97.94	14.15
2-2	—	74	31	—	—	55	7.89	0.49	98.34	16.65
2-3	—	—	84	37	—	53	8.77	0.46	102.82	14.82
2-4	—	—	—	50	14	46	9.90	0.47	98.49	14.95
2-5	—	—	—	—	12	42	11.33	0.60	97.75	9.26
Total	254	328	323	275	91	53	8.26	1.29	97.36	14.83

Note. Cohort is a label for the group of children as they entered the study, by year and grade. For example, 1-2 refers to the first year, second grade students, and 2-4 refers to the second year, fourth grade students. Age is measured in years. KBIT is the standard score (M = 100, SD = 15). KBIT = Kaufman Brief Intelligence Test.

Recruitment of participants occurred during orientation sessions at the beginning of each academic year. A doctoral student assigned to the project attended the orientation, presented the project to parents, and distributed consent forms. Consents were distributed at seven different schools. All students who returned the consents and who were not receiving special education services were included.

Assessment Measures

Dialect status was measured using the Diagnostic Evaluation of Language Variation–Screening Test (DELV-ST; Seymour, Roeper, & de Villiers, 2003). The DELV-ST categorically characterizes children's responses along a continuum (i.e., mainstream, some variation from mainstream, or strong variation from mainstream) based on the number of phonological and morphosyntactic dialect features produced on 15 test items. Following the methods of Terry et al. (2010), we calculated the degree of language variation from children's responses to the DELV-ST using the following formula: dialect productions divided by the sum of dialect and MAE productions multiplied by 100, yielding a percentage of dialect use. Measuring dialect in this way is consistent with the work of other studies focused on AAE speakers that calculated dialect density by dividing AAE tokens by the total number of words or utterances (Connor & Craig, 2006; Horton & Apel, 2014; Oetting & McDonald, 2002; Terry et al., 2010).

Language performance was measured using selected subtests of the Test of Language Development–Primary: Fourth Edition (TOLD-P:4; Hammill & Newcomer, 2008b) and the Test of Language Development–Intermediate: Fourth Edition (Hammill & Newcomer, 2008a). The TOLD-P:4 is designed for use with children under 8 years old, and the Test of Language Development–Intermediate: Fourth Edition is designed for children 8 years and older. Accordingly, participants in first and second grades were administered the picture vocabulary, syntactic understanding, and morphological completion subtests of the TOLD-P:4, and participants in third, fourth, and fifth grades were administered the subtests picture vocabulary, sentence combining, and morphological comprehension.

Unfortunately, the two versions of the TOLD are not vertically scaled—a score on the primary version cannot be compared in a meaningful mathematical way with a score on the intermediate version, except via norm-referenced standard scores (called “scaled scores” in the manual, with a mean of 10 and a SD of 3). To overcome this lack of an appropriate developmental scale in our longitudinal sample, we fit a single-factor model of language to the second grade students in the study. Second grade students are at the recommended age boundary between the versions of the test (8 years old) and, depending on their performance, were administered the primary or intermediate version. Our resulting sample of second grade students included 205 who took three primary subtests, 110 students who took three intermediate subtests, and 16 students who took a mixture of subtests from each version. Because the intention of the TOLD is to measure general language ability, we fit a confirmatory factor model of a single factor to all six subtests for second graders, which treated the test scores as missing at random and jointly scaled all tests to indicate latent language ability. This model fits excellently (χ² = 3.78, df = 6, Comparative Fit Index = 1.00, Tucker Lewis Index = 1.02, root-mean-square error of approximation < 0.01) with good standardized loadings for the six subtests (median loading = 0.73). We then applied the parameters (loadings and intercepts) of this second grade model to the full sample of students across all grades for the versions of the tests they took. This is a model of strong invariance (Meredith, 1993; Vandenberg & Lance, 2000), which allows latent variances and means to be estimated across grades. Their resulting factor scores indicate a longitudinally consistent z score of latent language ability, using whatever subtests or versions they took (estimated via full information maximum likelihood). This developmental z score is the language score used in the current longitudinal study, with the mean and variance centered on second grade performance. This score allowed us to meaningfully compare scores across grades and index growth within children, regardless of which version of the test they received.

Reading skill was measured using the Passage Comprehension subtest of the Woodcock–Johnson Test of Achievement–Fourth Edition (Schrank, Mather, & McGrew, 2014). Passage Comprehension was selected because it is a test of comprehension of connected text that starts with letter and word recognition (e.g., for first and second graders) and progresses to cloze comprehension of words in sentences and short passages. In our models of literacy-related skills, the passage comprehension test is a consistently strong indicator of general reading ability.

Design

The larger project obtained 5-year longitudinal data from first through fifth grade AA students using an accelerated cohort design tested across 2 years of the project for each participant. Specifically, in the first year of the project, we tested one cohort of participants including 137 first graders, 134 second graders, 133 third graders, and 126 fourth graders, and in the second year, we retested about 63% of these children who were now second graders, third graders, fourth graders, and fifth graders, respectively. Meanwhile, in the second year, we also tested a new cohort of participants including 127 first graders, 77 second graders, 90 third graders, 54 fourth graders, and 12 fifth graders, and in the third year, we retested about 41% of these children. Accordingly, 54% of the sample had two data points included in the data set. Children tested for the first time in fifth grade had only one data point. Table 1 shows the sample size of each cohort at each test occasion after removing the 55 children involved in special education services.

Administration and Scoring Procedures

Data were collected in quiet spaces identified for use by the project in each child's school. Examiners were trained to administer each instrument as presented in the Examiner's Manuals. All data were collected by graduate students in communication sciences and disorders and related disciplines (e.g., education, developmental psychology, counseling psychology), who varied by race and ethnicity and were all native speakers of American English. Measures were scored utilizing published scoring criteria. Graduate students who were not involved in data collection were responsible for scoring each measure.

Reliability

Scoring reliability was established by double entering and scoring approximately 20% of the data for every assessment instrument. Double-blind scoring of the data was designed to ensure consistency and accuracy of scoring. In addition to scoring reliability, entry reliability was established to ensure the quality and accuracy of data input. Scores were calculated electronically using scoring tables that were created based on raw scores from the published scoring criteria. Agreement for scoring reliability was 100%, and entry reliability was 96%.

Analysis

Univariate Growth Models

Growth was described using dual change score models (McArdle, 2001; McArdle & Hamagami, 2001), which are individual growth curve models, allowing for individual variability in starting point (intercept) and linear rate of change (slope). Technical details of the models used in this study are presented in the Appendix.

Such models are an extension of simple regression in which each student's score can be predicted as a function of time (grade), such that each student may differ in their starting point (intercept) or their rate of change (slope). In addition, there is a proportional change parameter that can describe status at any given time point as a function of the previous time point. Such a proportional change can be positive (accelerating growth, as in compound interest) or negative (decelerating growth, as in slowing to an asymptote). Thus, dual change score models can accommodate nonlinear growth.

Sometimes, in estimating growth models, the structure implied may not fit the data and the model will have to be modified (McArdle, 2001). For example, it is possible that the variance of the slope factor will be problematically small and the model should be reduced to suggesting all trajectories are parallel. In addition, with five time points, not all of the proportional change will be equal, and the rate of proportional change could be irregular (i.e., there could be a shift in the compound interest rate of change).

Bivariate Growth Models

Two dual change score models can be put together into a single model of growth, with cross-construct influences. Such a model is a system of two equations (see Appendix), with two interesting features. First, the intercepts and slopes may be related, revealing how starting point and rate of change correlate across constructs. Second, change in one construct can be estimated to affect later performance in the other construct via a “coupling” parameter. Beyond the simple relation between slopes, the coupling parameters can index how change in one outcome may drive or in turn be driven by change in the other. Because change is described by prior status as well as by prior status in the other construct, these models can yield complex dynamics of differing amounts of change due to different levels of performance (e.g., low-performing students may change faster than high-performing students). These results will be shown graphically.

Results

Univariate Growth Models

Table 2 presents the descriptive statistics for the three outcome variables for each cohort of the longitudinal design. Overall, means were decreasing for dialect and increasing for language and reading comprehension. However, we wish to examine these across cohorts in a population level model of growth, allowing for student variation (i.e., with dual change score models).

Table 2.

Descriptive statistics for each cohort at each grade.

Cohort	Grade 1	Grade 2	Grade 3	Grade 4	Grade 5
	Dialect density
1-1	75.77 (23.06)	60.06 (23.60)	—	—	—
1-2	—	56.93 (28.11)	47.78 (26.73)	—	—
1-3	—	—	54.56 (21.64)	49.27 (25.71)	—
1-4	—	—	—	51.35 (26.93)	40.74 (25.59)
2-1	54.51 (31.63)	30.15 (25.69)	—	—	—
2-2	—	52.73 (31.66)	29.73 (31.73)	—	—
2-3	—	—	44.21 (28.32)	26.63 (25.22)	—
2-4	—	—	—	45.85 (28.47)	32.22 (32.70)
2-5	—	—	—	—	31.33 (22.88)
	Language
1-1	−0.74 (0.85)	−0.19 (0.82)	—	—	—
1-2	—	−0.11 (0.96)	0.49 (1.15)	—	—
1-3	—	—	0.04 (0.81)	0.78 (0.80)	—
1-4	—	—	—	0.72 (0.87)	1.08 (0.95)
2-1	−0.36 (0.94)	0.63 (0.90)	—	—	—
2-2	—	0.11 (0.91)	1.26 (1.19)	—	—
2-3	—	—	0.55 (1.04)	1.47 (1.06)	—
2-4	—	—	—	0.88 (1.05)	2.08 (1.17)
2-5	—	—	—	—	1.34 (0.86)
	Passage comprehension
1-1	450.74 (19.52)	471.93 (13.67)	—	—	—
1-2	—	473.82 (13.60)	482.76 (11.10)	—	—
1-3	—	—	477.82 (13.50)	483.83 (9.74)	—
1-4	—	—	—	483.21 (10.38)	489.42 (8.42)
2-1	455.85 (20.89)	476.29 (13.90)	—	—	—
2-2	—	472.34 (16.81)	485.1 (11.28)	—	—
2-3	—	—	482.02 (10.59)	488.89 (10.50)	—
2-4	—	—	—	486.42 (11.72)	492.57 (12.64)
2-5	—	—	—	—	491.50 (7.66)

Note. Cohort is a label for the group of children as they entered the study, by year and grade. For example, 1-2 refers to the first year, second grade students, and 2-4 refers to the second year, fourth grade students. Dialect density is on a percentage scale. Passage comprehension is on a W score (Schrank et al., 2014). Language is on a longitudinally consistent z score, from first to fifth grade.

Table 3 shows the fit statistics for the dual change score models fit to each of the three outcomes. In all of these univariate models, the individual slopes estimated with zero variance. Therefore, they are excluded from all models, suggesting that students grow in parallel trajectories. Table 3 shows that the dual change score model fit excellently for dialect density and for language (for a discussion of fit in structural equation modeling, see Marsh, Hau, & Grayson, 2005; Marsh, Hau, & Wen, 2004). The dual change score model did not fit well for Passage Comprehension (Comparative Fit Index < 0.90; root-mean-square error of approximation > 0.10). Visual inspection of the growth trajectories suggested that there was far more change between Grade 1 and 2 than between the other grades, for passage comprehension. We therefore fit a model that relaxed the first proportional change parameter but kept the following proportional change parameters consistent for Grades 2–5. This model, on the fourth row of Table 3, fits reasonably. Because these models fit reasonably, we examined the specific parameters for each model (see Equations 1–2).

Table 3.

Fit for univariate growth models.

Model	χ2	df	CFI	TLI	RMSEA
Dialect density	24.56	9	0.96	0.98	0.05
Language	23.22	9	0.96	0.98	0.04
Passage comprehension	91.06	9	0.72	0.87	0.11
Passage comprehension, modified	45.04	8	0.87	0.94	0.08

Note. Because the passage comprehension model did not fit well, the first proportional change parameter was freely estimated, whereas the others were held constant. See text for description. Estimates are reported in Table 4. CFI = Comparative Fit Index; RMSEA = root-mean-square error of approximation; TLI = Tucker Lewis Index.

Dialect Growth

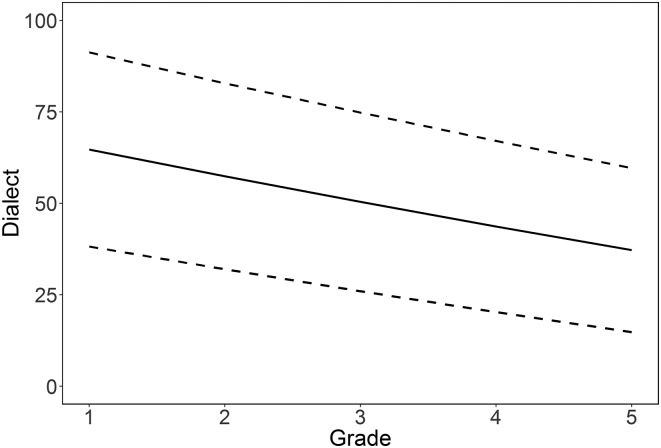
Table 4 presents the parameters from each of the three univariate growth models. The parameters presented here match those from Equation 1 (there is no variance for slopes because it estimated at zero). The first column of Table 4 shows that the average dialect density in Grade 1 was 64.72%, with an SD of 26% ($\sqrt{703.77}$). On average, students dropped 4.66% per year in dialect density. The proportional change (−0.04) was statistically significant but very small. Figure 1 presents the model expected trajectory for dialect density. The average downward trend is shown with the solid line, and dotted lines show high and low trajectories as well (±1 SD of the intercept factor). There is a slight curvature, showing the proportional change. Dialect density decreases in a nearly linear fashion from 65% in first grade by almost 5% per year (as suggested in Table 4).

Table 4.

Parameter estimates based on the univariate dual change score model for each outcome.

	Dialect density		Language		Passage comprehension
	Estimate	SE	Estimate	SE	Estimate	SE
Intercept mean	64.72	1.49	−0.55	0.05	22.69	0.05
Slope mean	−4.66	1.29	0.47	0.02	6.23	0.44
β Change	−0.04	0.02	0.03	0.02	−0.23	0.02
β Change, Grade 1	—	—	—	—	−0.25	0.02
Intercept variance	703.77	65.51	0.63	0.06	0.85	0.08
Residual variance	176.96	12.32	0.23	0.02	0.12	0.01

Note. All models were estimated with zero individual slope variance (i.e., parallel growth). Dashes indicate a parameter not applicable to the model. Passage comprehension W score was rescaled to 1/20th to obtain convergence.

Figure 1.

Predicted growth in dialect density from the univariate dual change score model. The solid line reflects mean growth, and the dotted lines are 1 SD above and below the mean. The metric is percent density.

Language Growth

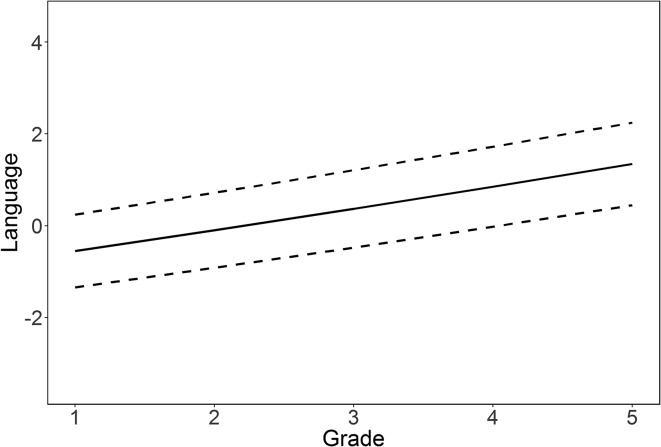
The language scores were on a z scale, across grades, centered at Grade 2. The mean intercept in Table 4 shows that first graders on average had a score of −0.55 and grew at 0.47 unit per year. The proportional change was not statistically significant (0.03), so growth was essentially linear. Figure 2 shows that language performance increased from a mean of −0.55 in first grade by about half a standard deviation per year, with average performance reaching above 1.0 unit by fifth grade.

Figure 2.

Predicted growth in language from the univariate dual change score model. The solid line reflects mean growth, and the dotted lines are 1 SD above and below the mean. The scale is a developmental z score centered at second grade (see text for details).

Reading Growth

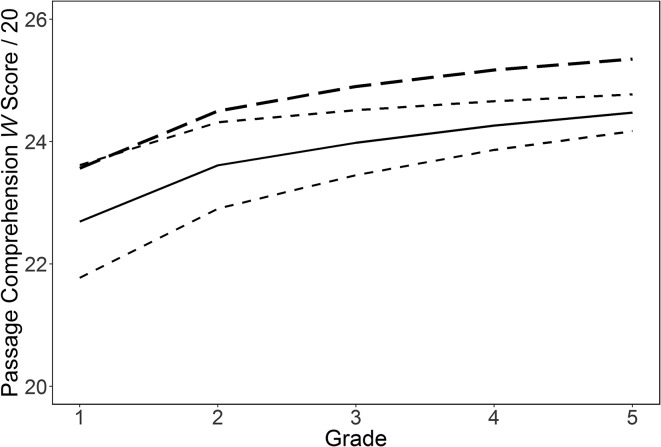
To get sensible estimation of the dual change model, we had to divide passage comprehension W scores by 20. ¹ Therefore, the mean intercept of 22.69 reflects an average W score of 452 units in first grade. The mean slope of 6.23 reflects a model-predicted change of 124.6 W score units per year. The proportional change was −0.23, suggesting that reading scores slowed down 23% per year in Grades 2–5. In Grade 1, the proportional change parameter was estimated to be −0.25. This is essentially a piecewise adjustment for the 5-year model of passage comprehension.

Figure 3 shows that growth in passage comprehension was substantially nonlinear, with sharp growth from Grade 1 to 2, followed by a slowing down from Grades 2 to 5. The effects of the proportional change parameter can be seen in the curvature of the trajectories. The proportional change was substantial, with lower-performing children accelerating but higher-performing children slowing down, producing a convergence seen in the dotted lines for high and low intercepts. In addition, the different first-grade proportional change, although seemingly similar to the subsequent proportional change parameters (−0.25 vs. −0.23), results in a clear bend in the model-predicted growth trajectory. For reference, we show the normative expected W score as a dashed line in the graph. This dashed line represents the average W score (50th centile) from the norm sample of the test (Schrank et al., 2014) for each grade, first through fifth.

Figure 3.

Predicted growth in reading from the univariate dual change score model versus normative expectation (dashed line). The metric is W score divided by 20. The solid line reflects mean growth, and the dotted lines are 1 SD above and below the mean. The heavy dashed line represents the normative expectation for students in that grade level (mean W score for each age level from the Technical Manual; Schrank et al., 2014). The proportional change is consistent from Grades 2 to 5 (−0.23) but steeper between Grades 1 and 2 (−0.25). See Table 4.

Bivariate Dual Change: Dialect and Language

As Equations 3a and 3b show, the bivariate version of the model is substantially more complex than the single-outcome univariate model. These are individual growth models: Students have their own level of intercepts (and slopes, if estimated). In a bivariate model, intercepts can be related: Performance in one construct can be related to performance in the other. In addition, the coupling parameters are particularly interesting as they suggest the extent to which performance in one construct precedes change in the other construct: the extent to which one construct seems to drive the other and vice versa. It is possible, however, that the data might not be so complex, and we can test whether some of these complex relations are zero (McArdle, 2001). For each of the full bivariate models, we tested whether the coupling effect of dialect was zero, whether the coupling effect on dialect was zero, and whether there was no coupling at all.

Table 5 shows the fit statistics for these bivariate models and the tests of the restrictions of the coupling parameters. The first line of Table 5 shows that the bivariate model for dialect density and language fits excellently. On their own, all these models of dialect density and language fit well. However, because the restricted models are nested within the freely estimated model with two change parameters (both coupling), we can statistically test the fit of the restriction. Results of this test are shown in the rightmost two columns of Table 5 as a chi-square difference test.

Table 5.

Fit for bivariate dual change score models, with tests of restriction.

Model	χ2	df	CFI	TLI	RMSEA	Δχ2 (Δdf)
Dialect and language
Both coupling	54.69	27	0.98	0.98	0.04
Dialect does not affect language	56.03	28	0.98	0.98	0.04	1.34 (1)
Language does not affect dialect	65.74	28	0.97	0.98	0.04	11.05 (1)*
No coupling at all	67.39	29	0.97	0.98	0.04	12.70 (2)*
Dialect and passage comprehension
Both coupling	64.81	26	0.96	0.97	0.04
Dialect does not affect reading	77.63	27	0.95	0.96	0.05	12.82 (1)*
Reading does not affect dialect	74.14	27	0.95	0.96	0.05	9.33 (1)*
No coupling at all	79.52	28	0.95	0.96	0.05	14.70 (2)*

Note. Each model represents a restriction tested against its respective full model (with both coupling parameters). Statistically significant model comparisons indicate substantial misfit, compared with the full model with both coupling parameters. CFI = Comparative Fit Index; RMSEA = root-mean-square error of approximation; Tucker Lewis Index.

^* p < .01.

The third row of Table 5 shows that restricting to zero the influence of dialect density upon language fit reasonably (Δχ²(1) = 1.02, p = .25). All of the other restrictions fit statistically worse than the freely estimated model. This model suggests that, although dialect density and language are related, dialect density does not appear to differentially affect change in language over time.

Table 6 shows the model estimated parameters for the bivariate “dialect density and language” model (see Equations 3a–3b). Some of these parameters are similar to the previous univariate estimates, but these models are dynamic, relating changes in one construct to subsequent changes in another construct. However, in the lower part of the table, we can see that individual status in dialect density is highly negatively correlated (r = −0.82) with individual status in language. Measurement error was essentially uncorrelated across constructs (r = −0.07).

Table 6.

Parameter estimates from the bivariate dual change score model for dialect density and language.

Parameter	Dialect		Language
	Estimate	SE	Estimate	SE
Intercept mean	6.61	0.15	−0.58	0.05
Slope mean	−0.99	0.20	0.48	0.02
Proportional (β)	0.05	0.03	0.03	0.02
Coupling (γ)	0.36	0.11	(0)	(0)
Intercept variance	6.99	0.63	0.62	0.06
Residual variance	1.74	0.12	0.24	0.02
	Covariance	SE	Correlation
Intercept covariance	−1.71	0.16	−.82
Residual covariance	−0.05	0.03	−.07

Note. Dialect density percentages were rescaled to 1/10th. Parentheses indicate a parameter restricted to zero. “Coupling” refers to the effect from the other construct (see Equations 3a–3b): The column name is the outcome, and the other construct is the predictor.

Table 7 shows the same estimates for the bivariate “dialect density and passage comprehension” model (see Equations 3a–3b). Both coupling parameters for the influence of dialect on change in reading comprehension and the effect of passage comprehension on change in dialect density were statistically significant. Individual status was highly negatively related across the constructs (r = −.65).

Table 7.

Parameter estimates from the bivariate dual change score model for dialect and passage comprehension.

Parameter	Dialect		Passage comprehension
	Estimate	SE	Estimate	SE
Intercept mean	6.61	0.15	22.67	0.05
Slope mean	−9.20	2.89	8.51	0.74
Proportional (β)	0.02	0.03	−0.33	0.03
Proportional 2 (β)	—	—	−0.34	0.03
Coupling (γ)	0.36	0.12	−0.03	0.01
Intercept variance	7.26	0.66	0.88	0.08
Residual variance	1.73	0.12	0.12	0.01
	Covariance	SE	Correlation
Intercept covariance	−1.64	0.18	−.65
Residual covariance	−0.01	0.02	−.01

Note. Dashes indicate that parameter is not applicable. Dialect density percentages were rescaled to 1/10th. Passage comprehension W scores were rescaled to 1/20th. “Coupling” refers to the effect from the other construct (see Equation 3a–3b): The column name is the outcome, and the other construct is the predictor.

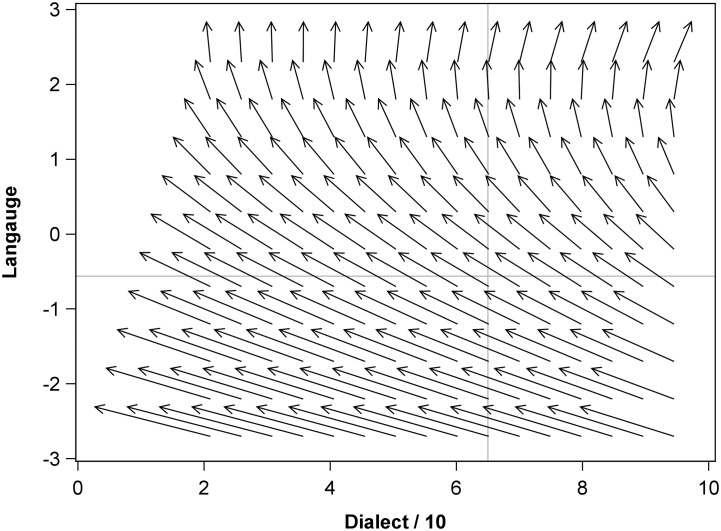
Just as it is difficult to interpret main effects in the presence of an interaction, we need graphs to illustrate this dynamic complexity. Figure 4 shows the dynamic relation between dialect and language performance. Each point has an arrow that starts at a particular level of dialect (horizontal axis) and language (vertical axis). Dialect is measured in deciles (10-point centiles, from zero to all-dialect, 10 = 100%). Language is on a z score, centered at Grade 2, so 1-unit change reflects growth of 1 SD (effect size = 1.0 of difference). The arrow extends from each point to the model-predicted next point, using Equations 3a and 3b simultaneously, taking into account the proportional change in each outcome as well as their mutual relation (coupling). Thus, each arrow shows the model-expected change at that level in each of the outcomes. Gray reference lines are shown for the Grade 1 means for each outcome (vertical for dialect, horizontal for language). These gray reference lines cross at the model-predicted Grade 1 start point for the sample.

Figure 4.

Vector field plot of the bivariate dual change score model of dialect density and language. The y axis for language is a developmental z score centered at second grade (see text for details). The x axis represents deciles of dialect density (percentage divided by 10). Gray reference lines are shown at the respective means for the first grade.

In Figure 4, the leaning of arrows upward and to the left shows the general increase in language (upward) and the decrease in dialect density (leftward). The arrows lean to the left more on the bottom and lean less leftward toward to the top, showing that there are higher degrees of dialect density decrease (leftward leaning) at lower levels of language, whereas at higher levels of language, dialect density is not expected to change much. Alternatively, dialect density has little impact upon the change of language, because the arrows have similar height (upward) at all levels of dialect density.

We can understand the implications of Figure 4 by taking two example cases. First, imagine a student in the lower left section of the graph, with low dialect density (e.g., 21%) and low language performance (e.g., −2.4 z score). The arrow leans heavily to the left and points slightly upward, suggesting a predicted drop in dialect density, perhaps from 2.1 to 0.3 (from 21% to 0%), and an upward gain in language, perhaps from −2.4 to −2.0 z units (effect size of 0.4).

Second, we can imagine a student in the upper right section of the graph, with high dialect density and high language performance. Although such a combination would be rare, the model would suggest that such a student would not change in dialect (no horizontal slant in the arrow) but would gain in language performance.

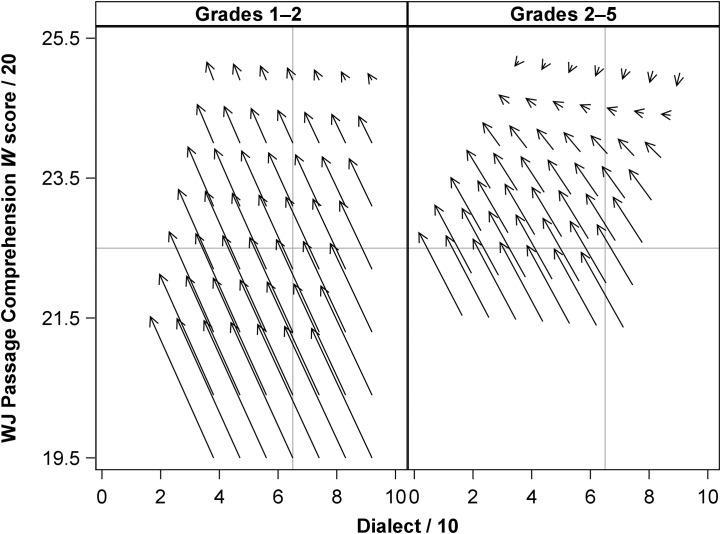
Because the proportional change for passage comprehension was different between the first 2 years and the subsequent 3 years, two vector plots are needed to show the dynamics of change. Figure 5 shows the pattern of results for change in dialect density and passage comprehension in two panels: from first to second grade (left) and from second to fifth grade (right). Most of the arrows face up and left, suggesting growth in reading comprehension (upward) and decrease in dialect density (leftward). Arrows are taller on the bottom and get shorter toward the top, suggesting that lower-performing children have a higher growth rate in passage comprehension but higher-performing children grow at a slower rate (see also Figure 3). Arrows get shorter farther on the right, showing that higher dialect density is related to slower growth in passage comprehension. Thus, students grow faster in passage comprehension at the lower ends of passage comprehension and lower dialect usage (see Figure 3). The leaning of arrows to the left is greater on the bottom, which likely reflects a higher degree of dialect density decrease at the lower level of passage comprehension.

Figure 5.

Vector field plot of the bivariate dual change score model of dialect density and passage comprehension, for Grades 1–2 and 2–5. The y axis represents W score divided by 20. The x axis represents deciles of dialect density (percentage divided by 10). Gray reference lines are shown at the respective means for the first grade. WJ = Woodcock–Johnson.

Discussion

The overarching question in this investigation was how dialect density impacts the growth of reading and oral language skills in AA children who speak AAE. Previous research studies indicate that dialect density has an important influence on reading and language outcomes. In many of these studies, AAE-speaking children who were high dialect users showed reduced reading and language skills compared with their peers who used less dialect. However, many of these investigations were cross-sectional, making it difficult to understand the details of growth in reading, language, and dialect within and across children. The outcomes of the current longitudinal study demonstrated that AAE-speaking children who are high dialect users tended to have weak overall language but dialect itself did not influence the growth of language skills over time. In the case of reading, a reciprocal relationship between reading and dialect was obtained, such that children who were strong readers were better at decreasing dialect use over time and children who were higher dialect users had slower reading growth. These outcomes suggest a complex and dynamic relationship between dialect and language and between dialect and reading.

The results of this investigation were indeed complex. Examination of univariate growth models demonstrated that the average level of dialect used in first grade was approximately 65% (SD = 26%), followed by a nearly linear decrease in dialect density through fifth grade (about 5% per year), with a slight slowing of the trajectory over time. These findings are not quite as dramatic as those of Craig and Washington (2004), who reported a significant decline in dialect density in first grade followed by a stabilization in second through fourth grades in their cross-sectional sample. In the current sample, the youngest participants were first graders, and the change score model used in the current study had the capacity to detect nonlinear shifts and stabilization at a plateau—but these were not found for dialect change. However, in the Craig and Washington sample, there were two younger groups, preschoolers and kindergarteners. Children were observed to make no measureable shifts in their use of dialect at these younger ages, but after 2–3 years of schooling, a shift toward the use of the classroom language standard was evidenced, although these changes were measured cross-sectionally rather than longitudinally. Whereas there were no data available to confirm that the participants in the current investigation attended either preschool or kindergarten, national data indicate that approximately 87% of children in the United States attend kindergarten (https://nces.ed.gov/programs/coe/indicator_cfa.asp) and about half (55%) attend preschool. Attendance in both prekindergarten and kindergarten in the state of Georgia, where the current sample was obtained, mirrors these national trends (https://gosa.georgia.gov/student-and-school-demographics). On the basis of these data, it can be assumed that most of the children in this study had the benefit of at least 1 year of schooling before first grade, the earliest grade that we sampled. It is unlikely that a shift toward decreased use of dialect occurred for all of the children in this sample, as previous studies have shown that not all children will make this change (Connor & Craig, 2006; Craig & Washington, 2004). However, taken together, the findings in the current investigation and the Craig and Washington (2004) findings suggest that, for AA children whose dialect density does change, it may take a minimum of 2 years in a Standard Classroom English environment to produce a measurable decrease in dialect density. It appears that this shift could occur earlier in schooling rather than later and then tapers off, suggesting that there may be a sensitive period for spontaneous decreases in dialect density. Alternatively, the current study could suggest that, although there is wide variability in dialect density, in this setting, students decrease only gradually but that change is highly related to language and reading.

Even with a potential decrease in dialect density for most children in first grade, the range of dialect density in this study was still wide, SD = 22%–33% per grade, confirming the high degree of variation in dialect use among low-income AA children. This variation is particularly important as there will be an approximately 5% change in dialect density for these children each year after their first grade year. Accordingly, children with the highest dialect density after the initial decrease in first grade may still be producing densities as high as 70% in fifth grade. The bivariate growth models suggest that failing to decrease density of dialect used may have consequences for both reading and language. Unfortunately, the relation between dialect density and reading (r = −.82) and dialect density and language (r = −.65) is highly negative. These findings confirm and extend those reported by others for AA children at various ages (Craig & Washington, 2004; Gatlin & Wanzek, 2015; Kohler et al., 2007).

The relations between dialect density and oral language and between dialect density and reading are dynamic. Although dialect density and language are highly related, dialect density appears to have no additional longitudinal effect on language change over time. A recent investigation by Terry et al. (2016) also found that children who used nonmainstream dialects (not necessarily AAE) and who had stronger language skills were more likely to decrease their use of dialect in second grade. The Terry et al. sample was composed of both low- and middle-income children, with a dialect change advantage reported for those in more affluent schools. The current findings suggest that, even within a sample of overwhelmingly low-income children, these relationships also exist. These findings suggest that a clinical or educational focus on improving language skills may increase the likelihood that children will shift to the use of the classroom standard spontaneously. In addition, as higher dialect levels are significantly related to lower performance in oral language, failure to decrease the use of dialect as expected by second grade may be a red flag for overall language difficulty in the future.

In the case of reading, the relation is reciprocal. Higher dialect use slows reading growth, suggesting that developing strong reading skills may be instrumental for driving code-shifting in AAE-speaking children. Perhaps, it is the development of these reading skills that is driving the small decreases in dialect density that were observed for second through fifth graders. Alternatively, both reading and dialect change are slowing in upper grades, and students with high dialect show very little change (Figure 5). For children in elementary school, it may not be enough to focus on strengthening oral language skills. Rather, it may be important to address language and reading in parallel. Further research is needed to understand the nature and causes of dialect shifting in relation to reading gains, especially concerning the role of basic reading skills in this population.

Reading was measured in this study using performance on a passage comprehension measure. Results showed that reading scores showed an acceleration in Grade 1 followed by a decelerating trajectory from second through fifth grades. In particular, children who were lower performing on the measure showed faster growth, compared with higher-performing children whose growth was considerably slower. This difference in growth between high- and low-performing children is not unexpected. Choi, Elicker, Christ, and Dobbs-Oates (2016) referred to this pattern as support for a compensatory hypothesis, whereby children who start out with weak skills make rapid growth compared with peers who start out with stronger skills. These authors provide this trajectory as evidence that these children will eventually catch up. Unfortunately, in the case of AA children, although this rapid growth from a weak skill base is certainly true, they do not appear to catch up in the later grades. The findings of the current study suggest that this early acceleration will begin to level off after second grade, being substantially slower than normative expectation (Figure 3). This decelerating pattern may in part be influenced by dialect use for AA children. The reciprocal relations between dialect and reading have interesting implications. They imply that higher dialect use may slow reading acquisition and that higher reading acquisition fosters a loss of dialect or more code-shifting.

Conclusions and Clinical Implications

Overall, dialect density is inversely related to language and reading. Change in dialect did not appear to have strong differential effects on oral language over time beyond the basic negative association. Dialect decreases appeared associated with gains in reading comprehension, and reading growth exhibited a substantial slowing down in Grades 4 and 5. The implications of these patterns for clinicians and reading specialists suggest that, to improve overall language and reading skills in AA children who use dialect, general language and reading skills likely should be addressed in parallel, as each skill has a measurable influence on the other and reading and dialect have reciprocal influences. Importantly, although it is clear that decreases in the use of dialect benefit AAE-speaking children's reading growth, it may not be necessary to target children's use of dialect directly, as some have suggested in the extant literature (Craig et al., 2014; Wheeler, 2006). Rather, it may be possible to impact dialect shifting by a focus on improving general oral language skills and strengthening foundational reading skills. Indeed, Terry et al. (2016) also reported the relationship between general oral language skills and changes in the use of dialect in their second-grade nonmainstream speakers, some of whom were AAE speakers and others were not. This reported relationship appears to hold true for children who are AAE speakers beyond the second grade as well, such that improving oral language skills, including syntax and morphology, may be important for encouraging decreased use of dialect. Furthermore, outcomes of the current study and others suggest that it may be beneficial to address oral language earlier rather than later, as spontaneous change in dialect use appears to taper off over time, and it may take as long as 2 years in the school context to see measurable change.

It is not clear that the lack of a longitudinal effect of dialect on language implies a resistance to change in dialect density. Instead, it appears that the general oral language skills of the child and the acquisition of reading skills may be driving changes in dialect at school age. Specifically, children who gain the most in language and reading skills experienced a subsequent decrease in dialect use that may be beneficial across the elementary school years. In fact, it is not clear whether the trends in dialect imply dialect shifting at all. Although these changes in dialect use by a particular grade are frequently interpreted as dialect shifting or switching, dialect switching is likely context dependent and the current study only measured students in the formal academic setting of their school, with a trained examiner on formalized instruments. The current models in this formal context suggest that decreases in dialect density are fairly consistent and almost linear.

The reciprocal relationship identified between dialect shifting and reading is an important finding of this study that has implications for educational contexts. These outcomes suggest that, for AAE-speaking children, the poor reading outcomes discussed nationally have previously unknown implications for development of Standard Classroom English. It is not a surprise that language skills have an influence on reading as this relationship is well documented (Arnold, Lonigan, Whitehurst, & Epstein, 1994; Scarborough, Neuman, & Dickinson, 2001; Storch & Whitehurst, 2002; Wasik & Bond, 2001; Whitehurst et al., 1988). Of importance here, the impact of reading on oral dialect skills suggests that poor reading skills can have an inhibitory effect on decreasing dialect density in AAE-speaking children. This impact may be compounded in children who are high dialect users and who also have weak general language skills, making these children least likely to shift from the use of AAE to the language of the classroom. That is, high dialect users who have poor oral language skills and who do not develop strong early reading skills are unlikely to be among the children who code-switch spontaneously.

It is important to note some limitations of the current study. The current models did not find appreciable differences between student rates of change—slope variances estimated at zero. The design was accelerated, with students only measured twice. More measurements per student could allow better estimation of differences in slopes between students. It is unclear whether the current results of parallel growth reflect true consistency across students or whether the limitation of two time points prevented detecting differences in growth rates. The current models of parallel growth may be sufficient for a broad characterization, but more intensive longitudinal data collection may find interesting differences in student rates of change and relations across constructs.

The current study explored complex relations at the child level across three constructs. Multilevel models examining variation across classrooms or differences between schools could be highly informative. It is possible that average dialect density may differ between classrooms and schools and that such context effects could be important. In addition, a trivariate model examining simultaneous relations across dialect, language, and reading could help to clarify some of the relations among these three developmental and educational processes.

The current study used a single measure of dialect density administered in a formal testing situation within the child's school. The DELV-ST is a criterion-referenced assessment and is administered in a standardized fashion. The method used to calculate dialect density is similar to other methods in that dialect density is based on the total number of AAE productions. Importantly, the DELV-ST and other dialect density indices calculated based on spontaneous language sampling, an informal method, have proven to be highly correlated (Horton & Apel, 2014; Oetting & McDonald, 2002). Thus, there is no current evidence to support that children's nonmainstream dialect productions are influenced by testing context, although this is an important area for future research. Although we did not measure student language use outside the formal school setting, it is possible that some students may use their language and dialect differently at home than they do at school. Further research is needed to understand the possible difference and impact of dialect use as distinct from formal language performance.

The findings of this study suggest that exposure to standard classroom language in either oral or written forms may be important for continued decreases in the use of AAE, after the initial drop experienced by most children at first grade. The big questions for future research are “How large must the decrease in dialect density be to benefit reading acquisition” and “At what age do these changes need to occur to prevent reading failures?” The results of this investigation indicate that being an AAE speaker does not lead to reading failure but that being a high dialect user may indeed lead to poorer overall language and reading outcomes.

Appendix

Dual Change Growth Models

This appendix provides general conceptual forms for the models used. Full details on dual change score models can be found elsewhere (McArdle, 2001; McArdle & Hamagami, 2001).

Univariate growth models. The general form of a dual change score model for a single outcome, Y _gi, for student i at grade g is:

$$Y_{gi}=Y_{\left(g-1\right)i}+\Delta Y_{gi}+e_{gi}$$ (1)

where the outcome at the first time point is Y _1i = Intercept _i and change is

$$\Delta Y_{gi}=\beta Y_{\left(g-1\right)i}+\mathit{Slop}{e}_i$$ (2)

Equation 1 states that a student's current score is their previous score (Y _{(g – 1)i}) plus the amount of change (ΔY _gi), plus random measurement error (e _gi), as is typical in regression or growth models. In the first year, the model is simply the predicted starting point or a student-specific Intercept.

Equation 2 describes ΔY _gi as the latent change score between score at grade g (Y _gi) and score at the previous grade (Y _{(g − 1)i}) for each individual, which includes the individual linear rate of change (Slope _i), with variability (i.e., some students may grow faster than others). β is the proportional change parameter that describes the curvature of the growth trajectories. The model is called “dual change” because of the linear growth combined with the proportional growth portion. If the proportional change parameter happens to be zero, the change score model reduces to a model of individual linear growth.

Bivariate growth models. Two dual change score models can be put together into a single model of growth, with cross-construct influences. Such a model is a system of two equations, with one additional subscript to distinguish one outcome (Y _gi) from the other (X _gi). The equations for change in each year are

$$\Delta Y_{gi}={\beta }_y{Y}_{\left(g-1\right)i}+\mathit{Slop}{e}_{yi}+{\gamma }_x{X}_{\left(g-1\right)i}$$ (3a)

$$\Delta X_{gi}={\beta }_x{X}_{\left(g-1\right)i}+\mathit{Slop}{e}_{\mathit{xi}}+{\gamma }_y{Y}_{\left(g-1\right)i}$$ (3b)

The parameters of Equations 3a and 3b are the same as those in Equation 2, with one new addition for each outcome: γ _x and γ _y, which are called coupling parameters as they describe the cross-influence of each outcome on the other: A prior score on one outcome predicts the change score of the other outcome. Specifically, γ _x captures the effect of the previous score (X _{(g − 1)i}) of variable X upon the change score (ΔY _gi) of variable Y; conversely, γ _y captures the effect of the previous score (Y _{(g − 1)i}) of variable Y upon the change score (ΔX _gi) of variable X.

There are additional parameters not shown in Equations 2a and 2b. The four factors of the two intercepts and two slopes may be freely related (up to four variances and six covariances): Performance in one construct might be related to performance in another. For example, levels of intercept in one measure might be highly related to levels in the other. Last, error in each of the outcomes (e _xgi and e _ygi) may be related with time.

Funding Statement

Research reported in this article was supported by the Eunice Kennedy Shriver National Institute of Child Health and Human Development of the National Institutes of Health under 1R24HDO75454-01, awarded to Julia A. Washington, Principal Investigator.