Dynamic PET of Human Liver Inflammation: Impact of Kinetic Modeling with Optimization-Derived Dual-Blood Input Function

Abstract

The hallmark of nonalcoholic steatohepatitis is hepatocellular inflammation and injury in the setting of hepatic steatosis. Recent work has indicated that dynamic ¹⁸F-FDG PET with kinetic modeling has the potential to assess hepatic inflammation noninvasively, while static FDG-PET is less promising. Because the liver has dual blood supplies, kinetic modeling of dynamic liver PET data is challenging in human studies. This paper aims to identify the optimal dual-input kinetic modeling approach for dynamic FDG-PET of human liver inflammation. Fourteen patients with nonalcoholic fatty liver disease were included. Each patient underwent 1-hour dynamic FDG- PET/CT scan and had liver biopsy within six weeks. Three models were tested for kinetic analysis: the traditional two-tissue compartmental model with an image-derived single-blood input function (SBIF), a model with population-based dual-blood input function (DBIF), and a new model with optimization-derived DBIF through a joint estimation framework. The three models were compared using Akaike information criterion (AIC), F test and histopathologic inflammation score. Results showed that the optimization-derived DBIF model improved liver time activity curve fitting and achieved lower AIC values and higher F values than the SBIF and population-based DBIF models in all patients. The optimization-derived model significantly increased FDG K₁ estimates by 101% and 27% as compared with traditional SBIF and population-based DBIF. K₁ by the optimization-derived model was significantly associated with histopathologic grades of liver inflammation while the other two models did not provide a statistical significance. In conclusion, modeling of DBIF is critical for dynamic liver FDG-PET kinetic analysis in human studies. The optimization-derived DBIF model is more appropriate than SBIF and population- based DBIF for dynamic FDG-PET of liver inflammation.

INTRODUCTION

Nonalcoholic fatty liver disease (NAFLD) affects approximately 30% of the general population and is emerging as a leading cause of liver-related morbidity and mortality (1,2). Nonalcoholic steatohepatitis (NASH) is a more severe form of NAFLD characterized by hepatocyte inflammation and injury, and can subsequently lead to cirrhosis and associated liver cancer and liver failure (3). NASH develops in 5–10% of NAFLD patients (i.e., 5–10 million people in the United States) and is associated with higher liver-related mortality than is hepatic steatosis alone (4). Differentiation of NASH from simple fatty liver is essential for future patient management in NAFLD, particularly as newer therapies become available (3,5).

The diagnostic hallmark of NASH is hepatocellular inflammation and injury in the setting of hepatic steatosis (3). Imaging methods have been developed to quantify hepatic steatosis (6), e.g. ultrasonography (7), computed tomography (CT) (8) or magnetic resonance imaging (MRI) (9–11). Other methods such as magnetic resonance elastography (MRE) (12) and ultrasound elastography (13) can measure liver stiffness and quantify advanced fibrosis of hepatic tissue (14–16). However, there is currently no effective imaging method for accurate characterization of liver inflammation in clinical practice and clinical trials (17). Liver biopsy followed by clinical histopathology remains the current standard practice (18).

¹⁸F-fluorodeoxyglucose (FDG) positron emission tomography (PET) is a widely used and effective method for imaging cell glucose metabolism. Previous studies have reported the use of FDG-PET for imaging infection and inflammation (19,20). Several studies have investigated the use of FDG-PET in the liver (21–27) with focus on evaluation of hepatic steatosis (24,26–32). Contradictory results have been reported (24,26–29) on the relation between FDG standardized uptake value (SUV) and hepatic steatosis. Keramida et al (30–32) have recently pointed out that SUV, if corrected for liver fat content, is increased in hepatic steatosis and may potentially relate to liver inflammation. However, no direct findings have been reported between FDG-PET and hepatic inflammation so far.

Current clinical usage of PET is largely limited to static PET imaging which provides SUV as a semi-quantitative measure of glucose utilization. SUV is related to steatosis (30) and is influenced by many patient factors including body habitus (33). This static way of using PET may not be able to explore the full potential of FDG-PET in imaging of hepatic inflammation. In contrast, dynamic FDG-PET acquires FDG activity images at multiple time points and can exploit quantitative tracer kinetics to characterize and separate the underlying molecular process of glucose metabolism (34). There are already several dynamic FDG-PET studies of liver, e.g., (21,23,32,35–37). However, existing studies mainly examined the overall glucose utilization using either glucose metabolic rate or FDG influx rate K_i. None of these studies have reported relevant or promising results for liver inflammation and NASH assessment. Our recent preliminary work has indicated a new promise (38). While we have not found FDG SUV by static PET or K_i by dynamic PET to be helpful, the FDG K₁ parameter, which represents the delivery rate of FDG from blood to hepatic tissue, is promising for characterizing liver inflammation in NASH (38).

The blood input function is essential for kinetic modeling in dynamic FDG-PET (34). Conventionally it is either obtained by invasive arterial blood sampling or noninvasively derived from the left ventricle or aortic regions in dynamic PET images (39–41). In the liver, both the hepatic artery and portal vein provide blood supply to the hepatic tissue (22). The portal vein input is not the same as the hepatic artery input and is difficult to obtain in human subjects (22). Neglecting the influence of portal vein can result in inaccurate kinetic modeling. A common approach to accounting for the effect of dual blood supplies is to use a flow-weighted model of dual-blood input function (DBIF) (21,36,42). The model parameters are often pre-determined by population means that were derived using arterial blood sampling in animal studies (22,37). Due to heterogeneity across patients and potential differences between arterial and image-derived input functions, the population-based DBIF model may become ineffective when arterial blood sampling is not available and in practice, image-derived input function is typically used in human studies.

The objective of this paper is to evaluate and identify an appropriate dual-input kinetic modeling approach for FDG kinetic quantification of liver inflammation using human patient data. Besides the population-based DBIF approach, we also examined a new optimization-derived DBIF model which employs mathematical optimization to jointly estimate the parameters of DBIF and liver FDG kinetics. This model directly utilizes image-derived aortic input function, requires no arterial blood sampling, and is more adaptive to individual patients. We used both statistical information criteria and histopathologic inflammation data to compare these methods.

MATERIALS AND METHODS

Patient Characteristics

Fourteen patients with NAFLD were included in this study. These patients had a liver biopsy as a part of routine clinical care or for enrollment in clinical trials. The University of California Davis Institutional Review Board and the University of California Davis Medical Center Radiation Use Committee approved the study. All patients signed informed consent before participating in the study. Patients with history of alcohol abuse, chronic hepatitis B or C, or other chronic liver disease other than NAFLD were excluded from the study.

Liver Histopathology

Liver biopsies were performed under ultrasound guidance and scored according to the nonalcoholic steatohepatitis clinical research network (NASH-CRN) criteria (43). The NAFLD activity score (NAS, range 0–8) is comprised of severity of steatosis, inflammation, and hepatocellular ballooning. While a NAS score greater than 4 has been reported to correlate with the presence of NASH, the scores of lobular inflammation and ballooning degeneration are noted to represent hepatic inflammation and injury, and are therefore combined to create an overall “hepatic inflammation” score (range 0–5). In this study, an inflammation score higher than 3 was considered indicative of high inflammation, while scores lower than 3 and equal to 3 suggested low and medium inflammation, respectively.

Dynamic ¹⁸F-FDG PET/CT

Scan Protocol:

Dynamic ¹⁸F-FDG PET studies were performed using the GE Discovery 690 PET/CT scanner at the UC Davis Medical Center. Patients fasted for at least 6 hours. Each patient was injected with 10 mCi ¹⁸F- FDG. List-mode time-of-flight data acquisition started right after the intravenous bolus administration and lasted for one hour. At the end of PET scan, a low-dose CT scan was performed for attenuation correction for PET. Dynamic PET data were binned into 49 time frames using the sampling schedule: 30 × 10s, 10 × 60s, and 9 × 300s. Dynamic PET images were then reconstructed using the vendor software with the standard ordered subsets expectation maximization (OSEM) algorithm with 2 iterations and 32 subsets.

Extraction of Blood and Tissue Time Activity Curves (TACs):

Eight spherical regions of interest (ROI), each with 25 mm in diameter, were placed on the eight segments of the liver avoiding any major blood vessels. These ROI placements were tuned and confirmed by an abdominal radiologist. The averaged FDG activity in all 8 ROIs was extracted from the dynamic images to form a global liver TAC of low noise. An additional ROI is placed in the descending aorta region to extract image-derived aortic input function.

Dual-Input Kinetic Modeling

Compartmental Model with Dual-blood Input Function (DBIF):

FDG kinetics commonly follow the two-tissue compartmental model (34) as shown in Figure 1(a). Glucose transporters transport ¹⁸F-FDG from blood to hepatic tissue with the rate constant K₁ (mL/min/mL) and from hepatic tissue to blood with the rate k₂ (1/min). FDG is phosphorylated by hexokinase in cells into FDG 6-phosphate with the rate k₃ (1/min) and the dephosphorylation process occurs with the rate k₄ (1/min). C_p(t), C_f(t) and C_m(t) represent the FDG concentration in the plasma compartment, free-state FDG in the hepatic tissue compartment, and metabolized FDG 6-phosphate in the tissue, respectively. In traditional kinetic modeling with single-blood input function (SBIF), only blood supply from the aorta is considered and thus the input function C_p(t) is equivalent to the aortic input function C_A(t). To account for the effect of dual blood supplies in the liver, a flow-weighted sum of the aortic input C_A(t) and portal vein input C_PV(t) can be used to model the DBIF (22):

$$C_p(t)=\left(1-f_A\right)C_{PV}(t)+f_A{C}_A(t)$$ Eq. 1

where f_A is the fraction of hepatic artery contributing to the overall liver blood flow. The portal vein input function C_PV(t) follows an analytical solution

$$C_{PV}(t)=k_a\exp \left(-k_{a}t\right)\otimes C_A(t),$$ Eq. 2

which is equivalent to a dispersed version of the aortic input function C_A(t) (44). The dispersion is because FDG in the portal vein flows through the gastrointestinal system before entering into the liver. Thus, portal vein can be considered as an additional compartment, as shown in Figure 1(b). As a result, the combined compartmental model is equivalently described by a set of differential equations:

$$\frac{d}{dt}\mathit{c}(t)=\mathit{A}\mathit{c}(t)+\mathit{b}{C}_A(t),$$ Eq. 3

where

$$\mathit{c}(t)=\left[\begin{array}{c}{C}_f(t)\\ C_m(t)\\ C_{PV}(t)\end{array}\right],\mathit{A}=\left[\begin{array}{ccc}-\left(k_2+k_3\right)& k_4& K_1\left(1-f_A\right)\\ k_3& -k_4& 0\\ 0& 0& -k_a\end{array}\right],\mathit{b}=\left[\begin{array}{c}{K}_1{f}_A\\ 0\\ k_a\end{array}\right].$$ Eq. 4

The total activity that can be measured by PET is the sum of different compartments:

$$C_T(t;\mathit{\theta })=\left(1-v_b\right)\left[C_f(t)+C_m(t)\right]+v_b\left[\left(1-f_A\right)C_{PV}(t)+f_A{C}_A(t)\right],$$ Eq. 5

where v_b is the fractional blood volume and θ = [v_b,K₁,k₂,k₃,k₄,k_a,f_A]^T is a vector collecting all unknown parameters. Note that this DBIF model becomes the traditional SBIF model when k_a = 0 and f_A = 1.

FIGURE 1:

Kinetic modeling of dynamic liver FDG-PET data with a dual-blood input function from the hepatic artery and portal vein.

Joint Estimation of Kinetic and Input Parameters:

All model parameters are jointly estimated by fitting a measured liver TAC č using the model equation and following nonlinear least square estimation:

$$\widehat{\mathit{\theta }}=\arg \underset{\mathit{\theta }}{\min }WRSS(\mathit{\theta }),WRSS(\mathit{\theta })={\sum }_{m=1}^M{w}_m{\left[{\check{c}}_m-C_T\left(t_m;\mathit{\theta }\right)\right]}^2.$$ Eq. 6

where WRSS(θ) denotes the weighted residual sum of squares of the curve fitting and w_m denotes the weighting factor for time frame m. In this study, a uniform weight was used as suggested by Thiele and Buchert (45) and Winterdahl et. al (37). We used the classic Levenberg-Marquardt algorithm with 100 iterations to solve the optimization problem. The fitting process was implemented using C/C++ programing similar to our previous work (46,47). In this paper, we refer this joint estimation as the optimization-derived DBIF approach for clarity. It would become equivalent to the population-based DBIF if the parameters f_A and k_a are assigned with fixed population means (if known). Based on our initial analysis of the patient data sets, we set the initials of kinetic parameters to v_b = 0.01, K₁ = 1.0, k₂ = 1.0, k₃ = 0.01, k₄ = 0.01, k_a = 1.0, f_A = 0.01.

Comparison of Kinetic Models

We compared three input models: the traditional model with SBIF, a model with population-based DBIF and a model with optimization-derived DBIF. In this study, the SBIF was derived from the descending aorta region in dynamic FDG-PET images. To utilize reported population means for the population-based DBIF, we used the following portal vein input model (22,37)

$$C_{PV}(t)=\left(\overline{\beta }/{(\overline{\beta }+t)}^2\right)\otimes C_A(t),$$ Eq. 7

which is very similar to the exponential-based model in Eq. 2 but not easily integrated into the differential equations for joint estimation. $\overline{\beta }=0.5$ and f_A = 0.25 were previously reported for FDG (37).

Comparison Using Statistical Criteria:

The three models were compared using two established statistical criteria for model selection for TACs: the corrected Akaike information criterion (AIC) and the F test (48,49). The AIC is defined by

$$\mathrm{AIC}=M\ln \left(\frac{WRSS}{M}\right)+2n+\frac{2n(n+1)}{M-n-1},$$ Eq. 8

where n denotes the total number of unknown parameters. Note that n=5 for the SBIF and population-based DBIF models and n=7 for the optimization-derived DBIF model. Here AIC was corrected for finite sample sizes due to the ratio $\frac{M}{n}\le 40$. A lower AIC value indicates a better selection of model (50).

The F test compares a complex model 2 with a simple model 1 using

$$F=\frac{\left({\text{WRSS}}_2-{\text{WRSS}}_1\right)/\left(n_2-n_1\right)}{{\text{WRSS}}_2/\left(M-n_2\right)},$$ Eq. 9

where the degree of freedom (number of unknown parameters) n₂ > n₁ larger F value indicates better fit. If the p value of F test is 0.05 or less, the model 2 is then considered significantly better than model 1.

Evaluation Using Histopathological Inflammation Data:

Patients in this study were divided into three groups according to their histopathological inflammation scores: low inflammation (<3), medium inflammation (=3), and high inflammation (>3). To examine the capability of FDG kinetic parameters for differentiating different inflammation groups, a two-sample 2-sided t-test at the 0.05 level was used to test the difference of group means and the Mann-Whitney U test was used to test difference of group medians. Other FDG-PET parameters that were reported to be associated with hepatic steatosis were also examined for their potential association with inflammation. These parameters include SUV, fat-adjusted SUV (31), and the metabolic rate of glucose by Keramida’s Patlak analysis (32). The SUV was calculated using the last frame (55–60 minutes) in the dynamic sequence. All statistical analyses were conducted using MATLAB (Natick, MA). P-values less than 0.05 were considered as statistically significant in this study.

RESULTS

Patient Characteristics

A majority of the patients were white (75%) while 25% were Hispanics. Female patients formed 67% of the cohort with 75% of the patients between the ages 40–70 years and 25% between 18–39 years. The mean BMI was 34±6 kg/m². The mean fasting glucose prior to PET scan was 115±33 mg/dL. The patient population had an equitable spread across NAS score (≥ of 58%). Two thirds of patients had hepatic inflammation score of ≥3.

Demonstration of dual-blood input function

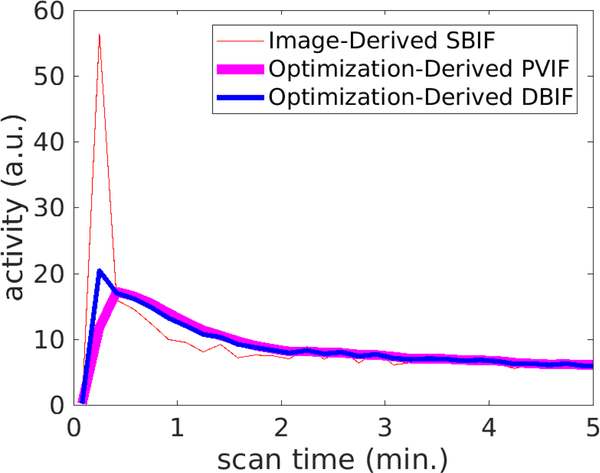
Figure 2 demonstrates an optimization-derived DBIF from a patient data set. Only the first 5 minutes are shown in the figure and the curves after 5 minutes are very similar among others. The DBIF is a weighted combination of the image-derived SBIF and the PVIF derived from the optimization. In this example, the weighting factor f_A was 0.19. The DBIF has a much lower peak value than the SBIF because the contribution from hepatic artery is small (19%) while the contribution from portal vein is great (81%).

FIGURE 2:

Example of optimization-derived DBIF and its components from the hepatic artery and the portal vein: image-derived SBIF and portal vein input function (PVIF).

Figure 3 compares the optimization-derived PVIF with two image-derived PVIFs. To measure the PVIF, a spherical ROI was manually placed within the region of the portal vein on the CT image by a radiologist. Both ROI mean and ROI max were used to derive the image-derived PVIF, respectively. The PVIF by ROI mean has lower noise than that of ROI max but has a notable decrease in activity quantitation, which can be explained by the effect of partial volume. The PVIF by ROI max is consistent with the optimization-derived PVIF but the former is compromised by substantial noise, especially in early frames.

FIGURE 3:

Comparison of optimization-derived PVIF minutes; Right: Zoom-in of (A) for the first 5 minutes.

Evaluation of TAC Fit Quality

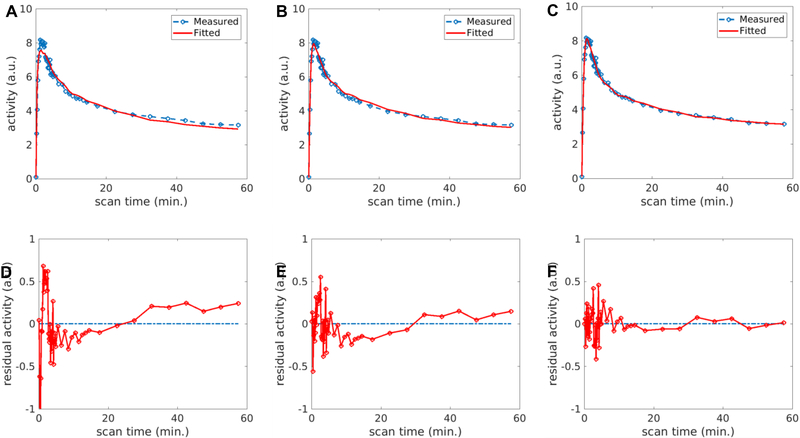
Figure 4A–4C show the fittings of the liver TAC using the image-derived SBIF, population-based DBIF and optimization-derived DBIF, respectively. The residual plots of these fits are shown in Figure 4D–4F. The fitting with SBIF could not fit the early-time peak and late time points due to lack of the portal vein component in the input function. The population-based DBIF provided an improved fit of the peak but still suffered error for late time points due to inaccuracy of the population means for a specific patient data set. A linear trend was observed in the residual plots (Figure 4D and4E) for these two approaches, indicating a systematic bias in the fitting. The optimization-derived DBIF estimated the input parameters from the data and fit both the peak at early time and late time points closely. The linear trend was removed and the residuals became asymptotically normal.

FIGURE 4.

Fit of a liver TAC using different input models: (A) SBIF, (B) population-based DBIF, (C) optimization-derived DBIF; (D-F) corresponding residual plots of the fits in (A-C).

The AIC values of the three fittings were −81, −140 and −159, respectively. AIC values of the three input models are further compared in Figure 5 for all individual patients in the cohort. The AIC difference was −105±23 between SBIF and optimization-derived DBIF, and −59±27 between population-based DBIF and optimization-derived DBIF, respectively. The optimization-derived DBIF model had the lowest AIC amongst the three models in all patients.

FIGURE 5:

AIC values of liver TAC fitting with different input function models.

The results of F test are given in Table 1. The minimum F value among different patients was 80.5 for comparing the optimization-derived DBIF with SBIF and 13.4 for comparing the optimization-derived DBIF with population- based DBIF model, both greater than the F critical value 3.2 calculated with n₁ = 5 and n₂ = 7 for a p value of 0.05. The p values of F test in individual patients are all small (<0.0001), indicating the optimization-derived DBIF is more appropriate for TAC fitting than the traditional SBIF and population-based DBIF models.

Table 1:

F statistics of model comparison (F critical value is 3.2 at the significance level of 0.05)

Model Comparison	F values			p values
	Mean±SD	Min	Max
Optimization-Derived DBIF vs SBIF	200.2±102.7	80.5	389.9	<0.0001
Optimization-Derived DBIF vs Population-Based DBIF	67.5±43.7	13.4	137.7	<0.0001

Change in Kinetic Parameters

The three input models resulted in different estimates in kinetic parameters. The mean and standard deviation of kinetic parameters v_b,K₁,k₂,k₃,k₄ and K_i = 𝐾₁𝑘₃/(𝑘₂+𝑘₃) estimated by the three approaches are listed in Table 2. Results of f_A and k_a are also included. It is worth noting that a reversible kinetic model (i.e., k₄ ≥ 0) was required for accurately modeling FDG TACs in the liver due to possible high level of glucose-6-phosphatase, as discussed in the literature (21,36,51,52). Neglecting k₄ in the model reduced TAC fit quality with higher AIC values (results not shown). Compared with the image-derived SBIF, the optimization-derived DBIF significantly increased the mean values of v_b (0.0000 vs 0.0229), K₁ (0.5112 vs 0.9829), k₂ (0.4983 vs 1.1053), k₃ (0.0008 vs 0.0141) and K_i (0.0008 vs 0.0119), all with p<0.0001 .The difference in K₁ in individual patients was 101% on average with a maximum of 150%, as shown in Figure 6. Compared with the population-based DBIF, the optimization-derived DBIF significantly increased the mean values of k₃ (0.0011 vs 0.0141, p<0.0001), k₄ (0.0196 vs 0.0534, p=0.0034), K_i (0.0010 vs 0.0119, p<0.0001) and v_b (0.0003 vs 0.0229, p<0.0001). Although the mean values of K₁ by the optimization-derived DBIF and population-based DBIF models are similar to each other (0.9787 vs. 0.9829), K₁ values by the two models were very different in each individual patient (Figure 6). The change was 27% on average with a maximum of 44%.

Table 2:

Mean and standard deviation of FDG kinetic parameters estimated by different input function approaches

	SBIF	Population-Based DBIF	Optimization-Derived DBIF
K1	0.5112±0.2064	0.9787±0.5509	0.9829±0.2730
k2	0.4983±0.1760	0.9197±0.4222	1.1053±0.2488
k3	0.0008±0.0010	0.0011 ±0.0011	0.0141±0.0070
k4	0.0512±0.0465	0.0196±0.0291	0.0534±0.0263
Ki	0.0008±0.0010	0.0010±0.0011	0.0119±0.0051
vb	0.0000±0.0000	0.0003±0.0010	0.0229±0.0252
fA	-	0.25	0.0440±0.0544
ka (or β)	-	0.50	1.9002±1.2560

FIGURE 6:

FDG K₁ values estimated by different input function models.

Association with Histopathologic Data

Figure 7 shows the associations of histopathologic grades of liver inflammation with FDG K₁ by different input models. The standard boxplots reflect the median, 25% percentile and 75% percentile of K₁ in each of low, medium and high inflammation groups. Overall, FDG K₁ value decreased as inflammation grade increased. The results of statistical t test for comparing group means and U test for comparing group medians are summarized in Table 3. Neither the SBIF model nor the population-based DBIF model could differentiate low, medium and high inflammation groups (p>0.05). Because of the larger overlap between the low and high inflammation groups in K₁ by the SBIF and population-based DBIF models, the p values of the t test were even higher than that of differentiating medium versus high inflammation groups. In comparison, K₁ by the optimization-derived DBIF model was better associated with the inflammation grades and differentiated low versus high inflammation groups and medium versus high inflammation groups (p<0.05).

FIGURE 7:

Association of histopathological inflammation score with FDG-K₁ estimated by different input models. (A) Image-derived SBIF; (B) Population-based DBIF; (C) Optimization-derived DBIF

Table 3:

P values of t test and U test for comparing different liver inflammation groups using FDG K₁ estimated by SBIF, population-based (PB) DBIF, and optimization-derived (OD) DBIF.

Group Comparison	T test			U test
	SBIF	PB DBIF	OD DBIF	SBIF	PB DBIF	OD DBIF
Low vs. medium inflammation	0.2733	0.3158	0.3121	0.5556	0.5556	0.5556
Medium vs. high inflammation	0.0826	0.0941	0.0242	0.1508	0.1508	0.0317
Low vs. high inflammation	0.1206	0.1707	0.0116	0.0635	0.1905	0.0317

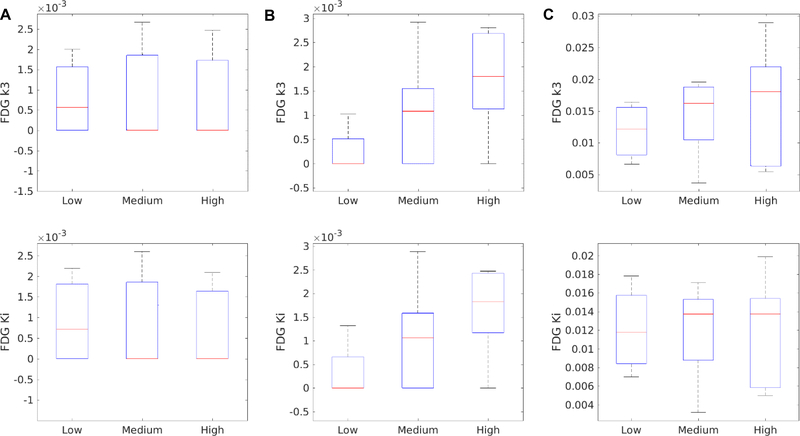
The capability of other kinetic parameters 𝑘2,3,𝑘4 and 𝐾𝑖 for differentiating different inflammation groups are summarized in Table 4. No kinetic parameter was able to differentiate inflammation groups, though k₃ and K_i by the population-based DBIF tended to differentiate low versus high inflammation groups. The boxplots of k₃ and K_i by different input models are shown in Figure 8. k₃ by the population-based DBIF achieved statistical significance (p=0.0444) in the t test but not in the U test (p=0.0794), both p values larger than that of K_i. The optimization-derived DBIF did not improve the p values of k₃ and K_i as compared with the population-based DBIF. This may indicate there is no inherent association between these kinetic parameters and liver inflammation, given that the former had better statistical fit quality than the latter as demonstrated by AIC (Figure 5) and F test (Table 2).

Table 4:

P values of T test and U test for comparing different liver inflammation groups using other FDG kinetic parameters estimated by SBIF, population-based (PB) DBIF, and optimization-derived (OD) DBIF.

Group Comparison	FDG Parameter	T test			U test
		SBIF	PB DBIF	OD DBIF	SBIF	PB DBIF	OD DBIF
	k2	0.5894	0.5465	0.7848	0.7302	0.9048	1.0000
Low vs. medium	k3	0.9321	0.2755	0.5661	1.0000	0.2381	0.5556
inflammation	k4	0.8121	0.2861	0.9427	1.0000	0.4603	1.0000
	Ki	0.9367	0.3345	0.9509	1.0000	0.5556	0.9048
	k2	0.1123	0.1320	0.1021	0.1508	0.3095	0.1508
Medium vs. high	k3	0.9355	0.3478	0.7661	0.8413	0.4127	0.6905
inflammation	k4	0.9975	0.7663	0.7269	1.0000	1.0000	1.0000
	Ki	0.8636	0.3862	0.9702	0.8413	0.4127	1.0000
	k2	0.3112	0.3276	0.2042	0.7302	0.9048	0.2857
Low vs. high	k3	0.9955	0.0444	0.4885	1.0000	0.0794	0.5556
inflammation	k4	0.8140	0.2223	0.7107	0.8095	0.2540	1.0000
	Ki	0.7955	0.0580	0.9263	0.9683	0.0794	1.0000

FIGURE 8:

Association of liver inflammation score with FDG k₃ (top row) and K_i (bottom row) estimated by different input models. (A) Image-derived SBIF; (B) Population-based DBIF; (C) Optimization-derived DBIF.

The associations of liver inflammation grades with SUV, fat-adjusted SUV (31), and the metabolic rate of glucose by Keramida’s Patlak analysis (MRglu-KP) (32) are shown in Figure 9. The p values of t and U tests are reported in Table 5. No association was statistically significant. While SUV had no association with inflammation (p>0.5), the fat-adjusted SUV corrected by CT values (31) tended to increase in high-grade inflammation (p≈0.1). MRglu- KP was calculated using blood glucose level and the Patlak intercept in addition to the Patlak slope (32) and thus had a trend different from K_i in Figure 8. We also applied the correction factor of fat-adjusted SUV to obtain fat-adjusted K₁, which however reduced the association between K₁ and inflammation (Table 5).

FIGURE 9:

Association of liver inflammation score with different glucose utilization parameters. (A) Standard SUV; (B) Fat-adjusted SUV; (C) Metabolic rate of glucose by Keramida’s Patlak analysis (MRglu-KP).

Table 5:

P values of t test and U test for comparing in different liver inflammation groups using standard SUV, fat-adjusted SUV (fSUV), metabolic rate of glucose by Keramida’s Patlak analysis (MRglu-KP), and fat-adjusted K₁ (fK₁).

Group Comparison	T test				U test
	SUV	fSUV	MRglu- KP	f K1	SUV	fSUV	MRglu- KP	fK1
Low vs. medium inflammation	0.7678	0.7386	0.4543	0.3110	0.9048	0.9048	0.7302	0.4127
Medium vs. high inflammation	0.9709	0.1287	0.1139	0.1672	1.0000	0.2222	0.2222	0.3095
Low vs.high inflammation	0.7494	0.1069	0.3690	0.0827	0.7302	0.1111	0.5556	0.1111

DISCUSSION

Determination of liver inflammation in nonalcoholic fatty liver disease patients is crucial in differentiating serious NASH from simple hepatic steatosis. Dynamic FDG-PET with kinetic modeling has the potential to provide a noninvasive imaging biomarker for characterizing hepatic inflammation. Accurate kinetic modeling of dynamic liver FDG-PET data requires consideration of the effect of dual-blood supplies in the liver. Although the input function from the hepatic artery can be derived from the aorta in the dynamic images, it is difficult to derive the portal vein input function from dynamic PET because the size of portal vein (10–15mm) is small compared to the spatial resolution of clinical PET scanner (4–8mm). Partial volume effects, noise and respiratory motion all can contaminate the accuracy of the portal vein input function.

The standard SBIF model simply neglects the portal vein input which theoretically represents more than 80% of the total blood input. Neglecting the PVIF causes overestimation of the peak value of the input function and subsequently results in inaccurate estimation of FDG kinetic parameters. The K₁ parameter, which reflects the scale between the blood input function and the tissue TAC (see Eq. 4 and Eq. 5), can hence be underestimated by the fitting process to compensate for the higher peak value of the SBIF. To account for the dual-blood supply effect, we applied the population-based DBIF model (21,36) in this study. It improved TAC fitting with lower AIC and higher F values than SBIF but did not improve association of the FDG biomarker with inflammation grades. This can be explained by the fact that the population model is not adaptive to individual objects and thus might not provide the optimal estimation.

The optimization-derived DBIF model estimated the PVIF adaptively and provided the best performance according to TAC fitting quality and association with histopathological inflammation grades. Because the parameters of the input model were jointly estimated with liver tissue kinetic parameters, the estimation was more adaptive to individual patients and achieved lower AIC and higher F values. In this study, the v_b estimates were very small but increased by the new model, though the values were still smaller than expectation in the liver (36). This is possibly explained by the difference between image-derived input function and arterial blood input. Similarly, the f_A estimates were far smaller than the population mean 0.25 that was reported based on arterial sampling. This may also be in part due to the capability of being adaptive to individual patient data. The resulting K₁ parameter estimates were different from those by population-based DBIF. Both were higher than those by SBIF thanks to the correction on overestimation of the input function peak. Although there was no ground truth of K₁ values for validating the estimates, evaluation of statistical information criteria and analysis of association of K₁ with liver inflammation grades provided a feasible way to prove the improved performance of the modified DBIF model.

In addition to establishing the kinetic modeling method for dynamic FDG-PET characterization of liver inflammation, this work adds a new contribution to the methodology of dual-input kinetic modeling. We extended and validated the method of DBIF modeling using a joint optimization framework. Previously, Kudomi et al estimated both aortic input function and parameters of input model from multiple regional liver TACs in dynamic FDG-PET (42). Their method, however, is more complex for practical use with multiple steps involved. When the tracer distribution is uniform in the liver, TAC data would also be less helpful for the estimation of the many parameters in their model. Our method is simpler and can be implemented voxel-by-voxel to easily derive parametric images which will allow the future study of liver heterogeneity. The proposed method shares a similar spirit with the work by Chen and Feng (53) designed for modeling a different tracer ¹¹C-acetate. The compartmental model used in (53) was irreversible while a reversible model was required in our study for FDG modeling. Rani et al also used a similar DBIF model for modeling FDG kinetics in rat liver (54). Their model uses a fixed f_A and 4 free dispersion parameters (as opposed to 1 parameter in this work), which is more flexible but results in higher variability. Garbarino et al proposed a more complex model for mouse imaging by including the gut as another compartment (35). The model has 9 free parameters if f_A is included and requires definition of the gut TAC. Thus, the current work has complemented existing studies to establish the optimization-derived DBIF modeling method. Our method can be easily implemented without additional operations.

Another notable aspect of this work is the validation of dual-input kinetic modeling using histopathological reference. All existing studies of dual-input kinetic modeling were only able to validate the DBIF approaches in animal studies (e.g., pigs (36,37), foxhounds (21), rodents (35,54)) or demonstrated the improvement using statistical TAC fitting quality in human patients (53). No studies had demonstrated an impact on physiological measurements by using a histopathological ground truth. In comparison, the present work provided direct evidence on the impact of DBIF on improving association of the FDG-PET biomarker with histopathological inflammation in human patients.

Using the optimization-derived DBIF model, we found that FDG K₁ decreases as liver inflammation grade increases (Figure 7). This result is consistent with previous findings that perfusion reduces in NASH (55,56), given that FDG K₁ from a 3-minute early-dynamic FDG-PET scan reflects hepatic blood flow (37). Nevertheless, FDG K₁ in this study was derived from one-hour dynamic data. It characterizes the overall delivery rate of FDG from blood to hepatic tissue and may also relate to the expression level of glucose transporters (34), though FDG has a high extraction fraction in the liver as compared to other organs such as the brain. Winterdahl et al. (37) also pointed out that FDG K₁ estimated by a scan longer than 3 minutes was less correlated with liver blood flow. It is worth further investigation to determine whether blood flow only or its combination with glucose transporters decides the association of FDG K₁ with liver inflammation. Our study also indicated that SUV and other kinetic parameters were not correlated with inflammation grades. FDG k₃ and fat-adjusted SUV tended to increase in liver inflammation, but the associations did not achieve statistical significance. Thus, FDG K₁ can be the major parameter of interest in future studies.

Earlier studies showed that liver fat content has a modulating effect on hepatic physiology including perfusion, fatty acid metabolism, and glucose metabolism as measured by PET (57) and it is necessary to correct FDG SUV and K_i for the fat content (30). This study showed that fat-adjusted K₁ had poorer association with liver inflammation than non-adjusted K₁, suggesting a potential effect of liver fat content on hepatic inflammation. This result complements existing observations.

There are limitations with the present study. Histopathological inflammation can vary across different spatial locations in the liver. The statistical analysis of PET data in the study was not specific to the location of biopsy. This is because accurate biopsy location information was difficult to obtain even with ultrasound guidance and was not available in this study. We chose to analyze the PET data based on the whole liver region to achieve robustness to locations and to noise in PET data. It is noted that all the evaluated kinetic models did not achieve a statistical significance (p>0.05) in differentiating low versus medium inflammation levels (Table 3), though the FDG K₁ values by the optimization-derived DBIF model tended to differ in the two groups (Fig. 6C). This might be limited by the number of samples (N=14) in this study and is worth further investigation in a larger number of subjects. Note that this study did not include healthy subjects. It is therefore more difficult to reach statistical significance than in other studies comparing patients to healthy subjects. The optimization-derived DBIF model contains two additional parameters as compared with the standard 3-compartment model, which may result in higher variability in parameter estimates. The nonlinear least-square estimation by the Levenberg-Marquardt algorithm may also suffer from local minima. While the better fit quality of the new model has been confirmed by statistical criteria including AIC and F test, our future work will investigate the structural identifiability of the new model using mathematical analysis and investigate practical identifiability using Monte Carlo simulation.

It is possible that k₃ is inherently associated with liver inflammation but the association could not be extracted from the data because of noise. k₃ may physiologically represent FDG transport instead of phosphorylation, as indicated by Bertoldo et al. in the study of a 4-compartment model in skeletal muscle (58). Also, in contrast to standard Patlak plot which underestimates K_i when k₄ is not small, the generalized Patlak plot (59,60) considering the effect of nonzero k₄ can be potentially used to improve Keramida’s analysis. In addition, advanced image reconstruction algorithms (61) such as direct reconstruction (62) or the kernel method (63) may provide a hope to reduce the variability of kinetic parameter estimates, given vendors have started to implement sophisticated four-dimensional reconstruction algorithms for whole-body parametric imaging on new PET scanners (64,65). Recent development of high-sensitivity PET scanners such as the EXPLORER (66,67) further provides a new opportunity for obtaining reliable estimation of k₃ and even k₄ to examine their possible role in characterizing liver inflammation. All these are of interest and value in future studies.

CONCLUSION

In this study, we examined three different kinetic models for analyzing dynamic FDG-PET data for characterizing liver inflammation. Statistical fit quality metrics and analysis of association with histopathology indicated that modeling of DBIF is crucial for accurate kinetic modeling of liver time activity curves. The optimization-derived DBIF model improved the association of FDG K₁ with liver inflammation grades and was more appropriate than traditional single-blood input function and population-based DBIF for dynamic FDG-PET kinetic analysis in human NASH studies.