Small airway segmentation in thoracic computed tomography scans: a machine learning approach

Abstract

Small airway obstruction is a main cause for Chronic Obstructive Pulmonary Disease (COPD). We propose a novel method based on machine learning to extract the airway system from a thoracic computed tomography (CT) scan. The emphasis of the proposed method is on including the smallest airways that are still visible on CT. We used an optimized sampling procedure to extract airway and non-airway voxel samples from a large set of scans for which a semi-automatically constructed reference standard was available. We created a set of features which represent tubular and texture properties that are characteristic for small airway voxels. A random forest classifier was used to determine for each voxel if it belongs to the airway class. Our method was validated on a set of 20 clinical thoracic CT scans from the COPDGene study. Experiments show that our method is effective in extracting the full airway system and in detecting a large number of small airways that were missed by the semi-automatically constructed reference standard.

1. Introduction

Chronic obstructive pulmonary disease (COPD) is a prevalent obstructive lung disorder characterized by long-term limited airflow. COPD is a complex, progressive disease and constitutes the third leading cause of death world-wide (Vos et al 2015). The societal burden of COPD is enormous.

Imaging, in particular computed tomography (CT), is of vital importance to elucidate the mechanisms underlying COPD. It is generally believed that the small airways are the major sites of obstruction (McDonough et al 2011, Burgel 2011). Small airways are defined as those with a diameter below 2.0mm (Barnes 2004), which is close to the resolution of CT. Since it is difficult to find these small airways in CT scans, researchers have instead analyzed expiratory CT scans for the presence of air-trapping as a surrogate marker of small airway disease (Gietema et al 2011). In this work we aim to specifically extract small airways from inspiratory thoracic CT scans. Although many algorithms have been proposed for the segmentation of airways in CT, none has focused specifically on extracting the smallest airways visible on CT.

Accurate airway segmentation from CT scans has multiple applications. A primary one is measuring global and local morphological properties of the airway tree, e.g., generation level, branch diameter, wall thickness, cross-sectional lumen area, and lumen circularity. These measurements have been shown to correlate with disease severity and progression. Another application is planning for virtual bronchoscopic navigation (Kiraly et al 2011). Finally, a precise delineated airway tree can aid segmentation of other structures, such as pulmonary lobes and segments (van Rikxoort and van Ginneken 2013), and pulmonary arteries and veins (Charbonnier et al 2016).

Radiologists carry out hand-operation to extract airways from CT scans, and measure the airway lumen diameter and wall thickness. The disector method (which focuses on a pair of serial sections separated by a fixed distance) is preferably adopted when counting the number of visible small airways per volume. All these tasks are extremely laborious and therefore infeasible in clinical routine. Therefore, many fully automated methods have been developed, reviewed by van Rikxoort and van Ginneken (2013) and Pu et al (2012), and compared in a collaborative study by Lo et al (2012). The key challenge of airway segmentation is to avoid false positive detections, as many algorithms have a tendency to “leak” into the lung parenchyma. The airway lumen and lung parenchyma both appear as regions with low intensity on CT, separated by high intensity wall tissues. It should thus be easy to separate airway lumen voxels from lung parenchyma voxels. However, at every bifurcation, the airway walls become thinner, and imaging noise and partial volume effect make it much more difficult to discriminate those walls from their surroundings. Therefore, extracting the airways by connecting voxels, starting at the trachea and main bronchi and progressing downwards, often oversteps the airway walls and spreads into lung tissues. A range of solutions have been proposed to tackle this issue (Lo et al 2012). Gray-scale morphological reconstruction can be used to selectively enhance tubular airways (Aykac et al 2003). A 3D version of this approach was proposed in Irving et al (2014) which may improve results but increases computational complexity. Various assisted rules encoded anatomical knowledge have been proposed, including exploiting the parallel adjacency of airways to arteries (Sonka et al 1996), the cross-sectional lumen area around the centerline (Wood et al 1995), local contrast to airway walls (Kitasaka et al 2003) and rules of thumb regarding branching angles (Bauer et al 2009). An optimal combination of such rules may improve airway extraction. In literatures front propagation is guided under constraints of fuzzy connectivity (Sonka et al 1996) or cylindrical regions of interest (Kitasaka et al 2003) to detect a connected airway tree. However, these methods tend to generate a fairly high amount of false positives (Lo et al 2012). None of these features are able to capture airway appearance perfectly.

Additionally, several researchers have used machine learning and developed supervised airway segmentation schemes. Lo et al (2010) sampled the airway and leaked parenchyma voxels from a conservative and a leaked segmentation, respectively. A kNN classifier categorized voxels by eigenvalue-based tubular features and oriented similarity features between airways and vessels. This method extracted a high quality airway tree and low false positive rate at the cost of extremely long run-time (55 minutes to segment the airway tree from a single CT scan). Meng et al (2016) initialized a relatively leaky segmentation based on multi-scale tubular enhancement and local intensity information. An SVM classifier with 32 Hessian-based features was trained to remove the false positives from the leaked segmentation. The remaining candidate patches were linked with the trachea and main bronchi using a graph-cut method. Charbonnier et al (2017) proposed an airway leakage removal scheme: a set of 2D patches that capture the 3D airway appearance were extracted along the centerline and a convolutional network was used to classify the patches and remove leaked segmentation branches.

In general, whatever additional strategy adopted, traditional region growing or wave front propagation, the need to reduce leakage has the consequence that many very small airways are not segmented at all. It is still far from maximizing the potential of machine learning. Some only existing efforts were made to convince machine learning’s ability to find airways and to avoid over-segmentation. The diversity of small airways’ morphology and CT characteristics leaves a complete blank in the automation of their extraction. We therefore proposed a fully automated machine-learning based airway segmentation framework focused specifically on extracting more small airways from CT images, which has never been reported, even when we cannot find the connection of those airways to the main airway tree. In this study, we had to face with the fact that a perfect reference standard was unavailable. A dedicated sampling method was presented to address this problem without any further manual involvement apart from obtaining the incomplete reference data. Another main contribution was that the image texture features were combined with traditional tubular features in the airway segmentation. Our framework was developed and evaluated using data from COPDGene, the largest genetic COPD study that includes imaging. The proposed framework could increase the detection measurements in full airway system and especially in small airways against the reference data under a relatively low false positive rate.

The paper is organized as follows. Section 2 describes the data and methods. Section 3 details the experiments and provides quantitative results. Section 4 contains the discussion and, finally, Section 5 draws conclusions.

2. Methods

In this section we explain our method in detail. We start by describing the data we used. We then explain the initial detection of the trachea and main bronchi, elaborate on the airway voxel candidate selection, and describe the features, classifier and post-processing steps we employed.

2.1. Data

Our project was conducted and evaluated on a randomly selected data set of 100 high resolution thoracic CT scans taken at full inspiration provided by the COPDGene Study (Regan et al 2010). Each scan was reconstructed to 512 * 512 slices (ranging from 360 to 659 axial slices). In-plane voxel size varied from 0.50 to 0.96mm and slice thickness was 0.625mm. Each scan was processed by the COPDGene imaging core (Thirona, The Netherlands) to identify the lung masks and extract a connected airway tree marked with branch labels. A description of the lung mask extraction and airway segmentation methods can be found in van Rikxoort et al (2009) and van Ginneken et al (2008). Then an annotation process was performed semi-automatically. Trained human analysts manually corrected and extended computer generated lung segmentation and airway trees. Leakages were removed and the missed segmental and sub-segmental branches belonging to a pre-defined set were added following strict protocols. This final airway segmentation served as reference standard in this study. We used these segmentation to obtain airway and non-airway voxels for training, as explained below. We note that the semi-automatically produced segmentation still misses smaller airways. We therefore investigate in Section 3 if our method can find additional airways.

2.2. Trachea and main bronchi removal

The trachea and main bronchi were not detected with our machine-learning based framework, because these branches are relatively easy to find with standard techniques. It is necessary to extract them as a starting point to obtain a 3D-connected tree structure. For this purpose, we implemented a simple region growing scheme that started with the detection of a tracheal seed point similar to Tan et al (2014). The initial region growing threshold was defined as the average intensity I_avg of the voxel in a 26-neighborhood of the seed point plus an additional 350HU. The 26-neighborhood voxels were repeatedly clustered as new seed points until a bifurcation was found, indicating the segmentation of the trachea was complete. Next, the mean tracheal intensity μ_tra and standard deviation σ_tra were calculated and a new region growing threshold for main bronchi segmentation was set to μ_tra + 2σ_tra. The main bronchi segmentation algorithm terminated when the second generation bifurcations were encountered.

2.3. Training sample selection

In order to capture the image characteristics of airway and non-airway voxels in the training phase, a representative set of positive and negative samples have to be selected. This subsection describes our sampling method in detail.

2.3.1. Airway sample selection

In order to specifically sample small airways in a given airway tree A, we first estimated the diameter of each branch labeled with B₁, B₂, … , B_n in A. A was skeletonized using a topology thinning method (Bian et al 2014) to form a 26-connected, one-voxel wide and central-located structure (centerline). The diameter D_Bi of individual branches B_i was estimated based on the centerline voxels c₁, c₂, … , c_k belonging to it. The centerline c_j was increasingly dilated by a spherical element (one voxel at a time) until the dilation surface collided with background voxels. The sphere diameter d_cj was then set to be c_j’s diameter with respect to image resolution. The branch diameter was computed as the average of all its centerline voxels’ diameters:

$$D_{B_i}=\frac{1}{k}{\displaystyle \sum }_j^k{d}_{c_j,}{C}_j\in B_i.$$

Although the main focus of this study is on small airways, we found it was not optimal to extract positive candidates from small branches exclusively. The main reason for this is that in some cases the reference did not contain a sufficient amount of small branch voxels. Hence, we extended the sampling to the whole reference tree. However, uniform sampling would lead to an imbalanced training set in which larger airway voxels would dominate the final positive candidate set.

Therefore, a diameter-focused airway sampling process was implemented by initially categorizing airway branches into small airways (D_Bi ≤ 2.0mm), medium airways (2.0mm < D_Bi ≤ 5.0mm) and large airways (D_Bi 5.0mm). The voxels belonging to each branch type were further sub-divided into four subsets according to their branch measurements and locations:

• (1)Voxels from small airways;
• (2)Voxels from central lumen area of medium airways;
• (3)Voxels from periphery lumen area of medium airways;
• (4)Voxels from large airways.

Subset 1 entirely consisted of small airway samples. The samples formed Subset 2 and 3 are all extracted from medium airways. The central lumen area in Subset 2 was defined as the branch centerline voxels and their 26-connected neighborhoods. The periphery lumen area in Subset 3 formed the remaining medium airway voxels. The primary consideration of distinguishing Subset 2 from Subset 3 was to simulate small branches in the central part of medium branches. Subset 4 was added to ensure that the proposed method was capable of extracting larger airway voxels as well, which was needed to obtain a connected airway tree. It should be noted that the trachea and main bronchi are not included in Subset 4. We randomly selected an equal amount of voxels from each subset for training.

2.3.2. Non-airway sample selection

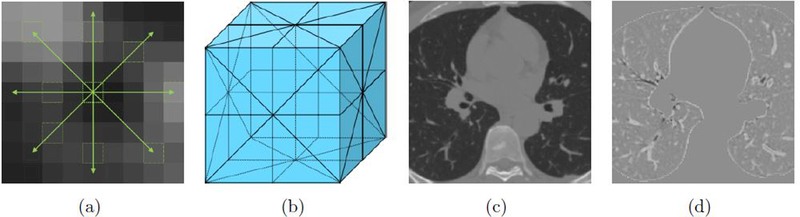
If we would randomly select negative voxels from all voxels in the lung masks not labeled as airway, we ran into the risk of selecting some voxels from small airways that were missed in the semi-automatically created reference. We therefore opted to use an airway-like removal sampling, which employed image processing procedure to enhance the possibly unlabeled airways in the training data, so as to avoid sampling those as non-airways. The lung fields were processed using a modified subtraction algorithm proposed in Lassen et al (2013). For a given voxel v with intensity value I_v in the lungs, the maximum intensities I_max were identified along 8-neighborhood directions with a range of k voxels (marked in green as 1(a)). k was a dimensional scale whose range covered one small airway diameter threshold, aiming to capture small airway completely within one direction. The subtracted scale of v was obtained from this equation: $I_{sub}=Avg(I_{\text{max}1-8})-Iv-Var(I_{\text{max}1-8}).$ The average maximum minus intensity item was the contrast between v and its spatial surroundings; subtracting the variance ensured that I_sub would only get a high response when v was uniformly surrounded by high-intensity voxels. The underlying idea was that genuine airway lumen voxels had a low attenuation and were uniformly surrounded by higher density wall tissue. Other airway-like structures, such as small clusters of emphysema and imaging noise had a more heterogeneous surrounding and received lower subtraction results. The lung parenchyma and other dense voxels were essentially unchanged, or might even be intensified by this preprocessing. With the procedure outlined above, only planes that cut almost orthogonally through the bronchi showed high responses. Therefore we took the average of three largest responses from the 9 plane filter responses (see Figure 1(b)) I_sub1−9 as the subtraction scale (see Figure 1(d)). Negative samples were randomly extracted in the lung fields apart from the highly-subtracted region.

Figure 1.

A specific display of the subtraction procedure: (a) From the center voxel (highlighted by a bold green dashed square) the maximum intensities (highlighted by green dash squares) were calculated for all of the 8-neighborhood directions (green arrows); each arrow covered a range of 2.0mm spatially which was the small airway scale. (b) Nine filter cutting planes (marked by straight and dashed black lines in 3D space). (c) An original CT slice. (d) Subtraction scale image of (c); the airway lumen attenuates significantly, whereas the high density tissue intensified and lung parenchyma kept almost unchanged compared with (c).

2.4. Features

Two categories of image features were utilized to express the airway’s tubular shape. The first category represented local intensity structure and was derived from Gaussian scale space (Frangi et al 1998). We used the three eigenvalues λ₁, λ₂, λ₃ of the Hessian matrix computed from the second-order derivatives of the image intensity after a Gaussian convolution. These features have been widely used in prior work to distinguish blob-like, plate-like and tube-like structures. The eigenvalues were sorted according to their absolute values as |λ₁| ≤ |λ₂| ≤ |λ₃| (Lo and de Bruijne 2008). To obtain additional rotationally invariant three eigenvalues combinations (Laplacian, Gaussian curvature, eigen magnitude) were also included in the feature set.

The second category of features was based on image texture. We extracted 2D local binary pattern (LBP) values as a visual descriptor (He and Wang 1990). Since the dimensions of small airways are below 2.0mm, it su ced to use a small neighborhood. For each candidate voxel centered in a square window, we compared the voxel to each of its 8 neighbors in a clockwise direction. This resulted in a binary value with 8 digits which was 0 when a candidate was lighter than its neighbor and 1 conversely. The value was further transferred to become rotationally invariant by a digit shifting operation to find its minimum conversion. We preferred these LBP values as features, rather than the full LBP vectors, because even a normal cell size in the classical LBP vector was larger than the diameters of small airways. To capture the airway appearance orthogonal to different spatial directions, the 2D LBP windows included the nine cut planes shown in Figure 1(b).

To cope with branches with variable diameters, the Hessian features were computed at multiple scales, and the LBP values were determined for different window sizes. Table 1 lists all features extracted at one scale.

Table 1.

Image features used for airway classification.

Feature ID	Description	Format
f1	Gaussian blurred intensity	I*G
f2, f3, f4	Hessian eigenvalues	λ1, λ2, λ3
f5	Laplacian	λ1 + λ2 + λ3
f5	Gaussian curvature	λ1λ2λ3
f7	Eigen magnitude	$\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}$
f8, … , f16	LBP values in 9 planes

2.5. Classifier

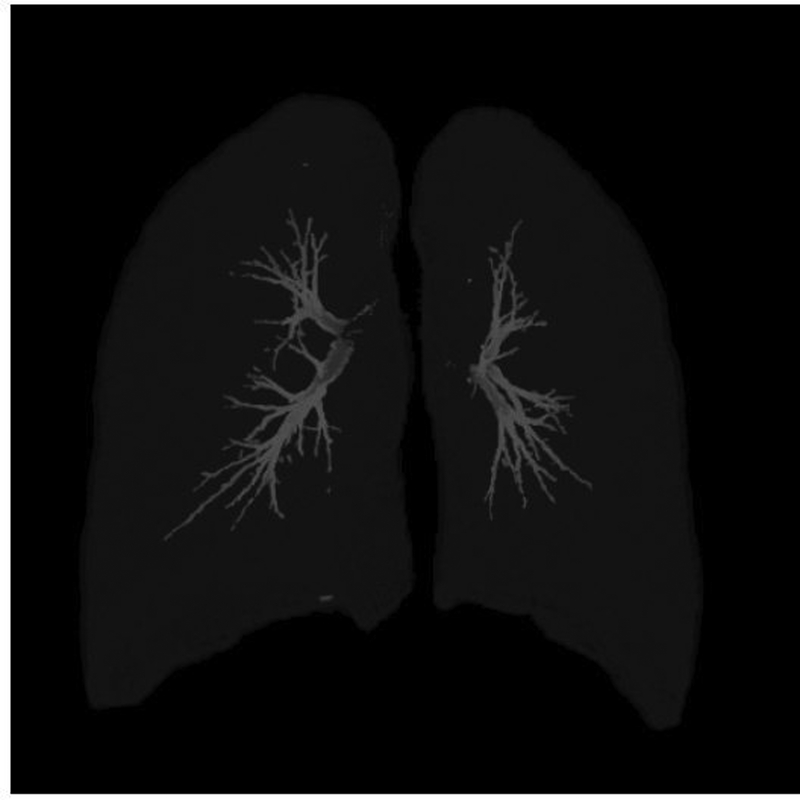
Random forest (RF) has been widely recognized as an accurate ensemble learning method, and is known to perform well for classification, regression and other tasks (Friedman et al 2001). It has attracted the pulmonology research community’s attention in lung nodule analysis and organ segmentation (Lee et al 2010, Mansoor et al 2014).A random forest consists of a collection of independently trained decision tree classifiers T₁, T₂,···, T_N. Input a previously unseen voxel v, processing via each subtree T_i starts at its root and pushes the voxel feature vector through the corresponding sequenced nodes. The prediction procedure terminates when a leaf node is reached. The forest returns for v a probability K/N, in which K is the number of subtrees voting for v representing an airway and N is the total number of trees. All voxels within the lung masks were processed and this generated a probability map (shown in Figure 2), which was used to construct a final airway segmentation.

Figure 2.

A resulted probability map shown in Maximum Intensity Projection Mode. The background outside lungs was in black. Individual lung or airway voxels’ probability was with respect to its gray-scale. Higher gray-scale indicated larger probability.

2.6. Post-processing

We applied a threshold T_prob to the probability map to label the voxels as airway. This resulted in a number of connected components, including small patches not connected to the trachea and main bronchi. We could only choose a limited number of them, due to the time-consuming and labor-intensive manual evaluation required. Therefore, a volume threshold, which was set as 30 voxels, was used to eliminate very small connected components from all extracted structures.

3. Experiments and Results

We designed two experiments to show the performance of our method to segment airways and small airways. The first experiment compared our results with the reference data to determine how many airway branches and small branches we could find correctly within the reference segmentation. The second experiment focused on additionally detected airways, i.e., those not contained in the semi-automatically constructed reference set. We expect these additional airways to be mainly small airways. For the quantitative measurements provided, we followed the approach of the MICCAI Challenge “Extraction of Airways from CT 2009” (EXACT’09) (Lo et al 2012). Three key measurements from the challenge were implemented for our evaluation: detected branch count percentage, detected tree length percentage and false positive volume percentage.

The trachea and main bronchi were excluded from the quantitative evaluation because they were not segmented by the machine-learning based method. Those branches were only used to make a connected tree structure for 3D visualization.

For each experiment, our results were evaluated in two ways: First, since the reference data is a tree structure, we constructed a completely connected airway tree based on our segmentation; rooted from the trachea seed point in Subsection 2.2, airway voxels were successively joined under a 26-connected rule. Second, we performed an evaluation not restricted to the tree structure – as researchers implemented before (Lo et al 2012) – but also extended to those components disconnected from the main tree. Measurements are shown for all branches (both larger and small branches) and for only small branches separately.

3.1. Parameters and implementation

80 scans were randomly selected from our dataset as training set, and the remaining 20 as test set. Airway and non-airway samples were extracted as described in Subsection 2.3. A total of 80, 000 positive samples were randomly selected from the airway reference data (1000 samples per scan) and a similar procedure was followed for the negative samples. For the positive sample selection (Subsection 2.3.1), each airway group contributed 25% of the samples. For the negative sample selection (Subsection 2.3.2), the subtraction radius was set to be the same as the small airway diameter threshold of 2.0mm, so that the border voxels of small airways could be attenuated significantly, just like the lumen center ones; the subtraction scale threshold to distinguish potential airways and lung parenchyma was set to be −30 HU.

For feature extraction (Subsection 2.4), the CT images were convolved by three scales similar to the small branch radius: σ = 0.5, 1.0 and 1.5mm. For the LBP features we used three different window sizes: 3 * 3, 5 * 5, and 7 * 7 voxels. The 5 * 5 window was resampled window from 3 * 3 and 7 * 7 was resampled from 5 * 5. In total, this resulted in 7 * 3 + 9 * 3 = 48 features.

In our classifier design, we implemented a forest consisted of 100 subtrees. For each tree, $\sqrt{48}\approx 7$ features were randomly selected from the feature vector for node training. A voxel was classified as airway if its probability T_prob was larger than 0.5.

The proposed method was implemented on a standard PC with an Intel Core i5–2400 CPU and 12GB memory. All code was written in C++. In the training procedure, the positive and negative sampling procedure took 20 seconds per CT scan, around 30 minutes in total. Most time, 2.5 hours, was spent on forest construction and training. In the test procedure, feature extraction took less than 5 minutes; the execution time for one scan was between 2 and 3 minutes.

The reference segmentation measurements of the 20 test scans are listed in Table 2. The tree length measure was calculated in mm and volume in mm³.

Table 2.

Reference airway measurements of the 20 test scans used for evaluating the proposed method.

	Branch count		Tree length(mm)		Volume (mm3)
Case	All branches	Small branches	All branches	Small branches	All branches	Small branches
1	150	49	2339.3	501.9	9119.8	573.2
2	110	24	1724.1	234.9	10893.6	294.8
3	122	23	1944.8	246.0	12366.7	327.7
4	98	8	1690.4	50.0	10272.4	72.4
5	219	31	3673.1	221.3	16960.8	292.3
6	119	21	2062.3	286.0	8649.9	384.7
7	368	113	5328.8	1031.1	22509.7	1326.7
8	209	42	3324.3	397.5	31066.7	590.4
9	110	9	2044.1	82.6	10108.9	147.2
10	168	42	2591.7	430.3	13596.3	524.7
11	139	43	1892.0	475.7	8204.7	583.9
12	356	69	5394.8	586.4	24438.4	767.2
13	263	64	4850.3	643.6	23814.5	826.3
14	196	64	2942.9	818.0	12827.3	1036.4
15	162	39	2412.0	349.4	13507.2	413.1
16	176	33	2904.4	339.7	14022.3	502.4
17	138	12	2006.6	87.5	13490.5	141.5
18	279	58	4431.6	569.5	18406.6	779.3
19	112	28	1579.2	289.4	11934.1	366.5
20	188	37	2773.5	296.9	14434.8	376.0
Total	3682	809	57909.9	7937.3	300625.0	10326.5

3.2. Detection performance relative to the reference standard

We first assessed the performance of our method relative to the reference standard. In Table 3, the percentage of detected branch branch count and percentage of detected tree length are reported. To compute these measurements, all the detected voxels which were not included in the reference data were discarded. Centerlines of our results and of the reference segmentation were extracted using topology-thinning (Bian et al 2014). There were sometimes one-voxel biases between the two segmentations at the border regions due to different airway decision rules by computer and the reference. In order to guarantee a coherent analysis, our centerline voxels were projected to its 26-neighborhood reference centerline locations if they were not found at the corresponding reference coordinates. A detected branch B was defined as correct if it met the following two conditions: 1) the detected branch overlapped more than 80% volume of the corresponding reference branch; 2) every centerline voxel from B could be projected correctly within 26-neighborhood range to the corresponding reference centerline.

Table 3.

Branch and length detected percentage results of the proposed method.

	Completely-connected airway tree				All segmented airway components
Case	All branches		Small branches		All branches		Small branches
	Branch count	Branch length	Branch count	Branch length	Branch count	Branch length	Branch count	Branch length
1	97.3	92.9	91.8	75.7	99.3	98.8	98.0	94.8
2	100.0	99.9	100.0	99.0	100.0	99.9	100.0	99.5
3	100.0	99.5	100.0	97.3	100.0	99.7	100.0	97.7
4	99.0	98.9	87.5	86.8	100.0	99.4	100.0	88.5
5	99.5	99.9	96.8	97.8	100.0	99.9	100.0	98.7
6	99.2	95.5	100.0	77.9	99.2	99.3	100.0	97.2
7	99.5	98.5	98.2	95.7	99.7	99.9	99.1	99.7
8	100.0	91.1	100.0	91.5	100.0	99.9	100.0	99.4
9	99.1	95.5	88.9	85.0	100.0	99.8	100.0	94.9
10	99.4	98.9	97.6	95.4	100.0	99.7	100.0	98.3
11	97.8	98.0	93.0	91.9	100.0	99.3	100.0	97.2
12	97.8	97.8	89.9	91.3	98.9	99.6	94.2	98.8
13	98.9	97.0	95.3	84.0	100.0	99.8	100.0	98.7
14	99.0	97.4	96.9	92.8	100.0	99.6	100.0	98.8
15	99.4	99.0	100.0	94.9	99.4	99.9	100.0	99.2
16	98.3	95.8	84.9	79.6	100.0	99.4	93.9	97.8
17	99.3	99.8	91.7	98.3	99.3	100.0	91.7	99.2
18	98.9	97.5	96.6	89.3	99.3	99.9	96.6	99.0
19	100.0	98.4	100.0	95.1	100.0	99.8	100.0	99.5
20	95.7	96.3	81.1	92.3	99.5	99.4	97.3	97.5
Avg	98.9	97.4	94.5	90.6	99.7	99.6	98.5	97.7
±Std	±1.1	±2.3	±5.7	±7.0	±0.4	±0.3	±2.5	±2.6
Total	98.8	97.3	95.1	90.5	99.7	99.7	98.5	98.3

Our method contained a few key elements, i.e., the type of positive and negative sampling scheme, and the set of extracted features. In order to evaluate the influence of these elements, 6 combination workflows of the key components were investigated, listed in Table 4. Note that uniform sampling of positive and negative classes means to select samples randomly from the airway and lung fields. The average results of the measurements of the 6 workflows are presented in Table 5.

Table 4.

6 compared combinations of airway segmentation workflow.

Workflow	Positive sampling	Negative sampling	Feature set
1	Uniform	Uniform	Tubular only
2	Uniform	Uniform	Tubular + texture
3	Diameter-focused	Uniform	Tubular + texture
4	Uniform	Airway-like removal	Tubular + texture
5	Diameter-focused	Airway-like removal	Tubular only
6	Diameter-focused	Airway-like removal	Tubular + texture

Table 5.

Comparison results of different workflows against the reference over the 20 test cases (measured in branch and tree length detected percentage of total detected components).

	Completely-connected airway tree				All segmented airway components
Workflow	All branches		Small branches		All branches		Small branches
	Branch count	Branch length	Branch count	Branch length	Branch count	Branch length	Branch count	Branch length
1	87.3	86.6	70.5	69.6	89.8	88.3	79.0	78.2
2	89.5	88.7	73.2	73.1	92.4	90.7	84.7	82.3
3	92.2	91.4	79.3	78.0	94.9	93.0	94.0	91.5
4	92.0	91.1	77.3	75.0	94.4	91.9	90.0	86.3
5	93.7	92.3	89.2	88.1	95.2	94.5	94.7	92.8
6	98.8	97.3	95.1	90.5	99.7	99.7	98.5	98.3

3.3. Additionally segmented airways

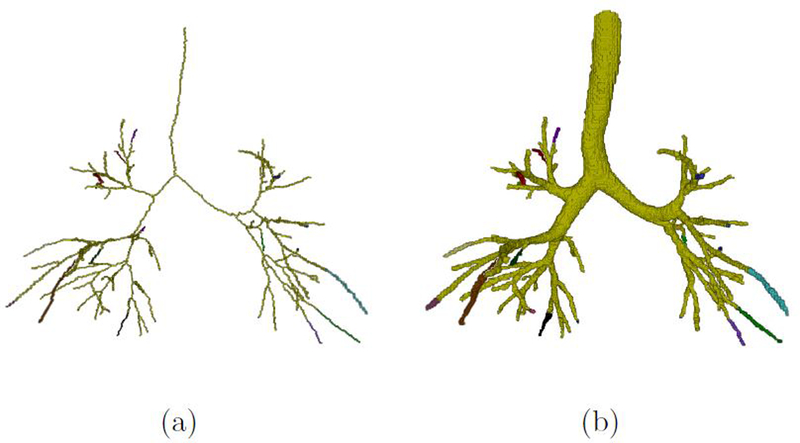
Occasionally, our method detected additional airway voxels very close to the reference. To be able to ignore this effect, we dilated the reference data with a 3 * 3 * 3 cube element and only the voxels outside the dilated reference were regarded as potentially newly discovered airways. The centerline structures of our small-component removal results and reference data were generated as described in Subsection 3.2. The topology structure was extracted to obtain tree or patch roots (voxels with only one neighboring voxels on centerlines) and branching points (voxels with three or more neighborhood on centerlines). Skeletonized branch B_S was marked with an independent label between root, bifurcation or terminal voxels (shown in Figure 3(a)). B_S was dilated by a set of binary sphere structures to include its lumen voxels continually until the morphology fronts collided with background or other labels, forming a reconstructed airway system for subsequent inspection. Figure 3(b) presents the final reconstructed airway system.

Figure 3.

An example of the labeling of airway system. The greened region indicates the overlap between our segmentation and the reference standard. The other colorful regions indicate the additionally detected branches with independent labels. (a) is the rendered centerline structure of a selected airway segmentation; (b) is the rendered reconstruction airway of (a).

All additionally discovered branches were presented to a human observer who was experienced with CT imaging, airway extraction and thoracic anatomy. The purpose of this observer study was to investigate which additionally discovered branches and which branches in the reference that were not detected by our method corresponded to actual airways, and which were leakages. The observer carefully inspected the post-processed test scans overlaid with rendered branches in a dedicated viewer. The platform visualized our segmentations in both 2D and 3D views. For 2D views, the scan was displayed synchronously on axial, sagittal and coronal sections. The observer could zoom, scroll and jump to labels through three orthogonal views to determine whether a branch B was an actual airway or not. The observer was required to classify each branch B as either correct or wrong. The observer received a training session about how to use the scoring platform and to become familiar with correct and wrong examples. It took 2 hours in total to complete the training session. On average, the observer needed 15 minutes to inspect all potentially additionally detected branches for a single case.

The results of this observer study experiment are provided in Table 6. We report the percentage of additionally detected airway and small airway length and volume, with respect to the reference measurements. Furthermore, in order to quantify the amount of erroneously segmented voxels, FPVP, the false positive volume percentage performance measure was introduced from Lo et al (2012). Let V_C and V_W represent the volumes of correct and wrong branches determined by the observer, FPVP was defined as:

Table 6.

Additionally segmented airway length and volume percentage for the proposed method.

	Completely-connected airway tree						All segmented airway components
Case	All branches			Small branches			All branches			Small branches
	Extra correct length	Extra correct volume	False positive volume	Extra correct length	Extra correct volume	False positive volume	Extra correct length	Extra correct volume	False positive volume	Extra correct length	Extra correct volume	False positive volume
1	2.6	1.2	0.4	9.7	15.8	2.9	7.5	3.6	0.9	18.4	31.7	2.6
2	14.3	5.0	0.0	33.9	50.4	0.0	37.8	13.2	0.0	47.9	67.5	0.0
3	23.5	8.2	0.5	56.1	81.7	1.0	54.3	18.2	1.5	87.0	108.2	4.1
4	11.4	5.2	0.1	35.8	56.0	4.9	36.2	14.7	0.4	99.3	131.9	3.0
5	6.9	3.3	0.1	38.7	49.9	2.5	24.9	11.7	0.8	94.2	129.0	3.1
6	3.3	2.4	0.1	1.9	1.5	1.5	19.4	11.0	0.2	18.4	23.3	1.8
7	8.6	2.6	1.7	15.5	20.0	1.5	24.6	10.9	2.6	39.1	54.0	2.8
8	23.6	5.8	1.1	36.5	37.4	9.7	56.3	16.4	1.9	58.4	70.6	10.7
9	39.4	26.9	0.4	19.6	27.6	2.9	77.8	53.3	0.5	24.2	33.5	2.4
10	7.9	3.0	0.3	13.7	17.9	0.0	23.6	10.5	0.3	25.8	38.4	0.0
11	4.0	1.5	0.2	10.8	11.9	0.9	16.1	7.6	0.5	29.5	38.0	0.7
12	12.4	4.7	3.3	20.7	23.0	10.4	23.1	11.3	4.0	26.7	37.8	7.7
13	5.5	2.6	0.1	11.1	14.6	0.6	16.1	7.2	1.1	33.3	44.7	0.6
14	7.3	2.9	0.8	5.0	7.0	0.0	20.6	8.3	3.7	17.5	24.7	2.8
15	6.4	2.3	0.4	13.7	24.7	0.0	23.0	9.0	1.6	35.3	67.2	0.0
16	12.6	3.3	3.7	26.9	22.1	12.1	29.7	12.7	3.7	35.3	36.0	8.9
17	46.4	14.0	6.1	114.4	74.9	25.6	83.2	31.3	6.2	177.1	178.6	16.5
18	7.9	2.7	3.3	11.9	6.8	14.3	24.0	12.9	4.2	29.9	40.2	7.4
19	1.6	0.2	0.4	4.7	2.5	2.0	15.7	2.4	2.8	27.6	29.2	7.4
20	5.8	1.9	1.0	7.9	9.5	4.7	16.1	6.7	1.1	29.7	39.8	3.4
Avg	12.6	5.0	1.2	24.4	27.8	4.9	31.5	13.6	1.9	47.7	61.2	4.3
±Std	±12.1	±6.0	±1.6	±25.5	±23.4	±6.5	±20.7	±11.1	±1.7	±39.3	±42.7	±4.3
Total	11.9	4.7	1.4	17.5	21.1	4.4	30.0	13.3	2.6	37.2	49.4	4.2

$$FPVP=\frac{V_W}{V_c+V_W}*100\%$$

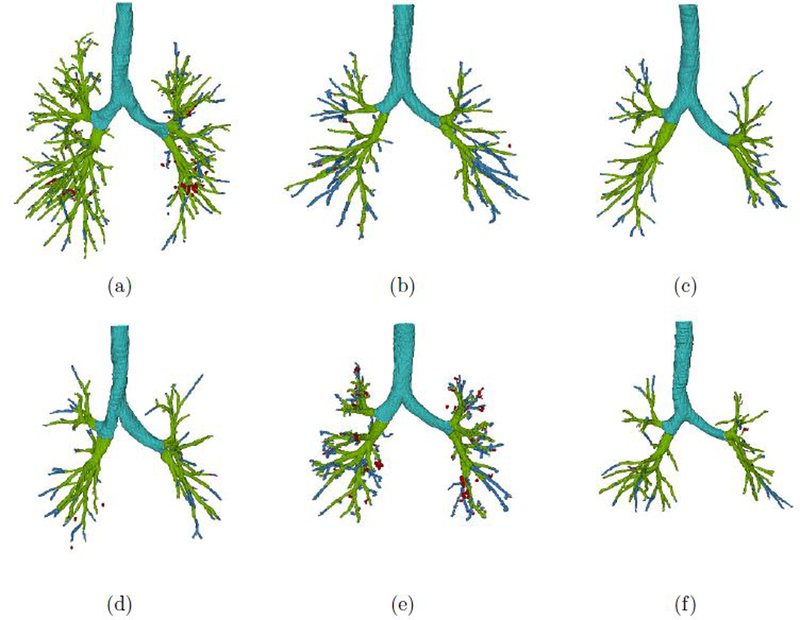
Six representative airway segmentations are presented in a 3D rendering in Figure 4. Figure 4(a) (Case07) and 4(b) (Case09) were the cases with the most/least small airways according to the reference data, respectively. Figure 4(c) (Case02) and 4(d) (Case04) achieved the highest/lowest measurements in terms of detection relative to the reference standard, respectively. Figure 4(e) (Case17) and 4(f) (Case06) were the cases with the most/least additionally detected small airway measurements, respectively. It should be noticed that in Case02 in Figure 4(c) no false positive detection occurred; On the contrary, Figure 4(e) obtained the highest false positive volume.

Figure 4.

3D rendering of selected airway segmentations. The light blue part indicates the trachea and main bronchi; light green is used for overlap between our segmentation and the reference standard; purple indicates missed airway voxels; green indicates false positive voxels in the reference data which are identified by the proposed method; blue indicates additionally detected airway branches; red indicates false positives among the additionally segmented voxels.

4. Discussion

Our experiments show that the proposed machine learning method is able to find a substantial amount of additional small airways, when compared to a reference standard created by manual adaptation of the results of a state-of-the-art airway segmentation. Additionally, we show that an optimized voxel sampling procedure can improve segmentation performance and that the incorporation of our dedicated feature set substantially improves the segmentation. These constitute our main results.

If we consider all extracted components by our proposed fully automated method, we detect nearly all airways in the semi-automatically constructed reference standard. As listed in Table 3, 99.7% of the branches are detected in the reference data and 99.7% for the tree length; for small airways the measures are 98.5% and 98.3%, respectively.

But our method is capable to explore more bronchial structures in the lung fields. Table 6 shows that our method can segment 13.3% more volume, and when we only consider the small airways this number even increases to 49.4%. The improvements are generated under a low false positive rate of 2.6%, and 4.2% for small airways. Moreover, even if we only consider the connected tree system, performance is competitive. It finds 4.7% more volume and 21.1% more small branch volume, and in this scenario the false positive rate drops to 1.4% and 4.4%. Furthermore, the proposed method extends the tree length by 30.0% and the total length of small branches by 37.2%.

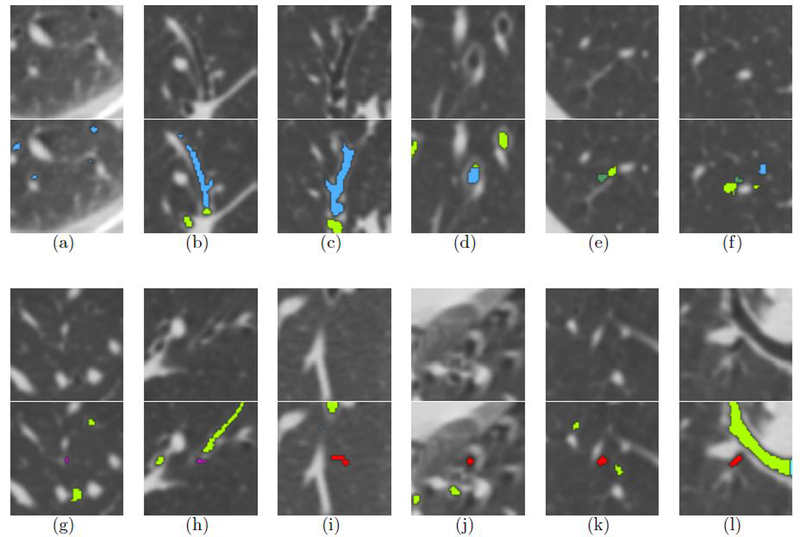
The method can identify airways in the periphery lungs (see Figure 5(a)). When an area of increased intensity occurs in the middle of the airways, the reference standard method regards that as the segmentation frontier encountering non-airway tissue (see Figure 5(b) and Figure 5(c)). Or when a terminal branch locally expands its width, the traditional method considers this a leak and fails to further segment the airways. The proposed method, driven by machine learning, processes the entire CT scan voxel by voxel and thus detects additional airways (see Figure 5(d)).

Figure 5.

2D CT image patches and the overlaps with rendered airway segmentations. The first and third row list the original CT image patches, and the second and fourth row list the corresponding 2D rendering results. The light blue part is the trachea and main bronchi; the light green part indicates the overlap between our segmentation and the reference standard; the purple part corresponds to the missing airway voxels; the green part are false positive voxels in the reference stadard which are identified by the proposed method; the blue parts are the additionally detected airway branches; the red parts are false positives among the newly segmented airways.

Our method, on the other hand, misses some parts of the reference data. This can be explained by considering two specific situations. Firstly, although the reference data sets were manually checked, some tiny leakages might have been accepted erroneously. This is illustrated in Figure 5(e) and Figure 5(f). The other situation pertains to false negatives. These mostly happen when a branch has just bifurcated into new terminal branches (see Figure 5(g) and Figure 5(h)).

In this work we report results for 6 different workflows. A limitation of this study is that the inspections at branch level by a human expert were only performed for Workflow 6, the proposed method. This was done since this visual inspection was extremely time consuming.

4.1. Effectiveness of Sampling

Table 5 indicates that our method achieves a significant improvement through the use of a well-designed candidate sampling. In the absence of a complete airway reference, a fully random candidate sampling turns out to be less reliable. Admittedly, the fully random sampling workflow (Workflow 2) is able to extend the tree length and find some extra branches. However, the disadvantages are: (1) it reveals poor performance in small branch detection with only 84.7% small branches and 82.3% small airway length detected on average; (2) it segments more false positives as well. Both airway-focused and lung-focused sampling have a positive influence on the final results, as Workflow 3 and 4 obtain better performance than Workflow 2. However, these approaches still fall short of the performance of the proposed method.

Lo et al (2010) adopted a sampling method in which airway candidates were extracted evenly with respect to their distance from trachea and main bronchi.

Inspired by this approach, we devised our strategy that samples more extensively from small branches and that is shown to improve results. Furthermore, literatures (Lo et al 2012, Lassen et al 2013) present several other airway sharpening filters such as multi-scale morphological reconstruction, Laplacian of Gaussian filter, and lumen subtraction. Although these approaches are not good enough in practice to completely distinguish airways and lung parenchyma, they can be used to improve the sampling of lung parenchyma voxels, as we did in Subsection 2.3.2. As a result, 98.5% of all small branches and 98.3% of small airway length were identified correctly.

4.2. Effectiveness of Features

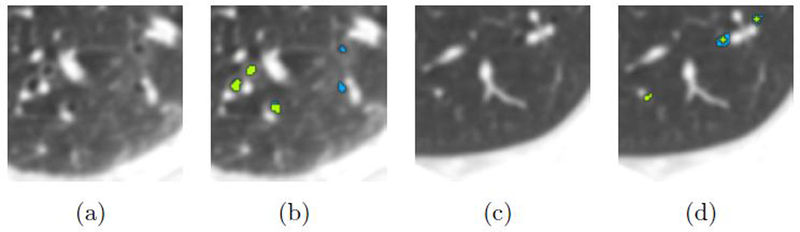
Previous work on machine learning based airway detection features was based on local image descriptors derived from eigenvalues of Hessian matrix, see (Meng et al 2016) and (Lo and de Bruijne 2008). This approach has thus been shown to be effective, and in our study 94.7% of small branches and 92.8% of small airway length are identified (Workflow 5). Figure 6 shows an example of how the proposed method (Workflow 6) outperforms the method using only tubular features (Workflow 5).

Figure 6.

A specific display of the di erence between combined feature segmentation and tubular feature-based segmentation. (a, c) Original CT slice. (b, d) Rendered segmentation; green part: overlay segmented by Workflow 5 and 6; blue part: segmented only by Workflow 6 (the proposed method).

The individual feature importance was also analyzed based on normalized Gini measurements. Among the 48 features, Gaussian blurred intensity at 1.0mm scale achieved the maximum feature importance (0.0558), indicating that no feature had significant influence in segmenting voxels. In general, tubular features’ importance (averaged 0.0335) was larger than the texture ones (averaged 0.0110). For tubular features, the Hessian-derived features generated at 1.0mm blurred scale(0.0443 in average) was slightly better than those at 0.5mm (0.0368 in average), and those at 1.5mm was 0.0192. The Gaussian blurred intensity and Hessian matrix eigenvalues weigh more in the classifier compared with Laplacian, Gaussian curvature, and Eigen magnitude. For texture features, the LBP values generated at 5*5 window size (0.0157 in average) performed better than those at 3*3 window size (0.0107 in average), and then at 7*7 window size (0.0063 in average).

There may still be room for further improvement. Lo et al (2010) introduced the vessel orientation similarity feature, derived from anatomical knowledge. It would however be time-consuming to segment pulmonary vessels and calculate intersection angles between airway and parallel vessel eigenvectors. Hence, we attempted to employ texture features in this work. We show this has a positive influence on the results: performance measurements increased to 98.5% and 98.3%, respectively.

Admittedly, the presented results su er from some false positives: 1.4% in the connected tree and 2.6% in terms of total components. For small airways the FPVP increased to 4.4% and 4.2%, respectively. The average connective tree FPVP (1.2%) of the 20 cases is almost the same as the average measurement (1.22%) across 15 EXACT’09 challenge participants.

4.3. Possible further improvements

Our method does not guarantee a completely connected airway tree. Several refinement procedures could be applied in future work. For instance, a morphological operator can fill the holes encircled by generated airway voxels in large branches. Meng (Meng et al 2016) proposed a graph-cut connecting method to link the dispatched structures with the airway trunk. Our main focus was to obtain as many small airways as possible. We argue that the fact that all components do not form a connected tree is in most cases not a limitation: global descriptors and imaging biomarkers can usually also be computed from a not necessarily connected set of airway branches or voxels.

We carefully inspected all erroneously segmented voxels and noticed several consistent mistakes. Most of those findings take place at the airway lumen-like areas. A set of 4 typical examples are presented in Figure 5(i) – Figure 5(l). Because of the use of ionizing radiation, the dose used in CT imaging is always as low as possible. CT scans therefore often suffer from imaging noise. Some highly noisy parts form a variety of random structures, which happens frequently in the periphery of the lungs (see Figure 5(i)). Moreover, motion artifacts, caused by respiration, heartbeat, and patient movement, commonly occur in thoracic CT. The artifacts cause artificially attenuated regions around dense tissues that have moved and these darker regions may mimic airways. This occurs throughout the lungs but mainly in the left lower lobe due to the impact of heartbeats (see Figure 5(j)). Furthermore, several false positive regions were noticed close to bright pulmonary vessel borders. Here, the vessel may be mistaken for an airway wall. Those regions form “shadow trenches” parallel to vessels (see Figure 5(k)). Finally, we noticed some false positives at relatively low-intensity areas surrounded by large airway walls and vessels (see Figure 5(l)).

Additional samples in these false positive regions may decrease the output of the classifier on these quasi-airway structures. Non-airway candidates could be specifically extracted from these regions, as well as from the false positives confirmed by the human observer.

Finally, we note that our method was capable to segment airways regardless of morphological deformation such as branch narrow and expansion. This makes it feasible to apply the method to a large amount of lung CT scans to investigate small airway diseases, e.g., asthma and bronchiectasis, and to research the relationship between small airway disorders and COPD.

5. Conclusion

This paper presents a fully automated small airway segmentation method from thoracic CT scans. The core of the method is a random forest voxel classification scheme, using an optimal set of features. A dedicated airway voxel sampling method is shown to be important to obtain good performance and specifically detect small airways with high accuracy. The method was shown to substantially increase the number of detected small airways at a low false positive rate, compared to a reference obtained with a semi-automatic method that involves manual post-processing. This method could be the basis for imaging biomarkers focused on small airway disease.