Concerted Nucleophilic Aromatic Substitutions

Abstract

Nucleophilic aromatic substitution (S_NAr) is one of the most widely applied reaction classes in pharmaceutical and chemical research, providing a broadly useful platform for the modification of aromatic ring scaffolds. The generally accepted mechanism for S_NAr reactions involves a two-step addition–elimination sequence via a discrete, non-aromatic Meisenheimer complex. Here we use ¹²C/¹³C kinetic isotope effect (KIE) studies and computational analyses to provide evidence that prototypical S_NAr reactions in fact proceed through concerted mechanisms. The KIE measurements were made possible by a new technique that leverages the high sensitivity of ¹⁹F as an NMR nucleus to quantitate the degree of isotopic fractionation. This sensitive technique permits the measurement of KIEs on 10 mg of natural abundance material in one overnight acquisition. As a result, it provides a practical tool for performing detailed mechanistic analyses of reactions that form or break C–F bonds.

Graphical Abstract

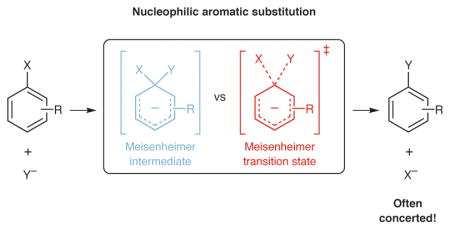
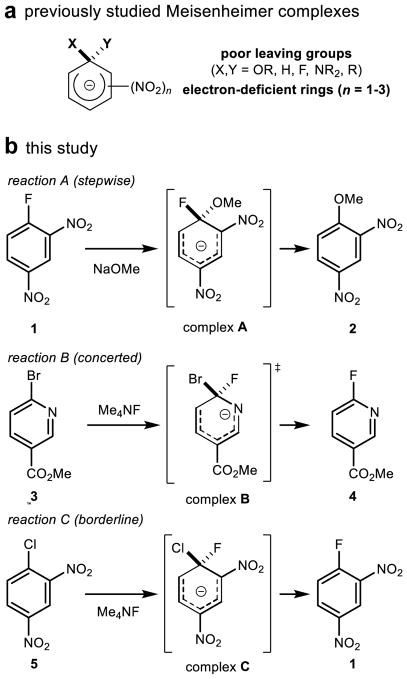
Whether a given chemical transformation proceeds through a stepwise or concerted mechanism is a question of both fundamental interest and practical importance, with direct implications for the stereospecificity, sensitivity to medium effects, and product distribution of the reaction.¹ In general, stepwise pathways are favored when productive reactive intermediates are energetically accessible. For example, the isolation and characterization of the direct products of nucleophilic addition to aromatic rings, termed Meisenheimer complexes (Figure 1a), have led to the widely held notion that S_NAr reactions² generally proceed via stepwise, addition/elimination mechanisms.^1,2

Figure 1.

Scope of study. (a) Previously observed Meisenheimer complexes have always been highly stabilized by poor leaving groups and electron-deficient rings. (b) The S_NAr reactions studied here. Bold letters denote Meisenheimer complexes, which span a range of stabilities. (The term ‘complex’ does not necessarily indicate that the structure is a true intermediate.)

The participation of a discrete Meisenheimer complex as an intermediate in an S_NAr mechanism requires that the anionic adduct be more thermodynamically stable than the transition state (TS) for the concerted pathway, as well as possess sufficient kinetic stability to have a significant lifetime prior to elimination. Nearly all known Meisenheimer complexes contain both strongly electron-withdrawing substituents, such as nitro groups, and poor leaving groups, such as fluoride, that are expected to retard elimination.³ In the S_NAr reactions that are typically employed in pharmaceutical synthesis,⁴ which involve less stabilized anions or good leaving groups, the intermediates are not detectable but have nonetheless been assumed to exist.²

However, recent theoretical and experimental work, most notably from the Ritter group,^5,6 has challenged this assumption. More broadly, concerted nucleophilic substitution reactions at sp² carbons have long been established for reactions of vinyl halides,^7–11 as well as acyl,^12–24 phosphorus,^25–29 and sulfur group transfer reactions.^30–34 In the context of S_NAr reactions, Williams et al. have shown that the quasi-symmetric¹ addition of substituted phenoxides to phenoxytriazines is concerted,^35,36 while the apparently analogous addition of pyridines to pyridyltriazines is stepwise.^37,38 For many other reactions, computations^39–50 predict concerted mechanisms, contradicting the textbook view that S_NAr reactions proceed via stepwise addition-elimination mechanisms.⁵¹

We sought to use experiments to ascertain whether stepwise mechanisms are indeed generally operative in S_NAr reactions by studying three transformations with putative intermediates that would be either strongly, moderately, or weakly stabilized (Figure 1b). Structure A is strongly stabilized by nitro group substituents and poor leaving groups (fluoride and methoxide), and related reactions have been demonstrated to be stepwise in nature.⁵² In contrast, structure B is only weakly stabilized by its nitrogen-containing heterocycle and ester substituent and contains a good leaving group (bromide), which are all factors that might be expected to favor a concerted reaction. Reaction C represents a borderline case, in which structure C is stabilized by strongly electron-withdrawing substituents, but destabilized by a good leaving group (chloride).

Kinetic isotope effects (KIEs) can provide direct insight into the bonding in transition states, and are therefore useful tools for the evaluation of reaction concertedness.¹ In S_NAr reactions, the primary ¹²C/¹³C KIE at the carbon undergoing substitution is expected to provide the most useful information. One powerful strategy for measuring such KIEs is to use quantitative ¹³C NMR spectroscopy, ideally at natural isotopic abundance.⁵³ However, the high precision required for the determination of intrinsically small (<10%) heavy-atom KIEs, combined with the low natural abundance and gyromagnetic ratio of the of ¹³C nucleus, renders this type of experiment generally challenging to implement. When the carbons of interest are not bound to a proton, as is the case for the sites undergoing substitution in S_NAr reactions, dipolar relaxation is particularly inefficient. This requires long delays (minutes) between scans and further reduces sensitivity.

Results

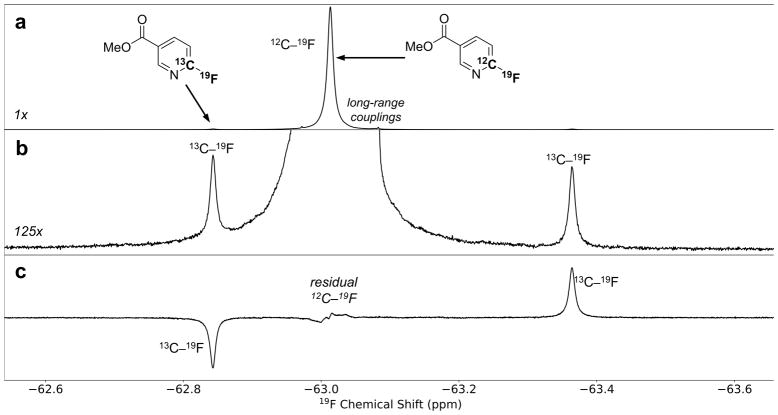
We envisioned an alternative approach for the quantification of ¹³C in the specific case of transformations involving C–F bond formation or cleavage, which are characteristic of many S_NAr reactions. In ¹H-decoupled ¹⁹F NMR spectra of organofluorine compounds at natural abundance, resonances appear as a large ¹²C–¹⁹F parent singlet flanked by a small ¹³C–¹⁹F satellite doublet (Figure 2a). In principle, integration of these satellite integrals could provide a highly sensitive means of determining ¹²C/¹³C isotope fractionation because the signal to noise ratio (S/N) of each ¹³C–¹⁹F satellite is theoretically 13.6 times greater (per fluorine) than that of the corresponding peak in a ¹³C spectrum. This increase in sensitivity translates to a potential 185-fold reduction in acquisition time.⁵⁴

Figure 2.

Assessing ¹³C isotopic fractionation by suppressing NMR signals from fluorine atoms bound to ¹²C. (a) Standard ¹⁹F{¹H} spectrum showing the parent ¹²C–¹⁹F peak flanked by two ¹³C–¹⁹F satellites. (b) The standard spectrum in (a), enlarged 125×. Accurate satellite integrals cannot be obtained directly due to overlap with the parent peak. (c) MQF ¹⁹F{¹H} spectrum. Suppression of the parent peak allows accurate integration of the satellites.

Unfortunately, it is not possible to obtain accurate satellite integrals directly⁵⁵ because of interference from the much larger parent peak, as well as possible overlapping impurities (Figure 2b). However, we found that accurate satellite integrals could be obtained from multiple-quantum-filtered (MQF) spectra in which the ¹²C signals are suppressed (Figure 2c).⁵⁴ This technique was validated by determining the ¹²C/¹³C KIE for a simple nucleophilic substitution reaction using both the traditional ¹³C NMR and new MQF methods (Table 1). The MQF method was found to require far less material (as little as 10 mg with overnight acquisition; see entry 6) and acquisition time (under one hour with 50 mg of material; see entry 7). The consensus value of 1.059(3) determined by the new method agrees with the predicted S_N2 KIE of 1.057 (M11/jun-cc-pVTZ/PCM). Consistent with prior studies,^56,57 the predicted KIE is insensitive to both TS geometry and computational method (see Supplementary Information Section 4b).

Table 1.

Comparison of KIE Measurements

method	time (h)	KIE (std. err.)
1 Singleton (300 mg)	9.9	1.058(6), 1.060(6)
2 MQF (50 mg)a	4.6	1.057(5), 1.065(6)
3 MQF (50 mg)	5.2	1.057(3), 1.062(4)
4 MQF (50 mg)b	5.2	1.059(4), 1.060(4)
5 MQF (10 mg)c	9.9	1.061(6)
6 MQF (50 mg)	0.7	1.055(10)
consensus (std. dev.): 1.059(3)

Samples are pure unless otherwise noted. Acquisition times are given for each pair of partial and full conversion samples. Pairs of KIEs refer to independent chemical replicates. The error bars (in parentheses) refer to standard errors of the mean (t-distribution) and reflect technical variation due to errors in the measurement of conversion and satellite area. KIEs are referenced to ¹²C–¹⁹F unless otherwise noted.

^aKIEs are referenced to ¹³C-¹⁹F.

^bUnpurified sample.

^cShigemi tube used.

The greatly increased sensitivity of the MQF method results from the larger gyromagnetic ratio and shorter T₁ relaxation times of ¹⁹F over ¹³C nuclei. Sensitivity can be further increased by using the parent ¹²C–¹⁹F peak from a routine ¹⁹F{¹H} spectrum, rather than a different ¹³C–¹⁹F satellite in the MQF spectrum, as an internal reference⁵⁸ (entries 4–7). Additionally, because a fluorination or defluorination reaction generally involves the appearance or disappearance of a well-separated ¹⁹F resonance, unpurified material can be used (entry 5).

The accuracy and sensitivity of the MQF method allowed us to determine the ¹²C/¹³C KIEs for several S_NAr fluorination and defluorination reactions. To provide a theoretical basis for interpreting these measurements, we assessed the accuracy of various computational methods in describing the potential energy surfaces of reactions A, B, and C. Using geometries spanning a range of carbon/nucleophile and carbon/leaving group distances, we found that B3LYP-D3BJ/jun-cc-pVTZ⁵⁹ most closely reproduced the energies calculated using the benchmark coupled cluster method DLPNO-CCSD(T)⁶⁰/aug-cc-pVTZ (see Supplementary Information Sections 4c–e).

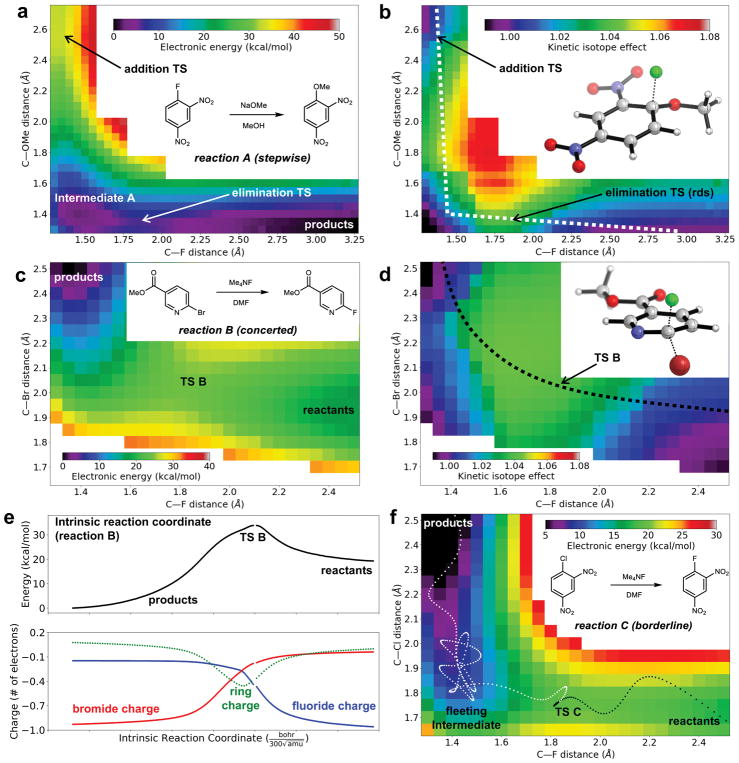
The surface for reaction A in implicit solvent (PCM) clearly shows an intermediate (Figure 3a), and is consistent with the second step being rate-determining. The experimental KIE of 1.035(3) agrees closely with the calculated KIE of 1.033. This provides strong evidence for the validity of the stepwise mechanism in the case of reaction A.

Figure 3.

Computational analysis of the transition from stepwise to concerted behavior (B3LYP-D3BJ/jun-cc-pVTZ). (a) Potential energy surface for reaction A. An intermediate is apparent (lower left). (b) Predicted KIE as a function of geometry for reaction A. The lowest-energy stepwise mechanism follows the white path, avoiding the region of large KIEs. (c) Potential energy surface for reaction B. The “Meisenheimer region” is very high in energy (white). (d) Predicted KIE as a function of geometry for reaction B. The lowest-energy concerted mechanism follows the black path, resulting in a KIE that approaches the maximum possible value. (e) Potential energy (top) and charge distribution (bottom) along the intrinsic reaction coordinate for reaction B. Negative charge is distributed between the nucleophile, the leaving group, and the ring in the non-aromatic TS. Breaks in the curves indicate the position of transition state B. (f) Potential energy surface for reaction C. A typical trajectory (dotted path) reflects a fleeting intermediate or long-lived TS in the Meisenheimer region (lower left).

In contrast, computational analysis of reaction B reveals no evidence of an intermediate, either on its energy surface (Figure 3c) or intrinsic reaction coordinate (Figure 3e). Additionally, quasiclassical⁶¹ dynamics initialized from transition state B proceed quickly to product (mean time, 91 fs) and nearly all trajectories are productive (94%), indicating that the reaction is truly concerted. The predicted KIE of 1.039 is in reasonable agreement with the experimental value of 1.035(3).

Discussion

Although the experimentally determined KIEs for stepwise reaction A and concerted reaction B are the same (1.035), the calculations reveal that those values are in fact of very different magnitudes relative to the maximum values possible for the two reactions. For a given reaction, a ‘KIE surface’ (e.g., Figure 3b) can be generated by predicting KIEs for each point on the energy surface (e.g., Figure 3a). The largest value on this KIE surface may then be defined as the maximum KIE. When the bonds in the ground state are strong, more vibrational energy can be lost in the TS, resulting in a larger maximum KIE. In reaction A, a strong C–F bond is broken, and the maximum KIE is 1.070 (Figure 3b, red). By contrast, in reaction B, a weak C–Br bond is broken, and the maximum KIE is 1.045 (Figure 3d, green).

The maximum KIE in any particular reaction is obtained when the bonds to both the nucleophile and electrophile are weakest in the transition state. Thus, the size of the actual KIE relative to its theoretical maximum is diagnostic of a stepwise or concerted mechanism. Stepwise mechanisms alter one bond at a time, leading to small KIEs (47% of the maximum value for reaction A). Conversely, concerted mechanisms alter both bonds simultaneously, passing through a nearly symmetric region in which both bonds are relatively weak, leading to large KIEs (87% of the maximum value for reaction B). This correspondence between small relative KIEs for stepwise mechanisms and large relative KIEs for concerted mechanisms parallels the behavior of S_N2 reactions.⁶²

Reaction C is a borderline case. Once again, the experimentally determined ¹²C/¹³C KIE of 1.045(3) is in good agreement with the predicted KIE of 1.040. This prediction is 73% of the maximum calculated value of 1.055, and lies between the values for the stepwise (47%) and concerted (87%) pathways. Borderline behavior is observed because the putative intermediate would be stabilized by two electron-withdrawing groups (NO₂), but destabilized by a good leaving group (Cl). Accordingly, the minimum energy path does not pass through an intermediate, even though structures in the vicinity of the Meisenheimer complex are relatively stable (Figure 3f). As a result, trajectories exiting the formal TS encounter this shallow region and linger for multiple vibrations before passing to product (mean time: 233 fs). The reaction mechanism can therefore be viewed either as concerted, with a long-lived TS, or stepwise, with a short-lived intermediate.

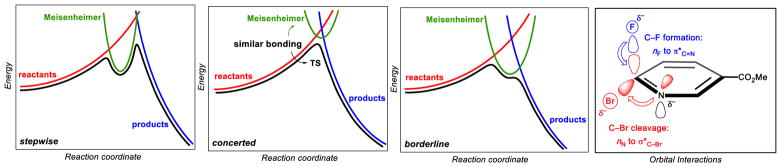
The transition from stepwise to concerted behavior can be rationalized using qualitative Marcus theory.^63–65 When the Meisenheimer complex is lower in energy than the intersection of the potential energy surfaces of the starting materials and products, the reaction is stepwise (Figure 4a). When the intermediate is higher in energy than the intersection, the reaction mechanism is concerted with the TS resembling the minimum of the Meisenheimer curve (Figure 4b). In borderline cases, such as when a stabilized anion is adjacent to a good leaving group, the Meisenheimer complex may intersect the reaction coordinate as a shallow minimum or shoulder (Figure 4c).

Figure 4.

Simplified Marcus analysis of stepwise vs. concerted S_NAr reactions. (a) In stepwise reactions, the Meisenheimer structure is highly stabilized, leading to a minimum along the reaction coordinate (reaction A). (b) Concerted reactions result if the Meisenheimer structure is less stable. This is the typical situation (reaction B). (c) When the Meisenheimer structure is highly stabilized, but leaving group elimination is facile, a borderline situation (reaction C) results. (d) Meisenheimer transition states are stabilized by concurrent donor-acceptor interactions (transition state B is shown).

At first glance, concerted S_NAr mechanisms may appear difficult to rationalize on stereoelectronic grounds given that backside attack by the nucleophile on the C–X σ* orbital of an aryl halide is precluded.⁶⁶ However, this argument assumes that the bonding in the transition state resembles that of the starting material. In fact, concerted transition structures actually possess characteristics of a Meisenheimer intermediate. For example, charge,⁶⁷ NICS,⁶⁸ and NBO⁶⁹ analyses all confirm that TS B is essentially a delocalized, but non-aromatic, anion (Figure 3e). This anion is generated by two concurrent, but asynchronous processes: C–F bond formation by donation of the fluoride lone pair into the C=N π* orbital, and C–Br bond cleavage by donation of the incipient nitrogen lone pair into the C–Br σ* orbital (Figure 4d). The result can be viewed as a ‘Meisenheimer transition state’.

The qualitative picture of a continuum between stepwise and concerted S_NAr mechanisms depicted in Figure 4 is supported quantitatively by the close agreement between the theoretical and experimental KIEs. To evaluate the overall prevalence of concerted S_NAr pathways, we carried out a computational survey of 120 S_NAr reactions spanning a variety of typical ring types, nucleophiles, and leaving groups using B3LYP/6–31+G*/PCM(DMSO). This more economical level of theory also corresponds closely to the coupled cluster energy surface (see Supplementary Information Section 4g), and similar outcomes would be expected from other DFT methods. Remarkably, 99 of these reactions (83%) are predicted to proceed via concerted mechanisms.

Where an S_NAr reaction lies on the stepwise/concerted continuum is determined primarily by the structural features of the reactants, rather than by the rate of their reaction. For nucleophilic substitutions on aryl rings, stepwise mechanisms are only predicted to occur when both a strongly electron-withdrawing substituent (e.g., nitro) is present and fluoride is the nucleophile or leaving group. For substitutions on pyridine, pyrazine, and pyrimidine, no stepwise mechanisms are predicted. Given that many S_NAr reactions of interest are performed on heterocycles with good leaving groups (e.g. Cl, Br),^1,2 it is likely that concerted mechanisms are actually very common.

The mechanistic analysis described herein was enabled by the sensitivity and practicality of the MQF method for determining ¹²C/¹³C KIEs. Our observations confirm that the nucleophilic adducts identified by Jackson⁷⁰ and Meisenheimer⁷¹ over a century ago are indeed involved in S_NAr reactions, but often as transition states rather than intermediates. We anticipate that the MQF method will enable the study of other fluorination and defluorination pathways of synthetic interest.

Methods

Data Availability

User-friendly software pipelines that can be used to measure and predict KIEs are freely available at www.github.com/ekwan/PyKIE and www.github.com/ekwan/PyQuiver. Raw NMR spectra and computed quasiclassical trajectories are available from the corresponding author upon reasonable request. All other data supporting the findings of this study are available within the paper and its supplementary information files.

Synthesis

Reactions were carried out in round-bottomed flasks under nitrogen. Commercially available reagents were purchased and used as received unless otherwise noted. The conversion of reactions was determined by quantitative ¹⁹F NMR spectroscopy using p-difluorobenzene as an internal standard, with the exception of reaction A, which was analyzed by HPLC using naphthalene as an internal standard. Products and recovered starting materials were purified by column chromatography, except for ‘impure’ samples, which were only subjected to an aqueous extraction. For detailed procedures and spectroscopic characterization data, please see Supplementary Information Section 1.

Isotope effect methodology

NMR samples greater than 10 mg in mass were prepared in Wilmad 528-PP-9 tubes and flame-sealed under air at room temperature. 10 mg samples were prepared in Shigemi tubes and sealed with parafilm. All spectroscopic measurements were performed at 25 °C on a Varian Inova 500 MHz machine fitted with an indirect detection probe (HFC) and a gradient driver. Specific details of the MQF pulse sequence can be found in Supplementary Information Section 3 and the PyKIE repository. For ¹²C-referenced experiments, standard ¹⁹F and MQF experiments were interwoven (eg. MQF then ¹⁹F then MQF). This pattern was repeated throughout the duration of the measurement.

NMR data were processed using Python and the nmrglue package³² using the PyKIE pipeline. Each FID was zero-filled (4×), apodized (exponential), Fourier transformed, and baseline corrected. Peaks were picked manually and centered on regions of interest. Widths of the peak-containing regions of interest were held constant as follows: MQF 0.045 ppm, ¹⁹F 0.15 ppm, ¹H 0.08 ppm, ¹³C 0.12 ppm and 0.14 ppm. S/N ratios were calculated for each peak by dividing the signal intensity at half height by the root-mean-square deviation of the signal in a noisy region.

Each KIE measurement was made by comparing the fractionation between a partial conversion sample and a full conversion sample (for product-based analyses) or between recovered and unreacted starting material. When multiple samples were available, data for the full conversion (or unreacted starting material) sample was pooled to give two independent estimates of the kinetic isotope effect. The values reported in the text correspond to the average of these estimates. Error bars for individual measurements correspond to standard errors and were propagated from known standard deviations in conversion and integral area. Detailed procedures and Excel spreadsheets for reproducing these calculations can be found in Supplementary Information Section 3 and the PyKIE repository.

Calculations

DFT calculations were performed with Gaussian 09 or Gaussian 16.⁷³ Bigeleisen–Mayer KIE predictions were made using PyQuiver.⁷⁴ Tunnelling corrections were calculated using the one-dimensional Bell method. For the M06-2X prediction of the S_N2 isotope effect, a multidimensional CVT/SCT correction was also calculated using GAUSSRATE⁷⁵/POLYRATE⁷⁶ and found to agree closely with the Bell correction. Coupled cluster calculations were carried out using ORCA 4.0.0 using TightPNO cutoffs.⁷⁷

Direct quasiclassical trajectory studies were carried out on the B3LYP-D3(BJ)/6–31+G*/PCM surface as previously described. Trajectories were initialized from a thermal distribution (298 K) of vibrational states using the position eigenstates of a quantum harmonic oscillator. No displacements were made in any modes with a frequency of less than 50 cm⁻¹, including the transition vector. The sign of the velocity in all modes was randomized except for the transition vector, which was directed towards product. 1.0 fs timesteps were calculated by the velocity Verlet method and each simulation was run 500 fs in both the forward and reverse directions.

The predicted KIEs for reactions A, B, and C were calculated with B3LYP-D3BJ/may-cc-pVQZ at 298 K (jun-cc-pVTZ is extremely similar) using PCM (i.e., IEFPCM) implicit solvation and a scaling factor^78–80 of 1.2 for the sphere radii. The addition of explicit methanol molecules to reaction A or explicit water molecules to reaction B had a negligible effect. The inclusion of at least one explicit water molecule was crucial for reaction C. The effect of solvation parameters is examined thoroughly in Supplementary Information Section 4f.

The energy and KIE surfaces shown in Figure 3a–d and 3f were calculated at B3LYP-D3BJ/jun-cc-pVTZ/PCM with no explicit solvent molecules. The intrinsic reaction coordinate energetics and charges shown in Figure 3e were calculated at B3LYP-D3BJ/6–31+G*/PCM. Each colored square in Figure 3 corresponds to a structure in which the carbon–nucleophile and carbon–electrophile bond distances have been held frozen, but all other geometric parameters have been allowed to relax. Bigeleisen–Mayer KIEs were then calculated for each grid point using the harmonic frequencies of the isolated substrate and the grid point geometry at 298 K. The maximum KIE was then taken as the maximum predicted KIE over the entire grid. The trajectory overlaid on Figure 3f was calculated with an explicit water molecule at B3LYP-D3BJ/6–31+G*. All calculations in Figure 3 used default PCM settings.

120 S_NAr reactions spanning a range of ring types (benzene, (NO₂)_n=1,2,3-benzene, H₃C-C=O-benzene, pyridine, pyrazine, pyrimidine), nucleophiles (F⁻, MeO⁻, N₃⁻, Me2N⁻, formate⁻), and leaving groups (F⁻, Cl⁻, Br⁻) were thoroughly examined at B3LYP-D3(BJ)/6–31+G*/PCM(DMSO). Consistent with previous studies,^39–50 in all but 21 cases, it was not possible to locate a Meisenheimer intermediate by beginning optimizations in the expected neighborhood of the intermediate. Intrinsic reaction coordinate (IRC) searches were attempted for each reaction. In no case did any converged IRC calculation show the unexpected existence of an intermediate. For the significant number of remaining unconverged cases, growing string⁸¹ calculations were performed. Likewise, no string calculations revealed the unexpected existence of an intermediate. Transition states and intermediates were located for nearly all of the reactions and each transition state was confirmed to connect to the expected starting materials and products by the means above. In a small number of cases involving highly exothermic reactions it was not possible to locate saddle points on the potential energy surface (details are given in Supplementary Information Section 4g).