Abstract
Coding EMRs with diagnosis and procedure codes is an indispensable task for billing, secondary data analyses, and monitoring health trends. Both speed and accuracy of coding are critical. While coding errors could lead to more patient–side financial burden and mis–interpretation of a patient’s well–being, timely coding is also needed to avoid backlogs and additional costs for the healthcare facility. In this paper, we present a new neural network architecture that combines ideas from few–shot learning matching networks, multi–label loss functions, and convolutional neural networks for text classification to significantly outperform other state–of–the–art models. Our evaluations are conducted using a well known deidentified EMR dataset (MIMIC) with a variety of multi–label performance measures.
1. Introduction
Electronic medical record (EMR) coding is the process of extracting diagnosis and procedure codes from the digital record (the EMR) pertaining to a patient’s visit. The digital record is mostly composed of multiple textual narratives (e.g., discharge summaries, pathology reports, progress notes) authored by healthcare professionals, typically doctors, nurses, and lab technicians. Hospitals heavily invest in training and retaining professional EMR coders to manually annotate all patient visits by reviewing EMRs. Proprietary commercial software tools often termed as computer–assisted coding (CAC) systems are already in use in many healthcare facilities and were found to be helpful in increasing medical coder productivity (Dougherty et al., 2013). Thus progress in automated EMR coding methods is expected to directly impact real world operations.
In the US, the diagnosis and procedure codes used in EMR coding are from the Interna tional Classification of Diseases (ICD) terminology (specifically the ICD–10–CM variant) as required by the Health Insurance Portability and Accountability Act (HIPPA). ICD codes facilitate billing activities, retrospective epidemiological studies, and also enable researchers to aggregate health statistics and monitor health trends. To code EMRs effectively, medical coders are expected to have thorough knowledge of ICD–10–CM and follow a complex set of guidelines to code EMRs. For example, if a coder accidentally uses the code “heart failure” (ICD–10–CM code I50) instead of “acute systolic (congestive) heart failure” (ICD–10–CM code I50.21), then the patient may be charged substantially more1 causing significant unfair burden. Therefore, it is important for coders to have better tools at their disposal to find the most appropriate codes. Additionally, if coders become more efficient, hospitals may hire fewer coders to reduce their operating costs. Thus automated coding methods are expected to help with expedited coding, cost savings, and error control.
In this paper, we treat medical coding of EMR narratives as a multi–label text classification problem. Multi–label classification (MLC) is a machine learning task that assigns a set of labels (typically from a fixed terminology) to an instance. MLC is different from multi–class problems, which assign a single label to each example from a set of labels. Compared to general multi–label problems, EMR coding has three distinct challenges. First, with thousands of ICD codes, the label space is large and the label distribution is extremely unbalanced – most codes occur very infrequently with a few codes occurring several orders of magnitude more than others. Second and more importantly, a patient may have a large number of diagnoses and procedures. On average, coders annotate an EMR with more than 20 such codes and hence predicting the top one or two codes is not sufficient for EMR coding. Third, EMR narratives may be very long (e.g., discharge summaries may have over 1000 words), which may result in a needle in a haystack situation when attempting to seek evidence for particular codes.
Recent advances in extreme multi–label classification have proven to work well for large label spaces. Many of these methods (Yu et al., 2014; Bhatia et al., 2015; Liu et al., 2017) focus on creating efficient multi–label models that can handle 104 to 106 labels. While these models perform well in large label spaces, they don’t necessarily focus on improving prediction of infrequent labels. Typically, they optimize for the top 1, 3, or 5 ranked labels by focusing on the P@1, P@3, and P@5 evaluation measures. The labels ranked at the top usually occur frequently in the dataset and it is not obvious how to handle infrequent labels. One solution would be to ignore the rare labels. However, when the majority of medical codes are infrequent, this solution is unsatisfactory.
While neural networks have shown great promise for text classification (Kim, 2014; Yang et al., 2016; Johnson and Zhang, 2017), the label imbalances associated with EMR coding hinder their performance. Imagine if a dataset contains only one training example for every class leading to one–shot learning, a subtask of few–shot learning. How can we classify a new instance? A trivial solution would be to use a non–parametric 1–NN (1 nearest neighbor) classifier. 1–NN does not require learning any label specific parameters and we only need to define features to represent our data and a distance metric. Unfortunately, defining good features and picking the best distance metric is nontrivial. Instead of manually defining the feature set and distance metric, neural network training procedures have been developed to learn them automatically (Koch et al., 2015). For example, matching networks (Vinyals et al., 2016) can automatically learn discriminative feature representations and a useful distance metric. Therefore, using a 1–NN prediction method, matching networks work well for infrequent labels. However, researchers typically evaluate matching networks on multi–class problems without label imbalance. For EMR coding with extreme label imbalance with several labels occurring thousands of times, traditional parametric neural networks (Kim, 2014) should work very well on the frequent labels. In this paper, we introduce a new variant of matching networks (Vinyals et al., 2016; Snell et al., 2017) to address the EMR coding problem. Specifically, we combine the non–parametric idea of k–NN and matching networks with traditional neural network text classification methods to handle both frequent and infrequent labels encountered in EMR coding.
Overall, we make the following contributions in this paper:
We propose a novel semi–parametric neural matching network for diagnosis/procedure code prediction from EMR narratives. Our architecture employs ideas from matching networks (Vinyals et al., 2016), multiple attention (Lin et al., 2017), multi–label loss functions (Nam et al., 2014a), and convolutional neural networks (CNNs) for text classification (Kim, 2014) to produce a state–ofthe–art EMR coding model.
We evaluate our model on publicly available EMR datasets to ensure reproducibility and benchmarking; we also compare against prior state–of–the–art methods in EMR coding and demonstrate robustness across multiple standard evaluation measures.
We analyze and measure how each compo nent of our model affects the performance using ablation experiments.
2. Related Work
In this section we cover recent methodologies that are either relevant to our approach and problem or form the main ingredients of our contribution.
2.1. Extreme Multi–label Classification
Current methods for extreme MLC fall into two categories: embedding and tree–based methods. Embedding–based methods aim to reduce the training complexity. They effectively reduce the label space by assuming the training label matrix is low rank. Intuitively, rather than learning independent classifiers for each label (binary relevance) (Tsoumakas et al., 2010), classifiers are learned in a reduced label space ≪ L where L is the total number of labels. Likewise, a projection matrix is learned to convert predictions from the reduced label space back to the original label space. In general, embedding methods vary based on how they reduce the label space and how the projection operation is optimized. Tai and Lin (2012) use principal component analysis (PCA) to reduce the label space. Low–rank Empirical risk minimization for Multi–Label Learning (LEML) (Yu et al., 2014) jointly optimizes the label space reduction and the projection processes. RobustXML (Xu et al., 2016) is similar to LEML but it treats infrequent labels as outliers and models them separately. Liu et al. (2017) employ neural networks for extreme multi–label problems using a funnel–like architecture that reduces the label vector dimensionality. Tree–based multi–label methods work by recursively splitting the feature space. These methods usually differ based on the node splitting criterion. FastXML (Prabhu and Varma, 2014) partitions the feature space using the nDCG measure as the splitting criterion. PfastreXML (Jain et al., 2016) improves on FastXML by using a propensity scored nDCG splitting criterion and re–ranking the predicted labels to optimize various ranking measures.
2.2. Memory Augmented Neural Networks
Memory networks (Weston et al., 2014) have access to external memory, typically consisting of information the model may use to make predictions. Intuitively, informative memories concerning a given instance are found by the memory network to improve its predictive power. Kamra et al. (2017) use memory networks to fix issues of catastrophic forgetting. They show that external memory can be used to learn new tasks without forgetting previous tasks. Memory networks are now applied to a wide variety of natural language processing tasks, including question answering and language modeling (Sukhbaatar et al., 2015; Bordes et al., 2015; Miller et al., 2016).
Matching networks (Vinyals et al., 2016; Snell et al., 2017) have recently been developed for few/one–shot learning problems. We can interpret matching networks as a key–value memory network (Miller et al., 2016). The “keys” are training instances, while the “values” are the labels associated with each training example. Intuitively, the concept is similar to a hashmap. The model will search for the most similar training instance to find its respective “value”. Also, matching networks can be interpreted as a k–NN based model that automatically learns an informative distance metric. Finally, Altae–Tran et al. (2017) used matching networks for drug discovery, a problem where data is limited.
2.3. Diagnosis Code Prediction
The 2007 shared task on coding radiology reports (Pestian et al., 2007) was the first effort that popularized automated EMR coding. Traditionally, linear methods have been used for diagnosis code prediction. Perotte et al. (2013) developed a hierarchical support vector machine (SVM) model that takes advantage of the ICD–9–CM hierarchy. In our prior work, we train a linear model for every label (Rios and Kavuluru, 2013) and re–rank the labels using a learning–to–rank procedure (Kavuluru et al., 2015). Zhang et al. (2017) supplement the diagnosis code training data with data from PubMed (biomedical article corpus and search system) to train linear models using both the original training data and the PubMed data.
Recent advances in neural networks have also been put to use for EMR coding: Baumel et al. (2018) trained a CNN with multiple sigmoid outputs using binary cross–entropy. Duarte et al. (2017) use hierarchical recurrent neural networks (RNNs) to annotate death reports with ICD–10 codes. Vani et al. (2017) introduced grounded RNNs for EMR coding. They found that iteratively updating their predictions at each time step significantly improved the performance. Finally, similar to our work, memory networks (Prakash et al., 2017) have recently been used for diagnosis coding. However, we would like to note two significant differences between the memory network from Prakash et al. (2017) and our model. First, they don’t use a matching network and their memories rely on extracting information about each label from Wikipedia. In contrast, our model does not use any auxiliary information. Second, they only evaluate on the 50 most frequent labels, while we evaluate on all the labels in the dataset.
3. Our Architecture
An overview of our model is shown in Figure 1. Our model architecture has two main components.
Figure 1:
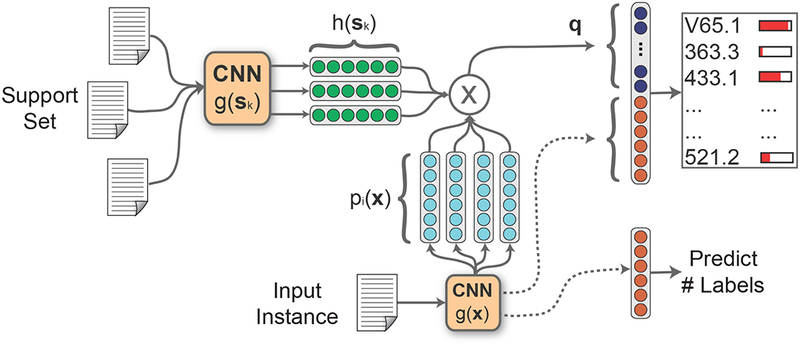
The matching CNN architecture. For each input instance, x, we search a support set using different representations of x and use the similar support instances and auxiliary features to the output layer.
We augment a CNN with external memory over a support set S, which consists of a small subset of the training dataset. The model searches the support set to find similar examples with respect to the input instance. We make use of the homophily assumption that similar instances in the support set are coded with similar labels. Therefore, we use the related support set examples as auxiliary features. The similar instances are chosen automatically by combining ideas from metric learning and neural attention. We emphasize that unlike in a traditional k–NN setup, we do NOT explicitly use the labels of the support set instances. The support set essentially enriches and complements the features derived from the input instance.
Rather than predicting labels by thresholding, we rank them and select the top k labels specific to each instance where k is predicted using an additional output unit (termed MetaL–abeler). We train the MetaLabeler along with the classification loss using a multi–task training scheme.
Before we go into more specific details of our architecture, we introduce some notation. Let X represent the set of all training documents and x be an instance of X. Likewise, let S represent the set of support instances and s be an instance of S. We let L be the total number of unique labels. Our full model is described in following subsections.
3.1. Convolutional Neural Networks
We use a CNN to encode each document following what is now a fairly standard approach consisting of an embedding layer, a convolution layer, a max–pooling layer, and an output layer (Collobert et al., 2011; Kim, 2014). However, in our architecture, the CNN additionally aids in getting intermediate representations for the multi–head matching network component (Section 3.2).
Intuitively, CNNs make use of the sequential nature of text, where a non–linear function is applied to region vectors formed from vectors of words in short adjacent word sequences. Formally, we represent each document as a sequence of word vectors, [w1, w2, . . . , wn], where represents the vector of the i–th word in the document. The region vectors are formed by concatenating each window of s words, into a local region vector . Next, cj is passed to a non-linear function
where ,, and ReLU is a recti fied linear unit (Glorot et al., 2011; Nair and Hinton, 2010). Each row of W represents a convolutional filter; so v is the total number of filters.
After processing each successive region vector, we obtain a document representation by concatenating each forming a matrix . Each row of D is referred to as a feature map, formed by different convolutional filters. Unfortunately, this representation is dependent on the length of the document and we cannot pass it to an output layer. We use max–over–time pooling to create a fixed size vector
where
3.2. Multi–Head Matching Network
Using the support set and the input instance, our goal is to estimate . The support set S is chosen based on nearest neighbors and its selection process is discussed in Section 3.4. Among instances in S, our model finds informative support instances with respect to x and creates a feature vector using them. This feature vector is combined with the input instance to make predictions.
First, each support instance is projected into the support space using a simple single–layer feed forward NN as
where and . Likewise, we project each input instance x into the input space using a different feed forward neural network,
where and Compared to the support set neural network where we use only a single network, for the input instance we have u projection neural networks. This means we have u versions of x, an idea that is similar to self–attention (Lin et al., 2017), where the model learns multiple representations of an instance. Here each pi(g(x)) represents a single “head” or representation of the input x. Using different weight matrices, and , we create different representations of x (multiple heads). For both the input multi–heads and the support instance projection, we note that the same CNN is used (also indicated in Figure 1) whose output is subject to the feed forward neural nets outlined thus far in this section.
Rather than searching for a single informative support instance, we search for multiple relevant support instances. For each of the u input instance representations, we calculate a normalized attention score
where Ai,k represents the score of the k–th support example with respect to the i–th input representation pi(g(x)) and
is the square of the Euclidean distance between the input and support representations.
Next, the normalized scores are aggregated into a matrix . Then, we create a feature vector
| (1) |
where , vec is the matrix vectorization operator, and is the support instance CNN feature matrix whose i–th row is h(g(si)) for . Intuitively, multiple weighted averages of the support instances are created, one for each of the u input representations. The final feature vector,
| (2) |
is formed by concatenating the CNN representation of the input instance x and the support set feature vector q.
Finally, the output layer for L labels involves computing
| (3) |
where ,, and σ is the sigmoid function. Because we use a sigmoid activation function, each label prediction (ŷi) is in the range from 0 to 1.
3.3. MetaLabeler
The easiest method to convert ŷ into label predictions is to simply threshold each element at 0.5. However, most large–scale multi–label problems are highly imbalanced. When training using binary cross–entropy, the threshold 0.5 is optimized for accuracy. Therefore, our predictions will be biased towards 0. A simple way to fix this problem is to optimize the threshold value for each label. Unfortunately, searching for the optimal threshold of each label is computational expensive in large label spaces. Here we train a regression based output layer
where estimates the number of labels x should be annotated with. At test time, we rank each label by its score in ŷ. Next, is rounded to the nearest integer and we predict the top ranked labels.
3.4. Training
To train our model, we need to define two loss functions. First, following recent working on multi–label classification with neural networks (Nam et al., 2014b), we train using a multi–label cross–entropy loss. The loss is defined as
which sums the binary cross–entropy loss for each label. The second loss is used to train the MetaL–abeler for which we use the mean squared error
where r is the vector of correct numbers of labels and is our estimate. We train these two losses using a multi–task learning paradigm (Collobert et al., 2011)
Similar to previous work with matching networks (Vinyals et al., 2016; Snell et al., 2017), “episode” or mini–batch construction can have an impact on performance. In the multi–label setting, episode construction is non–trivial. We propose a simple strategy for choosing the support set S which we find works well in practice. First, at the beginning of the training process we loop over all training examples and store g(x) for every training instance. We will refer to this set of vectors as T. Next, for every step of the training process (for every mini–batch M), we search T \ M to find the e nearest neighbors (using Euclidean distance) per instance to form our support set S. Likewise, we add e random examples from T \ M to the support set. Therefore, our support set S contains up to instances. The purpose of the random examples is to ensure the distance metric learned during training (captured by improving representations of documents as influenced by all network parameters) is robust to noisy examples.
3.5. Matching Network Interpretation
If we do not use the support set label vectors, then what is our network learning? To answer this question we directly compare the matching network formulation to our method. Matching networks can be expressed as
where a(,) is the attention/distance learned between two instances, k indexes each support instance, and yk is a one–hot encoded vector. a(,) is equivalent to A1,k assuming we use a single head. Traditional matching networks use onehot encoded vectors because they are evaluated on multi–class problems. EMR coding is a multi–label problem. Hence, yk is a multi–hot encoded vector. Moreover, with thousands of labels, it is unlikely even for neighboring instance pairs to share many labels; this problem is not encountered in the multi–class setting. We overcome this issue by learning new output label vectors for each support set instance. Assuming a single head, our method can be re–written as
| (4) |
where is the learned label vector for support instance s. Next, we define , the learned support set vectors, as
| (5) |
where both and are submatrices of Wc.Using this reformulation, we can now see that our method’s main components (equations (1)–(3)) are equivalent to this more explicit matching network formulation (equations (4)–(5)). Intuitively, our method combines a traditional output layer – the first half of equation 4 – with a matching network where the support set label vectors are learned to better match the labels of their nearest neighbors.
4. Experiments
In this section we compare our work with prior state–of–the–art medical coding methods. In Section 4.1 we discuss the two publicly available datasets we use. Next, Section 4.2 describes the implementation details of our model. We summarize the various baselines and models we compare against in Section 4.3. The evaluation metrics are described in Section 4.4. Finally, we discuss how our method performs in Section 4.5.
4.1. Datasets
EMR data is generally not available for public use especially if it involves textual notes. Therefore, we focus on the publicly available Medical Information Mart for Intensive Care (MIMIC) datasets for benchmarking purposes. We evaluate using two versions of MIMIC: MIMIC II (Lee et al., 2011) and MIMIC III (Johnson et al., 2016), where the former is a relatively smaller and older dataset and the latter is the most recent version. Following prior work (Perotte et al., 2013; Vani et al., 2017), we use the free text discharge summaries in MIMIC to predict the ICD–9–CM2 codes. The dataset statistics are shown in Table 1.
Table 1:
This table presents the number of training examples (# Train), the number of test examples (# Test), label cardinality (LC), and the average number of instances per label (AI/L) for the MIMIC II and MIMIC III datasets.
| # Train | # Test | # Labels | LC | AI/L | |
|---|---|---|---|---|---|
| MIMIC II | 18822 | 2282 | 7042 | 36.7 | 118.8 |
| MIMIC III | 37016 | 2755 | 6932 | 13.6 | 80.8 |
For comparison purposes, we use the same MIMIC II train/test splits as Perotte et al. (2013). Specifically, we use discharge reports collected from 2001 to 2008 from the intensive care unit (ICU) of the Beth Israel Deaconess Medical Center. Following Perotte et al. (2013), the labels for each discharge summary are extended using the parent of each label in label set. The parents are based on the ICD–9–CM hierarchy. We use the hierarchical label expansion to maximize the prior work we can compare against.
The MIMIC III dataset has been extended to include health records of patients admitted to the Beth Israel Deaconess Medical Center from 2001 to 2012 and hence provides a test bed for more advanced learning methods. Unfortunately, it does not have a standard train/test split to compare against prior work given we believe we are the first to look at it for this purpose. Hence, we use both MIMIC II and MIMIC III for comparison purposes. Furthermore, we do not use the hierarchical label expansion on the MIMIC III dataset.
Before we present our results, we discuss an essential distinction between the MIMIC II and MIMIC III datasets. Particularly, we are interested in the differences concerning label imbalance. From Table 1, we find that MIMIC III has almost twice as many examples compared to MIMIC II in the dataset. However, MIMIC II on average has more instances per label. Thus, although MIMIC III has more examples, each label is used fewer times on average compared to MIMIC II. The reason for this is because of how the label sets for each instance were extended using the ICD–9 hierarchy in MIMIC II.
4.2. Implementation Details
Preprocessing: Each discharge summary was tokenized using a simple regex tokenization scheme (\w\w+). Also, each word/token that occurs less than five times in the training dataset was replaced with the UNK token.
Model Details: For our CNN, we used convolution filters of size 3, 4 and 5 with 300 filters for each filter size. We used 300 dimensional skip–gram (Mikolov et al., 2013) word embeddings pre–trained on PubMed. The Adam optimizer (Kingma and Ba, 2015) was used for training with the learning rate 0.0001. The mini–batch size was set to 4, e – the number of nearest neighbors per instance – was set to 16, and the number of heads (u) is set to 8. Our code is available at: https://github.com/bionlproc/med-match-cnn
4.3. Baseline Methods
In this paper, we focused on comparing our method to state–of–the–art methods for diagnosis code prediction such as grounded recurrent neural networks (Vani et al., 2017) (GRNN) and multi–label CNNs (Baumel et al., 2018). We also compare against traditional binary relevance methods where independent binary classifiers (L1–regularized linear models) are trained for each label. Next, we compare against hierarchical SVM (Perotte et al., 2013), which incorporates the ICD–9–CM label hierarchy. Finally, we also report the results of the traditional matching network with one modification: We train the matching network with the multi–label loss presented in Section 3.4 and threshold using the MetaLabeler described in Section 3.3.
We also present two versions of our model: Match–CNN and Match–CNN Ens. Match–CNN is the multi–head matching network introduced in Section 3. Match–CNN Ens is an ensemble that averages three Match–CNN models, each initialized using a different random seed.
4.4. Evaluation Metrics
We evaluate our method using a wide variety of standard multi–label evaluation metrics. We use the popular micro and macro averaged F1 measures to assess how our model (with the MetaL–abeler) performs when thresholding predictions. For problems with large labels spaces that suffer from significant imbalances in label distributions, the default threshold of 0.5 generally performs poorly (hence our use of MetaLabeler). To remove the thresholding effect bias, we also report different versions of the area under the precision–recall (PR) and receiver operating characteristic (ROC) curves. Finally, in a real–world setting, our system would not be expected to replace medical coders. We would expect medical coders to use our system to become more efficient in coding EMRs. Therefore, we would rank the labels based on model confidence and medical coders would choose the correct labels from the top few. To understand if our system would be useful in a real–world setting, we evaluate with precision at k (P@k) and recall at k (R@k). Having high P@k and R@k are critical to effectively encourage the human coders to use and benefit from the system.
4.5. Results
We show experimental results on MIMIC II in Table 2. Overall, our method improves on prior work across a variety of metrics. With respect to micro F1, we improve upon GRNN–128 by over 1%. Also, while macro–F1 is still low in general, we also improve macro F1 compared to state–of–theart neural methods by more than 1%. In general, both micro and macro F1 are highly dependent on the thresholding methodology. Rather than thresholding at 0.5, we rank the labels and pick the top k based on a trained regression output layer. Can we do better than using a MetaLabeler? To measure this, we look at the areas under PR/ROC curves. Regarding micro and macro PR–AUC, we improve on prior work by ≈ 2.5%. This suggests that via better thresholding, the chances of improving both micro and macro F1 are higher for Match–CNN compared to other methods. Finally, we are also interested in metrics that evaluate how this model would be used in practice. We perform comparably with prior work on P@k. We show strong improvements in R@k with over a 4% improvement in R@40 compared to grounded RNNs and over 1% improvement when compared with Baumel et al. (2018). Our method also outperforms matching networks across every evaluation measure.
Table 2:
Results for the MIMIC II dataset.
| F1 | AUC (PR) | AUC (ROC) | P@k | R@k | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Prec. | Recall | Micro | Macro | Micro | Macro | Micro | Macro | 8 | 40 | 8 | 40 | |
| Flat SVM (Perotte et al., 2013) | 0.867 | 0.164 | 0.276 | – | – | – | – | – | – | – | – | – |
| Hier. SVM (Perotte et al., 2013) | 0.577 | 0.301 | 0.395 | – | – | – | – | – | – | – | – | – |
| Logistic (Vani et al., 2017) | 0.774 | 0.395 | 0.523 | 0.042 | 0.541 | 0.125 | 0.919 | 0.704 | 0.913 | 0.572 | 0.169 | 0.528 |
| Attn BoW (Vani et al., 2017) | 0.745 | 0.399 | 0.52 | 0.027 | 0.521 | 0.079 | 0.975 | 0.807 | 0.912 | 0.549 | 0.169 | 0.508 |
| GRU–128 (Vani et al., 2017) | 0.725 | 0.396 | 0.512 | 0.027 | 0.523 | 0.082 | 0.976 | 0.827 | 0.906 | 0.541 | 0.168 | 0.501 |
| BiGRU–64 (Vani et al., 2017) | 0.715 | 0.367 | 0.485 | 0.021 | 0.493 | 0.071 | 0.973 | 0.811 | 0.892 | 0.522 | 0.165 | 0.483 |
| GRNN–128 (Vani et al., 2017) | 0.753 | 0.472 | 0.58 | 0.052 | 0.587 | 0.126 | 0.976 | 0.815 | 0.93 | 0.592 | 0.172 | 0.548 |
| BiGRNN–64 (Vani et al., 2017) | 0.761 | 0.466 | 0.578 | 0.054 | 0.589 | 0.131 | 0.975 | 0.798 | 0.925 | 0.596 | 0.172 | 0.552 |
| CNN (Baumel et al., 2018)* | 0.810 | 0.403 | 0.538 | 0.031 | 0.599 | 0.127 | 0.971 | 0.759 | 0.931 | 0.585 | 0.207 | 0.586 |
| Matching Network* | 0.439 | 0.388 | 0.412 | 0.014 | 0.394 | 0.034 | 0.893 | 0.551 | 0.793 | 0.427 | 0.172 | 0.425 |
| Match–CNN (Ours) | 0.605 | 0.561 | 0.582 | 0.064 | 0.612 | 0.148 | 0.977 | 0.792 | 0.930 | 0.586 | 0.207 | 0.590 |
| Match–CNN Ens. (Ours) | 0.616 | 0.567 | 0.591 | 0.066 | 0.623 | 0.157 | 0.977 | 0.793 | 0.935 | 0.594 | 0.208 | 0.598 |
Models marked with * represent our custom implementations.
We present MIMIC III results in Table 3. We reiterate that MIMIC III does not have a standard train/test split. Hence we compare our model to our implementations of methods from prior efforts. For MIMIC III also we show improvements in multiple evaluation metrics. Interestingly, our method performs much better than the standard CNN on MIMIC III, compared to the relative performances of the two methods on MIMICII. Match–CNN improves on CNN in R@40 by almost 5% on the MIMIC III dataset. The gain in R@40 is more than the 1% improvement found on MIMIC II. We hypothesize that the improvements on MIMIC III are because the label imbalance found in MIMIC III is higher than MIMIC II. Increased label imbalances mean more labels occur less often. Therefore, we believe our model works better with less training examples per label compared to the standard CNN model.
Table 3:
Results for the MIMIC III dataset.
| F1 | AUC (PR) | AUC (ROC) | P@k | R@k | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| P | R | Micro | Macro | Micro | Macro | Micro | Macro | 8 | 40 | 8 | 40 | |
| Logistic (Vani et al., 2017)* | 0.711 | 0.242 | 0.361 | 0.026 | 0.419 | 0.147 | 0.961 | 0.751 | 0.554 | 0.211 | 0.414 | 0.686 |
| CNN (Baumel et al., 2018)* | 0.726 | 0.246 | 0.367 | 0.021 | 0.376 | 0.095 | 0.942 | 0.697 | 0.534 | 0.196 | 0.395 | 0.636 |
| Matching Network* | 0.248 | 0.237 | 0.242 | 0.008 | 0.183 | 0.028 | 0.823 | 0.554 | 0.310 | 0.128 | 0.231 | 0.431 |
| Match-CNN (Ours) | 0.466 | 0.447 | 0.456 | 0.041 | 0.421 | 0.119 | 0.963 | 0.726 | 0.557 | 0.206 | 0.413 | 0.670 |
| Match-CNN Ens. (Ours) | 0.488 | 0.449 | 0.468 | 0.043 | 0.441 | 0.129 | 0.965 | 0.760 | 0.570 | 0.211 | 0.422 | 0.683 |
Models marked with * represent our custom implementations.
In Table 4 we analyze each component of our model using an ablation analysis on the MIMIC III dataset. First, we find that removing the matching component significantly effects our performance by reducing micro PR–AUC by almost 5%. Regarding micro and macro F1, we also notice that the MetaLabeler heuristic substantially improves on default thresholding (0.5). Finally, we see that the multi–head matching component provides reasonable improvements to our model across multiple evaluation measures. For example, P@8 and P@40 decrease by around 1% when we use attention with a single input representation.
Table 4:
Ablation results for the MIMIC III dataset.
| F1 | P@k | R@k | AUC (PR) | |||||
|---|---|---|---|---|---|---|---|---|
| Micro | Macro | 8 | 40 | 8 | 40 | Micro | Macro | |
| Match-CNN | 0.456 | 0.041 | 0.557 | 0.206 | 0.413 | 0.670 | 0.421 | 0.119 |
| - Matching | 0.429 | 0.034 | 0.534 | 0.196 | 0.395 | 0.636 | 0.376 | 0.095 |
| - MetaLabler | 0.391 | 0.026 | 0.557 | 0.206 | 0.413 | 0.670 | 0.421 | 0.119 |
| - Multi-Head | 0.450 | 0.034 | 0.548 | 0.202 | 0.403 | 0.656 | 0.417 | 0.113 |
5. Conclusion
In this paper, we introduce a semi–parametric multi–head matching network with a specific application to EMR coding. We find that by combining the non–parametric properties of matching networks with a traditional classification output layer, we improve metrics for both frequent and infrequent labels in the dataset. In the future, we plan to investigate three limitations of our current model.
-
1.
We currently use a naive approach to choose the support set. We believe that improving the support set sampling method could substantially improve performance.
-
2.
We hypothesize that a more sophisticated thresholding method could have a significant impact on the micro and macro F1 measures. As we show in Table 4, MetaLabeler outperforms naive thresholding strategies. However, given our method shows non–trivial gains in PR–AUC compared to micro/macro F1, we believe better thresholding strategies are a worthy avenue to seek improvements.
-
3.
Both the MIMIC II and MIMIC III datasets have around 7000 labels but ICD–9–CM contains over 16000 labels and ICD–10–CM has nearly 70,000 labels. In future work, we believe significant attention should be given to zero–shot learning applied to EMR coding. To predict labels that have never occurred in the training dataset, we think it is vital to take advantage of the ICD hierarchy. Baker and Korhonen (2017) improve neural network training by incorporating hierarchical label information to create better weight initializations. However, this does not help with respect to zero–shot learning. If we can better incorporate expert knowledge about the label space, we may be able to infer labels we have not seen before.
Acknowledgments
Thanks to anonymous reviewers for their thorough reviews and constructive criticism that helped improve the clarity of the paper (especially leading to the addition of Section 3.5 in the revision). This research is supported by the U.S. National Library of Medicine through grant R21LM012274. We also gratefully acknowledge the support of the NVIDIA Corporation for its donation of the Titan X Pascal GPU used for this research.
Footnotes
In 2015, a federal mandate was issued that requires the use of ICD–10 instead of ICD–9. However because of this recent change, ICD–10 training data is limited. Therefore, we use publicly available ICD–9 datasets for evaluation.
Contributor Information
Anthony Rios, Department of Computer Science, University of Kentucky, Lexington, KY, anthony.rios1@uky.edu.
Ramakanth Kavuluru, Division of Biomedical Informatics, University of Kentucky, Lexington, KY, ramakanth.kavuluru@uky.edu.
References
- Altae–Tran Han, Ramsundar Bharath, Pappu Aneesh S, and Pande Vijay. 2017. Low data drug discovery with one–shot learning. ACS central science 3(4):283–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker Simon and Korhonen Anna. 2017. Initializing neural networks for hierarchical multi–label text classification. BioNLP 2017 pages 307–315. [Google Scholar]
- Baumel Tal, Nassour–Kassis Jumana, Elhadad Michael, and Elhadad Noemie. 2018. Multi–label classification of patient notes a case study on icd code assignment. In Proceedings of the 2018 AAAI Joint Workshop on Health Intelligence. [Google Scholar]
- Bhatia Kush, Jain Himanshu, Kar Purushottam, Varma Manik, and Jain Prateek. 2015. Sparse local embeddings for extreme multi–label classification. In Advances in neural information processing systems. pages 730–738. [Google Scholar]
- Bordes Antoine, Usunier Nicolas, Chopra Sumit, and Weston Jason. 2015. Large–scale simple question answering with memory networks. arXiv preprint arXiv:1506.02075. [Google Scholar]
- Collobert Ronan, Weston Jason, Bottou Léon, Karlen Michael, Kavukcuoglu Koray, and Kuksa Pavel. 2011. Natural language processing (almost) from scratch. Journal of Machine Learning Research 12:2493–2537. [Google Scholar]
- Dougherty Michelle, Seabold Sandra, and White Susan E. 2013. Study reveals hard facts on CAC. Journal of the American Health Information Management Association 84(7):54–56. [PubMed] [Google Scholar]
- Duarte Francisco, Martins Bruno, Pinto Cátia Sousa, and Silva Mário J. 2017. A deep learning method for icd–10 coding of free–text death certificates In Portuguese Conference on Artificial Intelligence. Springer, pages 137–149. [Google Scholar]
- Glorot Xavier, Bordes Antoine, and Bengio Yoshua. 2011. Deep sparse rectifier networks. In Proceedings of the 14th International Conference on Artificial Intelligence and Statistics. JMLR W&CP Volume. volume 15, pages 315–323. [Google Scholar]
- Jain Himanshu, Prabhu Yashoteja, and Varma Manik. 2016. Extreme multi–label loss functions for recommendation, tagging, ranking & other missing label applications. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining ACM, pages 935–944. [Google Scholar]
- Johnson Alistair EW, Pollard Tom J, Shen Lu, Lehman Liwei H, Feng Mengling, Ghas–semi Mohammad, Moody Benjamin, Szolovits Peter, Celi Leo Anthony, and Mark Roger G. 2016. Mimic–iii, a freely accessible critical care database. Scientific data 3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson Rie and Zhang Tong. 2017. Deep pyramid convolutional neural networks for text categorization. In Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers). volume 1, pages 562–570. [Google Scholar]
- Kamra Nitin, Gupta Umang, and Liu Yan. 2017. Deep generative dual memory network for continual learning. arXiv preprint arXiv:1710.10368. [Google Scholar]
- Kavuluru Ramakanth, Rios Anthony, and Lu Yuan. 2015. An empirical evaluation of supervised learning approaches in assigning diagnosis codes to electronic medical records. Artificial intelligence in medicine 65(2):155–166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kim Yoon. 2014. Convolutional neural networks for sentence classification. In Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP) Association for Computational Linguistics, Doha, Qatar, pages 1746–1751. [Google Scholar]
- Kingma Diederik P. and Ba Jimmy. 2015. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR). [Google Scholar]
- Koch Gregory, Zemel Richard, and Salakhutdinov Ruslan. 2015. Siamese neural networks for one–shot image recognition. In ICML Deep Learning Workshop. volume 2. [Google Scholar]
- Lee Joon, Scott Daniel J, Villarroel Mauricio, Clifford Gari D, Saeed Mohammed, and Mark Roger G. 2011. Open–access mimic–ii database for intensive care research. In Engineering in Medicine and Biology Society, EMBC, 2011 Annual International Conference of the IEEE IEEE, pages 8315–8318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Zhouhan, Feng Minwei, dos Santos Cicero Nogueira, Yu Mo, Xiang Bing, Zhou Bowen, and Bengio Yoshua. 2017. Automatic discovery and optimization of parts for image classification. In Proceedings of the International Conference on Learning Representations (ICLR). [Google Scholar]
- Liu Jingzhou, Chang Wei–Cheng, Wu Yuexin, and Yang Yiming. 2017. Deep learning for extreme multi–label text classification. In Proceedings of the 40th International ACM SIGIR Conference on Research and Development in Information Retrieval ACM, pages 115–124. [Google Scholar]
- Mikolov Tomas, Sutskever Ilya, Chen Kai, Corrado Greg S, and Dean Jeff. 2013. Distributed representations of words and phrases and their compositionality. In Advances in Neural Information Processing Systems. pages 3111–3119. [Google Scholar]
- Miller Alexander H., Fisch Adam, Dodge Jesse, Karimi Amir–Hossein, Bordes Antoine, and Weston Jason. 2016. Key–value memory networks for directly reading documents. In EMNLP. The Association for Computational Linguistics, pages 1400–1409. [Google Scholar]
- Nair Vinod and Hinton Geoffrey E. 2010. Rectified linear units improve restricted Boltzmann machines. In Proceedings of the 27th International Conference on Machine Learning (ICML–10) pages 807–814. [Google Scholar]
- Nam Jinseok, Kim Jungi, Mencía Eneldo Loza, Gurevych Iryna, and Furnkranz Johannes. 2014a. Large–scale multi–label text classification – revisiting neural networks In Machine Learning and Knowledge Discovery in Databases – European Conference, ECML PKDD 2014, Nancy, France, September 15–19, 2014. Proceedings , Part II pages 437–452. [Google Scholar]
- Nam Jinseok, Kim Jungi, Mencía Eneldo Loza, Gurevych Iryna, and Furnkranz Johannes. 2014b. Large–scale multi–label text classificationrevisiting neural networks In Machine Learning and Knowledge Discovery in Databases, Springer, pages 437–452. [Google Scholar]
- Perotte Adler, Pivovarov Rimma, Natarajan Karthik, Weiskopf Nicole, Wood Frank, and Elhadad Noémie. 2013. Diagnosis code assignment: models and evaluation metrics. Journal of the American Medical Informatics Association 21(2):231–237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pestian John P, Brew Christopher, Matykiewicz Paweł, Hovermale Dj J, Johnson Neil, Cohen K Bretonnel, and Duch Włodzisław. 2007. A shared task involving multi–label classification of clinical free text. In Proceedings of the Workshop on BioNLP 2007: Biological, Translational, and Clinical Language Processing Association for Computational Linguistics, pages 97–104. [Google Scholar]
- Prabhu Yashoteja and Varma Manik. 2014. Fastxml: A fast, accurate and stable tree–classifier for extreme multi–label learning. In Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining ACM, pages 263–272. [Google Scholar]
- Prakash Aaditya, Zhao Siyuan, Hasan Sadid A, Datla Vivek V, Lee Kathy, Qadir Ashequl, Liu Joey, and Farri Oladimeji. 2017. Condensed memory networks for clinical diagnostic inferencing. In AAAI. pages 3274–3280. [Google Scholar]
- Rios Anthony and Kavuluru Ramakanth. 2013. Supervised extraction of diagnosis codes from emrs: role of feature selection, data selection, and probabilistic thresholding. In Healthcare Informatics (ICHI), 2013 IEEE International Conference on IEEE, pages 66–73. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Snell Jake, Swersky Kevin, and Zemel Richard. 2017. Prototypical networks for few–shot learning In Guyon I, Luxburg UV, Bengio S, Wallach H,Fergus R, Vishwanathan S, and Garnett R, editors, Advances in Neural Information Processing Systems 30, Curran Associates, Inc., pages 4078–4088. [Google Scholar]
- Sukhbaatar Sainbayar, Weston Jason, Fergus Rob, et al. 2015. End–to–end memory networks. In Advances in neural information processing systems. pages 2440–2448. [Google Scholar]
- Tai Farbound and Lin Hsuan–Tien. 2012. Multilabel classification with principal label space transformation. Neural Computation 24(9):2508–2542. [DOI] [PubMed] [Google Scholar]
- Tsoumakas Grigorios, Katakis Ioannis, and Vlahavas Ioannis P.. 2010. Mining multi–label data In Data Mining and Knowledge Discovery Handbook, pages 667–685. [Google Scholar]
- Vani Ankit, Jernite Yacine, and Sontag David. 2017. Grounded recurrent neural networks. arXiv preprint arXiv:1705.08557. [Google Scholar]
- Vinyals Oriol, Blundell Charles, Lillicrap Tim, Wierstra Daan, et al. 2016. Matching networks for one shot learning. In Advances in Neural Information Processing Systems. pages 3630–3638. [Google Scholar]
- Weston Jason, Chopra Sumit, and Bordes Antoine. 2014. Memory networks. arXiv preprint arXiv:1410.3916. [Google Scholar]
- Xu Chang, Tao Dacheng, and Xu Chao. 2016. Robust extreme multi–label learning. In KDD. pages 1275–1284. [Google Scholar]
- Yang Zichao, Yang Diyi, Dyer Chris, He Xiaodong, Smola Alex, and Hovy Eduard. 2016. Hierarchical attention networks for document classification. In Proceedings of the 2016 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies pages 1480–1489. [Google Scholar]
- Yu Hsiang–Fu, Jain Prateek, Kar Purushottam, and Dhillon Inderjit S.. 2014. Large–scale multi–label learning with missing labels. In Proceedings of the 31th International Conference on Machine Learning, ICML 2014, Beijing, China, 21–26 June 2014 pages 593–601. [Google Scholar]
- Zhang Danchen, He Daqing, Zhao Sanqiang, and Li Lei. 2017. Enhancing automatic icd–9–cm code assignment for medical texts with pubmed. BioNLP 2017 pages 263–271. [Google Scholar]


