LINEAR SUMMATION OF INPUTS UNDERLIES DIRECTION SELECTIVITY IN DROSOPHILA

SUMMARY

While linear mechanisms lay the foundations of feature selectivity in many brain areas, direction selectivity in the elementary motion detector (EMD) of the fly has become a paradigm of nonlinear neuronal computation. We have bridged this divide by demonstrating that linear summation can generate direction selectivity in the fruit fly Drosophila. Using linear systems analysis and two-photon imaging of a genetically encoded voltage indicator, we measure the emergence of direction-selective (DS) voltage signals in the Drosophila OFF pathway. Our study is a direct, quantitative investigation of the algorithm underlying directional signals, with the striking finding that linear summation of inputs is sufficient for the emergence of direction selectivity. A linear stage of the fly EMD strongly resembles similar computations in vertebrate visual cortex, demands a reappraisal of the role of upstream nonlinearities, and implicates the voltage-to-calcium transformation in the refinement of feature selectivity in this system.

INTRODUCTION

A major goal in neuroscience is to define the algorithms underlying feature selectivity, the ability of neurons to respond to specific patterns in the sensory environment. Visual motion creates patterned changes in luminance over space and time, from which neurons can selectively respond to particular features. Many motion-sensitive neurons in vertebrate and invertebrate visual systems respond selectively to moving stimuli with a specific orientation, spatial frequency, velocity, or direction. As a tractable paradigm of functional specialization, direction selectivity has been the focus of extensive research, and defining its algorithmic basis has been a central goal for many years (Mauss et al., 2017; Priebe and Ferster, 2008; Vaney et al., 2012). Strikingly, the algorithms that underpin the emergence of direction selectivity in flies and vertebrates have been proposed to be fundamentally different (Jagadeesh et al., 1997; Mauss et al., 2017; Priebe and Ferster, 2005). Here we re-examine this issue, taking advantage of a genetically encoded voltage sensor to measure the first emergence of direction selectivity in the fly. In particular, we examine how DS neurons combine inputs across their receptive fields to become feature selective. These studies reveal, surprisingly, that flies, like vertebrates, use linear summation to produce the earliest DS signals in the brain.

Over the past 70 years, several models of motion detection have advanced competing theories of how non-DS inputs could be combined to generate a DS signal. In the initial stages of one influential model of motion detection, the Motion Energy model (Adelson and Bergen, 1985), spatiotemporally offset inputs are linearly combined to generate a DS signal that is then nonlinearly transformed to become more direction selective. In vertebrate simple cells there is now strong evidence supporting this initial computation of the Motion Energy model, as linear spatial summation of inputs generates a DS membrane potential, which becomes more selective through nonlinear action potential generation (Jagadeesh et al., 1993; Lien and Scanziani, 2018; Priebe and Ferster, 2005, 2008). By contrast, in invertebrates, direction selectivity has been proposed to be fundamentally nonlinear (Mauss et al., 2017), requiring nonlinear combination of inputs. However, this conclusion remains controversial, as other studies have proposed that direction selectivity in insects might employ linear mechanisms (Leong et al., 2016; Mizunami, 1990; Takemura et al., 2013; Wiederman et al., 2008).

In Drosophila, direction selectivity emerges three synapses downstream of the photoreceptors, in T4 and T5, which prefer contrast increments and decrements, respectively, and of which there are four subtypes, each responding selectively to motion in one of the four cardinal directions (Maisak et al., 2013). Several studies have examined the algorithmic basis of motion detection in T4 and T5 (Arenz et al., 2017; Fisher et al., 2015a; Haag et al., 2016, 2017; Leong et al., 2016; Salazar-Gatzimas et al., 2016; Strother et al., 2017). Among these studies, several have proposed algorithms which combine aspects of two prominent models of motion detection: the Hassenstein Reichardt Correlator (Hassenstein and Reichardt, 1956), and the Barlow-Levick Model (Barlow and Levick, 1965). The Hassenstein Reichardt Correlator generates preferred-direction enhancement (PDE, a supralinear signal) by nonlinearly combining inputs representing preferred-direction motion. The Barlow-Levick model generates null-direction suppression (NDS, a sublinear signal) by nonlinearly combining inputs representing null-direction motion. Several recent papers have shown that direction-selective intracellular calcium signals in T4 and T5 display both PDE and NDS (Haag et al., 2016, 2017; Leong et al., 2016). Furthermore, a recent study of T4 emphasized the importance of NDS in generating direction-selective changes in membrane potential (Gruntman et al., 2018). For the past few years, the prevailing view has been that PDE and NDS arise from complementary forms of nonlinear input integration (Haag et al., 2016, 2017), and that direction selectivity in T4 and T5 cannot exist without PDE and NDS. Thus, according to this view, direction selectivity requires nonlinear input integration, and cannot arise from linear input integration.

However, formally, both PDE and NDS can result from a nonlinear transformation of a linear DS signal. Most previous measurements of direction selectivity in T4 and T5 have examined intracellular calcium signals, an often nonlinear proxy for neural activity, and an indirect measure of input summation. It is therefore possible that these studies were unable to assess the linearity of input summation in T4 and T5 because their measurements were biased by nonlinearities governing the calcium signal. The voltage signal would provide a more direct readout of input summation. One recent study of T4 used the voltage signal to measure input summation, arguing for linear summation with a divisive nonlinearity, but could not account for all previous measurements of PDE in intracellular calcium signals (Gruntman et al., 2018). Here, we examine the linearity of input summation in T5 by measuring changes in voltage, and propose a unified linear-nonlinear model that relates the voltage to the calcium signal, and explains how PDE and NDS of intracellular calcium can arise from a linear DS voltage signal.

RESULTS

T5 projects to the lobula plate, where its axon terminals are organized into four layers according to directional preference (Figure 1A). To determine how linear mechanisms contribute to direction selectivity in T5, we expressed a genetically encoded voltage indicator, ASAP2f (Yang et al., 2016)), in T5, and imaged visually-evoked responses in the axon terminals of single-cell clones to the following visual stimuli: 1) moving dark and light edges, 2) stationary dark and light bars, 3) stationary, sinusoidally contrast-modulated gratings, and 4) moving sinusoidal gratings. In vivo and in vitro measurements demonstrate that changes in ASAP2f fluorescence are substantially linear across a wide range of changes in membrane potential (Yang et al., 2016). To verify that our measurements report single-cell function, we imaged the responses of a calcium indicator, jRGECO1a (Dana et al., 2016), that was co-expressed with ASAP2f, to a different set of visual stimuli for which the response properties of single T5 cells are known (Figure S1) (Fisher et al., 2015a; Maisak et al., 2013). Responses not satisfying our single-cell criteria were not included in further analysis.

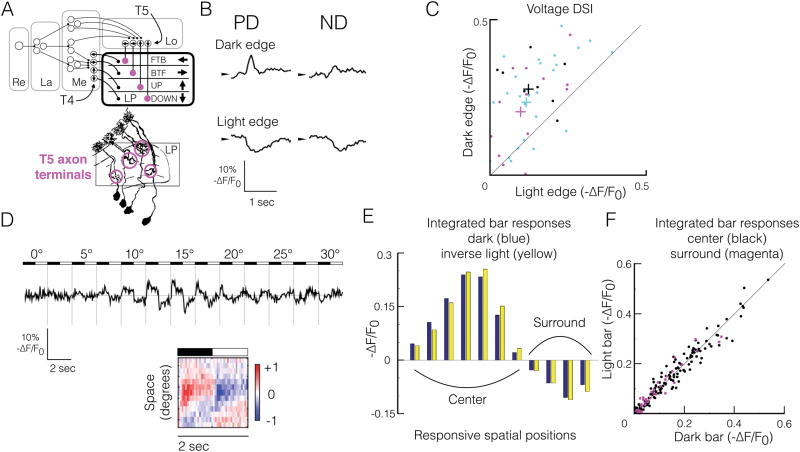
Figure 1. T5 voltage responses to moving and stationary local stimuli are consistent with a direction-selective linear system.

(A) Top, functional organization of the fly EMD. T4 and T5 project to the lobula plate (LP), where their axon terminals are arranged in layers according to their preferred direction (PD, arrows). Retina (Re), lamina (La), medulla (Me), lobula (Lo), lobula plate (LP). Bottom, golgi stain representation of T5 morphology (adapted, without magenta circles, from (Fischbach and Dittrich, 1989); axon terminals are highlighted with magenta circles.

(B) Mean ASAP2f fluorescence response timecourses (-ΔF/F₀) of a single T5 axon terminal to dark and light edges moving at 90°/s in PD and ND. ASAP2f decreases fluorescence with depolarization, so by convention, fluorescence timecourses are inverted.

(C) Direction selectivity indices (DSI) derived from ASAP2f responses to moving light vs dark edges. DSI defined as (PD-ND)/(PD+ND). Each point represents a single T5 cell responding to edges moving at either 30°/s (black, n = 9, from 5 flies), 60°/s (magenta, n = 15, from 7 flies), or 90°/s (cyan, n = 33, from 17 flies). Colored pluses indicate mean for each velocity.

(D) Top, ASAP2f fluorescence response timecourses of a single axon terminal (-ΔF/F₀) to individual 2.5°-wide bars, in the preferred orientation, on a grey background, alternating between dark and light contrast at 0.5 Hz, at 13 adjacent spatial positions, covering a 30° region of visual space. For each spatial position, the mean response to a single cycle of the stimulus is shown. Bottom, spacetime plot (XT plot) of responses depicted above. Each row represents the normalized mean response to one stimulus cycle (dark to light) for each spatial position. Red indicates depolarization (positive -ΔF/F₀), blue indicates hyperpolarization (negative -ΔF/F₀).

(E) Time-integrated dark bar voltage responses (blue) and inverse light bar voltage responses from panel D (yellow) at each spatial position eliciting responses.

(F) Time-integrated inverse light bar responses vs dark bar responses for all single T5 cells responding to stationary flashing bars at 0.5 Hz. Black dots correspond to single-cell responses from the receptive field center (depolarized to dark bars, hyperpolarized to light bars), integrated across the entire center; magenta dots correspond to responses from the receptive field surround (hyperpolarized to dark bars, depolarized to light bars), integrated across the entire surround. n=18 cells from 9 flies.

T5 voltage responses to moving edges are direction selective

To characterize T5 voltage responses to moving visual stimuli, we imaged ASAP2f responses in single axon terminals to full-contrast dark and light edges moving in the preferred direction (PD) and null direction (ND) (Figure 1B). T5 depolarized to dark edges moving in the PD, consistent with previous calcium measurements (Fisher et al., 2015a; Leong et al., 2016; Maisak et al., 2013). Dark edges moving in the ND elicited smaller depolarizations, demonstrating direction selectivity at the level of membrane potential for moving dark edges. Surprisingly, light edges moving in the PD and ND elicited robust hyperpolarizations of approximately equal amplitude, demonstrating non-DS voltage responses to moving light edges. For each edge direction and contrast, motion at 30°/s, 60°/s, and 90°/s elicited responses of similar amplitude (data not shown). Overall, voltage responses to moving dark edges were approximately twice as DS as voltage responses to moving light edges (Figure 1C). This asymmetry likely reflects the fact that only one of the major presynaptic inputs to T5, Tm9, can transmit both light and dark contrast, while all the other major inputs, Tm1, Tm2 and Tm4, are strongly rectified to favor dark contrast (Behnia et al., 2014; Fisher et al., 2015b; Serbe et al., 2016; Strother et al., 2014; Yang et al., 2016). Thus, the moving light edge response predominantly reflects input from Tm9, which alone will not be DS, while the moving dark edge response will incorporate more of the presynaptic inputs. Provided these inputs are spatiotemporally offset (forming a spatial gradient of response kinetics) simple linear summation could generate a DS signal (Adelson and Bergen, 1985; Watson, 1983).

T5 voltage responses to stationary local stimuli are linear with respect to contrast

To characterize T5 voltage responses to stationary visual stimuli, we imaged ASAP2f responses in single axon terminals to individual 2.5°-wide stationary bars, in the preferred orientation, alternating at full contrast between dark and light at 0.5 Hz (Figure 1D). Bars were presented on a gray background, at adjacent spatial positions, all together exploring a visual angle of 30–40° along the PD-ND axis of each cell. Such narrow, stationary stimuli can reveal how local visual responses, independent of motion and large-scale circuit interactions, vary across the receptive field.

T5 depolarized to dark bars, and hyperpolarized to light bars, presented within a contiguous 10–15° region of visual space (the center), consistent with T5’s previously reported OFF-center calcium response (Haag et al., 2017; Leong et al., 2016) (Figure 1D). T5 also hyperpolarized to dark bars, and depolarized to light bars, presented within a contiguous 10–15° region of visual space (the surround) that was adjacent to the OFF-depolarizing region, consistent with T5’s previously reported ON-surround calcium response (Leong et al., 2016). With respect to the cell’s preferred direction of motion, the center was always on the leading side of the receptive field, while the surround was on the trailing side. To quantify these responses, we used the integral of the response during the presentation of the dark or light bar. In general, center responses were approximately twice the amplitude of surround responses (Figure 1D–F). Strikingly, for each spatial position, the integrated dark and light bar responses were approximately equal and opposite (Figure 1E). Across the entire population of cells, contrast linearity did not depend on whether responses originated from a center or surround region (Figure 1F). For each spatial position, the timecourse of the dark and light bar responses were similar (Figure 1D). Furthermore, the timecourse of the bar responses varied in a systematic way across space, such that more sustained responses were on the preferred (leading) side of the receptive field, while more transient responses were on the null (trailing) side. Varying bar width (2.5° or 5°), duration (0.5 or 1 Hz), or cont rast (full or half contrast) did not affect the linearity of the responses with respect to contrast, nor the presence of a spatial gradient in response kinetics (data not shown). However, we note that faster bars, alternating at 1 Hz, elicited surround responses much less often than bars alternating at 0.5 Hz, consistent with differential temporal filtering among presynaptic inputs (Fisher et al., 2015b; Serbe et al., 2016). Taken together, our results indicate that local signaling onto T5 is linear, and reveals a spatial gradient of response kinetics that is a hallmark of a linear, direction-selective receptive field (Adelson and Bergen, 1985; Movshon et al., 1978; Reid et al., 1987; Watson, 1983).

T5 voltage responses to stationary global stimuli are predominantly linear

To assess the linearity of T5 voltage responses to global stimuli, we imaged ASAP2f responses in single axon terminals to stationary sinusoidally contrast-modulated gratings, a stimulus permitting linear systems analysis. We presented gratings in the preferred orientation, at eight equally-spaced spatial phases (each spatial phase shift is equivalent to shifting the grating in space along the PD-ND axis by one-sixteenth of a spatial period). To assess linearity across a range of stimulus parameters, we presented gratings at eight different spatial and temporal frequency combinations (25°/cycle at 0.5 Hz, 1 Hz, and 2 Hz, 50°/cycle at 0.5 Hz, 1 Hz, and 2 Hz, and 12.5°/cycle at 1 Hz and 2 Hz). We chose the se spatial and temporal frequencies to match, double, and halve T5’s previously-reported spatial frequency optimum (Leong et al., 2016) and temporal frequency optimum (Maisak et al., 2013). Because the major presynaptic inputs to T5 display different spatial and temporal frequency preferences, probing T5 with gratings across a range of spatial and temporal frequencies can differentially drive these presynaptic cells, revealing aspects of the functional circuitry underlying T5 voltage responses.

In response to a sinusoidal input, a linear system will only have significant power at the same frequency as the input (F1) (Hochstein and Shapley, 1976; Movshon et al., 1978). A response that instead shows a stimulus-dependent change in F0 (the mean), or a stimulus-dependent change in power at the even harmonics of the stimulus frequency (F2, F4, etc.) indicates a nonlinearity within the system.

Across six of the eight types of contrast-modulated gratings, T5 voltage responses were sinusoidal, and were overwhelmingly composed of oscillations at the temporal frequency of the stimulus (F1), with a very small positive F0 component (Figures S2A and S2C), consistent with a predominantly linear system. However, for 1 Hz gratings at 12.5°/cycle, although T5 voltage responses were sinusoidal, they displayed a significant response component at double the stimulus frequency (F2) (Figure S2B and S2C). The simplest operation that could produce this frequency doubling is presynaptic rectification, followed by linear summation. In particular, frequency doubling can arise if T5 linearly sums rectified presynaptic inputs with spatial receptive field centers roughly matching the spatial half period of the sinusoid (Hochstein and Shapley, 1976). That is, the spatial half period of the 12.5°/sec grating approximately matches the spatial extent of the OFF-depolarizing centers of presynaptic cells Tm1 and Tm2 (Arenz et al., 2017), which are rectified to prefer dark contrast (Behnia et al., 2014; Serbe et al., 2016; Yang et al., 2016). As a result, as the grating alternates contrasts at 1 Hz, if T5 linearly sums these presynaptic inputs, Tm1 and/or Tm2 cells with centers that are offset in space by approximately a half period of the grating will provide input during each dark half phase of the grating’s oscillation, resulting in a signal at 2 Hz. That the frequency doubling generally occurred only at certain spatial phases of the grating indicates that the rectified presynaptic cells’ receptive fields must be in register with the phase of the grating to generate this behavior. 2 Hz gratings at 12.5°/cycle did not reliably elicit vol tage responses from T5 (n = 9, data not shown), likely because it is both spatially and temporally poorly matched to the presynaptic inputs.

Although Tm1, Tm2, and Tm4, which provide the vast majority of the synapses onto T5 (Shinomiya et al., 2014), have been reported to have rectified voltage and calcium signals, preferring dark contrast (Behnia et al., 2014; Serbe et al., 2016; Strother et al., 2014; Yang et al., 2016), sinusoidal stimuli elicit sinusoidal voltage responses in T5 with only minor positive rectification (Figure S2D). This indicates that excitation and inhibition are nearly balanced at the level of T5, perhaps reflecting a sign-inverting input, and the functional importance of Tm9 (Fisher et al., 2015b), an input that responds linearly to both light and dark.

Finally, the amplitude and temporal phase of the responses to contrast-modulated gratings varied systematically with the spatial phase of the stimulus in a way characteristic of a linearly-summating direction-selective system (Figures S2E and S2F). In particular: (1) the response amplitude varied sinusoidally with stimulus spatial phase, (2) across all stimulus spatial phases, the response amplitude was never zero (that is, there was no “null response”, as there would be in a linear non-direction-selective system), (3) the temporal phase of the response varied proportionally with stimulus spatial phase (in a linear non-direction-selective system, response temporal phase would vary with stimulus spatial phase as a step-function, with a 180° shift at a particular spatial phase) (Enroth-Cugell and Robson, 1966; Movshon et al., 1978; Reid et al., 1987; Spitzer and Hochstein, 1985). In summary, voltage responses in single T5 axon terminals display classic features of a linear DS system, and also demonstrate that the T5 signals appear linear despite presynaptic rectification.

Mean and amplitude of the T5 calcium signal, but only amplitude of the T5 voltage signal, encode direction of motion

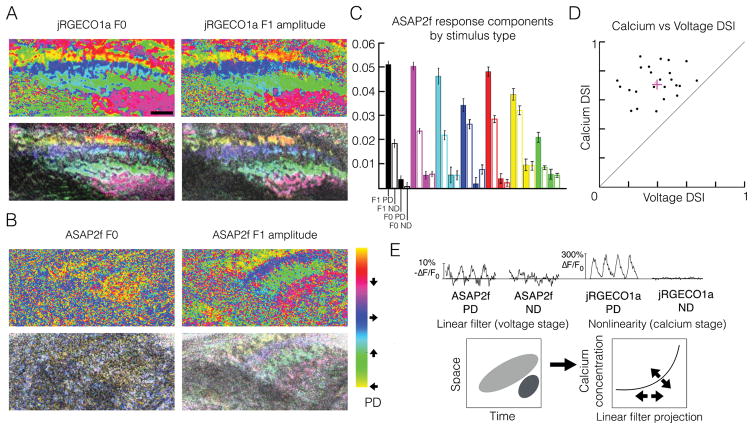
To determine whether T5 responds to moving stimuli with the same hallmarks of linearity, we imaged voltage and calcium responses of populations of T5 axon terminals while presenting moving sinusoidal gratings in 8 directions. From these responses, we generated hue-saturation-value (HSV) maps that represent the directional preference, directional tuning, and amplitude of the axon terminal responses across the layers of the lobula plate. Calcium maps of direction preference reflected this layered architecture when calculated from the jRGECO1a response mean (F0) and amplitude at the temporal frequency of the stimulus (F1) (Figure 2A). Because a DS F0 response requires a nonlinear mechanism (Movshon et al., 1978), our calcium maps are consistent with nonlinear models and measurements of the calcium response in T5. Voltage maps of direction preference calculated from the F1 amplitude of the ASAP2f signal matched the four-layer structure of the calcium maps, demonstrating that the voltage signal in T5 axon terminals is DS (Figure 2B). Notably, voltage maps calculated from the ASAP2f F0 response were not organized into any discernible functional architecture. Furthermore, voltage responses of single axon terminals to moving gratings across a range of spatial and temporal frequency combinations displayed DS F1 amplitudes, and non-DS F0 responses (Figure 2C). That the T5 voltage response to moving gratings was DS in F1 but not F0 suggests that nonlinear mechanisms may not be essential to the generation of a DS voltage signal in T5. Comparing the direction selectivities of individual cells at the level of voltage and calcium revealed that calcium responses to moving gratings, on average, were more than twice as direction selective as voltage responses to the same gratings (Figure 2D).

Figure 2. Mean and amplitude of the T5 calcium signal, but only amplitude of the T5 voltage signal, encode direction of motion.

(A) Hue (top) and hue-saturation-value (HSV, bottom) direction preference maps of the calcium signal in T5 axon terminals responding to sinusoidal gratings moving in eight directions, calculated from the response mean (F0, left) or amplitude at the fundamental frequency of the stimulus (F1, right). For each pixel, hue represents PD (colorbar), saturation represents direction selectivity index (DSI), and value represents maximum response across all 8 directions. Data from a single recording. Scale bar, 5 μm.

(B) Hue and HSV direction preference maps as in (A) calculated for voltage signals. The F1 amplitude of the voltage signal captures the directional preference of each LP layer, while the F0 amplitude displays no layer-specific organization. Data from a single recording, but a different recording from panel A. Colorbar applies to panels A and B. Scale is the same as in panel A.

(C) Quantification of ASAP2f responses in single T5 axon terminals to moving gratings of different spatial and temporal frequency combinations, each represented by a different color: 12.5°/s, 25°/cycle (black, n=14, from 8 flies), 25° /s, 25°/cycle (magenta, n=24, from 16 flies), 50°/s, 25°/cycle (cyan, n=12, from 8 flies), 25°/s, 50°/cycle (blue, n=5, from 2 flies), 50°/s, 50°/cycle (red, n=12, from 6 flies), 100°/s, 50°/cycle (yellow, n=9, from 3 flies), 12.5°/s, 12.5°/cycle (green, n=9, from 6 flies). Gratings we re presented in PD and ND. For each grating type and direction of motion, responses were averaged across cells. For each grating type, bars (from left to right) represent F1 amplitude in PD (solid), F1 amplitude in ND (hollow), F0 amplitude in PD (solid), and F0 amplitude in ND (hollow). Error bars indicate +/− 1 SEM.

(D) Calcium DSI vs voltage DSI in response to moving sinusoidal gratings at 1 Hz, 25°/cycle. Each point represents a single T5 axon terminal (n=24). DSI = (PD_R − ND_R) / (PD_R + ND_R), where PD_R represents the response amplitude to preferred-direction motion, and ND_R represents the response amplitude to null-direction motion. The same cells are depicted in magenta in Figure 2C and S2C–F.

(E) Top, representative example ASAP2f and jRGECO1a mean responses to four cycles of moving sinusoidal gratings, measured from the same single axon terminal, demonstrating enhanced calcium DS, relative to voltage DS, and demonstrating a calcium signal with prominent F0 and F1 components that are both DS, and a voltage signal with a minor, non-DS F0 component, and a prominent DS F1 component. Bottom, model of direction selectivity in T5, in which a linear filter generates an initial direction-selective signal, which is enhanced by an adaptive (arrows) nonlinear voltage-to-calcium transformation. T5 single-cell linear filter and nonlinearity, without arrows, adapted from (Leong et al., 2016).

Taken together, these data are consistent with a model in which linear summation followed by a nonlinearity, as from a voltage-to-calcium transformation, generates both PDE and NDS, enhancing the direction selectivity of the initial linear signal (Figure 2E). This model makes the explicit prediction that T5 sums inputs linearly to generate an initial DS signal. To test this model, we examined whether T5 voltage responses to moving stimuli could be predicted by a linear model constructed from responses to stationary stimuli.

Direction selectivity of the voltage signal in single T5 axon terminals arises from linear input summation

To determine whether linear summation underlies direction selectivity in T5, we again measured the voltage responses in single axon terminals. We used T5 voltage responses to non-moving stimuli to generate a prediction of how T5 would respond to moving stimuli if it were summing inputs linearly. Because T5 responds strongly to gratings, we used responses to stationary, contrast-modulated gratings to make a linear prediction of responses to moving gratings.

If and only if a cell sums inputs linearly, its response to the sum of a set of inputs is equal to the sum of its responses to the individual inputs. A moving sinusoidal grating is mathematically equivalent to the sum of spatially and temporally offset stationary sinusoidally contrast-modulated gratings of the same contrast, spatial frequency, temporal frequency, and orientation (Figure S3, and see STAR Methods). Visual intuition clarifies why this is the case. In space-time, a moving grating is represented as a “barber pole,” or periodic tilted stripes (Figure S3). Motion in the opposite direction corresponds to a reflection of the barber pole across the time axis. A stationary contrast-modulated grating is represented in spacetime as a “checkerboard.” Phase shifts in space and time correspond to translations of the checkerboard along the space and time axes. Thus, to synthesize the tilted stripes of a moving grating, stationary contrast-modulated gratings at different spatial phases must be temporally offset (advanced or delayed) to match the tilt, then summed, and finally scaled. To achieve a tilt corresponding to the opposite direction of motion, the temporal shifts are reversed.

Given this relationship between moving and stationary contrast-modulated gratings, we used T5 responses to stationary sinusoidally contrast-modulated gratings presented at different spatial phases to make a linear prediction of responses to moving gratings (Figure 3) (Enroth-Cugell and Robson, 1966; Jagadeesh et al., 1993; Movshon et al., 1978; Reid et al., 1987; Spitzer and Hochstein, 1985). If a single T5 cell sums its inputs linearly, its response to a moving grating will equal the scaled sum of its temporally phase-shifted responses to stationary contrast-modulated gratings presented at different spatial phases. This experiment can demonstrate whether DS responses to moving stimuli require nonlinear summation, that is, whether moving stimuli elicit nonlinear input interactions that are absent from responses to non-moving stimuli. The same experimental logic has been applied to demonstrate linear summation in vertebrate simple cells (Jagadeesh et al., 1993, 1997).

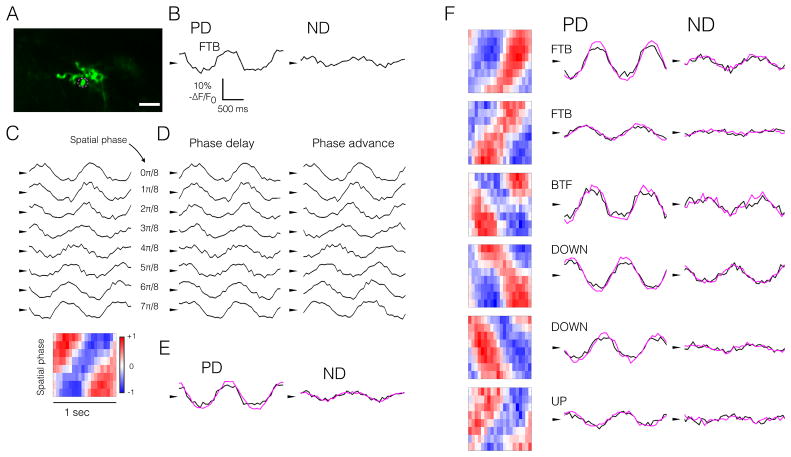
Figure 3. Single T5 axon terminals sum inputs linearly.

(A) Representative T5 axon terminal (single bouton). Scale bar, 5 μm. Magenta circle indicates the ROI depicted in (B–E).

Response timecourses in all panels represent the measured (black) or predicted (magenta) mean responses to two cycles of moving or stationary contrast-modulated gratings at 1 Hz, 25°/cycle. Spacetime plots in all panels, however, represent responses to a single stimulus cycle, to highlight temporal shifts in the responses. Arrowheads in all panels denote the mean response.

(B) ASAP2f response timecourses (− ΔF/F₀) of a single axon terminal to sinusoidal gratings moving in PD and ND.

(C) Top, ASAP2f response timecourses (− ΔF/F₀) of a single axon terminal to stationary sinusoidally contrast-modulated gratings (1 Hz, 25°/cycle) at 8 spatial phases. Bottom, spacetime plot of responses to contrast-modulated gratings above. For the spacetime plot, each row represents the average response to one stimulus cycle for each spatial phase. Red indicates positive ΔF/F₀, blue indicates negative ΔF/F₀. Normalization and colorbar as in Figure 1D.

(D) Same responses as in panel C with temporal phase delay (left) or advance (right), proportional to the spatial phase of the stimulus.

(E) Summed, scaled responses from panel D (magenta), overlain with responses from panel B (black), reproduced for comparison.

(F) Six additional representative ROIs, representing all four T5 subtypes, presented as in panel E. PD is indicated: Front-to-back (FTB), back-to-front (BTF), UP, DOWN. See also Figure S3.

T5 responses to moving and stationary gratings were sinusoidal, and phase-locked to the temporal frequency of the stimulus, consistent with linear mechanisms underlying these voltage signals (Figures 3B and 3C). Temporally shifting the responses to stationary gratings in one direction aligned the responses constructively, so that the scaled sum had a larger amplitude than the analogous procedure with the opposite temporal shift, which aligned the responses destructively (Figures 3D and 3E). These linear predictions, derived from responses to stationary gratings, matched quantitatively the responses of the same cell to moving gratings (Figure 3E). For all four T5 subtypes, the linear model accurately predicted voltage responses to moving gratings (Figure 3F).

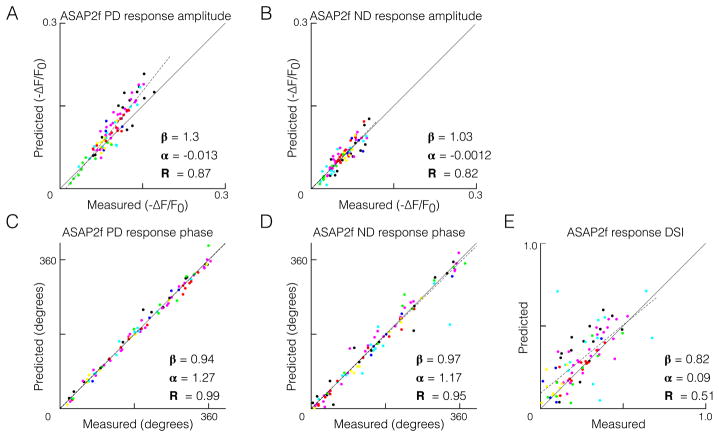
We applied this test of linear summation to responses to gratings across the same range of spatial and temporal frequencies depicted in Figures 2C and S2. Across the entire dataset, there was no difference in the linear model’s predictive performance in the preferred versus the null direction for either response amplitude or temporal phase (Figure 4A–D, and Figure S4). A linear model accounted quantitatively for the direction selectivity observed in voltage responses (Figure 4E) across a range of direction selectivity indices. Finally, the accuracy of our linear model did not appear to be influenced by adaptation to repeated presentations of the visual stimuli (Figures S5–S6).

Figure 4. A linear model quantitatively predicts direction-selective responses in T5.

(A–E) Comparison of measured responses and linear predictions of responses to moving sinusoidal gratings, each having a unique spatial and temporal frequency combination, and each represented by a different color (same set of cells and same color coding as in Figure 2C, S2C-F, S5, and S6). ASAP2f response amplitude was quantified as the 95th percentile minus the 5th percentile, and response phase was quantified as the phase of the component signal at the frequency of the stimulus (F1). Dotted lines represent least-squares fits to the data, with slope, intercept, and R-squared values indicated. See also Figure S4.

DISCUSSION

Here we find that voltage signals in T5 are 1) direction selective, 2) linear in response to local and global stationary stimuli, and 3) have direction-selective responses to motion that emerge from linear input summation. That T5, like vertebrate simple cells, can generate DS responses from non-DS inputs using a simple algorithm based on linear summation is a provocative finding given the role of nonlinearities previously thought to be essential determinants of direction selectivity in Drosophila (Mauss et al., 2017). We observed neither PDE (supralinear responses) nor NDS (sublinear responses) in T5 voltage signals. However, a nonlinear voltage-to-calcium transformation could accommodate all published measurements of calcium responses in T5 that support nonlinear models of direction selectivity involving PDE or NDS or both (Fisher et al., 2015a; Haag et al., 2017; Salazar-Gatzimas et al., 2016; Strother et al., 2017). Indeed, our direct observations of T5 support a recent model of T4 and T5 (Leong et al., 2016) that postulated an initial linear stage of direction selectivity, followed by a nonlinear stage (Figure 2E). We speculate that this nonlinear transformation is adaptive, allowing the system to perform contrast normalization and maintain direction selectivity across a wide range of conditions. These adaptation mechanisms do not, themselves, need to be direction selective, but could exploit upstream nonlinear computations (Behnia et al., 2014; Haag et al., 2017; Yang et al., 2016). Upstream nonlinearities like rectification can be detected in T5 voltage responses - as evidenced by responses to moving edges (Figure 1B), frequency doubling (Figure S2B–C), and modest rectification in responses to gratings (Figure S2D) - and appear to operate in addition to the linear operations we have uncovered, but are not essential determinants of DS. Indeed, upstream nonlinear mechanisms have been proposed to modulate direction selectivity in simple cells, which are nevertheless modeled as linear filters (Tolhurst and Heeger, 1997). Regardless, our data demonstrate that nonlinear processing is not required for the emergence of DS responses in T5.

We are the first to measure voltage signals in T5, and in doing so, have made a significant step toward understanding the computations T5 performs. Our model of direction selectivity in T5 stands in contrast to a recently proposed model of T4 that relies on a biophysical nonlinearity for the initial generation of DS (Gruntman et al., 2018), differences that will require further exploration. Finally, our data indicate that evolution has converged on a similar algorithm of direction selectivity in vertebrates and invertebrates, and organize the genesis of feature selectivity in distantly related organisms around the mechanistic linchpin of linear filtering.

STAR METHODS

Contact for Reagent and Resource Sharing

Further information and any requests for resources should be directed to and will be fulfilled by Lead Contact Prof. Tom Clandinin (trc@stanford.edu)

Experimental Model and Subject Details

Fly Husbandry and Preparation

Drosophila melanogaster were raised on molasses based food at 25°C. For two -photon imaging of T5, we used the enhancer fragment VT025965 to drive expression of Gal4 in T5 with high specificity (Leonhardt et al., 2016). For Figure 2A–B, dense expression of ASAP2f and jRGECO1a was achieved using the genotype +/+;UAS-ASAP2f/+;UAS-jRGECO1a/VT025965-Gal4. For all figures except Figure 2A–B, sparse expression of ASAP2f and jRGECO1a was achieved using a FLP-out strategy in the genotype +/yw,hs-FLP;UAS-ASAP2f/tub-FRT-Gal80-FRT;UAS-jRGECO1a/VT025965-Gal4, with heat-shock at 37°C for 2–3 minutes during the late 3^rd instar stage of development (Fisher et al., 2015a; Gruntman and Turner, 2013). All flies were female, and were imaged within 4–7 days of eclosion. To prepare for imaging, flies were immobilized by ice, and affixed to a custom built mount with UV-cured optical epoxy (NOA 63, Norland Optical Adhesives). The cuticle, fat bodies, and trachea of the left hemisphere were removed under ice-cold, artificial hemolymph without calcium to expose the brain for imaging from above. During imaging, standard, carbogen-gassed, room-temperature artificial hemolymph (Wilson et al. 2004) was perfused across the brain at 150 mL/h.

Method details

Imaging and Delivery of Visual Stimuli

Imaging and delivery of visual stimuli were followed as in Leong et al. 2016. Fluorescence was monitored in vivo using two-photon microscopy. For two-photon voltage and calcium imaging, we used a Leica SP 5 II (ASAP2f excitation @ 920 nm, ~15 mW at the stage, jRGECO1a excitation @ 1040 nm, ~15 mW at the stage). Recordings lasted ~1 h. Voltage and calcium signals were acquired at ~15 Hz (bidirectional scanning at 1.4 kHz, across a FOV of 128 pixels x 256 pixels, rows x columns). Pixels measured ~290 x ~290 nm. ASAP2f and jRGECO1a fluorescence signals were acquired with different bandpass filters (525/50m and 585/40m, respectively). The stimulus screen subtended ~ 60° x 90° (azimuth x elevation) of the left visual field. Visual stimuli were delivered with a Lightcrafter 4500 DLP, configured to deliver exclusively blue LED illumination, using a 100 Hz frame rate. The stimulus was attenuated with a 447/60 bandpass filter (Semrock), and a ND1 filter (Thorlabs). The mean radiance was 0.04 W sr⁻¹ m⁻².

Experiment and Stimulus Design for ASAP2f recordings

Each experiment (one fly per experiment) consisted of a series of jRGECO1a recordings (see below) followed by a single ASAP2f recording. For each ASAP2f recording, we presented one of three sets of visual stimuli:

1. moving light and dark edges (full contrast) in PD and ND, and individual stationary light and dark flashing bars at multiple spatial locations (Figure 1)

2. moving sinusoidal gratings (full contrast) in 8 directions (Figures 2B and 2D)

3. moving sinusoidal gratings (full contrast) in PD and ND, and stationary sinusoidally contrast-modulated gratings (full contrast) at 8 spatial phases, of matching orientation, spatial frequency, and temporal frequency (Figures 2C–E, 3, 4, S2, S4–S6)

For each of the above 3 stimulus sets, a single bout always lasted 8 seconds, and consisted of 4–16 presentations (or cycles, for periodic stimuli) of each stimulus condition, followed by a 2–4 second “blank” (the “blank” is a gray screen, of luminance matching the mean luminance of the preceding stimuli). The 8 second bout consisted of 4–16 presentations of each stimulus condition because multiple temporal frequencies were used. Within a single bout, stimulus conditions were presented in random order. Depending on the experiment, 20–40 bouts were presented, for a total of 80–320 presentations of each stimulus condition.

For Figure 1B–C, full-contrast moving edges were presented in series (for each direction, dark edge followed by light edge), at either 30°/s, 60°/ s, or 90°/s, in PD and ND. For Figure 1D–F, individual 2.5°-wide bars, in the preferred orientation, were presented on a gray background, at adjacent spatial positions covering 30–40° in total , alternating at 0.5 hz at full contrast between dark and light. For Figures 2A–B, moving gratings were presented at 1 Hz, 25°/cycle, in 8 directions, to a population of T5 axon terminals. For Figures 2C, 3, 4, S2, and S4–S6 moving and stationary contrast-modulated gratings were presented at various spatial and temporal frequencies, as indicated in the text and figure legends.

Experiment and Stimulus Design for jRGECO1a recordings

In addition to a single ASAP2f recording, each experiment also included a series of three jRGECO1a recordings, in which we presented three sets of stimuli, in the following order:

1. full-field (full screen) contrast steps alternating between dark, light, and gray, every 3 seconds

2. dark and light edges moving at 50°/s on a gray background, in the preferred and null directions

3. sinusoidal gratings (1 hz, 30°/cycle, full contrast) moving in 8 equally-spaced directions, between 0 and 315°, for 5 seconds

For each of the above 3 stimulus sets, a single bout consisted of a single presentation of each stimulus condition, followed by a 3-second “blank” (the “blank” is a gray screen, of luminance matching the mean luminance of the preceding stimuli). For each of the above 3 stimulus sets, 5 bouts were presented. The total duration of all three jRGECO1a recordings was ~10 minutes. Responses were averaged across all bouts to obtain the mean response to each stimulus condition, on which all analyses below were performed (except for analysis of responses to full-field contrast steps, see below). For each experiment, the jRGECO1a recordings always preceded the single ASAP2f recording.

Quantification and Statistical Analysis

Identification and Selection of ROIs

Identification and selection of ROIs, and quantification of calcium responses follows Leong et al., 2016. jRGECO1a recordings were used for ROI selection. ROI selection involved two stages: (1) automated segmentation (Pnevmatikakis et al., 2016) of jRGECO1a responses to moving sinusoidal gratings to obtain an initial set of ROIs that represent single cells or a mixture of cells at a single retinotopic location (2) systematic thresholding to exclude ROIs from this initial set if they did not match the known calcium response properties of T5 single cells (Fisher et al., 2015a; Leong et al., 2016), yielding a final set of ROIs that represent T5 single cells. jRGECO1a responses to moving gratings and moving light and dark edges were used to determine direction selectivity indices (DSI) and contrast selectivity indices (CSI), respectively. For jRGECO1a responses, DSI was calculated as the vector average of response amplitudes to the 8 directions of motion, normalized by the sum of response amplitudes to all 8 directions of motion; here, and only here, response amplitude was calculated as the F0 component plus the amplitude of the F1 component. For jRGECO1a responses, CSI was calculated as (R^max − R^null)/(R^max+R^null), where R^max is the maximum amplitude of largest response to either of the moving dark edges (PD or ND), and R^null is the maximum amplitude of the response to the moving light edge in the same direction.

To exclude ROIs from the initial set that may represent a mixture of T4 and T5 cells at the same retinotopic location, only ROIs having a CSI>0.6 were retained for further analysis. To exclude ROIs that may represent a mixture of T5 cells at the same retinotopic location, but having different preferred directions (a mixture of T5 subtypes), only ROIs having a DSI>0.5 were retained for further analysis. These thresholds were set based on previous measurements of T5 single cells, and DSI and CSI distributions obtained from an initial set of jRGECO1a recordings in the present study (283 ROIs from 28 flies). Because T5 responds poorly to full-field contrast steps, jRGECO1a responses to full-field contrast steps were used to determine whether the cell’s spatiotemporal receptive field was entirely on the stimulus screen; responses to full-field contrast steps were quantified as the integral of the response during the entire 3-second presentation of each stimulus condition (dark, light, or grey); we then performed ANOVA on the responses to each full-field contrast step; ROIs that responded to full-field contrast steps, relative to baseline (ANOVA p-value<0.01), were considered to lie partially off screen and were excluded from further analysis. As an additional precaution, we used the timing of responses to moving edges to verify that the cell’s receptive field was near the center of the screen. See Figure S1 for representative data used for ROI selection.

Analysis of ASAP2f recordings

Because moving edges and stationary flashing bars were always presented in the same recording, all cells in Figure 1F are also represented in Figure 1C. The dataset for Figure 1C consists of 57 single T5 cells from 29 flies, responding to edges moving in one of three velocities: 30°/s (black, n = 9, from 5 flies), 60° /s (magenta, n = 15, from 7 flies), or 90°/s (cyan, n = 33, from 17 flies). The dataset for Figure 1F consists of 18 single T5 cells, from 9 flies, responding to stationary flashing bars. Because moving and stationary contrast-modulated gratings were always presented in the same recording, all cells in Figure 4 are also represented in Figures 2C, S2C–F, S5, and S6. This dataset consists of 85 single T5 cells from 49 flies, responding to gratings across 7 different spatial and temporal frequency combinations: 12.5°/s, 25°/cycle (black, n=14, from 8 flies), 25°/s, 25°/cycle (magenta, n=24, from 16 flies), 50°/s, 25°/cycle (cyan, n=12, from 8 flies), 25°/s, 50°/cycle (blue, n=5, from 2 flies), 50°/s, 50°/cycle (red, n=12, from 6 flies), 100°/s, 50°/cycle (yellow, n=9, from 3 flies), 12.5°/s, 12.5°/cycle (green, n=9, from 6 flies). Different subsets of this dataset are also represented in Figure 2D–E, 3, and S4.

In all figures, ASAP2f fluorescence response was quantified as −ΔF/F₀, since ASAP2f decreases fluorescence intensity in response to depolarizations. For ASAP2f responses, F₀ was defined as the mean fluorescence during the final several frames of the “blank”, averaged across all “blank” presentations.

For all experiments, responses were averaged across bouts to obtain the mean voltage response to a single bout of each condition. All analyses were performed on these mean responses. Depending on the experiment and analysis, the mean voltage response may have been averaged further, prior to analysis: for example, in Figure 3 and Figure S4, response timecourses represent the mean response to 2 cycles of gratings, so responses were also averaged across the mean bout.

In Figure 1C, dark edge response amplitude was quantified as 95th percentile (a robust measure of the max), and light edge response amplitude as 5th percentile (a robust measure of the min), of this mean response. In Figure 1D, the spacetime plot of responses to stationary, flashed bars were normalized to the maximum depolarizing response. In Figure 1E–F responses having a positive (depolarizing) mean response integral during the presentation of the dark bar were classified as center, while responses having a negative (hyperpolarizing) mean response integral during presentation of the dark bar were classified as surround.

In Figure S2A–B, spacetime plots of responses to contrast-modulated gratings are normalized to the maximum depolarizing response. To calculate the power spectral density, we computed the discrete Fourier transform (DFT) of the mean response of each single cell to each of the 8 spatial phases, then averaged these 8 spectra, and across all cells responding to stationary contrast-modulated gratings at 1 Hz, 25°/cycle (Figure S2A), or at 1 Hz, 12.5°/cycle (Figure S2B). Spectra were normalized by the length (number of frames) of the signal. For Figure S2C, for each stimulus spatial and temporal frequency combination, we used the DFT with interpolation to compute the F0, F1, and F2 components of the mean response of each single cell to each of the 8 spatial phases, then averaged these values across all 8 spatial phases, and across all cells. For Figure S2D, for each stimulus spatial and temporal frequency combination, the response maximum and minimum were calculated from the mean response of each single cell to each of the 8 spatial phases, then averaged across all 8 spatial phases, and across all cells; response maximum was defined as 95th percentile, response minimum was defined as 5th percentile, and rectification was defined as 95th percentile/abs(5th percentile). In Figure S2E, response temporal phase was defined as the phase of the component signal at the frequency of the stimulus (F1); for each stimulus spatial and temporal frequency combination, response phase was normalized across spatial phases for each cell; then, across all cells, the 8 response temporal phases were registered by placing the response with the maximum amplitude at the rightmost position of the figure. For Figure S2F, amplitude was defined as the difference between the 95th percentile, and the 5th percentile; for each stimulus spatial and temporal frequency combination, for each cell, the amplitudes of responses to the 8 spatial phases were registered to place the the response with the maximum amplitude at the rightmost position of the figure. Because of this registration protocol for S2E–F, the x axes are labeled “relative spatial phase”.

In Figures 2A–B, HSV maps were computed as in (Leong et al., 2016), in response to sinusoidal gratings moving in 8 equally-spaced directions. In Figure 2C, the same protocol was followed as in Figure S2C, except here for moving sinusoidal gratings in PD and ND, and for only F1 and F0 response components. In Figure 2D, DSI was computed as (PD_R − ND_R) / (PD_R + ND_R), where PD_R represents the response amplitude to preferred-direction motion, and ND_R represents the response amplitude to null-direction motion; response amplitude was calculated as 95th percentile minus 5th percentile.

For Figure 3, linear predictions (magenta) were obtained by following the linearity test outlined in Jagadeesh et al., 1993. To make a linear prediction of responses to gratings moving in one direction, we temporally shifted the responses to stationary, contrast-modulated gratings by an amount proportional to the stimulus spatial phase offset, then summed these shifted responses, then divided by 4 (a scalar determined by the number of spatial phases presented). Opposite temporal shifts are used to obtain linear predictions of responses to opposite directions of motion (temporal advance for one direction, temporal delay for the opposite). In Figure 3C (bottom) and 3F, spacetime plots of responses to contrast-modulated gratings were normalized to the maximum depolarizing response.

In Figure 4A–B, response amplitude was quantified as 95th percentile minus 5th percentile. In Figure 4C–D, response phase was quantified as the phase of the component signal at the frequency of the stimulus (F1); some points were shifted 360° to help clarify the trend. In Figure 4E, DSI was calculated as in Figure 2D. In Figures 4A, 4B, and 4E, quantification of responses was carried out on the average single cycle of response (rather than the average 2 cycles, as in Figure 4C and 4D, and as presented in response timecourses in Figure 3 and S4).

All methods to produce Figure S4 match those used to produce Figure 3. All methods to produce Figure S5 and S6 match those used to produce Figure 4, except the following: rather than averaging responses across the bout (consisting of responses to multiple cycles of gratings), analysis was carried out only on the mean responses to the first period of stimulus presentation (Figure S5), or the last period of stimulus presentation (Figure S6); this applies to the linear prediction as well: that is, the linear prediction was formed from the first period (Figure S5) or last period (Figure S6) of mean responses to each of the 8 contrast-modulated gratings.

Data and Software Availability

Code availability

All analysis was carried-out using custom-written MATLAB code. Visual stimuli were programmed with the OpenGL 1.0 API in Visual C#. All code is available on github and will be made available upon request from the corresponding author.

Data availability

All data will be made available upon request from the corresponding authors.

Supplementary Material

supplement. Supplementary video: Stimuli for linearity test. Related to Figures 2–4, and S2–S6.

This video shows the stimuli used for the linearity test: sinusoidal gratings moving in 2 directions, and stationary contrast-modulated gratings at 8 spatial phases. Each of these stimulus conditions is separated by a “blank” (gray screen, or luminance matching the mean luminance of the gratings). As described in the text, and in Figure S3, a moving grating can be synthesized from the scaled sum of stationary, contrast-modulated gratings. It is this equivalence that underlies the test of linear summation we employ.