SUMMARY
A large amount of multi-species functional genomic data from high-throughput assays are becoming available to help understand the molecular mechanisms for phenotypic diversity across species. However, continuous-trait probabilistic models, which are key to such comparative analysis, remain under-explored. Here we develop a new model, called phylogenetic hidden Markov Gaussian processes (Phylo-HMGP), to simultaneously infer heterogeneous evolutionary states of functional genomic features in a genome-wide manner. Both simulation studies and real data application demonstrate the effectiveness of Phylo-HMGP. Importantly, we applied Phylo-HMGP to analyze a new cross-species DNA replication timing (RT) dataset from the same cell type in five primate species (human, chimpanzee, orangutan, gibbon, and green monkey). We demonstrate that our Phylo-HMGP model enables discovery of genomic regions with distinct evolutionary patterns of RT. Our method provides a generic framework for comparative analysis of multi-species continuous functional genomic signals to help reveal regions with conserved or lineage-specific regulatory roles.
Keywords: comparative genomics, continuous-trait probabilistic model, phylogenetic hidden Markov Gaussian process, replication timing
Graphical Abstract
INTRODUCTION
Multi-species functional genomic data from various high-throughput assays (e.g., ChIP-seq of transcription factor proteins or histone marks) are highly informative for the comparative analysis of gene regulation conservation and differences between human and other mammalian species (Villar et al., 2015; Cotney et al., 2013; Brawand et al., 2011). The signals from such data are continuous in nature. However, in most analyses, the continuous signals are often discretized by selected thresholds or being transformed to discrete values for distinctive feature patterns before subsequent cross-species comparisons, causing loss of information from the original data. Continuous-trait models, which are key to the modeling of functional genomic signals, are gaining increasing attention in genome-wide comparative genomic studies (Naval-Sánchez et al., 2015; Rohlfs et al., 2013). However, computational methods are under-explored to fully model continuous functional genomic data in the context of multi-species comparisons. In particular, to the best of our knowledge, there are no existing algorithms available to simultaneously infer heterogeneous continuous-trait evolutionary models along the entire genome.
Several types of continuous-trait evolutionary models have been developed for individual loci. One basic model (Felsenstein, 1985; Pagel, 1999; Freckleton, 2012) assumes that continuous traits evolve by Brownian motion. This model has been extended to more complicated Gaussian processes such as the Ornstein-Uhlenbeck (OU) process (Hansen, 1997; Butler and King, 2004; Hansen et al., 2008). However, the existing methods that use continuous-trait evolutionary models in comparative genomics either apply a single evolutionary model to signals of selected regions, or test different evolutionary model assumptions with prior knowledge at selected regions (Rohlfs et al., 2013; Brawand et al., 2011; Naval-Sánchez et al., 2015; Drummond et al., 2012). In other words, the continuous-trait evolutionary models have not been utilized in simultaneously estimating heterogeneous phylogenetic trees across different loci along the entire genome based on functional genomic data.
In this paper, we develop a new continuous-trait probabilistic model for more accurate state estimation based on multivariate features from different species using functional genomic signals. We call our model phylogenetic hidden Markov Gaussian processes (Phylo-HMGP). Our new method incorporates the evolutionary affinity among multiple species into the hidden Markov model (HMM) for exploiting both temporal dependencies across species in the context of evolution and spatial dependencies along the genome in a continuous-trait model. Note that our Phylo-HMGP is fundamentally different from the existing models that are restricted to discrete state space of the studied traits (Siepel and Haussler, 2005; Hobolth et al., 2007; Liu et al., 2014; Jensen and Pedersen, 2000; Lunter and Hein, 2004; Qu et al., 2018). In particular, Phylo-HMMs define a stochastic process of discrete-trait character changes (Siepel and Haussler, 2005), where different states estimated by Phylo-HMMs can reflect different patterns of substitutions or background distributions. However, Phylo-HMMs do not handle continuous signals. The models in (Jensen and Pedersen, 2000; Lunter and Hein, 2004) share similar mechanisms and have the same limitations. In the recent phylo-epigenetic model (Qu et al., 2018), the nature of the method is still based on transitions between discrete levels of observed signals, with the need to discretize the traits. In this work, our Phylo-HMGP explores a new integrated attempt to utilize continuous-trait evolutionary models with spatial constraints to more effectively study the genome-wide features across species. Our model is also flexible such that various continuous-trait evolutionary models or assumptions can be incorporated according to the actual problems. We believe that Phylo-HMGP provides a generic framework, which can be applied to different types of functional genomic signals, to more precisely capture the evolutionary history of regulatory regions across different species.
In this work, we generated a new cross-species DNA replication timing (RT) dataset from the same cell type in five primate species (human, chimpanzee, orangutan, gibbon, and green monkey). The RT program in eukaryotic cells duplicates the genome with a highly regulated temporal pattern. Genome-wide RT maps have revealed replication profile domains that correlate with chromatin structure (Gindin et al., 2014; Comoglio et al., 2015) and higher order genome organization, such as Hi-C A/B compartments and topologically associating domains (TADs) (Rhind and Gilbert, 2013; Ryba et al., 2010; Pope et al., 2014; Dileep et al., 2015; Solovei et al., 2016). It is known that RT changes across half of the genome during cell differentiation and disease (Ryba et al., 2011, 2012; Yue et al., 2014; Rivera-Mulia et al., 2015; Dileep et al., 2015). In addition, studies have shown conservation of RT between human and mouse (Yaffe et al., 2010; Ryba et al., 2010; Yue et al., 2014; Pope et al., 2014). Microscopy also revealed that chromosome regions with early and late RT have specific spatial localization preferences in the nucleus that are conserved in evolution (Solovei et al., 2016). However, we have limited understanding of how the RT program has evolved in mammals. To the best of our knowledge, there is no existing study to investigate the RT conservation and dynamics for more than two mammalian species beyond the human-mouse comparison. Here we apply Phylo-HMGP to reveal genome-wide distributions of distinct evolutionary patterns of RT in five primates. We found that constitutive early and constitutive late RT regions, as defined from human ES cell differentiation (Ryba et al., 2011; Dileep et al., 2015), exhibit a strong correlation with the predicted conserved early RT and conserved late RT patterns. We also found distinct gene functions associated with different RT evolution patterns. In addition, the predicted RT patterns across species show correlations with other genomic and epigenomic features, including higher order genome organization, cis-regulatory elements, chromatin marks, and transposable elements. Our results from the comparative RT analysis in five primate species demonstrate the potential of our Phylo-HMGP model to help reveal regions with conserved or lineage-specific regulatory roles for the entire genome.
RESULTS
Overview of the phylogenetic hidden Markov Gaussian processes (Phylo-HMGP) model
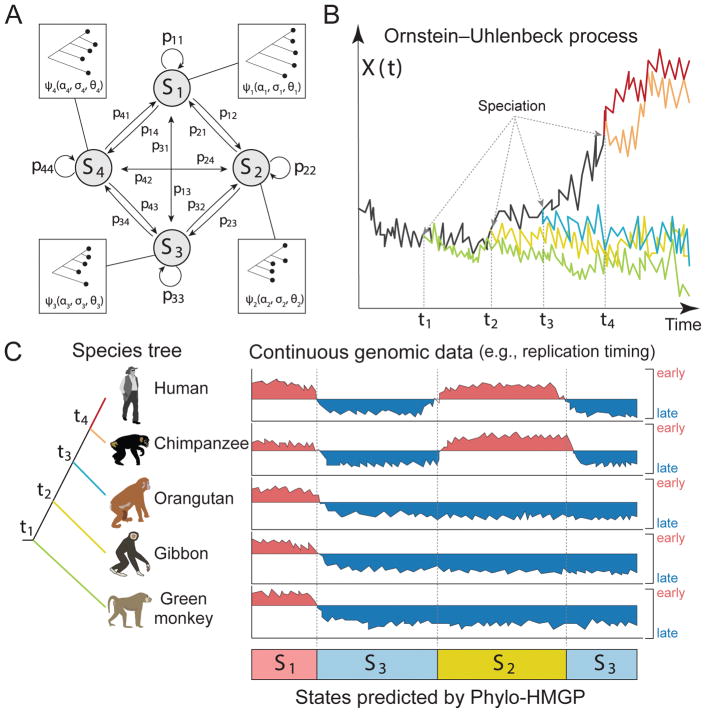
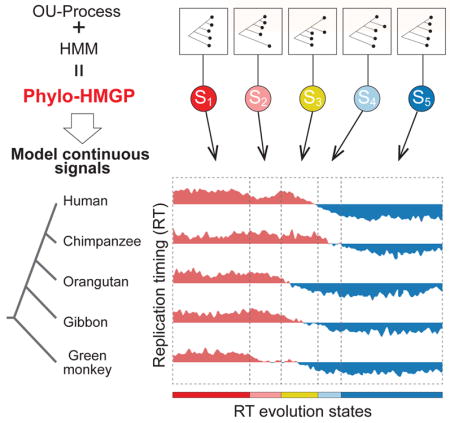
Here we first provide an overview of the proposed model (Figure 1). The details of the model are described in STAR METHODS. Our model aims to estimate different evolutionary patterns from multi-species functional genomic signals. As illustrated in Figure 1C, the input contains the observed continuous-trait signals from orthologous genomic regions from multiple species. The output is a genome-wide partition where neighboring genomic segments have different predicted states of multi-species signals, reflecting different evolution patterns of the signals being considered.
Figure 1. Overview of the Phylo-HMGP model.
(A) Example of the state space and state transition probabilities of the Phylo-HMGP model associated with the continuous genomic data in (C). Si represents a hidden state. Each hidden state is determined by a phylogenetic model ψi, which is parameterized by the selection strengths αi, Brownian motion intensities σi, and the optimal values θi of ancestor species and observed species on the corresponding phylogenetic tree. αi, σi, and θi are all vectors. (B) Illustration of the Ornstein-Uhlenbeck (OU) processes along the species tree specified in (C). X(t) represents the continuous trait at time t. The trajectories of different colors along time correspond to the evolution of the continuous trait in different lineages specified by the corresponding colors in (C), respectively. The time points t1, t2, t3, and t4 represent the speciation time points, which correspond to the speciation events shown in (C). The observations of the five species also represent an example of state S2 in (C). (C) Simplified representation of input and output of the Phylo-HMGP model. The five tracks of continuous signals represent the observations from five species. Si represents the underlying hidden states. Specifically, the example is the replication timing data, where ‘early’ and ‘late’ represent the early and late stages of replication timing, respectively. The species tree alongside the continuous data tracks shows the evolutionary relationships among the five species in this study. See also Figure S2, Figure S8, and Figure S9.
We define a Phylo-HMGP model as h = (S, ψ, A, π), where S is the set of states, ψ is the set of phylogenetic models, A is the state-transition probability matrix, and π represents the initial state probabilities, respectively. Suppose there are M hidden states. We have S = {s1, ···, sM},ψ = {ψ1, ···, ψM}, A = {aij}, 1 ≤ i, j ≤ M, and π = {π1, ···, πM}. Figure 1A shows the state space where different states are associated with varied phylogenetic tree models. Each phylogenetic tree model is parameterized with the Ornstein-Uhlenbeck (OU) processes, an example of which is shown in Figure 1B. Note that in this paper, we focus on the OU process and apply it to analyze cross-species RT data. We also discuss and compare with Brownian motion process within the framework (see STAR METHODS), which is also used as the Gaussian process for realizations of ψj to construct the emission probability distributions, j = 1, ···, M. ψj differs under different evolutionary models. The framework is flexible and other Gaussian processes can also be embedded into the framework by alternative definitions of ψj.
Phylo-HMGP provides a generic framework to more effectively incorporate multi-species functional genomic data into the HMM for analyzing both temporal dependencies across species in the phylogeny and spatial dependencies along the entire genome in a continuous-trait model. The source code of Phylo-HMGP can be accessed at: https://github.com/ma-compbio/Phylo-HMGP.
Simulation study demonstrates the robustness of Phylo-HMGP
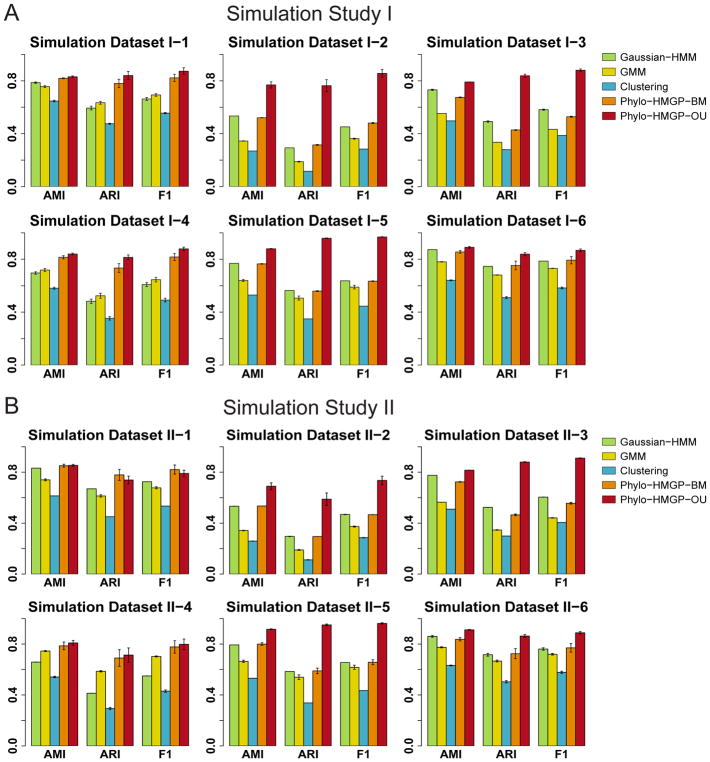
To explore whether incorporating evolutionary temporal constraints into the HMM can improve the accuracy of identifying different evolutionary patterns, we applied our method to 12 synthetic datasets in two types of simulation studies. We assessed the performance based on Adjusted Mutual Information (AMI), Normalized Mutual Information (NMI), Adjusted Rand Index (ARI), Precision, Recall, and F1 score (Manning et al., 2008; Vinh et al., 2010) by comparing the predicated states with the ground truth states (see STAR METHODS). We used HMM to generate the samples in simulation study I (SS-I), while simulation study II (SS-II) did not use HMM and was instead based on a Gaussian Mixture Model (GMM). Both SS-I and SS-II contained six synthetic datasets (sample size = 50,000 each), respectively. Detailed descriptions of the simulated datasets are in STAR METHODS.
We compared Phylo-HMGP-OU and Phylo-HMGP-BM with the Gaussian-HMM method, the GMM method, and the K-means clustering method in both SS-I and SS-II. For each dataset, we ran each method 10 times. Each method was started from different initializations and given the state number as 10. We reported the average performance of the 10 runs as the final performance of the respective method. We applied the same regularization parameter to Phylo-HMGP-OU on all of the 12 datasets, without tuning the parameter specifically on each dataset. The results show that Phylo-HMGP-OU outperforms the other methods on AMI, ARI, and F1 score on all of the six datasets in SS-I (Figure 2A and Table S1). In particular, Phylo-HMGP-OU shows significant advantage in reaching higher ARI on average in different datasets, as compared to the other methods. In SS-II (Figure 2B and Table S2), the performance of Phylo-HMGP-OU decreases occasionally (SS-II-1 and II-2) as compared to its performance in SS-I. However, Phylo-HMGP-OU still outperforms the other methods in five of the six datasets. Phylo-HMGP-BM reaches the highest performance on SS-I-1, while Phylo-HMGP-OU maintains comparable performance to Phylo-HMGP-BM on this dataset. These simulation results strongly suggest that Phylo-HMGP-OU can achieve robust performance even when the data are simulated from a non-HMM model such as the Gaussian mixture model. Note that in the rest of the Results section, we use “Phylo-HMGP” to refer to “Phylo-HMGP-OU”.
Figure 2. Evaluation using simulated datasets.
(A) Evaluation of Gaussian-HMM, GMM, K-means Clustering, Phylo-HMGP-BM, and Phylo-HMGP-OU on six simulation datasets in Simulation Study I in terms of AMI (Adjusted Mutual Information), ARI (Adjusted Rand Index), and F1 score. (B) Evaluation of Gaussian-HMM, GMM, K-means Clustering, Phylo-HMGP-BM, and Phylo-HMGP-OU on six simulation datasets in Simulation Study II in terms of AMI, ARI, and F1 score. In both (A) and (B), the standard error of the results of 10 repeated runs for each method is also shown as the error bar. See also Table S1, Table S2, and Figure S1.
Phylo-HMGP reveals genome-wide patterns of replication timing across primate species
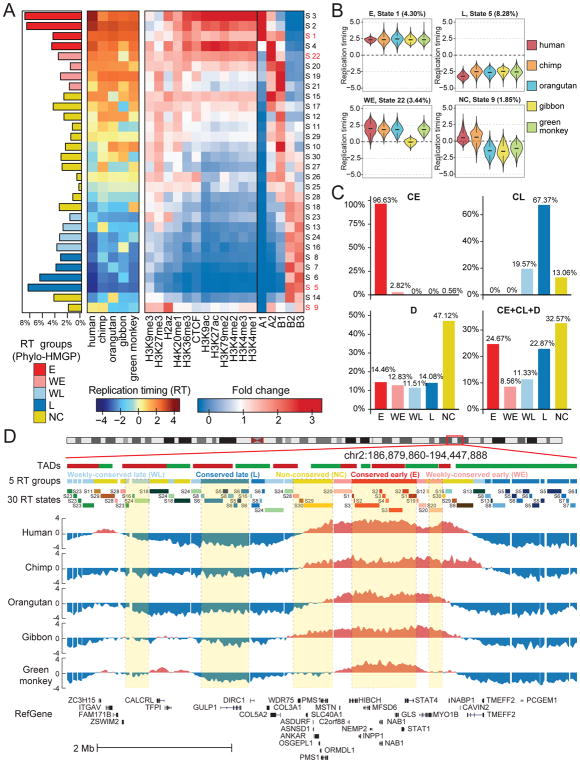
Next, we applied the Phylo-HMGP method to study different evolutionary patterns of RT in primate genomes. We generated genome-wide RT maps based on Repliseq (Marchal et al., 2018) in lymphoblastoid cells from five primate species, including human, chimpanzee, orangutan, gibbon, and green monkey. See STAR METHODS for the details on how we processed the data. We then applied Phylo-HMGP to this multi-species RT dataset. We set the state number as 30 based on estimation from K-means clustering (see STAR METHODS and Figure S3). We identified both conserved and lineage-specific states with differences in RT patterns across species. Here we classified the 30 states into five groups: conserved early (denoted as E), conserved late (L), weakly conserved early (WE), weakly conserved late (WL), and non-conserved (NC) (see STAR METHODS). In the E group, all five species have early RT. In the WE group, four species have early RT. We assign states to the L group and the WL group similarly. The remaining states are assigned to the NC group.
The representative RT signal patterns of the 30 predicted states are shown in Figure 3A, with examples of the states and groups shown in Figure 3B and Figure 3D. Distributions of RT signals of the five species in each of the 30 states are shown in Figure S2, including other lineage-specific patterns, conserved patterns, or divergent patterns. States 1–8 are conserved early or conserved late states of RT, making up approximately 47.7% of the whole genome. States 9–18 display different lineage-specific RT patterns. State 9 (Figure 3B) and 10 represent human-chimpanzee (hominini) specific patterns of early RT and late RT, respectively. State 11 shows human-chimpanzee-orangutan (hominid) specific early RT. States 12–18 reflect single-lineage specific patterns, where one species differs from all the other species.
Figure 3. RT evolution patterns identified by Phylo-HMGP.
(A) Panel 1 (leftmost): Proportions of the 30 RT states on the entire genome. The RT states are categorized into 5 groups: conserved early (E), weakly conserved early (WE), weakly conserved late (WL), conserved late (L), and other stages (NC), respectively. Panel 2: Patterns of the 30 states. Each row of the matrix corresponds to the state at the same row in Panel 1, and columns are species. Each entry represents the median of the RT signals of the corresponding species in the associated state. Panel 3: Enrichment of different types of histone marks and CTCF binding site (higher fold change represents higher enrichment). Panel 4: Enrichment of subcompartment A1, A2, B1, B2, and B3. (B) Four examples of RT signal distributions in states with different patterns (State 1: E; State 5: L; State 22: WE; State 9: NC with human-chimpanzee specific early RT). (C) Comparison of predicted RT patterns with the constitutively early/late RT regions identified across cell types. (D) Examples of different RT states and RT groups in five species predicted by Phylo-HMGP. TADs called by the Directionality Index method are shown at the top. See also Figure S2, Figure S3, Figure S4, Figure S5, Figure S6, and Figure S7.
Phylo-HMGP estimated the transition probabilities between the 30 predicted states (Figure S4). We noticed that overall the transition probabilities are higher within the E group and L group. Phylo-HMGP also simultaneously estimated the model parameters of selection strength, Brownian motion intensity, and optimal values of the phylogenetic model associated with each state (Figure S5 and Figure S6). We found that the estimated parameters correspond very well to the lineage-specific RT patterns. For example, for state 9 and 10, the human-chimpanzee specific states, the estimated strongest selection strength happened on the branch leading to human and chimpanzee, and strong Brownian motion intensity is also estimated for human and chimpanzee. We observed similar correlations for other states. We also compared Phylo-HMGP with the other methods on an evaluation dataset constructed from the RT data and found that Phylo-HMGP outperforms other methods (see STAR METHODS and Figure S7).
RT evolution patterns correlate with A/B compartments and histone marks
Analysis based on Hi-C data has shown that the genome can be divided into two compartments called A/B compartments (Lieberman-Aiden et al., 2009), with at least five subcompartments, namely A1, A2, B1, B2 and B3, which have different genomic and epigenomic properties (Rao et al., 2014). A1 and A2 subcompartments both show early RT, with the difference that replications in A2 regions finish later than A1. B2 and B3 subcompartments show late RT, while replications in B1 happen in the middle of S-phase (Rao et al., 2014). We used the subcompartment definitions in the human lymphoblastoid cell line GM12878 from (Rao et al., 2014) and calculated the enrichment of the five subcompartments in the 30 predicted RT states. We observed that different predicted RT evolution patterns show distinct enrichments of the subcompartments. For example, the predicted RT states in the E group (state 1–4) show the strongest correlation with A1 or A2, while the predicted RT states in the L group are enriched with B2 and B3. The majority of the states in the NC group are most enriched with A2 or B1. States in the WE group and WL group are enriched with A2/B1, and B2/B3, respectively.
We next compared the enrichments of different histone marks and CTCF binding site within each RT state. Figure 3A panel 3 shows the enrichment distributions of histone marks and CTCF binding site across the five predicted RT groups. These distributions are consistent with the epigenomic feature patterns of the subcompartments that are enriched in the corresponding states. We found that RT states in the E group show strong positive correlation with active histone marks (e.g., H3K27ac, H3K36me3, and H3K4me1) and the CTCF binding sites. On the contrary, RT states in the L/WL groups show distinct depletion of these histone marks and the CTCF binding sites. The majority of predicted states in the NC group instead exhibit variations in the enrichments of different types of histone marks.
Among the NC states, state 9 is identified as a human-chimpanzee specific early RT state (Figure 3B). It displays a unique pattern of histone mark enrichment, showing the strongest correlation with H2A.Z (p-values<1e-07) as compared to other predicted states. Recent studies have reported that H2A.Z is progressively enriched towards early RT loci (Du et al., 2018). Another state with interesting features is state 4, a conserved early state. The RT is significantly early in human in state 4, similar to other states in the E group. All of the other states in the E group (state 1–3) are strongly correlated with A1 subcompartment. State 4, however, is enriched with A2 subcompartment and is more positively correlated with H3K9me3, which generally has stronger enrichment in A2 than A1 (Rao et al., 2014). Therefore, state 4 represents a distinct state in the E group. These results demonstrate that Phylo-HMGP has the sensitivity to distinguish within similar evolutionary patterns of RT.
Different RT evolution patterns reflect different functions
Previous studies have shown that different genomic regions have different levels of cell type specificity for RT, including constitutively early, constitutively late, and more dynamic across different cell types (Ryba et al., 2011; Dileep et al., 2015). We compared the states from Phylo-HMGP with the constitutive and developmental RT patterns discovered during ES cell differentiation (Dileep et al., 2015), including constitutively early (CE), constitutively late (CL), developmentally regulated (D), and undetermined. We found that overall the constitutively early or constitutively late RT regions in the human genome have high consistency with the strongly conserved RT evolution patterns (Figure 3C). The findings are consistent with previous observations in human-mouse RT comparison (Ryba et al., 2011).
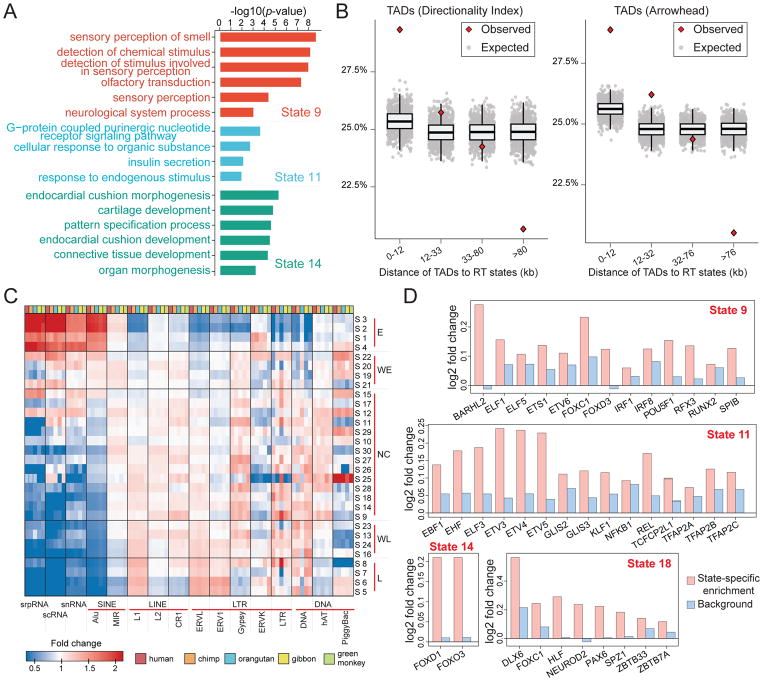
Among the CE regions that are also covered in the cross-species RT comparisons by Phylo-HMGP, 99.45% of the regions are assigned to the states of conserved early or weakly conserved early (p-value<2.2e-16). Also, 86.94% of the CL regions in human are within states of conserved late or weakly conserved late (p-value<2.2e-16). In contrast, the D regions show more diverse patterns across the five RT groups predicted by Phylo-HMGP. This also suggests that the RT regions in lymphoblastoid cells with similar RT profile across different cell types are highly likely to be conserved in primates. However, a significant fraction of conserved RT regions in primates also shows cell-type specific RT patterns in human. We performed Gene Ontology (GO) analysis for the conserved RT early regions with respect to the constitutive/non-constitutive RT patterns using DAVID (Huang et al., 2007), and found clear differences in gene functions (Table S3). We further performed GO analysis for the lineage-specific RT states (see Figure 4A and Table S4). We found that genes associated with different states have different functions and biological processes. For example, the hominini-specific early RT state (state 9) is enriched with genes having sensory functions. These analyses suggest that regions with different RT evolution patterns may contain genes with distinct functions.
Figure 4. Comparisons between the RT evolution patterns and other genomic features.
(A) Example gene ontology (GO) analysis results of state 9, state 11, and state 14. (B) Percentages of the distances between TAD boundaries and boundaries of predicted states in different intervals. The expected distances are calculated based on randomly shuffled TADs. Two types of TADs from different methods are used, namely TADs called by the Directionality Index method and TADs called by Arrowhead. (C) Transposable element enrichment in different RT states. (D) Motif enrichment in different lineage-specific RT states. State 9: human-chimpanzee specific early RT. State 11: human-chimpanzee-orangutan specific early RT. State 14: orangutan specific early RT. State 18: green monkey specific early RT. See also Figure S2, Table S3, and Table S4. The GO analysis results of other lineage-specific RT states are included in Table S4.
Boundaries of RT evolution patterns correlate with TAD boundaries
Earlier studies discovered that TADs defined from Hi-C data have high correspondence with replication domains (Pope et al., 2014; Dileep et al., 2015). We next asked whether the states found by Phylo-HMGP correlate with the boundaries of TADs. We used the TADs called by two methods, Directionality Index (DI) (Dixon et al., 2012) and Arrowhead (Rao et al., 2014). We named the TADs as DI TADs and Arrowhead TADs, the median lengths of which are 440kb and 185kb, respectively. For each boundary of a TAD, we calculated the distance between the TAD boundary and the nearest state boundary from Phylo-HMGP. We then calculated the percentages of boundary distances that fall into four distance intervals respectively, and estimated the empirical distributions of boundary distances in the different intervals by shuffling the TADs (see STAR METHODS).
We found that the boundary distances between the DI TADs and the predicted RT states are significantly more enriched in the interval [0,12kb] than expected (Figure 4B, empirical p-value<1e-03). The percentage drops in the intervals that correspond to increased boundary distances. The percentage is significantly lower than expected in the fourth interval that covers the largest distances (empirical p-value<1e-03). The comparison based on Arrowhead TADs show similar results. This analysis demonstrates the correlation between the boundaries of RT evolution states and the TAD boundaries.
RT evolution patterns have enrichment of different transposable elements
It is known that RT correlates with certain transposable element (TE) families, e.g., the early RT regions are typically enriched with SINE elements (Rhind and Gilbert, 2013). We next looked at the connection between RT evolution patterns and the involvement of TEs based on RepeatMasker annotation. We obtained the RepeatMasker annotations for each of the five primate species from the UCSC Genome Browser (Casper et al., 2017). For the TE families shared among the five primate species, we calculated the fold change of their enrichment in the orthologous regions of each species in each state (Figure 4C). We found that there exist distinct patterns of TE enrichment across different RT states and RT groups. Alu elements are strongly involved in conserved early RT states and depleted in conserved late RT states across the five species, with a clear changing correlation with RT across the five RT groups. On the contrary, L1 and LTR elements ERVL and ERV1 correlate negatively with early RT but positively with late RT. TEs in the LTR class and DNA class generally have more diversity in their distributions over states in the WE, WL, and NC groups. We also found that the repetitive sequence elements srpRNA, scRNA, and snRNA (based on RepeatMasker annotations) have a strong positive correlation with conserved early RT and negative correlation with conserved late RT (p-value<1e-04), having a similar enrichment pattern to Alu in the E, WL, and L groups. Although some of these correlations (such as those with srpRNA, scRNA, and snRNA) have not been reported before and further investigations are needed, this nevertheless demonstrates the potential of our method to provide new insights into the impact of sequence evolution on DNA replication timing.
Lineage-specific early RT regions harbor unique TFBS
We then asked whether there are specific transcription factor binding sites (TFBS) that are enriched in regions with specific types of RT evolution patterns. We used FIMO (Grant et al., 2011) to perform motif scanning in the orthologous open chromatin regions of each species (STAR METHODS), using 635 position weight matrices (PWMs) of TF binding motifs from the JASPAR 2016 core vertebrate motif database (Mathelier et al., 2016). We then computed the motif frequency for each of the PWMs for each species, using the threshold of p-value<1e-04, and normalized the frequency by the open chromatin region size. We used two types of tests jointly to identify TF binding motifs that may be enriched in predicted lineage-specific RT states. First, within each lineage-specific RT state, we performed binomial tests to find the motifs that are more enriched in the particular lineage than expected (p-value<0.05). Second, we examined if the species-specific enrichment of a motif in a state is also significantly different from the genome-wide background distribution (STAR METHODS).
We identified sets of motifs that show lineage-specific enrichment for the lineage-specific early RT states (Figure 4D). Note that we checked whether the TFs in the lineage-specific RT states that involve human are expressed and found that the majority of them are expressed (STAR METHODS). Also, we found that the identified lineage-specific enriched TF binding motifs vary in different states. However, there are still a number of TF binding motifs (or motifs with similar PWMs) shared between different states. For example, FOXC1 is significantly enriched in human and chimpanzee in the hominini-specific state (state 9), and also enriched in green monkey in the green monkey-specific state (state 18). Interestingly, many of corresponding TFs associated with species-specific early RT are from the FOX family (e.g., FOXC1, FOXO3, and FOXD1), the ELF family (e.g., ELF1 and ELF3), and the ETV family (e.g., ETV3 and ETV6). TFs of the FOX family are known regulators in B cells (Laurenti et al., 2013) (lymphoblastoid cells are B cells) and FOXO3 was previously found to be crucial for regulating cell cycle progression through its binding partnership with DNA replication factor Cdt1 (Zhang et al., 2012). Many of the other identified TFs are also regulators in B cells, such as EBF1, IRF8, RUNX2, and POU5F1 (Laurenti et al., 2013). Although these findings need further studies to evaluate their functional significance in lineage-specific biology, our analysis points to the direction that connects lineage-specific changes in cis-regulatory elements with lineage-specific changes in RT.
DISCUSSION
In this paper, we developed Phylo-HMGP, which is a new continuous-trait probabilistic model for more accurate genome-wide state estimation based on features from different species using functional genomic signals. The proposed Phylo-HMGP explores a new integrated framework to utilize the continuous-trait evolutionary model with spatial constraints to more effectively study the heterogeneous evolutionary feature patterns encoded in the genome-wide functional genomic datasets across multiple species. Both simulation studies and real data application demonstrate the advantage of Phylo-HMGP as compared to other methods. Importantly, we generated a new cross-species RT dataset from the same cell type in five primate species (human, chimpanzee, orangutan, gibbon, and green monkey) to study RT evolution patterns in primates for the first time using Phylo-HMGP. Our results from the comparative RT analysis demonstrate the potential of the model to help reveal regions with conserved or lineage-specific regulatory roles for the entire genome.
There are a number of areas that our model can be further improved. For Phylo-HMGP, the number of model parameters increases linearly with the number of species. There can be many local minima in parameter estimation for large scale evolutionary trees. Therefore, both more effective parameter constraints in accordance with the tree structure and more effective optimization methods need to be developed. Also, hierarchical state estimation methods can be developed to group similar predicted patterns for state prediction refinement. In addition, the current Phylo-HMGP assumes that all the phylogenetic tree models have the same tree topolopy. But in certain application domains this may not be accurate. Therefore, it would be useful to improve the model by incorporating inference of alternative tree topologies (Friedman et al., 2002). Furthermore, we need to improve the interpretation of the estimated model parameters of the evolutionary models associated with the predicted states, to gain deeper understanding of the evolutionary mechanisms underlying the different functional genomic feature patterns.
Genetic variation can contribute to differences in RT (Koren et al., 2014; Mukhopadhyay et al., 2014; Rivera-Mulia et al., 2018). Our current study has the limitation that it does not specifically consider the impact of intra-species variation on RT evolutionary patterns we identified. We did, however, compare the RT variant loci (among different individuals) identified in human lymphoblastoid cells (Koren et al., 2014) with the cross-species RT evolution states we found. We observed that the RT variations among individuals are distributed sparsely on the genome, with a small percentage of the whole genome and of each predicted RT evolution state. This suggests that the impact of the intra-species variation on RT patterns across different species we found is likely to be very minor. However, it would be an important methodological improvement to model both the inter-species differences and intra-species variations when population level functional genomic data are available for different species.
We believe that Phylo-HMGP provides a generic framework to more precisely capture the evolutionary history of functional genomic signals across different species. In addition to the cross-species RT comparisons, we also applied Phylo-HMGP to predict the evolution of cis-regulatory modules and demonstrated the advantage and the generic utility of our new method (see STAR METHODS, Figure S8, and Figure S9). From the application to the RT data, we found that different RT evolution patterns predicted by Phylo-HMGP correlate with RT patterns across different cell types and various other genomic and epigenomic features, including higher-order genome organization features, cis-regulatory elements, transposons, and gene functions. Such insights from comparative functional genomic analysis may in turn help interpret the impact of sequence evolution on genome organization and function. One important future direction would be to develop more integrated models to holistically consider sequence features (from mutations and small insertions/deletions to large-scale genome rearrangements) and functional genomic signals across multiple species.
STAR METHODS
KEY RESOURCES TABLE
| REAGENT or RESOURCE | SOURCE | IDENTIFIER |
|---|---|---|
| Antibodies | ||
| Anti-BrdU antibody | BD biosciences | Cat#555627; RRID: AB 395993 |
| Anti-mouse IgG | Sigma-Aldrich | Cat#M7023; RRID: AB 260634 |
| Deposited Data | ||
| Repli-seq data of five primate species | This paper | GEO: GSE111733 |
| Experimental Models: Cell Lines | ||
| Human: lymphoblastoid GM12878 | Coriell Cell Repositories | Cat#GM12878; RRID: CVCL 7526 |
| Pan troglodytes (Common Chimpanzee): lymphoblastoid cell line | E. Eichler and M. Ventura (Johnson et al., 2006) | PTR |
| Pongo pygmaeus (Bornean Orangutan): lymphoblastoid cell line | E. Eichler and M. Ventura (Johnson et al., 2006) | PPY |
| Nomascus leucogenys (Northern White Cheeked Gibbon): lymphoblastoid cell line | L. Carbone | NLE |
| Cercopithecus aethiops (Green Monkey): lymphoblastoid cell line | Coriell Cell Repositories | Cat#PR01205; RRID: CVCL 2Y01 |
| Software and Algorithms | ||
| Phylo-HMGP | This paper | https://github.com/ma-compbio/Phylo-HMGP |
| FastQC | web portal | http://www.bioinformatics.babraham.ac.uk/projects/fastqc |
| FASTX-Toolkit | web portal | http://hannonlab.cshl.edu/fastxtoolkit |
| Bowtie2 | Langmead and Salzberg, 2012 | http://bowtie-bio.sourceforge.net/bowtie2/index.shtml |
| liftOver | Hinrichs et al., 2006 | https://genome.ucsc.edu/cgi-bin/hgLiftOver |
| HMMSeg | Day et al., 2007 | https://noble.gs.washington.edu/proj/hmmseg |
| Other | ||
| Repli-seq protocol | Marchal et al., 2018 | N/A |
| Heat-inactivated FBS | Seradigm | Premium Grade HI FBS 1500–500H Lot #: 035B15 |
CONTACT FOR REAGENT AND RESOURCE SHARING
Further information and requests for resources and algorithms should be directed to and will be fulfilled by the Lead Contact Jian Ma (jianma@cs.cmu.edu).
EXPERIMENTAL MODEL AND SUBJECT DETAILS
The five primate species included in this study are Homo Sapiens (Human), Pan troglodytes (Common Chimpanzee), Pongo pygmaeus (Bornean Orangutan), Nomascus leucogenys (Northern White Cheeked Gibbon), and Cercopithecus aethiops (Green Monkey). We used GM12878 cell line from human. The GM12878 cell line is a lymphoblastoid cell line established from EBV (Epstein-Barr Virus)-transformed B-lymphocytes from a female donor. The GM12878 cell line was obtained from the Coriell Cell Repositories of Coriell Institute for Medical Research. Only three passages were performed after the GM12878 cell line was received from the Coriell Cell Repositories, and no other cell line was cultured together at the same time. We captured cell morphology image immediately before the BrdU labeling (the first step of the Repli-seq procedure, the details of which are included in METHOD DETAILS). The image supports that the cells were from the GM12878 cell line, providing evidence for cell authentication. As shown in the cell culture protocol defined in https://data.4dnucleome.org/biosources/4DNSRH17RFKR/, healthy lymphoblastoid cells including GM12878 cell line grow in suspension culture with cells clumped in loose aggregates, which was shown in the cell morphology image, and this characteristic is not observed in ES cells or fibroblast cells. The information of the GM12878 cell line used in this study and the cell morphology image are available at: https://data.4dnucleome.org/biosamples/4DNBS3I5U7BY/. We used lymphoblastoid cell lines from the other four non-human primate species, each of which is from one biological individual. The lymphoblastoid cell line of each of the species was derived from B-lymphoctyes by EBV transformation. The cells of Common Chimpanzee (abbreviated as Chimpanzee) are male. The cells of Bornean Orangutan (abbreviated as Orangutan) are male. The cell lines of Chimpanzee and Orangutan have been used in (Johnson et al., 2006). The cells of Northern White Cheeked Gibbon (abbreviated as Gibbon) are male. The cells of Green Monkey are female and the cell line was obtained from the Coriell Cell Repositories. Authentication of the lymphoblastoid cells from each of the four primate species was performed using standard karyotyping. For each species, metaphase chromosomes were isolated for the cell line and inverted DAPI images were used to assess the full karyotype of the species, which are of species-specific distinguishing characteristics. For each species, we only used autosomes for data analysis and excluded data from the sex chromosomes.
METHOD DETAILS
Ornstein-Uhlenbeck process in the Phylo-HMGP model
Overall framework
We define a Phylo-HMGP model as h = (S, ψ, A, π), where S is the set of states, ψ is the set of phylogenetic models, A is the state-transition probability matrix, and π represents the initial state probabilities, respectively.
In Phylo-HMGP-OU, we can model the continuous traits with the Ornstein-Uhlenbeck process, which is a stochastic process that extends the Brownian motion with the trend towards equilibrium around optimal values. It is characterized by the following stochastic differential equation (Hansen, 1997; Butler and King, 2004):
| (1) |
where Xi(t) represents the observation of the i-th species at time point t, Bi(t) is the Brownian motion, α, θ, and σ are parameters that represent the selection strength, the optimal value, and the Brownian motion intensity, respectively. For example, Xi could be the ChIP-seq signal of a certain histone mark from a specific cell type at a specific locus in a species. Under the assumption of the OU process, we can derive the expectation, the variance, and the covariance of the observations of species given the phylogenetic model ψj. The phylogenetic model is the combination of multiple OU processes that share parameters along common branches. Suppose that Xp is the trait value of the ancestor of the i-th species, and Xa is the trait value of the common ancestor of the i-th and j-th species. Following Butler and King (2004); Rohlfs et al. (2013), we have:
| (2) |
| (3) |
| (4) |
where tip is the length of the branch from p to i, and lij represents the set of the ancestor nodes of i and i itself after its divergence with j.
In the Phylo-HMGP model with OU process, ψj is defined as: ψj = (θj, αj, σj, τj, βj), j = 1, ···, M, where θj, αj, σj denote the OU process parameters of the j-th state, respectively. τj, βj represent the topology of the phylogenetic tree and the branch lengths, respectively. We allow varied selection strength and Brownian motion intensity along each branch and varied optimal values at interior nodes or leaf nodes. Suppose there are r branches. We have θj ∈ ℝr+1, αj, σj ∈ ℝr. Suppose x = (x1, ···, xN) are observations of consecutive regions along a sequence of length N, and y = (y1, ···, yN) are the underlying hidden states, respectively. Each observation xi is a multi-dimensional vector of the trait values of the compared species with respect to a certain type of functional genomic feature for an orthologous genomic region. Suppose there are d species, which correspond to the d leaf nodes in the phylogenetic tree. We have xi ∈ ℝd, yi ∈ {1, ···, M}, i = 1, ···, N. The hidden state yi indicates a specific phylogenetic model ψj from which the observation xi is generated. represent different evolutionary patterns of the genomic features across the multiple species. For example, one phylogenetic model ψi may represent conserved evolution of the feature across species, while another model ψj may represent strong selection strength along one lineage that results in a lineage-specific pattern. Given the input of multi-species functional genomic signals over a range of regions, which can be processed into the observations x, we are trying to infer the underlying evolutionary patterns and predict the evolutionary states y through model parameter estimation. Each yi represents an evolutionary pattern, parameterized by the inferred phylogenetic model ψyi. The output includes the estimated model parameters ĥ and predicted states ŷ. Note that our Phylo-HMGP-OU is different from the HMMSDE methods that use a temporal HMM to simulate a single OU process (Dittmer, 2009). Phylo-HMGP-OU embeds phylogenetic models constructed by complex of OU processes into a spatial HMM to utilize both temporal and spatial dependencies between variables.
Parameter estimation
Let Θ be the model parameters. The joint probability of the observations x and states y is (Bilmes et al., 1998). We use Expectation-Maximization (EM) algorithm (Dempster et al., 1977) for parameter estimation. Suppose Θg is the current estimate of model parameters. The EM algorithm computes the expectation of the complete-data log likelihood, which is defined as the Q function Q(Θ,Θg):
| (5) |
where 𝓢N is the set of all state sequences of length N. We have:
| (6) |
Model parameters π, A and ψ can be updated separately in the Maximization-step (M-step), corresponding to the three parts of Q(Θ,Θg), respectively. The parameters of the Ornstein-Uhlenbeck (OU) model are involved in p(xi|yi) of the third term of Q(Θ,Θg). Define that q−i = (y1, ···, yi−1, yi+1, ···, yN). We represent the third part as:
| (7) |
p(x, yi = l|Θg) can be computed using forward-backward algorithm (Rabiner, 1989; Bilmes et al., 1998). Assume that continuous-trait variables follow multivariate Gaussian distributions. We have for a given state l. The underlying phylogenetic model ψl is embedded into and by Eq. (2)–(4). Then the negative expected log likelihood of state l is:
| (8) |
Therefore, multiplied by 2/N, the third part of the negative Q function with respect to a given state l can be represented as:
| (9) |
where , and Θ(l) represents the phylogenetic model parameters associated with state l.
We need to perform parameter estimation for each of the possible states. We assume τl is given. βl can be combined in effect to αl and σl. In practice, if the real branch lengths are unknown, we perform the transformation that α̃v = αvβv, , where βv represents the length of the branch from the parent of node v to node v. Using this approach the branch lengths are incorporated into {αl, σl}. Then Θ(l) = {θl, αl, σl}. A challenge is that there are approximately two times more model parameters than the feature dimension for each state. We apply ℓ2-norm regularization to the parameters Θ(l). In each M-step, the objective function of a given state l is defined as:
| (10) |
where and are defined as above. We define , and tune λ0 based on a fixed simulation dataset. We estimated the range of λ0 that can improve the performance of Phylo-HMGP-OU (see later section and Figure S1). Accordingly, we applied the same λ0 to all the simulation datasets and the real data as a fixed coefficient, without tuning λ0 on each dataset specially, in order to avoid overfitting of λ0 on a particular dataset.
From the first two parts of Q(Θ,Θg) we can update the estimates of π and A accordingly. Let A = {akl}, where akl = p(yi = l|yi−1 = k), k, l = 1, ···, M. We have:
| (11) |
| (12) |
Therefore, in each E-step, given the present estimated model parameters Θg, we compute p(x, yi = l|Θg) and p(x, yi−1 = k, yi = l|Θg) using the forward-backward algorithm (Rabiner, 1989; Bilmes et al., 1998), k, l = 1, ···, M. In each M-step, we solve the maximum expected likelihood estimation problem to update the parameters π, A, and . Given the estimated model parameters, we can predict a most likely sequence of hidden states ŷ using the Viterbi algorithm (Viterbi, 1967).
Specifically, we compute in the E-step using the forward-backward algorithm and current model parameter estimates Θg. Let x = (x1, ···, xT) be the observation sequence. We define:
| (13) |
and
| (14) |
According to the forward-backward algorithm, we have:
| (15) |
Both αl(t) and βl(t) can be computed recursively. Let πl = p(y1 = l) be the initial state distribution, l = 1, ···, M. The forward procedure to compute αl(t) is as follows.
| (16) |
| (17) |
| (18) |
The backward procedure to compute βl(t) is as follows:
| (19) |
| (20) |
| (21) |
We also update the transition probability between any two states. Define that εkl(t) = p(yt = k, yt+1 = l|x, Θ). We have:
| (22) |
Equivalent to Eq. (12), the transition matrix can be updated as:
| (23) |
With p(x, yi = l|Θg) and p(x, yi−1 = k, yi = l|Θg) computed in each E-step, k, l = 1, ···, M, we update the parameters π, A, and in each M-step.
Note that the existing discrete-trait Phylo-HMMs (Siepel and Haussler, 2005; Hobolth et al., 2007) can also be represented as h = (S, ψ, A, π), where ψj is defined according to the substitution process with respect to an alphabet Σj of discrete characters, e.g., Σj = {A, C, G, T} for nucleotides. In discretetrait Phylo-HMMs, ψj is defined as ψj = {Qj, bj, τj, βj}, where Qj is the substitution rate matrix, bj is the vector of the background character frequencies, τj is the tree topology, and βj represents the branch lengths. This realization of ψj is limited to the discrete characters, where transition probabilities between two characters can be computed to model evolution of characters, e.g., the HKY85 model (Hasegawa et al., 1985). For the continuous traits, we need to use continuous-trait evolutionary model assumptions to define ψj.
Initialization of the Expectation-Maximization algorithm in Phylo-HMGP
Phylo-HMGP uses the Expectation-Maximization (EM) algorithm for parameter estimation. The EM algorithm seeks local minima and the results of EM algorithm are influenced by initializations. We designed different ways for parameter initialization. The first approach is to estimate OU model parameters initially based on the primitive state estimation results from K-means clustering. We perform model estimation for each cluster separately as single-state estimation, and use the estimates as initial model parameter values for the EM algorithm.
The second approach is to generate initial values randomly. There are three types of parameters in the OU model for a single state, which are optimal values θ, selection strength α, and Brownian motion intensity σ. We sample random variables from uniform distributions for the initial values of θ, α, and σ, respectively.
The third approach is to use linear combination of the initial parameter values obtained from the first approach and the second approach. We estimate the initial parameter values as Θ0 = w1Θ1 + (1 − w2)Θ2, where Θ1 and Θ2 are parameter estimates from the first and second approaches. By changing the initial weight w1, we have different initialization schemes. Based on the performance with respect to varied w1 in simulation study I, we observed that Phylo-HMGP is not very sensitive to initialization on four datasets, while on the other datasets the performance is improved as w1 increases within a range. Given w1 ∈ [0.2, 1.0], the performance of Phylo-HMGP on each simulated dataset is comparable to the best performance it can achieve on the corresponding dataset. For performance comparison with other methods in the simulation study, we fixed w1 = 0.8 for all the datasets to prevent overfitting on a particular dataset. The initialization weight w1 is an input parameter to the implemented program and can be adjusted within [0, 1] by the user’s choice.
Estimation of the regularization coefficient in Phylo-HMGP
For the objective function defined in Eq. (10), we define , where N is the sample size, and we observe how performance of Phylo-HMGP-OU changes with respect to λ0 based on a fixed simulation dataset (simulation dataset I-1), in order to estimate a range of λ0 in which the performance of Phylo-HMGP-OU can be improved with the l2-norm regularization. We tuned λ0 from 0 to 5, with the step size of 0.5, and compared the performance of the model with respect to the different choices of λ0. We found that the model with λ0 ∈ [3.0, 5.0] reaches relatively higher F1 score than the other choices of λ0 on this dataset (Figure S1). We selected λ0 = 4.0 and applied it to all the simulation datasets and the RT data as a fixed coefficient, without tuning λ0 on each dataset specially, in order to avoid overfitting of λ0 on a particular dataset. We also repeated the experiment on dataset I-1 and observed how the performance of Phylo-HMGP-OU changes with λ0 on the other datasets in simulation study I. We found that the performance of Phylo-HMGP-OU is not sensitive to λ0 ranging in [3.0,5.0] on most of the simulation datasets (I-1,I-3,I-4,I-5,I-6). Phylo-HMGP-OU still reaches comparable performance to the highest performance it can achieve on dataset I-2. We only used the performance resulted from λ0 = 4.0 on all the simulation datasets for performance evaluation and comparison.
Brownian motion in the Phylo-HMGP model
For more comprehensive method evaluation of the proposed framework, we also developed the Phylo-HMGP-Brownian Motion (Phylo-HMGP-BM) method, where the embedded continuous-trait model is the Brownian motion model. Phylo-HMGP-BM is also built from h = (S, ψ, A, π). For Phylo-HMGP-BM, ψj is defined as ψj = (μj, τj, βj, λj), j = 1, ···, M, where μj denotes the mean values of leaf nodes, and τj, βj, λj denote the phylogenetic tree topology, the branch lengths, and the evolution rates on branches, respectively. Under the Brownian motion assumption, the covariance between observations of two species depends on the depth of their nearest common ancestor in the phylogenetic tree. The covariance matrix based on the BM model can therefore be presented as a linear combination of covariance matrices (Zwiernik et al., 2017).
Suppose r is the number of branches of the phylogenetic tree, and d is the number of leaf nodes (i.e., the number of observed species). We have λj ∈ ℝr, βj ∈ ℝr, and μj ∈ ℝd, j = 1, ···, M. We number the branches with 1, ···, r. For any vector f, let f(k) be the k-th element of f. Let vj ∈ ℝr, and vj(k) = λj(k) · βj(k), k = 1, ···, r, which reflects the combined effect of branch length and evolution rate along each branch. Without loss of generality, suppose v ∈ ℝr is the transformed branch length vector for an arbitrary state. Then v(k) represents the transformed branch length of the k-th branch. Suppose Xi is the observation of a species. Based on the model of Brownian motion, the mean value of Xi is identical to that of the observation of its ancestor and the variance of Xi is proportional to the evolution time from its ancestor. We have:
| (24) |
| (25) |
| (26) |
where Xp represents the observation of the nearest ancestor of species i, v(k) represents the transformed branch length from the nearest ancestor of species k to species k, Sa(i) represents the set of ancestors of species i, and Sa(i, j) represents the set of common ancestors of species i and j. The covariance matrix based on the Brownian motion model can therefore be presented as (Zwiernik et al., 2017):
| (27) |
where Gk is a binary matrix representing contribution of a specific branch to the covariance matrix. Suppose x = (x1, ···, xN) are observations of consecutive genome regions along a sequence of length N, and y = (y1, ···, yN) are the corresponding hidden states. Similar to Phylo-HMGP-OU, we use EM algorithm for parameter estimation. We define the Q function Q(Θ,Θg) in the same way as Eq. (6), which is the expectation of the complete-data log likelihood function, but with different realization of p(x, y|Θg) according to the assumption of the Brownian Motion model. Here Θ represents the model parameters and Θg is the current estimate of the parameters. Based on the original Brownian motion model, the expectation of observation of descendant species is always identical to that of its ancestor. We have 𝔼(Xi) = 𝔼(X0) under this assumption, where X0 corresponds to the most remote ancestor. However, we can observe shift of the mean value of the phenotype in real world problems (Thomas et al., 2009, 2006). Therefore, we relax this constraint on the expectation of the observations, using a weaker assumption that allows the expectation to be shifted on branches. Then we considers the phenotype expectation of each species as model parameters, allowing the expectation to vary between species.
Similar to the derivations in Eq. (7–9), we compute the third part of the negative Q function with respect to each state, i.e., the negative expected log likelihood of each state (multiplied by 2/N), which is denoted by L̃(Θ(l)), l = 1, ···, M. Here Θ(l) represents the model parameters associated with state l. We have Θ(l) = {vl, μl}. We minimize L̃(Θ(l)) to estimate Θ(l). Accordingly, the objective function of a given state l is:
| (28) |
where , and , l = 1, ···, M. Using EM algorithm, in each E-step, given the estimated parameters Θg, we compute p(x, yi = l|Θg) using the forward-backward algorithm, l = 1, ···, M. In each M-step, we solve the maximum expected likelihood estimation problem to update the parameters associated with each state. Different optimization algorithms can be applied to solve the optimization problem. Let vl,k = vl(k), k = 1, ···, r. For the Phylo-HMGP-BM, the gradient with respect to vl,k can be computed explicitly (Zwiernik et al., 2017) and we implemented the gradient descent method based on the derived gradient as an alternative optimization approach:
| (29) |
Data simulation for the simulation studies
We used two types of models for data simulation, corresponding to Simulation Study I (SS-I) and Simulation Study II (SS-II). Each study consists of six synthetic datasets. In SS-I, for each dataset, samples were generated from an HMM with 10 states and with multivariate Gaussian distribution as the emission probability distribution. The Gaussian distribution of each state follows a different OU model on the same phylogenetic tree topology. The OU model parameters of each state were randomly generated with non-negative constraints of selection strength and Brownian motion intensity (M is the state number). Phylogenetic trees with four leaf nodes and with five leaf nodes were used as tree topologies for parameter simulation, each used for three datasets. The transition probability matrix of the HMM was randomly generated with the assumption that self-transition probability of a state is the dominant probability as compared to probabilities of transitions to other states.
In SS-II, samples were generated from a Gaussian mixture model instead of an HMM. For each dataset, samples were generated based on a mixture model with 10 states where Gaussian distributions are the emission probability distributions. We defined a transition probability matrix between the 10 states as we defined in SS-I, and computed the equilibrium probability distribution of the 10 states from the transition probability matrix. We then divided the genome into continuous segments of varied lengths. Each segment represents a series of samples that share the same state, e.g., adjacent fixed-size bins of the same state on the genome. We randomly sampled the segment length from a truncated Normal distribution by which the length is non-negative. The state of each segment was drawn randomly and independently from the computed equilibrium probability distribution of the 10 states. Parameters of the Gaussian distribution of each state were shared between two corresponding datasets in SS-I and SS-II. For example, simulation dataset I-1 (dataset 1 in SS-I) and simulation dataset II-1 (dataset 1 in SS-II) are assigned with the same set of Gaussian distributions for 10 states. However, different assumptions (HMM and non-HMM models) were used to simulate the two types of datasets.
In both simulation study I (SS-I) and II (SS-II), phylogenetic trees with four leaf nodes and with five leaf nodes were used as tree topologies. Datasets with even-number (I-2, I-4, I-6, II-2, II-4, and II-6) were based on the same topology of five leaf nodes, which is identical to the topology of the species tree specified in Figure 1C and is also the topology used in the RT data study. Datasets with odd-number (I-1, I-3, I-5, II-1, II-3, and II-5) were based on the same topology of four leaf nodes, which is identical to the topology of the sub-tree of the species tree specified in Figure 1C that contains human, chimpanzee, orangutan, and gibbon. 50,000 samples were generated for each dataset.
The emission probability distribution of each state in each dataset is Gaussian distribution, parameterized by a multivariate OU model ψj = (θj, αj, σj), where j is the index of the state, and θj, αj, σj represent the optimal value vector, the selection strengths and the Brownian motion intensities along the branches, respectively. The selection strength αj,k and Brownian motion intensity along each branch are each randomly and independently sampled from the uniform distribution Unif[0, 2], k = 1, ···, r (r is the number of branches). The optimal value θj,l (l = 1, ···, r + 1) of each node is randomly and independently sampled from a Normal distribution 𝓝(0, 2). In the transition probability matrix A of one dataset in SS-I, the self-transition probability of state j is defined as ajj = a0 + (1 − a0) × p, where p is randomly sampled from uniform distribution Unif[0, 1] and a0 is set to be 0.7. The transition probabilities of state j to other states are first randomly sampled from uniform distribution Unif[0, 1] and then normalized to be summed to 1−ajj. In SS-II, the fragment length (the number of continuous bins of the same state) is sampled from the a truncated Normal distribution 𝓝(50, 30) with the minimal fragment length to be 5. We first sampled a transition probability matrix à in the same way as in SS-I. Then we estimated the equilibrium probability distribution π̃ of the states from à based on π̃ = π̃ Ã. We sampled the state of each fragment from π̃ randomly and independently.
We calculated the Davies-Bouldin Index (DBI) (Davies and Bouldin, 1979) for each dataset in SS-I and SS-II, to estimate the difficulty in state prediction in different datasets. DBI can be used to measure how discriminative is each cluster (state) compared to the others. A high DBI represents that the states have large variances within themselves while the state-to-state distances are small, making it difficult to distinguish the states. The DBIs for the six datasets in SS-I are 2.3127, 2.0770, 1.9706, 1.3127, 1.5045 and 1.4623, respectively. The DBIs for datasets in SS-II are 2.2677, 2.0608, 1.9597, 1.3116, 1.4987, and 1.4864, respectively. We found that datasets I-1, I-2, II-1, and II-2 have relatively higher DBIs.
Cell culture, replication timing profiling, and Repli-seq data processing
The GM12878 cells were grown according to the protocol defined in https://data.4dnucleome.org/biosources/4DNSRH17RFKR/. Cell cultures were maintained in T25 flasks with 10–20 ml medium in upright position at 37°C, 5% CO2-95% air to keep cell density between 200,000 cells/ml and 500,000 cells/ml in RPMI 1640 supplemented with 15% heat-inactivated FBS. For the other primate species, lymphoblastoid suspension cells were grown in RPMI 1640 media supplemented with 15% FBS and 2mM L-glutamine. Cultures were maintained in T25 flasks at 37°C, 5% CO2 and passaged to maintain adequate confluency. Next, we performed Repli-seq for the cultured cells of each species. The Repli-seq data of one replicate of each species were used for algorithm input and analysis in this study. The detailed procedure of Repliseq is described in (Marchal et al., 2018). Specifically, exponentially growing cells were pulse-labeled with 100μM BrdU for 2 hours and then harvested and fixed in 70% ethanol. The fixed cells were stained with propidium iodide (50μg/mL) in the presence of RNase A (250 μg/mL) in phosphate-buffered saline with 1% FBS. Then early and late S fractions were collected according to the DNA content measured by propidium iodide signal strength on BD FACS SORP. Sorted cells were lysed in SDS-Proteinase K buffer (0.2 mg/mL Proteinase K, 50mM Tris-HCl pH 8, 10mM EDTA, 1M NaCl, 0.5% SDS). Subsequently, 10–40K cells equivalent lysate depending on the cell availability was used to make each Repli-seq library. First, from early S and late S fraction of each cell line, total genomic DNA was extracted respectively using DNA Clean & Concentrator-5 (Zymo Research, cat. no. D4014), and eluted into 50μL water. Then each DNA preparation was sheared into 200bp on average using Covaris E220 system. Next, end-repair and adaptor ligation were done using NEBNext Ultra DNA Library Prep Kit for Illumina (NEB, cat. no. E7370) and adaptor-ligated DNA was purified using DNA Clean & Concentrator-5 (Zymo Research, cat. no. D4014). From these adaptor-ligated DNA samples, BrdU-labeled DNA fragments were precipitated by mouse monoclonal anti-BrdU antibody (BD, cat. no. 555627) and rabbit anti-mouse IgG (Sigma-Aldrich, cat. no. M7023). The DNA was purified from this DNA-antibody complex using Proteinase K digestion and subsequent DNA Clean & Concentrator-5 (Zymo Research, cat. no. D4014) procedure, indexed and amplified using NEBNext Multiplex Oligos for Illumina (Dual-Index Primers Set 1; NEB, cat. no. E7600S), and purified using Agencourt AMPure XP (Beckman Coulter, cat. no. A63880). After the size distribution of each library was checked on Bioanalyzer, libraries were pooled and sequenced on HiSeq 2500 with 50 base single-end mode to obtain approximately 10 million reads/library.
We performed quality control of the Repli-seq reads using FastQC (http://www.bioinformatics.babraham.ac.uk/projects/fastqc) and removed adapter sequences using FASTX-Toolkit (http://hannonlab.cshl.edu/fastxtoolkit) for data preprocessing. To obtain RT signals in orthologous genome regions across the multiple species, we collected the RT signal values for each 6kb bin of human genome and its orthologous regions in each of the other species if RT measurements are available. Specifically, first, we mapped the preprocessed sequencing reads to the genome assemblies of hg19 (Human), panTro4 (Chimpanzee), ponAbe2 (Orangutan), nomLeu3 (Gibbon), and chlSab2 (Green Monkey), respectively, using Bowtie2 (Langmead and Salzberg, 2012). The genome assemblies were downloaded from the UCSC genome browser (Kent et al., 2002; International Human Genome Sequencing Consortium, 2001; The Chimpanzee Sequencing and Analysis Consortium, 2005; Locke et al., 2011; Carbone et al., 2014). Second, we used human genome (hg19) as the reference and divided the reference genome into 6kb bins. We then aligned each bin in human genome to each of the other species with reciprocal mapping using liftOver (Hinrichs et al., 2006) to obtain the orthologous regions. Third, for each species, we calculated Repli-seq read count within a given genomic window (an orthologous region) in early and late phases of RT, respectively, normalized by the total read count in early or late RT phase on the whole genome accordingly. The RT signal in each orthologous region is defined as the base 2 logarithm ratio of read count per million reads between the early and late phases of RT within this region.
For each species, we identify each sequence of consecutive bins without RT signals as a gap. The bin size (6kb in human) is much smaller than the scale of the RT signals (the replication domain is typically at the scale of 400–800kb (Pope et al., 2014)). We assume that RT does not change sharply at a small size gap if the gap is between both early RT signals or both late RT signals. We then performed data imputation for gaps smaller than 48kb using nearest neighbor imputation. In this way we can reduce missing data and have more continuous segments where cross-species observations are available. More specifically, if the RT signals on both sides of a gap smaller than 48kb are both early RT signals or both late RT signals with difference smaller than 1/3, we assign to each bin in the gap the RT signal of a signal-available bin that is nearest to this bin. We then used the software HMMSeg (Day et al., 2007) to perform wavelet smoothing (Percival and Walden, 2006) of the RT signals in each species, using the window size of 24kb.
Next, we found the orthologous regions where the RT signals across five species are all available. We then performed data normalization of the signals of each species in the regions. We observed that the different species have varied RT scales around [−5,5]. We performed feature scaling to scale non-negative RT signals (primarily early RT) in each species to [0,5] and scale non-positive RT signals (primarily late RT) in each species to [−5,0]. We formed the normalized RT signals in orthologous regions across five species into a five-dimensional feature vector and assigned it to the corresponding reference 6kb bin in human genome as a sample. We excluded the orthologous regions on the sex chromosome and only used autosomes of each species for data analysis. We obtained 419,754 samples in the orthologous regions across species.
Initial estimation of the state number in the RT data study
To apply Phylo-HMGP to the replication timing data, we first estimated the possible number of states using K-means clustering. We performed K-means clustering to the datasets with an increasing cluster number K, computed the Sum of Squared Error (SSE) of each clustering result, and observed how SSE changed with respect to K. We estimated the state number to be approximately 20–40 based on the K-means clustering results, as the decreasing rate of SSE with respect to the increasing K slows down in this range (Figure S3). Based on the observation the ‘elbow point’ of the SSE curve is around 30, and small fluctuation of the state number around 30 does not present significant change of the reduction of the SSE decreasing rate compared to the state number of 30. We therefore set the state number to be 30.
RT state prediction and RT state grouping
We applied Phylo-HMGP-OU to the multi-species Repli-seq data to perform state estimation, with the state number set to be 30. We used λ0 = 4.0 for l2-norm regularization and w1 = 0.2 for parameter initialization. We repeated the estimation 10 times with different initializations. We choose the result with the highest objective function value for further analysis.
We classified the 30 RT states predicted by Phylo-HMM-OU into 5 RT groups, namely, conserved early (noted as E), conserved late (L), weakly conserved early (WE), weakly conserved late (WL), and non-conserved (NC). If the majority (>98%) of the regions in a state share the pattern that all of the five species consistently have positive RT signals (early in RT), we assign this state to the conserved early (E) group. If a state does not satisfy this criteria, but instead satisfy that at least four species are consistently early in RT in more than 90% regions of this state, we assign this state to the weakly conserved early (WE) group. We assign states to the L and WL groups in a similar way accordingly. The remaining states are assigned to the NC group. Specifically, states 1–4 and states 5–8 are E states and L states, respectively. States 19–22, and states 13, 16, 23, 24 are WE and WL states, respectively. States 9–18 and 25–30 are NC states.
QUANTIFICATION AND STATISTICAL ANALYSIS
Performance evaluation in the simulation studies
We used Adjusted Mutual Information (AMI), Normalized Mutual Information (NMI), Adjusted Rand Index (ARI), Precision, Recall and F1 score (Manning et al., 2008; Vinh et al., 2010) for performance evaluation in the simulation studies. Suppose X = {x1, ···, xN} is the set of samples. Suppose Ω = {ω1, ···, ωK} is the set of predicted states which represents a partition of X into K states, and C = {c1, ···, cM} is the ground truth set of states. Let I(Ω, C) be the mutual information between Ω and C, and NMI(Ω, C) be the normalized mutual information. We have:
| (30) |
| (31) |
where H(Ω) and H(C) represent the entropies of Ω and C, respectively. The entropy is defined as . P(ωk), P(cj), and P(ωk, cj) represent the probabilities that a sample is in state ωk, in state cj, and in both ωk and cj, respectively. The maximum likelihood estimates of P(ωk), P(cj), and P(ωk, cj) are |ωk|/N, |cj |/N, and |ωk ∩ cj |/N, respectively, where |ωk| denotes the size of ωk and N is the number of samples.
Adjusted Mutual Information (AMI) is an adjustment of the mutual information to correct the effect of agreement between two partitions that is solely due to chance. We have:
| (32) |
where 𝔼(I(Ω;C)) represents the expectation of I(Ω;C), which can be estimated using Ω and C (Vinh et al., 2010).
The Rand Index (RI) (Manning et al., 2008) is another metric to compare two partitions, which is defined as:
| (33) |
TP (true positive) represents the number of pairs of samples in X that are in the same subset in Ω and also in the same subset in C. FP (false positive) is the number of pairs of samples in X that are in the same subset in Ω but in different subsets in C. FN (false negative) is the number of pairs of samples in X that are in different subsets in Ω but in the same subset in C. TN (true negative) is the number of pairs of samples in X that are in different subsets in Ω and also in different subsets in C.
The Adjusted Rand Index (ARI) corrects the Rand Index for the effect of agreement that is solely due to chance between partitions. ARI is defined as
| (34) |
where 𝔼(RI) represents the expectation of RI.
Precision, Recall, and F1 score are defined as
| (35) |
| (36) |
| (37) |
For the compared methods, we used the functions GaussianMixture and KMeans in the scikit-learn library (Pedregosa et al., 2011) to implement the Gaussian Mixture Model (GMM) method and the K-means clustering method, respectively. We used the hmmlearn library (https://github.com/hmmlearn/) to implement the Gaussian-HMM method. Each compared method is repeated 10 times with different initializations and guaranteed convergence each time. Specifically, the parameter initializations of the Gaussian-HMM method and the GMM method were based on K-means clustering. In each experiment, the best result from 10 randomly-initialized K-means clustering results (based on the clustering evaluation criteria used in hmmlearn or scikit-learn, respectively) was selected for estimating the initial parameters of Gaussian-HMM or GMM, respectively. 10 random initializations were also used for K-means clustering in each experiment, and the clustering with the best performance was chosen as the result. 10 experiments were repeated for the compared methods as well as Phylo-HMGP, and the average of the 10 runs was reported as the final performance of the corresponding method.
Comparison between the predicted RT states and TADs
When calculating the distances between the TAD boundaries and the RT state boundaries, to filter the TADs that are far away from any predicted states, we extended each boundary of a TAD with 30kb and used the states that overlap with the extended TAD to calculate the boundary distance. We then calculated the percentages of boundary distances that fall into four intervals. The first interval is [0,12kb]. The remaining three intervals are determined by the empirical distance distribution obtained from TAD shuffling, and equally cover the distances that are larger than 12kb. We shuffled the TADs 1000 times by randomly relocating them along the genome. We calculated and merged the boundary distances of each shuffle of TADs to form the empirical boundary distance distribution. Furthermore, for each shuffle of TADs, we computed the percentage of boundary distances that fall into each distance interval to form empirical distributions for each interval.
Motif feature analysis in lineage-specific RT states predicted by Phylo-HMGP
We performed motif scanning in the orthologous open chromatin regions of each of the five primate species. We identified open chromatin regions in human genome as DNase-seq peak regions with +/− 250bp extension, using DNase-seq data of the GM12878 cells downloaded from the ENCODE annotation data in the UCSC genome browser (Rosenbloom et al., 2012). We used the liftOver tool (Hinrichs et al., 2006) to project the identified open chromatin regions in human genome to genomes of the other primate species, obtaining orthologous open chromatin regions in other species. We used FIMO (Grant et al., 2011) and 635 position weight matrices (PWMs) of TF binding motifs from the JASPAR 2016 core vertebrate motif database (Mathelier et al., 2016) to perform motif scanning in the orthologous open chromatin regions of each species. In each orthologous region, we computed the motif frequency for each PWM within the open chromatin area for each species (p-value<1e-04 required for each motif). We then normalized the frequency by the open chromatin area size within this orthologous region.
To identify TF binding motifs that may be lineage-specifically enriched in predicted lineage-specific RT states, we used two types of tests and selected motifs that can pass both tests. First, within each lineage-specific RT state, we performed binomial tests to find the motifs that are significantly more enriched in the RT-specific species than expected (p-value<0.05). Second, for a motif that passes the binomial test in a lineage-specific RT state, we calculated the fold change of its motif frequency within the RT-specific species compared to the other species. To estimate the empirical p-value, we randomly sampled the same number of regions as the lineage-specific RT state from the whole genome for 2000 times, and calculated the same type of fold change to form empirical distribution. We selected the motifs that have empirical p-values<0.05.
We analyzed the expressions (in human) of those TFs with enriched motifs in the lineage-specific states that involve human (i.e., state 9 and state 11). The gene expression data were obtained from the ENCODE Project (ENCODE Project Consortium, 2012) (ENCODE Data Coordination Center accession: ENCSR000AEC; GEO accession: GSE78550). We found that 24 out of the 28 TFs (86%) associated with state 9 and 11 have FPKM greater than 0.01 (10/13 for state 9 and 14/15 for state 11). If we use the lower bound of the 95% credible interval for the FPKM greater than 0.1 as the threshold, 20 out of the 28 TFs (71%) associated with state 9 and 11 are expressed (10/13 for state 9 and 10/15 for state 11). For the TFs with low or no expression, we further searched for the most similar binding motifs using TOMTOM (Gupta et al., 2007). We found that all the TFs for the matching motifs are expressed. Therefore, if highly similar motifs are also considered, all the identified motifs correspond to expressed TFs.
Evaluation of Phylo-HMGP in comparsion with other methods on RT data
We also compared Phylo-HMGP-OU with Gaussian-HMM method, GMM method, K-means clustering method, and Phylo-HMGP-BM on the Repli-seq dataset, based on the average performance from 10 repeated runs of each method. We have applied each method to the RT data for state prediction, with state number set to be 30, as estimated before. However, there is no available ground truth for the RT data. For evaluation purpose, we constructed an evaluation state set. Specifically, we discretized the signals of each species into 5 levels, and identified 12 possible selected representative states (10 possible lineage-specific states and two conserved states) from all the combinations of the 5 levels in orthologous regions across the species. We fit a Gaussian-HMM with five hidden states independently for each species, with each state representing a discretized level of the RT signal values. High signal values (level 1 and 2) and low signal values (level 3 and 4) correspond to early phase and late phase in RT, respectively. For example, human early state represents early RT only in human and non-early RT in the other four species at the orthologous regions. The 10 possible lineage-specific states identified from discrete levels of RT signals are human early/late, chimpanzee early/late, orangutan early/late, gibbon early/late, and green monkey early/late, respectively. The two identified conserved states are conserved RT early and late, respectively. The 12 selected states cover around 60% of all the orthologous regions with cross-species RT signals. We constrained the evaluation of different methods to the regions where the 12 selected states are present. Within these regions, we used the 12 selected states as a known partition, and evaluated the relevance of the prediction of each method to this partition, using the evaluation metrics AMI, NMI, RI, and F1 (Figure S7). As each method predicted 30 states, which is a finer partition than 12 states, the evaluation measures are generally lower than those in the simulation studies. For example, regions in one state in the 12-state partition may be predicted to be in different states in the 30-state partition, which affects the F1 score by reducing the Recall and also affects the other metrics. Also, the selected states used for comparison were estimated using predictions from Gaussian-HMM in each species, which would favor Gaussian-HMM and GMM. The regions where 12 selected states are present are less continuous than the whole genome regions and have weaker spatial dependence between regions, which again would favor GMM. However, Phylo-HMGP-OU still outperforms the other methods in each of the four evaluation metrics. Phylo-HMGP-BM ranks second in performance. Even though the 12-state partition is not exactly ground truth, it nevertheless demonstrates that Phylo-HMGP outperforms the other methods in the RT data application, which is consistent with the results from the simulation studies.
Evaluation based on cis-regulatory module evolution
In addition to the real data application on the Repli-seq data, we also applied the models to predict different states of cis-regulatory module (CRM) evolution along the genome using features only from DNA sequences. We focused on a recent dataset for promoters and enhancers marked by H3K4me3 and H3K27ac in vertebrate liver cells (Villar et al., 2015). We used four species, including human (hg19), macaque (rheMac2), marmoset (calJac3), and mouse (mm10). We used hg19 as the reference and divide it into 5 kb bins. For each of the orthologous regions, we used the method Cluster-Buster (Frith et al., 2003) to compute a CRM score for presence of homotypic motif clusters within this region of the respective species, using a selected collection of 382 position weight matrices of TF binding motifs from the JASPAR 2016 core vertebrate motif database (Mathelier et al., 2016). We only used expressed TFs in liver cell based on gene expression data of human liver from GSE61260 (Horvath et al., 2014). We computed CRM sores for the 286,287 orthologous regions across the four species. We applied Phylo-HMGP to perform state prediction along the genome, with the state number set to be 16.
Here we assumed that the calculated CRM scores are associated with the activities of regulatory elements (e.g., enhancers or promoters). The ChIP-seq data, which can be used to identify and validate the existence of regulatory elements such as enhancers or promoters, were used to prepare benchmarks to evaluate the performance of the proposed model Phylo-HMGP in discovering different CRM patterns across species.
We used the peak regions called from ChIP-seq data of histone modification H3K27ac and H3K4me3 (Villar et al., 2015) to evaluate the different states estimated by Phylo-HMGP. For enhancer-evolution associated state prediction, we segmented the reference genome into different benchmark states based on the species-specific distribution of H3K27ac peaks. We then compared the states predicted by Phylo-HMGP-OU with the benchmark states, in comparison with the results from Gaussian-HMM, K-means clustering, and Phylo-HMGP-BM. We also performed the state evaluation using the H3K4me3 dataset. The results are shown in Figure S9. Phylo-HMGP-OU achieved the highest RI and F1 score among the different methods in the four experiments. Although the overall accuracy of using the CRM score for predicting enhancer/promoter activities seems not high and it remains an open problem to more accurately predict regulatory region activities from genome sequence, our evaluation again demonstrates the general utility and advantage of Phylo-HMGP.
DATA AND SOFTWARE AVAILABILITY
The Repli-seq dataset generated from this study is available under Gene Expression Omnibus (GEO) accession GSE111733. The data are also available at https://www2.replicationdomain.com/. The source code of Phylo-HMGP can be accessed at: https://github.com/ma-compbio/Phylo-HMGP.
Supplementary Material
Acknowledgments
This work has been supported primarily by the National Institutes of Health grant R01HG007352 (to J.M.). J.M. has been additionally supported by the National Science Foundation grants 1054309, 1262575, and 1717205. D.M.G. has been supported by the National Institutes of Health grant R01GM083337. J.M. and D.M.G. are also supported by the National Institutes of Health grant U54DK107965.
Footnotes
Supplemental Information includes four tables and nine figures and can be found with this article online.
DECLARATION OF INTERESTS
The authors declare no competing interests.
AUTHOR CONTRIBUTIONS
Conceptualization, J.M.; Methodology, Y.Y., Q.G., and J.M.; Software, Y.Y.; Investigation, Y.Y., Q.G., Y.Z., T.S., D.M.G., and J.M.; Resources, J.C. and R.J.O.; Visualization, Y.Z.; Writing – Original Draft, Y.Y. and J.M.; Writing – Review & Editing, Y.Y., Q.G., Y.Z., R.J.O., D.M.G., and J.M.; Funding Acquisition, D.M.G. and J.M.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bilmes JA, et al. Technical Report. International Computer Science Institute; 1998. A gentle tutorial of the EM algorithm and its application to parameter estimation for Gaussian mixture and hidden Markov models. ICSI TR–97–021. [Google Scholar]
- Brawand D, Soumillon M, Necsulea A, Julien P, Csárdi G, Harrigan P, Weier M, Liechti A, Aximu-Petri A, Kircher M, et al. The evolution of gene expression levels in mammalian organs. Nature. 2011;478:343–348. doi: 10.1038/nature10532. [DOI] [PubMed] [Google Scholar]
- Butler MA, King AA. Phylogenetic comparative analysis: a modeling approach for adaptive evolution. The American Naturalist. 2004;164:683–695. doi: 10.1086/426002. [DOI] [PubMed] [Google Scholar]
- Carbone L, Harris RA, Gnerre S, Veeramah KR, Lorente-Galdos B, Huddleston J, Meyer TJ, Herrero J, Roos C, Aken B, et al. Gibbon genome and the fast karyotype evolution of small apes. Nature. 2014;513:195–201. doi: 10.1038/nature13679. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casper J, Zweig AS, Villarreal C, Tyner C, Speir ML, Rosenbloom KR, Raney BJ, Lee CM, Lee BT, Karolchik D, et al. The UCSC Genome Browser database: 2018 update. Nucleic Acids Research. 2017;46:D762–D769. doi: 10.1093/nar/gkx1020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Comoglio F, Schlumpf T, Schmid V, Rohs R, Beisel C, Paro R. High-resolution profiling of Drosophila replication start sites reveals a DNA shape and chromatin signature of metazoan origins. Cell Reports. 2015;11:821–834. doi: 10.1016/j.celrep.2015.03.070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cotney J, Leng J, Yin J, Reilly SK, DeMare LE, Emera D, Ayoub AE, Rakic P, Noonan JP. The evolution of lineage-specific regulatory activities in the human embryonic limb. Cell. 2013;154:185–196. doi: 10.1016/j.cell.2013.05.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Davies DL, Bouldin DW. A cluster separation measure. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1979;2:224–227. [PubMed] [Google Scholar]
- Day N, Hemmaplardh A, Thurman RE, Stamatoyannopoulos JA, Noble WS. Unsupervised segmentation of continuous genomic data. Bioinformatics. 2007;23:1424–1426. doi: 10.1093/bioinformatics/btm096. [DOI] [PubMed] [Google Scholar]
- Dempster AP, Laird NM, Rubin DB. Maximum likelihood from incomplete data via the EM algorithm. Journal of the Royal Statistical Society: Series B (methodological) 1977:1–38. [Google Scholar]
- Dileep V, Ay F, Sima J, Vera DL, Noble WS, Gilbert DM. Topologically associating domains and their long-range contacts are established during early G1 coincident with the establishment of the replication-timing program. Genome Research. 2015;25:1104–1113. doi: 10.1101/gr.183699.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dittmer E. PhD thesis. Freie Universität Berlin; Berlin, Germany: 2009. Hidden Markov Models with time-continuous output behavior. [Google Scholar]
- Dixon JR, Selvaraj S, Yue F, Kim A, Li Y, Shen Y, Hu M, Liu JS, Ren B. Topological domains in mammalian genomes identified by analysis of chromatin interactions. Nature. 2012;485:376–380. doi: 10.1038/nature11082. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drummond AJ, Suchard MA, Xie D, Rambaut A. Bayesian phylogenetics with BEAUti and the BEAST 1.7. Molecular Biology and Evolution. 2012;29:1969–1973. doi: 10.1093/molbev/mss075. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Du Q, Bert SA, Armstrong NJ, Caldon CE, Song JZ, Nair SS, Gould CM, Luu PL, Khoury A, Qu W, et al. Replication timing shapes the cancer epigenome and the nature of chromosomal rearrangements. bioRxiv. 2018:251280. doi: 10.1038/s41467-019-08302-1. doi: https://10.1101/251280. [DOI] [PMC free article] [PubMed]
- ENCODE Project Consortium. An integrated encyclopedia of DNA elements in the human genome. Nature. 2012;489:57–74. doi: 10.1038/nature11247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Felsenstein J. Phylogenies and the comparative method. The American Naturalist. 1985;125:1–15. doi: 10.1086/703055. [DOI] [PubMed] [Google Scholar]
- Freckleton RP. Fast likelihood calculations for comparative analyses. Methods in Ecology and Evolution. 2012;3:940–947. [Google Scholar]
- Friedman N, Ninio M, Pe’er I, Pupko T. A structural EM algorithm for phylogenetic inference. Journal of Computational Biology. 2002;9:331–353. doi: 10.1089/10665270252935494. [DOI] [PubMed] [Google Scholar]
- Frith MC, Li MC, Weng Z. Cluster-Buster: Finding dense clusters of motifs in DNA sequences. Nucleic Acids Research. 2003;31:3666–3668. doi: 10.1093/nar/gkg540. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gindin Y, Valenzuela MS, Aladjem MI, Meltzer PS, Bilke S. A chromatin structure-based model accurately predicts DNA replication timing in human cells. Molecular Systems Biology. 2014;10:722. doi: 10.1002/msb.134859. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant CE, Bailey TL, Noble WS. FIMO: scanning for occurrences of a given motif. Bioinformatics. 2011;27:1017–1018. doi: 10.1093/bioinformatics/btr064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gupta S, Stamatoyannopoulos JA, Bailey TL, Noble WS. Quantifying similarity between motifs. Genome Biology. 2007;8:R24. doi: 10.1186/gb-2007-8-2-r24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hansen TF. Stabilizing selection and the comparative analysis of adaptation. Evolution. 1997;51:1341–1351. doi: 10.1111/j.1558-5646.1997.tb01457.x. [DOI] [PubMed] [Google Scholar]
- Hansen TF, Pienaar J, Orzack SH. A comparative method for studying adaptation to a randomly evolving environment. Evolution. 2008;62:1965–1977. doi: 10.1111/j.1558-5646.2008.00412.x. [DOI] [PubMed] [Google Scholar]
- Hasegawa M, Kishino H, Yano T-a. Dating of the human-ape splitting by a molecular clock of mitochondrial DNA. Journal of Molecular Evolution. 1985;22:160–174. doi: 10.1007/BF02101694. [DOI] [PubMed] [Google Scholar]
- Hinrichs AS, Karolchik D, Baertsch R, Barber GP, Bejerano G, Clawson H, Diekhans M, Furey TS, Harte RA, Hsu F, et al. The UCSC genome browser database: update 2006. Nucleic Acids Research. 2006;34:D590–D598. doi: 10.1093/nar/gkj144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hobolth A, Christensen OF, Mailund T, Schierup MH. Genomic relationships and speciation times of human, chimpanzee, and gorilla inferred from a coalescent hidden Markov model. PLoS Genetics. 2007;3:e7. doi: 10.1371/journal.pgen.0030007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horvath S, Erhart W, Brosch M, Ammerpohl O, von Schönfels W, Ahrens M, Heits N, Bell JT, Tsai PC, Spector TD, et al. Obesity accelerates epigenetic aging of human liver. Proceedings of the National Academy of Sciences. 2014;111:15538–15543. doi: 10.1073/pnas.1412759111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang DW, Sherman BT, Tan Q, Collins JR, Alvord WG, Roayaei J, Stephens R, Baseler MW, Lane HC, Lempicki RA. The DAVID Gene Functional Classification Tool: a novel biological module-centric algorithm to functionally analyze large gene lists. Genome Biology. 2007;8:R183. doi: 10.1186/gb-2007-8-9-r183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Human Genome Sequencing Consortium. Initial sequencing and analysis of the human genome. Nature. 2001;409:860–921. doi: 10.1038/35057062. [DOI] [PubMed] [Google Scholar]
- Jensen JL, Pedersen AMK. Probabilistic models of DNA sequence evolution with context dependent rates of substitution. Advances in Applied Probability. 2000;32:499–517. [Google Scholar]
- Johnson ME, Cheng Z, Morrison VA, Scherer S, Ventura M, Gibbs RA, Green ED, Eichler EE. Recurrent duplication-driven transposition of DNA during hominoid evolution. Proceedings of the National Academy of Sciences. 2006;103:17626–17631. doi: 10.1073/pnas.0605426103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kent WJ, Sugnet CW, Furey TS, Roskin KM, Pringle TH, Zahler AM, Haussler D. The human genome browser at UCSC. Genome Research. 2002;12:996–1006. doi: 10.1101/gr.229102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Koren A, Handsaker RE, Kamitaki N, Karlić R, Ghosh S, Polak P, Eggan K, McCarroll SA. Genetic variation in human DNA replication timing. Cell. 2014;159:1015–1026. doi: 10.1016/j.cell.2014.10.025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Langmead B, Salzberg SL. Fast gapped-read alignment with Bowtie 2. Nature Methods. 2012;9:357–359. doi: 10.1038/nmeth.1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laurenti E, Doulatov S, Zandi S, Plumb I, Chen J, April C, Fan JB, Dick JE. The transcriptional architecture of early human hematopoiesis identifies multilevel control of lymphoid commitment. Nature Immunology. 2013;14:756–763. doi: 10.1038/ni.2615. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lieberman-Aiden E, Van Berkum NL, Williams L, Imakaev M, Ragoczy T, Telling A, Amit I, Lajoie BR, Sabo PJ, Dorschner MO, et al. Comprehensive mapping of long-range interactions reveals folding principles of the human genome. Science. 2009;326:289–293. doi: 10.1126/science.1181369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu KJ, Dai J, Truong K, Song Y, Kohn MH, Nakhleh L. An HMM-based comparative genomic framework for detecting introgression in eukaryotes. PLoS Computational Biology. 2014;10:e1003649. doi: 10.1371/journal.pcbi.1003649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Locke DP, Hillier LW, Warren WC, Worley KC, Nazareth LV, Muzny DM, Yang SP, Wang Z, Chinwalla AT, Minx P, et al. Comparative and demographic analysis of orangutan genomes. Nature. 2011;469:529–533. doi: 10.1038/nature09687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lunter G, Hein J. A nucleotide substitution model with nearest-neighbour interactions. Bioinformatics. 2004;20:i216–i223. doi: 10.1093/bioinformatics/bth901. [DOI] [PubMed] [Google Scholar]
- Manning CD, Raghavan P, Schütze H. Introduction to Information Retrieval. Cambridge, UK: Cambridge University Press; 2008. [Google Scholar]
- Marchal C, Sasaki T, Vera D, Wilson K, Sima J, Rivera-Mulia JC, Trevilla-García C, Nogues C, Nafie E, Gilbert DM. Genome-wide analysis of replication timing by next-generation sequencing with E/L Repliseq. Nature Protocols. 2018;13:819–839. doi: 10.1038/nprot.2017.148. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mathelier A, Fornes O, Arenillas DJ, Chen C-y, Denay G, Lee J, Shi W, Shyr C, Tan G, Worsley-Hunt R, et al. JASPAR 2016: a major expansion and update of the open-access database of transcription factor binding profiles. Nucleic acids research. 2016;44:D110–D115. doi: 10.1093/nar/gkv1176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mukhopadhyay R, Lajugie J, Fourel N, Selzer A, Schizas M, Bartholdy B, Mar J, Lin CM, Martin MM, Ryan M, et al. Allele-specific genome-wide profiling in human primary erythroblasts reveal replication program organization. PLoS genetics. 2014;10:e1004319. doi: 10.1371/journal.pgen.1004319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Naval-Sánchez M, Potier D, Hulselmans G, Christiaens V, Aerts S. Identification of Lineage-Specific Cis-Regulatory Modules Associated with Variation in Transcription Factor Binding and Chromatin Activity Using Ornstein–Uhlenbeck Models. Molecular Biology and Evolution. 2015;32:2441–2455. doi: 10.1093/molbev/msv107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pagel M. Inferring the historical patterns of biological evolution. Nature. 1999;401:877–884. doi: 10.1038/44766. [DOI] [PubMed] [Google Scholar]
- Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, et al. Scikitlearn: Machine learning in Python. Journal of Machine Learning Research. 2011;12:2825–2830. [Google Scholar]
- Percival DB, Walden AT. Wavelet methods for time series analysis. Cambridge, UK: Cambridge University Press; 2006. [Google Scholar]
- Pope BD, Ryba T, Dileep V, Yue F, Wu W, Denas O, Vera DL, Wang Y, Hansen RS, Canfield TK, et al. Topologically associating domains are stable units of replication-timing regulation. Nature. 2014;515:402–405. doi: 10.1038/nature13986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qu J, Hodges E, Molaro A, Gagneux P, Dean MD, Hannon GJ, Smith AD. Evolutionary expansion of DNA hypomethylation in the mammalian germline genome. Genome Research. 2018;28:145–158. doi: 10.1101/gr.225896.117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabiner LR. A tutorial on hidden Markov models and selected applications in speech recognition. Proceedings of the IEEE. 1989;77:257–286. [Google Scholar]
- Rao SS, Huntley MH, Durand NC, Stamenova EK, Bochkov ID, Robinson JT, Sanborn AL, Machol I, Omer AD, Lander ES, et al. A 3D map of the human genome at kilobase resolution reveals principles of chromatin looping. Cell. 2014;159:1665–1680. doi: 10.1016/j.cell.2014.11.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rhind N, Gilbert DM. DNA replication timing. Cold Spring Harbor perspectives in biology. 2013;5:a010132. doi: 10.1101/cshperspect.a010132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivera-Mulia JC, Buckley Q, Sasaki T, Zimmerman J, Didier RA, Nazor K, Loring JF, Lian Z, Weissman S, Robins AJ, et al. Dynamic changes in replication timing and gene expression during lineage specification of human pluripotent stem cells. Genome research. 2015;25:1091–1103. doi: 10.1101/gr.187989.114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rivera-Mulia JC, Dimond A, Vera D, Trevilla-Garcia C, Sasaki T, Zimmerman J, Dupont C, Gribnau J, Fraser P, Gilbert DM. Allele-specific control of replication timing and genome organization during development. Genome Research. 2018 doi: 10.1101/gr.232561.117. gr–232561. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohlfs RV, Harrigan P, Nielsen R. Modeling gene expression evolution with an extended Ornstein–Uhlenbeck process accounting for within-species variation. Molecular Biology and Evolution. 2013;31:201–211. doi: 10.1093/molbev/mst190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rosenbloom KR, Sloan CA, Malladi VS, Dreszer TR, Learned K, Kirkup VM, Wong MC, Maddren M, Fang R, Heitner SG, et al. ENCODE data in the UCSC Genome Browser: year 5 update. Nucleic Acids Research. 2012;41:D56–D63. doi: 10.1093/nar/gks1172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryba T, Battaglia D, Chang BH, Shirley JW, Buckley Q, Pope BD, Devidas M, Druker BJ, Gilbert DM. Abnormal developmental control of replication-timing domains in pediatric acute lymphoblastic leukemia. Genome Research. 2012;22:1833–1844. doi: 10.1101/gr.138511.112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryba T, Hiratani I, Lu J, Itoh M, Kulik M, Zhang J, Schulz TC, Robins AJ, Dalton S, Gilbert DM. Evolutionarily conserved replication timing profiles predict long-range chromatin interactions and distinguish closely related cell types. Genome Research. 2010;20:761–770. doi: 10.1101/gr.099655.109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryba T, Hiratani I, Sasaki T, Battaglia D, Kulik M, Zhang J, Dalton S, Gilbert DM. Replication timing: a fingerprint for cell identity and pluripotency. PLoS Computational Biology. 2011;7:e1002225. doi: 10.1371/journal.pcbi.1002225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Siepel A, Haussler D. Phylogenetic hidden Markov models. In: Nielsen R, editor. Statistical Methods in Molecular Evolution. New York, USA: Springer; 2005. pp. 325–351. [Google Scholar]
- Solovei I, Thanisch K, Feodorova Y. How to rule the nucleus: divide et impera. Current Opinion in Cell Biology. 2016;40:47–59. doi: 10.1016/j.ceb.2016.02.014. [DOI] [PubMed] [Google Scholar]
- The Chimpanzee Sequencing and Analysis Consortium. Initial sequence of the chimpanzee genome and comparison with the human genome. Nature. 2005;437:69–87. doi: 10.1038/nature04072. [DOI] [PubMed] [Google Scholar]
- Thomas GH, Freckleton RP, Székely T. Comparative analyses of the influence of developmental mode on phenotypic diversification rates in shorebirds. Proceedings of the Royal Society of London B: Biological Sciences. 2006;273:1619–1624. doi: 10.1098/rspb.2006.3488. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thomas GH, Meiri S, Phillimore AB. Body size diversification in Anolis: novel environment and island effects. Evolution. 2009;63:2017–2030. doi: 10.1111/j.1558-5646.2009.00694.x. [DOI] [PubMed] [Google Scholar]
- Villar D, Berthelot C, Aldridge S, Rayner TF, Lukk M, Pignatelli M, Park TJ, Deaville R, Erichsen JT, Jasinska AJ, et al. Enhancer evolution across 20 mammalian species. Cell. 2015;160:554–566. doi: 10.1016/j.cell.2015.01.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vinh NX, Epps J, Bailey J. Information theoretic measures for clusterings comparison: Variants, properties, normalization and correction for chance. Journal of Machine Learning Research. 2010;11:2837–2854. [Google Scholar]
- Viterbi A. Error bounds for convolutional codes and an asymptotically optimum decoding algorithm. IEEE Transactions on Information Theory. 1967;13:260–269. [Google Scholar]
- Yaffe E, Farkash-Amar S, Polten A, Yakhini Z, Tanay A, Simon I. Comparative analysis of DNA replication timing reveals conserved large-scale chromosomal architecture. PLoS Genetics. 2010;6:e1001011. doi: 10.1371/journal.pgen.1001011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yue F, Cheng Y, Breschi A, Vierstra J, Wu W, Ryba T, Sandstrom R, Ma Z, Davis C, Pope BD, et al. A comparative encyclopedia of DNA elements in the mouse genome. Nature. 2014;515:355–364. doi: 10.1038/nature13992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Xing Y, Zhang L, Mei Y, Yamamoto K, Mak TW, You H. Regulation of cell cycle progression by forkhead transcription factor FOXO3 through its binding partner DNA replication factor Cdt1. Proceedings of the National Academy of Sciences. 2012;109:5717–5722. doi: 10.1073/pnas.1203210109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zwiernik P, Uhler C, Richards D. Maximum likelihood estimation for linear Gaussian covariance models. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2017;79:1269–1292. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.