Human Energy Expenditure: Advances in Organ-Tissue Prediction Models

Abstract

Humans expend energy at rest (REE), and this major energy exchange component is now usually estimated using statistical equations that include weight and other predictor variables. While these formulas are useful in evaluating an individual’s or group’s REE, an important gap remains: available statistical models are inadequate for explaining underlying organ- and tissue-specific mechanisms accounting for resting heat production. The lack of such systems level REE prediction models leaves many research questions unanswered. A potential approach that can fill this gap began with investigators who first showed in animals and later in humans that REE reflects the summated heat production rates of individual organs and tissues. Today, using advanced imaging technologies, REE can be accurately estimated from the measured in vivo mass of ten organ-tissue mass components combined with their respective mass-specific metabolic rates. This review examines the next frontier of energy expenditure models and discusses how organ-tissue models have the potential to not only better predict REE, but to provide insights into how perturbations in organ mass lead to structure-function changes across other interacting organ systems. The introductory ideas advanced in this review provide a framework for future human energy expenditure modeling research.

INTRODUCTION

Does high blood pressure in the absence of thyroid disease increase resting energy expenditure (REE) as reported by Mountain and colleagues in 1943 (1)? Do pathologic changes in organ size influence energy balance? At present, there is a lack of integrated physiological models that can answer these questions at a mechanistic level. An inability to answer these questions reveals important gaps in the study of human energy exchange: most current REE prediction formulas are based on statistically-derived equations that aggregate various organs and tissues together as if they are metabolically homogeneous; and such models are devoid of a systems-level mechanistic underpinning.

The lack of mechanistic systems-level REE prediction models is highlighted by the current empirical approach. Body size, characterized in adults mainly by weight and height, is strongly correlated with total daily energy expenditure and REE. One a century ago, total daily energy expenditure and REE were observed to correlate with body size (2), which was characterized mainly by weight and height. Harris and Benedict exploited these associations when they developed their now classic REE prediction equations (3). Measuring REE in a limited sample of individuals using indirect calorimetry, they developed statistically-derived sex-specific prediction equations that included weight, height, and age as model covariates.

Many years later, Keys and Brozek in 1953 extended the Harris-Benedict approach by replacing weight and height in REE prediction models with the “metabolically active” fat-free mass (FFM) compartment (4). Subsequent models that have descended from Keys and Brozek’s approach now predict REE from FFM, fat mass, age, and sex (2, 5), recognizing differences in energy expenditure even among metabolically active tissues. While such empirical models provide a great service to the field, they still fall short of explaining at a mechanistic physiological level why, for example, fat mass is a significant REE predictor variable (6, 7) and encapsulating how separate organs and tissue types that constitute FFM contribute to REE.

The inability of current REE prediction models to answer these types of questions and observations leaves important areas of human energy metabolism and obesity research relatively unexplored. Moreover, they suggest that the next frontier in developing a systems-level model of human energy expenditure is to understand the various contributions of organs and tissues to REE. We call such models that go beyond the standard FFM-fat mass model of energy expenditure organ-tissue and related organ-systems models. In this review we examine the progress, benefits, and challenges to creating organ-tissue and integrated organ-systems physiological models, and we discuss how such models can give insight into unforeseen linkages between body composition and physiologic and molecular mechanisms.

EMERGING MECHANISTIC APPROACHES

Organ-Tissue Model

An evolving set of mechanistic body composition REE prediction models are founded on the assumption that body heat generation can be understood at a physiological level by examining the individual organs and tissues and the way that they are integrated (2, 8, 9). These models trace their origin to Joseph Barcroft and colleagues who were working at Cambridge University’s Physiological Laboratory in the early twentieth century (10). The investigators conducted a classic series of studies systematically quantifying the mass-specific metabolic rates (K_i, rate of energy expended per unit mass) of different organs and tissues labeled i in animal models (11, 12). Multiplying each organ or tissues’ mass-specific metabolic rate by its mass (Ei = K_i × Mi), Barcroft was able to estimate the total energy expended (E_i) for each separate organ and tissue. By 1908, Barcroft reported that “summated tissue respiration” of all evaluated organs and tissues accounted for “82% of resting metabolism in the dog” (11, 13). Others extended these early efforts, and in meticulous experiments, Field and his colleagues working at Stanford University in 1939 reported that the cumulative sum of tissue respirations could account for 89% or more of the basal metabolic rate of albino rats (13). Serving as a proof-of-concept, these animal studies established that the total amount of heat produced at rest is largely accounted for by the sum of heat generated by individual organs and tissues.

Yet, these seminal animal studies remained of modest interest to investigators studying energy expenditure at the whole-body level in humans. Although metabolic rates could be quantified ex vivo, there was no way to measure either tissue mass or metabolic rates in vivo. This changed with the introduction of computerized axial tomography in the mid-1970s (14). This transformational imaging method, and magnetic resonance imaging (MRI) that followed a decade later, now enables investigators to non-invasively quantify the volume and mass of most major organs and tissues in healthy adults (14). With the reasonable assumption that K_i is approximately constant across adults of a given species, these imaging techniques enabled energy expenditure from various organs and tissues to be estimated non-invasively as E_i = K_i × M_i across individuals for the first-time (14).

Another imaging method that was introduced during the 1980s, ¹⁵³Gd-based dual-photon absorptiometry, offered a practical and safe means by which to measure bone mass across the lifespan (14). Although relatively less metabolically active than brain and visceral organs, quantifying bone mass is important as it accounts for a large fraction of residual (unmeasured) body mass and is a major component of the musculoskeletal system. Switched kVp or k-edge-filtered X-ray sources later replaced the radioactive isotope ¹⁵³Gd in modern dual-energy x-ray absorptiometry (DXA) systems (14). Magnetic resonance imaging, which has largely replaced computed axial tomography in the study of body composition in healthy subjects, does not quantify whole-body bone mass, and hence DXA remains important for estimating energy expenditure from body composition.

The next step in moving from in vivo animal studies of organ-tissue contributions to resting heat production was the critical 1992 review by Elia in which K_i values were proposed for human liver, brain, heart, kidneys, muscle, adipose tissue (AT), and residual mass (15). The growing recognition of organ contributions to resting heat production led Nelson et al. in 1992 (16) and Sparti et al. in 1997 (17) to put forth explanations for how REE and FFM relate to each other. Then Gallagher et al. in 1998 (8), and several years later, Illner et al. in 2000 (9), used Elia’s proposed mass-specific metabolic rates to achieve proof-of-concept in humans by showing close associations (meanΔ, 1-2%) between summated organ and tissue mass heat production rates and REE in healthy adults. The Gallagher-Illner approach involved quantifying the volumes of major organs and tissues with whole-body MRI and then assuming each of the measured components has a known and stable density. Mass was then calculated as the product of organ or tissue volume and the component’s density. Gallagher et al. (8) measured left ventricular (LV) mass with echocardiography, while Illner et al. (9) derived heart mass using a gated-MRI technique. The sum of six organ-tissue heat productions (i.e., brain, heart, liver, kidneys, skeletal muscle, and AT) and an unmeasured residual mass component was then used to derive a value for REE (8), (9).

The model has since been refined with addition of three model components: spleen, bone, and skin (18–21). This ten-component organ-tissue model requires MRI, DXA, and at some centers, echocardiographic measurements (8, 9, 22). The features of this model are summarized in Supporting Information I.

Advantages

The organ-tissue model has several benefits over current statistical prediction models. First, the organ-tissue model better predicts energy expenditure. To demonstrate this, we recently assembled a sample of 310 healthy adults from two research centers that had all of the required data to develop the ten-component organ-tissue model. The sample characteristics are summarized in Supporting Information II.

First, we found that our model’s REE predictions (X±SD; 1644±276 kcal/d) are highly correlated with REE as measured by indirect calorimetry (1613±294 kcal/d; R², 0.85; p<0.001) and a Bland-Altman plot indicates non-significant model bias (R², 0.004; p=0.3) (Supporting Information III). By comparison, R² values for the commonly used Harris-Benedict (3) and Mifflin St. Jeor (23) REE prediction models were 0.81 and 0.80 (both p<0.001), respectively.

Second, the organ-tissue models are useful in estimating a subject’s or group’s individual organ and tissue rates of heat production and their combined contributions to REE at baseline and over time with aging and interventions (24, 25). Estimated values for REE can be compared to those of reference populations as a means of deriving relative metabolic rates and determining whole-body as well as organ- and tissue-specific hypo- or hypermetabolism (2).

Third, by quantifying the organ- and tissue-specific contributions to E_R, such models also enable correlations to be made between individual and groups of organs and tissues and the cellular, neural, and hormonal modifiers of heat production and metabolic processes (26). In turn, we expect future observations to drive discoveries into the underlying molecular and physiologic modulators of energy expenditure.

Fourth, the reviewed organ-tissue models not only provide new options for developing physiological structure-function relationships, they underscore the need to further explore and understand classical statistical approaches for estimating resting heat production rates. As an example, most empirical REE prediction equations, such as those reported by Harris and Benedict, include three main covariates: weight, height, and age (3, 5). Using first-principles for guidance, it is assumed that body weight reflects the weights of all organs and tissues and that REE represents the sum of their respective heat production rates. Prediction equations can thus be derived for the mass of each organ and tissue, take the product of that result and respective K_i value, and then sum the individual organ heat production rates to derive a value for REE. In addition to body weight, our organ-tissue mass prediction equations are improved with height and age as potential covariates that further define body shape and organ proportions. The calculated REE values should theoretically approximate those derived by the Harris-Benedict equation and as measured by indirect calorimetry.

This hypothesis was tested in women by first deriving the ten organ mass/heat production prediction models using data from our demonstration sample and then testing it in an archived sample of 50 women who participated in previously reported studies (2, 27). No significant difference was observed between REE calculated by the Harris-Benedict equation (1385±230 kcal/d) and our organ-based derived value (1382±236 kcal/d) with a high correlation between the two REE estimates (R², 0.89 p<0.001). Both our calculated REE value and that by the Harris-Benedict equation closely approximate mean REE measured by indirect calorimetry (1359±251 kcal/d; both R²’s vs. measured REE, 0.57, p<0.001). Three components according to this model account for almost two-thirds of the group mean resting heat production rate: brain (24.3%), skeletal muscle (18.4%), and liver (19.9%); adipose tissue accounts for only a small percentage of REE (7.7%). These percentages are similar to those reported by Elia (15). Here, for the first time, we see an underlying quantitative physiological basis for one type of statistical REE prediction formula. The Harris-Benedict and related statistical REE prediction models can thus be envisioned as capturing the body’s collective organ and tissue mass heat production rates.

Another representative example relates to the “low” REE observed in African American adults that often is mistakenly used to explain this race group’s high risk for developing obesity (28). The “hypometabolism” observed in African Americans is largely an artifact caused when adjusting REE for weight or assumed metabolically homogeneous FFM: across-race group differences are present in the proportion of FFM as high and low-metabolic rate organs and tissues (29–31). These race differences in FFM organ-tissue proportions can account for the lower relative REE observed in people who are African American. This example illustrates an important potential limitation of statistical equations: a prediction formula developed on one group may not accurately predict REE when applied to another race/ethnic group.

Limitations

Despite the useful properties of current organ-tissue models, there remain important areas of potential improvement. One widely recognized limitation of current organ-tissue models is reliance on estimated K_i values that are usually assumed “constant” across all adult subjects and race/ethnic groups (8, 9). Organ mass-specific metabolic rates likely vary with age, during periods of weight gain and loss, in some chronic illnesses, and during pregnancy (19, 20, 24, 25). An important advance would be the introduction of new widely applicable methods for quantifying K_i values in vivo. While estimates of energy expenditure and total volume can be obtained using positron-emission tomography combined with computed tomography for organs such as brain (32), cost and radiation exposure are barriers to the practical use of this and related technologies as a means of deriving K_i values.

Another limitation of the organ-tissue model is that it cannot be reliably used to predict the effects on REE with hypothetical interventions or physiological changes that lead to alterations in the mass of organs or tissues. The organ-tissue model now functions largely as a static predictor of REE. without consideration for between-organ interactions. As an example, the question is posed: what happens to REE if total body AT mass increases with an intervention? In theory the change in REE could be calculated as ΔAT mass × K_i (i.e., 4.5 kcal/kg/d). The predicted result would, however, be incorrect based on the study of Nielsen et al. (33) who derived a K_i value of ~8 kcal/kg/d for fat mass (i.e., an equivalent molecular level measure of AT) using a statistical model in a sample of healthy adults. The current organ-tissue model is unable to provide an explanation for the kinds of observations made by Nielsen et al. (33), thus prompting the need for a working integrated organ systems model that reveals how a change in AT mass leads to corresponding changes in the mass of other interacting organs and tissues.

Organ-Systems Model

The organ systems model introduced in this review includes the ten classic organ systems and AT as a separate component (Figure 1). Adipose tissue is usually not included in organ system descriptions or is included in the integumentary system. The systems model includes the major components of energy exchange between the heat-generating subject and the external environment.

Figure 1.

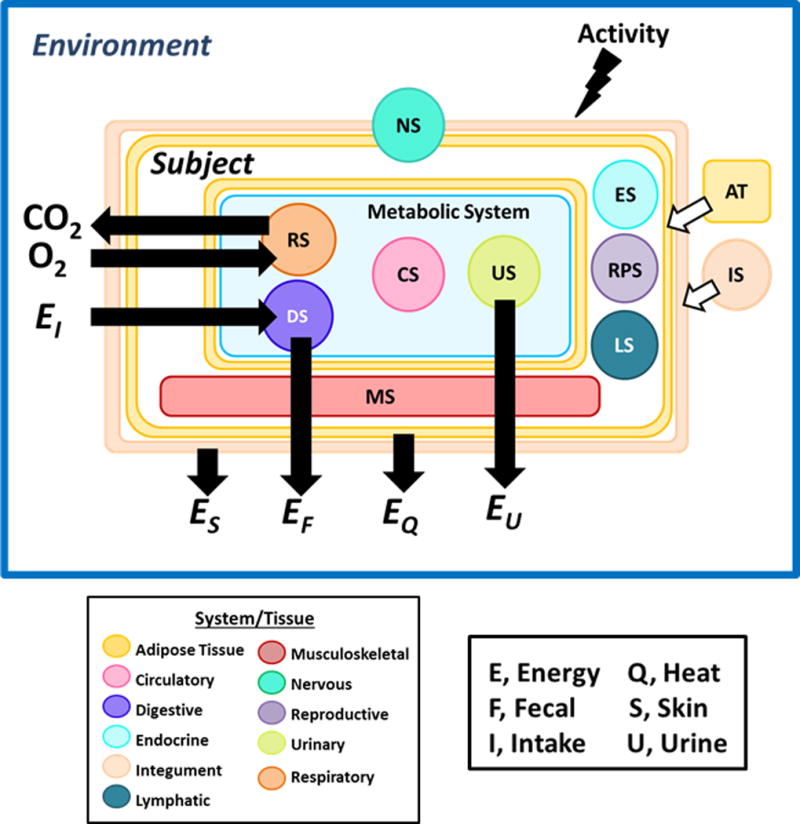
Organ tissue-based model of energy exchange. Four of the systems—digestive (DS), circulatory (CS), respiratory (RS), and urinary (US)—are within the visceral compartment and are directly involved in exchange of energy between the subject and environment. Adipose tissue (AT) is shown distributed in the subcutaneous compartment in association with the integumentary system (IS) and surrounding the visceral compartment organs. Heat (E_Q) is exchanged with the environment via conduction, convection, radiation, and evaporation. Urinary energy losses (E_U) are mainly as urea, the end-product of protein oxidation. Energy losses also arise from the skin (E_S) and in feces (E_F). Other systems include nervous (NS), musculoskeletal (MS), endocrine (ES), reproductive (RPS), lymphatic (LS), and integumentary. E_I is energy intake.

A feature of this illustration is the addition of activity levels as one driver of energy expenditure and thus energy throughput across the system. While the classic approach to examining body composition-energy expenditure relationships focuses on REE, the forces shaping the size and function of organ systems are integrated over 24 hours or even months and years. Although it is assumed that REE reflects these longer-term energetic processes (26), we explicitly recognize this factor as part of our model illustration.

We organize the organ tissue-energy exchange model according to systems with functions that are shared in common. Four systems—digestive, circulatory, respiratory, and urinary—are physically located primarily within the visceral compartment and together function as the main energy-processing portion of body mass. That is, these four systems are involved in dietary energy and oxygen uptake and distribution, metabolically useful energy production, and release of metabolic end products to the environment (Supporting Information IV). Three of the measured organs are included in this “metabolic” portion of body mass: liver, kidneys, and heart; they are representative of the digestive, urinary, and circulatory systems, respectively. The masses of these three organs are summed as an initial attempt to demonstrate how the collective “metabolic” system interacts with the other body systems, but the three organs remain separate in the organ-tissue mathematical REE prediction models. The mass of the major respiratory system components, notably lung mass, remain impractical at present to quantify using conventional imaging approaches in healthy adults (34).

A feature of the metabolic system is that a change in the mass of any one of the four main component systems will impact on the other three systems. As an example, increasing food intake from one level to a higher stable level will lead to activation of cardiovascular, respiratory, and urinary systems that respond to the greater metabolic and mechanical load imposed by nutrient ingestion, metabolism, and excretion of end-products.

The nervous system, mainly brain and spinal cord, serves to coordinate and integrate a wide range of body activities. Measured brain mass is used to represent the nervous system in the model. Spinal cord is less than 2% of the combined central nervous system weight with brain mass (35). Throughout the remainder of our review, the term brain mass serves as a term synonymous with the nervous system. Widely used Reference Human tables do not include a total nervous system mass (35).

Movement and support are provided by the musculoskeletal system, while AT serves as the main energy storage reservoir. Our introductory organ system model includes measured musculoskeletal (skeletal muscle plus bone) and total AT mass. Adipose-tissue free mass (ATFM) in our simplified model includes nervous, musculoskeletal, and metabolic systems and for discussion purposes is similar to the metabolically active molecular level component FFM that is incorporated into some statistical REE prediction formulas (2, 5, 33). Likewise, AT mass is similar but not identical to fat mass; the former is a “tissue” while the latter is a “chemical”, mainly in the form of triglycerides. Adipose tissue cells generate energy while fats do not, hence we cautiously use these two in their appropriate context throughout this report.

These four respective groupings—involved in metabolism, coordination, movement, and energy storage—collectively account for a large fraction of body mass (~70%) and heat production (~80%; Supporting Information II). We therefore focus the ensuing discussion on these four system model components in healthy adults.

Features

Nervous System

The four system components grow from birth onward at different rates, a finding that has important implications in understanding the structure of adult body composition. The nervous system, as represented by brain, reaches 90% of adult mass by the age of six years and 98% by ten years of age. This observation is supported by the cross-sectional autopsy study of Dekaban reported in 1978 (36) that is shown as a Scammon-type plot for males in Figure 2; similar growth patterns are observed for females (37). Scammon compared organ and system growth rates by expressing absolute mass values observed during childhood and adolescence as a percentage of adult values at the time of growth cessation. Once brain growth is complete, the organ remains relatively stable in mass throughout life, with small decrements in old age (36). Brain mass is either not or is weakly associated with body size, as measured by weight or height among healthy adults (38, 39) and similarly has limited correlations (R’s, 0.02-0.31, all p>0.05) with the mass of other systems and ATFM, as shown in Supporting Information V for our demonstration sample. Importantly, between-individual variability in adult brain mass is remarkably small, with a coefficient of variation (CV) in our demonstration sample of 7.1% and 7.8% in men and women, respectively. By comparison, the CVs for musculoskeletal and metabolic system components are more than double that of brain (e.g., musculoskeletal mass, 15.6%, 16.8%; kidneys, 18.5%, 24.8%; and liver, 19.8%, 20.1%). The adult human brain has a relatively small mass (~1.5 kg) but large mass-specific metabolic rate (240 kcal/kg/d; 15) that accounts for 22% of REE in our demonstration sample.

Figure 2.

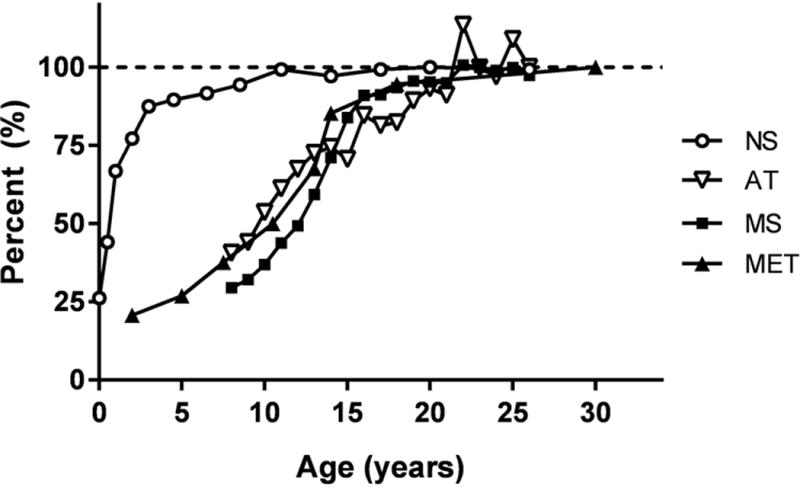
Plot of data from Scammon (37) showing percentage of adult male nervous, musculoskeletal, and metabolic system, and adipose tissue mass (NS, MS, MET, AT) achieved as a function of age. NS, represented by brain mass (36); MS, by appendicular lean soft tissue and bone mineral mass (30); MET, by LV mass (49); and AT by fat mass (30). A horizontal dashed line is placed at 100% growth. Details of the samples and measurement methods used to create the plots are provided in Supplementary Material VI. Qualitatively similar growth patterns are observed in females.

Musculoskeletal System

In contrast to the nervous system, the musculoskeletal system follows a growth trajectory that reaches adult levels towards the end of the second decade, as shown in Figure 2 using related DXA-derived measures in male National Health and Nutrition Examination Survey (NHANES) participants (Supporting Information VI). A similar growth trajectory is observed for the female NHANES participants.

The growth velocities of bone and attached skeletal muscle are determined by genetic, epigenetic, and nutritional factors (40, 41). These variable magnitude effects are important determinants of adult musculoskeletal system mass, shape, and dimensions, translating into much higher CVs for this tissue component than for brain mass. For instance, inadequate nutrition early in life can lead to stunting, with resulting short stature in adults and altered skeletal proportions (40). Similarly, excess adiposity in children leads to rapid growth with early closure of the epiphyseal growth plates (42). The potential impact on the adult phenotype is short stature and hyperplastic cellularity of adipose tissue (42). Developmental “plasticity” is a feature of organisms ranging from insects to vertebrates that involve nutrient sensing pathways and hormonal mechanisms (e.g., insulin-like growth factor) during critical growth periods (43).

Once adulthood is reached, the maximum linear dimension of the skeleton, represented by height, is relatively stable until stature declines following bone mineral loss later in life (44). By contrast, skeletal muscle and bone mass and their structure are modifiable following linear growth cessation with variation in “loading” conditions (45). Space flight and bed rest with reduced mechanical loading conditions lead to rapid loss of musculoskeletal mass (46, 47), while the opposite follows a strength-training program (48). As shown in the following section, “adaptability” is a fundamental characteristic of musculoskeletal and metabolic system components and a key mechanism by which they functionally integrate within their own and across other systems.

Both bone and resting skeletal muscle have low K_i values, 2.3 and 13 kcal/kg/d, respectively. Large in combined mass, the musculoskeletal system accounts for 29.9 kg or 21% of REE in our demonstration sample, about the same as much smaller brain mass (~1.5 kg).

Metabolic System

Heart mass, a representative organ of the metabolic system, follows a similar growth plane as the musculoskeletal system, according to data for LV mass in males acquired by echocardiography (Figure 2) (49).

Like the musculoskeletal system, the metabolic system components change in size, shape, and function to adapt to mechanical and metabolic demands. These variable loading conditions include, for example, changes in tissue oxygen consumption, intravascular fluid volumes, heart rate, arterial blood pressure, and glomerular filtration rate. This is important because such changes—including pathological ones—in tissue mass or function may impact energy expenditure, and we don’t fully understand all of the implications yet. There are many examples of these kinds of adaptations, perhaps the best studied of which is for the heart. Increasing LV afterload and/or preload through increasing arterial blood pressure and blood volume leads to enlargement of LV mass and distinct changes in LV wall thickness and chamber dimensions (50). Similarly, corresponding adaptive reductions in LV mass follow the hemodynamic effects of blood pressure lowering (51), voluntary weight loss (52), and detraining in athletes (53). A combination of variable loading conditions and neuro-hormonal effects mediate these adaptive changes (54).

Adipose Tissue

The energy storage component grows parallel to the musculoskeletal system (Figure 2); although, as expected, the amounts of AT present during adult life are highly variable. In our demonstration sample, the CV for AT is six times that for brain: 39.3% and 47.1% for men and women, respectively. Adipose tissue in our demonstration sample has a large mass (29 kg) but a low K_i (4.5 kcal/kg/d) and thereby accounts for only 5% of E_R.

Relatively small amounts of inducible high metabolic rate beige and brown adipocytes are present in adults (55) and as of yet are not included in organ-tissue REE prediction models. The K_i value for adipose tissue as currently evaluated (8, 9) may thus not be constant under some measurement conditions.

Integration

Our review of these four main systems provides a foundation for developing initial concepts related to an integrated organ-system model. To begin this process, several key observations emerge from our exploration of system features. First, the nervous system as represented by the brain is distinct, as it reaches full growth early in life and then remains largely stable in mass across the rest of the lifespan. Brain mass has limited associations with body size and the three other organ-tissue systems.

By contrast, the musculoskeletal and metabolic systems grow in tandem, reaching adult levels by the end of the second decade, with skeletal muscle and bone growth being sensitive to prevailing nutritional conditions. Both systems share in common “adaptive” properties with their components, capable of increasing or decreasing in mass with changes in mechanical or metabolic loading conditions. Both systems are strongly inter-correlated in our demonstration sample (R, 0.64 in men and 0.76 in women; both p<0.001) (Supporting Information V).

The energy storage compartment, AT, can increase or decrease in size with long-term trends in energy balance. Significant inter-correlations (R range, 0.42-069; both p<0.001) were present between AT mass and musculoskeletal and metabolic systems in our demonstration sample (Supporting Information V).

From the foregoing discussion, we observe that organs and tissues respond to imposed mechanical and metabolic loads with changes in structure and function. Beginning in 1981, Taylor and Weibel (56) advanced a theory referred to as “symmorphosis” that attempts to synthesize these types of observations into testable hypotheses. According to Taylor and Weibel, physiologic systems are “economically” designed and accommodate maximal metabolic and mechanical demands without energetic inefficiencies brought about by carrying “excess” structure (56, 57). Three useful concepts emerge from this viewpoint: (1) organs are structurally and functionally adaptable to loading conditions; (2) these responses are integrated within and across systems; and (3) these effects are optimized to maximize energetic efficiency.

While Taylor and Weibel’s symmorphosis hypothesis has stimulated considerable debate within the anthropology and evolutionary biology academic communities (58), the embodied ideas serve as a bridge from the static organ-tissue REE model to the more mechanistic and functionally-based organ systems model. Concepts surrounding structure, function, adaptability, optimization, and within- and across-system interrelationships are at the core of the organ systems model. Symmorphosis provides us a heuristic framework within which to examine questions such as why and how certain organs and tissues acquire a particular size and the extent to which they adhere to established rules related to biomechanics (45), hemodynamics (59), and other physiological processes. How the organs and their related systems grow in “harmony” during childhood and reach a stable mass and functional level in adulthood is one of the great research challenges of developmental biology (60, 61). This harmonization may explain why statistical REE formulas are so useful in healthy adults: the mass and functions of organs and tissues form highly stable interrelations across people differing in size and shape, thus allowing their prediction from simple equations that include weight, height, and age.

Another closely related concept advanced by Wells (62) contrasts “metabolic capacity” with “metabolic load” in the development of modern chronic diseases such as type 2 diabetes. According to Wells, maintenance of processes such as glucose homeostasis reflect metabolic capacity as represented by body compartments such as skeletal muscle mass. Demands on these processes are created by metabolic loading conditions, as for example by AT mass. Modern humans, according to Wells, have experienced a shift in the capacity-load balance (e.g., ↓ skeletal muscle/↑ AT mass) leading to susceptibility to chronic diseases such as type 2 diabetes.

Operation

With these concepts in place, the working parts of the physiological organ systems model are assembled by first allocating the nervous system to its own position with limited variation in size under most conditions (63). The nervous system places a large metabolic load on non-neural systems that are needed to generate glucose at a high rate of about 80.6 g/kg tissue/d (64) or about 130 g/d in order to sustain brain’s energy demands (15). Since the average size adult requires about 200 g/d of glucose, the brain’s high energy demands consume about 2/3 of that total, even during periods of energy deprivation when priority is given to the “pull” of central nervous system tissues (63).

Next, we consider the adult musculoskeletal system, which creates the fixed-in-size “frame” that accommodates the other body systems. The metabolic system components must adapt to this frame and the metabolic demands of its two main components, skeletal muscle and bone. This concept is intuitive: a short person with a small musculoskeletal system must have metabolic system components that are less energy-intensive to maintain compared to the higher metabolic demands experienced by their taller counterparts. While genetic mechanisms are important in determining frame size, environmental factors also contribute to peak adult height through developmental plasticity effects. Metabolic system components thus must be capable of adjusting their size and functional capacity related to the vagaries of musculoskeletal growth.

Lastly, variation in AT mass will impose vacillating mechanical loads on the musculoskeletal system and metabolic loads on metabolic system organs. Examples of these system mechanical and metabolic interrelations are shown in Figure 3.

Figure 3.

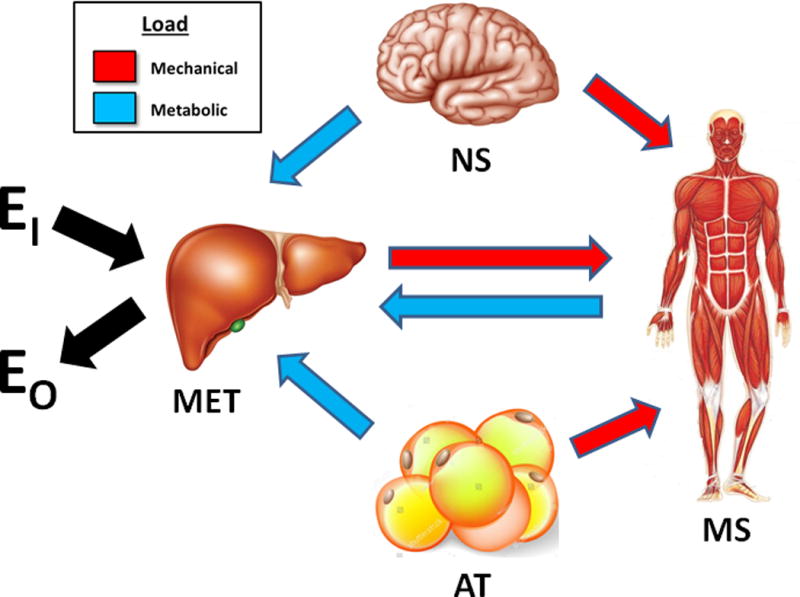
Mechanical and metabolic interrelations among the three major adult organ systems and adipose tissue. Liver is shown representative of the four metabolic system components. Metabolic loading conditions include, for example, tissue oxygen consumption, intravascular fluid volume, and arterial blood pressure effects. Although small in magnitude, brain contributes to the mechanical load on the musculoskeletal system. Abbreviations: E_I, energy intake; AT, adipose tissue; E_O, energy output or expenditure; MET, metabolic system; MS, musculoskeletal systems; and NS, nervous system.

Demonstrations

In this section we show in several examples how moving from statistical and static organ-tissue models to a systems approach can provide new and useful physiological insights.

Change in Adiposity

A descriptive example of how this model can operate is when a hypothetical person moves from a stable baseline level of adiposity to a higher level following a period of prolonged positive energy balance. Here, the pathways by which energy balance becomes positive will be ignored, although those considerations could also influence K_i values (24, 25) and body composition effects. The expanded AT compartment will increase loading conditions on the metabolic and musculoskeletal systems, as shown by the pathways in Figure 3. These combined responses to an expansion of the AT compartment will then lead to a greater level of resting heat production. The sources of the new level of REE thus go beyond that of AT mass alone; rather, both musculoskeletal and metabolic system components must adapt to the augmented mechanical and metabolic loading conditions (e.g., by increasing gluconeogenesis when basal insulin resistance is present (65)).

These integrated body composition effects can be observed in the demonstration sample. Twenty young adult women (age <30 years; Supporting Information VII) were matched on height (±3 cm) in the lowest and highest quartile for AT mass (18.4±3.8 kg vs. 54.1±9.3 kg). Their measured and organ-calculated group mean REE values (1440±117 kcal/d and 1404±103 kcal/d vs. 1785±160 kcal/d and 1773±232 kcal/d) displayed similar magnitude between-group differences of ~350 kcal/d. Brain mass was almost identical between the two groups (1.43±0.11 kg vs. 1.44±kg, p, non-significant), while the metabolic system organs were significantly larger in the high AT group (liver, 1.45±0.15 kg vs. 1.76±0.37 kg, p=0.007; kidney, 0.26±0.03 kg vs. 0.32±0.06 kg, p=0.017; heart, 0.24±0.07 kg vs. 0.37±0.11 kg, p=0.008), as was musculoskeletal mass (25.9±3.4 kg vs. 30.3±4.3 kg, p<0.002). Had the K_i value in this example been derived as ΔE_R (345 kcal/d)/ΔAT mass (37.5 kg), the results would have been a value of 9.7 kcal/kg/d, similar to that reported for fat mass by Nielsen et al. (~8 kcal/kg/d, (33) and not the value established through in vivo and in vitro measurements of ~4.5 kcal/kg/d (15, 33). The high AT K_i values appearing in statistical equations (i.e., slope of fat or AT mass regression model term) arises because energy expended by associated lean tissues are lumped in with that of AT.

These cross-sectional body composition changes are directionally similar to those reported in our longitudinal weight loss study of women with overweight and obesity (24). With a weight loss of 9.5 kg, the women had significant reductions (all p<0.05; 3.1-6.1%) in their skeletal muscle, heart, liver, and kidney mass, changes in brain mass were non-significant, and there was a small significant increase in bone mass (1.3%). Weight gain (6.5 kg over 23.5 to 43.5 months) in a related non-interventional longitudinal study of men and women (BMI range, 20.2-46.8 kg/m²) was accompanied by significant increases (all p<0.05; 3.9-8.3%) in skeletal muscle, liver, and kidney mass, no changes in heart mass and brain mass, and a small significant decrease in bone mass (1.0%) (25). These examples show the integrated effects of AT mass changes over time and provide a mechanistic basis for the observed changes in resting heat production.

To fully develop and test dynamic organ-specific models across a range of adiposities will require samples experiencing a wide range of weight changes. As noted, an as-yet unsolved measurement problem is capturing any changes in individual organ K_i values that reflect metabolic adaptations during periods of energy imbalance. An earlier voluntary weight loss study from our group in women who were overweight and obese reported a −3.2% “adaptive thermogenesis” relative to baseline REE following a 10% reduction in body weight (24). Adaptive thermogenesis was considered as the difference between measured and organ-calculated REE. Does adaptive thermogenesis as shown in this study reflect global changes across all organs in K_i values as would occur secondary to the actions of thyroid hormone (24, 25), or does it reflect metabolic effects in selected individual organs? This question remains to be answered.

Change in Blood Pressure

A second example explores the question posed at the beginning of our review: does high blood pressure in the absence of other pathological conditions increase E_R? High blood pressure increases cardiac afterload, to which the LV myocardium adapts by increasing in mass and changing in shape (50). Assume a normotensive adult has a LV mass of 150 g and that their mean blood pressure rises over time from 90 mm Hg to 110 mm Hg. The increase in afterload would cause a LV mass increase of about 50 g, from 150 g in the normotensive state to 200 g in the hypertensive state (66). Assuming kidney function and mass remain unchanged in the presence of high blood pressure (67), REE would increase by ΔLV mass × K_i for heart (440 kcal/kg/d) or 22 kcal/d. While extremely small in magnitude, the adaptive increase in cardiac mass and rise in myocardial oxygen consumption would theoretically lead to minute but finite respective mechanical and metabolic loads on the musculoskeletal and metabolic systems that would then respond by increasing in size accordingly. Unless these increases in energy expenditure were accompanied by an increase in energy intake or a reduction in activity levels, a state of negative energy balance would ensue with reductions in AT mass and the accompanying mechanical and metabolic effects on other systems.

Moving from a Statistical to Mechanistic Systems Model

Replacing weight and height in sex-specific empirical models with ATFM (or related FFM) is a widely used approach for assessing REE in clinical trials (2, 5). If ATFM is the main homogeneous source of body heat production, why is the REE versus ATFM regression line intercept significantly larger than zero, even after controlling for AT mass and other potential covariates (2)? This observation, one extensively discussed in the scientific literature (2), implies that REE/ATFM is not constant across people differing in size. Most investigators now avoid using the REE/ATFM ratio when comparing relative rates of REE between individuals and groups who differ in body size. Rather, alternative statistical means are used to adjust REE for body mass and composition when using ATFM as a predictor variable (2).

The proposed organ system model provides insights into this family of REE prediction models. First, ATFM is not a metabolically homogeneous compartment, but rather includes three systems differing in mass specific metabolic rates: nervous, musculoskeletal, and metabolic. The nervous system, mainly as brain, is largely independent of body size and it serves as a relatively stable source of absolute heat production across persons within the same sex and age group. Second, AT has a small heat production rate at rest and acts through the pathways examined earlier to impose metabolic and mechanical loads on musculoskeletal and metabolic system components. Adipose tissue therefore contributes to REE through these effects on musculoskeletal and metabolic component mass. Prediction equations for REE (kcal/d) that includes ATFM alone or ATFM and AT display large non-zero intercepts with AT as a significant covariate, as shown in demonstration sample of women (mass units all kg):

$$466+\left(22.5\times \text{ATFM}\right)\left[{\mathrm{R}}^2,0.45,\text{p<0}.001\right]$$ (1)

and

$$528+\left(14.6\times \text{ATFM}\right)+\left(9.1\times \text{ATmass}\right)\left[{\mathrm{R}}^2,0.74,\text{p<0}.001\right[$$ (2)

As predicted, and as previously reported by others (5, 33), these regression models have a large non-zero intercept (X±SE; 466±85 and 528±59 kcal/d) and the slope of the AT mass term is 9.1 kcal/kg/d, similar to that reported by Nielsen et al. for fat mass (~8 kcal/kg/d) (33) but larger than the mass specific metabolic rate of adipose tissue of ~4.5 kcal/kg/d (15).

When ATFM is replaced in the REE regression model with the mass of the three main constituent system components (nervous, musculoskeletal, and metabolic), the intercept is non-significantly different from zero (114±111 kcal/d, p=0.3) and the slope of the AT mass term (5.2 kcal/kg/d) is similar to the adipose tissue K_i value reported earlier (~4.5 kcal/kg/d) based on in vivo and in vitro studies (15, 33):

$$114+\left(227.2\times \text{NS}\right)+\left(17.2\times \text{MS}\right)+\left(205.4\times \text{MET}\right)+\left(5.2\times \text{AT}\right)\left[{\mathrm{R}}^2,0.81,p<0.001\right[$$ (3)

These observations are supported by the findings of Javed et al. (68) who developed a model similar to the one in equation 2 with addition of high metabolic rate trunk organ mass (sum of heart, liver, kidneys, and spleen mass) and brain mass. The intercept of their model, 69.1 kcal/d, was non-significantly different from zero and the fat mass covariate had a slope of 3.8 kcal/kg/d.

Here, again, use of the traditional empirical REE prediction models can obscure structure-function relations that have the potential to enlighten us on underlying sources of heat production and their interrelations. Moreover, by moving towards mechanistic models it is possible to deepen our understanding of REE differences across sex, race, and age groups even after controlling for ATFM and AT.

CONCLUSIONS

This review exposes an important gap in the study of human obesity: there are no current mechanistic body composition models that link REE with the functionally interrelated sources of heat production at the organ-tissue level. Examples are presented how an organ systems model can be used to gain physiological insights beyond those already provided by empirical REE prediction formulas. These examples expose gaps in current measurement capabilities, notably an inability to quantify K_i values in vivo and to produce a model that can accommodate dynamic changes in organ and tissue size and function. Another gap is that many investigators lack access to the imaging facilities needed to construct organ system REE models. Recent advances in automated whole-body MRI scan analysis promises to remove the important roadblock of long image analysis times by skilled technicians (69).

An important future need is to move the simple suggested physiological REE prediction model to a quantitative operational level, a task that will require focused extensive literature reviews and carefully designed cross-sectional and longitudinal experimental studies. The discussion of organ system models uncovers important aspects of people selected to serve in a Reference Human sample, such as type and amount of daily activities, diet composition, blood pressure, level of adiposity, and many other potentially subtle subject characteristics that likely influence body composition and energy exchange that have yet to be fully recognized (35, 70). 1,

As with other physiological models—such as those for the musculoskeletal system (45), heart (59), and blood pressure (71)—long time periods may be needed for initial development and then further refinement based on emerging new research. Mechanistic organ system models can also be connected to a vast array of hormonal, neural, and other physiological pathways (26). Mechanistic models also can and do play an important role in education, enlightening health care workers on the underlying sources of observed clinical body composition and metabolic phenomena and their responses to interventions. Future research need not be limited to humans as animal experiments may not only be more affordable, but body composition data can be acquired by organ weighing and direct chemical analysis of tissues. A next step is to move the reviewed qualitative descriptions towards an operational mathematically-rigorous quantitative dynamic organ-system REE model.

Abbreviations

AT

adipose tissue

ATFM

adipose-tissue free mass

CV

coefficient of variation

DXA

dual-energy x-ray absorptiometry

FFM

fat-free mass

Ki

mass-specific metabolic rate for each organ and tissue labeled i

LV

left ventricular

MET

metabolic system

Mi

mass of individual organ labeled i

MS

musculoskeletal system

NS

nervous system

REE

resting energy expenditure