User's guide to correlation coefficients

Abstract

When writing a manuscript, we often use words such as perfect, strong, good or weak to name the strength of the relationship between variables. However, it is unclear where a good relationship turns into a strong one. The same strength of r is named differently by several researchers. Therefore, there is an absolute necessity to explicitly report the strength and direction of r while reporting correlation coefficients in manuscripts. This article aims to familiarize medical readers with several different correlation coefficients reported in medical manuscripts, clarify confounding aspects and summarize the naming practices for the strength of correlation coefficients.

1. Introduction

Medical research is naturally based on finding the relationship between the known and the unknown.¹ Clinicians gather information via history, physical examination, laboratory tests and imaging; then, they use this information to infer clinical diagnosis, outcomes and treatment choices. Therefore, an endless struggle to link what is already known to what needs to be known goes on. We try to infer the mortality risk of a myocardial infarction patient from the level of troponin or cardiac scores so that we can select the appropriate treatment among options with various risks. We are trying to calculate the risk of mortality from the level of troponin or TIMI score. The most basic form of mathematically connecting the dots between the known and unknown forms the foundations of the correlational analysis.

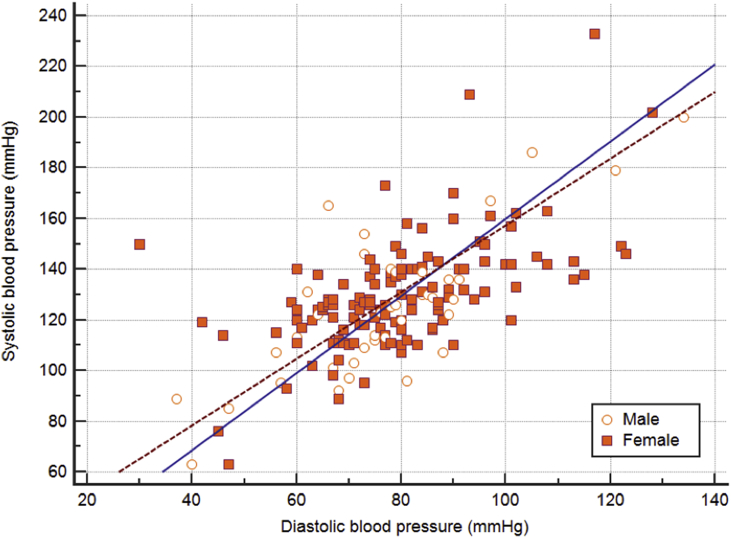
Correlation is defined as a relation existing between phenomena or things or between mathematical or statistical variables which tend to vary, be associated, or occur together in a way not expected by chance alone by the Merriam-Webster dictionary.² A classic example would be the apparent and high correlation between the systolic (SBP) and diastolic blood pressures (DBP). The correlation between two variables (eg., systolic and diastolic pressures) is called a bivariate correlation and can be shown on a scatterplot diagram if both are continuous (scale) variables (Fig. 1). It is clear from the figure that SBP and DBP increase and decrease together, therefore, they are highly correlated. If we want to remove the effect of a third variable from the correlation between two variables, then we have to calculate a Partial correlation. It is a form of correlation which quantifies the relationship between two variables while controlling the effect of one or more additional variables (eg., age, sex, treatment received, etc.). In the figure male and female subjects are colored separately to examine if sex affects the correlation between SBP and DBP, or not.

Fig. 1.

Scatterplot of systolic and diastolic blood pressures of a study group according to sex.

The most important fact is that correlation does not imply causation. As the ice-cream sales increase, the rate of deaths from drownings, and the frequency of forest fires increase as well. These facts happen at the same period, doesn't cause one another.³

The relationship (or the correlation) between the two variables is denoted by the letter r and quantified with a number, which varies between −1 and +1. Zero means there is no correlation, where 1 means a complete or perfect correlation. The sign of the r shows the direction of the correlation. A negative r means that the variables are inversely related. The strength of the correlation increases both from 0 to +1, and 0 to −1.

When writing a manuscript, we often use words such as perfect, strong, good or weak to name the strength of the relationship between variables. However, it is unclear where a good relationship turns into a strong one. The same strength of r is named differently by several researchers. Therefore, there is an absolute necessity to explicitly report the strength and direction of r while reporting correlation coefficients in manuscripts.

This article aims to familiarize medical readers with several different correlation coefficients reported in medical manuscripts, clarify confounding aspects and summarize the naming practices for the strength of correlation coefficients.

2. How to name the strength of the relationship for different coefficients?

2.1. Bivariate correlation coefficients: Pearson's r, Spearman's rho (r_s) and Kendall's Tau (τ)

Those tests use the data from the two variables and test if there is a linear relationship between them or not. Therefore, the first step is to check the relationship by a scatterplot for linearity. Pearson's r is calculated by a parametric test which needs normally distributed continuous variables, and is the most commonly reported correlation coefficient. For non-normal distributions (for data with extreme values, outliers), correlation coefficients should be calculated from the ranks of the data, not from their actual values. The coefficients designed for this purpose are Spearman's rho (denoted as r_s) and Kendall's Tau. In fact, normality is essential for the calculation of the significance and confidence intervals, not the correlation coefficient itself. Kendall's tau is an extension of Spearman's rho. It should be used when the same rank is repeated too many times in a small dataset. Some authors suggest that Kendall's tau may draw more accurate generalizations compared to Spearman's rho in the population.

After the calculation of the above coefficients, an interesting question arises: how can we name this strength? All researchers tend to report that there is a strong relationship between what they have tested. However, most of the time, the significance is incorrectly reported instead of the strength of the relationship. A statistically significant correlation does not necessarily mean that the strength of the correlation is strong. The p-value shows the probability that this strength may occur by chance. In the dataset shown in Fig. 1, the correlation coefficient of systolic and diastolic blood pressures was 0.64, with a p-value of less than 0.0001. This r of 0.64 is moderate to strong correlation with a very high statistical significance (p < 0.0001). In the same dataset, the correlation coefficient of diastolic blood pressure and age was just 0.31 with the same p-value. Even though, it has the same and very high statistical significance level, it is a weak one. The low level of the p-value reassures us that 99.99% of the time the correlation is weak at an r of 0.31.

In this context, the utmost importance should be given to avoid misunderstandings when reporting correlation coefficients and naming their strength. In Table 1, we provided a combined chart of the three most commonly used interpretations of the r values. Authors of those definitions are from different research areas and specialties.

Table 1.

Interpretation of the Pearson's and Spearman's correlation coefficients.

Correlation Coefficient		Dancey & Reidy (Psychology)	Quinnipiac University (Politics)	Chan YH (Medicine)
+1	−1	Perfect	Perfect	Perfect
+0.9	−0.9	Strong	Very Strong	Very Strong
+0.8	−0.8	Strong	Very Strong	Very Strong
+0.7	−0.7	Strong	Very Strong	Moderate
+0.6	−0.6	Moderate	Strong	Moderate
+0.5	−0.5	Moderate	Strong	Fair
+0.4	−0.4	Moderate	Strong	Fair
+0.3	−0.3	Weak	Moderate	Fair
+0.2	−0.2	Weak	Weak	Poor
+0.1	−0.1	Weak	Negligible	Poor
0	0	Zero	None	None

The naming on the 1) Left: Dancey & Reidy.,⁴ 2) Middle: The Political Science Department at Quinnipiac University, 3) Right: Chan et al.⁵.

2.2. Phi Coefficient and Cramer's V Correlation

Phi is a measure for the strength of an association between two categorical variables in a 2 × 2 contingency table. It is calculated by taking the chi-square value, dividing it by the sample size, and then taking the square root of this value.⁶ It varies between 0 and 1 without any negative values (Table 2).

Table 2.

Interpretation of Phi and Cramer's V.

Phi and Cramer's V	Interpretation
>0.25	Very strong
>0.15	Strong
>0.10	Moderate
>0.05	Weak
>0	No or very weak

Cramer's V is an alternative to phi in tables bigger than 2 × 2 tabulation. Cramer's V varies between 0 and 1 without any negative values. Similar to Pearson's r, a value close to 0 means no association. However, a value bigger than 0.25 is named as a very strong relationship for the Cramer's V (Table 2).

2.3. Concordance Correlation Coefficient (CCC)

Lin's concordance correlation coefficient (ρ_c) is a measure which tests how well bivariate pairs of observations conform relative to a gold standard or another set.⁷ Lin's CCC (ρc) measures both precision (ρ) and accuracy (Cβ).⁸ It ranges from 0 to ±1 similar to Pearson's. Altman suggested that it should be interpreted close to other correlation coefficients like Pearson's, with <0.2 as poor and >0.8 as excellent. On the contrary, McBride suggested another set for the interpretation (Table 3).

Table 3.

Interpretation of Lin's CCC according to McBride et al.⁷.

Value of the Lin's CCC	Interpretation
>0.99	Almost Perfect
0.95 to 0.99	Substantial
0.90 to 0.95	Moderate
<0.90	Poor

3. Conclusion

Interpretation of correlation coefficients differs significantly among scientific research areas. There are no absolute rules for the interpretation of their strength. Therefore, authors should avoid overinterpreting the strength of associations when they are writing their manuscripts.

Funding

None declared.

Conflicts of interest

HA reports no conflict of interest.

Author contributions

HA performed the literature search, designed the manuscript, drafted and approved the final version. HA take responsibility for the paper.