Geometric constraints during epithelial jamming

Abstract

As an injury heals, an embryo develops, or a carcinoma spreads, epithelial cells systematically change their shape. In each of these processes cell shape is studied extensively whereas variability of shape from cell-to-cell is regarded most often as biological noise. But where do cell shape and its variability come from? Here we report that cell shape and shape variability are mutually constrained through a relationship that is purely geometrical. That relationship is shown to govern processes as diverse as maturation of the pseudostratified bronchial epithelial layer cultured from non-asthmatic or asthmatic donors, and formation of the ventral furrow in the Drosophila embryo. Across these and other epithelial systems, shape variability collapses to a family of distributions that is common to all. That distribution, in turn, is accounted for by a mechanistic theory of cell-cell interaction showing that cell shape becomes progressively less elongated and less variable as the layer becomes progressively more jammed. These findings suggest a connection between jamming and geometry that spans living organisms and inert jammed systems, and thus transcends system details. Although molecular events are needed for any complete theory of cell shape and cell packing, observations point to the hypothesis that jamming behavior at larger scales of organization sets overriding geometrical constraints.

Grain in a silo, sand in a pile, or beans in a chute can flow in some circumstances or become jammed in others.^1–3 Even bubbles comprising a foam or colloid particles comprising a suspension can jam or unjam. In each case constituent particles interact with nearest neighbors to form a disordered collective, and the collective as a whole can exhibit a transition from a fluid-like unjammed phase toward a solid-like jammed phase. A characteristic feature of the jamming phenomenon is that thermal fluctuations by themselves are insufficient to drive local structural rearrangements. The collective can therefore become trapped away from thermodynamic equilibrium and stuck in packing geometries that remain disordered in solid-like and fluid-like phases alike. Disordered geometry near the solid-like phase is thought to result from caging of each constituent particle by its immediate neighbors, force chains that percolate from particle to particle, and associated cooperative particle-particle interactions.^1–3 Within such collective systems the jamming phenomenon is virtually ubiquitous.

To a surprising extent, similar phenomena typify the cellular collective comprising the confluent epithelial layer.^4–9 Constituent cells can migrate in multicellular packs and swirls reminiscent of fluid flow, with embryonic development, cancer invasion, and wound healing being classical examples. Or instead they can become quiescent, solid-like, and non-migratory, as in the mature, uninjured epithelium. Moreover, these solid-like versus fluid-like phases of the epithelial collective have been linked to cell caging by immediate neighbors, propagating force chains, and cooperative cell-cell interactions that typify cell jamming and unjamming.^4–9 Every analogy has its limits, however, and, compared to that within the inert granular collective, the cellular packing geometry that defines a confluent epithelial collective would seem to be quite a different matter controlled by altogether different mechanisms.^9–13

Detailed measurements of epithelial packing geometry and associated cell-to-cell shape variability described below lead to two striking findings. Here we report, first, that measurements spanning diverse confluent epithelial systems scale to a statistical shape distribution that is virtually common to all. As a result, cell shape and shape variability are mutually constrained through a relationship that is purely geometrical. We show, second, that these shape distributions are reminiscent of the Edwards conjecture, which holds that among the immense number of packing geometries that is possible within a jammed granular collective, all are equally likely.^14,15 But how the physics of granular matter can be adapted in a more satisfying way to the biology of the space-filling, highly adaptable, active particles that comprise a confluent epithelial collective remains an open question (Supplement 1). Nevertheless, the findings described here deepen the analogy between the physics of the inert granular collective and that of the living epithelial collective, thus making this analogy all the more striking, and all the more curious.^4–9

Shape and shape variability in vitro

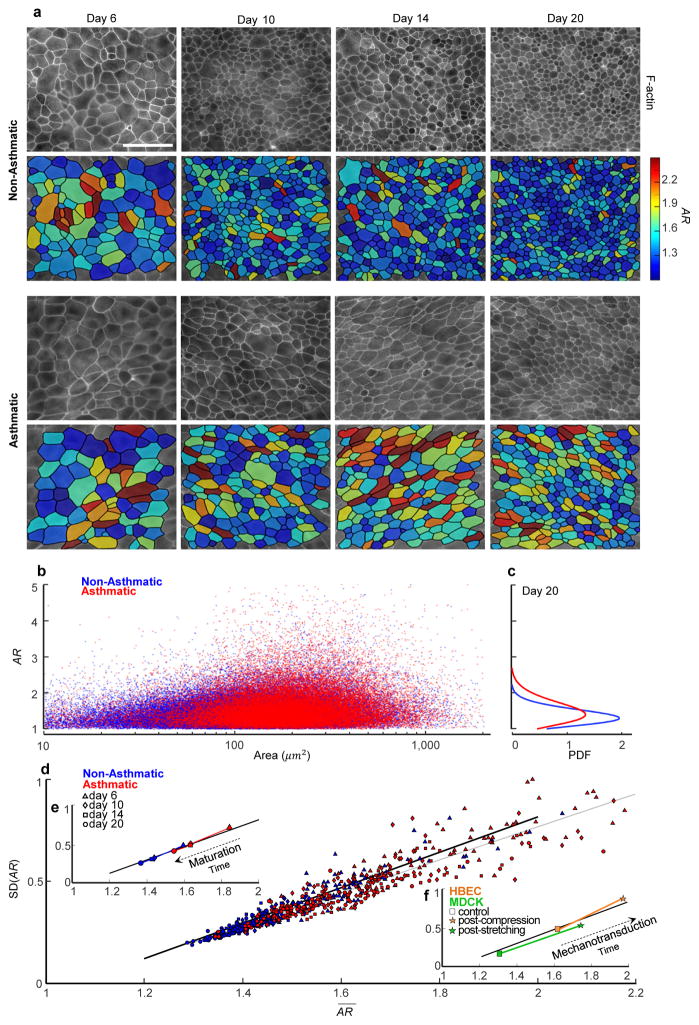
Human bronchial epithelial cells (HBECs) were grown to confluence in submerged conditions on a porous transwell for 5–6 days and then allowed to mature in air-liquid interface (ALI) culture conditions to become well-differentiated over the course of 6 to 20 days. Migratory dynamics were used to confirm evidence of progressive cell jamming⁴ (Supplement 2: Fig. S1), and a variety of imaging modalities were used to quantify cellular morphology (Methods; Supplements 3, 4). In HBEC layers from both non-asthmatic and asthmatic donors, areas and aspect ratios (ARs; Methods) were highly variable (Fig. 1a,b). Consistent with previous reports⁴, cells from asthmatic donors were more elongated than their non-asthmatic counterparts, and the distributions of ARs were broad and skewed (Fig. 1c; Fig. S2). As a simple measure of shape variability from cell-to-cell, we used the standard deviation of the aspect ratio, SD(AR). We had thought of this shape variability as representing biological noise. We were therefore surprised to find that data from all non-asthmatic donors and all days of maturation traced an unanticipated but clear linear relationship between the mean of the aspect ratio, $\overline{AR}$ , and its standard deviation, SD(AR), (p<0.0005; Fig. 1d; Table S1). Specifically, as the cell aspect ratio became progressively smaller with increasing days of maturation, its variability from-cell-to cell did so as well (Fig. 1e). Cells from asthmatic donors mature more slowly and migrate more quickly than do cells from non-asthmatic donors.⁴ We had therefore expected that any relationship between cell shape and its variability would be different as well between non-asthmatic versus asthmatic donors. To our further surprise, $\overline{AR}$ and SD(AR) from all asthmatic donors and all days of maturation defined a closely similar linear relationship, although with a slightly smaller slope (p<0.0005; Fig 1d; Table S1). Moreover, when we pooled all cells from all fields of view, and for each day of maturation, $\overline{AR}$ and SD(AR) for both asthmatic and non-asthmatic donors traced virtually the same relationship (Fig. 1d). Within this relationship, however, mature and/or non-asthmatic cells tended to fall at lower values of $\overline{AR}$ and SD(AR) whereas immature and/or asthmatic cells tended to fall at larger values (Fig. 1e, Fig. S2d).

Figure 1.

Across non-asthmatic and asthmatic donors of primary human bronchial epithelial cells (HBECs), and across all days of maturation, cell shape and shape variability in vitro are mutually constrained.

a, The apical actin ring was used to measure projected cell area and cell aspect ratio (AR; Methods, Fig. S9–11). With ongoing layer maturation, the AR of both non-asthmatic and asthmatic cells became progressively smaller and less variable (corresponding color maps). Scale bar, 50 μm. b, In cells from both non-asthmatic donors (n=87,066 cells, blue) and asthmatic donors (n=46,076 cells, red), AR was highly variable but did not co-vary with projected cell area. c, In the mature layer (20 days), the distributions of AR in both non-asthmatic and asthmatic cells were wide and skewed. d, AR from all donors and all days of maturation defined a clear relationship between the mean of $AR(\overline{AR})$ and the standard deviation (SD) of AR (each datum represents a different field of view), with non-asthmatic cells (day 6, 10, 14, 20; correspondingly n=13293, 23624, 20371, 29778) tending to fall at lower values of $\overline{AR}$ and SD(AR), and asthmatic cells (day 6, 10, 14, 20; correspondingly n=5372, 12629, 10019, 18056) tending to fall at larger values. e, With increasing days of maturation $\overline{AR}$ and SD(AR) decreased in tandem (each datum pools all cells for a given day of maturation), but were systematically increased in asthmatic compared with non-asthmatic controls. Nevertheless, all observations fell onto the same relationship. f, To rule out the possibility that this relationship might reflect an idiosyncrasy of layer maturation, we studied changes in cell shape and shape variability that occur acutely in response to an imposed mechanical perturbation. As demonstrated previously, for example, application of an apical-to-basal pressure difference (30cmH₂O) across the porous transwell causes the mature, jammed, HBEC layer to unjam^4,36,37 (Supplement 2, Video S1). Whereas maturation caused changes in cell shape to track in time from larger $\overline{AR}$ and SD(AR) to smaller, indicative of progressive jamming, mechanical compression caused changes in cell shape to track in the opposite direction with time, from smaller $\overline{AR}$ and SD(AR) to larger (control, n=6153; post-compression, n=5659), indicative of unjamming. Comparing unjamming vs. jamming, these changes with time were opposite in sign but tracked up or down a geometric relationship that in both instances was the same (cf. e and d). To complement results from HBEC compression, we applied sequential stretches to the mature MDCK layer plated on a deformable substrate (6% strain amplitude, isotropic in the cell plane, 1s duration, once every 6s for 20 min). Immediately after stretch cessation, cell shapes became elongated, but within 60 min these changes relaxed back to pre-stretch values (control, n=367; post-compression, n=422). These acute changes in cell shape could not be accounted for by changes in cell crowding, which were small (Fig. S2d for HBEC). As such, the geometrical relationship traced by the data (d,e,f) is not a specific effect of the passage of time, layer maturation, or cell crowding; these factors all mattered but no one among them could account for the observed geometric relationship. The dark continuous line (d,e,f) is not a regression line, but rather the prediction given by the computational model of cell-cell interactions (Supplement 6, Fig. S12). The light continuous line in d represents a linear regression for all data which gives SD(AR)=0.808 $\overline{AR}$−0.85 (R²=0.878).

Shape and shape variability in vivo

We then considered that this geometrical relationship might reflect a peculiarity of HBECs, an idiosyncrasy of layer maturation, or an artifact of cell culture. We show in Supplement 5 that the geometrical relationship traced by the data of Fig. 1d,e,f and Video S1 is not limited to HBECs, and is not a specific effect of the passage of time, layer maturation, or cell crowding; these factors all mattered but no one among them could fully explain the observations. To rule out artifacts of cell culture and, more importantly, to test the relationship between shape and shape variability in a completely distinct epithelial system in vivo, we studied ventral furrow formation in the developing embryo of the fruit fly Drosophila melanogaster.¹⁰

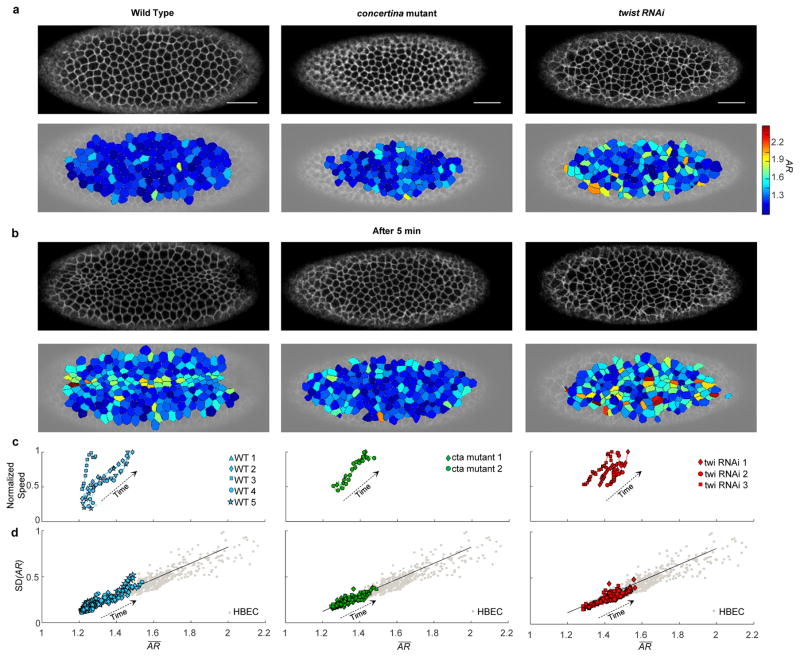
In Drosophila development, the ventral furrow forms to bring mesodermal precursor cells into the interior of the embryo. In this process cells exhibit pulsatile contractions that transition from a relaxed to a sustained contractile state.^16,17 These events are accompanied by changes of cell shape that include apical flattening, constriction of apical diameter, cell elongation, and subsequent shortening (Fig. 2a,b, left column).¹⁸ Across multiple wild type (WT) embryos, we characterized the aspect ratio of cell apical domains and its variability as cells constricted, increased their movement within the epithelial plane (towards ventral midline in wild type), and escaped their arrested state (Fig. 2c left column), but before the cells invaginated (Materials and Methods). Even though the Drosophila embryonic epithelium differs in many regards from HBEC and MDCK layers in vitro, cell shape data obtained in this system as the furrow forms traced the same geometric relationship (Fig. 2d, left; Video S2). To test how shape and shape variability are affected by genetic variability, we studied embryos that were mutant for concertina (cta). The cta gene encodes a Gα_12/13 protein, which is required for coordinated apical constriction.¹⁹ In cta maternal effect mutants, cells of the ventral furrow constrict in an uncoordinated manner and furrow formation becomes slow and uneven.²⁰ In addition, we used RNAi to knock down the transcription factor twist, which is essential for sustained apical contraction and ventral furrow formation. Unlike the maturing HBEC layer, but similar to compression-induced unjamming of the HBEC layer, these events in the embryo were accompanied by progressive increases of cellular speeds and $\overline{AR}$ s in tandem (Fig. 2c, center and right), and tracked with time from smaller toward larger $\overline{AR}$and SD(AR) (Fig. 2d center and right; Videos S3,4). Moreover, gradual transitions of layer structure (as reflected by changes of $\overline{AR}$) and cooperative dynamics (as reflected by changes in the self-overlap order parameter and the four-point susceptibility), occurred simultaneously (Fig. S1). These data suggest that certain changes in cell morphology during ventral furrow formation are associated with epithelial layer unjamming. It remains unclear, however, if unjamming and the associated solid-like to fluid-like transition in that particular context are permissive of the cellular flows that are driven by apical acto-myosin constriction, or are the effect.¹⁶

Figure 2.

During ventral furrow formation in Drosophila in-vivo, cell shape and shape variability follow the same geometrical relationship as do HBECs in vitro.

a,b, During Drosophila ventral furrow formation, a membrane marker was used to identify cell-cell boundaries in Wild Type (WT), concertina (cta) mutant, and twist (twi) RNAi embryos (n=5, 2 and 3 respectively). Aspect ratio (AR) was measured for 100–150 cells per frame, for 60–100 frames (6–8 seconds apart) per embryo. With time (b, after 5 minutes) cells constricted and attempted to form the ventral furrow, and cell AR in all embryos became progressively larger and more variable (corresponding color maps). Scale bar, 25 μm. c, Average speed in epithelial plane (across all cells) and $\overline{AR}$ increased in tandem for WT, cta mutant and twi-RNAi embryos. The speed is normalized to the maximum speed observed in each embryo, typically corresponding with the initiation of the fold, and ranging from 3 μm/min in WT to 1.5 μm/min in cta mutant and twist (twi) RNAi embryos. d, With time, $\overline{AR}$ and SD(AR) increased in tandem in WT embryos (c, left) and followed the same geometric relationship as seen in HBECs in-vitro (Fig. 1d,e,f; Video S2–4).This relationship persisted in embryos with genetic variability (c, center and left) that prevent or hinder the ventral furrow formation, as in cta mutant and twist (twi) RNAi embryos respectively. (Each datum represents a frame from an individual embryo). Each gray datum represents a different field of view for both asthmatic and non-asthmatic HBEC. The dark continuous line is the same as in Fig. 1, and corresponds to the prediction given by the computational model (Supplement 6, Fig. S12).

Diverse systems reveal common shape distributions

We found that explanations based solely upon the mathematics of randomness and tessellation are at best incomplete (Fig. S3). To explain these findings at a deeper level, we reasoned that the underlying statistical distributions of observed cell shapes across these diverse epithelial systems must comprise a special subclass of distributions that has yet to be determined. To fill that gap, we measured for each of the biological cases above the corresponding probability density functions (PDFs) of observed ARs, as described below. We then go on to ask what physical mechanism might account for that special subclass and its statistical properties.

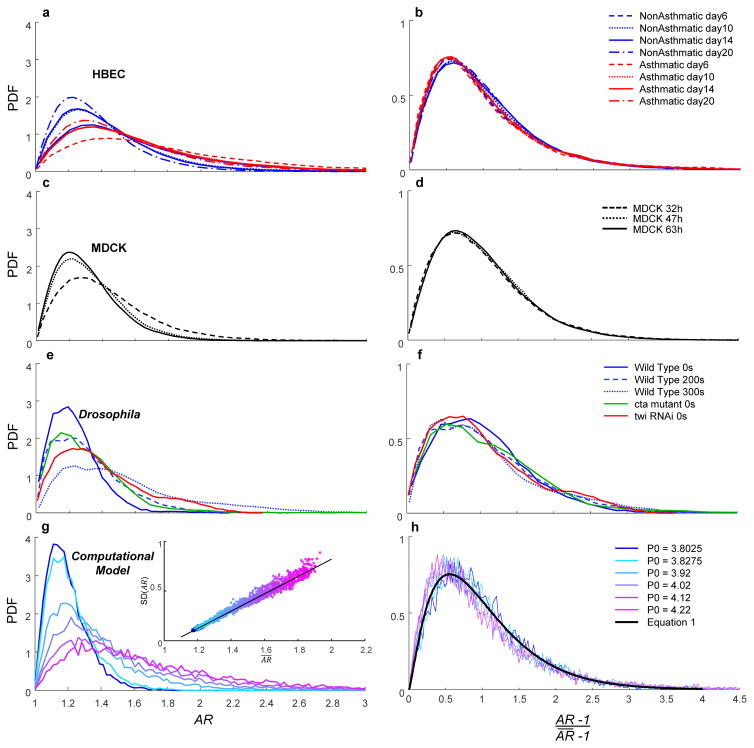
During maturation of HBECs or MDCKs, cell shapes became systematically less elongated and less variable with time (Fig. 3a,c). In contrast, during the approach to the formation of the ventral furrow in the wild type Drosophila embryo, cell shapes became more elongated and more variable with time (Fig. 3e). In the cta mutant compared with WT, cell shape was more elongated and more variable, and even more so in the twist knockdown (Fig. 3e). Despite differences in PDFs within and between these systems, and regardless of their trajectories over time, the functional form of all respective PDFs were unimodal and skewed in a manner suggestive of a common underlying mathematical basis (Fig. 3a,c,e). To assess this commonality in a quantitative fashion, we rescaled AR to the form $x=(AR-1)/(\overline{AR}-1)$; importantly, $\overline{AR}$ in HBECs progressively fell with increasing days of maturation (p<0.0005; Fig. S1), and was systematically greater in non-asthmatic versus asthmatic cells (p<0.0005). Rescaling in this fashion maps the lower limits of the abscissa and the ordinate to zero, and scales the mean of the distribution to unity. Across all days of maturation for HBEC data in all non-asthmatic donors, data thereupon collapsed onto a common distribution (Fig. 3a,b). For asthmatic donors, too, rescaled data again collapsed to a common distribution (Fig. 3a,b), as did data from MDCK cells (Fig. 3c,d), events preceding formation of the ventral furrow, and interventions that disrupt that furrow formation (Fig. 3e,f).

Figure 3.

Within and across vastly different epithelial systems, shape variability collapses to a family of probability density functions (PDFs) that is common to all, and perhaps universal.

a, PDFs of AR in HBECs (Fig. 1d,e) became systematically less skewed and less variable with maturation. b, PDFs of the rescaled parameter $x=(AR-1)/(\overline{AR}-1)$ of HBECs, where $\overline{AR}$ denotes the mean AR for each respective distribution, followed a k-gamma distribution (Eq.1) with k= 1.97. c,d, Similar to a,b respectively for MDCKs with k = 2.31. e,f, Similar to a,b respectively for Drosophila (Fig. 2d) with k = 2.52. g, Predicted distributions for AR given by the model of Bi et al.^25,26 For increasing values of the model’s input parameter P₀, the inset shows the predicted relationship for $\overline{AR}$ vs. SD(AR) (Supplement 6, Fig. S12). h, Collapse of predicted distributions. Black line shows maximum likelihood estimation (MLE) fit with k = 2.53.

Generic connections between jamming and geometry

Remarkably, within and across these diverse epithelial layers, observed variability of shape from cell-to-cell was well-described by a single distribution that, with small distinctions, was common to all. Importantly, a direct consequence of distributions that are invariant to scaling in this manner is a linear relationship between $\overline{AR}$ and SD(AR), as seen in Figs. 1–2.

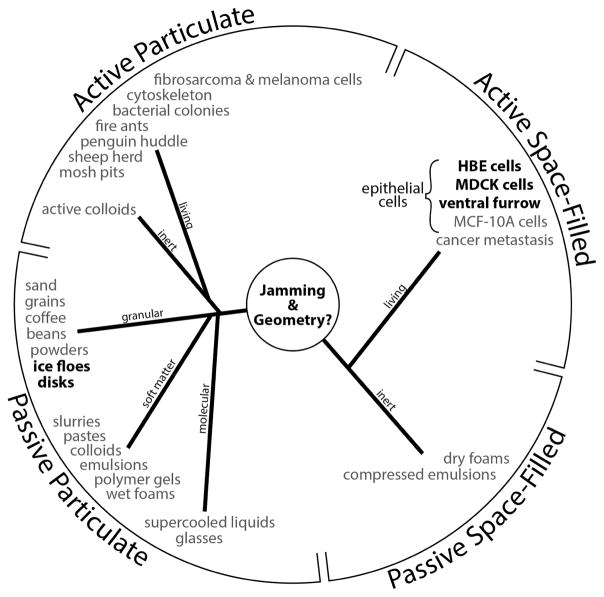
We wondered, therefore, if the findings above might be explained by a generic empirical connection between jamming and geometry that is not restricted to the particular effects of cell maturation, cortical tension or cell-cell adhesion, and instead points to a larger jamming reference class that transcends such system details (Fig. 4; Fig. S4). As a guide for thought, we start by considering the well-studied case of the disordered granular collective; recent evidence points to fluid-solid transitions in disordered granular matter as being similar in 2 and 3 dimensions.^21,22 In 3 dimensions, grain centers can be used to tessellate the volume around each individual grain. When packing is dense and disordered, these tessellated volumes necessarily vary from grain-to-grain. In such a physical system, the distribution of volumes, x, has been found theoretically and confirmed empirically to follow the k-gamma distribution²³,

Figure 4. The jamming superfamily.

Each entry denotes a phyical system in which jamming behavior has been reported, and is categorized here into four classes. In bold are systems described in this report; See also Fig. S4. The jamming mechanism was first introduced to explain the poorly understood behaviors that typify certain collective granular systems. Similarities in behavior between such inert granular systems and the migrating epithelial layer were quickly recognized however.^6,38,39 For example, both granular and cellular collective systems are close-packed, volume exclusion prevents two particles (or cells) from occupying the same space at the same time, and particle-particle (cell-cell) interactions are strong. Moreover, just as inert granular systems display swirling motions that arise in cooperative multi-particle packs and clusters, so too does the migrating epithelial layer.^8,40–44 But other physical factors do not fit so easily into this analogy. For example, within granular matter the state of internal mechanical stress is mainly compressive –these are fragile materials in the sense that they can support immense compressive stresses but can support no tensile stress whatsoever– whereas within the confluent cell layer the mechanical stress is overwhelming tensile.⁴² Within granular matter a principal control variable for jamming is free space between grains^2,45 whereas in the fully confluent cell layer there is by definition no free space between cells. Within granular matter neither a change of particle shape nor mutual particle-particle adhesion is required for jamming or unjamming – although either can influence jamming dynamics⁴⁶– whereas cell shape change and cell-cell adhesion are thought to be indispensable features of epithelial function and jamming ^5,24–26. And perhaps most importantly, the granular particle is neither active nor self-propulsive nor mechanosensitive whereas the epithelial cell exhibits all of these characteristics. In this report we show that the behavior of these diverse living and inert systems is unified to a remarkable extent by consideration of system geometry.

$$\text{PDF}(x;k)=k^k{x}^{k-\mathit{1}}{e}^{-kx}/\mathrm{\Gamma }(k)$$ (1)

where Γ(k) is the Legendre gamma function. This distribution is fully described by only a single parameter, k, and has a mean of unity.

Eq. 1 arises from statistical mechanics based in part upon volume exclusion, which prevents two grains from occupying the same space at the same time, and tessellated volume fluctuations that are additive so as to account for total system volume. We note that the derivation of this result²³ does not depend on the dimensionality of the system, and therefore applies as well to granular systems in 2 and 3 dimensions alike. In a confluent cellular system, however, cellular aspect ratios are in no sense additive, and for that reason and others there presently exists no rigorous basis for the applicability of the k-gamma distribution to metrics of cell shape. Nevertheless, when a layer remains confluent each individual cell can change not only its area but also its shape at the expense of complementary changes in neighboring cells. A central role for cell shape is demonstrated, for example, in the case of unjamming caused by acute layer compression which, compared with the case of layer maturation, reveals changes of area per cell and area distributions that are small but changes of cell shape and shape distributions that are not small (Fig. 1d inset; Fig. S2d).

For these reasons and others, the statistical physics of cell jamming emphasizes cell shape and its changes.^{4,5,9,24–27,28} Statistical physics of cell jamming also leads to a prediction for the distribution of energy barrier heights that act to impede local cellular rearrangements, where the k-gamma distribution is seen to arise yet again.²⁵ These hints lead us to the conjecture that cell shapes, too, are governed by a k-gamma distribution. We cannot prove this conjecture analytically, but using the extensive data sets described above we can test it empirically. Specifically, we take $x=(AR-1)/(\overline{AR}-1)$ and use maximum likelihood estimation (MLE; Materials and Methods). Eq. 1 is then seen to be faithful to observations with a high degree of statistical confidence (Fig. S5,6). In HBECs, the parameter, k, varied little over all days of maturation (p<0.0005, Fig. S5b) and, moreover, did not differ between non-asthmatic versus asthmatic cells (p=0.2147, Fig. S5b). Much as in the case of jammed granular packings²³, but quite unlike the case of unjammed granular packings, k changed only slightly as the system became progressively more jammed (Fig. S5b; see also Supplement 6; compare Fig. 4 in²³). Even though some differences in k were statistically significant, these differences were at most modest and, to a reasonable approximation, k in HBECs could be taken as a constant value of 1.97 (95% CI [1.89, 2.04]). In MDCK cells we found, similarly, that all data were well represented by a single k value of 2.31 (CI [1.90, 2.73]). In Drosophila, k values were not statistically different between WT and cta mutant (p=0.023), or twist RNAi (p =0.762) (Fig. S6b), and were well represented by a single k value of 2.52 (CI [2.43, 2.62]). Across these diverse epithelial systems, Eq. 1 pertained throughout and k was bounded to the relatively narrow range between 2 and 2.5. The near universal structure of shape distributions, and with a virtually common value of k, are therefore all the more striking.

Effective temperature in jammed packings

For disordered granular matter, the mathematical form of the k-gamma distribution (Eq. 1) constrains volume variability to mean volume according to the relationship $SD(V)=(\overline{V}-V_{\mathit{min}})/\sqrt{k}$, where V represents local tessellated volume associated with each individual grain, V̄ is the mean value of such volumes, and V_min is the minimal random packing volume that the system can attain.²³ But just as Eq. 1 requires volume variability SD(V) to change linearly with mean volume V̄ in the case of granular systems, so too Eq. 1 requires cell shape variability SD(AR) to change linearly with mean cell shape $\overline{AR}$ in the case of epithelial systems (Fig. 1d, 2d). But is there deeper insight that might help to explain these empirical findings?

Of the great many possible jammed packings into which a collective system might become trapped, all jammed packings become equally likely just as the system approaches the transition between fluid-like and solid-like phases; this is called the Edwards conjecture, and has been recently proven.^14,15 If no one jammed configuration is privileged over another, then the distributional entropy, S, becomes maximized, from which it has been shown that Eq. 1 follows directly.²³ In a jammed packing, however, thermal fluctuations are insufficient to drive local rearrangements, and for that reason the traditional statistical mechanics of Gibbs do not apply. Nevertheless, if volume in an athermal granular system were to play a role analogous to that of energy in a thermodynamic system, as suggested by Edwards, one can then define an effective temperature, T_eff, given by 1/(∂S/∂V).^23,14 Carried over from volume variability in granular jamming to shape variability in cellular jamming, T_eff then takes the form,

$$T_{\mathit{eff}}=\text{SD}(AR)/\sqrt{k}=(\overline{AR}-A{R}_{\mathit{min}})/k.$$ (2)

To the extent that Eq. 1 pertains (Fig. 3b,d,f) and to the extent that observed changes in k across diverse epithelial systems are small (Fig. S5b, S6b), then the cell jamming mechanism and Eq. 2 would explain not only the existence of a relationship between cell shape variability and cell shape, but also its linearity and its invariance. Through the lens of such a physical picture, data in the lower left of Fig. 1d might then be imagined as corresponding to effectively ‘cooler’ states, and those at the upper right to relatively ‘warmer’ states. It remains to be determined, however, if effectively warmer, unjammed, migratory, fluid-like phases are harnessed to enable wound healing, development, or invasion, and effectively cooler, jammed, non-migratory, solid-like phases are harnessed to slow those processes or arrest them. Experimental observations of cell shape spanning diverse epithelia, the statistical physics of disordered granular matter, and computational mechanics of cell-cell interactions (Supplement 6) are thus seen to converge in a manner that is qualitatively consistent and quantitatively reinforcing.

Geometrical constraints on cell shape variation

As early as 36 BC, the Roman Marcus Terentius Varro suggested that the bee’s honeycomb, in order to enclose a cellular space, makes optimal use of material. It was only much later, in 1611, when Johannes Kepler proposed that hexagonal packing of identical spheres corresponds to the densest possible arrangement. D’Arcy Thompson later argued that biological systems evolve toward and thus tend to recapitulate such optimal packing structures.²⁹ These conjectures and others dating even earlier have been proven only recently.^30,31 Cell divisions and apoptosis are known to drive cell arrangements away from such a hexagonal packing, however, and toward an equilibrium distribution of polydisperse cellular polygons.¹¹ Nevertheless, shape distributions measured throughout the jamming process of HBECs depart systematically from that predicted equilibrium distribution (Fig. S2e). Moreover, cell divisions tend to orient along the long axis of the interphase cell in a manner that facilitates both stress relaxation and isotropic growth within the cell layer – a phenomenon commonly known as Hertwig’s rule. ³²

A variety of dynamic events were likely at work in the datasets reported here, including but not limited to proliferation, crowding, extrusion, apoptosis, and even newly discovered nematic defects¹³, any of which might be expected to impact the jamming state of the epithelial collective. Nevertheless, in instances when $\overline{AR}$ and SD(AR) are relatively small the configurational options from which the cellular collective can sample are correspondingly limited, cell movements become highly constrained, rearrangements among neighboring cells become slowed, and the collective as a whole becomes solid-like. This is the essence of the jammed state. By contrast, in instances when $\overline{AR}$ and SD(AR) are relatively large a wider range of configurational options become available, cell movements become less constrained, rearrangements among neighboring cells become increasingly frequent, and the collective as a whole becomes fluid-like (Videos S1–4). This is the essence of the unjammed state.

The fundamental open questions are these. First, experimental results establish that scaled ARs are distributed in a fashion that is approximately common to all and follow the k-gamma distribution, which in turn requires a linear relationship between $\overline{AR}$ and SD(AR). But why this should be true, and why the numerical value of k in those systems should be so narrowly limited remain unexplained. Second, does structural disorder within a multicellular tissue represent noise, i.e., an inconsequential byproduct of more consequential biological events? Or instead might disorder be physiologically useful in its own right? New experimental evidence presented here and elsewhere increasingly ties cell jamming together with structural disorder, cell mechanics, and collective migration.^4–9 But the extent to which graded degrees of cell jamming and disorder might be regulated physiologically, or dysregulated pathologically, remains unclear. Importantly, both cell jamming and contact inhibition of locomotion (CIL) have argued to account for the progressive slowdown of cellular motions within the confluent epithelial layer.³³ But it remains unclear if these mechanisms are distinct, and, if so, the extent to which they are mutually independent, interdependent, or reinforcing. Finally, the biology of metastatic disease currently lacks a mechanistic explanation for how collective cancer cell migration can occur when the epithelial-to-mesenchymal transition (EMT) program is inactive.^34,35 The extent to which the unjamming transition comprises an alternative gateway to cancer cell migration and metastasis remains to be established (Supplement 1).

Data obtained across vastly different epithelial systems emphasize the generality of the cell jamming concept. Although molecular events are needed for any complete theory of cell shape and cell packing –whether during embryogenesis, cancer invasion, or wound healing– jamming behavior at a larger scale of organization is seen to set overriding geometric constraints. It is well-recognized that molecular events cannot exert their effects upon cell shape directly, but rather mediate their effects through the combined but indirect actions of genetic, cellular, and mechanical inputs that remain incompletely understood.¹⁰ Here we build directly upon this idea and extend it from the singe cell to the epithelial collective. To set the most primitive features of cell shape and shape variability, these indirect actions combine to modulate proximity of the confluent cell layer to the jammed state, and thereby shift the layer up or down the geometric relationship shown in Fig. 1–3. On the scale of cellular dimensions, therefore, these findings point to the hypothesis that cell jamming may be the principal determinant of epithelial cell shape and shape variability.

Methods

Culture of primary HBECs in ALI culture

Primary human bronchial epithelial cells (HBECs) were obtained at passage 0 or passage 1 from the Marsico Lung Institute/Cystic Fibrosis Center at the University of North Carolina, Chapel Hill. HBECs were cultured from three non-asthmatic and three asthmatic donors as previously described.⁴ Briefly, passage 2 HBECs were seeded onto a transwell insert coated with type I collagen (2 transwells per donor), and grown under submerged conditions for five to six days until the cells reached confluence. Upon reaching confluence, media was removed from the apical side of the transwell, but was kept in the basal side to initiate air-liquid interface (ALI) culture conditions. Cells were maintained in ALI conditions and became well-differentiated, expressing basal, goblet and ciliated cells (Fig. S8), as seen in airways in vivo. On specific days of ALI cells were fixed with 4% paraformaldehyde (PFA) and stained with phalloidin conjugated with alexa-488 to visualize F-actin (Life Technologies). Wide field fluorescent images (10–20 per transwell) were acquired at the apical plane on a Leica DMI 8 microscope using either a 40X or 63X-oil objective (Leica), and automatically segmented and analyzed using an in-house custom algorithm.

Cell morphology and metrics

Cell numbers progressively increased and projected areas progressively decreased with layer maturation (Fig. 1a; Fig. S2a,d). Both in ALI culture and in vivo, the mature HBEC layer comprises mainly basal cells, goblet cells, and ciliated cells arrayed in a complex pseudostratified structure (Fig. S9). Cell shapes vary dramatically along the apical-basal axis, with the cell body often bulging in the vicinity of the nucleus, which is relatively stiff. Analysis of such systems typically emphasizes the dominant mechanical effects attributable to apical regions and the apical actin ring.⁵ Fluorescent images labeled for F-actin show how these apical rings tile the cell layer (Fig. 1a; Fig. S9–11). These rings were segmented using a customized algorithm (Supplement 4), and from these segmented images we measured corresponding geometries across all donors and days of maturation in a total of 1.4×10⁵ cells. For each ring we determined the projected area and the aspect ratio, AR (Fig. S11); the more slender or elongated the profile, the higher is its AR. For any closed ring in the cell plane, AR thus serves as a simple, primitive, and robust metric of ring shape. In a previous study we had used as an index of shape the factor, q, which is the ring perimeter divided by the square root of area.⁴ In the dataset described here AR and q were correlated, but we found that the experimentally observed range of AR spanned roughly five-fold whereas that of q spanned less two-fold (Fig. S7). To better resolve changes in shapes, we found it preferable to use AR.

Migratory dynamics

Collective migratory dynamics in this experimental system have been characterized previously⁴, and we use a variety of metrics here to replicate and confirm those earlier findings (Fig. S1). For example, within the confluent layer cells move in cooperative swirls or packs of 10–100 cells. These packs display characteristic pack speed, size, and lifetime (as determined from the peak of the four-point susceptibility), and after several pack lifetimes any individual cell finds itself surrounded by a different set of immediate neighbors. As the jamming transition is approached, pack speed tends to decrease as pack size and pack lifetime tend to grow⁴, but there is no objective cutoff that defines a jamming transition. Rather, the transition is gradual and continuous, and jamming is said to occur when pack lifetime grows to exceed the laboratory measurement window (144 min). Using those criteria, the non-asthmatic maturing HBEC layer approaches jamming by day 8 of ALI culture, whereas the asthmatic layer approaches jamming no sooner than day 14.⁴

MDCK culture and live imaging

Cells were stably transfected with GFP-linked nuclear localization (NLS-GFP) and cultured in Dulbecco’s modified Eagle’s medium (DMEM) supplemented with 10% fetal bovine serum (FBS), 1% penicillin/streptomycin, and 0.5 mg/ml G418. Tissue culture plates were coated with collagen I and 50,000 cells were added to the center of the well and allowed to adhere for 24 hours. Cells were maintained at 37C and 5% CO₂ as images were recorded every three minutes for 54 hours using phase microscopy and confocal fluorescence using the 488 nm line of an argon laser on a Leica DMI6000 SP5 microscope with a stage top incubator. Images were processed to find centroids of each nuclei, which were used as seeds for a Voronoi tessellation in order to create a polygonal tiling of the cell layer. These polygons were then used to obtain cell aspect ratio using an in-house custom algorithm.

Fly stocks and live imaging

The following fly lines were used for imaging: sqh::GFP (myosin regulatory light chain, sqh, fused to GFP and expressed from endogenous promoter)⁴⁷, Gap43-mCherry (membrane marker driven by sqh promoter)⁴⁸. To make maternal effect concertina (cta) mutant embryos, the cta^RC10; sqh::GFP, Gap43::mCherry/TM3 flies were crossed with Df(2L)PR31/CyO, sqh::GFP flies and embryos from nonbalancer F1 females were imaged.

For live-cell imaging of Drosophila, embryos were dechorionated with 50% commercial bleach, washed with water, and mounted ventral side up on a glue-coated microscope slide. Two No. 1.5 coverslips were put between the slide and top coverslip to make a chamber and avoid compressing the embryo. Embryos were imaged in halocarbon 27 oil (Sigma-Aldrich). Images were acquired using a Zeiss LSM 710 confocal microscope equipped with a x 40/1.2 numerical aperture Apochromat water objective (Carl Zeiss). For each time point, z-projections of three consecutive slices were automatically segmented and analyzed using an in-house custom algorithm.

RNAi knock-down in Drosophila

To disrupt the twist transcription factor, we injected dsRNA generated using the Invitrogen MEGAscript T7 transcription kit, resuspended in 0.1 x PBS.¹⁶ The dsRNA against twist had to be injected at least 2.5 hours before imaging/gastrulation in order to observe the phenotype. The following primers were used to generate twist dsRNA: F: 5′-TAATACGACTCACTATAGGGGCCAAGCAAGATCACCAAAT-3′; R: 5′-TAATAC GACTCACTATAGGGGACCTCGTTGCTGGGTATGT-3′.

Maximum likelihood estimation (MLE)

We fitted the k-gamma probability density, PDF(x; k) = k ^k x ^k−1 e^{−k x}/Γ(k), to the data by the method of maximum likelihood. For each data set, aspect ratios were shifted and normalized by $x=(AR-1)/(\overline{AR}-1)$. For a given set of data {x_i} i = 1, …, N, the likelihood function is,

$$L(k)=\prod _{i=1}^N\rho (x_i;k)$$

The MLE estimate of k is then given by k̂ = argminI_k (−lnL(k)). The confidence intervals for k̂ were determined by parametric bootstrapping as follows. N simulated data points were generated from the cumulative distribution function (CDF) corresponding to the k̂ for that set. Maximum likelihood was again performed, yielding a parameter estimate k̂₁ from this first set of simulated data. This procedure was repeated over a large number S of simulations, typically >200. The standard deviation of the resulting set {k̂_s}, s = 1, …, S was used to construct 95% confidence intervals.

Finally, we tested goodness-of-fit for this approach by computing Chi squared values. For each data set, we constructed (uniform) decile bins from the cumulative distribution function, given k̂ for that set. We counted the observed number of data points O_j, j = 1, …, 10 occurring within each bin, and compared these with the expected number of occurrences E = N/10 within each bin by computing,

$${\mathrm{\chi }}^2=\sum _{j=1}^N{(O_j-E)}^2/E.$$

For decile binning, the number of degrees of freedom is 9; the threshold value of χ² for 95% confidence is given by ${\mathrm{\chi }}_{0.05,9}^2=16.9$. Observed values of ${\mathrm{\chi }}^2>{\mathrm{\chi }}_{0.05,9}^2$ indicate a rejection of goodness-of-fit with 95% confidence.

For HBEC data, we found that out of 646 frames only 22 had ${\mathrm{\chi }}^2>{\mathrm{\chi }}_{0.05,9}^2$, or approximately 3.4%. This is close to the expected false negative rate of 5%, given an appropriate distribution function with 95% confidence limits. Similarly, the data from Drosophila revealed a fraction of ${\mathrm{\chi }}^2>{\mathrm{\chi }}_{0.05,9}^2$ also approximately 3.4%, and the MDCK data exhibited a fraction 9.8%. This is striking confirmation at the level of goodness-of-fit that the underlying distribution over these cell types is well characterized by the k-gamma distribution given in Eq. 1.

Data Availability

Data that support the plots within this paper and other findings of this study are available from the corresponding author upon request.