Enhanced Real-Time Pose Estimation for Closed-Loop Robotic Manipulation of Magnetically Actuated Capsule Endoscopes

Abstract

Pose estimation methods for robotically guided magnetic actuation of capsule endoscopes have recently enabled trajectory following and automation of repetitive endoscopic maneuvers. However, these methods face significant challenges in their path to clinical adoption including the presence of regions of magnetic field singularity, where the accuracy of the system degrades, and the need for accurate initialization of the capsule’s pose. In particular, the singularity problem exists for any pose estimation method that utilizes a single source of magnetic field if the method does not rely on the motion of the magnet to obtain multiple measurements from different vantage points. We analyze the workspace of such pose estimation methods with the use of the point-dipole magnetic field model and show that singular regions exist in areas where the capsule is nominally located during magnetic actuation. Since the dipole model can approximate most magnetic field sources, the problem discussed herein pertains to a wider set of pose estimation techniques. We then propose a novel hybrid approach employing static and time-varying magnetic field sources and show that this system has no regions of singularity. The proposed system was experimentally validated for accuracy, workspace size, update rate and performance in regions of magnetic singularity. The system performed as well or better than prior pose estimation methods without requiring accurate initialization and was robust to magnetic singularity. Experimental demonstration of closed-loop control of a tethered magnetic device utilizing the developed pose estimation technique is provided to ascertain its suitability for robotically guided capsule endoscopy. Hence, advances in closed-loop control and intelligent automation of magnetically actuated capsule endoscopes can be further pursued toward clinical realization by employing this pose estimation system.

1 Introduction

Cancers of the gastrointestinal (GI) tract are among the top three leading causes of death in many parts of the world (Siegel et al. 2016; Torre et al. 2015; Jemal et al. 2010). In many cases, if the cancer is detected early, the chance of survival is significant (Siegel et al. 2016), thus physicians commonly use endoscopes to visually explore the reachable areas of the GI tract for signs of early cancer. However, due to their mechanics and method of actuation, current endoscopes have been reported to cause tissue damage and patient discomfort and, as a result, discourage patients from participating in recommended screening procedures (Bynum et al. 2012). Furthermore, certain areas of the GI tract (e.g. the small intestine) remain difficult to reach due to the use of semi-rigid conventional endoscopes. In the past two decades, attempts to mitigate these limitations have spurred the development of various devices that can be used to visually explore the GI tract (Slawinski et al. 2015; Valdastri et al. 2012b; Amoako-Tuffour et al. 2014). In this still active area of research, magnetically actuated mesoscale devices (capsules) have shown great promise in being maneuverable while significantly decreasing the risks associated with standard endoscopies (Sliker and Ciuti 2014). In particular, actively controlled devices, where magnetic fields are generated or manipulated via computer algorithms, have the potential to revolutionize GI endoscopy and transform the perception of patients toward recommended screening procedures (Slawinski et al. 2015).

In order to apply the necessary forces and torques, magnetic actuation systems need accurate estimates of the capsule’s pose. Despite their high levels of accuracy, commercially available electromagnetic tracking systems such as the NDI Aurora (Northern Digital Inc., Waterloo, ON, Canada) and the Ascension trakSTAR (Ascension Technology, Burlington, VT, USA) are incompatible with magnetic actuation due to magnetic distortions caused by the magnets found in the capsule and the actuator (Franz et al. 2014).

As such, several groups have proposed pose estimation methods with varying degrees of accuracy, workspace size, estimation time, and achievable degrees of freedom (Than et al. 2012). A subset (Salerno et al. 2012; Di Natali et al. 2013, 2016; Popek and Abbott 2015; Aoki et al. 2010) of these methods have contributed to the recent advances in robotically guided magnetic capsule endoscopy where trajectory following (Taddese et al. 2016b; Popek et al. 2017) and automation of repetitive endoscopic maneuvers (Slawinski et al. 2017) were demonstrated.

In particular, Salerno et al. (2012) demonstrated that an external permanent magnet (EPM) mounted on a robot manipulator, together with magnetic field and inertial sensors inside the capsule, can be used for estimating the position of the capsule. Their approach however was not real-time and required the separation of actuation and pose estimation steps. Di Natali et al. (2013) improved upon this system by creating an efficient algorithm that exploited the axial symmetry of cylindrical magnets to create a real-time 6 degrees-of-freedom (DOF) pose estimation system. They also provided a more computationally efficient iterative algorithm with an update rate faster than 100 Hz (Di Natali et al. 2016).

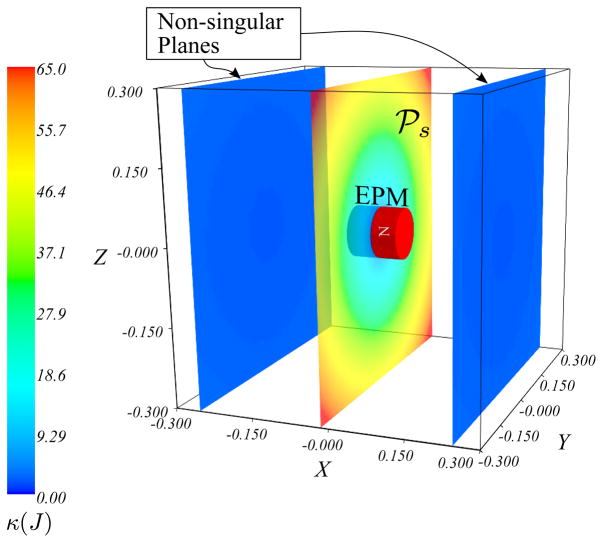
A thorough analysis of the workspace of the aforementioned real-time pose estimation methods (Di Natali et al. 2013, 2016) identifies singularities in certain regions of the workspace leading to the loss of estimation capability. The assumption made in these algorithms is that for a given pose of the EPM, there is a bijective mapping from all positions in the workspace to magnetic field vectors and that changes in magnetic field always occur for changes in position. We show in Section 3 of this paper that this assumption fails to hold on the singularity plane of the EPM defined as the plane normal to the dipole moment that passes through the center of the magnet (see Figure 2). Certain applications of robotically guided magnetic capsule endoscopy require the capsule to be nominally located in this region during clinical procedures, thus, this limitation hinders future clinical use of these devices (Taddese et al. 2016a,b; Slawinski et al. 2017; Mahoney and Abbott 2015). This problem requires additional sources of information to constrain the number of solutions found by the algorithms. Further drawbacks of these pose estimation methods come from the need for accurate initialization of the capsule’s yaw angle (see Figure 1) with respect to a global frame and the susceptibility of the estimated yaw angle to drift. Yaw angle errors arising from these issues lead to reduced accuracy in the overall estimated pose. Unlike pitch and roll angles, which are determined from the acceleration due to gravity, this issue exists for the yaw angle owing to the strong magnetic field from the EPM rendering the earth’s magnetic field unusable as an absolute reference. Aside from the inconvenience of performing accurate initializations every time the software is started, it is important to consider the implications in clinical settings. That is, if the algorithm is restarted for any reason during a procedure, it will be extremely difficult to reinitialize the yaw angle while the capsule is inside a patient.

Figure 2.

Application scenario of active magnetic manipulation of a capsule endoscope using a permanent magnet mounted at the end effector of a robot manipulator

Figure 1.

Definition of roll (ϕ), pitch (θ), and yaw (ψ) angles

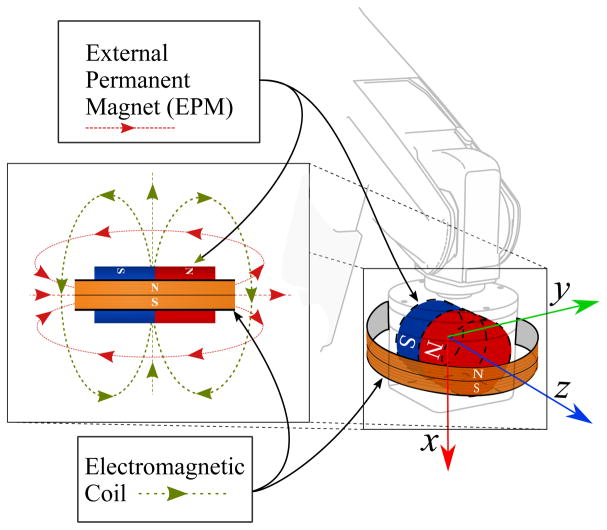
This paper introduces, for the first time, a hybrid system that combines static and time-varying magnetic field sources to create a robust and clinically viable magnetic pose estimation method for robotically guided magnetic capsule endoscopy. While this paper presents the method in the context of solving the singularity and yaw initialization problems in a specific magnetically actuated soft-tethered capsule endoscopy system shown in Figure 2, the approach presented here can be applied to other tethered and untethered devices. Furthermore, we note that any source of magnetic field that, for the purpose of actuation, can be sufficiently approximated by the point-dipole magnetic field model exhibits the singularity described in Section 3. This affects any pose estimation method that uses a single source of magnetic field with the exception of methods that make multiple measurements while rotating or translating the magnet, such as the one used by Popek et al. (2017). Therefore, the methods described herein can be adopted in other systems with different schemes of magnetic actuation. The assumption made in this paper is that, similar to the capsules in Salerno et al. (2012); Di Natali et al. (2013, 2016), the capsule contains one inertial sensor (IMU) and at least three single axis magnetic field (Hall effect) sensors arranged orthogonally so as to measure the magnetic field in all three axes. While it is further assumed that the capsule contains a permanent magnet in order to enable magnetic actuation, our method can be used in applications where this internal magnet is not necessary (Beccani et al. 2013). An additional contribution of this paper stems from our use of a state estimation technique based on a parallel implementation of a particle filter to combine all available sensor information in a stochastic framework. Experimental demonstration of closed-loop control of a tethered magnetic device making use of the developed pose estimation technique is also provided in order to ascertain that the technique is suitable for its intended application.

2 Related Work and Clinical Motivation

Systems for active magnetic actuation generally use either electromagnets or permanent magnets to generate and control external magnetic fields. The forces and torques created by these fields provide a mechanism for wirelessly actuating capsule-like magnetic devices inside the patient. The use of electromagnets has been reported in (Keller et al. 2012; Petruska and Abbott 2014; Lucarini et al. 2015). Despite their advantage of greater controllability, their limitations with respect to their cost, large size, small workspace, and need for large electrical currents have yet to be overcome. Consequently, permanent magnets are becoming the more common choice of actuation for these systems since they are able to maintain compact form factors while being able to efficiently induce relevant forces and torques on the capsule (Carpi and Pappone 2009; Valdastri et al. 2012a; Mahoney and Abbott 2015). While it is possible to have an arrangement of permanent magnets that are fixed in space but are allowed to rotate for actuation (Ryan and Diller 2016), their workspace is severely limited without using extremely large magnets (Carpi and Pappone 2009). A better trade-off between magnet size and workspace can be achieved by using a single permanent magnet mounted on a 6 DOF robot manipulator, as used by our group and other researchers worldwide (Wang et al. 2010; Salerno et al. 2013a; Valdastri et al. 2012a; Mahoney and Abbott 2014, 2015; Taddese et al. 2016a,b; Slawinski et al. 2017).

Notwithstanding how the external magnetic field is generated, existing magnetic actuation systems can also be classified based on the method of propulsion used: (1) rotational propulsion via magnetic torque where the capsule is rotated to create rolling (Yim and Sitti 2012; Mahoney and Abbott 2011; Maul and Alici 2013) or spiral motion (Ishiyama et al. 2001; Sendoh et al. 2003; Fountain et al. 2010; Zhou et al. 2013; Mahoney and Abbott 2014; Ye et al. 2015), and (2) direct propulsion by simultaneously using magnetic force and torque (Valdastri et al. 2012a; Lucarini et al. 2015; Mahoney and Abbott 2015; Taddese et al. 2016a) to translate the capsule and control its orientation. Since the force and torque induced by the external magnetic field drop as $\frac{1}{r^4}$ and $\frac{1}{r^3}$ respectively, where r is the distance between the source and the capsule, using the torque for propulsion is preferable. However, current rotational propulsion systems designed for GI exploration rely on friction against lumens, and thus can only be propelled in collapsed lumens resulting in reduced polyp detection efficiency in parts of the GI tract such as the colon.

In this paper, we focus on direct propulsion systems, which have been used on tethered (Valdastri et al. 2012a; Lien et al. 2012; Taddese et al. 2016a,b; Slawinski et al. 2017) and untethered (Mahoney and Abbott 2015; Denzer et al. 2015) devices. With the use of a robot manipulator, direct propulsion systems have been demonstrated on soft-tethered devices, which have extended capabilities such as video streaming, therapeutic tools, insuation and water irrigation (Valdastri et al. 2012a).

Despite the differences in how the driving magnetic fields are generated and what method of propulsion is used, actively controlled magnetic actuation systems require pose estimation in order to successfully translate to clinical settings. We make a distinction here from current clinical methods that localize the capsule relative to anatomical landmarks for subsequent treatment (Than et al. 2012; Slawinski et al. 2015). In this work, we focus on techniques that estimate the pose of the capsule with respect to a fixed global frame so as to enable closed-loop control. The majority of prior works in the literature assume that the capsule is free to move inside the patient once the lumen is distended with gas or liquid. Therefore, the externally generated magnetic field is controlled with the expectation that the capsule would align to it (Mahoney and Abbott 2015). While this assumption may hold true in most cases, there are often occasions when the capsule gets trapped in a tissue fold and the magnetic coupling is lost. This can be ascertained from results reported from comparative trials where open loop systems were used. In Arezzo et al. (2013), a robot manipulator with a permanent magnet was used to drive a tethered capsule in a phantom ex-vivo model of the colon and procedure times were three times longer when compared against standard endoscopy due to repeated loss of magnetic coupling. In Denzer et al. (2015), a magnetic resonance imaging (MRI) machine was modified by a joint team of researchers from Olympus and Siemens for magnetic actuation of an untethered device in the stomach. In their clinical trial, a low lesion detection sensitivity of 61.9% was reported suggesting difficulty in maneuvering. These results demonstrate the acute need for closed-loop systems that utilize pose estimation feedback.

The criteria for success of a pose estimation algorithm for robotic capsule endoscopy is three fold. First, a level of accuracy suitable for closed-loop control is needed. Since there is no established benchmark for accuracy in magnetic capsule endoscopy applications, our goal in this paper is to achieve equivalent or better performance as prior pose estimation methods where closed-loop control has been demonstrated. Second, the system must have an update rate appropriate for real-time operation. Although difficult to define precisely, a rate of 100 Hz or faster is generally considered acceptable. This allows the robotic controller to compensate for any deviation of the capsule from the commanded pose or trajectory promptly so as to ensure the safety and clinical efficacy of the system. Finally, the workspace for the pose estimation system must be compatible with endoscopic magnetic actuation, which has a typical working distance of 150mm (Ciuti et al. 2009).

3 Background

For the sake of completeness, a summary of the pose estimation methods described in Di Natali et al. (2013) and Di Natali et al. (2016) is given here. Then, the problems of singularity regions and yaw initialization are explained in further detail. Hereafter, bold letters indicate vectors (v) or vector valued functions (B), a hat over a bold letter indicates a unit vector (v̂), and except otherwise stated, an uppercase italicized letter indicates a matrix (M). I denotes the identity matrix.

In both methods of pose estimation, the capsule has six Hall Effect sensors in an arrangement that approximates a pair of 3-axis Hall Effect sensors separated by a known distance. Inertial sensors are also available and are used to rotate sensor readings into the frame of the EPM.

3.1 Summary of Existing Pose Estimation Methods

In the method reported in Di Natali et al. (2013), a look-up table mapping a uniform grid of positions in cylindrical coordinates to magnetic field vectors is generated offline using a finite element method (FEM) software according to the magnetic current model B : ℝ³ → ℝ³:

$$\mathbf{B}(\mathbf{p})=\frac{{\mu }_0}{4\pi }\underset{S^{″}}{\oint }{\mathbf{j}}_{\mathbf{m}}({\mathbf{p}}^{″})\times \frac{(\mathbf{p}-{\mathbf{p}}^{″})}{{\mid \mathbf{p}-{\mathbf{p}}^{″}\mid }^3}d{s}^{″}$$ (1)

where p is a point on the uniform grid, p′ is a point on the surface of the EPM and j_m is the equivalent surface current density of the EPM. The authors take advantage of the azimuthal symmetry of their cylindrical EPM to reduce the dimension of the look-up table to a plane. This symmetry can be exploited in cylindrical and spherical magnets, but is not available in other geometries such as cuboid magnets. During operation, the yaw angle of the capsule is first initialized to a known value. For each magnetic field measurement, a sequential search of the look-up table is performed to find the two points that closely match the measured magnetic fields from each pair of Hall sensors. The average of these two points is taken as the center of the capsule. A new yaw angle is then calculated based on the line segment between the two points.

In the approach described in Di Natali et al. (2016), an iterative method is used where small changes in magnetic field are linearly mapped to small changes in position by the Jacobian of (1):

$$\frac{\partial \mathbf{B}(\mathbf{p})}{\partial \mathbf{p}}=J=\left[\begin{array}{lll}\frac{\partial B_x}{\partial p_x}\hfill & \frac{\partial B_x}{\partial p_y}\hfill & \frac{\partial B_x}{\partial p_z}\hfill \\ \frac{\partial B_y}{\partial p_x}\hfill & \frac{\partial B_y}{\partial p_y}\hfill & \frac{\partial B_y}{\partial p_z}\hfill \\ \frac{\partial B_z}{\partial p_x}\hfill & \frac{\partial B_z}{\partial p_y}\hfill & \frac{\partial B_z}{\partial p_z}\hfill \end{array}\right]$$ (2)

In order to efficiently compute this Jacobian, a look-up table mapping positions in cylindrical coordinates to Jacobians is generated offline on a uniform grid of points. During operation, the position and yaw angle are first initialized to known values. Designating a measured magnetic field vector as b, for each iteration, changes in magnetic field are computed as Δb = b_new − b_old. The new position is then determined as:

$${\mathbf{p}}_{\mathit{new}}={\mathbf{p}}_{\mathit{old}}+J^{-1}\mathbf{\Delta }\mathbf{b}$$ (3)

The orientation is determined by applying inertial navigation algorithms on accelerometer and gyroscope measurements.

3.2 Limitations of Existing Pose Estimation Methods

For theoretical analysis, without any loss of generality, we will assume the EPM is an axially magnetized cylindrical magnet, but the principles of singularity described herein apply to all magnets that can sufficiently be approximated by a dipole model. The magnetic field of the EPM, B_E : ℝ³ → ℝ³, is then given by:

$${\mathbf{B}}_{\mathbf{E}}(\mathbf{p})=\frac{{\mu }_{\mathbf{0}}\Vert {\mathbf{m}}_{\mathbf{E}}\Vert }{\mathbf{4}\pi {\Vert \mathbf{p}\Vert }^{\mathbf{3}}}(\mathbf{3}\widehat{\mathbf{p}}{\widehat{\mathbf{p}}}^{\top }{\widehat{\mathbf{m}}}_{\mathbf{E}}-{\widehat{\mathbf{m}}}_{\mathbf{E}})$$ (4)

where p is the vector from the EPM to the capsule, $\widehat{\mathbf{p}}={[\begin{array}{lll}{\widehat{p}}_x\hfill & {\widehat{p}}_y\hfill & {\widehat{p}}_z\hfill \end{array}]}^{\top }$ is the unit vector along p, and m_E is the dipole moment of the EPM. Since the accuracy of this model increases as ||p|| gets larger (Petruska and Abbott 2013), it is adequate for characterizing singularity regions.

3.2.1 Regions of Magnetic Field Singularity

Assuming the orientation of the capsule is accurately determined, position estimation can be expressed by the nonlinear inverse problem ${\mathbf{B}}_{\mathbf{E}}^{-\mathbf{1}}(\mathbf{p})$. A region of singularity is where infinite solutions exist to this problem. Let ℘_s designate the plane that is normal to the dipole moment and passes through the center of the EPM, i.e., ${\mathcal{P}}_s=\{{\mathbf{p}}_s\in {ℝ}^3\mid {\mathbf{p}}_s^{\top }{\widehat{\mathbf{m}}}_{\mathbf{E}}=0\}$. On this plane, we have:

$${\mathbf{B}}_{\mathbf{E}}(\mathbf{p})=-\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{E}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}{\widehat{\mathbf{m}}}_{\mathbf{E}}$$ (5)

$$\widehat{{\mathbf{B}}_{\mathbf{E}}(\mathbf{p})}=-{\widehat{\mathbf{m}}}_{\mathbf{E}}$$ (6)

$$\Vert {\mathbf{B}}_{\mathbf{E}}(\mathbf{p})\Vert =\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{E}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}$$ (7)

Since $\widehat{{\mathbf{B}}_{\mathbf{E}}(\mathbf{p})}$ is constant in the EPM frame and ||B_E(p)|| changes only when |p|³ changes, the set of solutions to ${\mathbf{B}}_{\mathbf{E}}^{-\mathbf{1}}(\mathbf{p})$ is a circle of radius r on ℘_s defined as C_s = {c_s ∈ ℘_s | ||c_s|| = r}. That is, when the capsule is located on ℘_s, there exist an infinite number of vectors of equal magnitude and direction forming a circle C_s on ℘_s and centered on the EPM rendering infinite solutions to ${\mathbf{B}}_{\mathbf{E}}^{-\mathbf{1}}(\mathbf{p})$. Therefore, additional information is required to constrain the solution to a single pose.

Additional insight as to where the regions of singularity occur can be gained by analyzing the Jacobian, J, of (4) with respect to p. Figure 3 shows the condition number of J, defined as the ratio of the maximum and minimum singular values of J, i.e., $\kappa (J)=\frac{{\sigma }_{\mathit{max}}(J)}{{\sigma }_{\mathit{min}}(J)}$ on three different planes including ℘_s. As indicated by the colors in the figure, J becomes ill-conditioned near ℘_s and becomes singular on ℘_s while the planes parallel to ℘_s but farther from the center of the magnet are non-singular.

Figure 3.

Regions of magnetic field singularity as indicated by high condition numbers of the Jacobian matrix. Note that the plot shows a plane near the singularity plane ℘_s because the condition number on ℘_s is infinite. Two other planes parallel to ℘_s are displayed to show that the singularity region only exists near the center of the magnet.

3.2.2 Yaw Angle Initialization

Both algorithms in Di Natali et al. (2013) and Di Natali et al. (2016) require the accurate initialization of the yaw angle. Since both algorithms depend on converting the measured magnetic fields from the capsule’s reference frame to the EPM’s reference frame, the solutions found by the algorithms are sensitive to yaw angle errors. As discussed earlier, both algorithms use an incremental approach to estimate the yaw angle and are prone to sensor noise with errors increasing with longer periods of use.

To determine the sensitivity of these algorithms to yaw angle error, Monte Carlo simulations were performed at random positions in a 300mm × 300mm × 150mm workspace centered on the EPM. Position errors were obtained by computing the distance between the true position of the test point from the simulated point. At each point, the yaw angle error ranged from 0° to 5°. As shown in Figure 4, distance errors can be as high as 15mm in some regions of the workspace for a yaw angle error of 5°. While an error of 15mm might be acceptable for closed-loop control, with the addition of errors from sensor bias and noise, the total error might be much higher. Furthermore, although it can be argued that one can initialize the yaw angle to within 5° of the true yaw, accurate initialization of the yaw angle can be very difficult in clinical settings after a procedure has been started. The pose estimation methods in Di Natali et al. (2013) and Di Natali et al. (2016) would require the capsule be removed from the patient, reinitialized, and reinserted leading to prolonged procedure times.

Figure 4.

Position error as a function of yaw error. The errors can be as high as 15 mm in some regions of the workspace for a yaw angle error of 5°.

4 Methods

4.1 Hybrid Magnetic Field

As shown in Figure 5, if we augment the system with an electromagnetic coil that generates a weak time-varying magnetic field and attach it to the EPM such that their dipole moments are orthogonal, the static field of the EPM and the time-varying field of the coil can be used simultaneously to obtain an additional set of equations that allow for solving for the position and yaw angle of the capsule.

Figure 5.

EPM augmented with an electromagnetic coil.

Orthogonal collocation of the EPM and the electromagnetic coil ensures that in the singularity region of the EPM, the magnetic field of the coil is always orthogonal to the magnetic field of the EPM. If instead the coil was placed at a fixed location, e.g. embedded in the surgical table, it would be possible for the magnetic fields of the EPM and the coil to become aligned during magnetic manipulation. If this alignment were to happen in the singularity region of the EPM, the number of available equations for solving the inverse problem would be reduced. As a result, the singularity problem remains unmitigated. Another benefit of collocation is that it allows for a dynamic workspace that moves with the actuating magnet. This ensures that an adequate signal to noise ratio is maintained at the location of the capsule without requiring a large electromagnet.

For a given workspace, the time-varying field is made strong enough to be detected by the magnetic field sensors in the capsule without inducing enough force and torque to physically affect the capsule’s pose. A time-varying signal is used in order to measure the magnetic fields of the EPM and the coil separately. In contrast, if two static magnetic fields were used, it would not be possible to make separate measurements owing to the principle of superposition where the vector sum of the magnetic fields is measured. This is not desirable as it reduces the number of available equations. Goertzel’s tone-detection algorithm (Goertzel 1958; Turner 2003) is used to extract the magnitude and phase of the time-varying signal for each sensor. The measured values are assembled to create a vector that allows us to treat the coil as if it were another permanent magnet with the same origin as the EPM.

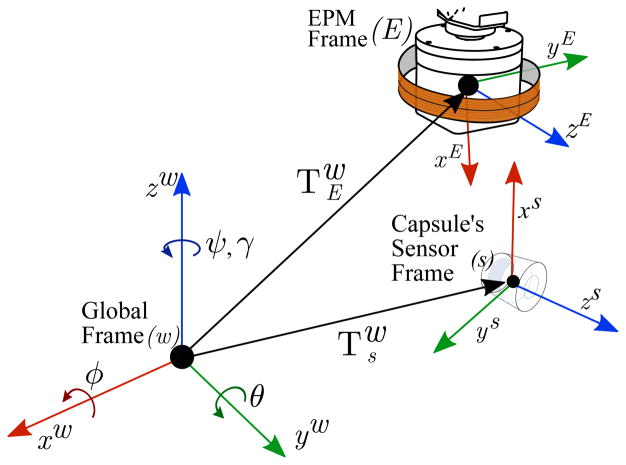
For the following analysis, measured magnetic fields from the EPM ( ${\mathbf{b}}_{\mathbf{E}}^s$) and electromagnetic coil ( ${\mathbf{b}}_{\mathbf{C}}^s$) are rotated to the EPM frame by the following expression:

$${\mathbf{b}}_{\mathbf{E}}=R_w^E{R}_s^w{\mathbf{b}}_{\mathbf{E}}^s$$ (8)

$${\mathbf{b}}_{\mathbf{C}}=R_w^E{R}_s^w{\mathbf{b}}_{\mathbf{C}}^s$$ (9)

For notational convenience, we omit the frame designator, (·)^E, for vectors expressed in the EPM frame (see Figure 6). The rotation matrix $R_w^E$ represents the rotation of the world frame (w) with respect to the EPM frame (E) and is assumed to be known from the robot manipulator. $R_s^w$ is the rotation of the capsule’s sensor (s) frame with respect to the world frame. Due to yaw angle initialization errors, $R_s^w$ is unknown and has to be solved for in our algorithm. It is useful to view this matrix as:

$$R_s^w=R_z(\gamma ){\stackrel{\sim }{R}}_s^w$$ (10)

where

Figure 6.

Coordinate frames of the magnetic pose estimation system showing the global frame (w), the capsule’s sensor frame (s) and the EPM frame (E).

$$R_z(\gamma )=\left[\begin{array}{ccc}cos(\gamma )& -sin(\gamma )& 0\\ sin(\gamma )& cos(\gamma )& 0\\ 0& 0& 1\end{array}\right],$$ (11)

${\stackrel{\sim }{R}}_s^w$ is the rotation of the capsule’s sensor frame (s) with respect to the world frame (w) computed using inertial measurements, and γ is the yaw angle error. The tilde symbol (·̃) is used to indicate that there is yaw angle error in the rotation matrix.

Incorporating the capsule orientation and the new additional magnetic field, the new system of equations is given by:

$$R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{E}}^s={\mathbf{B}}_{\mathbf{E}}(\mathbf{p})$$ (12)

$$R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{C}}^s={\mathbf{B}}_{\mathbf{C}}(\mathbf{p})$$ (13)

where

$${\mathbf{B}}_{\mathbf{E}}(\mathbf{p})=\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{E}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}(3\widehat{\mathbf{p}}{\widehat{\mathbf{p}}}^{\top }{\widehat{\mathbf{m}}}_{\mathbf{E}}-{\widehat{\mathbf{m}}}_{\mathbf{E}})$$ (14)

$${\mathbf{B}}_{\mathbf{C}}(\mathbf{p})=\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{C}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}(3\widehat{\mathbf{p}}{\widehat{\mathbf{p}}}^{\top }{\widehat{\mathbf{m}}}_{\mathbf{C}}-{\widehat{\mathbf{m}}}_{\mathbf{C}})$$ (15)

and m_E and m_C are the dipole moments of the EPM and coil respectively. Without any loss of generality, we will assign the dipole moment direction vectors to ${\widehat{\mathbf{m}}}_{\mathbf{E}}=\widehat{\mathbf{z}}={[\begin{array}{ccc}0& 0& 1\end{array}]}^{\top }$ and ${\widehat{\mathbf{m}}}_{\mathbf{C}}=\widehat{\mathbf{x}}={[\begin{array}{ccc}1& 0& 0\end{array}]}^{\top }$. Substituting into (12) and (13) and simplifying, we have:

$$R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{E}}^s=\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{E}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}(3{\widehat{p}}_z\widehat{\mathbf{p}}-\widehat{\mathbf{z}})$$ (16)

$$R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{C}}^s=\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{C}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}(3{\widehat{p}}_x\widehat{\mathbf{p}}-\widehat{\mathbf{x}})$$ (17)

which expands to

$$R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathrm{E}}^s=\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{E}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}\left(\left[\begin{array}{c}3{\widehat{p}}_z{\widehat{p}}_x\\ 3{\widehat{p}}_z{\widehat{p}}_y\\ 3{\widehat{p}}_z^2-1\end{array}\right]\right)$$ (18)

$$R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{C}}^s=\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{C}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}\left(\left[\begin{array}{c}3{\widehat{p}}_x^2-1\\ 3{\widehat{p}}_x{\widehat{p}}_y\\ 3{\widehat{p}}_x{\widehat{p}}_z\end{array}\right]\right)$$ (19)

We analyze these algebraic equations to determine if there are singularities in the hybrid system that would result in infinite solutions to the inverse problem of finding the pose given magnetic field measurements. We do not imply that the equations can be used directly to solve for the unknowns. Nevertheless, the analysis, without the need for extensive simulations, shows that an additional magnet placed orthogonally gives enough information so that a nonlinear solver can find a unique solution. However, the analysis does not take into account the stochastic nature of the signals; therefore, for practical implementation, we use the particle filter based state estimator described later in Section 4.2.

In most cases, the system is over-determined and the unknown values can be solved. However, due to the symmetry of magnetic fields, it is possible to find more than one solution to the system of equations, yet the number of solutions is always finite. Further, multiple solutions due to symmetry exist in disjoint regions of the workspace making it possible to choose proper solution based on previous poses of the capsule. From (16) and (17), we note that if γ is known as a result of accurate initialization as assumed in Di Natali et al. (2013, 2016), the singularity problem is eliminated. That is, if either p̂_x = 0 or p̂_z = 0, (16) or (17) can be used to estimate the capsule’s position respectively. If both p̂_x and p̂_z are zero, we immediately know p̂_y = ±1 and |p| can be determined from either (16) or (17).

If γ is not known, we have three conditions, namely, no singularity, singular region of one magnet (EPM or coil), and singular region of both magnets (EPM and coil):

1. p̂_x ≠ 0 and p̂_z ≠ 0: Not in singularity. The system is overdetermined and all unknowns, p̂_x, p̂_y, p̂_z, |p| and γ, can be solved.

2. Either p̂_x = 0 or p̂_z = 0 : The two cases represent singular regions for each magnet. However, p is only in the singularity region of one of the magnets. We show in either case that all unknowns can be solved.

   1. p̂_x = 0: Applying this constraint, we have:

      $$R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{E}}^s=\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{E}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}\left[\begin{array}{c}0\\ 3{\widehat{p}}_z{\widehat{p}}_y\\ 3{\widehat{p}}_z^2-1\end{array}\right]$$ (20)

      $$R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{C}}^s=\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{C}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right]$$ (21)

      $$\Vert R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{E}}^s\Vert =\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{E}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}\sqrt{3{\widehat{p}}_z^2+1}$$ (22)

      $$\Vert R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{C}}^s\Vert =\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{C}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}$$ (23)
      We note that |p| can be solved from (23) since

      $$\Vert R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{C}}^s\Vert =\Vert {\mathbf{b}}_{\mathbf{C}}^s\Vert .$$
      p̂_z can then be solved from (22), and p̂_y can be solved from the unity constraint |p̂| = 1. Although multiple solutions are possible for p̂_y and p̂_z due to the square root terms, as mentioned earlier, workspace and continuity constraints can be used to eliminate wrong solutions. Since only γ is left unknown, it can be solved as the angle between the measured and calculated magnetic field vectors projected on the the xy-plane. A more robust solution can be found by casting it as a least squares optimization problem,

      $$\gamma =\underset{R_z(\gamma )\in \mathbb{S}\mathbb{O}(3)}{argmin}{\Vert R_z(\gamma )P{\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{E}}^s-P{R_w^E}^{\top }{\mathbf{B}}_{\mathbf{E}}(\mathbf{p})\Vert }^2+{\Vert R_z(\gamma )P{\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{C}}^s-P{R_w^E}^{\top }{\mathbf{B}}_{\mathbf{C}}(\mathbf{p})\Vert }^2$$ (24)

      where P is a projection matrix onto the xy-plane and B_E(p) and B_C(p) are the calculated magnetic field vectors at p, which has already been determined. A well known closed form solution for (24) can be found in the literature (Arun et al. 1987).

   2. p̂_z = 0: Similarly, we have:

      $$R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{E}}^s=\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{E}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}\left[\begin{array}{c}0\\ 0\\ -1\end{array}\right]$$ (25)

      $$R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{C}}^s=\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{C}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}\left[\begin{array}{c}3{\widehat{p}}_x^2-1\\ 3{\widehat{p}}_x{\widehat{p}}_y\\ 0\end{array}\right]$$ (26)

      $$\Vert R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{E}}^s\Vert =\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{E}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}$$ (27)

      $$\Vert R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{C}}^s\Vert =\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{C}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}\sqrt{3{\widehat{p}}_x^2+1}$$ (28)

      Here, |p| can be solved from (27). p̂_x can then be solved from (28) and p̂_y from the unity constraint |p̂| = 1. Finally γ can be found using (24).

3. p̂_x = 0 and p̂_z = 0: This condition occurs when p is in the singularity region of both magnets. From the unity constraint, p̂_y = ±1. After substitution, we have:

   $$R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{E}}^s=\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{E}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}\left[\begin{array}{c}0\\ 0\\ -1\end{array}\right]$$ (29)

   $$R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{C}}^s=\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{C}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}\left[\begin{array}{c}-1\\ 0\\ 0\end{array}\right]$$ (30)

   $$\Vert R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{E}}^s\Vert =\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{E}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}$$ (31)

   $$\Vert R_w^E{R}_z(\gamma ){\stackrel{\sim }{R}}_s^w{\mathbf{b}}_{\mathbf{C}}^s\Vert =\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{C}}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}$$ (32)

   |p| can readily be solved from (31) or (32) and can be found using (24).

4.2 Magnetic Pose Estimation with Particle Filters

Particle filters or Sequential Monte Carlo methods (SMC) are a class of recursive Bayesian state estimation techniques often used for object tracking and localization (Chen 2003). In these methods, the posterior distribution, p(x_k|z_1:k), of the state x_k at time k conditioned on a time series of measurements z_1:k = {z_i, i = 1, 2, … , k} is represented by a set of point masses or particles with corresponding importance weights, $w_k^i$. The nonparametric representation of the probability density function (pdf) and the use of Monte Carlo techniques allow particle filters to overcome limiting assumptions made in other state estimation techniques such as Kalman filters (Chen 2003), where process and measurement models are linear and noise distributions are Gaussian.

In this paper, we use the sampling importance resampling (SIR) variant of the particle filter (Gordon et al. 1993). At each time step, the SIR algorithm performs a prediction, which consists of drawing samples from the prior density, $p({\mathbf{x}}_k\mid {\mathbf{x}}_{k-1}^i)$, creating a new set of particles. The process model of the system ${\mathbf{x}}_k={\mathbf{f}}_k({\mathbf{x}}_{k-1}^i,{\mathbf{v}}_{k-1}^i)$, where ${\mathbf{v}}_{k-1}^i$ is the process noise, can be used to generate a sample where the pdf $p({\mathbf{v}}_{k-1}^i)$ is assumed to be known. The importance weights of the newly sampled particles are then updated based on the likelihood function $p({\mathbf{z}}_k\mid {\mathbf{x}}_k^i)$, which makes use of the measurement model z_k = h(x_k, n_k) where n_k is the measurement noise. After normalization of the importance weights, a resampling step is performed. This step samples from the set of particles with replacement so as to eliminate particles with small weights and reinforce particles with large weights. Resampling is necessary in order to avoid a condition known as “weight degeneracy” or “sample impoverishment” where only a few particles are left with nonzero weights after a few iterations of the algorithm. The resampled set of particles is the discrete approximation of the posterior p(x_k|z_1:k). A more detailed account of particle filters and the SIR algorithm can be found in Arulampalam et al. (2002) or Chen (2003).

For the present problem of magnetic pose estimation and tracking, we first make use of the complementary filter of Mahony et al. (2008) for fusing accelerometer and gyroscope measurements. The output of the filter is an estimate of the capsule’s rotation with an unknown yaw offset, γ. The position of the capsule and the yaw angle offset comprise the state, ${\mathbf{x}}_k={[\begin{array}{cccc}x& y& z& \gamma \end{array}]}^{\top }$, to be estimated with respect to a world frame.

4.2.1 Process Model

It is known that using a process model that incorporates actuation control inputs would lead to better state estimation. However, in applications such as magnetically actuated capsule endoscopy, the motion of the object being tracked can be, at times, significantly different from commanded motion due to environmental factors (e.g., capsule trapped in a tissue fold, peristalsis), making it difficult to construct an accurate motion model. In this paper, we demonstrate that it is sufficient to use the random walk process model given by:

$${\mathbf{f}}_k({\mathbf{x}}_{k-1}^i,{\mathbf{v}}_{k-1}^i)={\mathbf{x}}_{k-1}^i+{\mathbf{v}}_{k-1}^i$$ (33)

where

$${\mathbf{v}}_{k-1}^i~\mathcal{N}(0,Q)$$ (34)

is a sample from a normal distribution and Q is a covariance matrix empirically chosen as a trade-off between convergence speed and jitter of the pose estimate. For our experiments, Q = diag(0.0015, 0.0015, 0.0015, 0.01)

4.2.2 Measurement Model

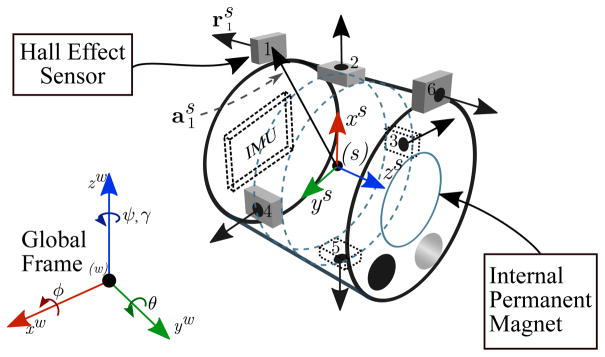
As shown in Figure 8, our system uses six single axis Hall effect sensors positioned in the capsule so as to approximate two triaxial sensors. We use a signal processing technique to separately measure the magnetic fields from the EPM and the electromagnetic coil (see Section 5). Given the relative position vector, ${\mathbf{a}}_i^s$, of each Hall sensor from the center of the capsule, the sensor output is computed as the projection of the magnetic field at the sensor in the direction of the sensor’s normal vector, ${\mathbf{r}}_i^s$.

Figure 8.

The six Hall effect magnetic field sensors and the inertial measurement unit (IMU) found inside the capsule. ${\mathbf{m}}_i^s$ is relative position vector of each Hall sensor from the center of the capsule and ${\mathbf{r}}_i^s$ is each Hall sensor’s normal vector, which corresponds its the sensing direction.

$$b_{{\mathbf{E}}_i}^s={{\mathbf{r}}_i^s}^{\top }{R}_E^s{\mathbf{B}}_{\mathbf{E}}(T_s^E({\mathbf{x}}_k^w){\mathbf{a}}_i^s)$$ (35)

$$b_{{\mathbf{C}}_i}^s={{\mathbf{r}}_i^s}^{\top }{R}_E^s{\mathbf{B}}_{\mathbf{C}}(T_s^E({\mathbf{x}}_k^w){\mathbf{a}}_i^s)$$ (36)

where i = 1, 2, … , 6 and $T_s^E:{ℝ}^3\times {\mathbb{S}}^1\to \mathbb{S}\mathbb{E}(3)$ is the homogeneous transformation of the capsule’s frame with respect to the EPM frame given by:

$$T_s^E({\mathbf{x}}^w)=T_w^E{T}_s^w({\mathbf{x}}^w)$$ (37)

$$=T_w^E\left[\begin{array}{cc}& x_x\\ R_z(\gamma ){\stackrel{\sim }{R}}_s^w& x_y\\ & x_z\\ \mathbf{0}& 1\end{array}\right]$$ (38)

and $T_w^E$ is the transformation of the world frame with respect to the EPM frame (see Figure 6), which is assumed to be known from the forward kinematics of the robot manipulator. We will denote magnetic field values calculated using (35) and (36) as ${\mathbf{z}}_k^{\ast }\in {ℝ}^{12}$. We assume that our the sensors’ noise is normally distributed. Thus, given a set of sensor measurements, z_k ∈ ℝ¹², our likelihood function is:

$$p({\mathbf{z}}_k\mid {\mathbf{x}}_k^i)=\frac{1}{{(2\pi )}^6{\mid R\mid }^{1/2}}{e}^{-\frac{1}{2}{({\mathbf{z}}_k-{\mathbf{z}}_k^{\ast })}^{\top }{W}_z{R}^{-1}({\mathbf{z}}_k-{\mathbf{z}}_k^{\ast })}$$ (39)

where R ∈ ℝ^12×12 is a covariance matrix that characterizes the noise in the magnetic field sensors and | · | is the determinant operator. W_z ∈ ℝ^12×12 is a diagonal weight matrix used to normalize the three orders of magnitude difference in the sensor outputs for the EPM and the coil. We found that the presence of W_z in the likelihood function to be of extreme importance. If left out, the likelihood function would be dominated by the error residuals from the EPM readings because the magnetic fields from the coil are very weak. This amounts to the algorithm completely ignoring the readings from the coil thereby facing the same challenges of singularity of a single EPM described in Section 3.2.1.

The choice of a magnetic field model for B_E and B_C directly impacts the accuracy of the pose estimate. Choosing the point-dipole model shown in (4) would result in reduced accuracy when the capsule is in close proximity to the source of external magnetic field. This is at odds with magnetic actuation because close proximity is necessary to induce enough force and torque; therefore, a better model is needed. Only spherical magnets would not exhibit this problem as (4) is known to perfectly model their magnetic fields (Petruska and Abbott 2013). For cylindrical magnets, while it is possible to employ finite element methods as used in (Salerno et al. 2013b; Di Natali et al. 2013, 2016), a more efficient closed form solution is available from Derby and Olbert (2009) using the generalized complete elliptic integral:

$$C(k_c,p,c,s)={\int }_0^{\pi /2}\frac{c{cos}^2\phi +s{sin}^2\phi }{({cos}^2\phi +p{sin}^2\phi )\sqrt{{cos}^2\phi +k_c^2{sin}^2\phi }}d\phi$$ (40)

which can be numerically solved in an efficient manner by using Bulirschs algorithm (Derby and Olbert 2009). For an electromagnetic coil with length 2b, radius a, turns per unit length n and current I, the magnetic field components in cylindrical coordinates (ρ, φ, z) are:

$$b_{\rho }=B_o[{\alpha }_{+}C(k+,1,1,-1)-{\alpha }_{-}C(k,1,1,1)]$$ (41)

$$b_{\phi }=0$$ (42)

$$b_z=\frac{B_{o}a}{a+\rho }[{\beta }_{+}C(k+,{\eta }^2,1,\eta )-{\beta }_{-}C(k_{-},{\eta }^2,1,\eta )]$$ (43)

where

$$B_o=\frac{{\mu }_0}{\pi }nI,$$ (44)

$$z_{\pm }=z\pm b,$$ (45)

$${\alpha }_{\pm }=\frac{a}{\sqrt{z_{\pm }^2+{(\rho +a)}^2}},$$ (46)

$${\beta }_{\pm }=\frac{z_{\pm }}{\sqrt{z_{\pm }^2+{(\rho +a)}^2}},$$ (47)

$$\eta =\frac{a-\rho }{a+\rho },$$ (48)

$$k_{\pm }=\sqrt{\frac{z_{\pm }^2+{(a-\rho )}^2}{z_{\pm }^2+{(a+\rho )}^2}}$$ (49)

For a permanent magnet with the same dimensions, the magnetic remanence B_r is equivalent to μ₀nI, thus (44) becomes

$$B_o=\frac{B_r}{\pi }$$ (50)

It is worth mentioning that in order to use this model at our desired update rate of 100 Hz, it was necessary to generate a look-up table that maps positions to magnetic field vectors. Without a look-up table, the update rate was reduced to 65 Hz using an Intel i7@3.60 GHz CPU.

4.2.3 Final Pose Estimate

The final pose estimate can be inferred from the posterior distribution, p(x_k|z_1:k), represented by the particles. The maximum a posteriori (MAP) estimate, defined as:

$${\mathbf{x}}_k^{\mathit{MAP}}=\underset{{\mathbf{x}}_k}{argmax}p({\mathbf{x}}_k\mid {\mathbf{z}}_{1:k})$$ (51)

is known to be a good estimate of the true state, especially in pose estimation applications where the posterior can be multimodal (Saha et al. 2009). One way to obtain the MAP estimate is to take the particle with the largest weight. The resultant estimate using this approach, however, can be very jittery. Therefore, in this paper, we use the robust mean, ${\overline{\mathbf{x}}}_k^{\mathit{MAP}}$, which is the weighted sum of particles inside a ball centered on the particle with the largest weight, x_{k;max weight}:

$${\overline{\mathbf{x}}}_k^{\mathit{MAP}}\approx \frac{{\sum }_i^{N}d({\mathbf{x}}_k^i)w_k^i{\mathbf{x}}_k^i}{{\sum }_i^{N}d({\mathbf{x}}_k^i)w_k^i}$$ (52)

where N is the number of particles. The function d : ℝ³ × 𝕊¹ → ℝ is given by

$$d({\mathbf{x}}_k^i)=\{\begin{array}{ll}1\hfill & \text{if}\Vert W_x({\mathbf{x}}_{k,max\_\text{weight}}-{\mathbf{x}}_k^i)\Vert <\eta \hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (53)

where W_x is a diagonal weight matrix and η is the desired radius of the ball. In our experiments, we set W_x = diag(1, 1, 1, 0) and η = 0.1.

When computing summations on γ ∈ 𝕊¹, we use the mean of circular quantities as the simple arithmetic mean is not suitable. This operation is given by:

$$\overline{\gamma }=\text{atan}2\left(\frac{{\sum }_i^{N}d({\mathbf{x}}_k^i)w_k^{i}sin({\gamma }^i)}{{\sum }_i^{N}d({\mathbf{x}}_k^i)w_k^i},\frac{{\sum }_i^{N}d({\mathbf{x}}_k^i)w_k^{i}cos({\gamma }^i)}{{\sum }_i^{N}d({\mathbf{x}}_k^i)w_k^i}\right)$$ (54)

The reconstructed pose estimate is finally given by:

$$T_s^w({\overline{\mathbf{x}}}_k^{\mathit{MAP}})=\left[\begin{array}{cc}& x_x\\ R_z(\gamma ){\stackrel{\sim }{R}}_s^w& x_y\\ & x_z\\ \mathbf{0}& 1\end{array}\right]$$ (55)

4.2.4 Initialization

Since our objective is to avoid accurate initialization, the particles are initialized by drawing from a uniform distribution within the bounds of a predefined workspace. Correspondingly, no initialization of the pose is required. The particle filter quickly converges solving for the position and the yaw offset. However, at least for initialization, the workspace should be set such that only one solution is available. This is accomplished by constraining the workspace to be contained in a single hemisphere of either the EPM or the electromagnetic coil. This constraint is necessary for all pose estimation techniques that use magnets with symmetrical magnetic fields.

5 System and Software Environment

5.1 Overview of the system

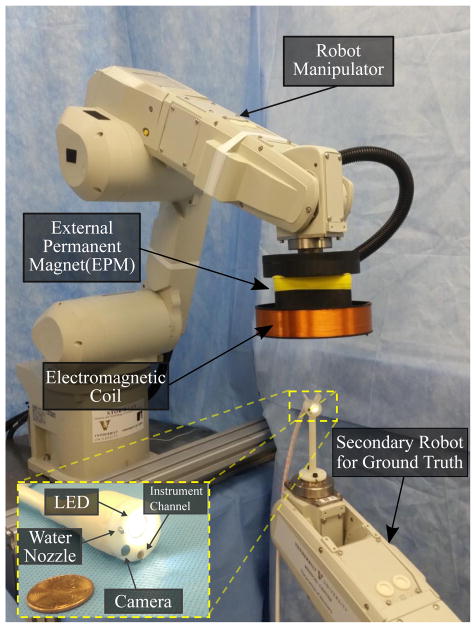
A general overview of the experimental setup is shown in Figure 7. At the end-effector of the 6 DOF robot manipulator (RV6SDL, Mitsubishi, Inc., Japan), a Neodymium Iron Boron (NdFeB) cylindrical permanent magnet (N52 grade, 101.6mm diameter and length, ND N-10195, Magnetworld AG, Germany) with axial magnetization and 1.48T remanence is held by means of a 3D printed box. An additional 3D printed structure holds the electromagnetic coil, which is built using 24 AWG wire with 160 turns arranged in two overlapping layers. Its diameter and height are, respectively, 180mm and 40mm. A second robot manipulator (RV6SDL, Mitsubishi, Inc., Japan) holds the capsule for precise ground truth measurements. The two robots are registered by least squares fitting a set of jointly measured 3D points (Arun et al. 1987).

Figure 7.

Experimental setup of the Magnetically Actuated Capsule (MAC) used in this paper.

The capsule (20mm diameter, 22mm length) has a soft-tether that enables functionalities that are commonly found in a traditional endoscope such as vision, illumination, insufflation, irrigation and the passage of endoscopic tools for biopsy. The soft-tether is also used as a channel for electrical wires connecting the internal sensors of the capsule to a signal acquisition unit. The capsule itself contains a small axially magnetized cylindrical NdFeB permanent magnet (N52 grade, 11.11mm diameter and length, D77-N52, K&J Magnetics, USA) with a magnetic remanence of 1.48 T. As shown in Figure 8, six Hall effect sensors (A1391, Allegro Microsystems, USA) are placed around the magnet so as to approximate two triaxial Hall sensors separated by a constant distance. The sensors are placed in locations where they are not saturated by the magnetic field from the internal magnet. Once assembled, a bias measurement of the magnetic fields is performed away from an external source of magnetic field. The biases are saved and are removed from sensor measurements during the operation of the pose estimation algorithm. In addition, the capsule contains an inertial measurement unit (LSM330DLC, STMicroelectronics, Switzerland) that is used to compute the orientation of the capsule with an unknown yaw offset. An illustration of the robotic magnetic actuation system is given in Extension 1. The generation of the input signal for the coil and the processing of data are achieved through a custom built circuit system that consists of the STM Nucleo development board (STM32F411RET, ARM Cortex M4) and a driver circuit, which are described more in detail in the following section.

5.2 Time-varying magnetic field

The electromagnetic coil, used to generate a time-varying magnetic field, is designed to satisfy two main constraints. First, it has to be small enough so as to not collide with the environment or the patient during a clinical procedure. Second, it needs to be able to generate a magnetic field strong enough to be detected by our sensors within the desired workspace. The design parameters were current, coil radius, number of wire turns, and number of wire layers. In order to determine the optimal values for the parameters, nonlinear optimization was performed using MATLAB (Mathworks, USA) where the volume of the coil was the minimization objective. In order to ensure adequate signal-to-noise ratio in the desired workspace, a larger workspace of 300mm was used in the optimization. The minimum magnetic field strength that can be measured by the Hall effect sensors at the boundary of this workspace was constrained to be above the noise floor of the sensors (10 μT).

The mechanical enclosure for the coil was designed to slide along the outer edges of the EPM in order to achieve the smallest volume for the whole assembly while minimizing the risk for collision with the other links of the robot. This implies that the coil and the EPM may not be centered at the same location; thus, the position of the coil with respect to the EPM was a parameter in our algorithm. For our experiments, the center of the coil was 45mm away from the center of the EPM along the x-axis of the EPM. It is worth mentioning, however, that varying this distance did not have a noticeable impact on the performance of the pose estimation system.

The time-varying signal was generated by the electromagnetic coil using an off-the-shelf H-bridge in combination with pulse width modulation (PWM) signals from the Nucleo development board. The resistance of the coil was measured to be 7 and its theoretical inductance was calculated to be 6.2 mH. A bench-top power supply was connected to the H-bridge with a set voltage of 17.3V resulting in an average current of 0.71A for a total power of 12.3W. The particular time-varying signal used was a square wave at a frequency of 300 Hz. This frequency was chosen because it allows for a sufficient number of wavelengths to be sampled within the sampling window of 10 ms. It is also low enough that no absorption of the magnetic field occurs as it passes through the human body (Sharma and Guha 1975). Furthermore, due to the high coercivity of NdFeB, from which the EPM is made, the effect of the relatively weak magnetic field generated by the coil on the EPM is negligible. Conversely, since the permeability of the EPM is very close to that of vacuum, the EPM does not act as a ux concentration device, such as soft iron. Thus, the magnetic field generated by the coil is not significantly affected by the presence of the EPM.

5.3 Signal Processing

The Nucleo development board was used to acquire data from the capsule’s internal sensors. The IMU was sampled at a rate of 100 Hz, while the Hall sensors were sampled at a rate of 18 kHz via a 16-bit analog-to- digital converter (AD7689, Analog Devices, USA) inside the capsule. By default, a Hall sensor measures the superposition of all static and time-varying signals at a point in space. In order to separately measure the strengths of the magnetic fields generated by the EPM and the coil, signal processing techniques were used. First, by using a sampling time window that was an integer multiple of the period of the time-varying signal, we ensured that the signal’s mean was zero. The EPM measurement was then obtained by simply averaging the raw sensor readings. To recover the amplitude of the time-varying signal, we used Goertzel’s algorithm (Goertzel 1958; Turner 2003), an efficient filter commonly used for tone detection. Two instances of the algorithm were run with 10 ms and 30 ms time windows respectively. The output from 10 ms instance was less reliable due to its relatively large bandwidth, but it provided the desired update rate for real-time pose estimation. The 30ms instance contained enough samples to apply data windowing functions (e.g. Blackman) making its bandwidth much narrower (Harris 1978). The particle filter described in Section 4 used the outputs of both instances, but assigned a lower weight to the 10 ms instance and only used it while the output from the 30 ms instance was pending.

It is worth mentioning that our scheme of sampling the sensors inside the capsule utilizes the serial peripheral interface (SPI) between the sensors and the microcontroller on the Nucleo board. To adapt our signal acquisition to wireless devices, it would be necessary to embed the microcontroller inside the capsule and only send the processed data wirelessly. This is because a wireless transceiver would be the most power intensive component in a wireless device that contains the same set of magnetic and inertial sensors as our capsule. Reducing the sampling rate of the magnetic field sensors would further conserve energy, however, doing so would negatively affect the tone detection algorithm by increasing its bandwidth. As a result, the overall system would be more susceptible to noise.

Examples of wireless devices that use a similar set of sensors can be found in the literature. The capsule in (Di Natali et al. 2014) contained the Allegro A1391 Hall effect sensors as well as the STMicroelectronics LIS331DLH accelerometer and used the Texas Instrument C2530 System-On-Chip microcontroller for data processing and wireless communication. The resulting capsule had a length of 60mm and diameter of 18mm which is approximately 2.3 times times the size of commercially available capsule endoscopes. Similarly, Popek et al. (2017) used the Allegro A1392 Hall effect sensors and the CC2530 in their capsule. The resulting capsule had a length of 42mm and diameter of 13.5mm which is approximately 1.4 times the size of commercially available capsule endoscopes (Popek et al. 2017).

5.4 Parallel Particle Filter Implementation

Our implementation of the particle filter makes use of the SMCTC C++ library (Johansen 2009). Modifications to the library were made to enable parallel computation where possible using the OpenMP API (OpenMP Architecture Review Board 2011). In particular, the update phase of the algorithm, where the likelihoods $p({\mathbf{z}}_k\mid {\mathbf{x}}_k^i)$ are computed, benefited from parallelization as the calculations for each particle are independent and computationally intensive. With these modifications, we were able to use 10000 particles on 4 cores of an Intel i7@3.60 GHz CPU with an average update rate of 100 Hz.

6 Experimental Validation and Results

In light of the criteria of success mentioned in Section 2, the pose estimation algorithm was experimentally validated in static and dynamic conditions. In the static condition tests, both the capsule and the EPM were fixed in known poses making it possible to compute average errors at each position including positions in the singular regions of the EPM and the coil. The dynamic test involved moving the capsule and/or the EPM at fixed speeds to characterize trajectory errors.

6.1 Validation in static conditions

As shown in Figure 7, the capsule was inserted into a 3D printed enclosure and secured to the secondary robot manipulator that was positioned in a known pose relative to the first robot. In the first set of static tests, the EPM was moved in a spiral trajectory along the surface of a hemisphere maintaining a constant distance from the capsule (see Figure 9). Six tests were performed with varying radii of the hemisphere ranging from 150mm to 200 mm. The maximum radius was limited to 200mm in order to constrain the test to regions of clinically relevant forces and torques induced on the capsule.

Figure 9.

Spiral trajectory used in static validation experiments. The red dots indicate the positions where the EPM was stopped and 25 points were collected.

6.1.1 Spiral Trajectory

A spiral trajectory was chosen to assess whether the accuracy of the system degraded with increasing distance. For each test, the EPM was stopped at 25 points along the trajectory and pose estimates were recorded for 30 seconds each. The pose estimation algorithm was restarted at each point to assess its ability to determine the yaw offset error. Pose errors were computed by taking the mean of the collected pose estimates and comparing them against the ground truth. Orientation errors are given in ZYX Euler angles, roll(ϕ), pitch(θ), and yaw(ψ), where the resultant rotation is:

$$R_s^w=R_{\mathbf{z}}(\psi )R_{\mathbf{y}}(\theta )R_{\mathbf{x}}(\varphi )$$ (56)

and the yaw(ψ) angle corresponds to the unknown yaw angle error γ, from Section 4.

Table 1 shows the overall accuracy of the system using the mean and standard deviations of the errors. In general, accuracy is expected to degrade with increasing distance as the magnetic field strengths weaken and become more susceptible to noise. The negligible differences in the standard deviations of the errors in Table 1, however, show that due to our high sampling rate, signal processing of the magnetic field measurements, and fusing of multiple sources of magnetic fields, this degradation was not observed. Yet, a larger position error was incurred in the y axis, which may be due to the fact that the capsule was in the singularity region of the EPM for a subset of the 25 points on the hemisphere reducing the number of constraining equations mapping poses to magnetic field vectors. Since the singularity plane of the EPM for these set of trials was the yz-plane, larger errors on the y axis can be expected. Additionally, the orientation error in ψ was larger than the other orientation angles since it was the only angle affected by the bias and noise characteristics of the magnetic field sources, while the other two angles were obtained from accelerometer measurements.

Table 1.

Average accuracy (mean ± std) of position estimates for static tests along a spiral trajectory

Radius of hemisphere	Δx	Δy	Δz	Δϕ	Δθ	Δψ
(mm)	(mm)	(mm)	(mm)	(°)	(°)	(°)
150	1.04 ± 1.42	3.67 ± 1.63	2.87 ± 1.05	0.93 ± 0.67	−0.95 ± 1.03	−4.73 ± 0.31
160	1.39 ± 1.42	3.81 ± 1.62	2.65 ± 1.00	1.00 ± 0.62	−1.05 ± 0.88	−5.06 ± 0.25
170	1.42 ± 1.39	3.97 ± 1.66	2.41 ± 0.92	1.00 ± 0.61	−1.09 ± 0.67	−5.62 ± 0.16
180	1.71 ± 1.42	4.19 ± 1.69	2.15 ± 0.94	1.02 ± 0.59	−0.86 ± 0.57	−5.62 ± 0.14
190	1.87 ± 1.40	4.32 ± 1.72	1.80 ± 0.91	1.05 ± 0.54	−0.84 ± 0.43	−5.65 ± 0.11
200	1.97 ± 1.38	4.35 ± 1.71	1.55 ± 0.88	1.11 ± 0.50	−0.84 ± 0.33	−5.66 ± 0.09

6.1.2 Evaluation in the Region of Singularity

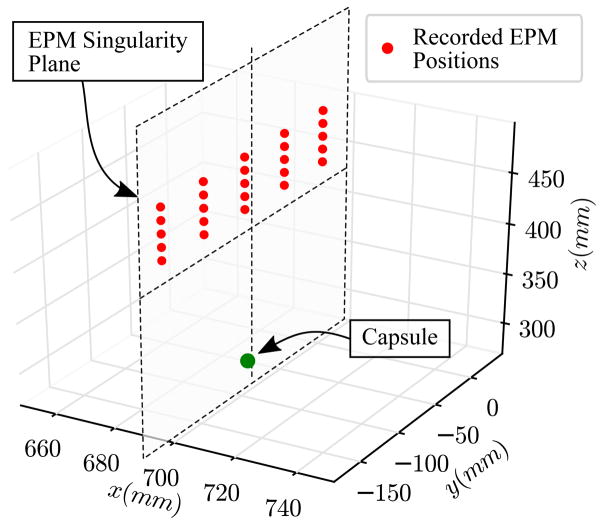
The second set of static tests evaluated the performance of the system in the singularity region of the EPM. As shown in Figure 10, the capsule was fixed in a single pose inside the EPM’s singularity region. The EPM was then placed on a grid of points defined by the plane of singularity. A total of 25 grid points spanning 200mm × 50mm were used where pose estimates were recorded for 30 seconds each. The average position errors were Δx = 2.85 ± 0.80 mm, Δy = 3.74 ± 1.53 mm, and Δz = 1.67 ± 0.88 mm. The average orientation errors were Δϕ =0.73 ± 0.60°, Δθ =−1.69 ± 0.15°, and Δψ = 3.76 ± 0.12°. To ensure the absence of singularity regions, the capsule was also placed on the line defined by the intersection of the singularity planes of the EPM and the coil. A total of 10 equally spaced points were used to record pose estimates for 30 seconds each. The average position errors were Δx = 1.21 ± 0.18 mm, Δy = 4.85 ± 1.34 mm, and Δz = 5.10 ± 0.68mm while the average orientation errors were Δϕ = 0.75 ± 0.10°, Δθ = −2.05 ± 0.13°, and Δψ = 1.08 ± 0.06°. The results show that the system performs well even in the singular regions of either magnet.

Figure 10.

Configuration for testing the singular regions of the EPM. With the capsule fixed in space, the EPM was placed on a grid of coplanar points. The EPM was oriented such that the capsule was always in its singularity plane.

The overall accuracy of the system for these set of tests was equivalent or better than the systems described in Di Natali et al. (2013) and Di Natali et al. (2016) without requiring an initialization step. For comparison, the accuracy of the system reported in Di Natali et al. (2013) was Δx = −3.4 ± 3.2 mm, Δy = −3.8 ± 6.2 mm, Δz = 3.4 ± 7.3mm in position and Δϕ = −6 ± 18°, Δθ = 3 ± 20°, Δψ = −19 ± 50° in orientation. With accurate initialization of both position and yaw angle, the system reported in Di Natali et al. (2016) achieved an accuracy of (in polar coordinates, r, z, θ′) Δr = 6.2 ± 4.4 mm, Δz = 6.9 ± 3.9 mm, Δθ′ = 5.4 ± 7.9° in position and Δϕ = 3.4 ± 3.2°, Δθ = 3.7 ± 3.5°, Δψ = 3.6 ± 2.6° in orientation. Given the results, we can conclude that our pose estimation algorithm readily satisfies the accuracy criteria.

6.1.3 Comparison with Prior Pose Estimation Methods

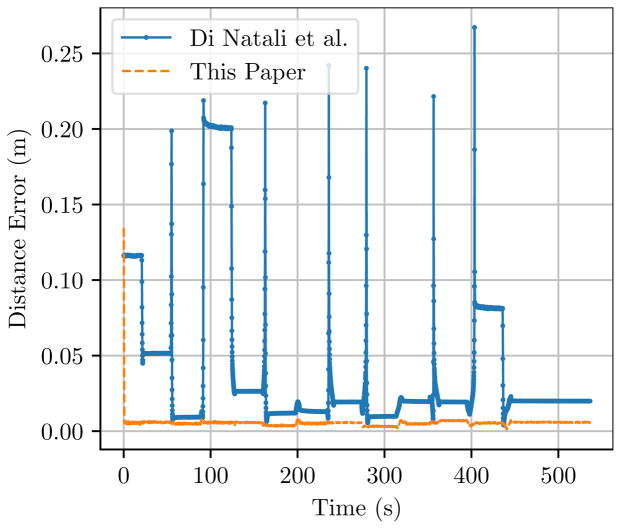
To provide a concrete example of the effect of magnetic singularity regions and demonstrate the scale of the singularity problem on previous 6 DOF pose estimation methods, we applied the algorithm described in Di Natali et al. (2013) to the data collected in the 150mm static spiral trajectory experiment. As the authors conclude in Di Natali et al. (2016), the long term performance of their iterative algorithm is susceptible to drift without periodic updates from their absolute pose estimation algorithm (Di Natali et al. 2013). The ill conditioning of the Jacobian in regions of singularity (Section 3.2) combined with the drift problem leads us to expect the performance of the iterative algorithm to be worse than their noniterative algorithm in Di Natali et al. (2013). Consequently, only a comparison between Di Natali et al. (2013) and the approach presented in this paper is given here. Figure 11 shows the distance error of the two methods during the spiral trajectory experiment. Severe performance degradation occurs in Di Natali et al. (2013) when the capsule is in or near the singularity region of the EPM. Large spikes can also be observed as the EPM moves along the spiral to one of the 25 test points (see Figure 12) and, in so doing, its singularity region crosses the position of the capsule. In contrast, the approach presented in this paper is robust to the presence of singularity regions.

Figure 11.

Comparison between the pose estimation algorithms in Di Natali et al. (2013) and this paper. Severe performance degradation occurs in Di Natali et al. (2013) when the capsule is in the singularity region of the EPM.

Figure 12.

Positions of the EPM where severe performance degradation occurs in Di Natali et al. (2013) when the capsule is in the singularity region of the EPM.

6.1.4 Effect of EPM Orientation

In order to explore the effect of the EPM’s orientation on the pose estimation algorithm, an additional static experiment was conducted. The EPM was moved to 10 points on a planar grid of 100mm × 100mm and at each point 10 different orientations were tested (see Figure 13). The grid was chosen to be in the xy plane so as to include singular and non-singular regions. The average position errors were Δx = −2.55 ± 2.89 mm, Δy = 2.60 ± 4.91 mm, Δz = −7.21 ± 1.84 mm. And the average orientation errors were Δϕ = 1.17 ± 0.30°, Δθ = −1.03 ± 4.18°, Δψ = 3.06 ± 0.65°. As can be seen from these values, the orientation of the EPM does not have a marked effect on the accuracy of the pose estimation algorithm.

Figure 13.

The ten orientations of the EPM and coil assembly that were tested in our experiment

6.2 Validation in dynamic conditions

Two types of experiments were conducted for validation under dynamic conditions. The static-dynamic experiment consisted of moving only the capsule along a trajectory while the EPM was static (see Extension 2). In the dynamic-dynamic experiment, both the capsule and the EPM moved along a trajectory keeping a constant relative speed (see Extension 3). In both cases, the trajectory was designed to mimic the general shape of a human colon (Alazmani et al. 2016). Moreover, in order to have ground truth measurements, a secondary robot manipulator was used to hold and move the capsule along the given trajectory. Errors were obtained by taking the average of the errors computed at each instance of time between the pose estimate and the ground truth.

6.2.1 Static-dynamic case

The motivation for the first case was to assess whether the particle filter, without an accurate motion model, could track the movement of the capsule. Table 2 shows the performance of the system at speeds of 10mm/s, 25mm/s and 50mm/s. The increase in the standard deviation of the position errors is correlated with increase in capsule speed indicating that the system is sensitive to the relative motion of the capsule. However, in most robotic capsule endoscopy applications, the relative motion of the capsule with respect to the EPM is expected to be minimal.

Table 2.

Average accuracy (mean ± std) of pose estimates for static-dynamic tests

Speed	Δx	Δy	Δz	Δϕ	Δθ	Δψ
(mm/s)	(mm)	(mm)	(mm)	(°)	(°)	(°)
10	−3.39 ± 6.76	−4.84 ± 5.23	4.06 ± 1.91	−0.96 ± 2.30	0.29 ± 1.73	−0.37 ± 2.84
25	−1.98 ± 7.70	−5.07 ± 5.67	4.49 ± 1.92	−1.75 ± 1.88	0.08 ± 1.55	−0.20 ± 2.79
50	0.70 ± 12.05	−3.33 ± 10.01	4.79 ± 2.74	−3.10 ± 2.14	−1.65 ± 3.44	−0.13 ± 2.69

6.2.2 Dynamic-dynamic case

The latter dynamic condition reects how the capsule would be used in a real scenario where the capsule is driven by a moving EPM. As such, the trajectory of the EPM was created by offsetting the capsule’s trajectory by a distance of 200 mm. Again, speeds of 10mm/s, 25mm/s and 50mm/s were tested, the results of which, are shown in Table 3. Unlike the static-dynamic case, the standard deviations in the position errors are not affected by the speed of the capsule because there was very little relative motion between the EPM and the capsule. Yet, a larger standard deviation is observed than the static test (Table 1), which can be attributed to the use of the random walk motion model in the particle filter algorithm. As mentioned in Section 4, better performance can be expected in applications with accurate motion models.

Table 3.

Average accuracy (mean ± std) of pose estimates for dynamic-dynamic tests

Speed	Δx	Δy	Δz	Δϕ	Δθ	Δψ
(mm/s)	(mm)	(mm)	(mm)	(°)	(°)	(°)
10	−2.05 ± 5.00	−1.60 ± 3.76	1.60 ± 0.57	−1.76 ± 1.15	0.07 ± 1.80	−0.27 ± 2.65
25	−1.39 ± 5.56	−1.50 ± 3.95	1.35 ± 0.65	−2.14 ± 1.45	−0.09 ± 1.96	−0.17 ± 2.60
50	−2.59 ± 5.44	−1.77 ± 5.63	1.16 ± 0.75	−3.01 ± 2.00	−1.44 ± 3.76	−0.08 ± 2.68

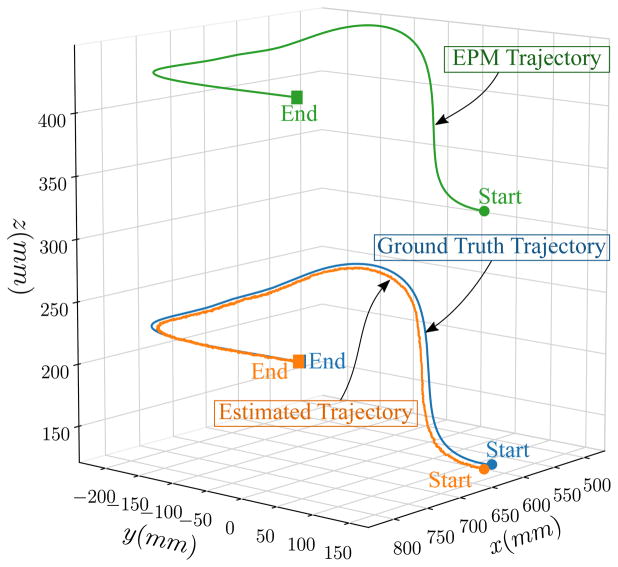
It is also evident from a qualitative assessment of Figure 14 that the system tracks the capsule’s trajectory with a steady bias. Further work is needed to determine whether this bias exists due to errors in the magnetic field model used or faulty sensor calibrations. Despite this, the errors reported in Table 3 are equivalent or better than the errors reported in Salerno et al. (2012); Di Natali et al. (2013, 2016) (see Table 4).

Figure 14.

Plot of the trajectories of the EPM and the capsule for the 10m/s dynamic-dynamic test. In order to establish ground truth, a secondary robot manipulator was used to hold and move the capsule at a constant speed along the trajectory. The trajectory was designed to mimic the shape of a human colon.

Table 4.

Average accuracy (mean ± std) of previous methods

Method	Δx(mm)	Δy(mm)	Δz(mm)	Δϕ(°)	Δθ(°)	Δψ(°)
Salerno et al. (2012)	−3.2 ± 18.0	5.4 ± 15.0	−13 ± 19
Di Natali et al. (2013)	−3.40 ± 3.20	−3.80 ± 6.20	3.40 ± 7.30	−6 ± 18	3 ± 20	−19 ± 50
	Δr(mm)	Δθ′(°)	Δz(mm)	Δϕ(°)	Δθ(°)	Δψ(°)
Di Natali et al. (2016)	6.2 ± 4.4	5.4 ± 7.9	6.9 ± 3.9	3.4 ± 3.2	3.7 ± 3.5	3.6 ± 2.6

7 Closed-Loop Magnetic Actuation

Equipped with a real-time 6 DOF pose estimation system without workspace singularities, it is now possible to perform closed-loop robotic manipulation of directly propelled magnetic capsule endoscopes. To demonstrate this possibility, we implemented a hybrid position and velocity control system that drove a soft-tethered capsule endoscope along a desired trajectory. Since it is not feasible to levitate the capsule using a single permanent magnet in a cavity that is not filled with liquid, the capsule’s position is controlled in 2D. Nevertheless, the vertical force on the capsule can be regulated and this capability can be used to keep the vertical force below a safety threshold. In addition, due to the nature of magnetically induced torque, it is not possible to control the rotation of the capsule along its axis of magnetization. Thus, our closed-loop control scheme admits 2 DOF control in position and 2 DOF control in orientation.

As is done in most magnetically actuated closed-loop control systems, we assume that the magnetic field of both the actuator and the magnet inside the capsule can be modeled by the point dipole model. This assumption allows us to efficiently compute the needed motion of the EPM to control the capsule, which would otherwise be computationally burdensome if we had employed more complicated models. Although the capsule is tethered, our formulations do not explicitly model the effect of tether and its interactions with the environment as our device is not equipped with the necessary shape and force sensors. Instead, we treat it as a disturbance and rely on the closed-loop system to compensate for it. We build on the formulation presented by Mahoney and Abbott (2015), as such, for further details of the approach, the reader is directed to their paper as well as our previous contributions (Taddese et al. 2016a,b; Slawinski et al. 2017). We denote the dipole moments of the EPM and the capsule’s magnet by m_E ∈ ℝ³ and m_ς ∈ ℝ³ respectively. The position of the EPM and the capsule’s magnet are similarly denoted by p_E ∈ ℝ³ and p_ς ∈ ℝ³ respectively.

With the dipole assumption, given a magnetic field B_E generated by the EPM, the force f and torque τ on the magnet inside the capsule is given by:

$$\mathbf{f}=({\mathbf{m}}_{\mathit{\varsigma }}·\nabla ){\mathbf{B}}_{\mathbf{E}}$$ (57)

$$\mathit{\tau }={\mathbf{m}}_{\mathit{\varsigma }}\times {\mathbf{B}}_{\mathbf{E}}$$ (58)

As such, the magnetic force f_m and torque τ_m on the capsule are:

$${\mathbf{f}}_{\mathbf{m}}(\mathbf{p},{\widehat{\mathbf{m}}}_{\mathbf{E}},{\widehat{\mathbf{m}}}_{\mathit{\varsigma }})=\frac{3{\mu }_0\Vert {\mathbf{m}}_{\mathbf{E}}\Vert \Vert {\mathbf{m}}_{\mathit{\varsigma }}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^4}({\widehat{\mathbf{m}}}_{\mathbf{E}}{{\widehat{\mathbf{m}}}_{\mathit{\varsigma }}}^{\top }+{\widehat{\mathbf{m}}}_{\mathit{\varsigma }}{{\widehat{\mathbf{m}}}_{\mathbf{E}}}^{\top }+({{\widehat{\mathbf{m}}}_{\mathit{\varsigma }}}^{\top }\mathbf{Z}{\widehat{\mathbf{m}}}_{\mathbf{E}})I)\widehat{\mathbf{p}}$$ (59)

$${\mathit{\tau }}_{\mathbf{m}}(\mathbf{p},{\widehat{\mathbf{m}}}_{\mathbf{E}},{\widehat{\mathbf{m}}}_{\mathit{\varsigma }})=\frac{{\mu }_0\Vert {\mathbf{m}}_{\mathbf{E}}\Vert \Vert {\mathbf{m}}_{\mathit{\varsigma }}\Vert }{4\pi {\Vert \mathbf{p}\Vert }^3}{\widehat{\mathbf{m}}}_{\mathit{\varsigma }}\times D(\widehat{\mathbf{p}}){\widehat{\mathbf{m}}}_{\mathbf{E}}$$ (60)

where p = p_ς − p_E, I ∈ ℝ^{3 × 3} is the identity matrix, D = 3p̂p̂^⊤ − I, and Z = I − 5p̂p̂^⊤.

The robot manipulator is controlled in joint position mode and its generalized coordinates are given by q ∈ ℝ⁶. The robot’s geometric Jacobian J_ℛ(q) ∈ ℝ^{6 × 6} is used to linearize the relationship between generalized joint velocities and the end effector twist as follows:

$$\left[\begin{array}{c}{\stackrel{•}{\mathbf{p}}}_{\mathbf{E}}\\ {\mathit{\omega }}_{\mathbf{E}}\end{array}\right]=J_{\mathcal{R}}(q)\stackrel{•}{\mathbf{q}}$$ (61)

We note that any component of ω_E that rotates the actuating magnet along the axis of the dipole moment m̂_E does not change m̂_E. That is, ${\stackrel{•}{\widehat{\mathbf{m}}}}_{\mathbf{E}}={\mathit{\omega }}_{\mathbf{E}}\times {\widehat{\mathbf{m}}}_{\mathbf{E}}$. To incorporate this into the mathematical formulation we define the EPM’s Jacobian J_E(q) as

$$\left[\begin{array}{c}{\stackrel{•}{\mathbf{p}}}_{\mathbf{E}}\\ {\stackrel{•}{\widehat{\mathbf{m}}}}_{\mathbf{E}}\end{array}\right]=\left[\begin{array}{cc}I& 0\\ 0& S{({\widehat{\mathbf{m}}}_{\mathbf{E}})}^{\top }\end{array}\right]J_R\stackrel{•}{\mathbf{q}}=J_{\mathbf{E}}\stackrel{•}{\mathbf{q}}$$ (62)

where S(a) ∈ 𝔰𝔬(3) denotes the skew-symmetric form of the cross product operation.

Furthermore, since it is difficult to solve for the necessary pose of the EPM that imparts a desired force and torque on the capsule using the nonlinear equations (59) and (60), we linearize them with respect to their parameters as follows:

$$\begin{array}{l}\left[\begin{array}{c}\stackrel{•}{\mathbf{f}}\\ \stackrel{•}{\mathit{\tau }}\end{array}\right]=\left[\begin{array}{lll}\frac{\partial {\mathbf{f}}_{\mathbf{m}}}{\partial \mathbf{p}}\hfill & \frac{\partial {\mathbf{f}}_{\mathbf{m}}}{\partial {\widehat{\mathbf{m}}}_{\mathbf{E}}}\hfill & \frac{\partial {\mathbf{f}}_{\mathbf{m}}}{\partial {\widehat{\mathbf{m}}}_{\mathit{\varsigma }}}\hfill \\ \frac{\partial {\mathit{\tau }}_{\mathbf{m}}}{\partial \mathbf{p}}\hfill & \frac{\partial {\mathit{\tau }}_{\mathbf{m}}}{\partial {\widehat{\mathbf{m}}}_{\mathbf{E}}}\hfill & \frac{\partial {\mathit{\tau }}_{\mathbf{m}}}{\partial {\widehat{\mathbf{m}}}_{\mathit{\varsigma }}}\hfill \end{array}\right]\left[\begin{array}{c}\stackrel{•}{\mathbf{p}}\\ {\stackrel{•}{\widehat{\mathbf{m}}}}_{\mathbf{E}}\\ {\stackrel{•}{\widehat{\mathbf{m}}}}_{\mathit{\varsigma }}\end{array}\right]\\ =J_{\mathcal{F}}(\mathbf{p},{\widehat{\mathbf{m}}}_{\mathbf{E}},{\widehat{\mathbf{m}}}_{\mathit{\varsigma }})\left[\begin{array}{c}\stackrel{•}{\mathbf{p}}\\ {\stackrel{•}{\widehat{\mathbf{m}}}}_{\mathbf{E}}\\ {\stackrel{•}{\widehat{\mathbf{m}}}}_{\mathit{\varsigma }}\end{array}\right]\end{array}$$ (63)

Since p = p_ς − p_E, we separate the contribution of the capsules velocity on the change in wrench from that of the EPM’s velocity. Using J_ℱ to designate J_ℱ(p, m̂_E, m̂_ς ):

$$\left[\begin{array}{c}\stackrel{•}{\mathbf{f}}\\ \stackrel{•}{\mathit{\tau }}\end{array}\right]=J_{\mathcal{F}}\left(\left[\begin{array}{c}{\stackrel{•}{\mathbf{p}}}_{\mathit{\varsigma }}\\ 0\\ {\stackrel{•}{\widehat{\mathbf{m}}}}_{\mathit{\varsigma }}\end{array}\right]+\left[\begin{array}{ccc}-I& 0& 0\\ 0& I& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}{J}_{\mathbf{E}}\\ 0\end{array}\right]\stackrel{•}{\mathbf{q}}\right)$$ (64)

Due to the fast dynamics of the system compared to our robot manipulator and the friction in our environment, the motion of the capsule is characterized by stick-slip motion. Thus, for practical purposes, we can neglect the contributions of ṗ_ς and ${\stackrel{•}{\widehat{\mathbf{m}}}}_{\mathit{\varsigma }}$ to the changes in force and torque. Defining J_{ℱ_E} as

$$J_{{\mathcal{F}}_{\mathbf{E}}}=J_{\mathcal{F}}\left[\begin{array}{ccc}-I& 0& 0\\ 0& I& 0\\ 0& 0& 0\end{array}\right]\left[\begin{array}{c}{J}_{\mathbf{E}}\\ 0\end{array}\right]$$ (65)

(64) can then be rearranged and succinctly written as:

$$\left[\begin{array}{c}\stackrel{•}{\mathbf{f}}\\ \stackrel{•}{\mathit{\tau }}\end{array}\right]=J_{{\mathcal{F}}_{\mathbf{E}}}\stackrel{•}{\mathbf{q}}$$ (66)

When discretized, (66) relates small changes in joint angles (δq) to changes in force (δf) and torque (δτ) on the capsule. Accordingly, the desired joint velocities are computed by inverting J_{ℱ_E}:

$$\stackrel{•}{\mathbf{q}}=J_{{\mathcal{F}}_{\mathbf{E}}}^{+}\left[\begin{array}{c}\stackrel{•}{\mathbf{f}}\\ \stackrel{•}{\mathit{\tau }}\end{array}\right]$$ (67)

where $J_{{\mathcal{F}}_{\mathbf{E}}}^{+}=J_W^{\top }{(J_W{J}_W^{\top }+\alpha I)}^{-1}$ is the damped weighted least-squares inverse of J_{ℱ_E} and J_W = J_{ℱ_E}W_q with W_q being the joint space diagonal weight matrix that is used to limit motion in specified robot DOFs. The damping term α serves to mitigate robot singularities.

7.1 Hybrid Position and Velocity Control

Despite the unavoidable stick-slip nature of magnetic manipulation in air, smoother motion can be achieved by decoupling forward velocity error from lateral position errors and providing two separate PI controllers that close the loop on the corresponding errors. Given a desired trajectory, the forward velocity controller attempts to propel the capsule forward (tangent to the trajectory) at a constant velocity while the position controller ensures that the lateral (normal to the trajectory) position error of the capsule from the desired trajectory remains small. As we do not assume automatic alignment of the capsules heading to a given magnetic field, as would be the case in liquid filled cavities (Mahoney and Abbott 2015), an additional controller operates on heading error.

In the following expressions, we denote the directions of the tangent and normal vectors at the point on the trajectory that is closest to the center of the capsule by t̂ and n̂.

The velocity error, e_v, is defined as the error between the current average velocity, ṗ_ς, and the desired velocity, ṗ_{ς_d}. Using the position estimates output by the algorithm presented in this paper, the average velocity of the capsule is computed by applying a low pass filter to differences in position in consecutive time steps. Thus, e_v = ṗ_{ς_d} − ṗ_ς. We remove any component of the velocity error in the lateral direction by projecting it onto the tangent direction, t̂, of the trajectory. The tangent velocity error, (e_v · t̂)t̂, is used as the error term in a proportional controller. The tangent projection of the velocity error, e_v · t̂, is also used to form a feed forward term f_res, that estimates and compensates for the resistance force applied by the tether.

$$f_{\mathit{res}}=-K_{i_{\mathit{vel}}}\int {\mathbf{e}}_v·\widehat{\mathbf{t}}$$ (68)

f_res is assumed to always be in the negative direction of the trajectory as it represents the resistance forces from the tether behind the capsule.

The position error is given by e_p = p_{ς_d} − p_ς. The projection of this error into the normal direction, (e_p · n̂)n̂, is used as the error term in a PI controller. Finally, the orientation error is computed as e_o = ĥ_ς × ĥ_{ς_d} where ĥ_ς and ĥ_{ς_d} are the current and desired capsule headings, respectively.

Using the matrices P_t̂ =t̂t̂^⊤ and P_n̂ = I −t̂t̂^⊤ to project error vectors onto t̂ and n̂ respectively, the overall expression for our control input, which is the vector of desired wrench on the capsule, is given by:

$$\left[\begin{array}{c}{\mathbf{u}}_f\\ {\mathbf{u}}_{\tau }\end{array}\right]=\left[\begin{array}{c}{K}_{p_{\mathit{vel}}}{P}_{\widehat{\mathbf{t}}}{\mathbf{e}}_v+K_{p_{\mathit{pos}}}{P}_{\widehat{\mathbf{n}}}{\mathbf{e}}_p+K_{i_{\mathit{pos}}}\int p_{\widehat{\mathbf{n}}}{\mathbf{e}}_p\\ K_{po}{\mathbf{e}}_o\end{array}\right]$$ (69)

The final changes in wrench on the capsule are computed by subtracting estimates of the wrench currently applied on the capsule:

$$\left[\begin{array}{c}\stackrel{•}{\mathbf{f}}\\ \stackrel{•}{\mathit{\tau }}\end{array}\right]=\left[\begin{array}{c}\delta \mathbf{f}\\ \delta \mathit{\tau }\end{array}\right]=\left[\begin{array}{c}{\mathbf{u}}_f-({\mathbf{f}}_{\mathbf{m}}+{\mathbf{f}}_{\mathit{res}})\\ {\mathbf{u}}_{\tau }-{\mathit{\tau }}_{\mathbf{m}}\end{array}\right]$$ (70)

7.2 Experimental Demonstration of Closed-Loop Control

In our experimental setup, the tethered capsule as described in Section 5, was inserted between two horizontal planes made of clear acrylic serving as vertical barriers for the capsule as shown in Figure 15. The two acrylic planes were lubricated with vegetable oil in order to reduce friction. A camera tracker was mounted below the bottom acrylic plane to provide ground truth on the 2D position of the capsule; however, its output was not used in the control algorithm. Since we do not have ground truth measurements for the heading of the capsule, we only report errors by comparing the commanded heading with the estimated heading provided by the pose estimation method described in this paper. The controller was implemented as a ROS node in Python and ran at a 100 Hz synchronized with the pose estimation algorithm. The two algorithms ran simultaneously on a single PC.

Figure 15.

Experimental setup of demonstrating closed-loop control. The capsule was painted so that it can be detected by the camera tracker with relative ease. The coil was covered with black tape to prevent erroneous color detection. The two acrylic planes were lubricated with vegetable oil in order to reduce friction.

Two sets of 10 trials were conducted where the system was commanded to propel the capsule along a straight line trajectory at a speed of 5mm/s. In both trials, the capsule’s heading was commanded to align with the forward direction of the trajectory.

In the first set of trials (see Extension 4), the initial capsule position was offset in the lateral direction by 55 mm. This experiment was used to assess the response of the controller to an initial offset and its ability to achieve a small steady state error. As seen in Figure 16a the capsule’s lateral error, on average, was reduced within the first 10 s of the trajectory. The steady state lateral error computed after the capsule has travelled 30 s was −5.30 ± 2.60 mm. The average heading error over the entire trajectory was 4.96 ± 2.20°. As shown in Figure 16e, the heading is consistently kept in the direction of forward motion.

Figure 16.

Traces of the capsule’s trajectory as it was propelled by the EPM with a closed-loop controller. Each colored solid line represents one of the 10 trials. (a, b) Traces obtained using a camera tracker based on color detection. (a) At time 0 s, the capsule’s position is offset from the trajectory in the x direction by approximately 55mm. (b) The tether is pushed in the +x direction as soon as capsule has travelled 100mm. This is indicated by the spike at time 20 s. The disturbance is maintained for approximately 10 s. (c, d) Traces obtained from the pose estimation algorithm. (e, f) Arrows representing the heading direction of the capsule at selected points along the two types of trajectories. For the purposes of good visualization, only a single trial from each set is shown. The color gradation shows the progression of time.

In the second set of trials (see Extension 5), the capsule starts without any intentional position error. Once the capsule has travelled 100 mm, a portion of the tether is manually pushed laterally thereby changing the position of the capsule by approximately 40 mm. This disturbance is maintained for approximately 10 s. This experiment was used to assess whether the controller was capable of compensating for sustained disturbances with its integral component all the while maintaining a desired orientation of the capsule. Figure 16b shows traces of the capsule trajectory as the controller responds to the disturbance. The average position error after the controller has recovered from the disturbance at T = 50 s was −7.90 ± 3.39 mm. The average heading error over the entire trajectory was 7.34 ± 1.77°. As shown in Figure 16f, the heading error increased during the disturbance, but quickly returned to its nominal direction.

The controller was commanded to maintain a vertical force of 0.45N on the capsule, a value empirically determined to balance the weight of the capsule without exerting excessive force on the vertical barrier. The system computed the magnetic force using the point-dipole model and pose estimates from the algorithm described in this paper. Accordingly, the average vertical force on the two sets of trials was 0.494 ± 0.093N and 0.502 ± 0.097N respectively. These forces are clinically relevant as they would not cause tissue damage (Slawinski et al. 2017). In maintaining this force, the vertical distance between the centers of the EPM and the capsule was kept at an average of 158 ± 4mm and 157 ± 6mm for the two sets of trials respectively. Considering the size of our EPM, this leaves close to 100mm of gap between the bottom of the EPM and the vertical barrier in the experiment.

In both sets of trials, it was observed that there was a constant offset between the position output of our pose estimation algorithm and the camera based ground truth. As Figures 16c and 16d show, the controller would have placed the capsule more accurately on the trajectory had this offset been absent. As mentioned in Section 6.2.2, further work is needed to determine the source of this error.

It was further observed that the capsule was frequently inside or near the singular region of the EPM. As such, successful control of the capsule in these trials would have been problematic if previous pose estimation methods were to be used.

8 Conclusion

In this paper, a novel pose estimation system that utilizes a hybrid assembly of a permanent magnet and an electromagnet was introduced. This approach overcomes two important limitations that hinder the use of prior pose estimation systems for magnetically driven robotic capsule endoscopy in clinical settings. A fundamental problem is that any source of magnetic field that can be sufficiently modeled by the point-dipole model is susceptible to ambiguities arising from regions of singularity when used as a source of information for pose estimation. This problem is mitigated by using a secondary source of magnetic field with an orthogonal dipole moment as shown in this paper. The extra information gained from the secondary source of magnetic field has the added benefit of enabling the computation of the initial yaw angle.

In order to use the two sources of information effectively, a particle filtering approach was used. By randomly initializing particles in the workspace, the filter was able to converge to the pose of the capsule, thereby eliminating the need for accurate initialization. Our experimental results show that the random walk motion model is sufficient to accurately track the capsule as long as the relative motion of the capsule with respect to the EPM remains low, as would be the prevalent case for robotic capsule endoscopy applications. However, in clinical application scenarios certain conditions, such as the sudden movement of the patient, could violate the assumption of low relative motion. This necessitates a higher-level system that monitors the sensor readings and the internal state of the pose estimation system and warns the user if the pose estimates cannot be relied upon. We hypothesize that the value of the likelihood function during the measurement update step of our particle filter algorithm can help to make this determination as we have observed the value to be extremely small when the capsule is out of range or it is intentionally moved to a new position rapidly.

In our static tests, the average errors were below 5mm in any single position axis and 6° in any orientation angle. How pose estimation errors affect the forces and torques induced on the capsule and closed-loop control in general needs further study, the result of which would be to establish a more meaningful benchmark. With our parallel implementation of the particle filter, our system was able to achieve an average update rate of 100 Hz. In comparison, the update rates reported in Di Natali et al. (2013) and Di Natali et al. (2016) were 71 Hz and 143 Hz respectively. In terms of workspace, our system exceeded the required radius of 150mm owing to size of our EPM, the use of multiple sources of magnetic fields, and the higher sampling rate used in our signal acquisition.

Moreover, our pose estimation method was experimentally shown to fulfill the criteria needed for closed-loop control in terms of accuracy, update rate and size of workspace making it suitable for use in tele-operated or autonomous operation of magnetically actuated robotic capsule endoscopes in clinical settings. In particular, tele-operated robotic manipulation can now be approached by combining our pose estimation algorithm and the closed-loop control scheme described in this paper with intuitive user interfaces and user feedback mechanisms.

Appendix A: Index to Multimedia Extensions

Table 5.

Table of Multimedia Extensions

Extension	Media type	Description
1	Video	Illustration of the components of the robotically controlled magnetic capsule endoscopy system
2	Video	Demonstration of the static- dynamic experiment
3	Video	Demonstration of the dynamic- dynamic experiment
4	Video	Demonstration of closed-loop control on a linear trajectory with an initial offset
5	Video	Demonstration of closed-loop control on a linear trajectory with added manual disturbance