Statistical Justification of Expansion Cohorts in Phase I Cancer Trials

Abstract

Background

Phase I cancer trials increasingly incorporate dose-expansion cohorts (DECs), reflecting a growing demand to acquire more information about investigational drugs. Protocols commonly fail to provide a sample-size justification or analysis plan for the DEC. In this study, we develop a statistical framework for the design of DECs.

Methods

We assume the maximum tolerated dose (MTD) for the investigational drug has been identified in the dose-escalation stage of the trial. We use the 80% lower confidence bound and the 90% upper confidence bound for the response and toxicity rates, respectively, as decision thresholds for the dose-expansion stage. We calculate the operating characteristics with reference to prespecified minimum effective response rates and maximum safe DLT rates.

Results

We apply our framework to specify a system of DEC plans. The design comprises three components: 1) the number of subjects enrolled at the MTD, 2) the minimum number of responses necessary to indicate provisional drug efficacy, and 3) the maximum number of dose-limiting toxicities (DLTs) permitted to indicate drug safety. We demonstrate our method in an application to a cancer immunotherapy trial.

Conclusions

Our simple and practical tool enables creation of DEC designs that appropriately address the safety and efficacy objectives of the trial.

INTRODUCTION

A typical phase I cancer clinical trial evaluates the safety of an antineoplastic agent not previously studied in humans. It commonly tests the drug initially in a dose-escalation phase in which cohorts of patients receive increasing doses until reaching a maximum tolerated dose (MTD). The cohort receiving the MTD is often small, typically only 6 subjects.^1,2 To further elucidate the drug’s properties, investigators may enroll an additional group of subjects, denoted a dose-expansion cohort (DEC), once the trial has identified the MTD.³

Trialists originally incorporated DECs into phase I trials to enable further study of safety and tolerability at the MTD. More recently, the role of the DEC has evolved to allow for acquiring preliminary efficacy information; characterizing pharmacokinetic and pharmacodynamic properties; and exploring outcomes in designated patient strata, such as those manifesting specific molecular aberrations or clinical features.^3,4

The expanded role of DECs reflects an impulse to expedite drug development by identifying promising drugs early and eliminating drugs with little chance of approval.⁵ As a result, there is increased emphasis on monitoring efficacy in phase I trials and in exploring novel surrogates for efficacy, particularly for molecularly targeted drugs whose toxicity is an unreliable predictor of efficacy.^1,3–7

The use of DECs is becoming more common. In a systematic review of published phase I cancer trials, the fraction incorporating a DEC increased from 12% in 2006 to 38% in 2011.⁴ Extrapolating to all 2,800 phase I cancer trials registered on clinicaltrials.gov in the past 5 years, we estimate that more than 1,000 of these trials included a DEC.⁸

Although there is a rich literature on designs that involve the collection of both safety and efficacy data within the current phase I/phase II taxonomy, few papers address phase I/DEC designs as they are currently implemented.^3,4 Unsurprisingly, an explication of statistical considerations for the DEC design is often absent from the protocol: Justification for DEC sample size is missing; the designation of endpoints is vague; and rules for evaluating trial success are lacking.

In this study, we propose a simple statistical framework to guide the design of DECs for phase I cancer trials. Retaining the currently popular framework for such studies, the key to our approach is the prospective specification of the efficacy and toxicity criteria that define trial success. These together yield a method for selecting the DEC sample size and conducting the data analysis.

METHODS

DOSE-ESCALATION AND DETERMINATION OF THE MTD

In the dose-escalation stage of a phase I trial, we monitor subjects for dose-limiting toxicities (DLTs), which are treatment-related adverse events defined a priori to satisfy criteria of type, severity, and time of occurrence. The aim is to identify the MTD, if one exists among the proposed doses. We describe our method in the context of a 3+3 design (Appendix 1), which is the most familiar and commonly implemented dose-escalation design,^9,10 but one can use other approaches as well.

DOSE-EXPANSION: THE DEC DESIGN

When dose escalation is complete, the trial begins enrolling subjects into a DEC at the declared MTD (or the highest planned dose if escalation did not reach the MTD). The aims of a DEC are twofold: 1) to obtain a preliminary assessment of the test drug’s efficacy, and 2) to further evaluate the safety of the drug at the MTD. Translating these objectives into statistical hypotheses permits determination of the DEC design. The following sections detail our approach to specifying the DEC plan: Its sample size; the number of responses necessary to deem a drug provisionally “effective”; and the number of DLTs necessary to deem it “unsafe”.

PROVISIONAL EFFICACY

Even at the early phases of drug evaluation, investigators recognize a minimum response probability below which further development would be futile. Thus, one can base a decision to continue development on the observation that the true response rate is likely to exceed a prespecified minimum response fraction. A statistical tool that summarizes the data to address this decision is the lower confidence bound (LCB)—the lower limit of a one-sided confidence interval. If the LCB exceeds the prespecified minimum response fraction, then there is preliminary evidence that the drug is effective, justifying further testing. If the LCB falls below the prespecified minimum response probability, there remains substantial uncertainty that the drug is effective. We use these considerations as a partial basis for the sample size and analysis plan for a DEC.

We assume the response outcome is dichotomous. The sample size, denoted n, includes subjects who receive the MTD during either the final stage of escalation or the DEC. We report the total sample size at the MTD instead of the DEC size to allow for flexibility in the number of subjects tested at the MTD during the dose-escalation phase, which typically is 6 subjects in a 3+3 design. We calculate the DEC sample size as the targeted n minus the number of subjects receiving the MTD during the dose escalation.

We calculate the 80% LCB for response counts r = 0,1,…,n using the Clopper-Pearson method.^11,12 We use an 80% confidence coefficient, rather than the conventional 90% or 95%, because the DEC portion of the trial is intended to be suggestive, not definitive.

We use the LCB for response to determine the minimum number of responses (NR) needed to declare the drug effective. Appendix 2 describes computation of NR.

A STOPPING BOUND FOR TOXICITY

We propose designating a stopping bound for toxicity based on a DLT probability threshold, specified a priori by the investigator, at which we deem the drug unacceptably toxic. In a manner comparable to the efficacy assessment, we use the upper confidence bound (UCB), the upper limit of a one-sided confidence interval, to judge the drug’s safety at the MTD. We declare the drug provisionally safe at the identified MTD if UCB is less than the prespecified DLT probability threshold. We declare the MTD provisionally unsafe, and therefore in need of revision downward, if UCB exceeds the threshold.

Defining d to be the count of DLTs in n subjects tested, we calculate the 90% UCB for the probability of a DLT at each possible DLT outcome, again using the Clopper-Pearson method.^11,12 With the 3+3 dose-escalation plan, this calculation does not fully account for the design, in that only doses that yield at most 1 DLT (in 6 subjects) can proceed to the dose-expansion phase. Thus, the distribution of DLTs is truncated to exclude values d > n–5. However, simulations reveal that the Clopper-Pearson UCB is adequate, particularly for DLT probability thresholds commonly used in phase I cancer trials (Appendix 3).

One derives the stopping bound by choosing the minimum number of DLTs, denoted ND, for which the 90% UCB exceeds the prespecified maximum DLT probability. If the number of subjects receiving the MTD and experiencing a DLT reaches ND, one stops enrolling subjects at the MTD and declares the MTD unsafe.

OPERATING CHARACTERISTICS OF THE DEC DESIGN

We evaluate the operating characteristics of various versions of our DEC designs as means to distinguish among these designs and to guide investigators to choose the DEC plan and sample size that best fits the trial.

A desirable DEC design has the following properties: 1) It rejects with high probability a treatment with an unsatisfactory response rate. 2) It accepts with high probability a treatment with a desirable response rate. 3) It rejects with high probability a treatment with a DLT rate that is higher than the prespecified maximum DLT rate. 4) It accepts with high probability a treatment with a safe DLT rate. Appendix 4 presents the formulas for the operating characteristics of our DEC design.

RESULTS

PROVISIONAL EFFICACY

Figure 1 presents 80% LCBs at various response counts for sample sizes 15, 20, 30, and 40. Using 80% LCBs, one can identify, for a specific sample size, the minimum number of responses, denoted NR above, necessary to claim a drug has provisional efficacy. For example, Figure 1C shows that if the minimum response probability is set at 5%, then among 30 subjects tested at the MTD, one declares the drug provisionally effective if there are at least 3 responses. The 80% LCB for 3 responses among 30 patients is 5.2%, which exceeds the prespecified minimum response probability, 5%. One uses the same algorithm to identify NRs at other samples sizes.

Figure 1.

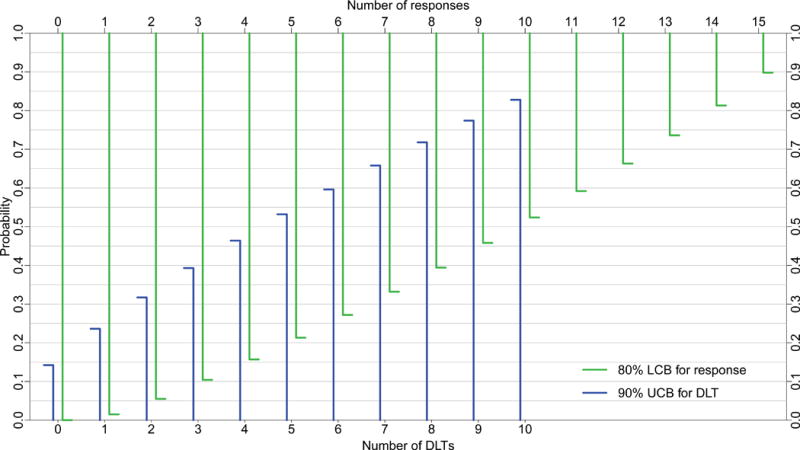
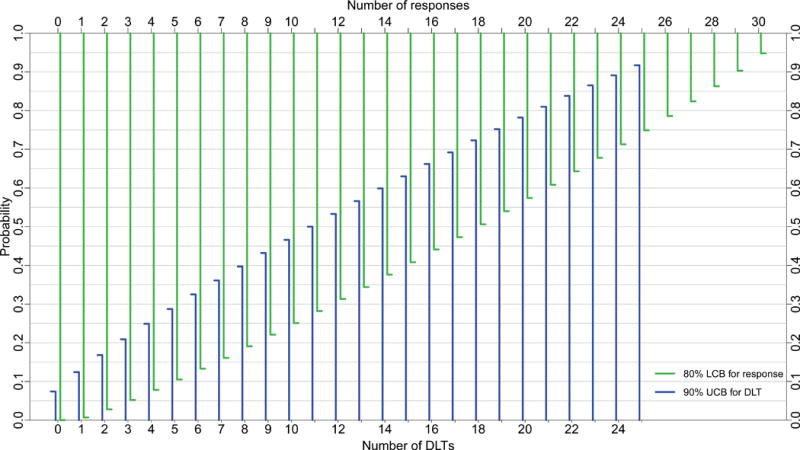
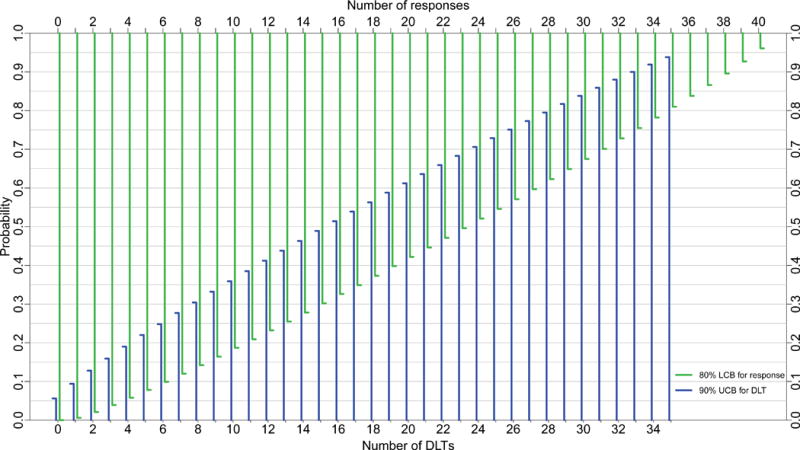
80% lower confidence bounds (LCBs, green) for response and 90% upper confidence bounds (UCB, blue) for toxicity for sample sizes A) 15, B) 20, C) 30, and D) 40 subjects; DEC sizes are A) 9, B) 14, C) 24, and D) 34 subjects, respectively. DLT= dose-limiting toxicity.

A STOPPING BOUND FOR TOXICITY

Figure 1 also depicts 90% UCBs for sample sizes 15, 20, 30, and 40, superimposed on the same graphs as the LCBs for response rate. One can use Figure 1 in an analogous manner to determine the stopping bound for toxicity, specifically, the number of DLTs, denoted ND above, that marks a drug unsafe. For example, if the maximum DLT probability is set at 30%, one stops for toxicity if the trial reaches 6 DLTs in a cohort of size 30. The 90% UCB for 6 DLTs among 30 patients is 32.5%, which exceeds the prespecified maximum DLT probability, 30%. Thus, upon reaching the 6^th DLT, one suspends enrollment for lack of safety, potentially abandoning the drug or revising its dose downward.

OPERATING CHARACTERISTICS OF THE DEC DESIGN

Table 1 summarizes the operating characteristics for DECs with a 5% minimum response probability, a 33% maximum DLT probability, and sample sizes between 15 and 40 subjects. The operating characteristics for DEC designs at some other probability combinations appear in Appendix Tables A.1, A.2, and A.3.

Table 1.

Operating characteristics of the DEC design. The minimum number of responses (NR) necessary to claim provisional efficacy, and the number of DLTs (ND) at which the MTD is deemed toxic are estimated according to an 80% lower confidence bound (LCB) that exceeds a prespecified minimum response probability p_Rmin=0.05 and a 90% upper confidence bound (UCB) that is less than a prespecified maximum acceptable DLT probability p_Dmax=0.33, respectively.

Sample sizea	DEC sizeb	Number of responses (NR)	Number of DLTs (ND, toxicity stopping bound)	Pr[reject] at pRmin=0.05	Pr[accept] at pRdesirable=0.20	Pr[reject] at pDmax=0.33	Pr[accept] at pDsafe=0.17
15	9	2	3	0.83	0.83	0.79	0.66
16	10	2	3	0.81	0.86	0.84	0.6
17	11	3	3	0.95	0.69	0.88	0.55
18	12	3	3	0.94	0.73	0.91	0.5
19	13	3	4	0.93	0.76	0.81	0.71
20	14	3	4	0.92	0.79	0.85	0.67
21	15	3	4	0.92	0.82	0.88	0.63
22	16	3	4	0.91	0.85	0.91	0.58
23	17	3	5	0.89	0.87	0.82	0.75
24	18	3	5	0.88	0.89	0.86	0.72
25	19	3	5	0.87	0.90	0.89	0.68
26	20	3	6	0.86	0.92	0.80	0.82
27	21	3	6	0.85	0.93	0.84	0.79
28	22	3	6	0.84	0.94	0.87	0.76
29	23	3	6	0.82	0.95	0.89	0.72
30	24	3	7	0.81	0.96	0.82	0.84
31	25	4	7	0.93	0.89	0.85	0.81
32	26	4	7	0.93	0.91	0.88	0.79
33	27	4	7	0.92	0.92	0.90	0.76
34	28	4	8	0.91	0.93	0.84	0.86
35	29	4	8	0.90	0.94	0.86	0.84
36	30	4	8	0.90	0.95	0.89	0.81
37	31	4	9	0.89	0.96	0.82	0.89
38	32	4	9	0.88	0.96	0.85	0.87
39	33	4	9	0.87	0.97	0.88	0.85
40	34	4	9	0.86	0.97	0.90	0.83

DEC=Dose-expansion cohort, DLT=Dose limiting toxicity, p_Rmin=prespecified minimum response probability, p_Rdesirable=prespecified desirable response probability, p_Dsafe=prespecified safe DLT probability, p_Dmax=prespecified maximum acceptable DLT probability.

^aSample size=Total number of subjects to be tested at the MTD; this includes subjects enrolled during the dose-escalation phase and subjects enrolled in the DEC

^bDEC size=Assuming 6 subjects are tested at the MTD during the dose-escalation phase, DEC size is calculated by subtracting 6 from the sample size

Table 1 reveals features of the DEC design:

1. The probability of rejecting a drug that has a 5% response rate is at least 81%, and the probability of declaring the MTD too toxic, given a DLT rate greater than 33% at the MTD, is at least 79%.

2. The probability of declaring a drug effective varies according to sample size: Among sample sizes with the same NR, the probability of accepting a drug increases as sample size increases. Notably, however, if the NR is not the same for two different sample sizes, there is no guarantee that a larger n will give a larger probability of accepting the drug at the same desirable response rate. For instance, the NR for sample size n=16 is 2, and the probability of accepting an “effective” drug is 86%. Whereas for sample size n=17, NR is 3, but the probability of accepting the drug is only 69%.

The probability of accepting a drug that is safe at the MTD varies markedly across sample sizes, and may be as low as 50%. Moreover, a larger sample size does not guarantee a higher probability of accepting a drug at a safe DLT rate. For instance, for sample sizes that have the same ND, a smaller sample size produces a higher probability of accepting a drug that is safe at the DLT.

EXAMPLE: NIVOLUMAB FOR REFRACTORY SOLID TUMORS

We demonstrate our method using a phase I trial reported by Brahmer et al.¹³ Their study evaluated the safety and efficacy of nivolumab (MDX-1106), a monoclonal antibody that enhances the responsiveness of immune cells to tumors by blocking the programmed death-1 coreceptor.¹⁴ Patients with advanced lung, colorectal, melanoma, renal cell, or prostate cancer refractory to prior treatments were eligible. Cohorts of participants were to receive MDX-1106 at 0.3, 1, 3, and 10 mg/Kg according to a 3+3 design, followed by a DEC at the MTD. Investigators evaluated tumor response radiographically at 8 and 12 weeks. They defined DLT as a grade 3 or 4 treatment-related adverse event or laboratory abnormality occurring within 28 days of drug administration.

We design the DEC for a minimum response rate of 5% and a maximum DLT rate of 33%. With these two inputs, we examine Table 1 to identify the DEC design with the most desirable operating characteristics; “desirable” here is subjective and reflects the investigator’s knowledge of the cancer under study, the properties of the test drug and similar drugs, and the resources available to the trial.

In a setting of constrained resources, for instance, enrolling 14 subjects into the expansion cohort (amounting to n=20 at the MTD—6 from the escalation and 14 from the DEC) produces reasonable operating characteristics. With this sample size, we deem nivolumab effective if 3 or more responses are recorded (NR=3) and excessively toxic if 4 or more subjects suffer a DLT (ND=4) (Figure 1). The probability of rejecting nivolumab is at least 92% if its true response rate is less than 5% and is at least 85% if its true DLT rate is greater than 33% (Table 1). By comparison, the probability of accepting nivolumab—and deeming the trial successful—exceeds 79% if the true response rate exceeds 20%, and is at least 67% if its true DLT rate is less than 17%.

The actual trial enrolled 15 subjects into the DEC, for a total of n=21 receiving the highest planned dose. The study did not reach the MTD, as the highest planned dose produced no DLTs. By including only 14 subjects rather than 15 in the expansion cohort, our hypothetical DEC design requires one less subject, has a similar probability of rejecting the drug if its true response rate is less than a 5%, and has a higher probability of deeming the trial successful if the drug’s true DLT rate is less than 17%. More importantly, the design reflects objective decision criteria defined prior to observing any study data.

DISCUSSION

We propose a simple method to design and analyze the DEC in a phase I cancer trial where one seeks a preliminary evaluation of drug efficacy and safety. Its components are the planned sample size and targeted response and DLT rates. Our method requires investigators to make explicit the characteristics of the trial design in light of their notions of drug safety and effectiveness.

Our method can accommodate multiple DECs, as would be applicable if one sought to acquire information on treatment performance in strata determined by patient baseline characteristics.⁴ For instance, in a trial that enrolls patients with different tumors, one could recruit a separate DEC for each tumor type represented in the escalation cohort. If there is no reason to expect toxicity to differ among cohorts, then one can apply a global stopping bound for toxicity, whereas response thresholds can be DEC-specific.

Numerous designs, many deploying variants of the continual reassessment method (CRM), simultaneously address safety and efficacy in early-phase trials.^15–27 As the DEC is a recent innovation, only a few papers recognize it as a formal design feature.^28–31 The emerging consensus is that 1) with the modest sample sizes of most phase I trials, one cannot estimate the MTD precisely; 2) the CRM is superior to the 3+3 as a general dose-finding tool; and 3) extending the study beyond its usual stopping point—either by recruiting a DEC or conducting additional CRM iterations—improves the estimated MTD. What then is the rationale for using our proposed approach?

First, compared to other designs it is simple to apply, and one can readily append it to the 3+3 design or any other dose-seeking plan.

Second, our design reflects well-established ideas of how one should conduct the early stages of a clinical research program. In the face of considerable uncertainty about a drug’s effects, it is reasonable to begin with a low dose, gradually escalate until toxicities appear, and then treat a few more patients to search for an efficacy signal.

Finally, our design conforms to the principle of “letting the students decide where the sidewalks should go”. The increasing use of DECs reflects the desire to unite the preliminary evaluations of safety and efficacy under a single protocol, rather than separate them arbitrarily into “phases”.

One can apply our DEC design with any dose-escalation plan, not just the 3+3. We generally favor the 3+3 for its simplicity and because it sensitively and conservatively detects DLTs that occur in the 15%–25% range.³¹ Such rates are likely to be of considerable concern to the patient and the clinician, regardless of the drug or the disease. Indeed, in simulation studies, a 3+3/DEC design was more likely than the CRM to correctly select the MTD with a desired 30% DLT rate for drugs that are highly toxic at low doses.³² More importantly, for all simulated dose-toxicity curves the 3+3/DEC was less likely to sojourn above the target MTD. The principal advantages of the CRM are that one can tune it to identify any target DLT rate, and that it is efficient, in that it will find the MTD rapidly if one exists. This is particularly important in studies with large numbers of candidate dose levels.

Unsurprisingly, clinicians prefer simple and familiar methods, which likely accounts for the continued popularity of 3+3 even 25 years after the promulgation of CRM.²⁷ (Similarly, the Simon (1989)³³ and Gehan (1961)³⁴ phase II designs continue to be popular despite many subsequent advances in the statistical design of such trials.) Our approach superimposes on this framework a way to justify a dose-escalation/DEC study by providing a means to signal a problem with safety or efficacy, and thereby to prompt a formal reconsideration of the drug’s usefulness.

What does the future hold for early-phase cancer trial design? The work of O’Quigley and others³¹ points to the creation of integrated systems for the collection and analysis of safety and efficacy data, likely founded on the Bayesian paradigm rather than the traditional idea of minimizing long-term error rates of rigidly enforced decision rules. It will be critical for biostatisticians to demonstrate the practical advantages of the integrated approach, as well as its feasibility in modestly funded, single-center, clinical research programs.

In conclusion, phase I trials in cancer increasingly incorporate DECs in order to obtain additional safety information together with preliminary drug efficacy data. We have proposed a simple practical tool to generate DEC designs that appropriately address the objectives of the extended phase I study.

Summary.

Phase I cancer trials increasingly incorporate dose-expansion cohorts (DECs) that are not subject to the same high level of statistical scrutiny as other trial components. We describe a statistical framework for the design of a DEC that involves prospectively specifying the efficacy and toxicity criteria that define trial success.