Predicting myofiber size with electrical impedance myography: a study in immature mice

Abstract

Introduction

Electrical impedance can be used to estimate cellular characteristics. We sought to determine whether it could be used to approximate myofiber size using standard prediction modeling approaches.

Methods

Forty-four C57BL/6J wild-type immature mice of varying ages underwent electrical impedance myography (EIM) using a needle electrode array placed in the gastrocnemius. Animals were then euthanized and muscle fixed, stained, and myofiber size quantified. Two different statistical prediction models were then applied.

Results

Impedance parameters showed major variation with increasing myofiber size. The prediction models based on EIM data alone were able to predict fiber size, with errors in the range of ±69.05–78.44 μm² (16.19–18.40% with respect to the average myofiber size).

Discussion

Using well-established statistical models, EIM data alone can provide a satisfactory estimate of myofiber size. Further study of this approach for approximating myofiber size without the need to remove tissue for histological analysis is warranted.

INTRODUCTION

Electrical impedance myography (EIM) is a neurophysiological technique in which a low-intensity, high-frequency current is passed through tissue and the resulting voltages measured.¹ From these values, the impedance of the tissue can be identified, including the major parameters of resistance, reactance, and phase angle. Changes in the impedance characteristics of tissue are altered in disease states. For example, muscle fiber loss, or an increase in fat or connective tissue in the muscle, will alter the impedance characteristics of the muscle. For this reason, the technology has been studied as a potential biomarker of disease status in a variety of disorders including amyotrophic lateral sclerosis,² Duchenne muscular dystrophy,³ and disuse.^4,5

Impedance techniques, however, can also be employed in more sophisticated ways then as simply “black box” measures of disease progression or response to therapy. In fact, impedance theory states that the major bioelectric outcomes are exquisitely sensitive to the cellular characteristics of the tissue.⁶ For example, cell size is related to the peak frequency of reactance values, with cell size being inversely related to the peak frequency value. Similarly, other measures, such as the ratio of the resistance values at very low and very high frequency, can provide information on cell density. Previous studies have also demonstrated significant correlations between impedance values and cell size and connective tissue deposition.^7–9 To our knowledge, however, these impedance values have not been used to specifically predict such morphological features of muscle.

In this study, we attempt to address this question by studying a group of wild-type immature mice of different ages to determine with what accuracy we can predict cell size based on the impedance multifrequency spectra. This effort represents the most basic step toward applying EIM as a tool to quantify the histologic characteristics of muscle without the need to remove tissue for microscopic analysis.

METHODS

Mice

The Beth Israel Deaconess Medical Center Institutional Animal Care and Use Committee approved all procedures. Wild type C57BL/6 mice were bred from mating pairs. Forty-four animals underwent EIM measured at each of the following ages: Post-natal day PND 5 (n=4), PND10 (n=7), PND15 (n=7), PND20 (n=7), PND25 (n=6), PND30 (n=7), PND35 (n=6). Because no specific hypothesis was being tested, we could not perform a sample size estimation. Thus, our choice of sample size was based entirely on practical considerations, including cost and time. There were fewer animals in the youngest group because it proved challenging to collect any data in these animals given their very small size.

EIM measurements

Measurements were performed with the mView System (Myolex, Inc., San Francisco, California, USA) to obtain multi-frequency data between 1 kHz and 10 MHz (a total of 41 logarithmically-spaced frequencies are measured to obtain a clear picture of the overall spectral characteristics of the tissue impedance). A 4-electrode needle array was created by employing 4 insulated monopolar needle electrodes (Natus, Inc., cat# 902-DMG50-S, Middleton, Wisconsin). The needle electrode spacing was approximately 1 mm (Figure 1A). The back ends of the needle electrodes were stripped off their connectors and soldered to wires that connected to a cradle device that connected directly to the mView system. The electrode array was placed in the right gastrocnemius as previously described (Figure 1A).¹⁰ The array was held in place using alligator clips secured to an iron base (Helping Hands by RadioShack, Fort Worth, TX). Data were collected twice to ensure stability of measurements.

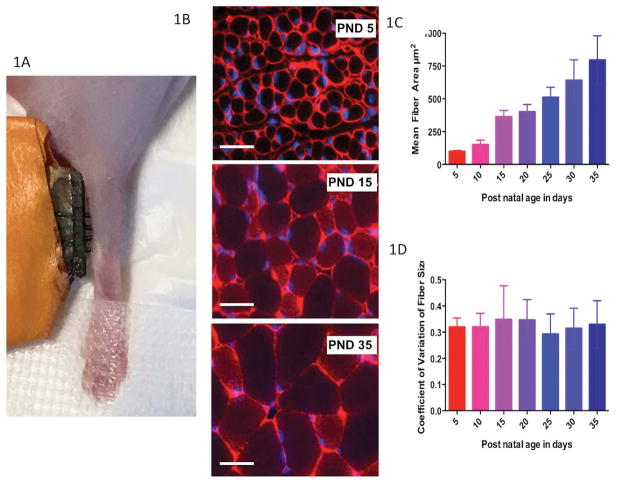
Figure 1.

A. Electrical impedance myography (EIM) measurement technique in a P5 mouse. B. Example images of gastrocnemius muscle stained with antibodies to collagen VI (red, cell membranes) and DAPI (blue, nuclei) in PND 5, PND 15, and PND 35 mice showing a uniform increase in muscle fiber size as mice age from PND 5 to PND 35; bar = 20 μm. C. Mean (± standard deviation) fiber size of each mouse group age. D. Coefficient of variation of fiber size (standard deviation/mean), demonstrating relative consistency of variation across all ages.

Animals were euthanized shortly after the measurements were completed and the contralateral gastrocnemius muscle was removed for histological analysis as described below (so as to avoid areas injured by the needle electrodes in the muscle studied).

Histological analysis

The gastrocnemius was fixed in 10% formalin. The tissue was then embedded in paraffin and sectioned into 10 μm slices. Sections were stained with collagen VI antibodies (Abcam #6588) to identify the cell membranes and 4′, 6-diamidino-2-phenylindole (DAPI) to stain nuclei. Individual sections were viewed and photographed using a Zeiss Axioimager M1 Epifluorescence Microscope. Using Volocity® Software, myofiber area was identified using the automated algorithms that identify the fiber membranes (see Figure 1B) and counts completed. On average, approximately 125 fibers were counted per muscle.

Data analysis

We were specifically interested in evaluating how different sets of impedance data predicted cell size. There were four sets of impedance data that we chose to evaluate separately: the single 50 kHz phase, resistance, and reactance values; the four Cole parameters (described below) that have been classically used to assess cellular/tissue characteristics; all the impedance data gathered across the 41 frequencies measured; and the impedance data gathered across all frequencies up to 1 MHz, the standard upper limit of most impedance measuring systems. In addition to evaluating each of these impedance data sets in isolation, we also evaluated how the addition of the animals’ age influenced prediction accuracy.

Cole impedance outputs

Multi-frequency resistance and reactance data were reduced to a set of four standard modeled parameters (the Cole parameters) using the standard impedance model described elsewhere.^6,11,12 The first parameter is R₀, the highest resistance value, if it were possible to measure at 0 Hz frequency. The second parameter is R_inf, which is the lowest resistance value if it were possible to measure at infinite frequency. The physiological interpretation of both R₀ and R_inf together (R₀/R_inf) is that they provide a measure of opposition to current flow through the extracellular and intracellular compartments of the tissue and hence an index of cell density. The third parameter is the characteristic frequency, f_c and is the frequency at which the electrical current is evenly split between the extra- and intracellular compartments (the cells’ membranes become permeable to the electrical current at higher frequency). Finally, the fourth parameter is alpha, α, which is a measure of cell size variation. Theoretically, α =1 in a perfectly homogenous tissue with equally sized cells; in contrast, α = 0 in an entirely heterogeneous tissue.

Statistical analysis and prediction models

We developed two different prediction models: (1.) A stepwise selection with Akaike Information Criterion (AIC) using a multivariable linear regression modeling framework (for 50 kHz values and Cole parameters);¹³ (2.) A penalized linear regression approach using least absolute shrinkage and selection operator (LASSO) for assessing the entire multifrequency set (up to 10 MHz) and the set up to 1 MHz.^14–16 “Shrinkage” refers to reducing a parameter’s coefficient in the regression equation if that parameter plays a very little or non-significant role in predicting the expected outcome. This is important in a multi-frequency prediction model, such as those studied here, in which the number of predictors is very large in comparison to the sample size. In these models, it is assumed that very few components of the multi-frequency set contribute to the prediction and that the remainder of the predictors’ effects is close to zero. There are several reasons for choosing the LASSO based estimate of model parameters, a) the least-squares estimate often has low bias but large variance, and prediction accuracy can be improved by shrinking the values of the regression coefficients. By doing so, we tend to introduce some bias but also reduce the variance of the predicted values; hence, often improving the overall predictive performance of the model, and b) secondly, we often are interested to identify a smaller subset of these predictors, just like in our current problem, that are strongly related to the outcome. Therefore, the underlying assumption of sparsity (i.e., using fewer values) for predictive model building allows for estimation of the parameters effectively, (using the LASSO and/or related approaches) even without having the knowledge of which unique set of parameters out of the entire set are actually nonzero. The tuning parameter, which controls the strength of the “penalty” in each LASSO model, which can further help simplify the model, was selected using the leave-one-out cross-validation (LOOCV) approach. In this procedure, we first choose a value of penalty and estimate model parameters using LASSO by leaving out one observation. The fitted model is then tested on the left out observation in terms of its predictive performance (to obtain an estimate of residual and hence mean square error for the left out observation). To obtain an estimate of mean squared error for the specified penalty, the above procedure of leaving out one observation and training on the remaining set is repeated on the entire set of observations. As a next step, the above LOOCV procedure is repeated for the specified range of penalty. The final penalty value is chosen to be one that provides an average minimum mean square error on the range of penalty terms using the LOOCV procedure. By taking this approach, it becomes possible to perform model selection while preventing over-fitting. Prior to modeling, the mean muscle fiber size and the impedance parameters were standardized to unit normal scale to provide equal weights to each predictor during cross-validation and to remove the effect of the underlying unit of measurement. In each case of the penalized linear regression approach, the estimates of parameters are generally biased but they perform extremely well in terms of providing prediction as they attain the minimum root mean square error (RMSE) on the training set while balancing the overall bias and variance trade-off.¹⁶

As a final step in assessing the effectiveness of each of these models, we then translated the scaled predicted muscle fiber size back into original scale of measurement by multiplying it by the standard deviation and adding the overall mean of the true fiber size in our training set. Similarly, we assessed the performance of prediction by multiplying the RMSE by the standard deviation of the true muscle fiber to estimate it in micrometers for each model.

RESULTS

Animal histology and raw impedance values

Figure 1B shows three representative images (each on the same scale) of gastrocnemius muscle stained with anti-Collagen VI antibodies (red, cell membranes) and DAPI (blue, nuclei) at selected time points to provide a general sense as to how the muscle fiber characteristics change with increasing age. An increase in muscle fiber cross-sectional area (i.e., muscle cell size) is apparent as the pups increase in age from PND5 (upper panel) to PND15 (middle panel) to PND35 (lower panel). Figure 1C shows the variation in the cell size, in terms of mean cross-sectional area, for each age cohort. Note that over the course of one month, the cross sectional area increases seven-fold from a mean of 97.6 μm² at p5, to 363 μm² at p15, to 737 μm² at p35. Figure 1D shows the coefficient of variation in the cell size at each age, confirming that all the cells are essentially enlarging to a similar extent, in agreement with the uniformity of the size of the muscle fibers shown in each of the images in Figure 1B.

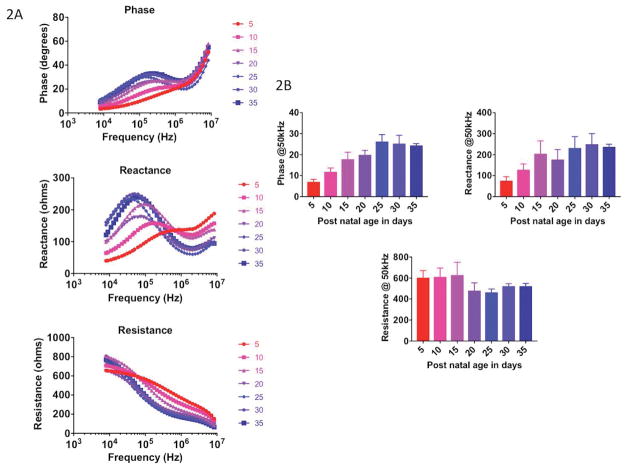
Figure 2A shows the complete multi-frequency data sets with increasing age, for all the animals averaged across each age group. As can be seen, the impedance spectra (phase, reactance, resistance) gradually shift as the animals grow, with the peak frequency decreasing in value and the whole curve increasing in value and shifting to the left. Figure 2B shows an example of the 50 kHz phase, reactance and resistance data. Whereas the reactance shows a general increase, resistance remains relatively unchanged; however, the phase shows the greatest relationship to age, although it plateaus at P25, despite increasing myofiber size (as seen in Figure 2A).

Figure 2.

Multifrequency (A) and single frequency (50 kHz) (B) impedance data in each group of mice aged PND 5 through PND 35.

Prediction models

We took several approaches for applying these prediction models. Because our main interest was in predicting muscle fiber size based on impedance parameters alone, we studied both prediction algorithms described above (stepwise and LASSO) without including age, focusing on 50 kHz values alone, the Cole parameters alone, the entire multifrequency set up to 10 MHz, and a more limited multifrequency set up to 1 MHz, the standard upper limit of most impedance measuring systems. Of note, for the 50 kHz parameters, only phase contributed to the model and thus is included here. Table 1 provides details as to the predicted error for each of the prediction models both in terms of raw scaled values and in terms of the final variation in area in μm². Table 1 also shows the effect of adding age to the prediction, demonstrating how much this one additional factor improves the prediction. Table 2 shows the relative contribution of the 50 kHz phase values and each of the Cole impedance parameters in the various prediction models, both with and without age. Table 3 provides the relative contribution of each of the frequencies to the various multifrequency models, with and without age included, and the associated coefficients for each value that would need to be used in the regression equation for each of the models. Only frequencies that contribute to the various multifrequency models are included in Table 3. As can be seen, a variety of frequencies/impedance parameters become important in the LASSO approach, their relevance not being intuitively obvious. Data from several frequencies between 1 and 10 MHz are also included in this model.

Table 1.

Summary of prediction models, associated root mean square errors (RMSE), and Pearson’s correlations between observed and predicted myofiber size along with 95% CI

Models without age	Prediction method	RMSE (scaled)	RMSE original scale, μm2	RMSE with respect to the overall mean of the myofiber size, %	Pearson’s correlation between observed and predicted myofiber size
50 kHz phase	Stepwise regression	0.541	122.89	28.83	0.836 (0.718, 0.908)
Cole parameters	Stepwise regression	0.635	144.12	33.81	0.766 (0.607, 0.866)
Multi-frequency Spectrum, all frequencies	LASSO	0.346	78.44	18.40	0.937 (0.887, 0.965)
Multi-frequency Spectrum, frequencies ≤ 1 MHz	LASSO	0.372	84.33	19.78	0.927 (0.869, 0.959)
Models with age included	Prediction method	RMSE (scaled)	RMSE original scale, μm2	RMSE with respect to the overall mean of the myofiber size, %	Pearson’s correlation between observed and predicted myofiber size
50 kHz phase	Stepwise regression	0.374*	84.92*	19.92	0.925 (0.867, 0.959)
Cole parameters	Stepwise regression	0.374*	84.92*	19.92	0.925 (0.867, 0.959)
Multi-frequency Spectrum, all frequencies	LASSO	0.304	69.05	16.19	0.951 (0.913, 0.974)
Multi-frequency Spectrum, frequencies ≤ 1 MHz	LASSO	0.323	73.21	17.17	0.945 (0.902, 0.970)

CI, confidence intervals; LASSO, Least absolute shrinkage and selection operator; RMSE, root mean square error

^*Only age is retained in these models using stepwise selection procedure, hence they provide identical values

Table 2.

Relative contribution of individual model parameters in various models

Prediction Model	Model parameters	Estimate	SE	P-value		RMSE (scaled)	RMSE original scale, μm2	RMSE, %
50 kHz phase without age	Phase 50 kHz	8.36E-01	0.085	<0.0001		0.541	122.89	28.83
50 kHz phase with age*	Age	9.26E-01	0.058	<0.0001		0.374	84.92	19.92
Cole parameters without age	fc	2.46E-01	0.120	0.047		0.635	144.12	33.81
	R0	−7.52E-01	0.237	0.003
	Rinf	−7.76E-01	0.176	<0.0001
	α	6.96E-01	0.184	0.001
Cole parameters with age*	Age	9.26E-01	0.058	<0.0001		0.374	84.92	19.92

RMSE, root mean square error

^*Both 50 kHz phase and Cole parameters are removed when included with age

Table 3.

Relative Contribution of Individual Frequencies and LASSO Penalty Estimates for Various Models

Model Parameters	Multi-frequency Spectrum (All Frequencies) Without Age	Multi-frequency Spectrum (All Frequencies) With Age	Multi-frequency Spectrum (Up to 1 MHz) Without Age	Multi-frequency Spectrum (Up to 1 MHz) With Age
Age	•	6.32E-01	•	6.25E-01
Phase 62 kHz	•	2.06E-01	3.46E-01	1.87E-01
Phase 178 kHz	4.52E-02	•	•	•
Phase 253 kHz	1.13E+00	•	7.50E-01	•
Phase 862 kHz	•	1.55E-01	7.62E-04	•
Phase 1027 kHz	•	•	2.50E-01	2.45E-01
Phase 4168 kHz	1.63E-01	•	•	•
Phase 5915 kHz	1.91E-04	•	•	•
Phase 8396 kHz	1.47E-01	1.51E-01	•	•
Reactance 8 kHz	−6.88E-02	•	−1.77E-01	−1.70E-02
Reactance 302 kHz	−4.52E-01	−4.25E-05	−3.87E-01	•
Reactance 359 kHz	•	−1.11E-01	•	•
Reactance 428 kHz	•	−3.48E-02	•	−1.26E-01
Resistance 1027 kHz	•	•	1.30E-01	•
Resistance 7047 kHz	1.97E-01	•	•	•
RMSE (scaled)	0.346	0.304	0.372	0.323
RMSE (original scale) (μm2)	78.44	69.05	84.33	73.21
Percentage RMSE	18.40%	16.19%	19.78%	17.17%
Pearson’s correlation between observed and predicted myofiber size	0.937 (0.887, 0.965)	0.951 (0.913, 0.974)	0.927 (0.869, 0.959)	0.945 (0.902, 0.970)

LASSO, Least absolute shrinkage and selection operator; RMSE, root mean square error; kHz, kilohertz; MHz, Megahertz; μm², micrometer squared.

Figure 3 shows the resulting actual and predicted cell size for each animal based on the regression analyses without age included. Figures 3A and 3B show the results using the 50 kHz phase and the Cole parameters, respectively. Figures 3C and 3D show the results obtained using the entire frequency spectrum as compared to using values of the frequency spectrum up to 1 MHz. As can be seen, the 50 kHz phase (Fig. 3A) somewhat surprisingly outperformed the Cole parameters (Fig. 3B), though both fared considerably worse than those analyses performed using all frequencies up to either 10 or 1 MHz (Figs. 3C and 3D).

Figure 3.

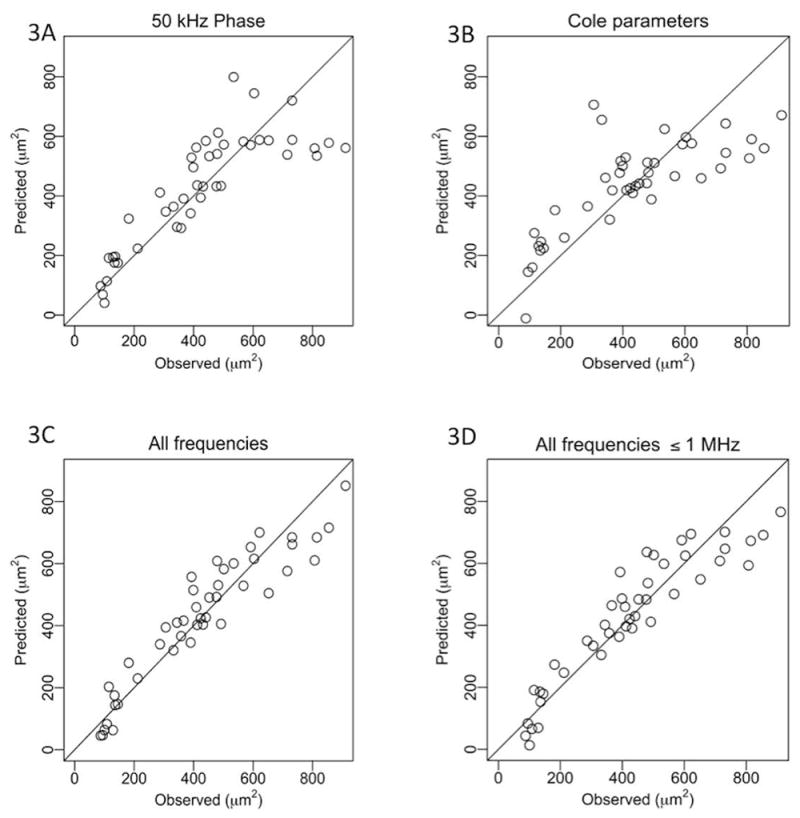
Comparison between actual and predicted muscle fiber sizes. A. 50 kHz phase impedance values alone using stepwise regression. B. Cole impedance parameters alone using stepwise regression. C. Full multifrequency impedance data set using LASSO. D. Up to 1 MHz multifrequency data set using LASSO.

DISCUSSION

The results of this study confirm the very strong relationship between impedance values and mean myofiber cross-sectional area, supporting general impedance theory. More specifically, the multifrequency model developed (using the data set up to 10 MHz) can predict muscle fiber size with a RMSE of 0.346, translating into an error of ~78.44 μm², in an “average” muscle fiber size of 426.25μm² in the combined group of immature and young mature animals, (representing an error of 18%). By adding age, that prediction becomes still stronger, with the RMSE dropping to 0.304, which translates into an error of 69.05 μm² (representing an error of 16%). However, using the Cole parameters or the 50 kHz phase values alone result in far less accurate predictions, as shown in Table 1. Although the penalized regression based models were built using LOOCV, further validation using a separate test would add more weight to this basic concept. Importantly, the LASSO based coefficients (Table 3) define the optimal weights needed for the multiplication with the standardized frequency components to perform prediction of muscle fiber size for future data sets.

This work represents only an initial attempt to refine EIM as a “virtual biopsy” technique in which impedance parameters along with proper modeling can be used to help provide histological information on muscle without the need to actually obtain tissue. Naturally, the complexity of muscle pathology makes our actually replacing biopsy impossible. However, the work described here represents a basic first step toward quantifying certain aspects of muscle histology without the need for actual tissue removal. While an error in prediction of 16–18% suggests a satisfactory estimate between histology and EIM for an early stage comparison, additional improvements will be required to reduce the error in prediction of fiber size to something more acceptable, perhaps to less than 5%. Achieving such a low error would help ensure greater success of the technique, especially as we begin to seek to identify more complex pathologies. Nevertheless, the wealth of potential impedance parameters, including frequency dependencies, anisotropic (i.e., direction dependent) characteristics, and the different impedance parameters themselves may help characterize other aspects of the tissue, including extracellular connective tissue and fat, the presence of inflammatory cells, or intracellular vacuolization. Performing these impedance measurements on tissue with needle electrodes in a very well controlled model represents a simpler paradigm as compared to the use of surface electrodes, in which the skin and subcutaneous fat may impact the data. Still, the model we developed here could be used in future animal studies or human work using needle electrodes for impedance measurements.

Clearly, it would be helpful if such a model could provide additional information beyond simply mean fiber diameter, such as a sense of the distribution of fiber size. This is theoretically possible, but the data set analyzed here did not readily allow for that possibility since these were all normal mice with consistent muscle fiber distributions. Stated another way, although the standard deviation in fiber sizes increased with age and increasing fiber area (see error bars in Figure 1C), the actual coefficient of variation (i.e., the standard deviation/mean) in fiber size remained virtually unchanged across all the groups of animals (see Figure 1D). Hence it would not be possible to predict the relative variation in fiber size in these animals since there was essentially nothing to predict (all animals had similar coefficients of variation in fiber size). Future studies can certainly seek to address assessing tissue with mixed fiber sizes.

Our main interest was in predicting muscle fiber size based entirely on the impedance data alone. The value of looking at animals of different ages was merely to provide a well-differentiated set of data so that we could create such a predictive model. As Table 3 shows, by adding in age as a predictor to either the entire multifrequency spectrum analysis or to analysis using the multifrequency spectrum up to 1 MHz, the predictions improve even further to yield a RMSE of 69.05 and 73.21 μm², respectively. There are two relevant points here. First, adding in the age, a clearly important and very informative predictor, as suggested by Figure 1C, only improves the prediction modestly for the two multifrequency models (i.e., RMSE decreased from 78.44 to 69.05 μm² for the 10MHz multifrequency data set, and from 84.33 to 73.21 μm², for the 1MHz multifrequency data set). Second, while small, this result does illustrate the fact that such non-impedance data could certainly be used to further improve the predictive capabilities of this EIM-based approach. However, it should be noted that the impact of a parameter such as age would likely be far less important in fully mature animals, where it would be unlikely to play as significant a role.

Another interesting fact about adding age to the prediction model is that it altered the frequency parameters used in the model, as shown in Table 3. This seems to be especially true when including the full frequency data set. As age itself was such a strong predictor—its presence tends to remove those frequencies that are strongly related with muscle fiber size and itself. To summarize, the LASSO approach is known to select only one variable from a group of highly correlated variables and it ends up selecting a set of frequency parameters in the presence of age that are not as strongly related to the age.

We also note that the increasing volume of the overall muscle would not be anticipated to have any impact on the spectral characteristics of the impedance that we evaluate here. In other words, we are not simply measuring gross muscle size. Changes in size could alter the actual values at a given frequency, but not the overall spectral characteristics.⁶

We evaluated two multifrequency sets: one going as high as the instrument could measure—10 MHz—and the other up to only up to 1 MHz. Although the system can obtain data between 1 and 10 MHz, there is likely considerable distortion in the impedance data at these higher frequencies due to a variety of unavoidable problems, including inductive effects from the wires and parasitic capacitances within the hardware. Despite this, several frequencies above 1 MHz did seem to improve the model fit, as shown in Table 3. If it were simple noise, it would not be expected to improve the model. Further investigations will be needed to clarify this issue.

There are several fine points and limitations that should also be highlighted. First, we also studied a second prediction model in the multifrequency set, called elastic net, which allows for selection of correlated predictors.¹⁷ This performed similarly to the approach shown, including identifying the same frequencies and impedance parameters that were identified as predicting cell size here; hence, for clarity, we decided not to show that data here. Second, we included phase as a separate parameter in all of these models. Phase is actually derived from reactance and resistance, (specifically via the equation phase = arctan (reactance/resistance)). While including this value in addition to reactance and resistance may seem duplicative, it is actually not. As can be seen, the phase contributes substantially to the final models presented in Table 2. Nevertheless, to see its effect, we re-ran the analysis, this time keeping reactance and resistance at all frequencies but omitting phase (data not shown). This weakened the predictive model, increasing the RMSE up to 74.87 μm² (from 69.05 μm²). In addition, we obtained the RMSE of 72.12 μm² in a model containing only phase, implying that all three components: resistance, reactance and phase, included in a single model improve prediction. A final limitation of the analysis performed is that it does not include any measurement of anisotropy.¹ Anisotropy, or the directional dependence of electrical current flow in muscle, plays a substantial role in muscle given the cylindrical shape of muscle fibers. However, given the very small size of each of these animals, it would have been challenging in the extreme to obtain two-directional data with any accuracy.

Having completed this initial work, the goal of future studies will be to begin to evaluate disease models using surface electrode arrays rather than the needle electrode arrays we utilized here. This approach may require the addition of a factor for the thickness of the skin/subcutaneous fat. Also, while we have achieved a satisfactory result, we believe we can still improve on these initial efforts and predict myofiber size more accurately. Moreover, we have, in fact, previously identified high-frequency impedance features that may allow the differentiation of slow-twitch from fast-twitch fibers.¹⁸ Thus it may be possible to predict relative proportions of these fiber types more accurately within a given muscle, in part by using the Cole alpha parameter, described above, which provides a measure of myofiber heterogeneity. In addition, we can begin to use such predictive methods to begin to assess more complex disease pathologies, including the endomysial deposition of fat and connective tissue and intracellular abnormalities, such as abnormal glycogen accumulation or vacuolization. Only by pursuing a varied group of neuromuscular pathologies will we be able to better understand both the possibilities and limitations of this approach to performing a “virtual biopsy.”

ABBREVIATIONS

AIC

Akaike information criterion

Arctan

arctangent

CIs

confidence intervals

EIM

electrical impedance myography

DAPI

4′, 6-diamidino-2-phenylindole

Hz

Hertz

kHz

kilohertz

LASSO

Least absolute shrinkage and selection operator

LOOCV

Leave one out cross validation

MHz

megahertz

PND

Post-natal day

RMSE

root mean square error

μm²

micrometer squared