High refractive index substrates for fluorescence microscopy of biological interfaces with high z contrast

Abstract

Total internal reflection fluorescence microscopy is widely used to confine the excitation of a complex fluorescent sample very close to the material on which it is supported. By working with high refractive index solid supports, it is possible to confine even further the evanescent field, and by varying the angle of incidence, to obtain quantitative information on the distance of the fluorescent object from the surface. We report the fabrication of hybrid surfaces consisting of nm layers of SiO₂ on lithium niobate (LiNbO₃, n = 2.3). Supported lipid bilayer membranes can be assembled and patterned on these hybrid surfaces as on conventional glass. By varying the angle of incidence of the excitation light, we are able to obtain fluorescent contrast between 40-nm fluorescent beads tethered to a supported bilayer and fluorescently labeled protein printed on the surface, which differ in vertical position by only tens of nm. Preliminary experiments that test theoretical models for the fluorescence-collection factor near a high refractive index surface are presented, and this factor is incorporated into a semiquantitative model used to predict the contrast of the 40-nm bead/protein system. These results demonstrate that it should be possible to profile the vertical location of fluorophores on the nm distance scale in real time, opening the possibility of many experiments at the interface between supported membranes and living cells. Improvements in materials and optical techniques are outlined.

Rapid advances in protein structure determination and in vivo fluorescence labeling have spurred the demand for high resolution, real-time optical imaging of macromolecular assemblies and the structural dynamics that accompany biological function. Remarkable advances in optical microscopy, including image deconvolution (1, 2), multiphoton excitation (3), standing-wave techniques (4–7), and point-spread function shaping (8, 9) have pushed the limits of resolution in ideal cases to 70 nm, substantially below the diffraction limit. This limit is still larger than the dimensions of many macromolecular assemblies. In the following work, we demonstrate a straightforward modification of variable incidence angle total internal reflection fluorescence microscopy (VIA-TIRFM) adapted to probe the interface between a supported lipid bilayer and cells with contrast on an even smaller scale.

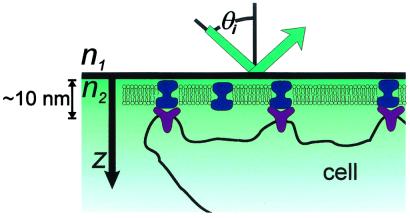
Lipid bilayers containing the appropriate ligands on solid supports can serve as an interface to living cells (10, 11). Because the supported bilayer, bilayer-associated ligands, and cell membrane receptors are all located within tens of nm of the interface (Fig. 1), we aim to achieve optical imaging contrast on this scale. In TIRFM, the evanescent field of the excitation light decays exponentially from the total internal reflection (TIR) interface with a 1/e distance or penetration depth d_p, on the order of 100 nm for a typical glass or SiO₂ (n = 1.5)/aqueous buffer (n = 1.3) interface (12–14). Thus, distance information is encoded in fluorescence intensity by the evanescent field gradient: a fluorophore near the TIR interface is excited to a greater extent than one further from the surface. For a given refractive index material, the penetration depth can be modulated by varying the incidence angle θ_i (Fig. 2); this method is VIA-TIRFM (15–17). Numerical modeling of the evanescent field as a function of n, θ_i, and other parameters discussed below can be used to obtain quantitative information on the profile of fluorophores in the z direction (15). Resolution in the context of VIA-TIRFM experiments is the minimum z displacement between two fluorescent objects that can be separately identified by numerical processing of images obtained at different θ_i's. For both TIRFM and VIA-TIRFM, resolution is fundamentally limited by detection of changes in fluorescence intensity, the validity of the model used to describe the evanescent field and fluorescence loss mechanisms, and suitable algorithms for inverting the observed dependence of the fluorescence intensity on θ_i into a measure of distance from the interface.

Figure 1.

Schematic of TIRFM imaging of a supported bilayer–cell interface illustrating the relevant vertical distance scale (the cell is not drawn to scale).

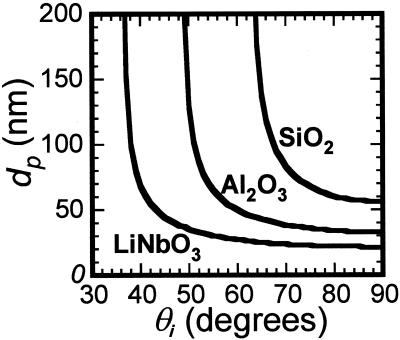
Figure 2.

Characteristic penetration depth, d_p, as a function of incidence angle θ_i for materials of different indices of refraction: SiO₂ (n = 1.5), Al₂O₃ (n = 1.8), LiNbO₃ (n = 2.3). The relation used was:

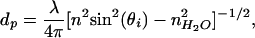with n = 1.33 and λ = 514 nm.

The differential illumination of objects separated by a given distance can be enhanced by making the gradient of the evanescent field steeper, thus enhancing resolution. As illustrated in Fig. 2, high refractive index substrates like lithium niobate can provide a steeper evanescent field gradient, with the greatest variation of d_p with θ_i on a scale that is relevant to the supported bilayer–cell interfacial region illustrated in Fig. 1. However, high refractive index optically transparent materials, such as lithium niobate, rutile, and zinc sulfide, exhibit different surface chemistries, and each presents unique challenges for defining biomolecular assemblies at the surface, a prerequisite for high-resolution TIR techniques. In contrast, many well developed strategies exist for modifying and tethering biomolecules to SiO₂ surfaces. Furthermore, SiO₂ surfaces are one of the few surfaces that can be used as substrates for supported lipid bilayers (10, 18, 19). Several high refractive index materials such as alumina (20) and in situ oxidized Ti (TiO_X) (21) can be used as barriers to pattern-supported lipid bilayers; that is, well defined bilayers do not assemble on these materials. In the following, we demonstrate that a thin interfacial layer of SiO₂ deposited on the high-index support provides a supported bilayer and cell-compatible surface that is ideal for VIA-TIRFM measurements.

Materials and Methods

Single-crystal lithium niobate was generously donated by Crystal Technology (Palo Alto, CA). Hybrid lithium niobate/SiO₂ substrates were prepared by deposition of SiO₂ (13-nm thick layer, unless otherwise specified) onto the +z face of an HF-cleaned lithium niobate substrate by diode-sputtering from a fused-quartz plate. Measurement of the thickness of SiO₂ films on lithium niobate by profilometry and by x-ray photoelectron spectroscopy (XPS) was used to calibrate the SiO₂ deposition rate. The variation in the SiO₂ thickness between depositions is estimated at 7%. A stair-step arrangement of SiO₂ on lithium niobate was fabricated by selective masking of the target during sputter deposition, and each step covered ≈50 mm² in area. The hybrid substrates were baked at 350°C in air for 4 h to improve surface flatness and bilayer assembly (P. Cremer and S. G. Boxer, unpublished work), with all heating and cooling steps done at ≈1°C per min to avoid crystal fracture. Before use, all substrates were rinsed with methanol, immersed in detergent (Linbro 7× detergent, ICN, diluted to 1:4 (vol/vol) in Millipore water), heated to 90°C, rinsed extensively with distilled water, and exposed to an oxygen plasma (Harrick Scientific, Ossining, NY) for 90 s. The substrate surface composition was characterized by XPS with an S-Probe Monochromatized XPS Spectrometer (Surface Science Instruments, Mountain View, CA) with an Al source (1,486 eV) providing a 1-mm spot size. XPS spectra of the hybrid lithium niobate/SiO₂ substrate showed Si and O in a 1:2 ratio, indicating that the SiO₂ film was stable all through the cleaning process. The substrate surface roughness was characterized by tapping mode AFM with a Digital Instruments MMAFM-2 scanning probe microscope.

Small unilamellar vesicles composed of egg phosphatidylcholine (egg PC, Avanti Polar Lipids) and either 1 mol % Texas red 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine (Texas red DHPE, Molecular Probes) or 0.5 mol % 1,2-dipalmitoyl-sn-glycero-phosphoethanolamine N-(biotinyl) (biotin PE, Avanti Polar Lipids) were prepared by vesicle extrusion through 50-nm filters. Fibronectin (Sigma) and BSA (Life Technologies, Rockville, MD) were labeled with cascade blue acetyl azide and Texas red X succinimidyl ester (Molecular Probes), respectively, in accordance with the manufacturer's instructions. Supported lipid bilayers on glass and on lithium niobate/SiO₂ hybrid substrates were formed by vesicle fusion and patterned by microcontact printing protein grids, as described (10, 22). The diffusion coefficient of fluorescent probes was determined as described (22, 23). Extraction and quantitative fluorescence of egg PC bilayers containing 1% Texas red was done as described (24). Epifluorescence images were collected by with a Nikon E800 microscope, appropriate filter sets, and a Photometrix Sensys KAF1400 CCD camera. In the SiO₂ stair-step experiment, the hybrid-supported Texas red DHPE-containing membrane was covered by an ≈1-μm thick water layer and a glass coverslip (no. 1, 0.16 mm thick). Epifluorescence images were collected by using a 10× objective (planar apochromatic, N.A. = 0.45, Nikon). Each experiment consisted of imaging bilayers on a single substrate containing multiple step heights and recording the average intensity observed on each step. For comparison between experiments, this intensity (corrected for background fluorescence) was normalized to that observed on a 65-nm step. The relative fluorescence intensity of Texas red-labeled membranes, prepared from the same vesicle solutions, supported on both plain glass and on a hybrid substrate, was compared by using the imaging conditions above.

For the VIA-TIRFM experiment, the bottom face of a 45° lithium niobate prism was coated with 13 nm of SiO₂ and then patterned with grid lines of Texas red-X labeled BSA (TR-BSA). A lipid bilayer containing 0.5% biotin PE was formed on this surface, incubated with 1 mg/ml unlabeled BSA for 30 min, and incubated with 40-nm diameter NeutrAvidin-labeled microspheres (TransFluoSpheres, λ_excite = 514 nm, λ_emit = 605 nm, Molecular Probes) diluted 1:400 (vol/vol) in 1 mg/ml unlabeled BSA for 30 min. According to the manufacturer, the dyes in these beads are distributed evenly and oriented randomly throughout the outer 50% radius of the bead, which corresponds to 80% of the volume. These samples were illuminated in a TIR configuration (14) on a Nikon TE300 microscope with an argon ion laser providing a 1 mm, 5 mW spot of s-polarized, 514-nm light. Images were collected with a 40× objective (planar apochromatic, N.A. = 0.75, Nikon), a Texas red filter set, and a PentaMAX Gen IV 512ET Intensified CCD camera (Princeton Instruments, Trenton, NJ).

Results and Discussion

Surface Characterization and Bilayer Assembly.

Lithium niobate/SiO₂ hybrid substrates support the formation of lipid bilayers by vesicle fusion that are identical to bilayers on glass, as evidenced by several criteria. First, epifluorescence microscopy of bilayers containing 1% Texas red DHPE on a hybrid support showed a single, uniform plane of fluorescence. Second, quantitative fluorescence of these bilayers after extraction from the substrate by detergent showed that the surface density of lipids on lithium niobate/SiO₂ (1.7 ± 0.2 × 10⁵ counts, mean ± 1 SD, for 324 mm²) is equivalent to that of a conventional glass-supported bilayer (1.6 ± 0.2 × 10⁵ counts for 324 mm²) (21). Third, the diffusion coefficient of Texas red DHPE in egg PC bilayers on hybrid supports (2.6 ± 0.3 μm²/s) was similar to that observed on glass (2.4 ± 0.2 μm²/s), with no detectable immobile fraction. Importantly, these labeled lipids can be patterned and manipulated by electric fields, just like glass-supported bilayers (20), as seen in Fig. 3. Thus, in every manner probed, lipid bilayers on this hybrid support behave and can be manipulated like glass-supported lipid bilayers.

Figure 3.

(a) Epifluorescence image of a supported lipid bilayer containing 1 mol % Texas red DHPE patterned with cascade blue-labeled fibronectin (50 × 50 μm grid, 4-μm wide grid lines) on a hybrid lithium niobate substrate with 13-nm SiO₂. (b) The same region after application of a lateral electric field of 18 V/cm for 10 min demonstrating the formation of gradients of negatively charged Texas red DHPE. (Bar = 50 μm.)

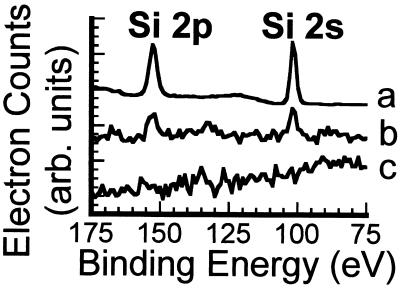
Deposition of SiO₂ onto lithium niobate is necessary for reproducible formation of fluid-supported lipid bilayers. When egg PC vesicles containing 1% Texas red DHPE are exposed to lithium niobate that was polished and then cleaned with dilute HF,† no fluorescence is present on the surface, indicating that supported lipid bilayers are not formed. By contrast, vesicle fusion onto lithium niobate that was polished and without subsequent HF-cleaning results in homogeneous fluorescence on the surface. Analysis of the photobleaching data for Texas red DHPE lipids on the latter surface, however, revealed that this structure does not constitute a fully connected fluid supported lipid bilayer, because the diffusion of these molecules is not Brownian across the surface.‡ Furthermore, upon multiple cycles of cleaning and reuse, progressively more bright points of light, which are likely intact vesicles, were found adsorbed to the surface, and the fluorescence was less homogeneous. XPS spectra of polished lithium niobate surfaces without subsequent HF-cleaning (Fig. 4b) show a small amount of Si in addition to Nb and O; for comparison, the XPS spectra of lithium niobate coated with 13-nm SiO₂ is shown in Fig. 4a. In contrast, the surface of the HF-cleaned lithium niobate (Fig. 4c) contained only Nb and O atoms in the expected 1:3 ratio.§ Consequently, we attribute these observations to the presence of colloidal silica residue from the polishing process on the polished surface, which is removed during HF cleaning. We conclude that supported lipid bilayers do not form on a clean lithium niobate surface, and these results highlight the importance of careful surface characterization.¶

Figure 4.

X-ray photoelectron spectra of a hybrid lithium niobate/SiO₂ substrate with 13-nm SiO₂ (intensity is divided by 10) (a), a polished lithium niobate substrate (polished with colloidal silica) (b), and a polished lithium niobate substrate after cleaning with HF (c).

Vertical Contrast of 40-nm Beads by VIA-TIRFM.

To illustrate the utility of hybrid high refractive index supports toward the goal of high z-resolution imaging, we used the model system schematically illustrated in Fig. 5a, which contains both 40-nm fluorescent beads tethered to a supported lipid bilayer and fluorescently labeled protein (TR-BSA) printed onto a hybrid substrate. This configuration provides two fluorescent structures with different z positions and extents that are spatially separated in the x–y plane. We can estimate the vertical separation of the various objects from the surface with reasonable certainty. The 13-nm thick SiO₂ layer, 2-nm water layer (26, 27), 5-nm thick membrane (27), and 3-nm biotin-NeutrAvidin linkage (28) position the center of the fluorescent bead 43 nm from the lithium niobate-SiO₂ interface. The position of the TR-BSA is less certain; we have shown elsewhere by atomic force microscopy (AFM) that microcontact printing of BSA leaves at most one or two layers of protein on the surface (22); therefore, the approximate thickness is 5 nm. Assuming that the Texas red dyes are randomly distributed and oriented on the BSA surface, the layer of BSA-associated fluorescence is an average of about 15 nm from the lithium niobate-SiO₂ interface. A significant concern in defining distances on this scale is the surface roughness. AFM analysis of both the bare lithium niobate surface and the 13-nm SiO₂ on lithium niobate hybrid surface showed a surface rms roughness of 0.3 nm and 1 nm over 500 × 500-nm regions, respectively. Because the protein and lipid layers are conformal, variations on the order of 1–2 nm are not important at the level of z resolution being considered here, as the relationship between the fluorescent objects and the evanescent field is approximately constant over the area of illumination.

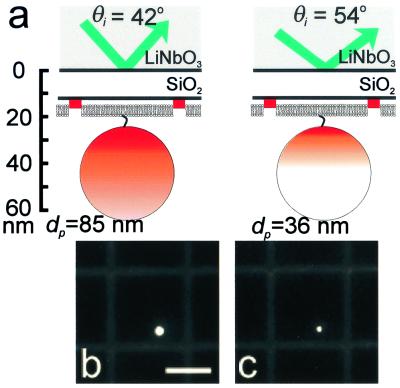
Figure 5.

(a) Schematic diagram of a 40-nm fluorescently labeled bead anchored to a TR-BSA-patterned supported bilayer by a biotin/NeutrAvidin linkage on a hybrid lithium niobate/SiO₂ substrate. The vertical scale provides approximate distances for a 13-nm SiO₂ layer. The shading further indicates the effects of excitation using TIRFM with two different angles of incidence. For simplicity, it does not reflect that only the outer 50% radius of the bead, corresponding to 80% of the volume, contains fluorescent dye, and it does not account for the collection factor discussed in the text. In the case on the left, the penetration depth is such that the excitation intensity covers the entire bead, whereas on the right, only a portion of the bead is excited. Corresponding TIRFM images of a 40-nm NeutrAvidin-coated bead anchored to a supported lipid bilayer containing 0.5 mol % biotin PE on a hybrid lithium niobate/SiO₂ substrate for (b) θ_i = 42° (corresponding to d_p = 85 nm), and (c) θ_i = 52° (corresponding to d_p = 36 nm). The supported membrane was patterned by microcontact printing 3.5-μm wide grid lines of TR-BSA that are separated by 25 μm. (Bar = 20 μm.)

As illustrated in Fig. 5a, illuminating this assembly at different values of θ_i, and thus at different penetration depths, differentially excites the fluorescent beads and the TR-BSA. Specifically, less of the bead is illuminated above a threshold value at a penetration depth of 36 nm than at a depth of 85 nm, compared with the layer of TR-BSA that is well illuminated at both penetration depths. In calculating d_p, we do not consider the birefringence of lithium niobate, and we use a single value for its refractive index as a first approximation.** The absolute intensity of either structure is related not only to d_p, but is also directly proportional to I_o(θ_i), the intensity at the TIR interface, which varies with incident angle and prism geometry. Our approach is to ratio the fluorescence intensity of the beads to the TR-BSA layer at each incident angle; this ratio is independent of I_o(θ_i). Thus, relative to the observed intensity of the TR-BSA layer, the observed fluorescence of the bead is greater at larger penetration depths (smaller incident angles) than for small penetration depths.

The ability of VIA-TIRFM to selectively excite the bead relative to the TR-BSA on the surface is shown in Fig. 5 b and c. For comparison between images collected at the two different incident angles, the contrast was linearly scaled such that the TR-BSA minus background intensity as well as the background intensity is the same between the images presented in Fig. 5 b and c. The bead is brighter for θ_i = 42° than for θ_i = 54°, demonstrating vertical contrast of an object that is ≈15 nm vs. 43 nm from the surface.

To quantitatively compare the fluorescence of beads and TR-BSA at different incident angles, image regions were chosen to encompass either an entire bead or a specific, nearby region of TR-BSA, and the charge-coupled device (CCD) pixel intensities were summed over these regions. These regions remained constant for each field of view between different incident angles of illumination. We assume that these summed intensities contain contributions from background signal that is composed of background fluorescence, scattered light, and CCD dark current, but it is constant over the area of interest in each image. Background-corrected, summed intensities of the bead and TR-BSA, F_bead(θ_i) and F_TR-BSA(θ_i), respectively, were calculated by measuring the average background intensity from a region near both a bead and a region of TR-BSA and subtracting this value from the intensity of each pixel in the summation. With these corrected fluorescence intensities, we define a contrast ratio R_42°/54° as:

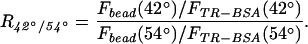1

For the conditions presented in Fig. 5, the average value for several beads is 2.2 ± 0.3 (mean ± SD). This ratio is greater than unity, demonstrating quantitatively the contrast between fluorescent structures differing in vertical position by only tens of nanometers.

Quantitative Imaging and Fluorophore Profiling.

The ultimate utility of the hybrid high refractive index substrate for VIA-TIRFM lies in the potential to generate profiles of fluorescence intensity in the z direction. As a step in this direction, we consider a more quantitative model. In a TIRFM configuration at a given θ_i, the detected fluorescence intensity of an object summed over its x–y extent, F_object(θ_i), can be modeled to a first approximation as:

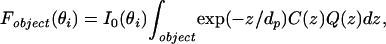2

where the vertical distribution of fluorophores in the object is described by C(z). The fluorescence collection factor Q(z), as defined by Hellen and Axelrod (29), captures the well established phenomenon that a radiating fluorophore near a high refractive index substrate exhibits altered fluorescence that depends on its distance from the interface (30, 31). This phenomenon is attributed to two effects (29, 32): (i) interference between emitted light propagating directly from the radiating dipole and light that is reflected from the material interface; and (ii) power dissipation into the high refractive index material as the radiating dipole is closer to the interface.

The model developed for the collection factor by Hellen and Axelrod considers a constant-amplitude oscillating dipole at a three-layer interface composed of two semiinfinite, nonattenuating dielectric regions 1 (the aqueous media) and 3 (the lithium niobate) with indices of refraction of n₁ and n₃, respectively, separated by an intermediate region 2 (the SiO₂ spacer) with index of refraction of n₂ and thickness l. The radiating dipole is located in region 1 at a distance z from the region 2–3 interface, and its transition dipole moment is oriented with polar angle Θ relative to the surface normal. The collection factor in region 1 is given by:

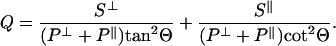3

S^⊥ and S^∥ represent the power collected through the microscope objective with numerical aperture N.A. from a dipole oriented perpendicular or parallel relative to the surface, respectively. These terms account for the interference effect of the propagating field; they are defined fully in ref. 29. P^⊥ and P^∥ describe the total dissipated power, including near-field effects, of a dipole oriented perpendicular or parallel, respectively, to the surface; these terms also are defined fully in ref. 29.

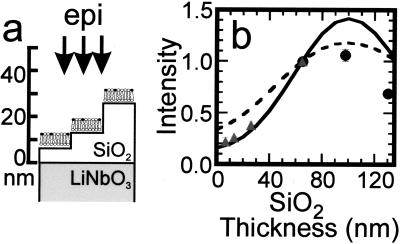
To obtain more quantitative information on the collection factor near lithium niobate, we assembled lipid bilayers containing a small percentage of Texas red DHPE on a stair-step arrangement of SiO₂ layers on lithium niobate (Fig. 6a). As shown in Fig. 6b, the observed fluorescence is substantially reduced as the fluorophore is brought close to the lithium niobate substrate. Making side-by-side comparisons, the fluorescence of the membrane on 13 nm of SiO₂ on lithium niobate is approximately half of what would be observed on plain glass, whereas on 65 nm of SiO₂ on lithium niobate, the fluorescence is approximately twice the intensity observed on glass (data not shown).

Figure 6.

(a) Schematic diagram of SiO₂ stair steps sputtered onto lithium niobate and used to probe the effect of the high refractive index substrate on the fluorescence from 1 mol % Texas red DHPE in assembled supported bilayers. Each region of SiO₂ was ≈50 mm², so the horizontal and vertical scales are very different in this schematic. (b) Intensity of Texas red fluorescence as a function of the SiO₂ thickness normalized to the fluorescence measured from the 65-nm SiO₂ layer. The fluorescence was excited and collected with an epifluorescence microscope, and background was subtracted as described in Materials and Methods. The gray triangles are data acquired from a single lithium niobate substrate containing 7, 13, 26, and 65-nm layers of SiO₂; the black circles are from a substrate containing 65, 98, and 130-nm layers of SiO₂. Q(l) is shown by the dashed line, whereas Q(l)⋅S^∥(l) is shown by the solid line, where both are normalized to 1 at l = 65 nm. The parameters used to calculate Q(l) and S^∥(l) (see text) were: N.A. = 0.45, distance of the fluorophore to the SiO₂/aqueous interface = 7 nm, n₃ = 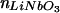= 2.29, n₂ =  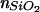= 1.46, n₁ = 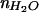= 1.33, λ_excite = 585 nm, λ_emit = 605 nm, and Θ = π/2 (transition dipole moment of Texas red is approximately parallel to the surface; ref. 33).

To compare these data to the model of Hellen and Axelrod, we assume that the Texas red DHPE fluorophores are confined to the top surface of the supported membrane, with an average distance of ≈7 nm from the SiO₂-aqueous interface.‡‡ As before, we assume that the water layer is 2 nm and that the SiO₂ and lithium niobate surfaces are flat. These uncertainties are small compared with the wavelength of light, which is the relevant distance scale for these effects; as discussed below, the interference effect dominates. The transition dipole moment of Texas red DHPE is taken to be oriented parallel to the interface, because linear dichroism measurements of dye-containing membranes show that structurally similar rhodamine chromophores are preferentially oriented parallel to the interface (33). Finally, in the epi-illumination configuration, the excitation intensity at different distances from the surface is influenced by interference between incident light and light reflected off the surface (30). According to the reciprocity theorem, this interference is identical in form to that for interference of emitted light (34), as modeled by Hellen and Axelrod. Consequently, the observed fluorescence should be modeled by Q(l)⋅S^∥(l), where Q(l) and S^∥(l) are calculated with the wavelength of emitted light (605 nm) and excitation light (585 nm), respectively.

By using the parameters outlined above, we calculated Q(l) and S^∥(l) for a three-layer interface composed of n₁ = 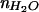= 1.33, n₂ = 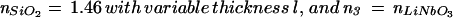= 2.29. The solid curve in Fig. 6b represents Q(l)⋅S^∥(l) for the specific conditions outlined above, whereas the dashed curve represents Q(l) alone; both curves and the experimental data have been normalized to 1 at l = 65 nm. It is seen that Q(l)⋅S^∥(l) quite accurately represents the relative collected bilayer fluorescence on the short SiO₂ stair steps (less than 65 nm in height) but fails to show quantitative agreement on layers of SiO₂ measuring 98 or 130 nm. Qualitatively, the Hellen and Axelrod model predicts that when the Texas red DHPE is closest to the lithium niobate surface, its parallel orientation causes destructive interference between light emitted directly toward the objective and light reflected off the lithium niobate surface, which is phase shifted by λ/2. This interference becomes constructive as the chromophore is moved away from the surface, with a maximum at a distance of λ/4. For a dipole parallel to the surface, the power dissipation effect is small relative to the interference effect because the dipole's near-field is oriented away from the lithium niobate. It is possible that in the 98- and 130-nm layers, which were prepared by 2 and 3 steps of SiO₂ sputtering, respectively, there is an accumulation of scattering defects and possible local density variations leading to lensing, which would tend to reduce the intensity of light that gets to the fluorophore and the fluorescence that gets to the objective. The origin of this discrepancy on these thickest layers is being investigated further. Nonetheless, the good agreement between the model and the data for the fluorophores within 65 nm of the interface, the region of greatest interest in our current experiments, suggests that we can use the Hellen and Axelrod treatment to model Q(z) in Eq. 2.

We are now in a position to predict R_42°/54° for the system presented in Fig. 5. Including the assumptions stated previously into Eq. 2, we have:

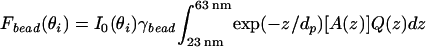4

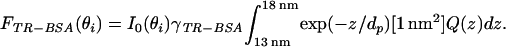5

Here, γ_bead and γ_TR-BSA are the number of fluorophores per nm³ in the bead and the region of TR-BSA, respectively. As for I₀(θ_i), γ_bead and γ_TR-BSA do not need to be known because they cancel out in the calculation of R_42°/54°. In Eq. 4, A(z) is the fluorophore-containing cross-sectional area of the bead at z, where A(z) = π[r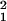 − (z − a)²] for 33 nm < z < 53 nm and A(z) = π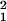(r − r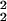) otherwise; r₁, r₂, and a are the bead radius (20 nm), radius of the region lacking fluorescent dyes (10 nm) in the bead, and center position (43 nm) of the bead, respectively. In Eq. 5, the term in square brackets describes the TR-BSA structure as a top-hat distribution of fluorophores in z and makes the expression dimensionally correct. The theory of Hellen and Axelrod was used to calculate Q(z)†† for randomly oriented fluorophores excited by s-polarized light that emit 650-nm light; then, Eqs. 4 and 5 were used to calculate R_42°/54° ≈ 1.5 ± 0.1, where the SD is based on the manufacturer's estimate of 20% variation in bead diameter. This ratio is on the same order as the observed value of 2.2 ± 0.3 but indicates that, relative to the TR-BSA, the observed fluorescence of the bead is less at the shorter d_p compared with the large d_p than we would expect. The experimental parameters that are subject to the most uncertainty are the thickness of the TR-BSA layer and the orientation of fluorophores in the TR-BSA and bead. It is likely that the weakest assumption in the model is the approximation that the evanescent field decays as a simple mono-exponential. Because of the short penetration depths involved in these experiments, the multiple layers with different refractive indices (SiO₂, water, lipid bilayer, protein, and polystyrene bead) and different shapes may alter the scattering and decay of the evanescent field, and this effect could make the observed value of R_42°/54° greater than the predicted value.

Conclusions and Prospects.

We have demonstrated that a very thin SiO₂ layer on lithium niobate renders it compatible with the demanding requirements for supported lipid bilayer assembly and fluidity. Although bilayers are of primary interest in our work, there is a huge literature on the adsorption of a variety of molecules to SiO₂ as well as its specific chemical modification for a wide range of purposes. Thus, SiO₂ serves as a generally useful interfacial layer for a wide range of underlying materials whose properties may not be so easily modified.

High refractive index materials promise enhanced resolution in a TIRFM configuration by increasing the steepness of the gradient of the evanescent field; based on the minimum attainable penetration depth at a substrate/water interface, lithium niobate provides a 50% and 130% improvement in resolution over sapphire and glass, respectively, for a given signal-discrimination threshold. Our quantitative demonstration of selective illumination of substrate-bound protein and membrane-tethered bead spaced nominally 28 nm apart is a first step in demonstrating the use of these hybrid supports. Subsequent VIA-TIRFM studies with appropriate nanometer calibration should yield highly accurate z positions for fluorescently labeled objects. Although we used lithium niobate for this first set of experiments, it is a poor choice for several reasons: lithium niobate is birefringent, pyroelectric, and exhibits a photorefractive effect that limits the long-term utility in an intense excitation beam. Several other materials—including ClearTran (ZnS, n = 2.3) and ytterium:aluminum garnet (YAG, n = 1.8)—that are not birefringent, are transparent throughout the visible and near infrared, thermally stable, insoluble in water and reasonably inexpensive are of potential use. By combining a true automated VIA-TIRFM apparatus (15, 16) and these materials, it should be possible to extend the limits of accuracy and utility of this approach.

Abbreviations

VIA

variable incidence angle

TIRFM

total internal reflection fluorescence microscopy

TIR

total internal reflection

XPS

x-ray photoelectron spectroscopy

Texas red DHPE

Texas red 1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine

TR-BSA

Texas red X-labeled BSA