Microstructural Parcellation of the Human Brain

Abstract

The human cerebral cortex is composed of a mosaic of areas thought to subserve different functions. The parcellation of the cortex into areas has a long history and has been carried out using different combinations of structural, connectional, receptotopic, and functional properties. Here we give a brief overview of the history of cortical parcellation, and explore different microstructural properties and analysis techniques that can be used to define the borders between different regions. We show that accounting for the 3D geometry of the highly folded human cortex is especially critical for accurate parcellation. We close with some thoughts on future directions and best practices for combining modalities.

A. Introduction

Current neuroimaging studies frequently refer to activated cortical locations using areas defined by Korbinian Brodmann more than a century ago (Brodmann 1909). Despite the well-known shortcomings of Brodmann’s map, the moderate resolution of volume-averaged neuroimaging data did not initially demand better. Activations in ‘Brodmann areas’ are not typically accompanied by rigorous statistical analysis of the uncertainty associated with the localization. Most commonly, a ‘Brodmann area’ (BA) is used colloquially in the sense of any structurally-defined region in the cerebral cortex. Heavily-smoothed and thresholded average activations are then assigned to ‘Brodmann areas’, sometimes subdivided ad hoc, using surrounding folding patterns (Turner and Geyer 2014, Turner 2016). This is a consequent of the fact that Brodmann’s iconic summary map was largely transmitted to modern neuroimaging via the noisy channel of a single pair of labeled 2D lateral and medial views of the folded cortex. That diagram summarized observations from multiple, small, usually non-overlapping samples of multiple brains. This approach has long been known to be problematic as: (1) there was no way to rigorously test the uncertainty of these localizations, and (2) the relationship between the Brodmann areas and cortical folding was little discussed and less quantified. While computational analysis of neuroimaging data has advanced remarkably in the last decade (Miller, Massie et al. 2000, Smith, Jenkinson et al. 2006, Ashburner 2007, Behrens, Berg et al. 2007, Davatzikos, Fan et al. 2008, Fischl, Stevens et al. 2009), relatively little research has explicitly attempted to relate cyto- and myeloarchitecture to the complex but observable geometry of the cortical surface (e.g. (Fischl, Rajendran et al. 2008, Sereno, Lutti et al. 2013, Waehnert, Dinse et al. 2014, Waehnert, Dinse et al. 2016)). A primary goal of this research is to develop high resolution multi-contrast acquisition methods that reveal putative cortical boundaries both within the cortical sheet (i.e. laminae) and along the cortical sheet (i.e. cortical areas).

Improvements in acquisition technology have advanced MRI to the point where we can now catch glimpses in vivo of the laminar and columnar architecture that is one of the defining features of the human cerebral cortex (Geyer, Weiss et al. 2011). Using phased-array receive coils and ultra-high-field scanners, researchers have demonstrated the importance of using our understanding of the laminar nature of cortical gray matter to guide functional and diffusion MRI (dMRI and fMRI respectively) analysis (Polimeni, Fischl et al. 2010, Polimeni, Fischl et al. 2010, Leuze, Anwander et al. 2014). Within-area modules in visual extrastriate areas (e.g., V2 stripes, V4 patches) initially discovered in non-human primates have just begun to be convincingly visualized in humans at high fields (Nasr, Polimeni et al. 2016, Tootell and Nasr 2017) and correlated with myelination density (Dumoulin, Harvey et al. 2017). The relatively stereotyped nature of the laminar origins and targets of cortico-cortical connectivity raises the importance of being able to accurately determine which cortical lamina a given signal arises from, as there is suggestive evidence that such a capability may allow the inference of the direction of information flow within the cortex from fMRI (Polimeni, Fischl et al. 2010) – a significant potential development. Finally, an array of disorders such as epilepsy, schizophrenia, dyslexia and autism, may result in subtle but detectable changes in laminar architecture that could be measured using improved tools for quantifying the laminar and columnar properties of the human cerebral cortex. Knowing the vertical (columnar) position of an effect is potentially as important as knowing its tangential location (cortical area).

Classical microstructural parcellation

The heterogeneous appearance of the local laminar and columnar structure of different parts of the cortical sheet suggested early on that it might be worth defining subregions in preparation to looking for functional differences between areas. The pioneers in this field focused on either stains for cell bodies (cytoarchitectonics) or stains for myelinated fibers (myeloarchitectonics)(Flechsig 1920) (Brodmann 1909, Vogt and Vogt 1919, Flechsig 1920, von Economo and Koskinas 1925). Many competing hemisphere-wide maps based on sectioning and histological staining of cadaver brains were published, demarcating the boundaries of cyto- and myelo-architectonic domains. Perhaps because of the accessibility and compactness of his two summary images, Brodmann’s cytoarchitectonic parcellation came to dominate, despite the fact that some of the competing myeloarchitectonic parcellations have turned out to better reflect our current understanding of cortical parcellation (Campbell 1905, Flechsig 1920). For example Flechsig (Flechsig 1920) correctly identified myelinated maxima in the region of what we now call the MT/FST complex, V3A, V6, and VIP, none of which were correctly identified by Brodmann (Sereno, Lutti et al. 2012). That these prescient early observations fell into obscurity was partly due to the difficulty of objectively comparing multiple incommensurate maps. Some of this early work of the Vogt school has only very recently been made more accessible by manual alignment with modern atlases (Nieuwenhuys 2013, Nieuwenhuys, Broere et al. 2015, Nieuwenhuys and Broere 2017).

The early architectonic maps subdivided the cortical sheet into a complex mosaic based on radial and lateral variations in the composition of tissue columns perpendicular to the pial and white matter surfaces. However, these parcellations were subject to many methodological criticisms. Their labor intensive nature limited sample size, which was problematic given: (1) inter-subject variability of cytoarchitectonic boundaries but also substantial within-area variation (see e.g., MT in Fig. 3 in (Sereno, McDonald et al. 2015); and (Kuehn, Dinse et al. 2017), on the hand-face border in somatomotor cortex), (2) the unavoidable artifacts of the histological process, such as idiosyncratic plastic deformation and tearing of sections, artefactual variations in fixation and staining density, and random angle of the plane of section relative to the intrinsic laminar coordinate system of the cortical sheet, (3) observer bias, and (4) limitation to a single tissue contrast per sample. In current invasive mapping studies on non-human primates, typically necessarily limited to small subject counts, these methods are practiced much the same way as they were 100 years ago (see e.g., (Seelke, Padberg et al. 2012), on electrophysiological mapping of higher level somatosensory areas followed by architectonic analysis).

Large-scale studies on post-mortem human tissue by Zilles, Amunts and colleagues have recently managed to address many of these limitations (Geyer, Schleicher et al. 1999, Schleicher, Amunts et al. 1999, Amunts, Malikovic et al. 2000, Morosan, Rademacher et al. 2001, Amunts, Schleicher et al. 2003, Zilles, Eickhoff et al. 2003, Eickhoff, Amunts et al. 2006, Amunts, Schleicher et al. 2007, Malikovic, Amunts et al. 2007). By expanding the number of tissue contrasts collected on individual post-mortem specimens beyond basic columnar density profiles to include immunohistochemical stains and polarized light(Axer, Axer et al. 2001, Axer, Amunts et al. 2011), by expanding sample sizes, by more closely controlling fixation and sectioning conditions, and by using probabilistic observer-independent methods, it has become possible to generate cortical area parcellations that are better matched to the kind of receptotopic and functional parcellations that can now be obtained in living subjects (see e.g., (Rosenke, Weiner et al. 2017)).

Resting state functional connectivity

A great profusion of studies of “resting state functional connectivity”’ have been undertaken since the ground-breaking PET work by Raichle in the late 1980s (see, for example (Raichle, MacLeod et al. 2001, Raichle and Snyder 2007) for review) and by Biswal (Biswal, DeYoe et al. 1994, Biswal, Yetkin et al. 1995) using MRI in the 1990s. This popular method merely requires that a subject lies ‘at rest’ in the scanner for a moderate amount of time. By analyzing the synchronization of signals between brain regions and then constraining the number of resulting regions using various combinations of topological neighborhood constraints, region size, local gradients, and seed region definitions, a large number of different tentative cortical parcellation schemes have been published (e.g. (Yeo, Krienen et al. 2011, Power, Schlaggar et al. 2014)). To a substantially greater extent than was the case with more technically difficult microstructural parcellations, the very large number of alternate resting state parcellations and data formats already in the literature has made it virtually impossible to objectively assess and compare them (for recent reviews, see e.g. (Glasser, Smith et al. 2016, Schaefer, Kong et al. 2017)), an unfortunate echo of the initial flowering of cortical architectonics.

White-matter and gray-matter diffusion

The use of diffusion-weighted imaging to trace white-matter tracts provides yet another method for parcellation of the cortex somewhat analogous to resting-state functional connectivity (see (Eickhoff, Thirion et al. 2015) for a review). Unlike invasive neural tracer methods, local diffusion-based tract tracing is a Markov process. Its memory-less nature means that a mistake capable of being propagated to the next step is possible in the passage through every voxel. Even assuming no mistakes, fiber tracts are like freeways, with multiple entrances and exits, so ‘connections’ can only be defined probabilistically. And mistakes are easy to make when there are crossing fibers within single voxels. Microscopic observations show this commonly occurs in the white matter, but also at the sudden right-angle turns that fibers make as they enter the gray matter in gyri. One huge advantage these methods have over injected tracer methods is that all ‘connections’ can be measured simultaneously in a single specimen/scan. Though these methods have not yet passed the acid test of correctly tracing connections between a single retinotopic location in one cortical visual area to the corresponding retinotopic points in its target cortical areas, their somewhat coarser image of connectivity has many uses(Johansen-Berg and Behrens 2014). While global methods (Jbabdi, Woolrich et al. 2007, Yendiki, Panneck et al. 2011) can avoid this sensitivity to errors, they are designed for probing the properties of known connections rather than exploratory techniques.

Another use for diffusion-weighted scans is to measure local differences in the ‘fabric’ of the fiber structure of the cortex, by analogy with the methods of early myeloarchitectonics. Though gray matter diffusion is much less anisotropic than white-matter diffusion, what anisotropy there is can be reliably measured and used to distinguish cortical areas (e.g. (Nagy, Alexander et al. 2013)). These methods are in their infancy. However, by combining high angular-resolution scans, multiple b-values (to measure aspects of local neurite orientation, dispersion and density), and by constructing features that measure diffusion relative to the orientation of the local cortical surfaces, it has been possible to distinguish cortical areas using both unsupervised and supervised methods (McNab, Polimeni et al. 2013, Ganepola, Nagy et al. 2017)

T1 mapping

T1 relaxation has long been known to be correlated with myelination density. However, the brightness of each voxel in a standard ‘structural’ MRI image is only weighted by T1 relaxation value (actually, since T1 is shorter for brighter voxels, ‘T1’ images are actually weighted by R1=1/T1). The reason for saying ‘weighted’ is that other factors affect the voxel brightness, such as proton density and B1 receive inhomogeneities. But more insidiously, B1 transmit inhomogeneities affect the contrast between different voxels; there is a large (25%) variation in B1 transmit flip angles across the head at 3T for a given nominal ‘flip angle’ (Lutti, Dick et al. 2014). A great deal of effort has been put into trying to repair these brightness and contrast artifacts after the fact, for example, for the purpose of distinguishing gray matter from white matter(Wells, Kikinis et al. 1994, Sled, Zijdenbos et al. 1998, Dale, Fischl et al. 1999, Weiskopf, Lutti et al. 2011). But given the comparatively small tangential variation in T1 between cortical areas (at maximum, only a 5% variation), post-hoc brightness and contrast correction methods risk ‘normalizing’ away the signal.

A different strategy is to acquire additional scans to more accurately estimate T1 in the first place. A large number of different methods have been proposed over the years; here are four recent ones. A qualitative method for removing B1 receive inhomogeneities is to divide a T1 scan by a 3D fast spin echo long-echo-train T2 scan, since receive inhomogeneities affect both scans similarly(Glasser and Van Essen 2011). However, different signal pathways (gradient echo vs. spin echo plus stimulated echo) result in different spatial distortion; and uncorrected transmit inhomogeneity locally affects contrast. An improved quantitative method is to collect multiple FLASH scans with different flip angles and use the signal equation to estimate T1(Fischl, Salat et al. 2004, Sigalovsky, Fischl et al. 2006). Another quantitative method for estimating T1 is MP2RAGE, where two MPRAGE images with different inversion times are combined (Marques, Kober et al. 2010). Finally, a fourth method is to collect two multi-echo FLASH scans with different flip angles, estimate the variable local flip angle with an independent dual-echo STEAM (spin-echo plus stimulated echo) scan (Jiru and Klose 2006), then solve directly for T1 and proton density after linearizing the FLASH signal equation (Helms, Dathe et al. 2008, Sereno, Lutti et al. 2012, Lutti, Dick et al. 2014). The greatest challenge in applying any of these methods to the cortex is that between-area, within-lamina (tangential) variation is actually substantially smaller than within-area, between-lamina (columnar) variation. This means that small errors in estimating laminar position can easily obscure the between-area differences that are critical for accurate parcellation.

In the following, we will concentrate on best practices for finding cortical laminae in both 2D and 3D contexts and in vivo and ex vivo, consider recent advances in parcellating the gray matter using structural and diffusion-weighted scans. In addition, we present a new method for computing correspondences between the gray/white and pial surfaces, which is needed to quantify the properties of the gray matter in the cortex, and hence detect changes that are indicative of architectonic boundaries. We build on previous techniques for computing corresponding locations that required the embedding of constraints on allowable thickness values and correspondence properties into the surface evolution itself (MacDonald, Kabani et al. 2000, Das, Avants et al. 2009). In contrast, our variational technique that can be applied post-hoc on any pair of surfaces, and doesn’t require assumptions about the geometry of the surfaces. We finish by discussing the difficult interrelated problems of how best to combine modalities and compare competing parcellations.

B. Methods

The Perils of Analyzing a folded surface in an arbitrary viewing plane

One of the central features of the mammalian cerebral cortex is its differentiation into areas with varying cyto-, myelo-, chemo- and vaso-architectonic properties, including changes in the density, morphology, and laminar distribution of cells and intracortical connections. The detection of the boundary between different areas is thus accomplished by quantifying these properties and looking for abrupt changes that mark the transition from one area to another. Automating this procedure requires extracting information that quantifies these properties at each point in the cortical ribbon, which in turn is based on some method of traversing the ribbon from the gray/white boundary to the pial surface. A dominant current method for carrying out this analysis is to treat the pial and white surfaces as capacitive plates, clamp the voltages to 0 and 1, respectively, then solve the Laplace equation of electromagnetism in the interior space (Jones, Buchbinder et al. 2000)}(Schleicher 1999). Streamlines of the solution that are perpendicular to the isopotential curves are followed from the white to the pial surface to establish a path for sampling gray matter properties. While in principle this analysis for computing intensity profiles within the cortical ribbon can be carried out using the pair of folded surfaces directly in their native 3D space, in practice, this is not possible with standard histological methods. The microscopic resolution needed to directly visualize architectonic features of the cortex, to uniformly infuse stains that highlight molecular properties, and finally to remove water and fat from human tissue to optically clear it currently require planar physical cutting of the tissue, following by staining, mounting, dehydration, and defatting. Polarized light imaging (Axer, Axer et al. 2001, Dammers, Axer et al. 2010, Axer, Amunts et al. 2011) does not require staining as it uses the intrinsic birefringence of the myelin sheath to produce contrast; but it still requires cutting, and hence, distortion prior to imaging. The Laplace analysis is then almost ubiquitously carried out on this two-dimensional slice (Schleicher, Amunts et al. 1999).

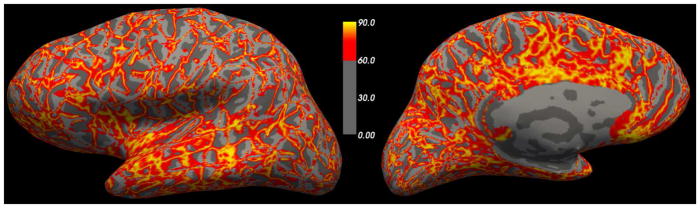
Recent work in tissue clearing (Chung and Deisseroth 2013), fast block-face imaging (Seiriki, Kasai et al.), and optical coherence tomography (Augustinack, Magnain et al. 2014, Wang, Zhu et al. 2014, Magnain, Augustinack et al. 2015) hold the promise of imaging before cutting has introduced irremediable distortions, but current histological techniques analyze the folded 2D surface embedded in three-dimensions by cutting through it along an arbitrary plane. In (Schleicher, Amunts et al. 1999) it was suggested that distortion induced by folding patterns is within acceptable limits if the angle between the cutting plane and the cortex is less than 60°. For cortical regions that exceed this limit, a different cutting plane should be used to analyze this region – by necessity in a different brain if the one brain had not been blocked. Unfortunately, due to the complexity and high spatial frequency of the folding patterns of the human neocortex, very little of the cortical sheet respects this constraint. This is shown in Figure 1, which displays an inflated surface with a color overlay of the angle between the coronal plane and the surface normal at each point on the white surface, with points that do not exceed the 60° threshold shown in gray. As can be seen, there are no large patches of the surface that fall below the 60° cutoff and in fact only 46% of the total cortical surface area falls below this threshold (52.6% and 52.9% for sagittal and horizontal planes respectively), suggesting that cortical folding patterns will introduce significant noise into this kind of analysis for almost every cortical region.

Figure 1.

Angle (in degrees) of dot product of coronal plane with pial surface normal (light/gray dark gray curvature maps shown for all regions < 60°).

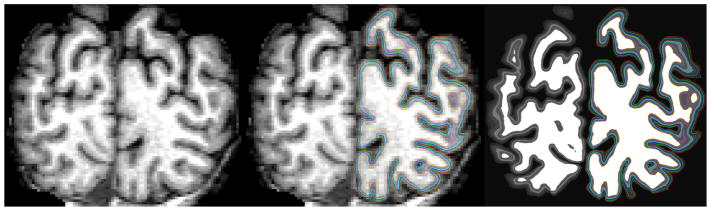
In order to assess the magnitude of these effects, we created a synthetic volume in which we take an actual (1mm³) MRI volume, derive white and pial surfaces from it, then divide the interior of the ribbon into 6 equally-spaced compartments meant to represent the 6 cortical layers. We then fill the interior of each layer with a unique value (WM=110, layer 6=70, layer 5=60, layer 4=80, layer 3=50, layer 2=40, layer 1=30, exterior =10) to create a volume with 200μm³ resolution. An example coronal slice from this procedure is given in Figure 2. We then solve the Laplace equation and compute streamlines as described in (Schleicher, Amunts et al. 1999, Jones, Buchbinder et al. 2000), but limit the Laplace solution and the resulting streamlines to be within each coronal slice, as would be the case for normal histological analysis. Given that that the original surface is topologically equivalent to a sphere, any planar cut will result in a set of closed curves lying within that plane, as can be seen in Figure 2, right which shows the laminar surfaces used to create the synthetic volume overlaid on an arbitrary coronal slice. As can be seen, this results in a set of non-intersecting closed curves in the plane. We note that the number of curves changes as a function of which laminar surface is used for the intersection. In this particular case, the white surface shown in yellow has 3 separate closed curves, but the pial surface shown in red has only a single closed curve in this slice plane, which highlights the problematic nature of using planar analysis techniques for a highly-folded surface.

Figure 2.

Example of synthesis procedure. Top, from left-to-right: original MRI, 6 equidistant compartments created between the white and pial surfaces, and rightmost, an image synthesized to have uniform intensity within each compartment or “layer”. Bottom: zoom to show individual surfaces.

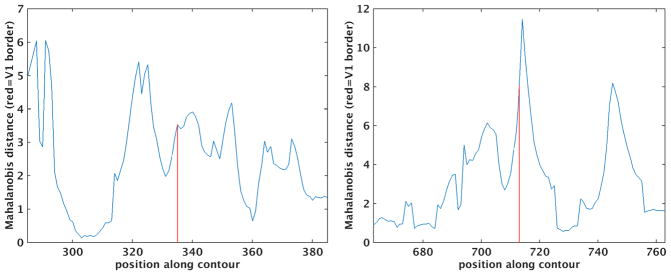
While the folds can change the planar topology as illustrated above, they also introduce significant geometric confounds into any laminar analysis. To illustrate this issue, we replicated the observer-independent laminar profile analysis procedure presented in (Schleicher, Amunts et al. 1999) and used in a number of important subsequent studies investigating the variability of architectonic boundaries in the human brain(Geyer and Ledberg 1996, Amunts, Schleicher et al. 1999, Amunts, Malikovic et al. 2000, Amunts, Kedo et al. 2005, Eickhoff, Amunts et al. 2006, Amunts, Schleicher et al. 2007, Eickhoff, Grefkes et al. 2007). In this approach, the Laplace streamlines are used to sample an intensity image in which the value at each pixel is related to the density of neurons at that location. Features representing each streamline are computed, then the equivalent of a spatial gradient is calculated by estimating the Mahalanobis Distance (MD) between the feature sets of adjacent blocks off streamlines (for details please see (Schleicher, Amunts et al. 1999)). Peaks in the MD then correspond to putative borders between architectonic areas.

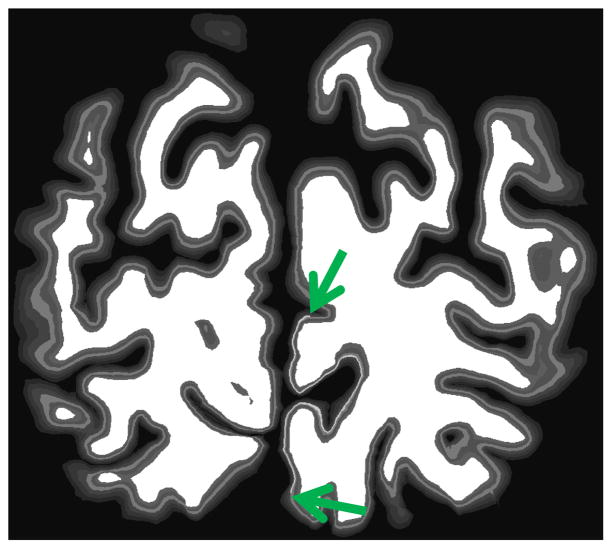
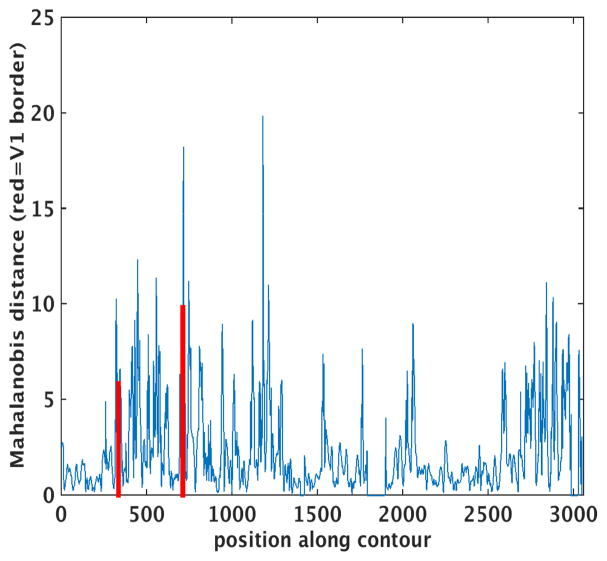
We applied this procedure to a coronal slice containing a synthetic stria of Gennari – a region in which the intensity of the simulated layer 4 is increased significantly, as shown in Figure 3. Finally, we extracted the largest curve from the intersection of an arbitrary coronal plane with the white matter surface and computed the Mahalanobis distance between neighboring blocks of 200-um-spaced Laplace profiles. The results of this analysis are shown in Figure 4, with the borders of the synthetic stria marked with vertical red lines. Recall that the synthetic data used as input to this cortical parcellation procedure has no boundaries other than the simulated V1. Every layer has exactly the same thickness and intensity everywhere in the brain. Nevertheless, the through-plane folding of the cortex induces apparent changes in laminar properties when viewed in an arbitrary coronal plane, giving rise to large spikes in the MD throughout the slice, some larger than those observed at the true boundary. And even those at the true boundaries are displaced relative to their true location by through-plane folding, as shown in Figure 4.

Figure 3.

Synthetic V1 with increased layer IV intensity in the “stria” (green arrows show end of stria).

Figure 4.

Mahalanobis distance across the cortex, red lines indicate boundaries of synthetic stria.

In order to elucidate the source of these large spikes in the MD, we zoom into a region of spikes completely within the boundaries of the simulated V1 in Figure 5, with the two blocks of contours used to compute the MD shown in different colors (cyan and red) in Figure 6. Examining this figure, it is clear that the large MD is a result of through-plane folding, with the cyan contours largely orthogonal to the gray/white boundary, but the red ones covering a region in which the through-plane folding of the cortex causes the profiles to be oblique to the cortex. This problem is exacerbated by the fact that the different layers are differentially affected. For example, in this region, the deep layers show a much greater apparent expansion than the superficial ones, although, of course, all the layers are exactly the same thickness in their native three-dimensional space.

Figure 5.

Zoom on MD around left-hand and right-hand V1 boundary.

Figure 6.

Laplace streamlines shown in region around the spike that occurs near profile 450 (cyan to left of spike, red to right of spike). The coronal view creates apparent changes in laminar intensity that are really just the result of typical cortical folding patterns.

B.1. Variational approach to finding a vector field connecting gray and white matter boundaries

In the previous section, we showed that the analysis of the folded cortex in an arbitrary plane introduces large artifacts into the resulting maps of putative areal boundaries. In this section, we extend this analysis to 3D and investigate the effects of different types of schemes for sampling between the two surfaces. Laminar modeling requires sampling cortical intensities along a path connecting the gray/white and pial boundaries, thus implicitly establishing a correspondence between the two surfaces. A simple and intuitively appealing way to compute this correspondence is simply to move outwards along the surface normal of the inner (white) surface until the pial surface is reached. Unfortunately, this method fails when the normal of one surface is tangential to the other, resulting in arbitrarily long traversals (e.g. when the inner surface is a flat large U and the outer one is a smaller flat U).

As discussed in the previous section, the most common approach to computing these traversals is to treat the two surfaces as capacitive plates with the outer (pial) surface clamped to a voltage of 1 and the inner (white) surface clamped to 0. The Laplace equation of electromagnetism is then solved to yield an EM field specifying a voltage at each location between the surfaces. The paths between the surfaces are then found by following the gradient of this field (e.g., using Euler integration). These paths have a number of desirable properties that account for their widespread use – they are smooth, non-self-intersecting (and hence invertible), and they intersect both boundaries at right angles to the surfaces.

While intellectually appealing and elegant, the Laplace approach has a number of drawbacks. The solution of the Laplace equation is carried out on a discrete mesh, limiting the resolution of the results. More importantly, the resulting correspondence is non-uniform if the surfaces are not parallel (as is frequently the case for the white and pial surfaces). In addition, while the traversals are perpendicular to the boundary surfaces (and the interior isopotential lines), they can be highly curved and hence may not be perpendicular to actual cortical layers.

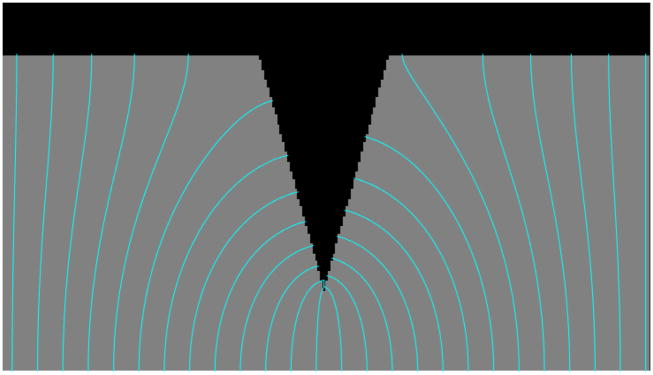
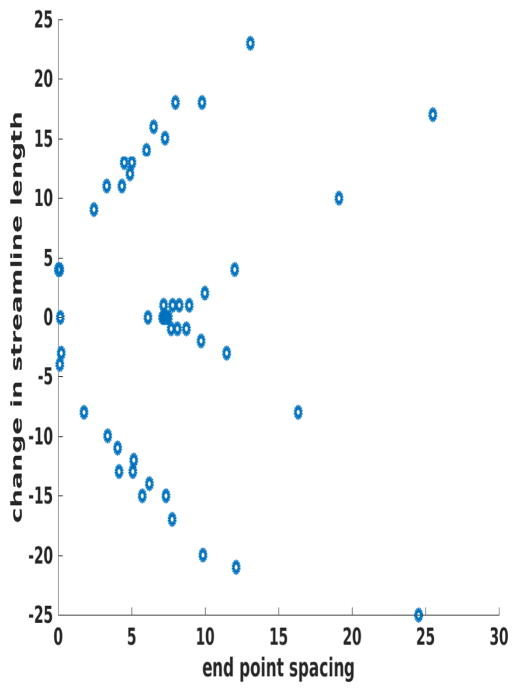
An example of this issue is given in Figure 7, which shows a synthetic CSF (dark, top), GM (gray, central), and WM (bright, bottom) image, with the Laplace equation solved between the two boundaries, then streamlines followed with Euler integration (shown in cyan). Examining this image, one can see how tightly bunched the streamlines are near the bottom of the downward facing “spike”, a situation that is common in deep cortical sulci. Further, we note the change in shape of the streamlines as they transition from terminating on the base of the spike to doing so on the upper horizontal boundary. Figure 8 quantifies this effect by plotting the change in the length of adjacent streamlines on the vertical axis and the spacing between neighboring terminations on the horizontal axis. As can be seen, the streamlines are least densely spaced in precisely those regions in which their length is changing most dramatically – exactly the opposite of what is needed. These variations in streamline length and in what “gray matter” they sample can result in large apparent spatial changes in gray matter properties that are solely due to the geometry of the pial surface.

Figure 7.

Synthetic image with Laplace solutions between ‘white matter’ (at bottom) and CSF (top).

Figure 8.

Change in the length of the streamlines on the vertical axis plotted against the spacing between the termination points on the horizontal. As can be seen, where the streamlines change length the most is where the sampling density is the smallest. The synthetic surfaces are spaced 128 pixels apart, so a change of 25 pixels is approximately 20%.

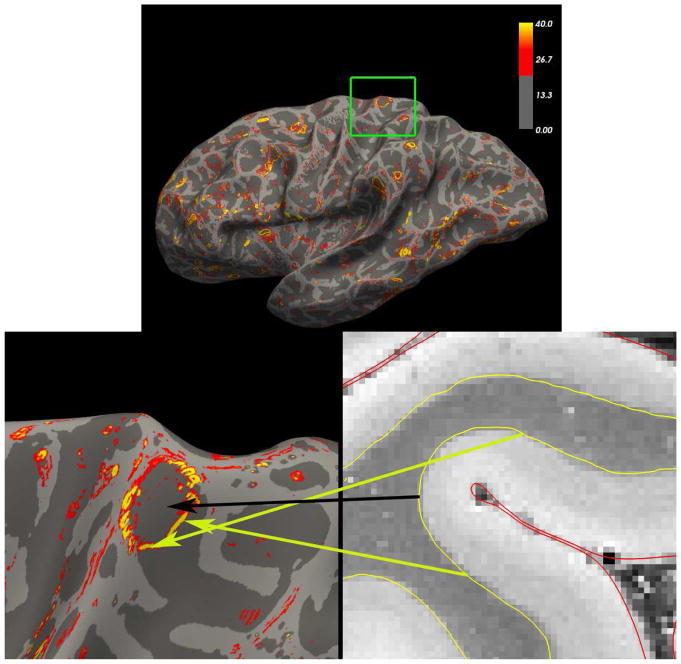
While this example may seem contrived, in fact we created it to better understand the ubiquitous artefactual borders seen in actual data in situations in regions in which the pial surface has much sharper curvature than the white surface. This is shown in real data in Figure 9, in which we applied this technique to 150μm isotropic ex vivo MRI. The same circular patterns surrounding fundi can be observed throughout the cortex, overwhelming any potentially useful information about the underlying cytoarchitecture contained in this data. Finally, we note that using the streamlines as measures of thickness is also problematic as can be seen examining the first few streamlines at either edge of the image in which the streamline distance is growing larger due to the nonlocal effects of the spike, despite the fact that the actual distance between the two boundaries is constant.

Figure 9.

Example of Laplace streamline sampling artifacts in ex vivo MRI data. Top: the magnitude (Frobenius norm) of the spatial derivative of the Laplace streamline samples of a 200μm ex vivo FLASH scan of a human brain (α=20°, TR=40ms, TE=20ms). Small circular regions of high gradient magnitude can be seen in many parts of the cortex. Bottom left: zoom on region in the green box. Bottom right: axial zoom of the surfaces over the intensity volume. The arrows show the correspondence between locations in the volume and those on the surface. The yellow arrows correspond to regions of high gradients and the black to low gradients. These gradients represent a change in the streamline solution from those that cluster at the deepest point of the pial surface (shown in red) to those terminating on the banks of the sulcus instead of the fundus, by analogy with the synthetic geometry shown in Figure 7

To resolve these issues and remove the geometric artifacts induced by the Laplace streamlines, we developed a procedure to explicitly construct a vector field connecting the two surfaces with the desired properties – a spatially coherent set of vectors that do not diverge too far from the surface normal direction. To achieve this, we take a variational approach and build an energy functional with two terms – one that one that maximizes the degree of parallelism of adjacent vectors, and a second that keeps each vector close to parallel to the surface normal.

The approach we take can be seen as treating the task of constructing a vector field as a registration problem, similar in spirit to the diffeomorphic surface evolution work of (Das, Avants et al. 2009), although our technique can work with an pair of existing surfaces. That is, we seek a vector field that establishes correspondence between the white and pial surfaces. Typically, this type of registration has two types of terms in the energy functionals that drive them – a “data” term that is derived from the geometric or intensity properties of the surfaces or volumes to be registered, and a “smoothness term” that encourages smooth, invertible transformations. In contrast, in our domain we have no “data” term, just a set of smoothness terms – one to keep the vectors reasonably close to the surface normal (that is, so that like the Laplace streamlines, they intersect the two boundary surfaces at approximately right angles) and another to ensure that they are parallel.

One technical detail that we must resolve is how to conduct the numerical minimization on a triangular mesh. That is, if we fix the base of each vector to be a (stationary) point on the gray/white surface, the minimization amounts to moving the vertices within the pial surface such that the energy is reduced, while maintaining an invertible mapping. We can phrase the minimization as a sequence of movements of each vertex within the tangent bundle (T_pS) of the pial surface, so that each differential update is computed as a vector that is a linear combination of the two principal directions at each point. However, these movements are not in general guaranteed to stay within the surface when they cross over the border of a triangular face. While one might imagine that this issue can be easily addressed by projecting the point back onto the surface at each step, this is not the case, as the projection operator for an arbitrarily folded manifold such as the pial surface is not well-defined (this can be seen in the case where the movement causes a vertex to leave one side of a sulcus and approach the opposing bank – the projection would then move the vertex back within the surface on the wrong bank of the sulcus).

Fortunately, part of our surface reconstruction procedure instantiates a spherical coordinate system for the cortex(Fischl, Sereno et al. 1999, Fischl, Sereno et al. 1999, Fischl, Liu et al. 2001). This allows us to phrase the minimization as a mapping from S² to itself in much the same way we carry out spherical registration across subjects. In this formulation, every point on each surface is mapped to exactly one point on the unit sphere, and we can therefore cast the movement of vertices on the surface as a movement on the unit sphere, then use the correspondence (and the chain rule) to compute what movement on the pial surface is equivalent to the movement on the sphere. Since the mapping is differentiable and invertible, we know that the principal directions, which are orthogonal on the sphere, will form a basis under the spherical mapping (that is, they will not be collinear). While we could cast the minimization in terms of longitude and co-latitude as was elegantly done in the development of Spherical Demons (Yeo, Sabuncu et al. 2010), we wish to avoid the difficulties of the nonuniform coordinates and multiple charts that must be used on the sphere. Instead, we take a simpler approach, and compute all vertex movement within the tangent bundle of the sphere, then project each vertex back onto the sphere after every update, taking advantage of the well-defined nature of projection onto the sphere (in contrast to an arbitrary folded manifold).

More specifically, the energy functional we minimize is given by:

$$E=(1-\lambda )J_N(\mathbf{x})+\lambda J_p(\mathbf{x})=(1-\lambda )\sum _{v=1}^V\left(1-\left|\langle t_v,o_v^w\rangle \right|\right)+\left(1-\left|\langle t_v,o_v^p\rangle \right|\right)+\lambda \sum _{v=1}^V\sum _{n=1}^{N_v}\left(1-\left|\langle t_v,t_n\rangle \right|\right)$$

where x is a location on the pial surface, J_p(x) is the term that encourages a parallel vector field, J_N(x) keeps the vectors close to the surface normal of the white and pial surfaces, t_v is the vector connecting the white and pial surfaces at the v^th vertex, normalized to have unit length, N_v is the number of neighbors of that vertex, $o_v^w$ and $o_v^p$ are the outwards-pointing surface normals of the white and pial surfaces respectively, and <> denotes the inner product operator. Note that the t and o vectors are all functions of x, but we have dropped this functional dependence for notational simplicity. In addition, we note that adding an additional term to encourage uniform vertex spacing is straightforward.

In order to minimize E, we represent x as a function of spherical coordinates r, and sample J_p and J_n at +−ε (where we set ε to be 1/10 of the average inter-vertex spacing on the surface) in the positive and negative principal directions in T_pS of the sphere:

$$\frac{dJ}{dr}=\frac{dJ}{dx}\frac{dx}{dr}=\frac{\lambda }{2\epsilon }(J(x(r+\epsilon e_v^1))-J(x(r-\epsilon e_v^1))e_v^1+J(x(r+\epsilon e_v^2))-J(x(r-\epsilon e_v^2))e_v^2$$

where x(r) is computed using barycentric interpolation of the face that the projection of r onto the unit sphere lies within (which is itself found using a spatial lookup table, so it not computationally costly), and $e_v^1$ and $e_v^2$ are the two principal directions on the unit sphere S at vertex v. This procedure is used for computing the values and derivatives of both J_p and J_n (with different functions returning the energy at the location r of course). A geometric intuition for the effects of modifying λ can be obtained by examining Figure 10, which shows the same toy example as above for various values of λ.

Figure 10.

Examples of minimizing equation (1) for various values of λ (from left to right: 0, 0.2, 0.4, 0.6, 1)

An example of minimizing equation (1) using gradient descent for a pair of cortical surfaces with λ=[0,0.2,0.4, 0.6, 0.8,1.0] is given in Figure 11. In this experiment, we minimize equation (1) using equation (2) to compute the gradients, continuing integration until the percent change in the error functional falls below a pre-specified tolerance of 10⁻³. To guarantee that the mapping is invertible, we add the penalty for triangles with area close to 0 proposed by Ashburner in (Ashburner 2000).

Figure 11.

Example of vector fields after energy minimization for various values of λ (left: λ=0, right: λ=1) in a region around the central sulcus (red = sulcal, green = gyral), shown on a white matter surface. Blue arrows indicate two locations of prominent differences.

In order to assess the value of the vector field we obtain using this approach we use the simulated laminar volume presented in the previous section. By construction, this synthetic volume should have no boundaries in it since each layer occupies the exact same fraction of the entire cortical ribbon everywhere in space. To quantify the true negative and false positive rates of the Laplace and variational formalizations, we computed the minimum energy vector field with λ=.9, a value chosen to produce a relatively smooth vector field, although other values (not shown) achieve comparable results. To compute boundaries, we use the same approach as previously utilized to compute spatial gradients of the Laplace-sampled intensity profiles: we fit a first order Taylor series to approximate the intensity profiles in a spatial neighborhood of each vertex, then minimize the RMS error of the Taylor expansion to compute the spatial derivatives. Finally, we take the Frobenius norm of this matrix of partial derivatives and use it to look for spurious boundaries. The results of this experiment are shown Figure 11. Example of vector fields after energy minimization for various values of λ (left: λ=0, right: λ=1) in a region around the central sulcus (red = sulcal, green = gyral), shown on a white matter surface. (we do not include p-values as the results are wildly significant with the Laplace gradient magnitude being mean +− standard deviation of 2.6+−2.55, and the variational one being 0.9+−1. Given the 140,000 vertices over the surfaces, these standard errors of the mean become so small that the p-value is meaninglessly tiny, assuming we could estimate the spatial covariance structure). This picture reveals the same critical flaw in the Laplace streamlines as seen previously – in regions where the pial surface is not parallel to the white surface the Laplace streamlines are distributed nonuniformly on the pial surface. This result in circular “swirls” of high gradients as the streamlines transition from being spaced evenly to all being drawn to a deep pinch in the pial surface, exactly as was seen in Figure 7. In contrast, the gradient magnitude derived from the vector field we derived from our energy minimization approach shown at the right does not have this freedom – parallel vectors that are uniformly spaced on the white surface cannot bunch too much on the pial surface, resulting in a more uniform distribution and more consistent spatial sampling of the intensity profiles.

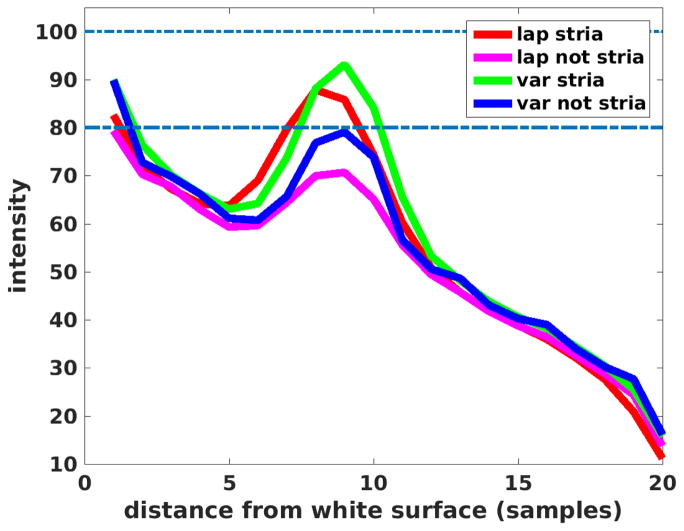
To assess true positives and false negatives we synthesize a “stria of Gennari”, the heavily myelinated layer 4 band in primary visual cortex, by increasing the intensity of a layer 4 in a small region to 100 (from 80), then recomputing the streamlines. The average intensity profiles for the Laplace approach and the variational one presented here are given in Figure 13. As can be seen, the variational streamlines more closely approach the true synthetic values inside the stria (green curve, true value=100) and outside (blue curve, true value=80), than does the Laplace approach in which the streamlines curve interior to the ribbon and hence intersect interior boundaries obliquely, increasing partial volume effects and reducing laminar contrast.

Figure 13.

Synthetic stria streamline results shown for variational (green=within stria, blue=outside of stria) and Laplace (red=within stria, magenta=outside of stria).

It is worth noting that this approach could be combined with a local-curvature-based laminar depth correction in order to approximate Bok-like ‘equivolume’ effects on laminar thickness (Waehnert, Dinse et al. 2014, Waehnert, Dinse et al. 2016) (see next).

C. Parcellations using structural MRI

As mentioned in the introduction, one greatest difficulties of using structural MRI estimates of myelination is the extreme sensitivity to small errors in the estimation of laminar position, which potentially overwhelm the small but significant tangential differences that indicate transitions between cortical areas. The methods just described for refining gray/white matter to pial surface streamlines is likely to improve the homogeneity of depth estimates across the folded cortex. But that assumes that cortical laminae can be picked out by depth fraction. It has long been known that the apparent position of cortical laminae within the cortical column is modulated by the curvature of the cortex (Bok 1929).

In a study of the relation between lamina-specific quantitative T1 and retinotopy (Sereno, Lutti et al. 2012), it was found that quantitative T1 and curvature were moderately correlated across the entire cortex (R² = 0.14). This correlation was simply regressed out to clean up the laminar-specific T1 maps. A deeper explanation of why this relationship exists in the first-place builds on the original ideas of Bok (Waehnert, Dinse et al. 2014, Tardif et al. 2015, Tardif, Schafer et al. 2015). Assume that as the cortex bends, each local tangential volume element of each cortical layer attempts to retain its original, unbent volume. In a sulcus, if one assumes that deeper layers are being stretched, then deeper layers will have to thin out to retain their original local volume, which is very clearly observed in histological sections cut perpendicular to a sulcus. One motivation for the deep-layer stretching force is that a number of general features of the adult cortical folding pattern can be reproduced in a mechanical model where a thin ‘cortical’ gel layer expands in volume like the thickening but also laterally-expanding cortex over an underlying armature of white matter that expands much less (Tallinen, Chung et al. 2014). The Bok-inspired ‘equivolume’ model of cortical folding does a better job of following the prominent layer 4B in V1 than does simple cortical thickness fraction. However, V1 is a unique area; it is unusually thin, unusually cell-dense, and its unusually prominent layer 4B is unique among cortical areas. Not surprisingly, V1 was one of the first cortical areas to be (macroscopically) distinguished by Meynert in the 19^th century. Because cortical laminae in most cortical areas are not nearly as distinct as V1 layer 4B, it is more difficult to explicitly test this hypothesis elsewhere.

By measuring lamina-specific quantitative T1 signals in living humans, it was possible to distinguish a number of heavily myelinated cortical regions as originally seen in the post-mortem myeloarchitectonic studies of Flechsig (1920) (Flechsig 1920, Sereno, Lutti et al. 2012). In the occipital and parietal visual cortex, these include V1 (of course), V6 (a visual-periphery-emphasizing motion area), MT/FST (which together formed the prominent maximum in lateral occipital cortex), V3A (a dorsolateral motion-sensitive area), V6A (a reach-related area anterior to V6), V8 (as originally defined by (Hadjikhani, Liu et al. 1998)), LIP+ (intraparietal areas involved in eye movements and attention), and VIP+ (a multisensory area, as defined in (Sereno and Huang 2006)). In auditory cortex, quantitative T1 defines the auditory core (areas A1 and R, (Dick, Tierney et al. 2012)), as well as a separate lateral maximum of myelination along the superior temporal gyrus. In frontal cortex, quantitative T1 outlines and distinguishes motor cortex from S1, the frontal eye fields, dorsolateral prefrontal cortex, and a multisensory area located near the boundary between the motor cortex representation of the face and hand (originally named PZ in (Huang and Sereno 2007), to respect the equivalent macaque monkey area originally discovered by (Graziano and Gandhi 2000), and later renamed area 55 in humans by (Glasser, Coalson et al. 2016)).

Though the number of areas distinguished by quantitative T1 might seem large, it represents a definite minority of the total number of cortical areas thought to exist. As initially recognized by early students of cortical myeloarchitectonics, there are substantial portions of inferior parietal cortex, precuneus cortex, insular cortex, inferotemporal and anterior temporal cortex, frontal cortex, anterior cingulate cortex, and frontal pole cortex that have very shallow gradients of change in myelination and in quantitative T1 that are near the practical threshold for detecting areal differences (<1%). Though it is possible to calculate gradients in these regions to try to find borders, gradients are extremely noisy unless the data is first very heavily spatially smoothed, which has the potential to tangentially displace borders. To reliably distinguish these regions with quantitative T1 alone is likely to require additional effort to measure and classify subtle differences in laminar (columnar) profiles, which will require higher fields and smaller voxels. As we see next, diffusion-weighted imaging may be able to more directly distinguish subtle interareal differences not accompanied by average differences in quantitative T1.

D. Parcellations using diffusion-weighted MRI in the gray matter

Diffusion-weighted MRI has been widely adopted to analyze white matter microstructure, but has been virtually ignored as a method for distinguishing regions in the gray matter because of the reduced anisotropy there. However as noted above, differences in the texture of the cortical fabric have long been used in myeloarchitectonic mapped by histologists to distinguish cortical areas. High angular resolution diffusion measurements conceivably contain information about area-specific fiber arrays (including both dendrites and local cortical axons). The first requirement is that slight deviations from isotropic diffusion – a constant radius diffusion surface – are present in the gray matter and are reproducible across scans. This is, in fact, the case (Nagy, Alexander et al. 2013). Since architectonic features of cortical areas have always been defined in a local coordinate system based on the two dimensions of the cortical surface and the third dimension of cortical depth, it was important to measure gray matter diffusion with respect to the cortical surface (see also (McNab, Polimeni et al. 2013)). By constructing features based on a spherical harmonic decomposition of the diffusion surface together with the local orientation of the cortical surface, it was possible to distinguish selected cortical areas from each other, but also to classify never-seen regions beyond training regions(Nagy, Alexander et al. 2013).

Subsequent studies using unsupervised group average cortical parcellations showed that some areas that could not be distinguished on the basis of T1/T2 measurements could be distinguished on the basis of a k-means clustering of the cortical-surface-based gray matter diffusion features (Calamante, Jeurissen et al. 2017, Ganepola, Nagy et al. 2017). More recent studies have examined how choice of feature sets, including data measured at different b-values, affects supervised performance in distinguishing each area in the Human Connectome Project parcellation from its neighbors (Calamante, Jeurissen et al. 2017).

Although these methods will likely benefit from ultra-high-field diffusion data capable of providing multiple measurements along cortical columns, these initial demonstrations suggest that gray matter diffusion may provide one or more additional effective dimensions orthogonal to quantitative T1 measurements, useful for distinguishing cortical areas.

E. Conclusion

Great strides have been made in the microstructural parcellation of the human brain. However, it is important not to underestimate how much work remains. We start by backing up and asking “what is a cortical area?”, then take stock of progress, and finish with a few suggestions for how to proceed.

What is a cortical area?

It’s worth remembering that a cortical area is a human label for local region of the neocortex after normal development. In the case of invasive experiments on animals, it has often been suggested that cortical areas are best defined on the basis of multiple converging criteria including at least: (1) receptotopic organization, (2) architectonic features, (3) connection patterns, (4) neurophysiological properties, and (5) effects of localized lesions. In the case of areas whose borders are not in dispute such as V1, these five measures can each be used separately to mark borders, and then these independently derived estimates can be compared. There are surprisingly few cortical areas whose borders are as well-agreed-upon as V1.

As with many scientific endeavors, the easier targets get investigated first. In the case of the visual system, this means V1, and then V2 and MT. Finding and characterizing these areas in living humans has turned out to be surprisingly difficult. Layer 4B of V1, the “stria” in striate cortex, makes V1 perhaps the most architectonically distinct cortical area. It was detected macroscopically by Meynert in post-mortem samples in 1867. However, reliably visualizing this feature across the extent of V1 with in vivo human structural imaging requires long, ultra-high field scans and uncommonly still subjects. With human V2, ultra-high field scanning was also required to finally functionally visualize the stripe compartments (Nasr, Polimeni et al. 2016), already known to exist 40 years ago from invasive work in non-human primates. Similarly, we can finally now reliably locate human area MT through a confluence of quantitative T1 mapping and retinotopic mapping (Sereno, Lutti et al. 2012), which recently showed that only the posterior one-third to one-half of the lateral occipital maximum of quantitative T1 (and by implication, myelination) actually corresponds to MT proper. Once again, the fact that MT was adjoined by several densely-myelinated, motion-related areas that are difficult to discriminate from MT was known long ago from work in non-human primates.

But even in the case of these three paragons of cortical areas, there are unsettling details as one digs deeper. In the case of V1, there are additional internal borders that will have to be ignored as in vivo resolution is improved. For example, at the cortical representation of the blind spot (which receives input only from ipsilateral dLGN layers) and the monocular crescent (which receives input only from contralateral dLGN layers), the pattern of ocular dominance columns is interrupted, which affects most of the criteria listed above. Or consider V2, where there seem to be at three subareas intercalated as side-by-side stripes into a single map. Or consider the case of the periphery of MT/V5, where there is an sharp drop in myelination within the boundaries of the retinotopic map ((Allman and Kaas 1971); Fig. 3, 4A in (Sereno, McDonald et al. 2015)).

Moving to the majority of visual areas beyond V1, V2, MT, and V6, where quantitative T1 is less diagnostic, most studies have turned primarily to retinotopy for parcellation. Although invasive studies in primates and other animals have suggested that there is a fair degree of variation even within species, most work in humans has implicitly assumed that individual brains all have the same number of cortical visual areas, that all visual cortical areas have the same neighbor relations, and that it makes sense to average across individuals (as we have ourselves). There is a fair amount of agreement about the layout of early visual areas. Nevertheless, outside of V1, V2, and MT, there are enough disagreements in detail that no generally agreed upon ‘ground truth’ exists for non-human primates, much less for humans. Moving to other modalities, mapping auditory areas is more difficult since there is currently only one main mapping coordinate, tonotopy, to distinguish areas on a 2D cortex. Mapping somatosensory areas is yet harder, since compared to the retina, the surface of the body is inconveniently shaped, and the subject is resting on it. Finally, with motor areas, it’s hard acquire good MRI data when the subject moves due to technological limitations such as motion-induced field changes. Attempts to map all 4 modalities at the same time in the same group of subjects (e.g., (Sood and Sereno 2016)) suggest that individual brains are similar, but not identical in areal number and neighbor relations; given that different primate species differ in these two measures, this should not be surprising. Comparative and development evidence suggests that cortical areas have arisen by duplication, subdivision, or fusion. These processes may still be at work in disturbed and perhaps even in normal development (the second author’s V3A appears to directly touch his V2 without an intervening V3).

Though we have implied otherwise above, fundamental questions about the definition of a ‘cortical area’ remain open, namely, whether boundaries between every pair of cortical areas are similarly sharp and smooth, and whether boundaries determined by different techniques should agree in the limit of ‘really good data’. It has long been known that some borders, such as the one between V1 and V2, are sharp and smooth, and well aligned across different techniques, but it is not known whether these features extend to all cortical areas. And even within early sensory areas, recent invasive experiments simultaneously measuring cerebral blood volume (CBV) and neural activity (Winder, Echagarruga et al. 2017) show that spontaneous CBV changes are closely associated with neural activity due to whisker stimulation and volitional whisker and body movements, but are only weakly coupled with neural activity during rest periods. This may complicate the task of combining non-invasive neuroimaging data from multiple techniques (e.g., receptotopic mapping versus resting state correlations) to generate omnibus parcellations, especially for locations where both types of data are not discriminative.

All of these findings suggest that it will be critical to establish probabilistic maps that are capable of handling not only substantial variation in cortical area size, but also variation in cortical area number and neighbor relations. Though implied by the word “probabilistic”, the variation in uncertainty of areal boundaries is often lost when viewing “ground truth” summary maps. Of course, researchers mainly interested in using rather than generating parcellations will gravitate toward a single, definitive, convenient-to-use “ground truth”. Keeping the “ground truth” communally editable is a difficult job.

In vivo and ex vivo

By analogy with the difficulty of combining and adjudicating between architectonics and topographical mapping, there is a similarly difficult passage between in vivo and ex vivo parcellation. Except in rare circumstances, in vivo and ex vivo data is not available from the same subject. Another MRI-imaging-specific difficulty is that in vivo and ex vivo structural contrast is markedly different for measures of T1, T2, T2*, and diffusion. Though ex vivo T2* contrast (inverted) is a reasonable substitute for in vivo T1 contrast, it is clear that fine points like the subvoxel position of the gray-white matter border – a critical stepping off point for laminar measures – might subtly differ between the two, and that no simple functional form appears to relate the tissue parameter changed induced by fixation. On the positive side, the greater resolution available with ex vivo data should be able to help with designing algorithms to help discern the more subtle contrast between laminae that can be measured in vivo with quantitative T1 scans.

A way forward for histology

Although we have been critical of methods applied to ex vivo histological sections, there are excellent reasons for continuing to cut and stain sections in the traditional way, and we do not mean to imply otherwise (and we note the world-class neuroanatomical expertise that was a significant component of these studies undoubtedly precluded serious errors). There are simply no alternatives; the volume of human tissue that can be currently cleared as an uncut block (e.g., CLARITY(Chung and Deisseroth 2013)) would cover only a small portion of one human cortical gyrus, and while promising alternatives such as optical coherence tomography (OCT) avoid the problem of cutting-induced distortions(Wang, Black et al. 2011, Magnain, Augustinack et al. 2014, Wang, Zhu et al. 2014, Magnain, Augustinack et al. 2015, Wang, Lenglet et al. 2015, Magnain 2016, Wang, Akkin et al. 2016), these techniques have also not yet been scaled up to image entire hemispheres or brains. Our critique is merely a motivation to try to find ways around the problems we have outlined, for example, by combining information from adjacent slices during the estimation of columnar paths. This is a substantially more difficult problem than computing streamlines in isotropically sampled MRI data of comparatively much lower resolution. While ex vivo MRI methods continue to advance in terms of resolution and contrast and provide an intrinsically 3D acquisition that does not suffer from the slice-based distortions that plague histology, the several orders of magnitude increase in resolution, and the panoply of molecularly-specific staining options that are only available via ex vivo histology, provide a strong impetus to try to resolve the problems we have presented (see for example, the detailed, whole-brain cellular-resolution atlas presented in (Ding, Royall et al. 2017)).

Comparing and combining parcellations

As the number of different cortical parcellation schemes increases, the difficulty of objectively comparing and combining them increases even faster. With low-subject-count invasive animal experiments, it is customary to illustrate single-subject data based on two or more of the area-defining criteria listed above (receptotopy, architectonics, etc.) in such a way that the reader can verify for themselves the extent to which the independently measured criteria do in fact support coincident borders. With neuroimaging data based on large group averages and multiple criteria, however, it can be more difficult to tell if parcellation borders derived independently from different criteria in fact agree. This is especially problematic when criteria have been combined to generate a single parcellation. First, cross-subject alignment methods differ. For example, surface-based alignment can be driven by sulcus depth, receptotopic map coordinates, connectivity measures, T1 values, or some combination; and 3D methods are somewhat incommensurate with surface-based methods. Second, one criterion may not detect any border within a region that is easily subdivided by a different criterion, making different borders differently supported; or researchers may insert ‘knowledge-based’ borders not directly supported by the data at hand. Third, different techniques have adjustable parameters to determine, for example, how many areas are generated, or what their general shape should be, or how smooth borders should be. It is often difficult to determine how much of a parcellation is determined by these priors and how much is more directly data-driven.

We are unfortunately in a situation similar to that of the first blossoming of cyto- and myeloarchitectonics. The profusion of schemes resulted in confusion, backlash, and the eventual almost universal adoption of the Brodmann map, despite its shortcomings. To avoid settling too quickly on a single cortical parcellation, it will be important to provide tools to allow researchers access to individual criteria components so that data can be recombined in different ways, or augmented with new criteria and compared across subject, modality and algorithm.

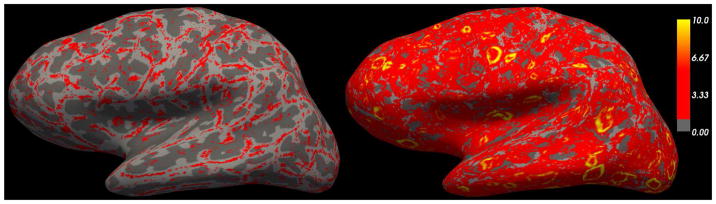
Figure 12.

Left: magnitude of the spatial gradient (Frobenius norm) using the vector field sampling. Right: magnitude of the spatial gradient using the Laplace streamlines for sampling the synthetic volume.