Spontaneous refolding of the large multidomain protein malate synthase G proceeds through misfolding traps

Abstract

Most protein folding studies until now focus on single domain or truncated proteins. Although great insights in the folding of such systems has been accumulated, very little is known regarding the proteins containing multiple domains. It has been shown that the high stability of domains, in conjunction with inter-domain interactions, manifests as a frustrated energy landscape, causing complexity in the global folding pathway. However, multidomain proteins despite containing independently foldable, loosely cooperative sections can fold into native states with amazing speed and accuracy. To understand the complexity in mechanism, studies were conducted previously on the multidomain protein malate synthase G (MSG), an enzyme of the glyoxylate pathway with four distinct and adjacent domains. It was shown that the protein refolds to a functionally active intermediate state at a fast rate, which slowly produces the native state. Although experiments decoded the nature of the intermediate, a full description of the folding pathway was not elucidated. In this study, we use a battery of biophysical techniques to examine the protein's folding pathway. By using multiprobe kinetics studies and comparison with the equilibrium behavior of protein against urea, we demonstrate that the unfolded polypeptide undergoes conformational compaction to a misfolded intermediate within milliseconds of refolding. The misfolded product appears to be stabilized under moderate denaturant concentrations. Further folding of the protein produces a stable intermediate, which undergoes partial unfolding-assisted large segmental rearrangements to achieve the native state. This study reveals an evolved folding pathway of the multidomain protein MSG, which involves surpassing the multiple misfolding traps during refolding.

Introduction

It is well known that a significant proportion of the complete proteome in nature belongs to the multidomain class of proteins, where the net content of such proteins is approximated to be higher than 75% in eukaryotic systems (1, 2). Despite their abundance and the functional implications of multiple domains, the folding studies until now have mainly focused on the simpler systems, e.g. single domain or truncated domains of multidomain proteins. The recent systematic advances in decoding the folding pathway of multidomain proteins have revealed a number of insights that point toward the inherent complexity of such systems and a need for further exploration. It is found that the highly favorable inter-domain interactions in proteins often result in a frustrated energy landscape (3, 4), forming nonproductive domain-swapped or amyloidogenic species that interfere with the actual folding pathway (5–8). The studies reveal that despite the autonomous folding nature of individual domains, the proteins with a highly shared domain interface may behave in a cooperative manner (9, 10). The competition between individual domain folding (intra-domain interactions) and their rearrangement (inter-domain interactions), which again is a question of structural topology and relative orientation, proves decisive in folding of the multidomain proteins (11–13). As it requires a fine orchestration of a conformational search for polypeptide and the folded domains, it becomes necessary to explore the mechanism further.

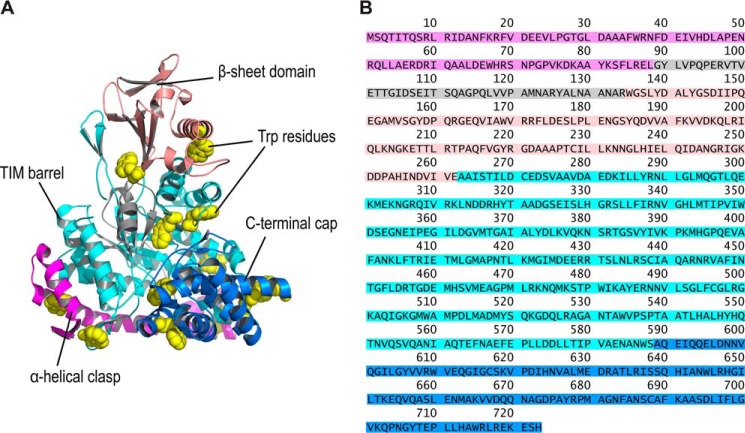
To understand the folding behavior for such macromolecules, studies have been carried out by probing the global conformation of a large multidomain protein malate synthase G (MSG).³ MSG is an enzyme of the glyoxylate bypass mechanism and has been extensively studied for its structural characteristics in the past decade (14–17). In this work, we focus on Escherichia coli MSG, an 82-kDa protein with four different domains whose active site is located between the predominant TIM barrel domain and the C-terminal helical plug structure (Fig. 1) (14, 18, 19). The folding studies in such large multidomain proteins are often limited due to their poor solubility, aggregation propensity, and irreversibility in unfolding, which present stiff experimental challenges in their study (20–23). However, such limitations for MSG have been overcome in previous studies under optimized reducing conditions to maintain all six Cys residues free and by using 10% glycerol in the buffer to enhance its solubility (24). The protein was shown to spontaneously refold from a chemically denatured state with population of burst phase species within ∼6 ms of refolding. The previous studies also revealed the formation of an on-pathway functional intermediate, which is prone to aggregation and converts to the native state via slow reaction. Interestingly, the protein, despite its high entropic cost to search for correct native contacts, did not populate any misfolded species, which remains counterintuitive due to the presence of long-range contacts in the native structure. Although the nature of transient intermediates populating during MSG refolding was studied, a mechanistic pathway of folding reaction remains to be established.

Figure 1.

Arrangement of Trp residues in MSG. A, cartoon representation of MSG (PDB code 1D8C) is shown to contain four domains: α-helical clasp (magenta); β-sheet domain (salmon); TIM barrel domain (cyan); and the C-terminal cap (blue) covering the active site. The residues in gray represent the inter-domain–connecting region in the sequence. The Trp residues are shown in yellow (with spherical heavy atoms) for distinction. B, amino acids sequence is colored in accordance with the domains shown in structure.

A conventional and informative method of studying multidomain proteins involves sectioning of the individual domains to study their folding behavior. The method is usually acceptable for systems with lesser inter-domain interfacial areas where truncation does not result in a complete destabilization of domains, e.g. γ-B crystalline (25), titin (26), and fnIII domains of fibronectin (27). The notion of studying the sectioned domains of MSG could not be considered due to a very significant interfacial surface area being shared among them. Although there are variants of the MSG in nature, where the N-terminal α-helical domain and the β-sheet domain are absent (fungus Laccaria bicolor), proving them to be less crucial for the activity of enzyme (14), the sequence of those variants of the protein aligns very poorly with the E. coli MSG and hence cannot be taken as the sole criteria to truncate the domain segments. Because of the reasons, we have mostly tried to avoid truncating the protein to maintain its structural integrity and mutual domain cooperation.

Here, by using multiple biophysical tools to monitor the conformational transition, along with computational kinetics modeling, we attempt to understand the folding behavior of the MSG. It was found that the unfolded protein undergoes an initial hydrophobic collapse to form transient misfolded species, which partially unfold to achieve the correct folding route. An equilibrium intermediate similar to the transient kinetic species is further proposed to stabilize at moderate urea concentrations (4–6 m) giving indications of residual tertiary structural elements in the polypeptide and lack of secondary structure content. We show that the increasing viscosity of the refolding medium impedes the late refolding step of MSG, and hence we propose it to be a domain reshuffling step to achieve a correct native state. Although MSG contains 31 Pro residues, the slow isomerization of prolyl–peptide bonds was not found to populate any transient intermediates during folding.

Results

Equilibrium unfolding studies of MSG

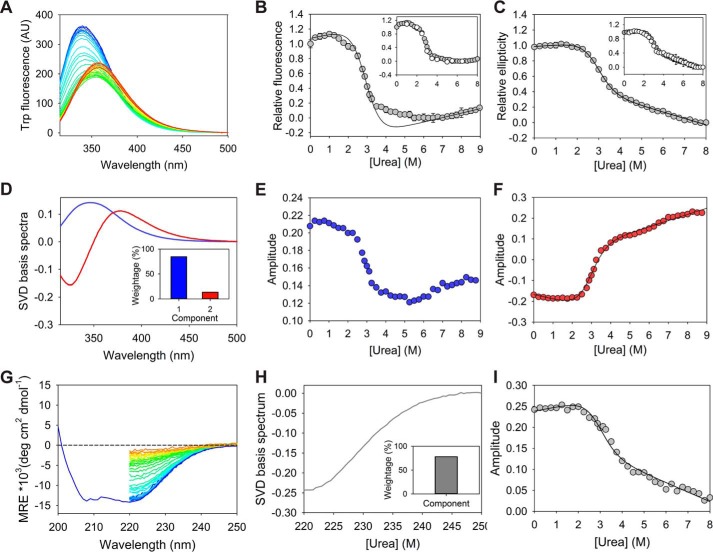
Because of the presence of four domains in MSG, there is a high possibility of observing stable intermediates in equilibrium studies. To characterize the stable conformational states present in the system and to determine the initial and final conditions for (un)folding kinetics studies, equilibrium unfolding studies were performed on MSG by using different probes. Twelve Trp residues scattered over the entire protein structure (Fig. 1A) allow us to probe the global tertiary structure by using intrinsic fluorescence. The fluorescence spectra of the protein equilibrated in increasing urea concentrations exhibit decreasing intensity, along with red-shift of the maximum peak (Fig. 2A). The equilibrium denaturation plot with Trp fluorescence at 340 nm shows a distinct reproducible and conformational transition in 1.5–2.5 m urea, which, however, could not be detected with ellipticity at 222 nm (Fig. 2, B and C). The observation indicates a partial tertiary structural loss without significant secondary structural change and hints toward the molten globule-type conformation of the intermediate species that populates in the urea concentration range (28, 29). Although the equilibrium plot with Trp fluorescence shows a transition at ∼6.5 m urea, it may be an artifact produced by the nonlinear rise of tryptophan's fluorescence under high urea concentration (Fig. S1A) (30). To distinguish the artifact from conformational transition, the behavior of the emission fluorescence spectrum shift was taken into account. It is expected that the exposure of the buried fluorophore residues to the polar aqueous environment should bring about an increase in the wavelength of maximum emission for the protein. As a red shift in wavelengths corresponding to maximum fluorescence, until 6.5 m of the denaturant was clearly observable, it validates a gradual conformational exposure and hence transition to the unfolded state near ∼6.5 m urea (Fig. S1B). Consequently, the unfolding baseline for MSG was assigned after 7 m urea concentration. The transition at ∼6.5 m urea in fluorescence data compared with equilibrium data with CD suggests the presence of a residual tertiary structure-containing entity (with no α-helical content) in 4–6 m of the denaturant, which melts completely at the higher urea concentrations.

Figure 2.

Urea-induced equilibrium denaturation of MSG. A, Trp fluorescence emission scans (excitation at 295 nm) recorded for 0–9 m denaturant are represented as color ramped from blue to red. B and C, solid line represents the global two-state fit of relative fluorescence intensity at 340 nm and relative ellipticity at 222 nm against urea concentration. The transition regions in 1.5–2.5 m urea and 3.25–6.5 m urea in relative fluorescence plots have been excluded from fitting due to the absence of corresponding baselines for the intermediate states. Insets display reversibility of MSG unfolding to various urea concentrations on the denaturation curve. Error bars represent standard deviation from three individual samples. D, significant basis spectra obtained by SVD analysis of the fluorescence scans in A. Only two distinguishable species corresponding to buried and exposed Trp residues (peak maximums near 345 and 377 nm, respectively) can be identified. E and F, amplitudes corresponding to major (weight = 84.6%) and minor (weight = 13.6%) basis spectra representing their population variation with urea concentration. G, molar residue ellipticity (MRE) scans of the protein equilibrated from 0 to 8 m of urea are represented as color ramped from blue to red. H, only significant SVD basis spectrum (weight = 77.9%) obtained from CD spectra. I, amplitudes corresponding to the basis spectrum from CD, showing respective population variation with denaturant concentration.

The singular value decomposition (SVD) analysis of the Trp fluorescence scans (Fig. 2A) could only identify two basis spectra of significant weighting factors (w) (Fig. 2D). The spectra with corresponding peak maxima at 345 and 377 nm can be associated with buried and exposed Trp residues of native and unfolded ensembles, respectively. The amplitude plot of the first component (w = 84.6%), with respect to urea, exhibits similar behavior as the equilibrium unfolding plot of the fluorescence intensity at 340 nm, indicating its correlation with the native structure (Fig. 2, B and E). However, the amplitudes of the second component (w = 13.6%) were found to display a single transition as shown by relative ellipticity (Fig. 2F). A similar SVD analysis of CD spectra at different urea concentrations (Fig. 2G) only identifies a single significant basis spectrum (Fig. 2H), whose amplitudes indicate a single transition as seen for the ellipticity at 222 nm (Fig. 2I).

As the fluorescence at 340 nm and the first SVD component from Trp fluorescence show multiple transitions with respect to the denaturant concentration, but no distinct baseline for stable intermediate states, it becomes impossible to fit the data in higher order equations (Fig. 2, B and E). However, the amplitudes of the second SVD component from fluorescence, relative ellipticity, and the SVD component from CD spectra, all exhibit a simple two-state–type transition with common transition region (Fig. 2, C, F, and I). With only two resolved SVD components from fluorescence, where the first one exhibits signatures of stable intermediate states, it becomes apparent that the spectra corresponding to the native state and the intermediate species are not highly distinguishable and hence could not be resolved. In the absence of the intermediate baselines and with poor knowledge of stability parameters of individual domains, the fitting of fluorescence signals was conducted only in native and unfolding baselines, along with the transition region (with exclusion of the transition regions in 1.5–2.5 m urea and 3.25–6.5 m urea) that resulted in a good correlation with the rest of the single transition equilibrium plots (relative ellipticity, second SVD component of the fluorescence, and SVD component from CD spectrum) (Fig. 2B). The global fitting was found to be agreeable and resulted in overall thermodynamic stability parameters as shown in Table 1. It should be noted that the two-state equation is applicable to cooperative transition in proteins and should not be applicable to MSG. The thermodynamic calculation in the current case is a mere approximation that provides the free energy of the native ensemble (probed by secondary structure content) as compared with the unfolded region, i.e. >3.5 m urea, and it does not alter the overall nature of folding pathway as proposed.

Table 1.

Equilibrium parameters of MSG from a two-state global fit of relative fluorescence and ellipticity data

The errors represent standard error of fitting.

ΔG(NU)	m(NU)	c(NU)
kcal/mol	kcal/mol m	m
4.23 ± 0.16	1.45 ± 0.05	2.91 ± 0.02

Misfolding events on the refolding pathway

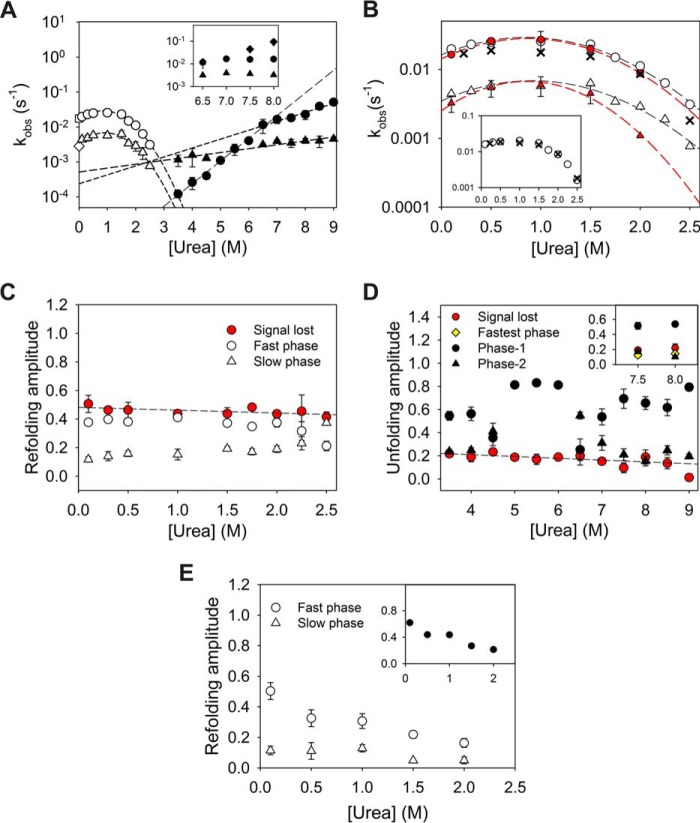
To explore the folding pathway of a protein, the refolding kinetics is often monitored using different conformational probes in varying refolding conditions. The behavior of refolding rates and initial signals (corresponding to zero time of refolding) with respect to denaturant concentration in refolding buffer provide insights into the nature of kinetic intermediates. In ensemble kinetics of MSG refolding, the global conformational change of the protein was probed using intrinsic Trp fluorescence (Fig. S2A). The kinetics of refolding, obtained via single-jump manual mixing as well as the stopped-flow technique, were biexponential and gave two apparent rates of refolding. Semi-logarithmic plot of these rates against urea concentration (chevron plot) exhibits a rollover, where assistance by urea in refolding for both phases can be seen under strongly native conditions (Fig. 3, A and B). It was seen that the refolding rates of MSG for both phases rise by ∼30% when refolding urea concentration is increased from 0.1 to 1 m urea. The observation implies an accumulation of misfolded intermediates in both the phases, which need to partially unfold to proceed toward the folding route. As the rates of refolding for both phases and corresponding relative amplitudes were found to be independent of protein concentration, the possibility of aggregation due to intermolecular interactions is ruled out (Fig. S2, C and D) (31). It is further noticed that the refolding amplitudes are not in proportion with the corresponding rates, which implies that the refolding phases may not be parallel reactions emanating from a common unfolded ensemble. The observation of two refolding phases can be explained in terms of the sequential nature of two reactions or as a result of unfolded state heterogeneity arising from cis/trans isomerization of the prolyl–peptide bonds in the protein with 31 Pro residues.

Figure 3.

Single-jump ensemble kinetics. A, ensemble refolding (white) and unfolding (black) rates of MSG shown as k_obs. Both phases of refolding, i.e. fast (circles) and slow (triangles), exhibit a rollover where denaturant-assisted refolding is observed under strongly native conditions, a classic sign of misfolded intermediate formation. The refolding rates at 0 m urea (white square and diamond) were obtained by pH jump (pH 11 to pH 7.9) refolding of MSG in the native buffer. Two unfolding arms of the chevron (black circles and triangles) intersect near 5.5 m urea. The inset represents origin of new fastest phase rates (diamonds) of unfolding at >7.5 m urea. B, comparison of refolding rates from Trp fluorescence (white), ANS fluorescence (red), and ellipticity (black cross) is shown. Inset represents a good correlation of averaged refolding rates from Trp fluorescence probe with the CD probe. C and D, fractional amplitudes of refolding and unfolding phases, respectively. The signal lost within the dead time of mixing (red) in both the cases is found to be independent of urea concentration. E, fractional amplitudes of two refolding phases as probed by ANS fluorescence. Error bars wherever shown represent standard deviation from three individual experiments.

1-Anilinonaphthalene-8-sulfonate (ANS) is a hydrophobic dye that gives a high fluorescence on binding to the hydrophobic patches of partially denatured entities that usually form at the beginning of refolding reactions. The bound dye molecules get kicked off of the polypeptide chain during refolding and hence are used as an extrinsic fluorescence probe for monitoring conformational change. ANS has been previously used to report on folding intermediates and to characterize the burst phase species for a number of cases (32–35). Refolding kinetics of MSG when probed by ANS showed a very high fluorescence at the beginning, which implies initial formation of species with an exposed hydrophobic surface that allows binding of ANS dye. The decrease in fluorescence was found to be biphasic with both the rates in satisfactory correlation with the rates obtained by Trp fluorescence probe (Fig. 3B; Fig. S3). The assistance in refolding by urea under strongly native conditions was seen for both the phases as expected. Although the amplitudes corresponding to the fast refolding phase were found to decrease with increasing urea concentrations in the refolding buffer, the slow-phase amplitudes were virtually unaffected (Fig. 3E). The observation can be explained by urea-induced destabilization of the misfolded intermediate species from which the fast refolding reaction takes place, and proceeds sequentially to the second slow refolding step.

The refolding kinetics probed by ellipticity at 222 nm could be fitted in single exponential kinetics reliably (Fig. S4). The averages of the two refolding rates obtained from fluorescence (weighted average based on fractional amplitudes of two phases) were found to be in agreement with the ones with ellipticity probe (Fig. 3B, inset).

Early misfolded species (I_M) and its correlation with equilibrium intermediates in 4–6 m urea

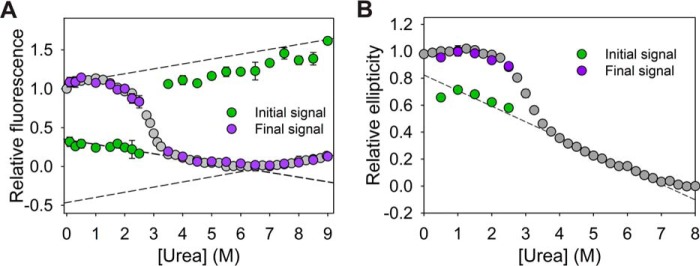
The initial Trp fluorescence signals obtained from extrapolated refolding traces to zero time of mixing were plotted on the equilibrium unfolding curve, which showed collinear behavior with the baseline for equilibrium intermediate populated in 4–6 m urea range rather than to the unfolded baseline at >6.5 m urea (Fig. 4A; Fig. S2A). The observation is independent of unfolding urea concentration (Fig. S2B) and has been also observed in earlier studies (24). The previous refolding studies of MSG from the guanidine hydrochloride (GdnHCl)-mediated unfolded state indicated a similar correlation of initial refolding signals with the intermediate baseline (1–2 m GdnHCl) and not with the fluorescence signals of the unfolded state. The consistency in the observation allows us to assume similarity in the nature of equilibrium intermediates in 4–6 m urea and 1–2 m GdnHCl concentration. Furthermore, it appears that the unfolded polypeptide undergoes an almost complete conversion to the intermediate state (I_M) within milliseconds. Although the kinetically populated misfolded intermediate should be a collapsed structure under native refolding conditions, a similar species being populated stably at higher urea (4–6 m) may imply a correlation between two entities.

Figure 4.

Initial and final signal analysis of single-jump kinetics studies. A and B, initial (green) and final (purple) signals of refolding (for Trp fluorescence and CD probe, respectively) and unfolding (Trp fluorescence probe) obtained by extrapolation of kinetics traces to the zero time of mixing are overlaid with corresponding equilibrium unfolding curves. Error bars represent standard deviation from three individual experiments.

The equilibrium studies using an ellipticity probe imply the absence of secondary structure in the 4–6 m urea region (unfolding baseline with CD probe, Fig. 2C). It was seen that an overlay of initial signals from refolding traces by ellipticity (222 nm) on a corresponding equilibrium curve displays agreement with the unfolded baseline (Fig. 4B). As the unfolding baselines of the equilibrium curves with fluorescence and ellipticity fit globally (Fig. 2, B and C), I_M is thought to be a species lacking α-helical structure but still having residual stability that only loses completely at >6.5 m of the denaturant.

Conformational transition in MSG probed by quencher accessibility of Trp residues

The native conformation of MSG contains buried Trp residues (Fig. 1A), which get exposed upon unfolding of the protein as confirmed by the urea-induced red shift in Trp fluorescence spectra (Fig. S1B). As a probe to monitor the refolding, the rate of sequestration of Trp residues was examined by using fluorescence quencher in the refolding solution. The single-jump refolding kinetics of MSG (at 1 m urea) with the Trp fluorescence probe were performed in varying concentrations of acrylamide, a neutral Trp fluorescence quencher. Assuming that the quencher molecules do not interfere with the folding pathway of the protein, the extent of buriedness of the fluorophores in the macromolecule during refolding can be probed (36). As the high concentration of acrylamide (i.e. >0.15 m) resulted in the appearance of a faster phase (Fig. S5A), the refolding kinetics at low quencher concentration, i.e. 0.05 m, was considered for qualitative analysis. The variation in the ratio of Trp fluorescence without and with the quencher (F₀/F) was plotted against time, which indicated the population of a compact species near 120 s at a fast rate that subsequently undergoes a slow partial conformational opening to the native state (Fig. 5A). The nature of the sequential reaction was further confirmed by double-jump interrupted refolding experiments.

Figure 5.

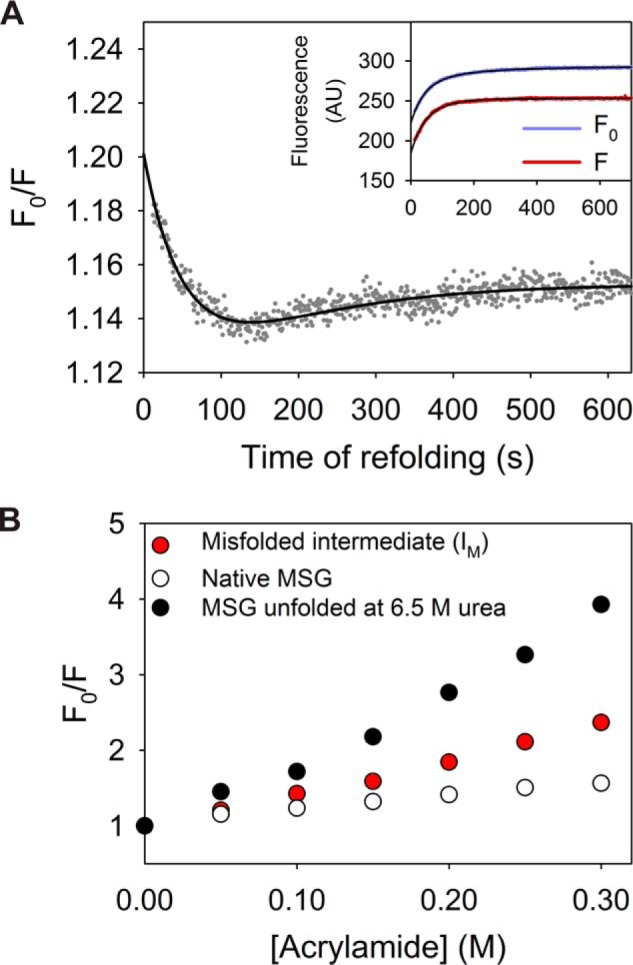
Refolding kinetics of MSG probed by the accessibility of its Trp residues to acrylamide. A, single-jump refolding kinetics (to 1 m urea) were probed by the ratio of Trp fluorescence intensities without and with 0.05 m acrylamide (F₀/F). The drop of F₀/F to 1.19 (from 1.45 for the unfolded state) within dead time of mixing indicates a collapse of the unfolded polypeptide. The inset represents refolding traces probed by Trp fluorescence in absence (purple) and presence (red) of quencher for reference. B, Stern-Volmer plot representation for comparison of structural compactness of I_M (red), as compared with native (white) and unfolded (black) protein at 6.5 m urea.

The refolding traces in different quencher concentrations, when extrapolated to zero time of mixing, should report on the extent of exposure of the I_M (Fig. 5B; Fig. S5B). A Stern-Volmer plot comparison of the initially formed misfolded species (I_M), with the unfolded protein, indicates much lesser acrylamide accessibility of the Trp residues and hence points toward the collapsed nature of the polypeptide (Table 2).

Table 2.

Stern-Volmer (K_SV) constants for fluorescence quenching in MSG by acrylamide

The values are calculated by nonlinear least-square fitting of the data (Fig. 5B) in the Stern-Volmer equation (F₀/F = 1 + K_SV × [quencher]). The errors shown represent standard error of fitting.

Conformational state	KSV
	m−1
Native	2.01 ± 0.07
Misfolded state (IM) in 1 m urea	4.39 ± 0.09
Unfolded (6.5 m urea)	9.10 ± 0.29

To assess the link between the kinetic misfolded species (I_M) and the equilibrium intermediate (4–6 m urea), the Stern-Volmer constants were also determined for equilibrium species in 3.5–5.5 m urea range (Table S1), but they were not found to be significantly different from the unfolded ensemble (6.5 m urea). It appears that the I_M intermediate, which transiently accumulates at the beginning of the fast refolding phase, is highly compact but still contains exposed hydrophobic sites for ANS binding. The equilibration of the protein at higher denaturant concentrations (4–6 m urea) renders it highly open, but probably with few intact structural elements as I_M.

Complex nature of the unfolding pathway of MSG

To explore the possibility of common intermediate states being accumulated during refolding and unfolding transition, the unfolding kinetics were studied for MSG. In addition, the analysis of protein refolding using an interrupted refolding method requires prior knowledge of unfolding behavior, which, in turn, was achieved by single-jump unfolding kinetics using Trp fluorescence probe. The protein was found to exhibit multiphasic kinetics, depending on the unfolding urea concentrations (Fig. S6; Fig. 3A). A loss of ∼10–15% signal is observed for unfolding traces under all urea concentrations and is probably due to the fast formation of unfolding intermediates hidden under refolding conditions (Figs. 3D and 4A). (37) The fastest unfolding phase that arises at >7.5 m urea conditions (Fig. 3A, inset) contributes to only <10% of the total signal change (Fig. 3D, inset) and can be modeled as an on-pathway unfolding intermediate. Moreover, an increase of unfolding amplitude of the phase-1 (fast unfolding phase at 7 m urea) at the cost of phase-2 (slower phase at 7 m urea) with increasing urea implies a common population giving rise to slow and fast unfolding phases (Fig. 3D). It can be noted that the apparent rate of unfolding for phase-1 is significantly sensitive to the urea concentration as compared with phase-2, indicating the highly exposed surface area of the unfolding transition state in the former case.

No role of cis/trans prolyl-peptide isomerization in MSG refolding

As the MSG contains 31 Pro residues, the cis/trans isomerization of prolyl–peptide bonds may result in heterogeneity in the unfolded ensemble, thereby exhibiting a slow refolding phase corresponding to correction in non-native prolyl–peptide bonds. To investigate whether the isomerization plays any role during refolding, interrupted unfolding experiments were conducted manually. The native protein was allowed to unfold in 8 m urea, for various delay time points followed by a fast refolding jump using dilution at 1 m urea. The amplitudes of refolding for two phases were plotted against delay time points to obtain kinetics of unfolding. Both the obtained amplitudes were found to be increasing with biexponential kinetics, with their weighted-averaged-rates (based on amplitudes) adding up to the rates of unfolding obtained from single-jump unfolding studies (Fig. 6). For the prolyl–peptide isomerization to be the rate-limiting step during refolding, a clear decrease in population corresponding to the correct isomeric state should have been observed. The behavior can be understood if the refolding pathway of the protein involves higher barriers of conformational transition, as compared with the ones corresponding to the isomerization step.

Figure 6.

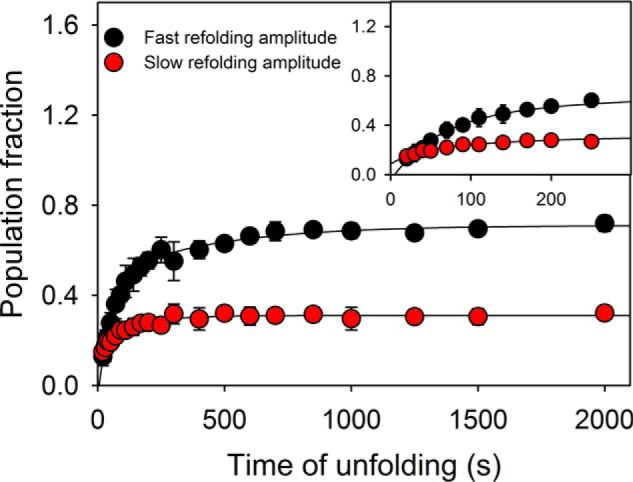
Interrupted unfolding experiments. The native protein unfolded at 8 m urea for different time periods was allowed to refold rapidly by dilution to 1 m urea. The biphasic refolding traces provide two amplitudes, which are plotted against time of unfolding. The plot excludes the possibility of prolyl-peptide isomerization mediated conformation heterogeneity in the unfolded population. The error bars represent standard deviation from three separate experiments.

Sequential nature of the refolding pathway of MSG using double-jump refolding

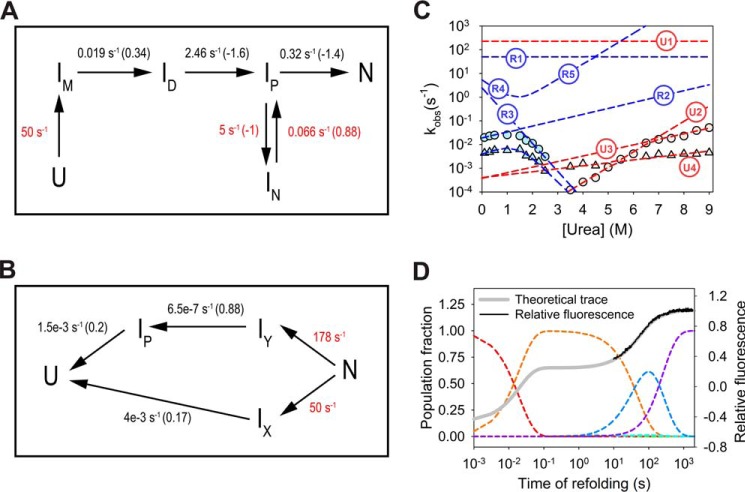
The rates of accumulation of stable intermediates or the native state can be obtained from interrupted refolding studies, provided the unfolding trace corresponding to the populated species can be captured. Although refolding kinetics experiments in the presence of quencher provide clues for sequential nature of two refolding phases, the interrupted refolding studies were further conducted for additional verification. The unfolded protein at 6.5 m urea was allowed to refold by manual dilution to 0.1 m (∼20 s dead time) for various time delays followed by interruption of refolding using a strong unfolding jump of 7 m urea. The biexponential unfolding traces (∼10 s dead time) provide two amplitudes whose plot with refolding time points result in kinetics plot of native protein or intermediate formation (Fig. 7A). Although the double-jump experiment provides data points with low signal to noise ratio, where each point represents the average of three independent experiments, the individual refolding kinetics plot using fast unfolding phase (phase-1) consistently shows a fast exponential increase until ∼200 s followed by a slow exponential decrease until the final signal of ∼50% (similar to the amplitude for native protein unfolding) is achieved (Table S2). The refolding curve from slow unfolding amplitudes (phase-2) exhibits a single exponential slow increase in population with the same rate as for the slow decrease in phase-1. The rates obtained for both the kinetics obtained (by phase-1 and -2), are in agreement with single-jump refolding studies. Thus, the observation can be modeled by assuming the fast phase to be conversion of misfolded intermediate to another intermediate, I_N (Fig. 10A), which in turn requires partial unfolding (to I_D) to proceed toward the native state, N. Interrupted refolding studies with a refolding urea concentration of 2 m also exhibit similar outcomes (Fig. 7B).

Figure 7.

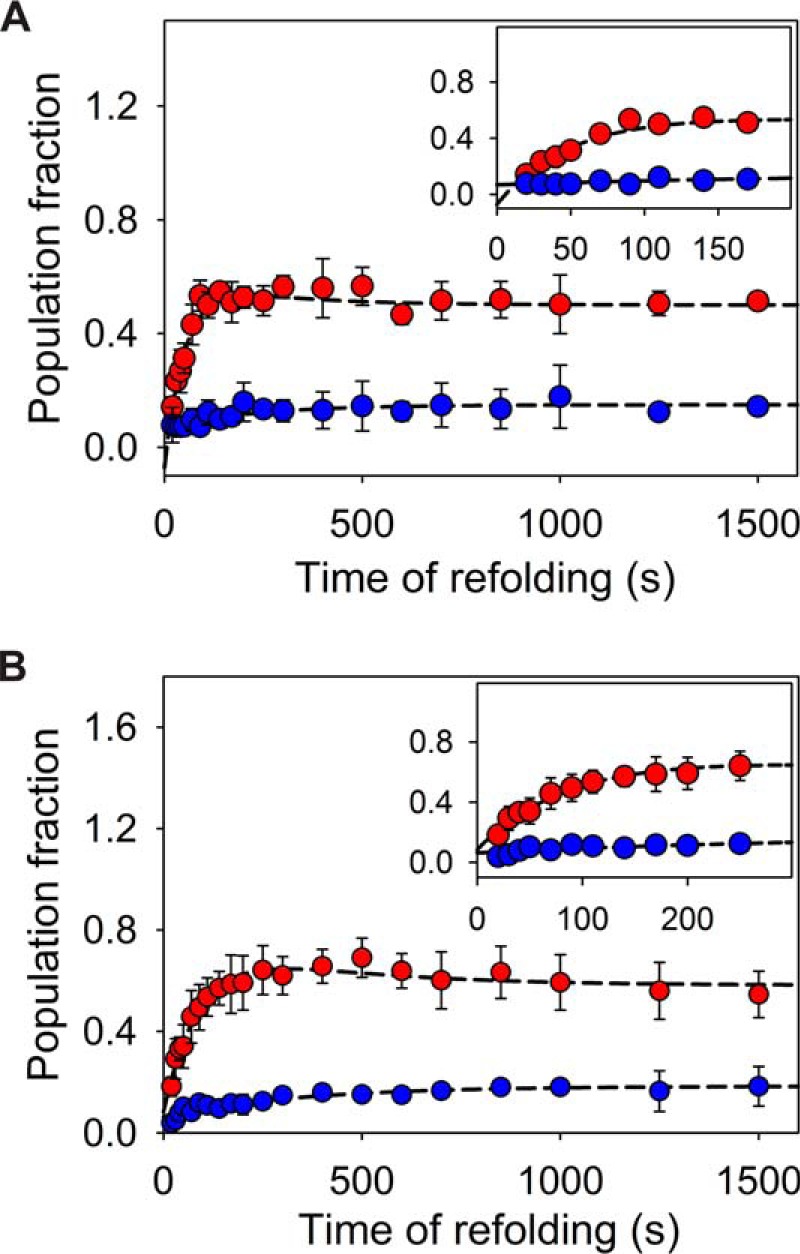
Interrupted refolding studies. A, MSG was allowed to refold at 0.1 m urea for different time points, followed by unfolding at 7 m urea. The plots of two unfolding amplitudes against time of refolding represent kinetics of stable species present in the system. The amplitudes probed by phase-1 (fast phase at 7 m urea) of unfolding (red) (Fig. 3D) show a rapid build-up of the intermediate species (fast refolding phase), which undergoes a slow decay (slow refolding phase) (Table S2). The amplitudes of slow unfolding phase (blue) exhibit slow single exponential increase. B, interrupted refolding study for refolding of MSG at 2 m urea. The error bars represent the standard deviation of three independent experiments. Although the slow decrease in the accumulated population near ∼150–200 s is found to be consistent (and easily perceptible for refolding at 2 m urea), the large error bars are obtained as a consequence of the range of amplitudes from independent set of experiments.

Figure 10.

Kinetic models for refolding and unfolding. A, refolding kinetics model for MSG under strong native conditions. Rates for unobservable kinetic steps are hypothetical values and are shown in red. The values in black represent rate-determining steps of refolding and are adjusted according to hypothetical rate values. I_N behaves as an off-pathway intermediate whose partial unfolding to I_P is a prerequisite for correct folding. The values in parentheses indicate the dependence of natural log of rates on urea concentration. The microscopic rates for reverse reactions are neglected due to the assumption of refolding under strong native conditions. B, unfolding kinetic model consists of initial rapid partition toward two unfolding pathways. The hypothetical rates (red) for initial partition are adjusted to obtain amplitudes corresponding to phase-1 (fast phase) and -2 (slow phase) for unfolding at 7 m urea within <100 ms dead time of mixing. The rest of the values (black) are proposed unfolding rates in the absence of urea whose variation with the denaturant is tuned by values shown in parentheses. A common kinetic model satisfying both refolding and unfolding data requires the inclusion of additional species in the system, and will be unreliable due to a large number of hypothetical rates. C, fitting of urea dependence of theoretical rates on the chevron plot. Where R1, R2, R3, R4, and R5 are the refolding model rates corresponding to U → I_M, I_M → I_D, I_D → I_P, I_P → I_N, I_N → I_P steps, respectively. U1, U2, U3, and U4 are the unfolding model rates corresponding to steps, N → I_Y, I_Y → I_P, I_P → U, and I_X → U, respectively. D, population variation of individual species; U (red), I_M (orange), I_N (blue), and N (purple) with time during refolding at 0.1 m urea (dashed lines). I_D and I_P do not populate to appreciable amounts during refolding (at 0.1 m urea). The net resultant signal (thick gray line) is hypothesized based on optical signals for individual species, where the fluorescence for U, I_M, and N have been fixed in accordance with observed kinetic trace.

Slow domain rearrangement step

To investigate the nature of two refolding phases in view of the size of diffusing segments in the macromolecule, refolding kinetics were studied in viscogenic conditions. In accordance with the Kramer's theory, the presence of microscopic viscogen, e.g. glycerol, should influence the dynamics of differentially structured parts of the protein differently (38–40). As the individual folded domains must be structurally bulkier units as compared with the mobile polypeptide, their diffusion should encounter more resistance from the viscous solvent as compared with less structured loosely packed chain segments and hence may assist in identifying any major structural shuffling step of the refolding.

The presence of glycerol and other similar viscogens also affect the stability of proteins significantly (41), thereby making it difficult to compare refolding rates under different viscogenic conditions. It becomes essential to quantify these stabilizing effects and to use only isostable conditions (with similar free energy difference between denatured and native state) for rate comparisons. The method of comparing kinetics under isostability is much more reliable with two-state folders and may not be apt for a protein such as MSG, which shows multiple intermediates in equilibrium and kinetic studies (42). However, the differential effects of viscosity on two refolding phases should be able to inform about the nature of structural changes in two phases.

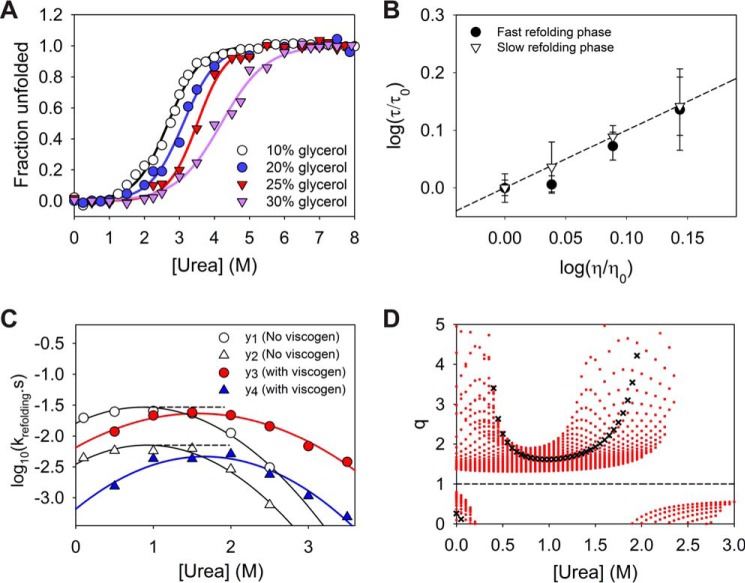
To perceive the effect of viscogen on protein stability, the equilibrium unfolding experiments were conducted under varying glycerol concentrations. Because of limited solubility of urea in glycerol-containing buffers, the studies were conducted only up to 8 m urea concentrations. As anticipated, the addition of glycerol tends to shift the mid-point of denaturation to higher urea concentrations (Fig. 8A). As a result of the shift of equilibrium curve and limitation to 8 m urea, the conformational transition of the protein appears to be much simpler (two-state), but it does not exclude the possibility of similar intermediate states as found under viscogen-lacking conditions. Although the equilibrium plots of MSG were found to be completely reversible under 10, 15, 20, and 25% glycerol, a higher glycerol concentration (30% glycerol) introduced hysteresis in the plot, making it unreliable for refolding experiments (Fig. S7). Unlike at 30% glycerol, the plots up to 25% glycerol simply shifted toward higher urea, without an appreciable effect on the cooperativity index (m-values), signifying negligible relative effects on the nature of free energy landscape (40, 42). Because of this reason, the refolding studies were performed at 25% glycerol under several urea concentrations to obtain a modified chevron arm under viscogenic conditions. It was observed that the refolding limb of the MSG under viscogenic conditions also indicates a rollover and kink near ∼1.5 m urea concentration, i.e. both the refolding phases were found to be assisted by the presence of urea under refolding conditions. Although the protein appears to follow two-state behavior under 25% glycerol, the observation confirms the population of transient misfolded species (I_M) during refolding.

Figure 8.

Effect of viscogenic conditions on refolding kinetics. A, effect of glycerol addition on the stability of MSG. The solid lines represent two-state fit of the data points considered until 8 m urea (limited solubility of urea in presence of glycerol). The equilibrium plots were found to be reversible except in case of 30% glycerol (Fig. S7). A similar cooperativity index until 25% of the viscogen ensures minimal relative alteration of the energy landscape due to glycerol. B, plot indicates a linear effect of dynamic viscosity of the solvent on two refolding rates and excludes any possibility of alteration in the free energy of refolding due to presence of glycerol. C, comparison of refolding rates for both phases under normal native conditions (10% glycerol) and viscogenic conditions (25% glycerol) where y_i = log₁₀k_i. The higher effect of the viscogen on the slow refolding phase can be observed visually. D, as the stability of protein increases appreciably in presence of viscogen like glycerol, the comparison in refolding rates is only viable under equal stability of native state with respect to denatured conformation (isostable conditions). For simpler systems (two-state systems) the isostability is achieved by addition of denaturant to the refolding solution under viscogenic conditions to exactly counter the resulting stabilization. For multistate protein MSG, the relative alteration in the slow refolding rate as compared with that of faster phase, i.e. q (= (y₂ − y₄)/(y₁ − y₃)), is explored under different practical urea increments for achieving isostability, and it was found to be greater than 1 always. The red dots for each urea concentration indicate multiple q values obtained for increments of 0.05 m urea intervals. The black crosses represent q values for isostable conditions under the approximation of two-state behavior of the protein as shown in A. Under two-state assumption, the rates of refolding in native buffer at 1 m urea can be directly compared with refolding rates at 1.61 m urea in viscogenic conditions. Error bars represent the standard deviation of three individual studies.

A simple linear dependence of time constants of refolding for both the phases on the relative viscosity of the medium displays the significance of diffusive motions in folding of the protein (Fig. 8B) (38, 42). Although it can be clearly perceived that the slower phase of refolding is affected more by increased viscosity (Fig. 8C), a quantitative evaluation is further achieved theoretically.

Usually, for two-state proteins, the time constants in the absence and presence of viscogen, are compared under isostable conditions, where the rates without glycerol are compared with the ones with glycerol under higher urea concentrations so that the increased stability due to viscogen is exactly countered by destabilization due to denaturant concentration (42). Although the method is reliably achieved with two-state folding proteins, for proteins like MSG (with equilibrium intermediates present in the system), a direct calculation of higher urea to compensate for increased stability is not straightforward. For this reason, the chevron refolding plot under native buffer (10% glycerol) conditions is compared with the one at higher glycerol (25% glycerol), considering an entire practical range of possible urea increments.

For comparison, two chevron refolding plots on a log₁₀ scale (with and without viscogen) are fitted to quadratic equations that provide a good fit for all the curved refolding arms under denaturant range (Fig. 8C). Theoretical y_i values (where y_i = log₁₀k_i; k₁ and k₂ are apparent rates of refolding for fast and slow phases under low viscosity conditions (10% glycerol), and k₃ and k₄ are apparent rates for fast and slow phases in the presence of 25% glycerol, respectively) from fits as a function of urea concentrations are then compared in terms of the quotient “q,” a ratio of apparent change of y_i values in the presence of high glycerol to the change in the native buffer, i.e. q = (y₂ − y₄)/(y₁ − y₃).

By definition, q with a value greater than 1 would imply an increased time constant and hence higher resistance of the viscogen on the slow-refolding phase as compared with the faster phase. It is found that for the practical range of such urea increments (0.25 to ∼2 m) in achieving isostability, q was always found to be greater than 1 (Fig. 8D). To achieve a rough approximation, thermodynamic parameters were obtained from the two-state fit of protein under native and viscogenic conditions (0–8 m urea), which then provides an estimate of urea increment to be compared with the native condition (10% glycerol) kinetics (38). Calculated values of q for this rough approximation are shown by ×.

Discussion

The previous studies of the large multidomain protein MSG gave hints of burst phase intermediate formation within milliseconds, which later on resulted in the formation of native-like intermediate. The detailed mechanism of the folding pathway of the protein could not be interpreted. Our investigations of the (un)folding pathway of MSG, probed by multiple biophysical tools, give information regarding the mechanism as discussed below.

I_M is on-pathway misfolded intermediate

The refolding from the I_M shows a denaturant-assisted refolding behavior, characteristic of off-pathway type species. However, the placement of I_M, on the off-pathway to the unfolded state, requires its complete unfolding before proceeding to the correct folding route (Fig. 9A). The notion would require I_M → U conversion to be a rate-limiting step during refolding for the fast phase (∼0.197 ± 0.003 s⁻¹ under strongly native conditions). As the I_M populates within dead time of mixing (<100 ms), the rate for U → I_M conversion can be modeled to >50 s⁻¹ to allow rapid equilibration. The exact collinear behavior of the initial fluorescence with the intermediate equilibrated in 4–6 m urea should imply a significant conversion (probably complete) of the unfolded state to the I_M (Fig. 4A), and it requires a large bias of the U ⇌ I_M equilibria toward I_M; k(U → I_M) ≫ k(U ← I_M). As I_M → U is the unfolding step, proceeding to correction, the net folding reaction can only proceed to native state if the rate for subsequent reaction, i.e. U → I (Fig. 9A) is larger than that for U → I_M. The establishment will make it impossible to populate I_M in the initial stages of refolding.

Figure 9.

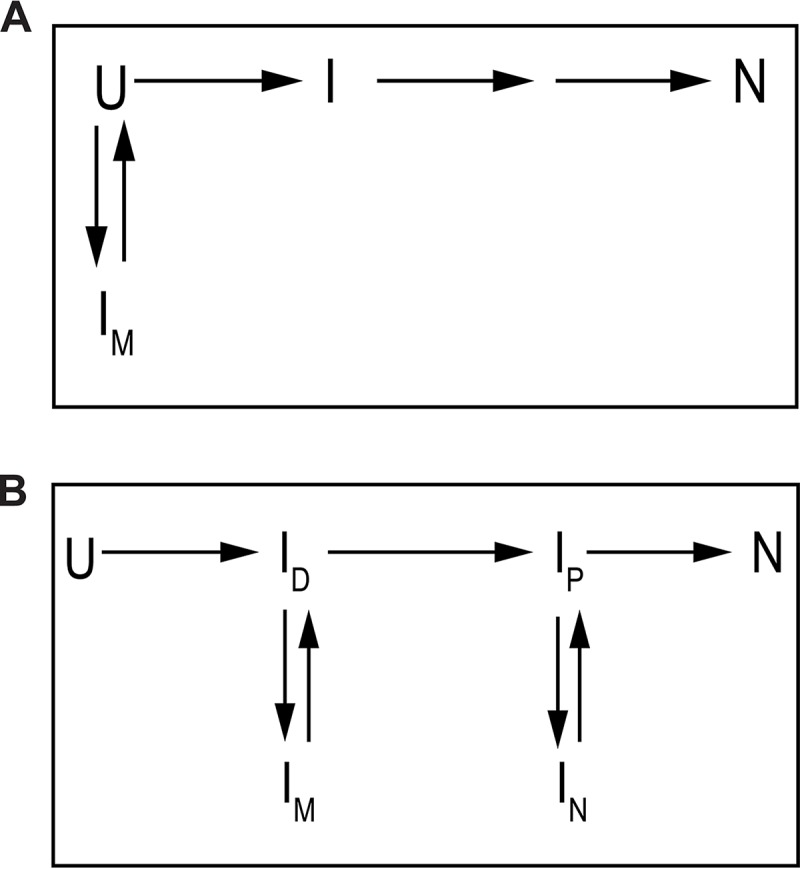
Alternative (incorrect) schemes for modeling I_M. A, model indicates off-pathway placement of I_M to unfolded state (U), and requires complete unfolding prior to achieving correct folding rate. B, model contains another possibility of placing I_M, where the intermediate is considered as off-pathway to another less unfolded on-pathway intermediate.

The additional possibility of placing I_M in refolding model could be as shown in Fig. 9B, where a fast rate (>50 s⁻¹) for U → I_D conversion is proceeded by another fast I_D → I_M (>50 s⁻¹) reaction, resulting in population of the misfolded intermediate. However, modeling of I_M → I_D in accordance with the fast refolding phase (∼0.0197 ± 0.003 s⁻¹), a partial unfolding before the correct route, would not allow the population to come out of the I_M trap due to huge bias toward it. As the following reactions, i.e. I_D → I_P etc., would have to be modeled according to the chevron refolding limb near mid-point, and they would have much lesser rates than ∼50 s⁻¹, it becomes impossible for the I_M to overcome misfolding trap.

The only feasible way to draw kinetics scheme for the fast phase of refolding could be if I_M lies as an on-pathway misfolded intermediate whose partial unfolding (to I_D) is modeled in accordance with the apparent refolding rates at <1 m urea (Fig. 10A). The further refolding step from I_D to the next species on the correct pathway becomes the rate determining step at higher urea (between 1.5 and 2.5 m), resulting in the formation of I_N, another off-pathway species.

Sequential nature of two refolding reactions

As both the refolding chevron arms indicate assistance by denaturant under strongly native conditions it can be inferred that both of them stem from kinetic traps. Although it seems intuitive to assume a common origin (I_M) for both the reactions, the slower phase with a slow rate of partial unfolding (another rate-limiting step) would not take place due to the availability of a parallel faster route. The two refolding reactions need to be sequential in nature, which is further confirmed by folding kinetics probed by fluorescence in the quencher's presence (Fig. 5A). The interrupted refolding experiments despite their low signal to noise ratio also support the notion of sequential nature of two refolding phases (Fig. 7).

As observed from the behavior of the interrupted refolding kinetics, the amplitudes corresponding to the phase-1 (fast unfolding phase at 7 m urea) do not reach to zero even after complete refolding of MSG (confirmed by native MSG unfolding kinetics). However, what appears to be the partial and slow decay of the amplitude after completion of fast reaction should result in a complete folding of the protein. The observation can be explained based on the unfolding behavior of the protein in which the fast unfolding phase is unable to distinguish native species from populated stable intermediates (Fig. 10B).

During unfolding, an initial partition of the native state (N) should result in fast and slow unfolding phases, where the slower phase would correspond specifically to the native state, with no intermediary species. However, the faster unfolding phase (phase-1) should involve I_Y → I_P → U reaction, where I_P should also populate during refolding. The scheme would imply that the population probed by the phase-1 in interrupted refolding kinetics corresponds to the combined population of native (N) and on-pathway intermediate species (I_P). Additionally, the fast rate of I_N → I_P at 7 m urea should remain unobserved, making amplitudes probed by phase-1, a result of combined population of native and I_N species together (I_P being less stable under native conditions).

Nature of initial collapse of unfolded polypeptide

Recent refolding studies with TIM barrel class of proteins and analysis of other folds have provided clues in the formation of misfolded intermediates and their correlation with the tightly packed hydrophobic clusters of ILV residues, also known as BASiC (for Branched Aliphatic amino acid Side Chain) clusters (43–45). The tendency of ILV residues to exclude water molecules combined with compaction due to dewetting transition (46) provides a driving force for hydrophobic collapse and may stabilize a compact core with unsuitable docking sites for further structure formation. The presence of several hydrophobic clusters in MSG structure (Table 3; Fig. S8) would result in polypeptide collapse and might be a feasible reason for I_M. The relatively lower absolute contact orders (ACO) of the ILV residues in two large clusters (clusters 1 and 2) ensures correspondingly low entropic cost, pointing toward their contribution to fast and stable core formation. However, cluster 3 with a large number of contacts along with higher ACO would require a much longer time, making the polypeptide vulnerable to non-native contact formation.

Table 3.

BASiC clusters (43, 50) in MSG

The absolute contact orders for the clusters were calculated based on the identified amino acids of the clusters (51, 52). The high values of absolute contact orders are due to the large size of the protein.

Major clusters identified by “BASiC networks (49, 50)” (>500 Å2 buried)	No. of amino acids involved	No. of total contacts formed	Absolute contact order (51, 52)
Cluster 1	24	41	67.19
Cluster 2	20	31	51.03
Cluster 3	23	31	106.9
Cluster 6	14	16	96.75
Cluster 7	14	20	80.5

Furthermore, as the compact clusters are known to impede penetration of water in the structure and are hypothesized to be stable enough to reside in the high-energy intermediates, the residual structure of MSG in 4–6 m urea might be a consequence of the resulting stabilized core. Although the analysis provides an intuitive molecular justification, it needs to be further verified by mutational analysis.

Refolding mechanism of MSG

The refolding of MSG starts with a sub-millisecond collapse of the unfolded polypeptide, resulting in the formation of compact I_M devoid of significant secondary structure. Although the transient species appears to encounter the misfolding trap only under strongly native conditions (<1 m urea), the collinear behavior of its fluorescence and relative ellipticity signals with that of equilibrium intermediate in 4–6 m urea point toward a correlation between the two species. It was found that the Stern-Volmer analysis of the equilibrium intermediates points toward their highly open conformation; however, the equilibrium unfolding curve (Trp fluorescence probe) hints toward a residual tertiary structure. At the molecular level, the kinetic intermediate I_M can be perceived as a product of hydrophobic compaction with the formation of stable hydrophobic clusters guiding the conformational search. Because of the large size of the protein (and hence huge conformational entropy cost of refolding), combined with the compact nature of I_M, it becomes highly probable for the polypeptide to form non-native interactions in the initially collapsed state (i.e. misfolding trap). In the same way, the equilibration of MSG to higher urea concentrations (4–6 m) probably does not result in a complete loss of tertiary structure due to the presence of stable hydrophobic clusters (Fig. S8). Consequently, the protein achieves a residual tertiary structure-containing state with lost α-helical content. It can be imagined that the protein maintains similar interactions in 4–6 m urea as formed in the kinetically populated I_M state; however, it remains open enough to have no helical content with a very high (similar to unfolded state) Stern-Volmer coefficient (Fig. 2, B and C, and Table S1). As the available evidence only allows us to propose the possible mechanism, the exact link between two entities needs to be determined by using techniques such as hydrogen-deuterium exchange probed by mass spectrometry.

After achieving the conformational collapse, the correction in misfolded state (I_M) is achieved via partial unfolding (breaking of non-native interactions), which subsequently leads it to another off-pathway trap, forming I_N. The slow conversion of I_N to the native state is assisted by denaturant concentrations (under strongly native conditions) (Fig. 3B) but meanwhile gets impeded in the presence of microscopic viscogen (Fig. 8). As a consequence, the molecular nature of I_N appears to be an entity with large sections (domains) of the protein folded but oriented incorrectly, forming several non-native interactions. The slow correction step involving partial disruption of the structure would result in native state formation.

Kinetic modeling of refolding and unfolding mechanism

A common kinetic model of refolding and unfolding pathways over entire urea range requires the inclusion of additional intermediate species. However, in the absence of sufficient information, the defined pathways were only proposed under strongly native and unfolding conditions (Fig. 10, A and B). As the microscopic rates of all the steps could not be calculated, hypothetical values (shown in red) were taken for obtaining fit of the chevron plot (Fig. 10C). The relative concentrations of the components in a kinetic model are a function of individual microscopic rate constants as well as their denaturant dependence, and hence the concentration of the putative intermediate species could not be derived based on the present evidence. Fig. 10D represents the fluorescence refolding trace for MSG, based on theoretical fluorescence of intermediate species.

The unfolding theoretical model (Fig. 10B) agrees with the initial missing signal of unfolding, which is modeled by a very fast parallel partition, in accordance with the amplitudes of two unfolding phases. The availability of two fast unfolding phases for >7.5 m urea is justified by development of a transition barrier (I_P → U) at high urea concentrations.

Scenario of the large multidomain protein folding

In this study, with the help of a number of biophysical tools and computational techniques, we were able to propose the sequence of events taking place during refolding of MSG. Because of the large size of the protein, it is intuitive that the high entropic cost of correct contacts formation, the complex domain topology, and dominant hydrophobic clusters in the protein should result in multiple misfolding traps on the folding pathway. However, the spontaneous reversibility from such local traps and the ability to achieve the final native state signify a highly efficient folding mechanism. Although the refolding of protein requires no assistance under in vitro (diluted) conditions, the apparently slow refolding rate along with aggregation-prone tendencies of the intermediates (24) may highlight a requirement of in vivo folding assistance under crowding cellular concentrations (47).

Experimental procedures

Protein production and buffer conditions

MSG was overexpressed and purified using nickel-nitrilotriacetic acid affinity chromatography as mentioned previously (24). The protein is known to be stable and exhibits reversible unfolding under optimized buffer conditions containing 20 mm Tris (pH 7.9), 10 mm MgSO₄, 300 mm NaCl, 10% glycerol, and 1 mm Tris(2-carboxyethyl)phosphine hydrochloride as reducing agent. All the studies, unless specified, were conducted in the described buffer conditions at 25 °C. Unfolding buffer was prepared fresh with the same composition and additional ultrapure grade urea as the denaturing agent. The concentration of urea was determined by refractive index (Abbe-3L refractometer).

Ensemble equilibrium unfolding experiments

The native MSG was equilibrated at a number of urea concentrations for a minimum of 10 h at 25 °C. Trp fluorescence scans were accumulated in 315–500 nm (slit width = 10 nm) range by excitation at 295 nm (slit width = 10 nm) in a 10-mm quartz cuvette using Cary Eclipse fluorescence spectrophotometer (Agilent Technologies). The emission signal intensity for specific wavelength, e.g. 340 nm, was collected for 30 s and averaged. Each data point is an average of three readings from individual samples where a correction of signals due to buffer as a background has been made. Reversibility was verified by equilibrium refolding studies starting from 6.5 m urea unfolded MSG.

Ellipticity scans and measurements at 222 nm were carried out for samples prepared similarly, in 1-mm path length optical cuvette using JASCO J-815 CD spectrophotometer (Jasco Inc.). The reversibility of unfolding was verified by conducting equilibrium refolding studies.

Ensemble kinetic experiments

All kinetic experiments were conducted in above-mentioned buffer conditions at 25 °C to achieve reversibility. The Trp fluorescence signals were collected at 340 nm by excitation at 295 nm and were corrected for background buffer fluorescence. Signals for ANS were obtained at 450 nm, by excitation at 350 nm. The ellipticity of the protein at 222 nm was recorded to monitor conformational transition.

Refolding

Unfolded MSG at 6.5 m urea was diluted in native buffer manually, as well as via RX2000 stopped-flow module (∼100 ms of dead time) to record the refolding traces in a 10-mm quartz optical cuvette. The refolding protein concentration was always kept between 0.1 and 0.4 μm, to achieve complete reversibility (24). Refolding traces using Trp fluorescence in the presence of acrylamide were corrected for inner filter effect (48).

Unfolding

Native protein was unfolded to a number of urea concentrations via stopped-flow module as well as manual method to obtain unfolding traces.

Interrupted refolding studies

The 6.5 m urea unfolded MSG was allowed to refold in 0.1 or 2 m urea (as mentioned above) for a definite amount of refolding time points, followed by a second unfolding jump in 7 m urea. The unfolding traces at different refolding time points were collected and analyzed for amplitudes.

Interrupted unfolding studies

The native protein was allowed to unfold in 8 m urea for a number of unfolding time points, followed by a fast refolding jump (in 1 m urea). Refolding kinetics traces were collected and analyzed.

Viscosity measurements

The viscosities of solutions were measured at 25 °C using Cannon-Fenske viscometer size 50, calibrated using double-distilled deionized water.

BASiC clusters in MSG

The BASiC clusters, with >500 Ų surface area buried, were identified using BASiC Networks on-line server (49, 50) and verified by an in-house computational algorithm that considers cluster as sets of contacts with a minimum six ILV side chains arranged in compact form (<4.2 Šdistance between heavy atoms counts as a contact) (43). The ACO for the clusters was calculated based on the identified amino acids of the clusters (51, 52),

$$\text{ACO}=\left(1/N\right)\times {\displaystyle \sum \Delta n_{ij}}$$ (Eq. 1)

where N is the total number of contacts, and Δn_ij represents number of residues separating the pairs in contact.

Data analysis

Equilibrium studies

Equilibrium unfolding scans with Trp fluorescence were subjected to singular value decomposition (SVD) analysis using MATLAB (The Mathworks Inc.) to determine distinguishable components and their amplitudes. The two-state global fit of equilibrium unfolding curves is carried out by nonlinear least-square regression to Equation 2,

$$y_{\text{obs}}=\frac{\left(a+b\left[\text{urea}\right]\right)+\left(\left(d+f\left[\text{urea}\right]\right)\exp \left(-m\left(c_{50\%}-\left[\text{urea}\right]\right)\right)\right)}{1+\exp \left(-m\left(c_{50\%}-\left[\text{urea}\right]\right)\right)}$$ (Eq. 2)

where y_obs = experimental signal; a, b, and d, f represent the y-intercept and slopes of native and unfolding baselines respectively. m and c_50% are the cooperativity index and denaturant concentration where half of the protein population is unfolded, respectively.

Kinetic studies and modeling

The kinetic traces were fitted to exponential equations to obtain apparent rates as shown in Equation 3,

$$y\left(t\right)=y\left(\infty \right)+{\displaystyle \sum _{i=1}^n{y}_i\exp \left(-kt\right)}$$ (Eq. 3)

where y(t) represents signals with respect to time and y(∞) is the final signal after completion of kinetics. k represents apparent rate, and t is the time. The pathways for refolding and unfolding were modeled separately by calculation of the eigenvalues and eigenvectors of the rate matrix (Fig. 10) as described previously (53). The eigenvalue decomposition of the rate matrix was conducted by MATLAB.

Author contributions

V. K. and T. K. C. conceptualization; V. K. data curation; V. K. software; V. K. formal analysis; V. K. validation; V. K. investigation; V. K. visualization; V. K. and T. K. C. methodology; V. K. writing-original draft; V. K. and T. K. C. writing-review and editing; T. K. C. resources; T. K. C. supervision; T. K. C. funding acquisition; T. K. C. project administration.