Abstract
The purpose of this review was to introduce readers of Child Development to the meta-analytic structural equation modeling (MASEM) technique. Provided are a background to the MASEM approach, a discussion of its utility in the study of child development, and an application of this technique in the study of reading comprehension development. MASEM uses a two-stage approach: first, it provides a composite correlation matrix across included variables, and second, it fits hypothesized a priori models. The provided MASEM application used a large sample (n = 1,205,581) of students (ages 3.5 – 46.225) from 155 studies to investigate the factor structure and relations among components of reading comprehension. The practical implications of using this technique to study development are discussed.
Keywords: Meta-analysis, structural equation modeling, reading development
Meta-analysis is not a new technique in the study of child development, particularly as related to educational research. Indeed, Gene Glass first coined the term meta-analysis in 1976: “[meta-analysis is] a rigorous alternative to the causal, narrative discussions of research studies which typify our attempts to make sense of the rapidly expanding research literature” (p. 3). In education, meta-analyses have pooled effect sizes from studies examining the effectiveness of programs designed for struggling readers (e.g., Lee, & Tsai, 2017; Wanzek, Wexler, Vaughn, & Ciullo, 2010), the effects of vocabulary training on reading comprehension (e.g., Elleman, Lindo, Morphy, & Compton, 2009), and the effectiveness of spelling instruction (e.g., Graham & Santangelo, 2014), to name only a few.
Meta-analysis is not limited to the pooling of effect sizes like Hedge’s g or Cohen’s d and can also be used to pool correlation coefficients across studies. For example, recent correlational meta-analyses involving reading skills have considered rapid naming ability and reading (Araújo, Reis, Petersson, & Faísca, 2015), word decoding and reading comprehension (García & Cain, 2014), and second language correlates of reading comprehension (e.g., Jeon & Yamashita, 2014). However, these studies investigated the univariate relations between one predictor and one outcome (or in the case of Jeon & Yamashita, multiple univariate analyses). These studies, particularly Jeon and Yamashita (2014), are missing valuable information provided by correlations that were unmeasured in a univariate meta-analysis framework.
Education researchers can use meta-analytic techniques and a structural equation modeling (SEM) framework to test multivariate models using a multivariate framework to address the limitations of univariate methods (e.g., Becker & Schram, 1994; Viswesvaran & Ones, 1995). The purpose of this article is to introduce the multivariate meta-analytic structural equation modeling (MASEM) approach, to discuss its usefulness in the study of child development, and to apply MASEM to the study of a multivariate skill (reading comprehension).
Meta-Analytic Structural Equation Modeling: A Primer
In a univariate approach, each element of a correlation matrix is treated as independent within a study, and correlations are thus pooled separately (e.g., Araújo, Reis, Petersson, & Faísca, 2015; García & Cain, 2014). Becker (2000, 2009) proposed a model-based meta-analysis approach: a pooled correlation matrix is estimated under a random effects model, and variation between studies is included in the confidence intervals of the estimates. The relations among variables that considers their covariances can be estimated through multiple regression models (Becker, 2000, 2009). This approach extended univariate meta-analysis, but resulted in the question: How do you choose an appropriate sample size for these analyses? Does one choose the average sample size, the harmonic mean of sample sizes, or another option?
Cheung and Chan (2005) extended the GLS method to a two-stage structural equation modeling (TSSEM) approach to address the question of choosing a sample size. TSSEM uses multiple-group SEM to pool correlation matrices in the first stage, and then uses weighted least squares (WLS) estimation in fitting the a priori proposed SEM(s) in the second stage. Using WLS, the sampling covariance matrix is used to assign different weights to the correlation matrix cells depending on their precision (i.e., the size of their variances). Thus, there is no need to decide on one sample size to use for the estimation of model effects (Cheung, 2015b).
The Utility of MASEM in the Study of Child Development
The number of effect sizes reported in primary studies can vary greatly, as researchers have different research questions and use different methods and samples to answer them. Multivariate approaches are exceptionally useful for education researchers, as the types of curricula, minutes or hours spent teaching various subjects, and even classroom environments are different across schools, districts, and states. The usefulness of MASEM is further emphasized by the increasing use of latent variables to extract common variance across similar, but separately norm-referenced educational tests. One example is a recent extension of the Direct and Inferential Mediated Effects (DIME) model of reading comprehension (Cromley & Azvedo, 2007). The DIME model defines direct and indirect pathways between vocabulary, decoding, background knowledge, inference, strategy usage, and reading comprehension using single manifest measures. Ahmed and colleagues (2016) extended the DIME model by using multiple measures of each construct to create latent variables in a large sample of students, thus extracting the common variance among similar measures to create a more reliable model of reading comprehension. Multivariate MASEM aims to increase the reliability of correlational meta-analyses in a similar manner that the inclusion of latent variables brought to path analyses.
MASEM Application: Component Skills of Reading Comprehension
Reading comprehension (RC) is vital for educational attainment (National Center for Educational Statistics, 2013). According to the Simple View of Reading (SVR, Gough & Tunmer, 1986; Hoover & Gough, 1990), skilled RC is the product of sufficient decoding and linguistic comprehension skills. Both decoding and linguistic comprehension are necessary for RC, but each component alone is not sufficient. Decoding, or word recognition, is the ability to interpret printed letters and words using the alphabetic principle (Adams, 1990) and to transform them into their phonetic code (Perfetti, 1985). Fluent and accurate decoding, at the word level and in the context of sentences or passages, facilitates RC (LaBerge & Samuels, 1974). Linguistic comprehension includes oral language skills such as listening comprehension and vocabulary knowledge. Listening comprehension is the ability to interpret the meaning of oral lexical information (Gough & Tunmer, 1986), and makes significant contribution to RC ability above word reading (Kim, 2015). Vocabulary knowledge is one of the most important predictors of RC (Anderson & Freebody, 1981; Beck & McKeown, 1991; Ouellette, 2006) and accounts for a large proportion of variance in listening comprehension ability at kindergarten (Florit, Roch, & Levorato, 2013; 2014). Vocabulary knowledge is also important for word recognition and facilitates reading (Chiappe, Chiappe, & Gottardo, 2004; Metsala & Walley, 1998). Failures in either decoding (i.e., reading impairment) or linguistic comprehension (i.e., language impairment) can result in delayed or impaired comprehension of written text (Gough & Tunmer).
Other important predictors of RC that were not explicitly included in the original SVR include background knowledge, working memory, and reasoning and inference skills. Background knowledge affects RC (e.g., Dole, Valencia, Greer, & Wardrop, 1991; Spires & Donley, 1998), and more strongly facilitates RC as a reader ages (Evans, Floyd, McGrew, & Leforgee, 2001). Second, working memory (see Baddeley, Eysenck, & Anderson, 2009, for a review; Baddeley, 1992) is a foundational cognitive skill that supports comprehension monitoring and inference making (e.g., Oakhill, Hartt, & Samols, 2005) and is an important predictor of RC (Cain, Oakhill, & Bryant, 2004; Seigneuric & Ehrlich, 2005; Swanson & Berninger, 1995). Third, reasoning skills are important for understanding spoken language, and verbal and non-verbal reasoning tasks are significantly correlated with reading (Pammer & Kevan, 2007). Inference uses background knowledge to interpolate or extrapolate missing information and is important for RC (Cain et al., 2004; Kendeou, Bohn-Gettler, White, & Van Den Broek, 2008; Oakhill & Cain, 2012; Tompkins, Guo, & Justice, 2013; Yuill & Oakhill, 1988). In contrast to the SVR, other multivariate models of RC such as the multicomponent view of reading (Cain, 2009; Cain et al., 2004), the DIME model (Cromley & Azvedo, 2007), the verbal efficiency theory (Perfetti, 1985), and the construction-integration model (Kintsch, 1988) provide evidence for the inclusion background knowledge, working memory, and reasoning and inference as separate from or in addition to the original SVR components.
The Present Study
Within the present application, we used the two-stage MASEM approach to analyze the correlations between common components of RC in order to answer the following questions:
What are the meta-analytic correlations between reading comprehension and its predictors?
What is the factor structure of the hypothesized predictors, and how much variance do these factors account for in reading comprehension?
Are there differences in the model structure or relations between younger and older children?
Methods
Literature Base
We used a multi-step process to identify relevant articles. The original literature search was conducted on March 25, 2015; it was then updated on April 3, 2016.
Search criteria
Using PsycINFO, ProQuest (Dissertations and Theses, PQTD), and ERIC, a primary search of the literature was conducted to identify studies that included one of the following phrases in the title of the document: reading comprehension OR text comprehension OR simple view of reading OR simple view. To ensure retrieval of empirical studies, the abstract must have also contained predict* or develop* or assoc* OR relat* OR depend* OR connect* OR occur* (the asterisk is to denote all extensions of the word are acceptable, e.g., prediction, development). All studies must have been published from 1990 on, as methods for teaching reading and measuring reading ability differed substantially prior to this time. Additionally, studies must have had one or more key words related to the predictor variables as a subject (e.g., decoding, working memory, background knowledge, vocabulary knowledge).
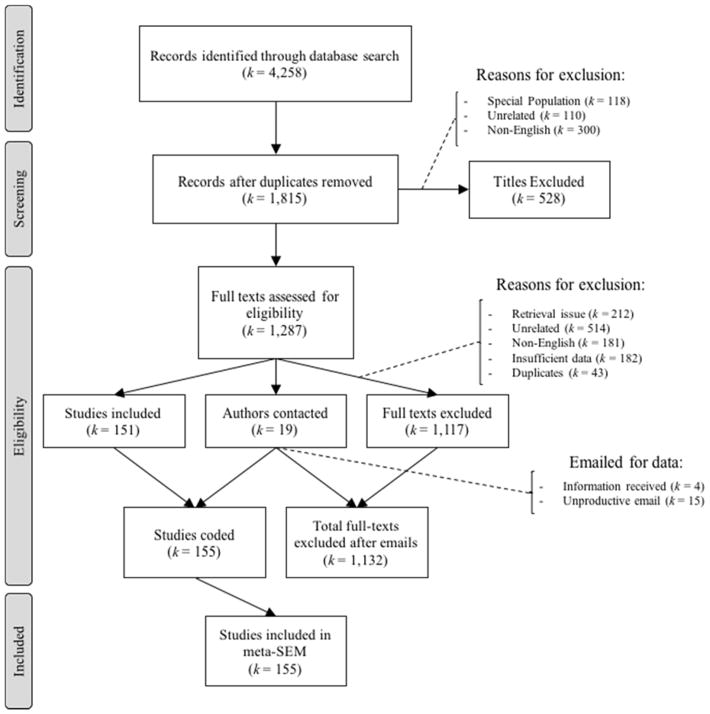
We identified 4,258 articles using these criteria; 2,404 studies after removing duplicate sources (1,350 from PsycINFO and ProQuest and 1,054 from ERIC). Due to issues with retrieval, the total number of studies subjected to exclusionary criteria was reduced to 1,815.
Exclusion criteria
Exclusionary criteria were applied in two steps. Within the first step, the titles of the articles were screened for three exclusionary criteria (See Figure 1): special population status (e.g., traumatic brain injury, autism spectrum disorder, intellectual disability, hearing or vision impairments), being unrelated to the meta-analysis (e.g., non-empirical, single-case studies, corrigendum, commentaries), or English language learners (ELL) or foreign language populations. We excluded studies with ELL samples because the relations between decoding and comprehension can be affected by transfer effects across languages (García & Cain, 2014), and foreign language populations were excluded because different writing systems may produce different relations between the included variables (Florit & Cain, 2011). An additional 212 studies could not be retrieved from the server. Applying these exclusionary criteria to the titles resulted in the exclusion of 1,117 total studies (See Figure 1).
Figure 1.
Flow chart of the record screening process. Reasons for exclusion are included in brackets to the right of the excluded boxes.
We consulted the full texts of the remaining 1,287 studies to determine eligibility for analysis using the following criteria. Studies must have measured individual constructs (i.e., no composite scores) and measures must have been collected within the same year (i.e., only concurrent correlations). Studies must have had a correlation coefficient between a measure of reading comprehension and at least one predictor variable, and must have met the exclusionary criteria applied to the article titles that may have been missed during the first step. The authors of 19 of 182 studies with insufficient could be contacted, but 15 could no longer provide the data. In total k = 155 studies, denoted with asterisks within the References (references used in the study that were not cited in text are included in Supplemental Online Materials A to preserve space), were included in the present analyses.
Moderator Variables
Both average age of the sample and reader ability status (e.g., reading or learning disability, typical readers) were coded. While there was enough information to group the correlation matrices by average age, there was not enough information to create full composite correlation matrices separately for the typical sample of readers and for readers with learning or reading disabilities. As such, we conducted moderator analyses using only average age.
Coding Scheme
Each study was coded for the following information: Study name and year, sample of students, age, reader status (e.g., reading disability, typical readers), and available correlations between reading comprehension and the eight predictor variables (word reading accuracy, word reading fluency, text reading fluency, vocabulary knowledge, listening comprehension, background knowledge, reasoning and inference, and working memory). Where correlations were missing from a study, we left the cell blank, and still included any available information in the coding scheme. Multivariate MASEM allows for missing correlations to be handled in the missing at random (MAR) framework when the correlation matrix is estimated in the first stage of the MASEM. This allows models to be fit using maximum likelihood estimation methods (Cheung, 2015b; Enders, 2010). If a cell had more than one correlation, we adopted the method used by the National Reading Panel (National Institute of Child Health and Human Development [NICHD], 2000) by averaging the effect sizes together. See Supplemental Materials B for a discussion on model robustness and correlation coverage across the included matrices.
Reliability of coding
To assess reliability, a graduate student independently coded 20 of the identified studies to establish acceptable inter-rater reliability. The mean kappa was .94 (.82–1) for the matrices, 1 for age, .95 for reader ability designation, and 1 for sample size.
Meta-Analytic Structural Equation Models
Fixed versus random effects models
It was reasonable to expect that there were study-specific differences in correlations due to variations in samples, measures, and study designs. As such, a random-effects model was adopted. Additionally, a random effects model allows for the generalization of findings to be outside of the studies used in a meta-analysis. The R package metaSEM (Cheung, 2015a) provides a two-stage structural equation modeling (TSSEM) method to first calculate the sampling covariance matrix of the correlations and to estimate a pooled correlation matrix. The second stage of the TSSEM analyzes the pooled correlation matrix according to the user’s hypothesized models. Using metaSEM, the I2 statistic was estimated to quantify heterogeneity in correlations by using the Q test of homogeneity (See Cheung, 2015b). After creating the pooled correlations using the first step, the estimated values of the stage 1 results were treated as sample statistics in the stage 2 analysis.
Hypothesized a Priori Models
Structural models fit using metaSEM differ from traditional SEMs fit in other programs in several ways. Traditional SEM fitting specifies latent variables to represent common variance across measures or items of the same construct. In meta-SEM, since the data are represented as correlations and not as scores on a particular measure, higher-order factors capture the common variance across constructs. Therefore, residual variances and disturbance terms in meta-SEMs represent the amount of variance unaccounted for in the constructs that may be attributable to heterogeneity in sampling and measurement.
Confirmatory factor analyses (CFAs)
We first explored the factor structure of the predictor variables before including reading comprehension. We fit a two factor model to test the true SVR (one factor for linguistic comprehension and a second factor for decoding) and a three factor model with the original two components of the SVR and a separate factor for the cognitive components (working memory and reasoning and inference). We include more information about the fitting of these models, including tests of model fit, in the supplemental materials (Online Supplemental Materials C).
Reading comprehension model
A modified version of the Simple View of Reading was fit to the complete set of matrices (k = 214). Three higher order factors were created from the eight predictors: a decoding factor was indicated by word reading fluency, text reading fluency, and word decoding accuracy, a linguistic comprehension factor was indicated by vocabulary knowledge and morphology, listening comprehension, and background knowledge, and a cognitive factor was represented by working memory and reasoning and inference. We then regressed reading comprehension onto these three factors.
Moderator Analyses
We used age as a moderator during the fitting of these models. We created two groups: a younger group including samples with average ages below 11 years (below the 6th grade) and an older group including samples with average ages at or above 11 years (at or above grade 6). We applied this method due issues with variable coverage in the correlation matrix (explained in detail in the results section).
Model Fit
We assessed model fit with the chi-square test of model fit, the confirmatory fit index (CFI), the standardized root mean square residual (SRMR), and the root mean square error of approximation and its confidence interval (RMSEA). Maximized CFI values (greater than .95), minimized RMSEA and SRMR values (less than .08), and a low ratio of the chi-square value to its degrees of freedom (less than or equal to 2) were preferred (Kline, 2011).
Results
First Stage Results
Descriptive statistics
Table 1 contains the results of the first stage of the TSSEM approach. Correlations (presented in the bottom half of Table 1) between the nine predictor variables ranged from low to moderate (0.265 – 0.695). The correlation between word reading fluency and listening comprehension was homogenous (I2 = 0.000). A homogenous correlation indicates that the relation between word reading fluency and listening comprehension was captured in a similar way across the studies that included these variables. All other correlations were heterogeneous across studies (I2s > 0.82, see the top half of Table 1). The average sample size across all included studies was n = 5,530. The harmonic mean was n = 114. A total of N = 1,205,581 participants from K = 155 studies were included in the present meta-analysis. The average age for the participants was 12.533 (3.5 – 46.225).
Table 1.
Correlations and heterogeneity statistics for the nine included constructs.
| Construct | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1. RC | -- | .988 | .989 | .992 | .986 | .980 | .978 | .963 | .982 |
| 2. WRF | .475 | -- | .990 | .990 | .975 | .000 | .823 | .945 | .983 |
| 3. TRF | .581 | .695 | -- | .991 | .990 | .934 | .973 | .966 | .989 |
| 4. DA | .540 | .588 | .579 | -- | .977 | .971 | .988 | .972 | .977 |
| 5. V/M | .553 | .411 | .520 | .480 | -- | .987 | .986 | .980 | .992 |
| 6. LC | .495 | .316 | .401 | .365 | .482 | -- | .963 | .982 | .949 |
| 7. R/I | .452 | .265 | .392 | .339 | .403 | .386 | -- | .985 | .990 |
| 8. WM | .336 | .286 | .349 | .327 | .331 | .331 | .350 | -- | .976 |
| 9. BGK | .471 | .381 | .417 | .423 | .535 | .433 | .379 | .329 | -- |
Note. Correlations are below the diagonal; heterogeneity statistics are above the diagonal. RC = reading comprehension; WRF = word reading fluency; TRF = text reading fluency; V/M = vocabulary and morphological knowledge; LC = listening comprehension. R/I = reasoning and inference; BGK = background knowledge. Bolded values indicate homogenous correlations.
Second Stage Results
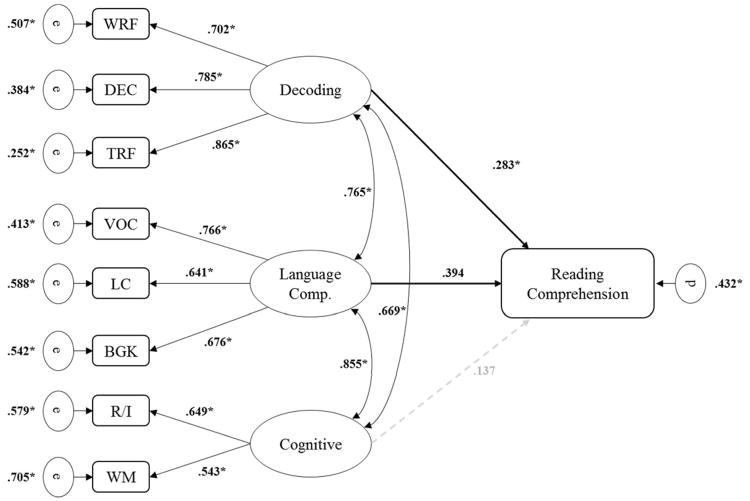
The three-factor model of RC was fit to the stage 1 results of the TSSEM approach. This model provided excellent fit to the data (χ2 (20) = 61.4902, p < .001, CFI = 0.9969, RMSEA = 0.0012 [0.0009 – 0.0016], SRMR = 0.0310). Figure 2 includes the path coefficients and factor loadings. The loadings of word reading fluency (λ = 0.702, p < .001), decoding accuracy (λ = 0.785, p < .001), and text reading fluency (λ = 0.865, p < .001) were all significant and positive, indicating that the latent construct of decoding captured significant common variance across the included studies. A similar pattern of loadings for vocabulary knowledge (λ = 0.766, p < .001) background knowledge (λ = 0.676, p < .001), and listening comprehension (λ = 0.676, p < .001) were estimated, indicating that the construct of linguistic comprehension was also capturing significant common variance between these three indicators.
Figure 2.
Meta-SEM path diagram for the three-factor model. * p < .001. Dashed, grey pathway is not significant. WRF = word reading fluency; DEC = decoding accuracy; TRF = text reading fluency; VOC = vocabulary knowledge; LC = listening comprehension; BGK = background knowledge; WM = working memory; R/I = reasoning and inference. e = residual variance error terms, d = disturbance term.
The standardized regression pathways from the higher order factors of linguistic comprehension (β= 0.394, p < .001) and decoding (β= 0.283, p < .001) were significant and positive. For every 1 standard deviation increase in linguistic comprehension and in decoding, RC increased by 0.394 and 0.283 standard deviation units, respectfully. After accounting for individual differences in decoding and linguistic comprehension, the factor that included the cognitive components (working memory and reasoning and inference) did not account for significant additional variance in reading comprehension (β= 0.137, p = .129). Approximately 56.8% of the variance in reading comprehension was accounted for by this model (R2 = 1 – d).
Moderator Analyses
The first stage of the TSSEM approach was used to create separate composite correlation matrices for these two groups. The expanded SVR model was then fit separately to these matrices in the second stage. To create two groups of matrices according to age, we dichotomized age at 11 years. This dichotomization represents children in approximately 5th grade and below for the younger sample (average age = 8.76 years, range = 3.5 – 10.67) and approximately 6th grade and older for the older sample (average age = 16.80, range 11.0 – 46.23).
Younger Sample
The composite correlation matrix and heterogeneity estimates for the younger children are contained in Table 2. Correlations ranged from low to moderately high (0.278 – 0.740). Three correlations were homogenous (denoted in bold in Table 2). During the first stage model fitting, it was discovered that there was not enough information across the included studies (k = 79) to estimate the meta-correlations for background knowledge. The first stage model failed to converge. For the purposes of this portion of the meta-analysis, background knowledge was removed from the models for the younger cohort.
Table 2.
Correlations and heterogeneity statistics for the younger cohort.
| Construct | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| 1. RC | -- | .979 | .958 | .986 | .979 | .973 | .941 | .911 |
| 2. WRF | .569 | -- | .984 | .988 | .984 | .000 | .946 | .000 |
| 3. TRF | .621 | .740 | -- | .982 | .991 | .939 | .984 | .000 |
| 4. DA | .610 | .593 | .642 | -- | .968 | .972 | .986 | .881 |
| 5. V/M | .542 | .450 | .533 | .470 | -- | .987 | .983 | .976 |
| 6. LC | .498 | .311 | .405 | .376 | .483 | -- | .967 | .970 |
| 7. R/I | .480 | .278 | .412 | .360 | .398 | .412 | -- | .881 |
| 8. WM | .360 | .312 | .318 | .312 | .367 | .380 | .329 | -- |
Note. Correlations are below the diagonal; heterogeneity statistics are above the diagonal. RC = reading comprehension; WRF = word reading fluency; TRF = text reading fluency; V/M = vocabulary and morphological knowledge; LC = listening comprehension; R/I = reasoning and inference. Bolded values indicate homogenous correlations.
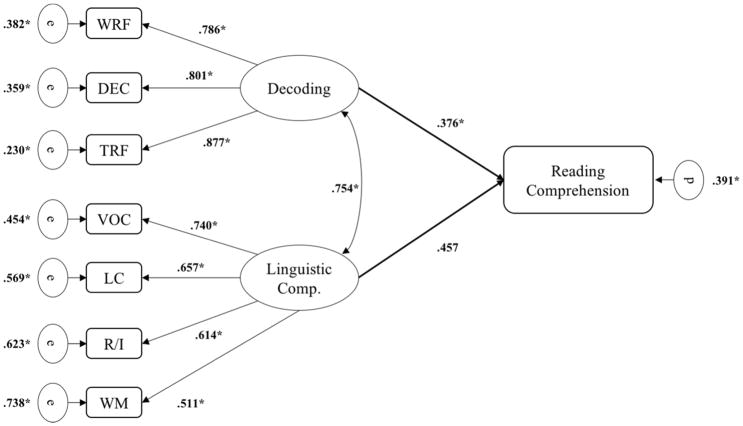
The two-factor model provided excellent fit to the data, (χ2 (18) = 31.0251, p = .0285, CFI = 0.9985, RMSEA = 0.0012 [0.0004 – 0.0018], SRMR = 0.0347). Increasing the model complexity to create three factors did not improve model fit (see Supplemental Materials C, Table C2). Figure 3 presents the path coefficients for this model. Both the linguistic comprehension and decoding factors captured significant common variance across their respective indicators with medium to high loadings (λs = 0.511 – 0.877). The regression pathways from the linguistic comprehension factor (β= 0.457, p < .001) and decoding factor (β= 0.376, p < .001) were both significant and positive, indicating that decoding and linguistic comprehension independently predict variance in reading comprehension. These units are standardized: for every 1-unit standard deviation increase in linguistic comprehension and in decoding, RC increases by 0.457 and 0.376 standard deviation units, respectfully. The two-factor model accounted for 60.9% of the variance in reading comprehension for younger children.
Figure 3.
Meta-SEM path diagram for the younger sample. *p < .001. Dashed, grey pathways are not significant. WRF = word reading fluency; DEC = decoding accuracy; TRF = text reading fluency; VOC = vocabulary and morphological knowledge; LC = listening comprehension; WM = working memory; R/I = reasoning and inference. e = residual variance error terms, d = disturbance term.
Older Cohort
The first stage of the TSSEM was conducted in R on the studies with samples of older children (k = 86). The composite correlation matrix and associated heterogeneity statistics for this sample are presented in Table 3. The correlations ranged from low to moderate (r = 0.243 – 0.596). There were four homogenous correlations (indicated in bold).
Table 3.
Correlations and heterogeneity statistics for the older cohort.
| Construct | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
|---|---|---|---|---|---|---|---|---|---|
| 1. RC | -- | .963 | .990 | .992 | .987 | .981 | .984 | .971 | .981 |
| 2. WRF | .394 | -- | .992 | .988 | .920 | .000 | .000 | .939 | .000 |
| 3. TRF | .527 | .596 | -- | .991 | .983 | .865 | .963 | .976 | .972 |
| 4. DA | .438 | .589 | .522 | -- | .981 | .955 | .981 | .982 | .964 |
| 5. V/M | .562 | .382 | .514 | .485 | -- | .986 | .987 | .979 | .989 |
| 6. LC | .494 | .313 | .393 | .346 | .477 | -- | .862 | .981 | .000 |
| 7. R/I | .434 | .243 | .362 | .304 | .401 | .358 | -- | .989 | .992 |
| 8. WM | .324 | .272 | .363 | .336 | .316 | .292 | .352 | -- | .979 |
| 9. BGK | .436 | .302 | .288 | .356 | .526 | .517 | .376 | .323 | -- |
Note. Correlations are below the diagonal; heterogeneity statistics are above the diagonal. RC = reading comprehension; WRF = word reading fluency; TRF = text reading fluency; V/M = vocabulary and morphological knowledge; LC = listening comprehension; R/I = reasoning and inference; BGK = background knowledge. Bolded values indicate homogenous correlations.
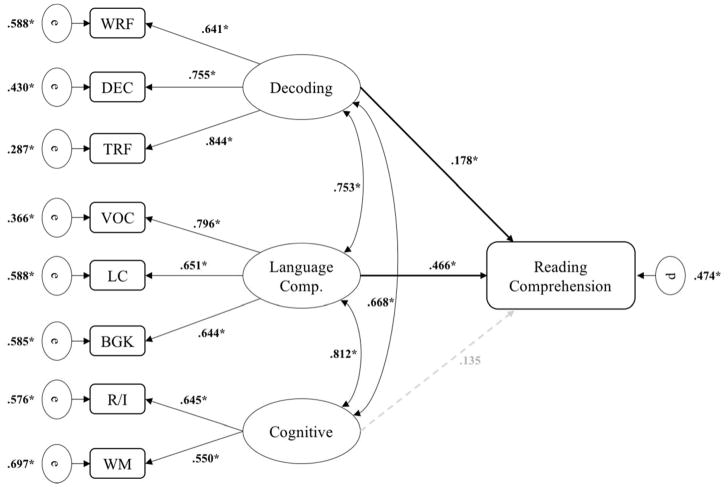
The three-factor expanded SVR provided an excellent fit to the data, (χ2 (22) = 53.8364, p < .001, CFI = 0.9951, RMSEA = 0.0015 [0.0010 – 0.0020], SRMR = 0.0451). The results of this model are presented in Figure 4. The loadings of each indicator were moderate to high (range 0.641 – 0.844). Linguistic comprehension (β= 0.466, p < .001) and decoding (β= 0.178, p < .001) accounted for significant unique variance in reading comprehension. For every 1 standard deviation increase in linguistic comprehension and in decoding, RC increases by 0.466 and 0.178 standard deviation units, respectfully. The linguistic comprehension factor accounted for a significantly larger portion of variance in RC than decoding. After accounting for decoding and linguistic comprehension, the cognitive component was not a unique predictor of reading comprehension (β= 0.135, p = .130). The three-factor model accounted for 52.6% of the variance in reading comprehension for the older sample.
Figure 4.
Meta-SEM path diagram of Model 2 for the older sample. *p < .001. Dashed, grey pathways are not significant. WM = working memory; R/I = reasoning and inference; BGK = background knowledge; WRF = word reading fluency; DEC = decoding accuracy; TRF = text reading fluency; VOC = vocabulary knowledge; LC = listening comprehension. e = residual variance error terms, d = disturbance term.
Discussion
The present study used a relatively new and advanced meta-analytic SEM approach to analyze correlation matrices from 155 studies with over 1 million students. The two-stage modeling approach supported a three-factor model that accounted for 57% of the variance in RC in the full sample. This estimate is similar to other relevant accounts of the SVR (e.g., Hoover & Gough, 1990). Once decoding and linguistic comprehension were accounted for, a cognitive factor made of reasoning and inference and working memory was a separable, but non-significant predictor of additional variance in RC. The factor structure was different across development: For the younger sample of students, the original specifications of the SVR were supported, whereby a two-factor model (decoding and linguistic comprehension) was the best fit to the data and accounted for 60% of the variance in RC. For the older students, the three-factor solution with a separate cognitive factor accounted for approximately 53% of the variance in RC. That we accounted for 50–60% of the variance in reading comprehension is impressive in itself: the portion of variance unaccounted for included error and measurement variance due to differences in samples, measures, and missing constructs.
Our expansion of the SVR was based on similar models of reading comprehension that include separate variables for background knowledge, working memory, and reasoning and inference (e.g., Cain, 2009; Cain et al., 2004; Cromley & Azvedo, 2007; Kintsch, 1988; Perfetti, 1985). However, the SVR argues that constructs not specifically relevant for word reading are subsumed under the linguistic comprehension factor. Background knowledge is argued to be a separate predictor important for reading comprehension (e.g., Cromley & Azvedo), but this construct loaded best on the factor for linguistic comprehension. While the SVR posits that constructs such as reasoning and inference and working memory should load on to the linguistic comprehension factor, we only supported this for the younger sample of students. The older sample supported a full three-factor model with a cognitive factor separate from the linguistic comprehension factor. We did not include all of the necessary additional components to compare our models properly to these other relevant models of reading comprehension, so our interpretations are limited in scope to the original specifications of the Simple View of Reading (Gough & Tunmer, 1986; Hoover & Gough, 1990).
Strengths of the MASEM Approach
There are multiple strengths and benefits for researchers who use SEM or meta-analytic approaches and want to incorporate a method that uses both in to their statistical toolbox.
Multivariate Approach
MASEM can be applied in a univariate or multivariate framework. However, the multivariate approach allows a researcher to analyze more than one effect size per study, presenting an increase of information that can be retained from a single study and incorporated in to a large meta-analysis. Similar to the models we fit, researchers can analyze data from correlation matrices across studies to test their theoretical model that provides an estimate of heterogeneity due to differences in measures, samples, and settings. Further, it is possible that researchers from the primary studies to be included in the analyses are interested in different construct relations. This can present as a missing data issue, whereby Study A may be interested in X related to Y, Study B is interested in Z related to Y, and Study C is interested in the inter-relations between X, Y, and Z. Multivariate applications allow for missing correlations to be handled in the missing at random (MAR) framework, so that the models can be fit using maximum likelihood estimation methods (Cheung, 2015b; Enders, 2010). In doing so, researchers do not have to only include studies that measure all variables (Study C) and instead can include all studies that include any of the variables (Studies A, B, and C).
Model robustness
We were in a unique position to attempt a test of robustness for our models given the large number of studies and large number of subjects. We randomly selected half (107) of the total number of matrices (220) for these tests; however, there was an issue of coverage for background knowledge across the included matrices, much like what was seen when we split the matrices according to age. Cheung (2015b) has reported that a minimum of four values are needed in each cell to properly estimate the value and its confidence interval. We decided to run the robustness tests on the remaining constructs; the results of these models are highly similar to those found in the overall model and separate models for age. These tests of robustness are further discussed in the online supplemental materials (B).
Limitations of the MASEM Approach
The limitations of the MASEM approach can apply to any researchers who use this method regardless of topic or field. We state limitations specific to our results below and explain how these limitations may affect researchers of any background.
Range restriction
We included studies from only the past 26 years. This reduces the amount of studies that would meet criteria had studies been accepted from years prior to 1990. The MASEM approach has the ability to include continuous and categorical moderators. Future applications of this method should consider publication year or a range of publication years as a moderator to test for historical differences in populations, settings, and measures.
Dichotomization
We dichotomized age to produce a matrix for children who were below age 11 and for children who were aged 11 and older. Dichotomizing continuous variables has been criticized (e.g., MacCallum, Zhang, Preacher, & Rucker, 2002; Maxwell & Delaney, 2004), as it produces a loss of effect size and power, loss of information regarding individual differences, and loss of measurement reliability. However, most of these criticisms are directed at dichotomizing scales that are normally distributed (e.g., using cut-points on a continuous scale of ability or skill). The solution in this study is justified in that there are reasons to believe children younger children will have different patterns of predictor importance than older children. However, we could not directly compare the model for the younger cohort to the model for the older cohort due to inability to analyze the same covariance structure in the models.
Reader ability status
We coded reader ability status for all studies but we were not able to include it as a moderator in the meta-SEM analyses. This limited our ability to investigate whether the parameter estimates and model structure were different across separable groups of impairment, which represents an important distinction. An additional study on the differences between these groups is warranted and necessary. Future applications of this method may encounter this same issue, and researchers should be aware of this limitation when considering subgroup analyses.
Coding of listening comprehension measures
We accounted for a smaller amount of variance (41%) in the construct of listening comprehension at the study level than we anticipated. One hypothesis is that the listening comprehension variable was coded to include tasks that measured students’ oral grammatical and syntactical skills in addition to tasks measuring their understanding of oral language. As a result, this construct was heterogeneous across studies. Researchers should exercise caution when coding for broad concepts, and carefully consider the ways in which primary studies measure their constructs of interest.
Reliability of measurement
One final limitation was that the reliability of the measures was not controlled for at the individual study level. Decoding, linguistic comprehension, and cognitive abilities were privileged in the final model, since these variables had their reliability accounted for through the estimation of latent variables. Reading comprehension was a single-criterion variable, even though every study included a measure of RC. Researchers should consider multiple indicators of constructs to create latent variables free of measurement error, or consider correcting for study-level reliability where feasible.
Despite its limitations, but given the likeliness that a researcher will encounter these limitations, the results still provide researchers the basic tools needed to not only conduct their own MASEMs but to understand and consider the methodological constraints and complexities.
Implications for Education Research
We were unable to test for potential indirect effects from the cognitive component to RC through either of the SVR components due to the usage of correlational data. However, previous research has suggested that improvements in reading fluency can reduce the demands on working memory, indirectly improving reading comprehension by reducing cognitive load (Swanson & O’Connor, 2009). Further, two of the linguistic comprehension components (vocabulary knowledge, background knowledge) have previously been indirectly linked to reading comprehension through inferencing skills (Ahmed et al., 2016; Cromley & Azvedo, 2007). Although a direct pathway was not supported, and an indirect pathway could not be estimated, there were large correlations between the cognitive component and decoding and linguistic comprehension. Additionally, text reading fluency fully mediates the relation between word reading and reading comprehension, and partially mediates the relation between listening comprehension and reading comprehension (e.g., Kim & Wagner, 2015). Further testing is needed to determine if there are constructs involved in indirect pathways that could benefit from targeted instruction and intervention. The usage of MASEM techniques with longitudinal data may be better suited for determining indirect and direct pathways in the development of reading comprehension skills.
Concluding Remarks: The Utility of MASEMs
The MASEM results were estimated from the first multivariate, large-scale meta-analysis to be conducted on individual differences in reading comprehension. The MASEM approach provided a composite correlation matrix of the included variables and fit multiple models to the data that supported both the original and expanded versions of the SVR. This promising two-stage statistical approach can benefit researchers of any field, but is particularly beneficial for the education sciences, where curricula, measures, and samples can vary extremely between studies. The two-stage approach to combining correlation matrices across multiple studies and considering the covariances between correlations provides a unique way to account for stochastic dependence and heterogeneity that has previously been ignored or underutilized.
Supplementary Material
Acknowledgments
Support for this research was provided by the Eunice Kennedy Shriver National Institute of Child Health and Human Development (Grants P50 HD052120; P50 HD052117-07). The content is solely the responsibility of the authors and does not necessarily represent the official views of the Eunice Kennedy Shriver National Institute of Child Health and Human Development, the National Institutes of Health, or the U.S. Department of Education.
Contributor Information
Jamie M. Quinn, The Meadows Center for Preventing Educational Risk
Richard K. Wagner, Florida State University
References
A list of the references included in the meta-analysis are presented in Supplemental Materials A.
- Adams M. Beginning to read: Thinking and learning about print. Cambridge, MA: M.I.T. Press; 1990. [Google Scholar]
- *.Ahmed Y, Francis DJ, York M, Fletcher JM, Barnes M, Kulesz P. Validation of the direct and inferential mediation (DIME) model of reading comprehension in grades 7 through 12. Contemporary Educational Psychology. 2016;44:68–82. doi: 10.1016/j.cedpsych.2016.02.002. [DOI] [Google Scholar]
- Anderson RC, Freebody P. Vocabulary knowledge. In: Guthrie JT, editor. Comprehension and teaching: Research reviews. Newark, DE: International Reading Association; 1981. pp. 77–117. [Google Scholar]
- Araújo S, Reis A, Petersson KM, Faísca L. Rapid automatized naming and reading performance: A meta-analysis. Journal of Educational Psychology. 2015;107:868–883. doi: 10.1037/edu0000006. [DOI] [Google Scholar]
- Baddeley A. Working memory. Science. 1992;255:556–559. doi: 10.1126/science.1736359. [DOI] [PubMed] [Google Scholar]
- Baddeley A, Eysenck MW, Anderson M. Memory. New York, NY: Psychology Press; 2009. [Google Scholar]
- Baddeley AD, Hitch GJ. Working memory. In: Bower GA, editor. The Psychology of Learning and Motivation: Advances in Research and Theory. New York, NY: Academic Press; 1974. pp. 47–89. [Google Scholar]
- Becker BJ. Multivariate meta-analysis. In: Tinsley HEA, Brown SD, editors. Handbook of applied multivariate statistics and mathematical modeling. San Diego: Academic Press; 2000. pp. 499–525. [Google Scholar]
- Becker BJ. Model-based meta-analysis. In: Cooper H, Hedges LV, Valentine J, editors. The Handbook of Research Synthesis and Meta-Analysis. 2. The Russell Sage Foundation; New York: 2009. pp. 377–394. [Google Scholar]
- Becker BJ, Schram CM. Examining explanatory models through research synthesis. In: Cooper H, Hedges LV, editors. The handbook of research synthesis. New York: Russell Sage Foundation; 1994. pp. 357–381. [Google Scholar]
- Cain K. Making sense of text: Skills that support text comprehension and its development. Perspectives on Language and Literacy. 2009;35:11–14. [Google Scholar]
- Cain K, Oakhill J. Profiles of children with specific reading comprehension difficulties. British Journal of Educational Psychology. 2006;76:683–696. doi: 10.1348/000709905X67610. [DOI] [PubMed] [Google Scholar]
- *.Cain K, Oakhill J, Bryant P. Children’s reading comprehension ability: Concurrent prediction by working memory, verbal ability, and component skills. Journal of Educational Psychology. 2004;96:31–42. doi: 10.1037/0022-0663.96.1.31. [DOI] [Google Scholar]
- Cheung MWL. metaSEM: an R package for meta-analysis using structural equation modeling. Frontiers in Psychology. 2015a;5:1521. doi: 10.3389/fpsyg.2014.01521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung MW-L. Meta-Analysis: A Structural Equation Modeling Approach. West Sussex, UK: John Wiley & Sons; 2015b. [Google Scholar]
- Cheung MWL, Chan W. Meta-analytic structural equation modeling: a two-stage approach. Psychological Methods. 2005;10:40–64. doi: 10.1037/1082-989X.10.1.40. [DOI] [PubMed] [Google Scholar]
- Chiappe P, Chiappe DL, Gottardo A. Vocabulary, context, and speech perception among good and poor readers. Educational Psychology. 2004;24:825–843. doi: 10.1080/0144341042000271755. [DOI] [Google Scholar]
- *.Cromley JG, Azevedo R. Testing and refining the direct and inferential mediation model of reading comprehension. Journal of Educational Psychology. 2007;99:311–325. doi: 10.1037/0022-0663.99.2.311. [DOI] [Google Scholar]
- Dole JA, Valencia SW, Greer EA, Wardrop JL. Effects of two types of prereading instruction on the comprehension of narrative and expository text. Reading Research Quarterly. 1991;26:142–159. doi: 10.2307/747979. [DOI] [Google Scholar]
- Elleman AM, Lindo EJ, Morphy P, Compton DL. The impact of vocabulary instruction on passage level comprehension of school age children: A meta-analysis. Journal of Research on Educational Effectiveness. 2009;2:1–44. doi: 10.1080/19345740802539200. [DOI] [Google Scholar]
- Enders CK. Applied missing data analysis. Guilford Press; New York: 2010. [Google Scholar]
- Evans JE, Floyd RG, McGrew KS, Leforgee MH. The relations between measures of Cattell–Horn–Carroll (CHC) cognitive abilities and reading achievement during childhood and adolescence. School Psychology Review. 2001;31:246–262. [Google Scholar]
- Florit E, Cain K. The simple view of reading: Is it valid for different types of alphabetic orthographies? Educational Psychology Review. 2011;23:553–576. doi: 10.1007/s10648-011-9175-6. [DOI] [Google Scholar]
- Florit E, Roch M, Levorato MC. The relationship between listening comprehension of text and sentences in preschoolers: Specific or mediated by lower- and higher-level components? Applied Psycholinguistics. 2013;34:395–415. doi: 10.1017/S0142716411000749. [DOI] [Google Scholar]
- Florit E, Roch M, Levorato C. Listening text comprehension in preschoolers: A longitudinal study on the role of semantic components. Reading and Writing: An Interdisciplinary Journal. 2014;27:793–817. doi: 10.1007/s11145-013-9464-1. [DOI] [Google Scholar]
- García JR, Cain K. Decoding and reading comprehension: A meta-analysis to identify which reader and assessment characteristics influence the strength of the relationship in English. Review of Educational Research. 2014;84:74–111. doi: 10.3102/0034654313499616. [DOI] [Google Scholar]
- Glass GV. Primary, secondary, and meta-analysis of research. Educational Researcher. 1976;5(10):3–8. doi: 10.3102/0013189x005010003. [DOI] [Google Scholar]
- Gough PB, Tunmer WE. Decoding, reading, and reading disability. Remedial and Special Education. 1986;7:6–10. doi: 10.1177/074193258600700104. [DOI] [Google Scholar]
- Graham S, Santangelo T. Does spelling instruction make students better spellers, readers, and writers? A meta-analytic review. Reading and Writing. 2014;27:1703–1743. doi: 10.1007/s11145-014-9517-0. [DOI] [Google Scholar]
- Hoover WA, Gough PB. The simple view of reading. Reading and Writing. 1990;2:127–160. doi: 10.1007/BF00401799. [DOI] [Google Scholar]
- Jeon EH, Yamashita J. L2 Reading comprehension and its correlates: A meta-analysis. Language Learning. 2014;64:160–212. doi: 10.1111/lang.12034. [DOI] [Google Scholar]
- Kendeou P, Bohn-Gettler C, White MJ, Van Den Broek P. Children’s inference generation across different media. Journal of Research in Reading. 2008;31:259–272. doi: 10.1111/j.1467-9817.2008.00370.x. [DOI] [Google Scholar]
- Kim YS. Language and cognitive predictors of text comprehension: Evidence from multivariate analysis. Child Development. 2015;86:128–144. doi: 10.1111/cdev.12293. [DOI] [PubMed] [Google Scholar]
- Kim YSG, Wagner RK. Text (oral) reading fluency as a construct in reading development: An investigation of its mediating role for children from grades 1 to 4. Scientific Studies of Reading. 2015;19:224–242. doi: 10.1080/10888438.2015.1007375. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kintsch W. The role of knowledge in discourse comprehension: A construction-integration model. Psychological Review. 1988;95:163. doi: 10.1037/0033-295X.95.2.163. [DOI] [PubMed] [Google Scholar]
- LaBerge D, Samuels SJ. Toward a theory of automatic information processing in reading. Cognitive Psychology. 1974;6:293–323. doi: 10.1016/0010-0285(74)90015-2. [DOI] [Google Scholar]
- Lee SH, Tsai SF. Experimental intervention research on students with specific poor comprehension: a systematic review of treatment outcomes. Reading and Writing. 2017;30(4):917–943. doi: 10.1007/s11145-016-9697-x. [DOI] [Google Scholar]
- MacCallum RC, Zhang S, Preacher KJ, Rucker DD. On the practice of dichotomization of quantitative variables. Psychological Methods. 2002;7:19–40. doi: 10.1037/1082-989X.7.1.19. [DOI] [PubMed] [Google Scholar]
- Maxwell SE, Delaney HD. Designing experiments and analyzing data: A model comparison perspective. 2. Mahwah, NJ: Erlbaum; 2004. [Google Scholar]
- Metsala JL, Walley AC. Spoken vocabulary growth and the segmental restructuring of lexical representations: Precursors to phonemic awareness and early reading ability. In: Metsala JL, Ehri LC, editors. Word Recognition in Beginning Literacy. Mahwah, NJ: Erlbaum; 1998. pp. 89–120. [Google Scholar]
- National Institute of Child Health and Human Development (NICHD) Report of the National Reading Panel. Teaching children to read: An evidence-based assessment of the scientific research literature on reading and its implications for reading instruction. Washington, DC: U.S. Government Printing Office; 2000. (NIH Publication No. 00-4769) [Google Scholar]
- National Center for Education Statistics. The Nation’s Report Card: A First Look: 2013 Mathematics and Reading. Institute of Education Sciences, U.S. Department of Education; Washington, D.C: 2013. (NCES 2014-451) [Google Scholar]
- Oakhill JV, Cain K. The precursors of reading ability in young readers: Evidence from a four-year longitudinal study. Scientific Studies of Reading. 2012;16:91–121. doi: 10.1080/10888438.2010.529219. [DOI] [Google Scholar]
- Oakhill J, Hartt J, Samols D. Levels of comprehension monitoring and working memory in good and poor comprehenders. Reading and Writing. 2005;18:657–686. doi: 10.1007/s11145-005-3355-z. [DOI] [Google Scholar]
- *.Ouellette GP. What’s meaning got to do with it: The role of vocabulary in word reading and reading comprehension. Journal of Educational Psychology. 2006;98:554. doi: 10.1037/0022-0663.98.3.554. [DOI] [Google Scholar]
- Pammer K, Kevan A. The contribution of visual sensitivity, phonological processing, and nonverbal IQ to children’s reading. Scientific Studies of Reading. 2007;11:33–53. doi: 10.1080/10888430709336633. [DOI] [Google Scholar]
- Perfetti CA. Reading ability. New York, NY: Oxford University Press; 1985. [Google Scholar]
- Seigneuric A, Ehrlich MF. Contribution of working memory capacity to children’s reading comprehension: A longitudinal investigation. Reading and Writing. 2005;18:617–656. doi: 10.1007/s11145-005-2038-0. [DOI] [Google Scholar]
- Spires HA, Donley J. Prior knowledge activation: Inducing engagement with informational texts. Journal of Educational Psychology. 1998;90:249–260. https://doi.org10.1037/0022-0663.90.2.249. [Google Scholar]
- Swanson HL, Berninger V. The role of working memory in skilled and less skilled readers’ comprehension. Intelligence. 1995;21:83–108. doi: 10.1016/0160-2896(95)90040-3. [DOI] [Google Scholar]
- Swanson HL, O’Connor R. The role of working memory and fluency practice on the reading comprehension of students who are dysfluent readers. Journal of Learning Disabilities. 2009;42:548–575. doi: 10.1177/0022219409338742. [DOI] [PubMed] [Google Scholar]
- Tompkins V, Guo Y, Justice LM. Inference generation, story comprehension, and language skills in the preschool years. Reading and Writing. 2013;26:403–429. doi: 10.1007/s11145-012-9374-7. [DOI] [Google Scholar]
- Tunmer WE, Chapman JW. The simple view of reading redux: Vocabulary knowledge and the independent components hypothesis. Journal of Learning Disabilities. 2012;45:453–466. doi: 10.1177/0022219411432685. [DOI] [PubMed] [Google Scholar]
- Viswesvaran C, Ones DS. Theory testing: combining psychometric meta-analysis and structural equations modeling. Personnel Psychology. 1995;48:865–885. doi: 10.1111/j.1744-6570.1995.tb01784.x. [DOI] [Google Scholar]
- Wanzek J, Wexler J, Vaughn S, Ciullo S. Reading interventions for struggling readers in the upper elementary grades: A synthesis of 20 years of research. Reading and Writing. 2010;23:889–912. doi: 10.1007/s11145-009-9179-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yuill NM, Oakhill JV. Understanding of anaphoric relations in skilled and less skilled comprehenders. British Journal of Psychology. 1988;79:173–186. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.