Evaluation of methods for detecting recombination from DNA sequences: Computer simulations

Abstract

Recombination is a key evolutionary process that shapes the architecture of genomes and the genetic structure of populations. Although many statistical methods are available for the detection of recombination from DNA sequences, their absolute and relative performance is still unknown. Here we evaluated the performance of 14 different recombination detection algorithms. We used the coalescent with recombination to simulate DNA sequences with different levels of recombination, genetic diversity, and rate variation among sites. Recombination detection methods were applied to these data sets, and whether they detected or not recombination was recorded. Different recombination methods showed distinct performance depending on the amount of recombination, genetic diversity, and rate variation among sites. The model of nucleotide substitution under which the data were generated did not seem to have a significant effect. Most methods increase power with more sequence divergence. In general, recombination detection methods seem to capture the presence of recombination, but they are not very powerful. Methods that use substitution patterns or incompatibility among sites were more powerful than methods based on phylogenetic incongruence. Most methods do not seem to infer more false positives than expected by chance. Especially depending on the amount of diversity in the data, different methods could be used to attain maximum power while minimizing false positives. Results shown here will provide some guidance in the selection of the most appropriate method/s for the analysis of the particular data at hand.

Recombination, defined here as the exchange of genetic information between two nucleotide sequences, is an important process that influences biological evolution at many different levels. Recombination explains a considerable amount of genetic diversity in natural populations and, in general, genes located in regions of the genome with low levels of recombination have low levels of polymorphism. Recombination reshuffles existing variation and even creates new variants at the amino acid level. Indeed, recombination shapes the genetic structure of natural populations (1, 2) and the action of natural selection (3). Characterization of the role of recombination across genomes is of major interest. The study of recombination events will allow us to better understand the dynamics of genomes (4, 5). Recombination breaks down linkage disequilibrium and, consequently, the characterization of recombination is essential for gene mapping, quantitative trait loci, and association studies (6). In addition, recombination has a significant impact on the evolution of several human pathogens (7–9) and consequently on their clinical treatment and prevention. Moreover, many applications in biology today are based on the estimation of phylogenetic trees. One main assumption of most phylogenetic methods is that there is only one phylogeny underlying the evolution of the sequences under study. Recombination violates this assumption by generating mosaic genes, where different regions have different phylogenetic histories. By ignoring the presence of recombination, phylogenetic analysis may be severely compromised (10–13).

For all these reasons, the accurate detection of recombination from DNA sequences becomes very relevant, and indeed a number of methods have been developed for that purpose (D. L. Robertson, http://grinch.zoo.ox.ac.uk/RAP_links.html). Surprisingly, only a few studies have attempted to examine the relative performance of these methods (14–17). Although useful, these studies have been limited in the number of methods compared and the set of conditions evaluated. In practice, researchers are unable to make an objective selection of the most suitable method to detect recombination in their data. Here we perform a comprehensive analysis of 14 different methods for detecting recombination to determine relative performance and associated conditions of performance. We simulated DNA sequences with different rates of recombination, diversity, and rate heterogeneity to investigate the statistical power and the rate of false positives of the 14 different recombination detection algorithms.

Methods

A glossary of terms is described in Table 1. To study the statistical power (1—rate of Type II error, or the probability of rejecting the null hypothesis—no recombination—when it is false) and the rate of false positives (Type I error, or the probability of rejecting the null hypothesis when it is true) of the methods evaluated, two sets of simulations were carried out. In the first set (Simulations I, power analysis; Table 2), an increasing recombination rate was simulated for different levels of variation. In the second set (Simulations II, false positives; Table 3), increasing rate variation among sites was simulated for different levels of variation and without recombination. This design allows us to examine the confounding effect of rate variation with recombination (10). For each set of conditions, 100 replicates were simulated. The range of parameter values used in the simulations is commonly observed in real data sets. Software to perform these simulations is available on request. The general simulation strategy was:

Table 1.

Glossary of terms

Symbol	Meaning
s	Number of replicates
k	Number of sequences at a given generation
n	Sample size
l	Sequence length
N	Effective population size
μ	Mutation rate per site per generation
θ	= 4Nμl = Population mutation parameter (per gene)
p	Average pairwise sequence divergence
r	Recombination rate per site per generation
ρ	= 4Nrl = Population recombination parameter (per gene)
R(n)	Expected number of recombination events
G	Number of potential locations for recombination to occur
κ	Transition/transversion rate
π	Base frequencies
α	Shape of gamma distribution
Γ	Gamma distribution
JC	Jukes–Cantor 1969 (49)
K80	Kimura-2-parameters (50)
F81	Felsenstein 1981 (51)
HKY	Hasegawa–Kishino–Yano 1985 (52)
x	Power to detect recombination

Table 2.

Parameter values in Simulations I (power analysis)

s	n	l	N	μ	θ	r	ρ	R(n)	Model	α*
100	10	1,000	1,000	0.25  × 10−5	10	0	0	0.00	JC	∝
				1.25  × 10−5	50	0.25  × 10−6	1	2.83	K80
				2.5  × 10−5	100	1  × 10−6	4	11.32	F81
				5  × 10−5	200	4  × 10−6	16	45.26	HKY
						16  × 10−6	64	181.05

^*α indicates the strength of rate variation among sites. When α = ∝, there is no rate variation among sites. The smaller the α the stronger the rate variation (53). 

Table 3.

Parameter values used in Simulations II (false positive analysis)

s	n	l	N	μ	θ	r	ρ	R(n)	Model	α
100	10	1,000	1,000	0.25  × 10−5	10	0	0	0	JC	∝
				1.25  × 10−5	50	0	0	0	K80	2.00
				2.5  × 10−5	100	0	0	0	F81	0.50
				5  × 10−5	200	0	0	0	HKY	0.05
						0	0	0

(i) Simulate recombinant genealogies by using the coalescent with recombination.

(ii) Evolve nucleotide sequences on the simulated genealogy to obtain a sequence alignment.

(iii) Apply 14 different methods to the simulated data and record how many times, of 100 replicates, a method infers the presence of recombination.

The Coalescent with Recombination.

Multiple genealogies for samples of n = 10 sequences were simulated under the coalescent with recombination (18–26). In the recombination model implemented here, there are n sequences with l sites, and the population consists of N diploid individuals. A continuous time approximation is used, and the time is scaled in units of 2N generations. The recombination rate (ρ) is defined as ρ = 4Nrl, where r is the rate of recombination per site per generation.

The coalescent is built backwards in time. It is constructed by waiting for recombination or coalescent events until all ancestral sites in the n sequences have found a most recent common ancestor (not necessarily the same ancestor for all sites). The waiting times to a coalescent event are exponentially distributed with mean k(k − 1)/2 (k is the number of sequences at a given generation). The waiting times to a recombination event are also exponentially distributed, but with mean 2NrG. G is the number of potential locations where recombination can happen (20). This quantity is a number between 0 and (l − 1)k, and it depends on the outcome of the previous events. G can be written as:

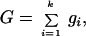1

where g_i is the number of ways a sequence can be a recombinant descendant of two sequences both ancestral to the sample. As an example, the values of g_i associated with the 4-tuples (a sequence with four sites) (1, 0, 0, 1) (1, 0, 1, 0), (1, 1, 0, 0), and (1, 0, 0, 0) are 3, 2, 1, and 0, respectively (20) (where 1 denotes that a site is ancestral and 0 that it is nonancestral). A site between two segments of ancestral material is called “trapped site;” in the tuple (1, 0, 1, 0), the first 0 is trapped, whereas the second is not (21).

Because coalescent and recombination events are independent, the time to one of these events happening is exponentially distributed with mean k(k − 1)/2 + 2NrG. The probabilities that a given event is either a coalescence or a recombination are:

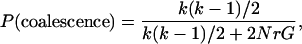2

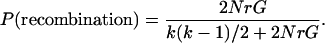3

Simulation of a single realization of this process is performed by starting with k = n sequences at time 0, and determining when the first event (coalescence or recombination) happens by drawing a random number u from the uniform distribution:

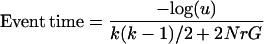4

A decision is made whether this event is a coalescence or a recombination based in their relative probabilities, and then the number of sequences k is updated. If the event is a coalescence, two sequences are chosen uniformly, and their material is coalesced. The number of sequences decreases by one (k = k − 1). In the case of a recombination event, one sequence is chosen at random by assigning probabilities to the sequences based on their relative g_i values. A recombination breakpoint is then chosen uniformly over the ancestral material and the nonancestral material that is trapped between two blocks of ancestral material. When a recombination event happens, the number of sequences increases by one (k = k + 1). After each event, the value of G is updated [initially, G = (l − 1)k]. The process is continued until each site in the extant sequences has found a most recent common ancestor (MRCA). With recombination, different parts of the alignment are likely to have different coalescent trees and different times to the MRCA.

The number of recombinational events in the history of a sample of size n, R(n), has the expectation

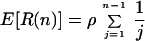5

(19). Not all recombination events, R(n) in total, are detectable. Regarding their effect on the genealogy, there are three types of recombination events: events that do not change the branch lengths, events that do change the branch lengths but do not change the topology, and events that change the topology. Wiuf et al. (15) provide the expectations for these three types of events.

Sequence Evolution.

Sequences were evolved on the simulated (potentially) recombinant genealogies. Several models of nucleotide substitution were used (Table 4) to study the effect of base frequency and transition/transversion ratio on the detection of recombination. Different mutation rates were used to obtain alignments with different levels of divergence (Tables 2 and 3). The expected average pairwise sequence divergence (p) depends on the parameters of the model of nucleotide substitution. A rough approximation for models with no rate variation would be

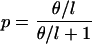6

where θ = 4Nμl, and μ is the mutation rate per site per generation. For example, a value of θ = 100 would indicate that a randomly chosen pair of sequences is expected to differ in 0.1/(1 + 0.1)≈9% of their sites (given that sequence length, l = 1,000).

Table 4.

Models of evolution and parameter values used in the simulations

Model	πA	πC	πT	πG	κ
JC	0.25	0.25	0.25	0.25	0.5
K80	0.25	0.25	0.25	0.25	2.0
F81	0.40	0.20	0.10	0.30	0.5
HKY	0.40	0.20	0.10	0.30	2.0

Performance Evaluation.

The recombination detection algorithms were applied to the simulated data sets, and the number of times a method inferred the presence of recombination of the 100 replicates was recorded. This number approximates the probability of detecting recombination for each method and therefore is a convenient indicator of performance. Although some methods provide a qualitative answer for the presence of recombination (yes or no), most methods calculate a P value. In the later case, recombination was inferred when the provided P value was smaller than 0.05.

Methods for Detecting Recombination.

We evaluated 14 methods for the detection of recombination (Table 5). A detailed description of these methods is published as supporting information on the PNAS web site, www.pnas.org. In general, we can tentatively classify these methods as:

Table 5.

Methods for detecting recombination evaluated for performance

Method		Implementation	Reference	Category
1	Bootscanning	simplot	33, 44	Phylogenetic
2	Geneconv	geneconv	37	Substitution
3	Homoplasy Test	homoplasy test*	42	Substitution
4	Informative Sites Test	pist	43	Substitution
5	Maximum χ2	maxchi*	41	Substitution
6	Maximum mismatch χ2	chimaera*	D.P., unpublished work	Substitution
7	Phylogenetic Profiles	phypro*	27	Distance
8	Partial Likelihood	plato	30	Phylogenetic
9	Rdp	rdp	32	Phylogenetic
10	Recombination Parsimony	recpars	28	Phylogenetic
11	Reticulate	reticulate	34	Compatibility
12	Runs Test	runs test*	40	Substitution
13	Sneath Test	sneath test*	38	Substitution
14	Triple	triple*	48	Phylogenetic

^*Local program written in c. 

(i) Distance Methods.

Distance methods look for inversions of distance patterns among the sequences (27). In general, they use a sliding window approach and the estimation of some statistic based on genetic distances among the sequences. Because the phylogeny does not need to be known, these are normally fast methods.

(ii) Phylogenetic Methods.

Several methods infer recombination when phylogenies from different parts of the genome result in discordant topologies or when orthologous genes from different species are clustered. When comparisons of adjacent sequences yield different branching patterns, there is reason to suspect the involvement of recombinational events. If the consequence of such changes results in reconciling different sequence phylogenies to a single phylogeny, then the existence of such events becomes a reasonable hypothesis (28–33). These are the methods most extensively used in the literature.

(iii) Compatibility Methods.

Compatibility methods test for partition phylogenetic incongruence in a site-by-site basis and do not require the phylogeny of the sequences analyzed to be known (34, 35).

(iv) Substitution Distribution.

Nucleotide substitution distribution methods examine the sequences for a significant clustering of substitutions or fit to an expected statistical distribution (S. A. Sawyer, http://www.math.wustl.edu/∼sawyer/geneconv/index.html; refs. 36–43).

Implementation of Methods for Detecting Recombination.

Unless otherwise noted, the number of permutations was 1,000, and the family significance level used was 0.05. Permuted alignments were obtained by randomizing the position of the columns in the alignment.

The windows program simplot (33) was generously modified by Stuart Ray (simplot's author) to implement the bootscanning (44) of every sequence in the alignment against the rest. We used a sliding window size of 200 base pairs and a step size of 10 nucleotides. Neighbor-joining trees were estimated by using F84 distances (45, 46), and bootstrap values were obtained from 100 replicates. Several bootstrapping thresholds for assignment of parenthood were explored (70, 90, and 95%), but only the 95% threshold provided reasonable false positive rates. To implement the method of Sawyer (http://www.math.wustl.edu/∼sawyer), we used a modified version of geneconv 1.81. The global permutation P values based on blast-like global scores, obtained from 10,000 replicates smaller than 0.05, were considered evidence of recombination. A multiple comparison correction is already built into these P values, so there was no need for further correction. The parameter gscale, which scales the mismatch penalty, was set to 0. To implement the homoplasy test (42), two qbasic programs written by Maynard Smith were translated into a single c program, which was benchmarked against the original implementation. Because an outgroup was not used, and to be conservative, the number of effective sites, Se, was taken to be 0.6 × the total number of sites.

The program pist (A. Rambaut and M. Worobey, http://evolve.zoo.ox.ac.uk/) was modified for simulations to implement the informative sites test (43). pist takes as input and alignment a tree and the parameter values of a model of evolution. For each data set, a maximum likelihood (ML) tree was estimated under the Hasegawa–Kinshino–Yano (HKY) + Γ model. At the same time, we obtained ML estimates of the parameters in the HKY + Γ model (π, κ, and α). The trees and model parameter estimates for each data set were used in the pist analysis. For the parametric simulation of the null distribution of the statistic (see supporting information, www.pnas.org), 100 replicates were used. A computer program was written in c implementing a modification of Maynard Smith's maximum χ² method (15, 41) by using only variable sites. The statistic is the maximum χ² in the original alignment. The P value equals the number of times the original statistic is smaller than the statistic from permuted alignments divided by the number of permutations. For all calculations, a sliding window was used, with the width of the windows set to the number of polymorphic sites divided by 1.5. This window moved in steps of one nucleotide at a time. A previous implementation calculated the P values by calculating the value of the statistic in the permuted data sets exactly at the same position (breakpoint and sequences) where the original maximum was found. This strategy resulted in many false positives and was discarded. The computer program chimaera was written in c, implementing the maximum mismatch χ² method (D.P., unpublished work) (see supporting information). The rest of the implementation is the same as in the maximum χ² method. A computer program was written in c implementing an extension of the Phylogenetic Profiles (phypro) method (27), which in its original form does not provide statistical significance. Only variable sites were used. The statistic is the minimum distance vector correlation in the original alignment. The rest of the implementation was the same as in the maximum χ² and chimaera methods.

The program plato (30) was also modified for simulations. For each data set, a maximum likelihood tree was estimated, with parameter estimates then obtained under the Hasegawa–Kinshino–Yano + Γ model of evolution. Those values were used in the calculation of the likelihoods in plato. A null distribution was simulated by 100 Monte Carlo replicates. The default window settings were used (minimum size, 5; step, 1). The windows program rdp (32) was generously modified by Darren Martin for the simulations. After exploring different conditions, the best settings were using internal and external reference sequences and a window size of 10 nucleotides. Turning off the multiple significance correction improved performance. The c program recpars (K. Fisker, ftp://ftp.daimi.aau.dk/pub/empl/kfisker/programs/RecPars) was modified for the simulations to implement the recombination parsimony method (28, 29). A recombination cost of three times the maximum substitution cost (d = 3 × s) was found to perform the best with the statistic below. The substitution costs were the true values of the parameters of the model. The statistic used was the number of histories recovered. If more than one history was recovered, recombination was inferred.

The c program reticulate (34) was modified for the simulations. The statistic used was the neighbor similarity score. A c program was written implementing the runs test (40). The program was benchmarked against results in Takahata's paper (40). Sneath's method (38, 47) implemented in qbasic was translated into c and benchmarked against the original implementation. Because P values are calculated for each pairwise comparison, P values were Bonferroni-corrected. To evaluate Stephens' method (36), an improved implementation written in fortran by Mary Kuhner (48) was translated into c and benchmarked against the original implementation. Because many tests are made, the Bonferroni correction was applied with a family α level of 0.01 (a 0.05 level gave an excess of false positives).

Results

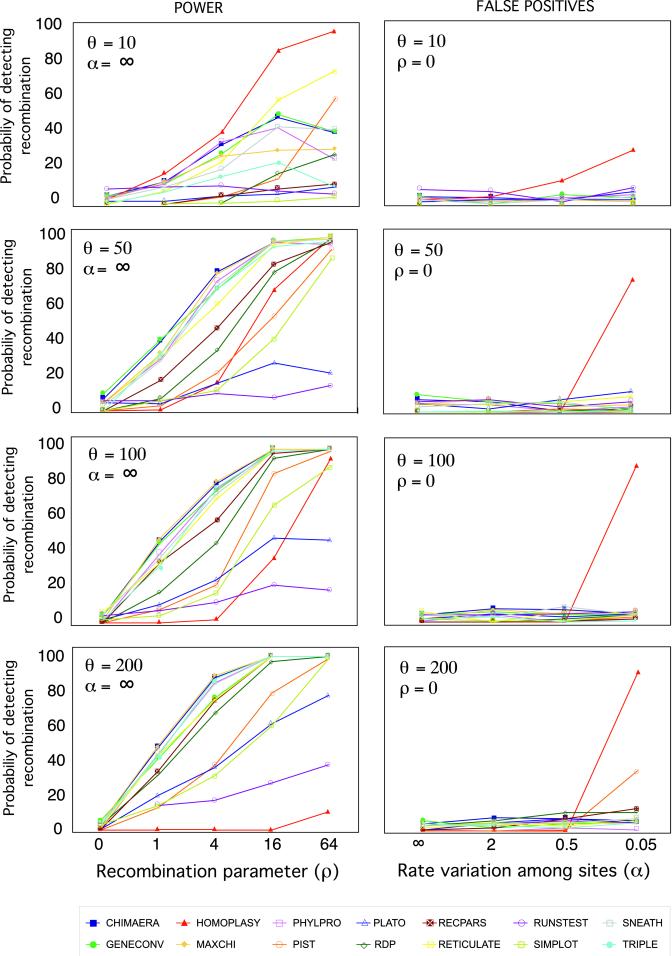
Different methods for detecting recombination showed very distinct performance in different conditions (Fig. 1).

Figure 1.

Power (Left) and rate of false positives (Right) corresponding to 14 recombination detection algorithms. The probability of detecting recombination is plotted against increasing levels of recombination (ρ) and nucleotide diversity (θ). Sequences were evolved under the Hasegawa–Kinshino–Yano model of evolution.

Power.

At very low divergence (θ = 10), the homoplasy test seems to be the more powerful method, attaining 80 and 100% detection levels when ρ equals 16 and 64, respectively. reticulate follows with 49 and 88% detection, respectively. pist attained 73% power only when ρ equals 64. Substitution methods like chimaera, maxchi, and geneconv show similar power compared with the methods above at low recombination levels, but do not increase detection even with increasing amounts of recombination after ρ = 16. These substitution methods (chimaera, maxchi, and geneconv) and phlypro were the most powerful in detecting recombination, followed by reticulate. Phylogenetic methods performed the worst. Some of them increased their overall power (rdp, recpars, triple) with increasing amounts of recombination (but the power was always lower relative to the substitution methods), whereas others detected recombination only when it was frequent (plato, bootscanning). At medium levels of divergence (θ = 100), power slightly increased for all methods, especially for low recombination rates, except for the homoplasy test, which detected recombination only when it was extremely frequent. At a high level of divergence (θ = 200), power again increased for low levels of recombination, except for the homoplasy test.

False Positives.

Most methods showed false positive rates around the expectation of 5%. However, the homoplasy test inferred recombination (30–86%), with extreme levels of rate variation (α = 0.05). At high levels of divergence, methods like pist and, to a lesser extent, recpars, rdp, and triple, also inferred recombination 11–49% of the time when rate variation was extreme. This false positive rate trend with high rate variation was more evident with increasing levels of divergence.

Models of Nucleotide Substitution.

The model of substitution used in the simulations did not have significant impact on the power of the different recombination detection methods (see supporting information on the PNAS web site). However, it seems that more complex models slightly increased the power and rate of false positives for some methods.

Discussion

Most methods showed more power with increased rates of recombination, which is the expected behavior for efficient methods. However, some methods are more efficient than others. Most methods showed better performance at higher levels of divergence, probably because in such cases there is more information available to recognize the footprint of recombination. The only method that showed decreased power with more sequence divergence was the homoplasy ratio. For most methods, a minimum sequence divergence of 5% seems necessary to attain substantial power. When the number of recombination events in the history of the sequences is around 3 (ρ = 1), the most powerful methods inferred the presence of recombination only 50% of the time, which indicates that several recombination events are needed in order for these methods to detect recombination. However, it should be kept in mind that around 10% of the data sets simulated under ρ = 1 contain no recombination events. For the most powerful methods to detect recombination around 80% of the time, 12 recombination events (ρ = 4) are needed.

In this simulation, methods based on the patterns of substitutions and in-site compatibility worked better than phylogenetic methods, a result also obtained by Brown et al. (16) and Wiuf et al. (15) in their comparison of four recombination detection methods. Simple implementations of methods like chimaera or maxchi, based on summary statistics, performed the best. Indeed, phylogenetic methods can detect only recombination events that change the topology (see supporting information on the PNAS web site), although at high recombination rates, there should be plenty of such events.

To maximize the chances of detecting recombination when it is present and to avoid, at the same time, the inference of recombination when it is absent, it will be useful to estimate the amount of divergence and rate heterogeneity in the data. Given those estimates and the performance graphs shown here, the most suitable methods for detecting recombination for the data at hand might be readily selected. For example, if variation is around 1%, the homoplasy test could be the method of choice, as long as there is not much rate variation. Indeed, this method was intended to work at low levels of divergence (42). For the more divergent data sets (5–20%), methods like chimaera, maxchi, phypro, reticulate, and geneconv are more powerful and do not infer false positives in excess.

The power of different methods for detecting recombination is not superb, but recombination is not an easy problem. Several methods seem to often capture the presence of recombination but detect far less recombination than possible, a fact also pointed out by Wiuf et al. (15). Fortunately, recombination methods do not seem to infer many false positives. Here we study only the different methods from a qualitative point of view. Of course, the problem of recombination is much more complex than that, and includes the identification of parentals and recombinant individuals (sequences) and the localization of the recombinational breakpoint/s. Indeed, in many cases it is important not only to detect the presence of recombination but also to measure its frequency (17).

There are two different contexts in which we may wish to detect recombination: rare recombination or frequent repeated recombination (17). In this study, we have tackled both problems by simulating data over a wide range of recombination rate values. Not surprisingly, most methods have trouble detecting rare recombinational events, especially when sequence divergence is low. Indeed, recent events should be more easily identifiable than older events, as the later may be obscured by subsequent mutation. On the other hand, when recombination rates are very high (higher than those simulated here), leading to situations close to linkage equilibrium, substitution methods might have trouble identifying site patterns (17).

Current recombination methods do not seem to make use of the information contained in the substitution pattern in the data (i.e., model of evolution). Nevertheless, this information could be used to better distinguish between those homoplasies produced by recombination and those produced by mutation.

Our results are based on computer simulations, which are simplifications of the problem. However, analysis of real data (D.P., unpublished work) seems to confirm and validate the conclusions obtained here. It should be noted that we used a limited number of replicates (100) to explore a reasonable parameter space within a practical computing time. The 95% confidence limits for the estimate of power, x, are given by x ± 1.96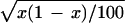. This confidence interval will be largest when x = 0.5, being ≈0.402–0.598, implying that the power of some methods would not be statistically distinguishable in some situations (see Fig. 1).

Indeed, the accurate inference of recombination is a key to understanding the role of the different molecular evolutionary processes and the architecture of genes and genomes. Hopefully, the results shown here will provide some guidance in the selection of the most appropriate method/s for analysis of the particular data at hand.