A personalized approach of the patient-healthcare provider communication regarding the colorectal cancer screening options

Abstract

Background

Current colorectal cancer screening guidelines by the US Preventive Services Task Force endorse multiple options for average risk patients and recommend that screening choices should be guided by individual patient preferences. Implementing these recommendations in practice is challenging because they depend on accurate and efficient elicitation and assessment of preferences from patients who are facing a novel task.

Objective

To present a methodology for analyzing the sensitivity and stability of a patient’s preferences regarding colorectal cancer screening options, and to provide a starting point for a personalized discussion between the patient and the healthcare provider about the selection of the appropriate screening option.

Methods

This research is a secondary analysis of patient preference data collected as part of a previous study. We propose new measures of preference sensitivity and stability that can be used to determine if additional information provided would result in a change to the initially most preferred colorectal cancer screening option.

Results

Illustrative results of applying the methodology to the preferences of two patients, of different ages, are provided. The results show that different combinations of screening options are viable for each patient and that the healthcare provider should emphasize on different information during the medical decision-making process.

Conclusion

Sensitivity and stability analysis can supply healthcare providers with key topics to focus on when communicating with a patient, and the degree of emphasis to place on each of them to accomplish specific goals. The insights provided by the analysis can be used by healthcare providers to approach the communication with patients in a more personalized way, by taking into consideration patients’ preferences before adding their own expertise to the discussion.

INTRODUCTION

Colorectal cancer is one of the leading causes of mortality among cancer patients in the United States.¹ It is also one of the most preventable forms of cancer. The current US Preventive Service Task Force guidelines recommend routine screening for patients 50 to 75 years old who are categorized as having an average risk.² The guidelines also recommend that the choice of screening method should be made using a shared decision-making process, which implies significant input from patients regarding their preferences with respect to the available screening options. A better understanding of the patient’s preferences would facilitate a more personalized discussion between the patient and the healthcare provider.

Current research supports an inference that clinicians frequently override patients’ preferences regarding the preferred screening test, indicating that the communication process between the patient and the healthcare provider should be improved.^3,4 An insufficient understanding of patients’ preferences by their healthcare providers might be the reason for suboptimal communication. Another reason might be that the provider does not have sufficient time to both discover the patient’s preferences and to fully discuss key topics related to those preferences.

But how can the desired level of personalized communication be achieved during the medical decision-making process? Dolan and his team conducted an extended pilot study⁵, created to help patients make the best medical decision regarding colorectal cancer screening using an Analytic Hierarchy Process-based model. The Analytic Hierarchy Process (AHP) is about breaking a problem down into its constituent parts and then aggregating the solutions of all the sub-problems created. It facilitates decision-making by organizing perceptions, feelings, judgments, and memories into a framework that exhibits the forces that influence a decision. The AHP methodology is based on the innate human ability to make sound judgments about problems structured like a hierarchy built to represent the influences involved. The proposed model includes four main criteria, one of which has three sub-criteria, to ascertain patients’ preferences among ten screening alternatives. In his initial results, Dolan et al. concluded that the AHP model improved the patients’ decision-making process, but he could not find any statistical evidence of the effect of the model on the implementation of the decision obtained.⁵ In their later studies, they emphasized even more the usefulness of the AHP-based model in identifying the preferences of individual patients and the necessity of including patients’ preferences in the medical decision-making process.⁶

The novelty of our research is the in-depth analysis of the patients’ preferences using the new sensitivity and stability analysis developed for AHP models. This methodology is taking the elicited preferences and analyzes the different alternatives rankings as changes are applied to the importance assigned to the criteria weights. Using the preferences assessment model proposed by Dolan et al., the methodology we developed aspires to close the gap in the communication between the patient and healthcare provider by exploring the evolution of the patient’s preferences as additional information is provided⁷. The process takes advantage of the initial elicitation of preferences, rather than requiring additional data collection, and it analyzes how sensitive and stable the patient preferences are when possible perturbations are applied to the information acquired by the patient. The purpose of the analysis is to facilitate an efficient discussion that accommodates both the patient’s preferences and the clinician's expertise.

METHODS

Data collection

At the time of the original study, colorectal cancer screening guidelines recommended ten alternative options, invasive, non-invasive, or both, for patients who are classified as having an average risk for colorectal cancer (Table 1)⁸.

Table 1.

Screening options for colorectal cancer

Screening options
Annual fecal occult blood test with sensitivity 20%	A1	Non-invasive
Annual fecal occult blood test with sensitivity 40%	A2	Non-invasive
Flexible sigmoidoscopy every 5 years	A3	Invasive
Fecal DNA test every 5 years	A4	Non-invasive
Annual immunochemical fecal occult blood test	A5	Non-invasive
Annual fecal occult blood test and flexible sigmoidoscopy every 5 years	A6	Both
CT colonography	A7	Non-invasive
Double contrast barium enema	A8	Invasive
Annual immunochemical fecal occult blood test and flexible sigmoidoscopy every 5 years	A9	Both
Colonoscopy every 10 years	A10	Invasive

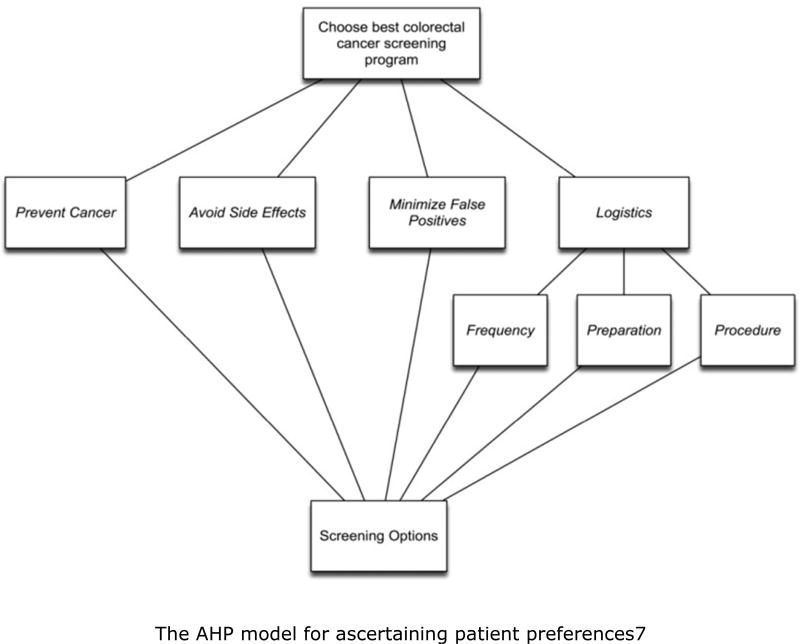
In their initial study, Dolan et al. proposed an Analytic Hierarchy Process (AHP)–based model (see Figure 1) to ascertain patients’ preferences among the alternatives in Table 1⁵.

Figure 1.

The AHP model for ascertaining patient preferences.<7> Avoid Side Effects – Screening procedure possible side effects Frequency – How often the screening procedure needs to be performed Minimize False Positives – Screening procedure level of a false alarm Preparation – Length of time and what steps are needed to prepare for the screening procedure Prevent Cancer – Screening procedure level of accuracy in detecting cancer Procedure – Level of complexity and invasiveness of the screening procedure

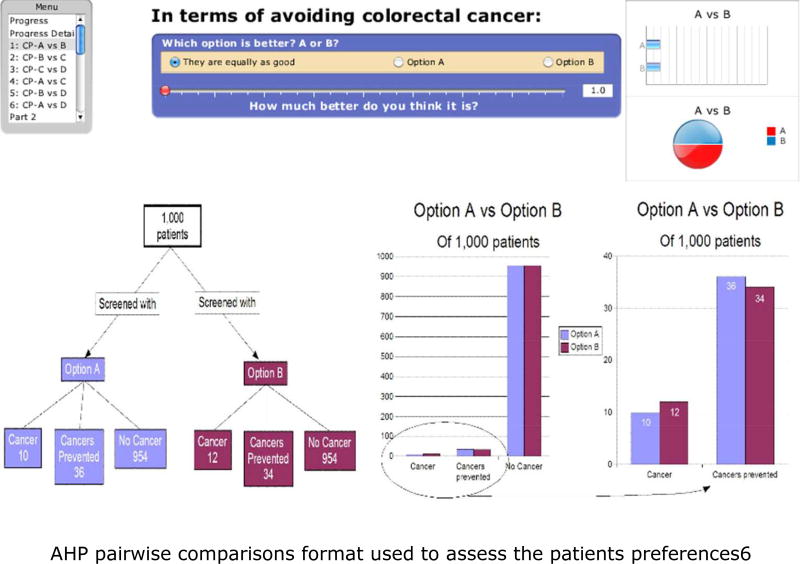
First, participants were presented with generic descriptions of the six criteria used in the model and of the ten colorectal cancer screening options available as alternatives. All participants were able to use the standard AHP pairwise comparison method to compare the screening options, and to judge the relative priorities of the criteria involved in the decision⁹. This was done using an interactive computer program created for the project to perform the pairwise comparisons. A research assistant was present to give the participants a brief introduction to the procedure and provide help assistance completing it if required. An example comparison is shown in Figure 2.

Figure 2.

AHP pairwise comparisons format used to assess the patients preferences.<6>

Data were collected from 484 patients from primary healthcare practices in Rochester, NY, Birmingham, AL, and Indianapolis, IN. Because the selection of a screening alternative should be a decision made by the patient and the healthcare provider jointly, we illustrate the applicability of our methodology by analyzing the sensitivity and the stability of the initial selection of single patients. The results of the analysis provide information to the healthcare provider about the patient’s preferences over the set of screening alternatives and the ways those preferences might change if the patient is presented with additional information about the criteria used to discriminate among the alternatives. For example, if the patient is older, the healthcare provider can emphasize the risks associated with undergoing an invasive procedure like colonoscopy. Based on this additional information, the patient could change the importance (weight) assign to the criterion Procedure complexity (C6). If large enough, this change will consequently alter the initial ranking of the preferred screening options.

Analytic Hierarchy Process (AHP) - model assumptions

The Analytic Hierarchy Process (AHP) methodology is structuring the decision-making process as shown in the following diagram:

The process described above was applied to elicit Patient A’s preferences and it is presented in Appendix 1.

Sensitivity and stability methodology for AHP models

Most of the multi-criteria decision-making methods, including AHP/ANP, lack in-depth sensitivity and stability analysis of the results. Whenever a sensitivity analysis is performed, it focuses on a single change at a time. Our methodology extends the sensitivity analysis of AHP/ANP models by enabling simultaneous changes in the inputs for a better understanding of the evolution of the results over time, with the ultimate purpose of choosing the most appropriate/stable alternative to be implemented. The methodology is developed for the n-dimensional case¹³ (n changes made simultaneously), but, for the purpose of illustrating its implications for a challenging medical decision-making problem, only the two-dimensional case is presented.

In the next diagram we synthetized the steps of the methodology we developed to accommodate the two criteria application:

Measures of sensitivity and stability

To analyze and interpret the changes that happen at the level of preferences when additional information regarding the six criteria used in the model is brought to the patient, we developed a set of measures. The measures quantify: (1) the sensitivity of the patient’s initial preference, with respect to a given colorectal cancer screening option, when additional information is provided; (2) the stability of the initially most preferred screening option, in terms of implementing it as the best screening option; and (3) the stabilities of competitive screening options.

The study of our measures begins with the most preferred screening alternative in the initial study, that is, the screening option that was ranked first, based on the elicitation of patient’s preferences using the model described in Figure 1; let’s denote that alternative as Alternative F. The core stability measure identifies all possible combinations of criteria weights for which the patient will continue to rank Alternative F first, despite the additional information given to him/her. Core stability is specific only to Alternative F. The combinations of criteria weights associated with core stability are the ones that describe the largest sphere around the point characterized by the initial set of criteria weights.

The direction of change in stability defines the shortest way in which a switch in the preferences between two screening alternatives can result from a change in the importance of the criteria weights (e.g., an increase in importance for one criterion and decrease in importance for the second criterion). The perturbations applied to the initial criteria weights are equivalent to the different levels of additional information provided to the patient. For example, if additional information provides more emphasis on the complexity of the screening procedure and the risks associated given the patient advanced age, the patient may decide to change the relative importance he/she assign to these two criteria. The perturbation stability defines the minimum changes necessary to be made to the criteria weights that will result in a switch in preferences.

The solution stability measure is defined for all the screening alternatives that are ranked first in the patient’s preferences, as different changes are applied to the criteria. Solution stability identifies all the possible combinations of criteria weights for which a certain screening alternative is ranked first, and for which it remains ranked first as changes in the criteria weights happen. Mathematically, the measure is described by the volume of the preference region of a screening alternative. The preference region of an alternative is the set of all possible combinations of criteria weights for which a given alternative always remains the most preferred one. The initially most preferred screening option is the only alternative characterized by both core stability and solution stability.

The mathematical definitions of the sensitivity and stability measures are provided in Appendix 2. Numerical examples of all these concepts are given in Appendix 3.

Patients’ characteristics

Custom-tailoring a sensitivity and stability analysis for an individual patient is appropriate if the goal is to personalize the medical decision-making process, by increasing the patient’s level of involvement. We consider, in detail, two patients, with different demographic characteristics, to illustrate the differences and similarities that a sensitivity and stability analysis of preferences can provide.

Consider a 70-year-old male patient from the Midwest (Patient A), and an 80-year-old female patient from the Southeast (Patient B). For both patients, we used the model depicted in Figure 1 to ascertain their preferences among the ten colorectal cancer screening alternatives. The importance given to each of the six criteria by the two patients is shown in Table 2.

Table 2.

Importance of the criteria for the two patients

	Patient A		Patient B
Ranking	Criteria	Criteria weights	Criteria	Criteria weights
1	Prevent Cancer (C1)	0.6890	Prevent Cancer (C1)	0.5810
2	Avoid Side Effects (C2)	0.2060	Minimize False Positives (C3)	0.2480
3	Minimize False Positives (C3)	0.0770	Avoid Side Effects (C2)	0.1130
4	Procedure Preparation (C5)	0.0220	Procedure Complexity (C6)	0.0379
5	Procedure Complexity (C6)	0.0054	Procedure Frequency (C4)	0.0145
6	Procedure Frequency (C4)	0.0015	Procedure Preparation (C5)	0.0056

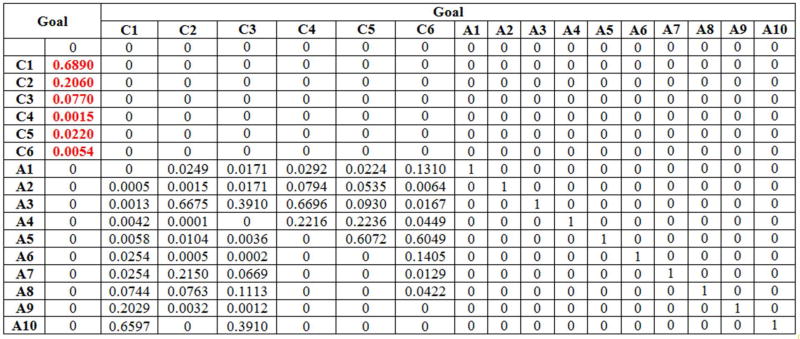
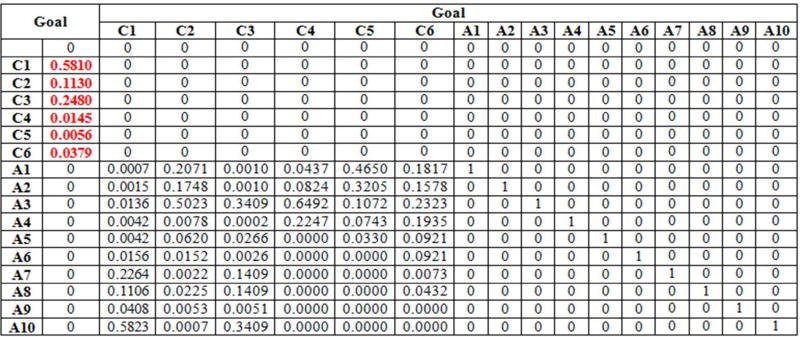
Both Patient A’s judgments and Patient B’s judgments, with respect to the six criteria (Table 2) and to the ten screening alternatives, are summarized in the supermatrices presented in Appendix 1, Table 10 and Table 11. These matrices are known as supermatrices because they are matrices whose entries are in turn matrices. Thus, the supermatrix structure consists of blocks as follows:

Each entry in the supermatrix is matrix of priorities. The structure shown above is the supermatrix corresponding to a hierarchy, where I is the identity matrix (see, e.g., Table 10 in Appendix 1)

The supermatrix is the mathematical representation of all the priorities generated by the model depicted in Figure 1. The synthesis of the patient preferences regarding the ten-available colorectal cancer screening options are obtained by raising the supermatrix to powers. Based on the preliminary information synthesized in the supermatrix, the corresponding limiting priorities are generated for both patients and they are given in Table 4. The priorities represent the ranking of the ten screening options based on the patient preferences.

Table 4.

Priorities and ranking of the ten screening alternatives for Patient A and Patient B

		Patient A		Patient B
Alternative		Ranking	Priority	Ranking	Priority
Annual fecal occult blood test with sensitivity 20%	A1	9	0.0077	5	0.0342
Annual fecal occult blood test with sensitivity 40%	A2	10	0.0033	6	0.0299
Flexible sigmoidoscopy every 5 years	A3	2	0.1715	2	0.1681
Fecal DNA test every 5 years	A4	8	0.0084	10	0.0144
Annual immunochemical fecal occult blood test	A5	6	0.0230	8	0.0197
Annual fecal occult blood test and flexible sigmoidoscopy every 5 years	A6	7	0.0184	9	0.0149
CT colonography	A7	5	0.0669	3	0.1670
Double contrast barium enema	A8	4	0.0757	4	0.1034
Annual immunochemical fecal occult blood test and flexible sigmoidoscopy every 5 years	A9	3	0.1404	7	0.0256
Colonoscopy every 10 years	A10	1	0.4842	1	0.4229

RESULTS

Single patient sensitivity and stability analysis for pairs of criteria

Eliciting the patient’s preferences with respect to the set of screening alternatives available it is not enough for a complete analysis of what should be the most appropriate screening option to be implemented. The new sensitivity and stability analysis developed for the AHP models can provide the necessary in-depth analysis for models with an arbitrary number of criteria. For simplicity, we consider only the simultaneous perturbations of two criteria in this paper.

According to the priorities in Table 4, the alternative initially most preferred by both patients is Colonoscopy every 10 years (A10). But the two most important criteria for each of the two patients differ. For Patient A, they are Prevent Cancer (C1) and Avoid Side Effects (C2). For Patient B, they are Prevent Cancer (C1) and Minimize False Positives (C3).

So, both the healthcare provider and the patient are interested in determining:

1. Is the initially most preferred screening alternative also the most stable one?

   The stability of an alternative, in this context, is a function of the set of conditions, that is, the combinations of criteria weights, for which the initially most preferred screening alternative remains the one most preferred by the patient. The results of the stability analysis may help guide the patient and the healthcare provider towards implementing the most appropriate screening option for the patient, taking into consideration all the possible changes that might occur.

2. Which pairs of criteria are the most/least sensitive to changes in the information provided to the patient?

To answer those two questions, we considered all 15 pairs of criteria that result from the six criteria associated with the model presented in Figure 1. We perturbed simultaneously both criteria in the pair, using a perturbation increment chosen to provide “enough” sampling data for the sensitivity and stability analysis to return relatively precise results. Using the results of the perturbations, we calculated: (a) the volume of each preference region present in the perturbation space; and (b) the volume of the core stability sphere around the origin. In addition, we identified the sets of perturbations that would lead to a change in preference away from A10.

Comparing the sensitivity and stability analysis of two patients

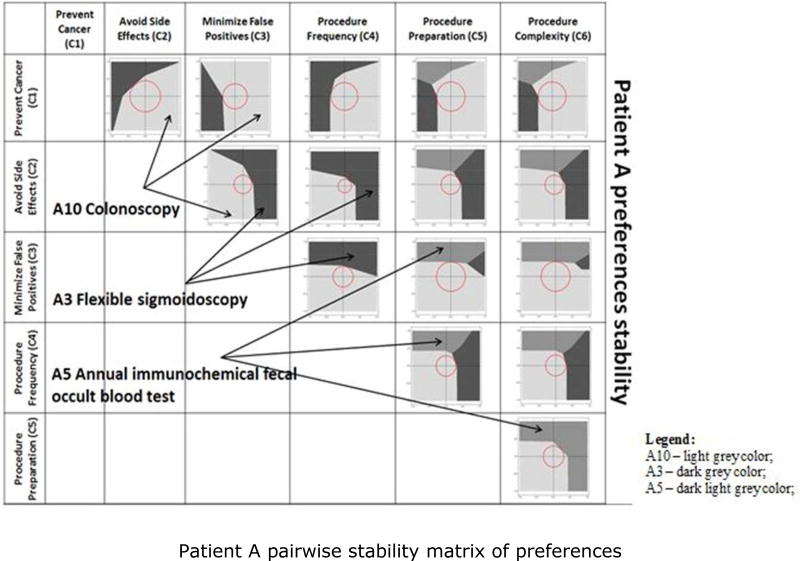
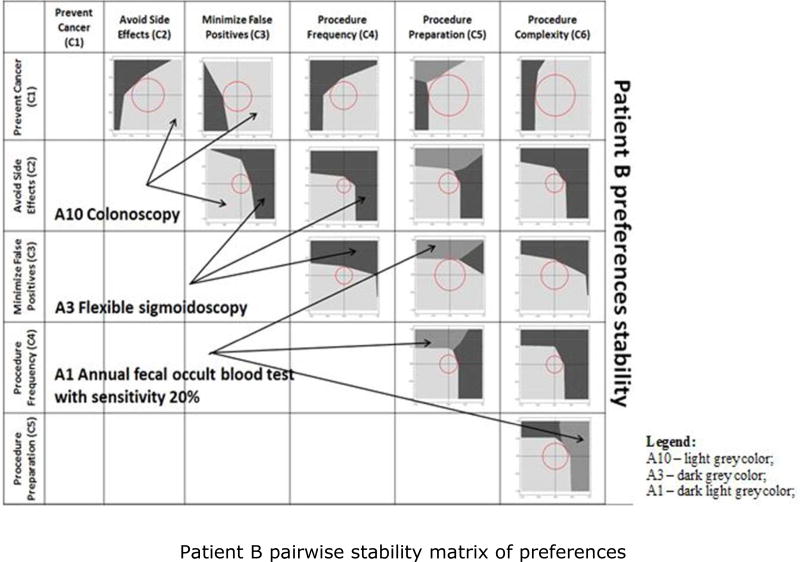
In this section, we illustrate how our sensitivity and stability analyses detect differences in preference structure for different patients. We compare the sensitivity and stability analyses of Patients A and B, focusing on the elements that might be the basis for different discussions between the patient and the healthcare provider. Figures 5 and 6 graphically depict which alternatives dominate within the perturbation space, as perturbations are applied to each of the 15 pairs of criteria. A pairwise stability matrix of preferences was defined for each of the two patients, for Patient A in Figure 6 and for Patient B in Figure 6, to display the preference regions and core stability spheres. The numerical results associated with the two figures are presented in Appendix 3, Tables 12 and 13.

Figure 5.

Patient A pairwise stability matrix of preferences. A3 – dark grey color; A5 – dark light grey color; A10 – light grey color.

Figure 6.

Patient B pairwise stability matrix of preferences. A1 – dark light grey color; A3 – dark grey color; A10 – light grey color.

Consider the first representation from Figure 5, its enlarged version depicted in Figure 7, and the numerical results presented in Appendix 3, Table 12. We first selected the pair of criteria that are perturbed simultaneously – Prevent Cancer (C1) and Avoid Side Effects (C2). We then identified the resulting preference regions for all alternatives that are most preferred across all perturbations of the two selected criteria. The axes in Figure 7, represent the proportional change toward the lower bound of 0 (for a negative perturbation) or toward the upper bound of 1 (for a positive perturbation) for a range from −1 to +1. For perturbations of C1 and C2, only Flexible Sigmoidoscopy every 5 years (A3) and Colonoscopy every 10 years (A10) would be selected. We approximated the areas of the two associated regions as a percentage of the total perturbation space.

Figure 7.

Perturbation space for Patient A's pair of criteria C1–C2.

Next, we estimated the volume of the core stability sphere and its relative volume with respect to the preference region of the initial most preferred alternative, A10. The center of the perturbation space for C1–C2 represents the initially most preferred screening option based on the patient’s preferences elicitation; it is the point where no changes have been applied. To determine the direction of the shortest-length vector that results in a switch in the most preferred alternative, i.e., from A10 to A3, we identified the associated perturbation pair. We also determined what would be the “new” most preferred alternative, A3, based on the minimum change necessary in the criteria weights, as given by the perturbation pair. A more detailed numerical example following the same notions is presented in Appendix 3.

The similarities and differences between Patients A and B are summarized in Table 5. For the two patients analyzed, only three out of the ten screening alternatives ever dominate in any of the perturbation spaces: A3, A5, and A10 for Patient A, and A1, A3, and A10 for Patient B. Note that A3 and A10 are invasive procedures; A1 and A5 are non-invasive.

Table 5.

Similarities and differences between Patients A and B

Similarities		Patient A	Patient B
	Most stable alternative	A10	A10
	Initially most preferred option (A10) is least stable with respect to the pair of criteria	C2 & C4	C2 & C4
	Perturbing the most stable pair leads to a switch from A10 to	A3	A3
Differences
	Most important criteria	C1 & C2	C1 & C3
	Potentially dominating alternatives	A3, A5, A10	A1, A3, A10
	Initially most preferred option (A10) is most stable with respect to the pair of criteria	C1 & C2	C1 & C5
	Perturbing the most stable pair leads to a switch from A10 to	A3	A1
	Patient will switch to a non-invasive procedure under perturbations of the pairs	C3–C5, C3–C6, or C5–C6	C1–C5, C3–C5, or C5–C6

Given that for both patients, only three out of the ten screening alternatives ever dominate in the perturbation space, the solution stability is approximated by the volume of the preference regions. Those regions represent all possible combinations of criteria weights for which a given screening alternative will remain the most preferred one, independent on the changes applied to the criteria. For Patient A, for all pairs of criteria, the volume of the solution stability region is greater for A10, between 42% and 75% of the perturbation space. The solution stability regions for A3 and A5 cover between 3% and 57% of the space and between 15% and 51%, respectively. That suggests that as the importance of the criteria is changed, A10 might be the most stable solution to be implemented on the long run. The results are similar for Patient B. A10 covers between 42% and 77% of the perturbation space, A1 between 14% and 33% and A3 between 8% and 57%. We are also interested in how the patients’ preferences for the most preferred screening alternative, A10, change or remain unchanged as the criterion weights varies. For both patients, the initially most preferred alternative is pairwise most stable with respect to all pairs of criteria, because the solution stability regions for A10 have greater volumes than do the stability regions of other dominating alternatives. That means that A10 is the most stable alternative among all sets of alternatives, because it is the most stable screening alternative with respect to the other screening options for both patients.

Core stability is the process of identifying all possible combinations of criteria weights, based on the initial patient preferences, that will maintain the initially preferred alternative, A10, as the most preferred screening alternative. Changes in criteria weights may be the result of additional information the patient receives about the criteria (e.g. medical statistics or possible risks associated with the procedures given his age group), which will lead him to adjust their importance.

For both patients, alternative A10 is the initially most preferred screening option. For Patient A, A10 is most stable with respect to the pair of criteria Prevent Cancer (C1) and Avoid Side Effects (C2), the combination of criteria that determines the largest core stability sphere. For Patient B, the most preferred alternative A10 is most stable with respect to the pair of criteria C1 and Procedure Preparation (C5). The greatest stability of the initially most preferred screening alternative A10 is achieved under different conditions for the two patients. Even though both patients consider the criterion C1 to be very important, the second criterion from the pair determining the highest stability is different. For Patient A, it is C2, and, for Patient B, it is C5. Age may be a differentiator. Patient A is younger, and may be more concerned with avoiding the possible side effects. Patient B may be more concerned with the complexity of the preparation for the procedure. At the other extreme, the most preferred screening alternative A10 is least stable with respect to the pair of criteria Avoid Side Effects (C2) and Procedure Frequency (C4) for both patients, because that combination of criteria generates the smallest core stability sphere. The implication is that, for both patients, the initially most preferred screening alternative A10 is more sensitive with respect to the pair of criteria C2–C4. Perturbing that pair results in the fastest change in patients’ preferences. The differences in core stability are determined by the variations in the criteria weights for the two patients (Table 2). Patient A gives a greater weight to criteria C1 and C2. Patient B considers the criteria C1 and C3 to be more important.

The core stability sphere provides information about the direction of change in stability, and about the perturbation stability, given by the magnitude of the minimum perturbation in the importance of the criteria necessary to bring about the change in the patient’s preference.

Consider the situation in which the initially most preferred screening option for Patient A is also the most stable one for the pair of criteria C1–C2. The vector of minimum perturbations associated with that pair of criteria results in a change from A10 to A3. The direction of change in stability indicates that the change in preferences occurs when a decrease in the importance of C1 is combined with an increase in the importance of C2. The perturbation stability indicates that the magnitude of the perturbations needs to be such that the two criteria end up being almost equal in importance. Initially, criterion C1 had the greatest importance. For Patient B, the initially most preferred screening alternative A10 is most stable with respect to the pair of criteria C1 and C5. Following the perturbation vector associated with C1–C5 brings about a change in preference from A10 to A1. The direction of change in stability shows that the switch in preferences happens if the importance of C1 decreases while the importance of C5 increases. The perturbation stability indicates that the magnitude of perturbations necessary to be applied to the two criteria weights need to be significant for C1. Its importance needs to decrease by almost a half, accompanied by a slight increase in C5.

For both patients, the initially most preferred screening option is least stable with respect to the pair of criteria C2–C4. For both patients, the unique vector of minimum perturbations is associated with a change in preferred alternative from A10 to A3. The direction of change in stability is the same for both patients. A simultaneous increase in both criteria weights of approximately equal magnitude leads to the switch in preferences.

A different change in patients’ preferences occurs when the pair of criteria analyzed contains, for Patient A, either Procedure Preparation (C5) or Procedure Complexity (C6), and for Patient B only Procedure Preparation (C5). In such a situation, Patient A is inclined to choose a non-invasive screening procedure, switching from A10 to A5, and the direction of change in stability is a function of the pair of criteria considered. For Patient A, there are three possibilities: (1) C3–C5; (2) C3–C6; and (3) C5–C6. For (1) or (2), the weight of criterion C3 requires a small positive perturbation, while either C5 or C6 needs to be increased considerably. For (3), the change in preferences occurs when both criteria are increased by almost the same amount.

Patient B switches from A10 to the non-invasive screening option A1 when perturbations occur to: (1) C1–C5; (2) C3–C5; or (3) C5–C6. The direction of change in stability is a function of the criterion with which C5 is paired. For case (1), the change in preferences occurs when C1 is significantly decreased while C5 is just slightly increased. For cases (2) or (3), the switch to A1 occurs when criterion C5 is increased considerably more than is either C3 or C6.

In conclusion, for both patients, Colonoscopy every 10 years (A10) is not only the most preferred one; it is also the most stable of the entire set of alternatives. But slight changes in a patient’s judgments could drastically change the preferred screening option. The switch in preference can be either in the direction of a less invasive screening option, e.g., Flexible Sigmoidoscopy every 5 years (A3), or towards a non-invasive screening alternative, A5 for Patient A and A1 for Patient B.

DISCUSSION

At the current stage of the methodology development, a complete elicitation and analysis of the patients’ preferences is required to understand the preferences evolution as changes in the pair of criteria are made. This might be considered a limitation, given the time necessary to both elicit the preferences and to analyze their stability.

Our on-going work is focusing on identifying the key elements that will enable the implementation of our methodology as a support system that could be used in the medical decision-making process. Currently, we are focusing on identifying the minimum number of questions that a patient needs to answer to elicit his/her preferences without overwhelming him/her in the process. To achieve this goal, we are currently in the process of performing complete sensitivity and stability analysis for all the patients available in the data sample. By performing both an individualized analysis and one at the aggregate level, we will be able to extract the common characteristics that will help simplify the elicitation process.

We are also working on developing a decision support system that will be available to both the patient and the healthcare provider. Given the limited time the healthcare provider has available during the medical encounter with the patient, implementing this approach to the clinical setting via a decision support system should be a two-step process. First, the patient will have access, in advance, to the necessary information about the colorectal cancer screening alternatives available and the six most important criteria chosen for the comparison purposes. He/she will be using the system to express its preference regarding the colorectal cancer screening options available and personally understand what he/she would prefer based on the sensitivity and stability analysis performed “behind the scenes”. Second, the healthcare provider will have access, with the patient permission, to the results of the analysis before the medical encounter to be able to take into consideration the patient’s preferences during the medical decision-making process. At this point, he/she will combine the patient’s preferences with the medical history and his/her expertise to recommend the most appropriate colorectal cancer screening to be implemented.

Our approach does not want to replace any steps of the medical process, but to enhance the information exchange between the patient and the healthcare provider to improve the medical outcome. The decision support system will be developed using an increased emphasize on data visualization.

Conclusions and implications for practice

Our analyses suggest to the healthcare provider that the two patients have both similarities and differences in preferences. Either patient prefers only three screening options. The preferred invasive screening procedures are the same, A3 and A10, but the non-invasive one is different – A5 for Patient A and A1 for Patient B. One of the factors that might determine the similarity in preferences is test accuracy - Colonoscopy every 10 years (A10) and Flexible Sigmoidoscopy every 5 years (A5) have the greatest accuracy rates. Age may also drive the difference in preferences. Medically, the Annual Immunochemical Fecal Occult Blood Test is preferred for the younger patients.

If, from a medical perspective, the healthcare provider would like to recommend A10 as the screening option to be chosen by the patients, he should highlight to Patient A how minimal are the possible side effects at his age, while, to Patient B, he should emphasize that the procedure preparation is not as complex as in the past. Alternatively, if the care provider considers that A10 is not the most appropriate screening procedures to be used, he should emphasize, to both patients, the importance of avoiding side effects at their age, and that a more frequent colorectal cancer procedure might be preferable at their age. As patients consider C2 and C4 to be more important, they are predicted to switch their preferences to A3.

The perturbation stability results mean that if it is to Patient A’s benefit to follow-up with a less invasive and more frequent alternative, such as A3, even though A10 has the greatest stability, the healthcare provider should talk with the patient about the importance of avoiding any possible side effects at his age, while assuring him that the accuracy of the test in detecting and preventing cancer is as great as the accuracy for Colonoscopy. For Patient B, if the healthcare provider places increased emphasis on the extensive procedure preparation, combined with the assurance that, at the patient’s current age, an annual non-invasive colorectal cancer screening option might be more beneficial to prevent cancer, the patient is predicted to switch her preference to A1.

The core stability analysis implies that even though the two patients have the same initially most preferred alternative, Colonoscopy every 10 years (A10), the stability of that solution differs. A primary reason for the stability differences is the differences in weights assigned to the six criteria by the two patients. Medically, these findings are important for the healthcare provider. Using the stability results, the healthcare provider can decide which pair of criteria to emphasize when discussing the possible screening options with the patient. Based on the patient’s age and medical history (which was not accessible to us during this research), the healthcare provider can “guide” the patient towards the most appropriate colorectal cancer screening option, while taking into consideration the patient’s preferences.

Clinically, the greater level of solution stability may tell the care provider that it might be easier to influence Patient A’s preferences, and to recommend either a less invasive screening option or a non-invasive one, than it would be to influence the preferences of Patient B. Age might be the differentiating factor in this situation. As patients age, they may be increasingly reluctant to change or to adjust their preferences, leading to longer discussions between the patient and the healthcare provider.

Figure 3.

AHP model steps for eliciting and synthetizing patient's preferences.

Figure 4.

The steps of the new sensitivity and stability analysis for AHP models.

Table 3.

Supermatrix structure for the AHP model

	Goal	Criteria	Alternatives
Goal	0	0	0
Criteria	Priorities of the Criteria wrt the Goal	0	0
Alternatives	0	Priorities of the Alternatives wrt the Criteria	I

Appendix 1

Eliciting Patient A’s preferences via the AHP-based model for the colorectal cancer screening problem

• Step 1: In the case of colorectal cancer screening the hierarchy consists of the Goal (Choose the best colorectal cancer screening option), Criteria as listed in Figure 1 and Alternatives as shown in Table 1.

• Step 2: The 70 year-old male patient (Patient A) provided judgments to represent his relative preferences for the criteria. The judgments are obtained by comparing the criteria in pairs as a response to the following question: Given two criteria, e.g., Prevent Cancer and Avoid Side Effects, which criterion is more important, in this decision, and by how much?

• Step 3: We are using the absolute scale 1 to 9 to represent the patient’s judgments. For example, if Prevent cancer (C1) criterion is extremely more important than Avoid side effects (C2) criterion, then we are saying that the weight of Prevent cancer should be 9 times the weight of Avoid side effects. Hence, the weight of Avoid side effects should be 1/9 the weight of Prevent cancer. Patient A provided the following judgments when comparing the criteria:

  Table 6.

  Patient A’s judgments with respect to the criteria

  Criteria comparison with respect to the Goal	Prevent cancer (C1)	Avoid side effects (C2)	Minimize false positives (C3)	Logistics	Priorities
  Prevent cancer (C1)	1	9.00	9.00	9.00	0.691
  Avoid side effects (C2)	0.1111	1	7.00	7.00	0.203
  Minimize false positives (C3)	0.1111	0.1428	1	7.00	0.077
  Logistics	0.1111	0.1428	0.1428	1	0.029

  Table 7.

  Patient A’s judgments with respect to the sub-criteria

  Comparison of Logistics’ sub-criteria	Frequency (C5)	Preparation (C6)	Procedure (C7)	Priorities	Global Priorities
  Frequency (C4)	1	0.140	0.140	0.054	0.002
  Preparation (C5)	7.00	1	8.00	0.757	0.022
  Procedure (C6)	7.00	0.125	1	0.189	0.005

• Step 4: Based on the calculations performed in Step 3 we determined the priorities of the six criteria considered in the model for Patient A as:

  Table 8.

  Patient A’s priorities for the six criteria

  		Local priorities	Global priorities
  Prevent cancer (C1)		0.691	0.691
  Avoid side effects (C2)		0.203	0.203
  Minimize false positives (C3)		0.077	0.077
  Logistics		0.029
  Frequency (C4)		0.054	0.002
  Preparation (C5)		0.757	0.022
  Procedure (C6)		0.189	0.005

  And the priorities of the alternatives under each criterion as:

  Table 9.

  Patient A’s priorities for the ten alternatives

  	C1	C2	C3	C4	C5	C6
  A1	0	0.0249	0.0171	0.0294	0.0227	0.1310
  A2	0.0009	0.0015	0.0171	0.0794	0.0535	0.0064
  A3	0.0013	0.6675	0.3910	0.6696	0.0930	0.0167
  A4	0.0042	0.0007	0	0.2216	0.2236	0.0449
  A5	0.0058	0.0104	0.0036	0	0.6072	0.6049
  A6	0.0254	0.0005	0.0008	0	0	0.1405
  A7	0.0254	0.2150	0.0669	0	0	0.0134
  A8	0.0744	0.0763	0.1113	0	0	0.0422
  A9	0.2029	0.0032	0.0012	0	0	0
  A10	0.6597	0	0.3910	0	0	0

• Step 5: The syntheses of the results obtained in Step 4 are organized in the following supermatrix:

  Table 10.

  The supermatrix for the 70 year-old male patient (Patient A)

Using the same procedure described above, we generated the supermatrix for the second patient used in the analysis:

Table 11.

The supermatrix for the 80 year-old male patient (Patient B)

Appendix 2

Measures of sensitivity and stability – mathematical definitions

Core stability tells us about the preferentiality of the initially most preferred alternative, denoted A_i, after perturbations have taken place. It is given by the maximum sphere, centered at A_i, that can be inscribed in the space of all perturbations, where the dimensionality of the perturbation space is given by the number of criteria perturbed simultaneously.

The direction of change in stability of an alternative is a direction, d, in the perturbation space, along which A_i is replaced by another alternative A_j. The perturbation stability over a set of criteria C₁, C₂, …, C_m is given by the distance from the center of the core solution stability sphere for the most preferred alternative to the closest boundary, i.e., the radius, r, of the core stability sphere. Combining the perturbation stability with the direction of change in stability, we obtain insight about the minimum change in the weights of the criteria that will make another alternative most preferred.

We determine the solution stability for all the alternatives dominating in the perturbation space, as the volume of the preference region. For the most preferred alternative, the relation between the maximum core stability sphere and the volume of the region, described as a ratio, is a measure of the level of stability of a decision.

An alternative A_i is pairwise more stable than another alternative A_j with respect to a set of criteria if the solution stability volume of A_i is larger than that of A_j. An alternative is more stable than all other alternatives with respect to a set of criteria if the alternative is pairwise more stable than all other alternatives. An alternative is the most stable alternative among a set of alternatives if it is more stable than all other alternatives with respect to a set of criteria.

The theoretical guidelines described in this Appendix can be a starting point for any sensitivity and stability analysis performed on practical multi-criteria decision-making models.

Appendix 3

Results of the sensitivity and stability analysis for the two patients

In this Appendix we present the complete sensitivity and stability analysis for the patients discussed in the paper.

Consider the first row of the Table 12. The first column of Table 12 records the pair of criteria that are simultaneously changed. For example, in the first row, criteria Prevent Cancer (C1) and Avoid Side Effects (C2) are considered. Column 2 indicates the set of alternatives that dominate for some set of values of the criteria. In the first row, alternatives Flexible Sigmoidoscopy every 5 years (A3) and Colonoscopy every 10 years (A10) dominate; Annual Immunochemical Fecal Occult Blood Test (A5) does not. The numbers in the body of the table are the volume of regions over which the alternatives dominate, and the percentage of the total volume of each dominance region. In row 1, alternative A3 has a volume of 1.2105, and dominates over 30.26% of the total volume; note that the total volume of the perturbation space is 4. Alternative A10 dominates over the remaining volume (2.7804; 69.74% of the total volume). Column 3 records the radius of the stability sphere constructed around the original solution. In row 1, the sphere has radius 0.4511. The greatest possible sphere radius is 1.0. The value for the C1–C2 combination, 0.4511, is greater than the radius for any of the other combinations in Table 12, so A10 is more stable with respect to changes in criteria C1 and C2 than it is to changes in any other pair of criteria. Column 4 indicates the volume of the core stability sphere based on the radius recorded in Column 3, and the proportion of the volume over which A10, the originally dominant alternative, dominates. For row 1, the volume of the stability sphere is π*(0.4511)² = 0.6393, which is 22.92% of the volume, 2.7894, in which A10 dominates.

Column 5 provides information about what combination of changes in the weights for the pair of criteria leads to the nearest point at which the preferred alternative changes to the alternative in Column 6. For row 1, the values (−0.304 and 0.333) indicate that a decrease in criteria C1 combined with an increase in criteria C2, of about the same magnitude, will lead to a change in dominance from A10 to A3.

Table 12.

Sensitivity and stability analysis results for Patient A

1.	2.			3.	4.	5.		6.
Criteria pair	Solution stability			Stability sphere radius*	Core stability	Direction of fastest change (perturbation stability)		New preferred alternative
	A3	A5	A10		A10	pi	pj
C1–C2	1.2105 (30.26%)	-	2.7894 (69.74%)	0.4511	0.6393 (22.92%)	−0.304	0.333	A3
C1–C3	0.9840 (24.60%)	-	3.0160 (75.40%)	0.3607	0.4087 (13.55%)	−0.360	−0.024	A3
C1–C4	1.5750 (39.38%)	-	2.4250 (60.63%)	0.3939	0.4874 (20.10%)	−0.380	0.104	A3
C1–C5	0.8210 (20.53%)	0.6112 (15.28%)	2.5676 (64.19%)	0.4173	0.5471 (21.31%)	−0.416	0.034	A3
C1–C6	0.7849 (19.62%)	0.6224 (15.56%)	2.5926 (64.82%)	0.4100	0.5281 (20.37%)	−0.410	0.006	A3
C2–C3	1.8190 (45.48%)	-	2.1809 (54.52%)	0.2649	0.2205 (10.11%)	0.232	0.128	A3
C2–C4	2.2841 (57.10%)	-	1.7158 (42.90%)	0.1980	0.1232 (7.18%)	0.122	0.156	A3
C2–C5	1.3428 (33.57%)	0.8249 (20.62%)	1.8322 (45.81%)	0.2800	0.2463 (13.44%)	0.316	−0.114	A3
C2–C6	1.2791 (31.98%)	0.8841 (22.10%)	1.8367 (45.92%)	0.2733	0.2347 (12.78%)	0.236	0.138	A3
C3–C4	1.5221 (38.05%)	-	2.4778 (61.95%)	0.2960	0.2753 (11.11%)	0.090	0.282	A3
C3–C5	0.2047 (5.12%)	1.0773 (26.93%)	2.7179 (67.95%)	0.4267	0.5720 (21.05%)	0.048	0.424	A5
C3–C6	0.1237 (3.09%)	1.1064 (27.66%)	2.7698 (69.25%)	0.4287	0.5774 (20.85%)	0.026	0.428	A5
C4–C5	1.2672 (31.68%)	0.8883 (22.21%)	1.8443 (46.11%)	0.2918	0.2675 (14.50%)	0.266	0.120	A3
C4–C6	1.2142 (30.36%)	0.9347 (23.37%)	1.8509 (46.27%)	0.3010	0.2846 (15.38%)	0.286	0.094	A3
C5–C6	-	2.0421 (51.05%)	1.9578 (48.95%)	0.3012	0.2850 (14.56%)	0.213	0.213	A5
Min	0.1237	0.6112	1.7158	0.1980	0.1232
Min (%)	3.09%	15.28%	42.90%		7.18%
Max	2.2841	2.0421	3.0160	0.4511	0.6393
Max (%)	57.10%	51.05%	75.40%		22.92%

^*Calculated from the origin (0,0) where the most preferred alternative is A10

Table 13.

Sensitivity and stability analysis results for Patient B

1.	2.			3.	4.	5.		6.
Criteria pair	Solution stability			Stability sphere radius*	Core stability	Direction of fastest change (perturbation stability)		New preferred alternative
	A1	A3	A10		A10	pi	pj
C1–C2	-	1.1502 (28.76%)	2.8497 (71.24%)	0.4765	0.7133 (25.03%)	−0.337	0.337	A3
C1–C3	-	0.9411 (23.53%)	3.0588 (76.47%)	0.4268	0.5723 (18.71%)	−0.420	−0.076	A3
C1–C4	-	1.5476 (38.69%)	2.4523 (61.31%)	0.3979	0.4974 (20.28%)	−0.266	0.296	A3
C1–C5	0.5816 (14.54%)	0.5723 (14.31%)	2.8460 (71.15%)	0.5860	1.0788 (37.91%)	−0.586	0.006	A1
C1–C6	-	0.9066 (22.67%)	3.0933 (77.33%)	0.5849	1.0748 (34.74%)	−0.580	0.076	A3
C2–C3	-	1.6898 (42.25%)	2.3101 (57.75%)	0.2682	0.2260 (9.78%)	0.252	0.092	A3
C2–C4	-	2.3139 (57.85%)	1.6860 (42.15%)	0.2016	0.1277 (7.57%)	0.120	0.162	A3
C2–C5	1.0256 (25.64%)	1.0930 (27.33%)	1.8813 (47.03%)	0.2874	0.2595 (13.79%)	0.244	0.152	A3
C2–C6	-	2.0670 (51.68%)	1.9329 (48.32%)	0.2612	0.2143 (11.09%)	0.208	0.158	A3
C3–C4	-	1.5992 (39.98%)	2.4007 (60.02%)	0.2479	0.1931 (8.04%)	0.076	0.236	A3
C3–C5	0.9207 (23.02%)	0.3538 (8.85%)	2.7254 (68.14%)	0.4451	0.6224 (22.84%)	0.032	0.444	A1
C3–C6	-	1.3108 (32.77%)	2.6891 (67.23%)	0.3971	0.4954 (18.42%)	0.176	0.356	A3
C4–C5	0.7728 (19.32%)	1.4062 (35.16%)	1.8209 (45.52%)	0.2600	0.2124 (11.66%)	0.244	0.090	A3
C4–C6	-	2.1197 (52.99%)	1.8802 (47.01%)	0.2424	0.1846 (9.82%)	0.214	0.114	A3
C5–C6	1.3252 (33.13%)	0.5602 (14.01%)	2.1145 (52.86%)	0.3711	0.4326 (20.46%)	0.320	0.188	A1
Min	0.5816	0.3538	1.6860	0.2016	0.1277
Min (%)	14.54%	8.85%	42.15%		8.04%
Max	1.3252	2.3139	3.0933	0.5860	1.0788
Max (%)	33.13%	57.85%	77.33%		37.91%

^*Calculated from the origin (0,0) where the most preferred alternative is A10.