Solving high-dimensional partial differential equations using deep learning

Significance

Partial differential equations (PDEs) are among the most ubiquitous tools used in modeling problems in nature. However, solving high-dimensional PDEs has been notoriously difficult due to the “curse of dimensionality.” This paper introduces a practical algorithm for solving nonlinear PDEs in very high (hundreds and potentially thousands of) dimensions. Numerical results suggest that the proposed algorithm is quite effective for a wide variety of problems, in terms of both accuracy and speed. We believe that this opens up a host of possibilities in economics, finance, operational research, and physics, by considering all participating agents, assets, resources, or particles together at the same time, instead of making ad hoc assumptions on their interrelationships.

Abstract

Developing algorithms for solving high-dimensional partial differential equations (PDEs) has been an exceedingly difficult task for a long time, due to the notoriously difficult problem known as the “curse of dimensionality.” This paper introduces a deep learning-based approach that can handle general high-dimensional parabolic PDEs. To this end, the PDEs are reformulated using backward stochastic differential equations and the gradient of the unknown solution is approximated by neural networks, very much in the spirit of deep reinforcement learning with the gradient acting as the policy function. Numerical results on examples including the nonlinear Black–Scholes equation, the Hamilton–Jacobi–Bellman equation, and the Allen–Cahn equation suggest that the proposed algorithm is quite effective in high dimensions, in terms of both accuracy and cost. This opens up possibilities in economics, finance, operational research, and physics, by considering all participating agents, assets, resources, or particles together at the same time, instead of making ad hoc assumptions on their interrelationships.

Partial differential equations (PDEs) are among the most ubiquitous tools used in modeling problems in nature. Some of the most important ones are naturally formulated as PDEs in high dimensions. Well-known examples include the following:

• i)The Schrödinger equation in the quantum many-body problem. In this case the dimensionality of the PDE is roughly three times the number of electrons or quantum particles in the system.
• ii)The nonlinear Black–Scholes equation for pricing financial derivatives, in which the dimensionality of the PDE is the number of underlying financial assets under consideration.
• iii)The Hamilton–Jacobi–Bellman equation in dynamic programming. In a game theory setting with multiple agents, the dimensionality goes up linearly with the number of agents. Similarly, in a resource allocation problem, the dimensionality goes up linearly with the number of devices and resources.

As elegant as these PDE models are, their practical use has proved to be very limited due to the curse of dimensionality (1): The computational cost for solving them goes up exponentially with the dimensionality.

Another area where the curse of dimensionality has been an essential obstacle is machine learning and data analysis, where the complexity of nonlinear regression models, for example, goes up exponentially with the dimensionality. In both cases the essential problem we face is how to represent or approximate a nonlinear function in high dimensions. The traditional approach, by building functions using polynomials, piecewise polynomials, wavelets, or other basis functions, is bound to run into the curse of dimensionality problem.

In recent years a new class of techniques, the deep neural network model, has shown remarkable success in artificial intelligence (e.g., refs. 2–6). The neural network is an old idea but recent experience has shown that deep networks with many layers seem to do a surprisingly good job in modeling complicated datasets. In terms of representing functions, the neural network model is compositional: It uses compositions of simple functions to approximate complicated ones. In contrast, the approach of classical approximation theory is usually additive. Mathematically, there are universal approximation theorems stating that a single hidden-layer neural network can approximate a wide class of functions on compact subsets (see, e.g., survey in ref. 7 and the references therein), even though we still lack a theoretical framework for explaining the seemingly unreasonable effectiveness of multilayer neural networks, which are widely used nowadays. Despite this, the practical success of deep neural networks in artificial intelligence has been very astonishing and encourages applications to other problems where the curse of dimensionality has been a tormenting issue.

In this paper, we extend the power of deep neural networks to another dimension by developing a strategy for solving a large class of high-dimensional nonlinear PDEs using deep learning. The class of PDEs that we deal with is (nonlinear) parabolic PDEs. Special cases include the Black–Scholes equation and the Hamilton–Jacobi–Bellman equation. To do so, we make use of the reformulation of these PDEs as backward stochastic differential equations (BSDEs) (e.g., refs. 8 and 9) and approximate the gradient of the solution using deep neural networks. The methodology bears some resemblance to deep reinforcement learning with the BSDE playing the role of model-based reinforcement learning (or control theory models) and the gradient of the solution playing the role of policy function. Numerical examples manifest that the proposed algorithm is quite satisfactory in both accuracy and computational cost.

Due to the curse of dimensionality, there are only a very limited number of cases where practical high-dimensional algorithms have been developed in the literature. For linear parabolic PDEs, one can use the Feynman–Kac formula and Monte Carlo methods to develop efficient algorithms to evaluate solutions at any given space–time locations. For a class of inviscid Hamilton–Jacobi equations, Darbon and Osher (10) recently developed an effective algorithm in the high-dimensional case, based on the Hopf formula for the Hamilton–Jacobi equations. A general algorithm for nonlinear parabolic PDEs based on the multilevel decomposition of Picard iteration is developed in ref. 11 and has been shown to be quite efficient on a number of examples in finance and physics. The branching diffusion method is proposed in refs. 12 and 13, which exploits the fact that solutions of semilinear PDEs with polynomial nonlinearity can be represented as an expectation of a functional of branching diffusion processes. This method does not suffer from the curse of dimensionality, but still has limited applicability due to the blow-up of approximated solutions in finite time.

The starting point of the present paper is deep learning. It should be stressed that even though deep learning has been a very successful tool for a number of applications, adapting it to the current setting with practical success is still a highly nontrivial task. Here by using the reformulation of BSDEs, we are able to cast the problem of solving PDEs as a learning problem and we design a deep-learning framework that fits naturally to that setting. This has proved to be quite successful in practice.

Methodology

We consider a general class of PDEs known as semilinear parabolic PDEs. These PDEs can be represented as

$$\frac{\partial u}{\partial t}\left(t,x\right)+\frac{1}{2}Tr\left(\sigma {\sigma }^{\mathrm{T}}\left(t,x\right)\left({\mathrm{H}\mathrm{e}\mathrm{s}\mathrm{s}}_{x}u\right)\left(t,x\right)\right)+\nabla u\left(t,x\right)\cdot \mu \left(t,x\right)+f\left(t,x,u\left(t,x\right),{\sigma }^{\mathrm{T}}\left(t,x\right)\nabla u\left(t,x\right)\right)=0$$ [1]

with some specified terminal condition $u\left(T,x\right)=g\left(x\right)$. Here $t$ and $x$ represent the time and $d$-dimensional space variable, respectively, $\mu$ is a known vector-valued function, $\sigma$ is a known $d\times d$ matrix-valued function, ${\sigma }^{\mathrm{T}}$ denotes the transpose associated to $\sigma$, $\nabla u$ and ${\text{Hess}}_{x}u$ denote the gradient and the Hessian of function $u$ with respect to $x$, $Tr$ denotes the trace of a matrix, and $f$ is a known nonlinear function. To fix ideas, we are interested in the solution at $t=0$, $x=\xi$ for some vector $\xi \in {\mathbb{R}}^d$.

Let ${\left\{W_t\right\}}_{t\in \left[0,T\right]}$ be a $d$-dimensional Brownian motion and ${\left\{X_t\right\}}_{t\in \left[0,T\right]}$ be a $d$-dimensional stochastic process which satisfies

$$X_t=\xi +{\int }_0^t\mu \left(s,X_s\right)ds+{\int }_0^t\sigma \left(s,X_s\right)d{W}_s.$$ [2]

Then the solution of Eq. 1 satisfies the following BSDE (cf., e.g., refs. 8 and 9):

$$u\left(t,X_t\right)-u\left(0,X_0\right)=-{\int }_0^{t}f\left(s,X_s,u\left(s,X_s\right),{\sigma }^{\mathrm{T}}\left(s,X_s\right)\nabla u\left(s,X_s\right)\right)ds+{\int }_0^t{\left[\nabla u\left(s,X_s\right)\right]}^{\mathrm{T}}\sigma \left(s,X_s\right)d{W}_s.$$ [3]

We refer to Materials and Methods for further explanation of Eq. 3.

To derive a numerical algorithm to compute $u\left(0,X_0\right)$, we treat $u{\left(0,X_0\right)\approx \theta }_{u_0},\nabla u{\left(0,X_0\right)\approx \theta }_{\nabla u_0}$ as parameters in the model and view Eq. 3 as a way of computing the values of $u$ at the terminal time $T$, knowing $u\left(0,X_0\right)$ and $\nabla u\left(t,X_t\right)$. We apply a temporal discretization to Eqs. 2 and 3. Given a partition of the time interval $\left[0,T\right]$: $0=t_0<t_1<\dots <t_N=T$, we consider the simple Euler scheme for $n=1,\dots ,N-1$:

$$X_{t_{n+1}}-X_{t_n}\approx \mu \left(t_n,X_{t_n}\right)\mathrm{\Delta }{t}_n+\sigma \left(t_n,X_{t_n}\right)\mathrm{\Delta }{W}_n,$$ [4]

and

$$u\left(t_{n+1},X_{t_{n+1}}\right)-u\left(t_n,X_{t_n}\right)\approx -f\left(t_n,X_{t_n},u\left(t_n,X_{t_n}\right),{\sigma }^{\mathrm{T}}\left(t_n,X_{t_n}\right)\nabla u\left(t_n,X_{t_n}\right)\right)\mathrm{\Delta }{t}_n+{\left[\nabla u\left(t_n,X_{t_n}\right)\right]}^{\mathrm{T}}\sigma \left(t_n,X_{t_n}\right)\mathrm{\Delta }{W}_n,$$ [5]

where

$$\mathrm{\Delta }{t}_n=t_{n+1}-t_n,\hspace{1em}\mathrm{\Delta }{W}_n=W_{t_{n+1}}-W_{t_n}.$$ [6]

Given this temporal discretization, the path ${\left\{X_{t_n}\right\}}_{0\le n\le N}$ can be easily sampled using Eq. 4. Our key step next is to approximate the function $x\mapsto {\sigma }^{\mathrm{T}}\left(t,x\right)\nabla u\left(t,x\right)$ at each time step $t=t_n$ by a multilayer feedforward neural network

$${\sigma }^{\mathrm{T}}\left(t_n,X_{t_n}\right)\nabla u\left(t_n,X_{t_n}\right)=\left({\sigma }^{\mathrm{T}}\nabla u\right)\left(t_n,X_{t_n}\right)\approx \left({\sigma }^{\mathrm{T}}\nabla u\right)\left(t_n,X_{t_n}{|\theta }_n\right),$$ [7]

for $n=1,\dots ,N-1$, where ${\theta }_n$ denotes parameters of the neural network approximating $x\mapsto {\sigma }^{\mathrm{T}}\left(t,x\right)\nabla u\left(t,x\right)$ at $t=t_n$.

Thereafter, we stack all of the subnetworks in Eq. 7 together to form a deep neural network as a whole, based on the summation of Eq. 5 over $n=1,\dots ,N-1$. Specifically, this network takes the paths ${\left\{X_{t_n}\right\}}_{0\le n\le N}$ and ${\left\{W_{t_n}\right\}}_{0\le n\le N}$ as the input data and gives the final output, denoted by $û\left({\left\{X_{t_n}\right\}}_{0\le n\le N},{\left\{W_{t_n}\right\}}_{0\le n\le N}\right)$, as an approximation of $u\left(t_N,X_{t_N}\right)$. We refer to Materials and Methods for more details on the architecture of the neural network. The difference in the matching of a given terminal condition can be used to define the expected loss function

$$l\left(\theta \right)=\mathbb{E}\left[|g\left(X_{t_N}\right)-û\left({\left\{X_{t_n}\right\}}_{0\le n\le N},{\left\{W_{t_n}\right\}}_{0\le n\le N}\right){|}^2\right].$$ [8]

The total set of parameters is $\theta =\left\{{\theta }_{u_0},{\theta }_{\nabla u_0},{\theta }_1,\dots ,{\theta }_{N-1}\right\}$.

We can now use a stochastic gradient descent-type (SGD) algorithm to optimize the parameter $\theta$, just as in the standard training of deep neural networks. In our numerical examples, we use the Adam optimizer (14). See Materials and Methods for more details on the training of the deep neural networks. Since the BSDE is used as an essential tool, we call the methodology introduced above the deep BSDE method.

Examples

Nonlinear Black–Scholes Equation with Default Risk.

A key issue in the trading of financial derivatives is to determine an appropriate fair price. Black and Scholes (15) illustrated that the price $u$ of a financial derivative satisfies a parabolic PDE, nowadays known as the Black–Scholes equation. The Black–Scholes model can be augmented to take into account several important factors in real markets, including defaultable securities, higher interest rates for borrowing than for lending, transaction costs, uncertainties in the model parameters, etc. (e.g., refs. 16–20). Each of these effects results in a nonlinear contribution in the pricing model (e.g., refs. 17, 21, and 22). In particular, the credit crisis and the ongoing European sovereign debt crisis have highlighted the most basic risk that has been neglected in the original Black–Scholes model, the default risk (21).

Ideally the pricing models should take into account the whole basket of underlyings that the financial derivatives depend on, resulting in high-dimensional nonlinear PDEs. However, existing pricing algorithms are unable to tackle these problems generally due to the curse of dimensionality. To demonstrate the effectiveness of the deep BSDE method, we study a special case of the recursive valuation model with default risk (16, 17). We consider the fair price of a European claim based on 100 underlying assets conditional on no default having occurred yet. When default of the claim’s issuer occurs, the claim’s holder receives only a fraction $\delta \in \left[\mathrm{0,1}\right)$ of the current value. The possible default is modeled by the first jump time of a Poisson process with intensity $Q$, a decreasing function of the current value; i.e., the default becomes more likely when the claim’s value is low. The value process can then be modeled by Eq. 1 with the generator

$$f\left(t,x,u\left(t,x\right),{\sigma }^{\mathrm{T}}\left(t,x\right)\nabla u\left(t,x\right)\right)=-\left(1-\delta \right)Q\left(u\left(t,x\right)\right)u\left(t,x\right)-R\hspace{0.17em}u\left(t,x\right)$$ [9]

(16), where $R$ is the interest rate of the risk-free asset. We assume that the underlying asset price moves as a geometric Brownian motion and choose the intensity function $Q$ as a piecewise-linear function of the current value with three regions ($v^h<v^l,\hspace{0.17em}{\gamma }^h>{\gamma }^l$):

$$Q\left(y\right)={\mathbb{1}}_{\left(-\infty ,v^h\right)}\left(y\right)\hspace{0.17em}{\gamma }^h+{\mathbb{1}}_{\left[v^l,\infty \right)}\left(y\right)\hspace{0.17em}{\gamma }^l+\hspace{0.17em}{\mathbb{1}}_{\left[v^h,v^l\right)}\left(y\right)\left[\frac{\left({\gamma }^h-{\gamma }^l\right)}{\left(v^h-v^l\right)}\left(y-v^h\right)+{\gamma }^h\right]$$ [10]

(17). The associated nonlinear Black–Scholes equation in $\left[0,\hspace{0.17em}T\right]\times {\mathbb{R}}^{100}$ becomes

$$\frac{\partial u}{\partial t}\left(t,x\right)+\overline{\mu }x\cdot \nabla u\left(t,x\right)+\frac{{\overline{\sigma }}^2}{2}\sum _{i=1}^d|x_i{|}^2\hspace{0.17em}\frac{{\partial }^{2}u}{\partial x_i^2}\left(t,x\right)-\left(1-\delta \right)Q\left(u\left(t,x\right)\right)\hspace{0.17em}u\left(t,x\right)-R\hspace{0.17em}u\left(t,x\right)=0.$$ [11]

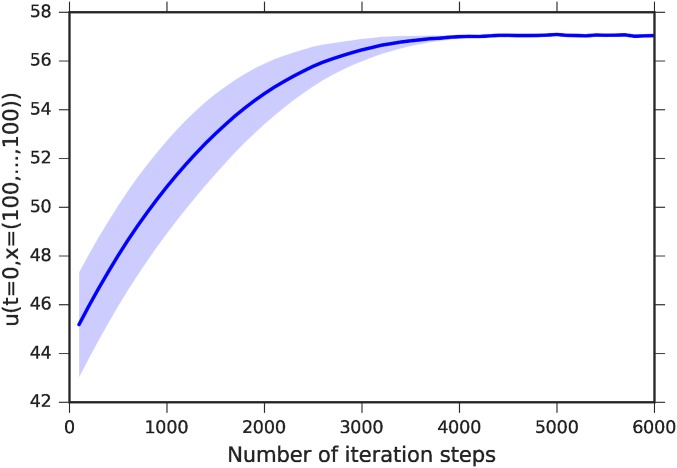
We choose $T=1,\delta =2/3,\hspace{0.17em}R=0.02,\hspace{0.17em}\overline{\mu }=0.02,\hspace{0.17em}\overline{\sigma }=0.2,\hspace{0.17em}{v}^h=50,\hspace{0.17em}{v}^l=70,\hspace{0.17em}{\gamma }^h=0.2,\hspace{0.17em}{\gamma }^l=0.02$, and the terminal condition $g\left(x\right)=min\left\{x_1,\dots ,x_{100}\right\}$ for $x=\left(x_1,\dots ,x_{100}\right)\in {\mathbb{R}}^{100}$. Fig. 1 shows the mean and the SD of ${\theta }_{u_0}$ as an approximation of $u\left(t=0,x=\left(100,\dots ,100\right)\right)$, with the final relative error being $0.46\%$. The not explicitly known “exact” solution of Eq. 11 at $t=0,\hspace{0.17em}x=\left(100,\dots ,100\right)$ has been approximately computed by means of the multilevel Picard method (11): $u\left(t=0,x=\left(100,\dots ,100\right)\right)\approx 57.300$. In comparison, if we do not consider the default risk, we get $ũ\left(t=0,x=\left(100,\dots ,100\right)\right)\approx 60.781$. In this case, the model becomes linear and can be solved using straightforward Monte Carlo methods. However, neglecting default risks results in a considerable error in the pricing, as illustrated above. The deep BSDE method allows us to rigorously incorporate default risks into pricing models. This in turn makes it possible to evaluate financial derivatives with substantial lower risks for the involved parties and the societies.

Fig. 1.

Plot of ${\theta }_{u_0}$ as an approximation of $u\left(t=0,x=\left(100,\dots ,100\right)\right)$ against the number of iteration steps in the case of the $100$-dimensional nonlinear Black–Scholes equation with $40$ equidistant time steps ($N=40$) and learning rate $0.008$. The shaded area depicts the mean $\pm$ the SD of ${\theta }_{u_0}$ as an approximation of $u\left(t=0,x=\left(100,\dots ,100\right)\right)$ for five independent runs. The deep BSDE method achieves a relative error of size $0.46\%$ in a runtime of $\mathrm{1,607}$ s.

Hamilton–Jacobi–Bellman Equation.

The term curse of dimensionality was first used explicitly by Richard Bellman in the context of dynamic programming (1), which has now become the cornerstone in many areas such as economics, behavioral science, computer science, and even biology, where intelligent decision making is the main issue. In the context of game theory where there are multiple players, each player has to solve a high-dimensional Hamilton–Jacobi–Bellman (HJB) type equation to find his/her optimal strategy. In a dynamic resource allocation problem involving multiple entities with uncertainty, the dynamic programming principle also leads to a high-dimensional HJB equation (23) for the value function. Until recently these high-dimensional PDEs have basically remained intractable. We now demonstrate below that the deep BSDE method is an effective tool for dealing with these high-dimensional problems.

We consider a classical linear-quadratic Gaussian (LQG) control problem in 100 dimensions,

$$d{X}_t=2\sqrt{\lambda }\hspace{0.17em}{m}_t\hspace{0.17em}dt+\sqrt{2}\hspace{0.17em}d{W}_t$$ [12]

with $t\in \left[0,T\right]$, $X_0=x$, and with the cost functional $J\left({\left\{m_t\right\}}_{0\le t\le T}\right)=\mathbb{E}\left[{\int }_0^T\Vert m_t{\Vert }^2\hspace{0.17em}dt+g\left(X_T\right)\right]$. Here ${\left\{X_t\right\}}_{t\in \left[0,T\right]}$ is the state process, ${\left\{m_t\right\}}_{t\in \left[0,T\right]}$ is the control process, $\lambda$ is a positive constant representing the “strength” of the control, and ${\left\{W_t\right\}}_{t\in \left[0,T\right]}$ is a standard Brownian motion. Our goal is to minimize the cost functional through the control process.

The HJB equation for this problem is given by

$$\frac{\partial u}{\partial t}\left(t,x\right)+\mathrm{\Delta }u\left(t,x\right)-\lambda \Vert \nabla u\left(t,x\right){\Vert }^2=0$$ [13]

[e.g., Yong and Zhou (ref. 24, pp. 175–184)]. The value of the solution $u\left(t,x\right)$ of Eq. 13 at $t=0$ represents the optimal cost when the state starts from $x$. Applying Itô’s formula, one can show that the exact solution of Eq. 13 with the terminal condition $u\left(T,x\right)=g\left(x\right)$ admits the explicit formula

$$u\left(t,x\right)=-\frac{1}{\lambda }\ln \hspace{0.17em}\left(\mathbb{E}\left[\exp \hspace{0.17em}\left(-\lambda g\left(x+\sqrt{2}{W}_{T-t}\right)\right)\right]\right).$$ [14]

This can be used to test the accuracy of the proposed algorithm.

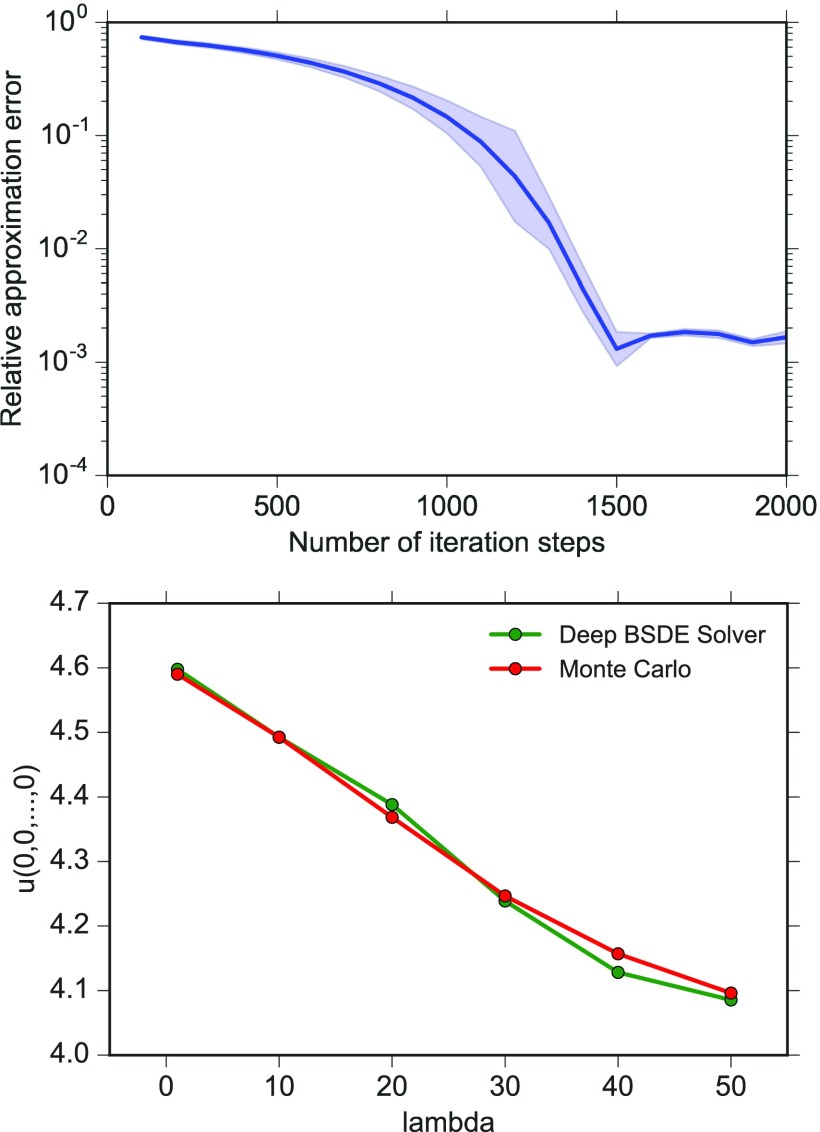
We solve the HJB Eq. 13 in the 100-dimensional case with $g\left(x\right)=\ln \left(\left(1+\Vert x{\Vert }^2\right)/2\right)$ for $x\in {\mathbb{R}}^{100}$. Fig. 2, Top shows the mean and the SD of the relative error for $u\left(t=0,x=\left(0,\dots ,0\right)\right)$ in the case $\lambda =1$. The deep BSDE method achieves a relative error of $0.17\%$ in a runtime of $330$ s on a Macbook Pro. We also use the BSDE method to approximatively calculate the optimal cost $u\left(t=0,x=\left(0,\dots ,0\right)\right)$ against different values of $\lambda$ (Fig. 2, Bottom). The curve in Fig. 2, Bottom clearly confirms the intuition that the optimal cost decreases as the control strength increases.

Fig. 2.

(Top) Relative error of the deep BSDE method for $u\left(t=0,x=\left(0,\dots ,0\right)\right)$ when $\lambda =1$ against the number of iteration steps in the case of the $100$-dimensional HJB Eq. 13 with $20$ equidistant time steps ($N=20$) and learning rate $0.01$. The shaded area depicts the mean $\pm$ the SD of the relative error for five different runs. The deep BSDE method achieves a relative error of size $0.17\%$ in a runtime of $330$ s. (Bottom) Optimal cost $u\left(t=0,x=\left(0,\dots ,0\right)\right)$ against different values of $\lambda$ in the case of the $100$-dimensional HJB Eq. 13, obtained by the deep BSDE method and classical Monte Carlo simulations of Eq. 14.

Allen–Cahn Equation.

The Allen–Cahn equation is a reaction–diffusion equation that arises in physics, serving as a prototype for the modeling of phase separation and order–disorder transition (e.g., ref. 25). Here we consider a typical Allen–Cahn equation with the “double-well potential” in 100-dimensional space,

$$\frac{\partial u}{\partial t}\left(t,x\right)=\mathrm{\Delta }u\left(t,x\right)+u\left(t,x\right)-{\left[u\left(t,x\right)\right]}^3,$$ [15]

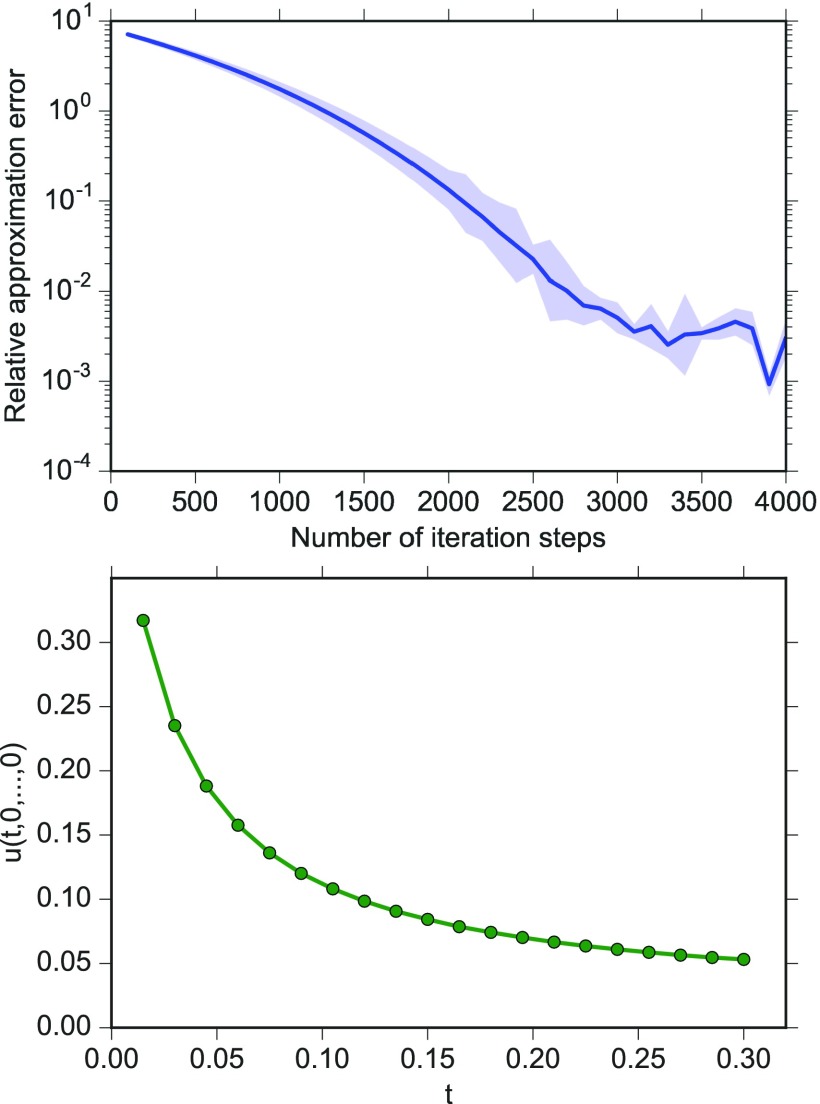
with the initial condition $u\left(0,x\right)=g\left(x\right)$, where $g\left(x\right)=1/\left(2+0.4\hspace{0.17em}\Vert x{\Vert }^2\right)$ for $x\in {\mathbb{R}}^{100}$. By applying a transformation of the time variable $t\mapsto T-t\hspace{0.17em}\left(T>0\right)$, we can turn Eq. 15 into the form of Eq. 1 such that the deep BSDE method can be used. Fig. 3, Top shows the mean and the SD of the relative error of $u\left(t=0.3,x=\left(0,\dots ,0\right)\right)$. The not explicitly known exact solution of Eq. 15 at $t=0.3$, $x=\left(0,\dots ,0\right)$ has been approximatively computed by means of the branching diffusion method (e.g., refs. 12 and 13): $u\left(t=0.3,x=\left(0,\dots ,0\right)\right)\approx 0.0528$. For this $100$-dimensional example PDE, the deep BSDE method achieves a relative error of $0.30\%$ in a runtime of $647$ s on a Macbook Pro. We also use the deep BSDE method to approximatively compute the time evolution of $u\left(t,x=\left(0,\dots ,0\right)\right)$ for $t\in \left[\mathrm{0,0.3}\right]$ (Fig. 3, Bottom).

Fig. 3.

(Top) Relative error of the deep BSDE method for $u\left(t=0.3,x=\left(0,\dots ,0\right)\right)$ against the number of iteration steps in the case of the $100$-dimensional Allen–Cahn Eq. 15 with $20$ equidistant time steps ($N=20$) and learning rate $0.0005$. The shaded area depicts the mean $\pm$ the SD of the relative error for five different runs. The deep BSDE method achieves a relative error of size $0.30\%$ in a runtime of $647$ s. (Bottom) Time evolution of $u\left(t,x=\left(0,\dots ,0\right)\right)$ for $t\in \left[\mathrm{0,0.3}\right]$ in the case of the $100$-dimensional Allen–Cahn Eq. 15 computed by means of the deep BSDE method.

Conclusions

The algorithm proposed in this paper opens up a host of possibilities in several different areas. For example, in economics one can consider many different interacting agents at the same time, instead of using the “representative agent” model. Similarly in finance, one can consider all of the participating instruments at the same time, instead of relying on ad hoc assumptions about their relationships. In operational research, one can handle the cases with hundreds and thousands of participating entities directly, without the need to make ad hoc approximations.

It should be noted that although the methodology presented here is fairly general, we are so far not able to deal with the quantum many-body problem due to the difficulty in dealing with the Pauli exclusion principle.

Materials and Methods

BSDE Reformulation.

The link between (nonlinear) parabolic PDEs and BSDEs has been extensively investigated in the literature (e.g., refs. 8, 9, 26, and 27). In particular, Markovian BSDEs give a nonlinear Feynman–Kac representation of some nonlinear parabolic PDEs. Let $\left(\mathrm{\Omega },\mathcal{F},\mathbb{P}\right)$ be a probability space, $W:\left[0,T\right]\times \mathrm{\Omega }\to {\mathbb{R}}^d$ be a $d$-dimensional standard Brownian motion, and ${\left\{{\mathcal{F}}_t\right\}}_{t\in \left[0,T\right]}$ be the normal filtration generated by ${\left\{W_t\right\}}_{t\in \left[0,T\right]}$. Consider the following BSDEs,

$$X_t=\xi +{\int }_0^t\mu \left(s,X_s\right)\hspace{0.17em}ds+{\int }_0^t\sigma \left(s,X_s\right)\hspace{0.17em}d{W}_s,$$ [16]

$$Y_t=g\left(X_T\right)+{\int }_t^{T}f\left(s,X_s,Y_s,Z_s\right)\hspace{0.17em}ds-{\int }_t^T{\left(Z_s\right)}^{\mathrm{T}}\hspace{0.17em}d{W}_s,$$ [17]

for which we are seeking a ${\left\{{\mathcal{F}}_t\right\}}_{t\in \left[0,T\right]}$-adapted solution process ${\left\{\left(X_t,Y_t,Z_t\right)\right\}}_{t\in \left[0,T\right]}$ with values in ${\mathbb{R}}^d\times \mathbb{R}\times {\mathbb{R}}^d$. Under suitable regularity assumptions on the coefficient functions $\mu$, $\sigma$, and $f$, one can prove existence and up-to-indistinguishability uniqueness of solutions (cf., e.g., refs. 8 and 26). Furthermore, we have that the nonlinear parabolic PDE is related to the BSDEs 16 and 17 in the sense that for all $t\in \left[0,T\right]$ it holds $\mathbb{P}$-a.s. that

$$Y_t=u\left(t,X_t\right)\hspace{1em}\text{and}\hspace{1em}{Z}_t={\sigma }^{\mathrm{T}}\left(t,X_t\right)\hspace{0.17em}\nabla u\left(t,X_t\right)$$ [18]

(cf., e.g., refs. 8 and 9). Therefore, we can compute the quantity $u\left(0,X_0\right)$ associated to Eq. 1 through $Y_0$ by solving the BSDEs 16 and 17. More specifically, we plug the identities in Eq. 18 into Eq. 17 and rewrite the equation forwardly to obtain the formula in Eq. 3.

Then we discretize the equation temporally and use neural networks to approximate the spatial gradients and finally the unknown function, as introduced in the methodology of this paper.

Neural Network Architecture.

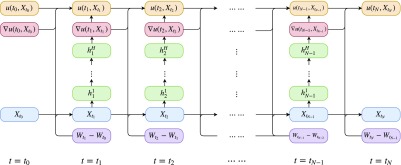
In this subsection we briefly illustrate the architecture of the deep BSDE method. To simplify the presentation we restrict ourselves in these illustrations to the case where the diffusion coefficient $\sigma$ in Eq. 1 satisfies that $\forall \hspace{0.17em}x\in {\mathbb{R}}^d:\sigma \left(x\right)={\mathrm{I}\mathrm{d}}_{{\mathbb{R}}^d}$. Fig. 4 illustrates the network architecture for the deep BSDE method. Note that $\nabla u\left(t_n,X_{t_n}\right)$ denotes the variable we approximate directly by subnetworks and $u\left(t_n,X_{t_n}\right)$ denotes the variable we compute iteratively in the network. There are three types of connections in this network:

Fig. 4.

Illustration of the network architecture for solving semilinear parabolic PDEs with $H$ hidden layers for each subnetwork and $N$ time intervals. The whole network has $\left(H+1\right)\left(N-1\right)$ layers in total that involve free parameters to be optimized simultaneously. Each column for $t=t_1,t_2,\dots ,t_{N-1}$ corresponds to a subnetwork at time $t$. $h_n^1,\dots ,h_n^H$ are the intermediate neurons in the subnetwork at time $t=t_n$ for $n=\mathrm{1,2},\dots ,N-1$.

• i)$X_{t_n}\to h_n^1\to h_n^2\to \cdots \to h_n^H\to \nabla u\left(t_n,X_{t_n}\right)$ is the multilayer feedforward neural network approximating the spatial gradients at time $t=t_n$. The weights ${\theta }_n$ of this subnetwork are the parameters we aim to optimize.
• ii)$\left(u\left(t_n,X_{t_n}\right),\nabla u\left(t_n,X_{t_n}\right),W_{t_{n+1}}-W_{t_n}\right)\to u\left(t_{n+1},X_{t_{n+1}}\right)$ is the forward iteration giving the final output of the network as an approximation of $u\left(t_N,X_{t_N}\right)$, completely characterized by Eqs. 5 and 6. There are no parameters to be optimized in this type of connection.
• iii)$\left(X_{t_n},W_{t_{n+1}}-W_{t_n}\right)\to X_{t_{n+1}}$ is the shortcut connecting blocks at different times, which is characterized by Eqs. 4 and 6. There are also no parameters to be optimized in this type of connection.

If we use $H$ hidden layers in each subnetwork, as illustrated in Fig. 4, then the whole network has $\left(H+1\right)\left(N-1\right)$ layers in total that involve free parameters to be optimized simultaneously.

It should be pointed out that the proposed deep BSDE method can also be used if we are interested in values of the PDE solution $u$ in a region $D\subset {\mathbb{R}}^d$ at time $t=0$ instead of at a single space-point $\xi \in {\mathbb{R}}^d$. In this case we choose $X_0=\xi$ to be a nondegenerate $D$-valued random variable and we use two additional neural networks parameterized by $\left\{{\theta }_{u_0},{\theta }_{\nabla u_0}\right\}$ for approximating the functions $D\ni x\mapsto u\left(0,x\right)\in \mathbb{R}$ and $D\ni x\mapsto \nabla u\left(0,x\right)\in {\mathbb{R}}^d$. Upper and lower bounds for approximation errors of stochastic approximation algorithms for PDEs and BSDEs, respectively, can be found in refs. 27–29 and the references therein.

Implementation.

We describe in detail the implementation for the numerical examples presented in this paper. Each subnetwork is fully connected and consists of four layers (except the example in the next subsection), with one input layer ($d$ dimensional), two hidden layers (both $d+10$ dimensional), and one output layer ($d$ dimensional). We choose the rectifier function (ReLU) as our activation function. We also adopted the technique of batch normalization 30 in the subnetworks, right after each linear transformation and before activation. This technique accelerates the training by allowing a larger step size and easier parameter initialization. All of the parameters are initialized through a normal or a uniform distribution without any pretraining.

We use TensorFlow (31) to implement our algorithm with the Adam optimizer (14) to optimize parameters. Adam is a variant of the SGD algorithm, based on adaptive estimates of lower-order moments. We set the default values for corresponding hyperparameters as recommended in ref. 14 and choose the batch size as 64. In each of the presented numerical examples the means and the SDs of the relative $L^1$-approximation errors are computed approximatively by means of five independent runs of the algorithm with different random seeds. All of the numerical examples reported are run on a Macbook Pro with a 2.9-GHz Intel Core i5 processor and 16 GB memory.

Effect of Number of Hidden Layers.

The accuracy of the deep BSDE method certainly depends on the number of hidden layers in the subnetwork approximation Eq. 7. To test this effect, we solve a reaction–diffusion-type PDE with a different number of hidden layers in the subnetwork. The PDE is a high-dimensional version ($d=100$) of the example analyzed numerically in Gobet and Turkedjiev (32) ($d=2$),

$$\frac{\partial u}{\partial t}\left(t,x\right)+\frac{1}{2}\hspace{0.17em}\mathrm{\Delta }u\left(t,x\right)+min\hspace{0.17em}\left\{1,{\left(u\left(t,x\right)-u*\left(t,x\right)\right)}^2\right\}=0,$$ [19]

in which $u*\left(t,x\right)$ is the explicit oscillating solution

$$u*\left(t,x\right)=\kappa +\sin \hspace{0.17em}\left(\lambda \sum _{i=1}^d{x}_i\right)\exp \hspace{0.17em}\left(\frac{{\lambda }^{2}d\left(t-T\right)}{2}\right).$$ [20]

Parameters are chosen in the same way as in ref. 32: $\kappa =1.6,\hspace{0.17em}\lambda =0.1,\hspace{0.17em}T=1$. A residual structure with skip connection is used in each subnetwork with each hidden layer having $d$ neurons. We increase the number of hidden layers in each subnetwork from zero to four and report the relative error in Table 1. It is evident that the approximation accuracy increases as the number of hidden layers in the subnetwork increases.

Table 1.

The mean and SD of the relative error for the PDE in Eq. 19, obtained by the deep BSDE method with different numbers of hidden layers

	No. of layers†
Relative error	29	58	87	116	145
Mean, %	2.29	0.90	0.60	0.56	0.53
SD	0.0026	0.0016	0.0017	0.0017	0.0014

The PDE is solved until convergence with 30 equidistant time steps (N=30) and 40,000 iteration steps. Learning rate is 0.01 for the first half of iterations and 0.001 for the second half.

^†We count only the layers that have free parameters to be optimized.