Significance
Influenza hemagglutinin (HA) is the viral membrane protein that guides entry of flu viruses into host cells. A global refolding of the stem domain of HA, , is crucial to successful viral membrane fusion, but the molecular mechanism relating this conformational change of to its fusogenic properties remains unclear. We use molecular dynamics simulations to quantify the thermodynamic importance of the B loop domain for driving the overall rearrangement. We find that the B loop’s loop-to-coiled-coil refolding is not strongly downhill and thus is a possible target for therapeutics. A buried hydrophilic amino acid is implicated in destabilizing the coiled coil, and the sequence divergence at this position may indicate functional differences between group 1 and 2 HAs.
Keywords: all-atom molecular dynamics, B-loop transition, structural heterogeneity, buried water, sequence divergence
Abstract
Influenza hemagglutinin (HA) mediates viral entry into host cells through a large-scale conformational rearrangement at low pH that leads to fusion of the viral and endosomal membranes. Crystallographic and biochemical data suggest that a loop-to-coiled-coil transition of the B-loop region of HA is important for driving this structural rearrangement. However, the microscopic picture for this proposed “spring-loaded” movement is missing. In this study, we focus on understanding the transition of the B loop and perform a set of all-atom molecular dynamics simulations of the full B-loop trimeric structure with the CHARMM36 force field. The free-energy profile constructed from our simulations describes a B loop that stably folds half of the postfusion coiled coil in tens of microseconds, but the full coiled coil is unfavorable. A buried hydrophilic residue, Thr59, is implicated in destabilizing the coiled coil. Interestingly, this conserved threonine is the only residue in the B loop that strictly differentiates between the group 1 and 2 HA molecules. Microsecond-scale constant temperature simulations revealed that kinetic traps in the structural switch of the B loop can be caused by nonnative, intramonomer, or intermonomer -sheets. The addition of the A helix stabilized the postfusion state of the B loop, but introduced the possibility for further -sheet structures. Overall, our results do not support a description of the B loop in group 2 HAs as a stiff spring, but, rather, it allows for more structural heterogeneity in the placement of the fusion peptides during the fusion process.
Influenza hemagglutinin (HA) is the membrane surface glycoprotein responsible for guiding the invasion of flu viruses into their host cells. It is a homotrimer with each monomer composed of two domains, a globular head domain () that wraps around a stem domain ( together with termini) (Fig. 1). contains a C-terminal transmembrane peptide that anchors it to the viral membrane and a buried N-terminal fusion peptide (FP). The overall picture that has emerged from many years of study (1) is that the low-pH conditions in the endosome trigger a large conformational change in that (i) allows the burial of the FPs into the endosomal membrane and (ii) guides the subsequent fusion of the viral and endosomal membranes. While the endpoints of the structural rearrangement (2–4) are known from X-ray crystallography, how the intermediate steps of the conformational rearrangement are coordinated to perform these two crucial functions remains unclear. Thus, an understanding of the pH-induced structural transition of will shed light on the physical mechanism of the invasion of influenza viruses.
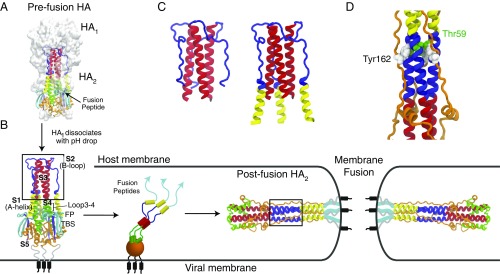
Fig. 1.
The pH-induced HA transition. (A) The prefusion configuration of HA [Protein Data Bank (PDB) ID code 2HMG (2)] including the head domain (white surface representation) and stem domain (colored cartoon representation). (B) The reduction of pH triggers the dissociation of from , which starts an extensive structural rearrangement ending in the postfusion configuration [PDB ID code 1QU1 (4)]. Successful membrane fusion presumably places the FPs and transmembrane helices in the same membrane. Note that remains localized near because of a disulfide bond between regions S5 and TBS (two -strands). The B-loop domain (blue) changes from a random loop to a coiled-coil structure (highlighted by boxes). The central stalk, S3, maintains its coiled-coil structure during the transition. The A-helix domain (yellow) shifts >100 Å from the preconfiguration to postconfiguration. Little is known about intermediate configurations during this transition. (C) The simulation constructs: the entire B loop and S3 (Left); and A helix, B loop, and S3 (Right). (D) The long coiled coil in the postfusion structure is wrapped by S5 (orange domain), which may provide additional stabilization to the coiled-coil configuration. In the crystal structure, Tyr162 is the only residue in S5 that buries deeply into the B loop. A buried water is coordinated between Thr59 and Tyr162.
A seminal discovery was that the postfusion structure of is significantly more stable than the prefusion structure of in the absence of (3, 5). This means that the free energy released during refolding can be used to help drive the fusion process. At the end of the conformational rearrangement, the postfusion structure (Fig. 1) shows that the transmembrane region and the FPs are located in the same membrane. Completing the rearrangement before inserting FPs into the host membrane leads to a nonfusogenic, dead-end state, where the FPs are stuck at the viral membrane (6, 7). Thus, the conformational rearrangement must take place in at least two stages: a membrane insertion stage, followed by a final rearrangement, where the final rearrangement is sufficiently delayed to allow for host membrane insertion. How the kinetics of the HA rearrangement are controlled remains unclear, but likely involves differential kinetic barriers and stabilities of the various prefusion to postfusion refolding substeps. divides into at least five subdomains, S1–S5, that undergo distinct structural rearrangements during the refolding (Fig. 1). An attractive model, first described in terms of a “spring-loaded” model (5, 8), suggests that S1 (A helix) and S2 (B loop) refold at an early stage, with the resulting coiled coil extending the FPs away from and the viral membrane and toward the host membrane. The C-terminal portion of the protein (S4 and S5) then refolds at a later stage. Although direct observation of the HA rearrangement is complicated, this general model of an extended intermediate is supported by several studies (5, 9, 10).
It is now well recognized that, similarly to HA, some protein sequences can fold into multiple folded structures (11–13). While the global folds of these proteins can stably switch based on solvent conditions or binding partners, the various subdomains or foldons (14) of these proteins are likely to be frustrated on their own, preferring one local fold only marginally more than the alternative. The postfusion B loop has a coiled-coil structure, but in the context of the crystal, it is wrapped by loops coming from S5 (Fig. 1D). Here, our central question is whether the B loop is able to quickly and stably refold from its random loop structure attached to S3 in the prefusion structure to its trimeric coiled-coil postfusion structure in the absence of the S5 interactions. We study the B loop’s ability to act as a structural switch with detailed molecular simulations. Some indications for the pH sensitivity of the B loop itself have been seen in vitro by using a 36-residue B-loop construct, showing monomers with little helical structure at pH 7 and trimers with significant helical content at pH 4.8 (5).
The energy landscape theory of protein folding (15–17) describes folding as a diffusive process across a high-dimension energy landscape, where the competition between configurational entropy and energetics can lead to free-energy barriers to folding. Fast refolding of the B loop implies a refolding barrier small enough that the B loop can reconfigure much faster than the time scale of the full transition. Additionally, involvement of the B loop with the removal of the buried FPs would imply a large free-energy bias toward the postfusion coiled-coil structure. By studying the folding landscape of the B loop, the ability of the B loop to shape the overall HA refolding process can be tested. The postfusion B loop has a coiled-coil fold (18, 19), a motif where two or more -helices associate together with complimentary amphipathic sequence patterns. The simplest description of the folding of a coiled coil is as a hydrophobic “zipper,” where each turn of the coiled coil quickly nucleates the folding of the next turn because of the low effective loop length (20). Thus, the folding speed for stable coiled coils can be as fast as several microseconds (21, 22). Real sequences though, with deviations from ideal hydrophobic packing, can show more complicated folding kinetics. For example, studies of the leucine zipper protein GCN4 revealed a double-exponential fit to the unfolding rate, indicating the existence of intermediate states (23, 24). GCN4 folding, recently observed with pH-jump experiments (25), can be as fast as 30 s when tethered. An additional complicating factor is that the symmetry of a homotrimer can lead to frustration on the folding landscape (26, 27). Even considering these factors able to slow the folding, it is very likely that the refolding time of a stable B loop is much shorter than the long time scale of fusion [tens of seconds (28)]. Thus, the question of the thermodynamic stability of the final coiled-coil fold is of greatest functional importance.
In this work, we use all-atom explicit-solvent simulations using the CHARMM36 forcefield to characterize the refolding of the B loop from the group 2 H3 HA variant. Simulations follow the B loop from the prefusion loop to the postfusion trimeric coiled coil. The pH-sensitive residues in the B loop are protonated to model a low-pH environment. The free-energy profiles derived from these simulations indicate that the B loop can rapidly and stably fold half of the coiled coil, but further folding is not favorable. The burial of Thr59 in group 2 HAs is implicated as the source of the destabilization of the N-terminal region of the coiled coil by creating a water pocket in the hydrophobic core. In sharp contrast, group 1 HAs have a hydrophobic Met59. Kinetic unfolding simulations confirm that a Thr59Met mutant has a dehydrated hydrophobic core and is more stable, providing evidence that Thr59 is destabilizing the N-terminal half of the B-loop coiled coil. Additional long unbiased kinetic trajectories were consistent with the free-energy profiles and gave information on possible kinetic traps to B-loop refolding, consisting of nonnative -sheet formation.
Results
The B-loop domain of influenza HA subtype H3 folds into a trimeric coiled coil in the absence of the head domain. The B-loop sequence features a heptad repeat pattern creating amphipathic helices able to form a continuous hydrophobic core buried among the three helices (Fig. 1B). From the A helix (S1), the B loop (S2), and the stable central coiled coil (S3), there is a 45-residue stretch where the residues at positions “a” and “d” are hydrophobic, interrupted only by Thr59 in the B loop, and flanked by Thr87 and Thr41. Additionally, coiled coils can be stabilized by salt-bridge interactions at positions “e” and “g,” of which the B loop has one, Lys62 and Glu67. The B loop has several charged residues. Including the flanking Arg54 and Arg76, there are 12 charged residues per monomer. The coiled-coil structure is known to be sensitive to pH, with little helicity and probable loss of the trimer at pH 7 and strong helicity and trimer formation at pH 4 (5), where the charge is between +4 and +5 per monomer. Secondary structure prediction algorithms predict the B loop to be helical (29), although recent experiments on B-loop monomers have suggested that the B loop is only 12% helical at pH 4.8 (30).
The formation of the B-loop coiled coil is inconsistent with the prefusion HA structure. Thus, a highly stable and downhill refolding B loop has been suggested as the force that drives the initial stages of the HA conformational change (5, 8). To test this hypothesis, we characterized the folding and free-energy landscape of an S2–S3 trimer, where the B-loop trimer is folding from a prenucleated S3 coiled coil, as it does in nature. As simulating the full HA molecule is prohibitively expensive, our choice of this subset of deserves a brief discussion. The prefusion loop structure was stabilized by interaction with (Fig. 1A), which is believed to be destabilized and dissociated from the B loop through electrostatic repulsion caused by the lowered pH in the endosome (31). Here, we assumed that any remaining interaction between and the B loop was weak and nonspecific, and, thus, we were able to remove it from the simulation. S1 (the A helix) is a second structural feature that is missing from the simulation. S1 makes extensive contacts with the anchored portion of and, additionally, is attached to the FPs buried within S4. In the initial stages of the HA conformational rearrangement, if B-loop refolding is to be a dominant force for driving the dissociation of S1 and the FPs, the B loop will be refolding without interaction with S1 apart from its N-terminal attachment. Thus, to focus on the B loop’s early role in driving subsequent refolding, we removed S1 from the simulation. We explore the consequences of including S1 later (Microsecond-Scale Kinetic Simulations).
Coiled-Coil Formation Is Not Downhill for the B Loop.
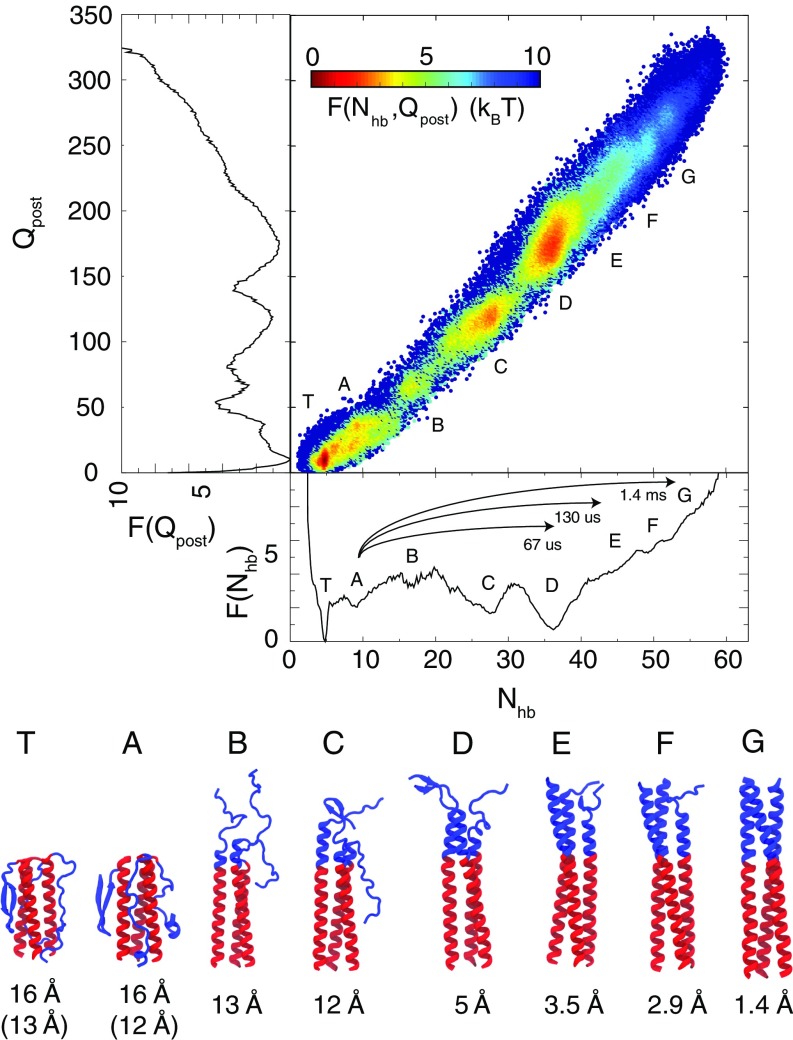
We characterized the folding of the B-loop trimer with fully atomistic molecular dynamics simulations, in which the protein was protonated as if at pH 4 (see Materials and Methods for details). The folding was monitored with two reaction coordinates. counted the number of -helical hydrogen bonds formed in the B-loop trimer and indicated the degree of helicity. counted the number of postfusion contacts that were formed and was a good monitor of the formation of tertiary interactions existing in the crystallographic coiled-coil structure of the B loop. Fig. 2 shows the free energy as a function of these two reaction coordinates. Also shown are the centroid structures from eight different ensembles, a long-lived trapped structure () and structures with roughly zero to six formed -helical turns per B-loop monomer (). The overall folding was seen to be a zipping-like mechanism, where progressive helical structure was formed from C- to N-terminal and in lock-step with tertiary interactions.
Fig. 2.
Free-energy profiles of the B-loop transition and the centroid structures from eight representative ensembles at physiological temperature (310 K). (Upper) The two-dimensional free-energy profile as a function of and , colored by free energy. The one-dimensional plots to the left and below show the projection of the free energy onto and , respectively. The prefusion crystal structure has and . The postfusion crystal structure has and . Also indicated are the mean first passage times for the B-loop transitions from basin A to basin D, E, and G. (Lower) The backbone rmsd of the B loop in the representative ensembles relative to the postfusion crystal structure is shown. If the rmsd to the prefusion structure is smaller, its value is shown in parentheses.
The most striking result was that the B loop was thermodynamically most stable near , where only half of the coiled-coil structure is formed, as opposed to the post-fusion-like . Unbiased simulations only sampled between (SI Appendix, Fig. S3A) and, thus, umbrella simulations were necessary to connect the unbiased sampling to the postfusion ensemble (). A simple lack of conformational sampling was not a good explanation for the absence of in the unbiased simulations because the conformational entropy of is more restricted than due to the forming coiled coil. Thus, the absence of in the unbiased simulations suggested a free-energy penalty preventing sampling of . This hypothesis was confirmed by performing two umbrella simulations of increasing helical bias, which connected with (SI Appendix, Fig. S3B) and with (SI Appendix, Fig. S3C), respectively.
The resulting free-energy profile was computed by using the combined data. The folding progressed from a disordered B-loop ensemble 1–2 T above over a T barrier to and then over a T barrier to . was seen to be T above . The existence of an intermediate at was corroborated by an additional set of melting simulations starting from the full postfusion coiled-coil structure of S1–S3 (SI Appendix, Fig. S10).
The free-energy profiles shown in Fig. 2 describe a B loop that spends most of its time in . Significant time was also spent in a particular configuration where each monomer of the B loop made extensive and unique contacts with S3 (SI Appendix, Fig. S9). In , the N termini of the B loop are interacting with the C termini of S3, which is likely an artifact of introducing the artificial termini for the simulation. Nevertheless, this trap along with highlights that there is residual tendency for the B loop to interact with S3. Despite the high -helical secondary structure propensity, the B loop spent % of the time as a monomer in -strand structures (SI Appendix, Fig. S8). As can be seen in the centroid structures of and , these -strand structures can associate with S3. This behavior was consistent with the frustrated and slow folding B loop observed with dual-basin structure-based models (9).
Thr59 Interrupts the Coiled-Coil Hydrophobic Core.
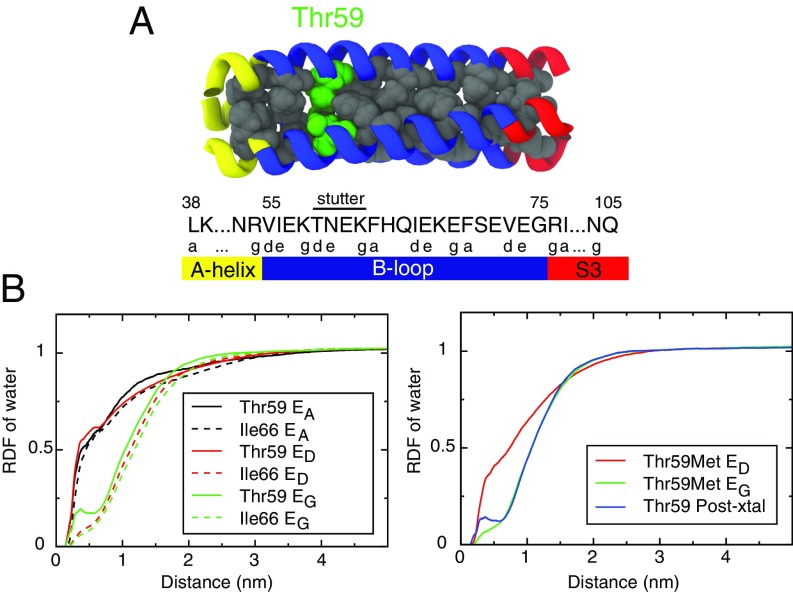
The stability of coiled-coil structures stems from a heptad repeat pattern of buried hydrophobic residues (positions and ) flanked by highly polar residues locking the coiled-coil configuration (18, 19). The most stable ensemble, , buried the C-terminal heptad repeat pattern of Ile77–Val73–Phe70–Ile66–Phe63 until its interruption at the small polar Thr59, which was surrounded by the polar Asn60 and the charged Lys58 (Fig. 3A). A heptad repeat stutter (19, 32) had a 3–4–4–3–4 hydrophobic pattern instead of the canonical 3–4–3–4. There was a heptad stutter at positions 62–59, and the heptad pattern then continued from Lys58 into S1. Conspicuously, the configurations zipping up past Phe63 () were destabilized relative to .
Fig. 3.
The radial distribution function (RDF) of water around side-chain atoms of core residues. (A) The sequence and location of Thr59. (B, Left) RDFs around Thr59 and Ile66 in , , and . The RDF of Thr59 has a peak at the radius of water, indicating solvation even in the fully coiled-coil . As a comparison, Ile66 is dehydrated in states D and G. (B, Right) RDFs around Met59 in a single-residue mutant B loop at and . Also, as a control, a simulation starting from the postfusion coiled-coil B loop was performed, and the RDF around Thr59 was calculated.
The formation of the hydrophobic core was quantified by the radial distribution function (RDF) of water molecules around residues forming the hydrophobic core of the coiled coil (Fig. 3B). The burial of the C-terminal hydrophobic core was quantified by the RDF of Ile66 (the rest of the RDFs can be found in SI Appendix, Fig. S6), which was solvated in , but dry in and . In contrast, even in , Thr59 had a peak at the radius of a water, showing that it was hydrated even when folded into the core. Note that the neighbors of Thr59, Asn60 or Lys58, were not observed to fold into the core in and displaced Thr59. Seemingly, Thr59 reduced the free-energy gain of the next zipping step after by maintaining water in contact with the hydrophobic residues. Put another way, there is a likely free-energy penalty in confining waters to the empty space left by Thr59 and surrounded above and below by hydrophobic residues. The presence of a polar residue inside the coiled-coil hydrophobic core is not a unique trait of the B loop. A similar cavity is seen in the GCN4 coiled coil, where two ordered water molecules cling to a buried asparagine (33).
Thr59 Is the Hallmark of Group 2 HA Molecules.
Bioinformatic studies of influenza HA sequence evolution (34, 35) classify HA into two groups (36). These two groups are believed to have separated 1,500 y ago (37). Thr59 is the only residue of the B loop strictly conserved within group 2 HA sequences, despite its disruption of the heptad repeat pattern and its apparent disruption of the hydrophobic core. Group 1 HAs have instead a conserved hydrophobic Met59. Position 59 is the strongest differentiator between the two groups (SI Appendix, Fig. S1).
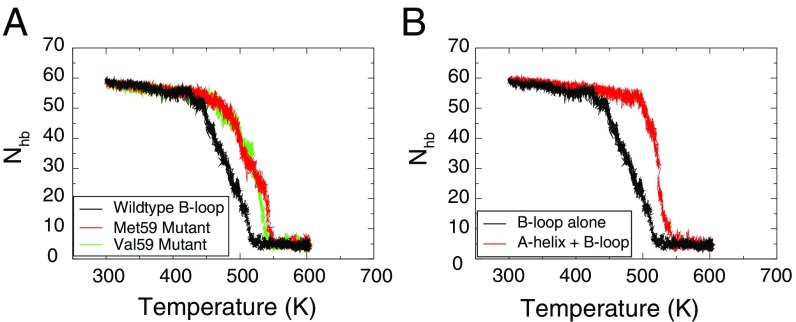
Although a full thermodynamic characterization of a Thr59Met mutant or a group 1 B loop is beyond the scope of the current study, we performed a 130-ns constant temperature simulation on Thr59Met mutant. The mutation was introduced into the centroid structure of and led to a dry core (Fig. 3B). As a control, to show that the time scale of the simulation was long enough to calculate the water dynamics, a simulation of the same duration showed water penetrating into the core at position 59 for wild type started from the postfusion crystal structure. Additionally, thermal unfolding simulations indicated that hydrophobic mutations at position 59 were stabilizing. When started from the postfusion structure and subjected to a temperature ramp, wild-type B loop unfolded at 450 K, whereas Thr59Met and Thr59Val were shifted up by 25 K (Fig. 4A).
Fig. 4.
Stability to thermal unfolding. of the B loop is used to monitor the unfolding during a 500-ns simulation with a temperature ramping from 300 K to 600 K. (A) Comparison of melting curves between the wild-type H3 B loop (black) with two mutants where Thr59 of the sequence was mutated to Met59 (red) and Val59 (green). The melting temperatures of these two mutants have been raised by 25 K. (B) Comparison of melting curves between the wild-type S2 + S3 and with A helix added. With the stability provided by the A helix (red), the B loop has a 50 K higher melting temperature than without the A helix (black). Also, the A-helix-included system melts more cooperatively, with a steeper slope downward than the S2 + S3 system. All melting curves are averages over three independent simulations. The individual curves are shown in SI Appendix, Fig. S10.
As evidenced by the postfusion crystal structure, any residual disruption of the B-loop coiled coil was eventually overcome by the refolding of the S1 coiled coil and/or S5 wrapping around the B loop. Tyr162 may be important: It is positioned to coordinate a buried water in the hydrophilic pocket created by Thr59 (Fig. 1D). Bioinformatic analysis does not indicate any significant sequence deviations between group 1 and 2 in the S5 region interacting with the B loop. In the case of position 162, tyrosine was completely conserved for group 2, but in group 1 it was phenylalanine in 9% of sequences. In the future, a group 1 postfusion crystal structure would provide insight on any side-chain packing differences in the B-loop region between group 1 and 2 HAs.
Estimating the Kinetics of the B-Loop Transition from Free-Energy Profiles.
To calculate rates from free-energy profiles, we describe the folding of the B loop in terms of diffusive motion on a free-energy landscape (see Materials and Methods for details). While one-dimensional reaction coordinates can provide intuitive descriptions of the dynamics, the full dynamics are multidimensional. In the case of protein folding, collective coordinates based on the degree of nativeness (e.g., ) have been shown to behave diffusively and capture transition-state ensembles (38, 39). Here, for the case of B-loop folding, the high degree of similarity between free-energy profiles and diffusion coefficients calculated for two different collective coordinates gives additional evidence that they are appropriate for estimating rates. The rates calculated here for B-loop folding are likely an upper bound since the additional energetic roughness from nonspecific interactions with or the drag of S1 should further slow the folding.
Mean first passage times obtained from our free-energy profiles are indicated in Fig. 2. It took over a millisecond for the B loop to reach a post-fusion-like coiled coil () from the prefusion ensemble (). In comparison, the folding time for a fast-folding helical bundle protein is s (40, 41) and for a tethered leucine zipper is s (25). The dimeric, pH-sensitive leucine zipper was thermodynamically two-state, but showed multiphase folding kinetics on a microsecond time scale similar to our current B-loop folding landscape. For the B loop, the large free-energy penalty to fully fold was the main factor in slowing down the folding. Reaching the most stable intermediate took s, a bit slower than a tethered leucine zipper.
Microsecond-Scale Kinetic Simulations.
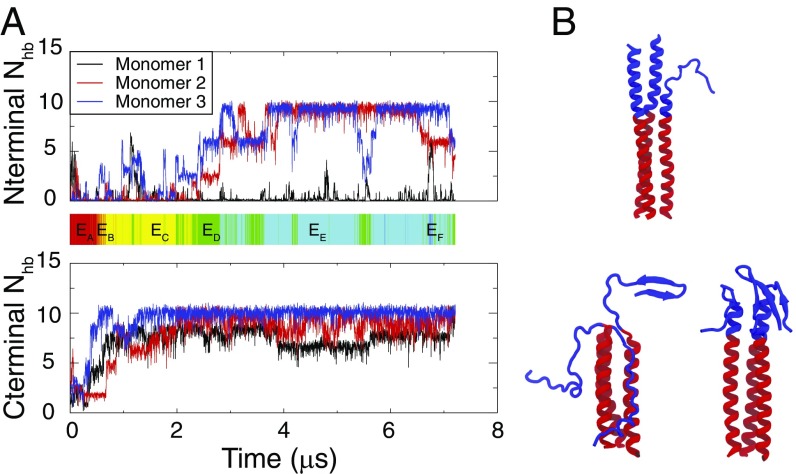
To connect the thermodynamic sampling data more directly to the kinetic behavior of the B-loop transition, we further performed unbiased, microsecond-scale, constant-temperature simulations (42). Three runs with S2 + S3 were performed for 1, 3, and 7.2 s. The shorter runs formed long-lived -structures and were terminated for this reason. The final snapshots from the 1- and 3-s runs are shown in Fig. 5B.
Fig. 5.
Constant-temperature (T = 350 K) kinetic simulations of S2 + S3 system. (A) of each B-loop monomer changes with simulation time in one simulation trajectory. (A, Upper) of the N-terminal half of the B loop. (A, Lower) of the C-terminal half of the B loop. The C-terminal half of the B loop is almost fully folded in a stable state after 2 . The color bar shows the corresponding states reached by the B loop during this simulation. Color code: red, ; orange, ; yellow, ; green, ; cyan, ; blue, . The B loop reaches after 3 while eventually returns to . (B, Upper) One snapshot from the latter half of the simulated trajectory showing a typical structure of the B loop kept from forming the hydrophobic core around Thr59. (B, Lower) Snapshots of the B loop showing nonnative structures from the end of the two other independent runs.
In the 7-s trajectory, the B loop quickly reached (3 s) but did not form the full coiled coil during the remaining 4 s (Fig. 5A). The C-terminal half of the B loop folded into a helical bundle, followed by the complete folding of two helical monomers. However, progress stopped at this stage, as the third monomer had difficulty zipping up or docking to create the hydrophobic core. In line with the thermodynamic sampling, this kinetic run suggests that a barrier exists to forming the hydrophobic core and that the core is not seen to form around Thr59. Also consistent with the thermodynamics, the kinetic run relaxed back into at 7.0 s rather than remaining stably in before continuing toward the full coiled coil as downhill folding would suggest.
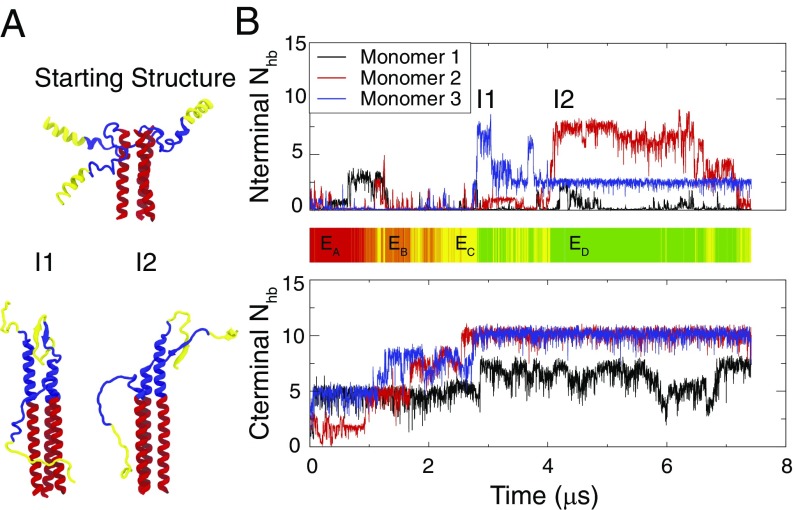
In the full molecule, the N termini of the B loop were attached to a 16-residue A helix (S1, residues 38–53; Fig. 1). Experimentally, the B loop was found to be more stable in a coiled-coil structure when the A helix was present (5). To investigate how the A helix may affect the kinetics of the B-loop transition, similarly to the S2 + S3 simulations, two runs were performed for 6 and 7 s for S1 + S2 + S3 (Fig. 6). These simulations showed some structural similarity to the S2 + S3 simulations. Specifically, we found several intermediate structures of the B loop, where one or two monomers went almost completely helical, while the third stayed as a random loop, unable to form the hydrophobic core. While there was no indication that a free A-helix helps speed the folding of the B loop, the short time scale of the kinetic simulations makes such a determination difficult.
Fig. 6.
Constant temperature kinetic simulations of the S1 + S2 + S3 system. The simulations show similar behavior to the simulations of S2 + S3 system. (A, Upper) Simulations start from a prefusion-like structure, where the A helix has been lifted slightly away from S3 to reduce their initial interactions. (A, Lower) Two intermediate structures, I1 and I2, taken from the simulations shows the existence of nonnative structures formed between the B loop and the A helix. (B) of each B-loop monomer changes with simulation time. (B, Upper) of the N-terminal half of the B loop. (B, Lower) of the C-terminal half of the B loop. The color bar shows the corresponding state reached by the B loop during this simulation. Color bar code same as Fig. 5.
The most interesting feature of the kinetic simulations was the prevalence of secondary structure in both the B loop and A helix. Both segments showed almost no helical secondary structure when surrounded by solvent and showed affinity for forming -strands. As an isolated monomer, the B loop had on average 20% secondary structure (SI Appendix, Fig. S8). Existence of the other two monomers and the A helices can stabilize these secondary structures. Intramonomer -hairpins were seen both between A helix and B loop (Fig. 6A, I1) and within the B loop alone (Fig. 5B). Intermonomer -strands were also seen both between the A helix and B loop (Fig. 6A, I2) and within the B loop (Fig. 5B). structures were also observed in the thermodynamic simulations, including the centroids of , , and (Fig. 2). This propensity was not observed in the bioinformatic prediction by Psipred (SI Appendix, Fig. S5) (43). This could be because Psipred is based on crystal structures, and the A helix and B loop have clear coiled-coil-like sequences that indeed form coiled coils in their folded end states. These simulations suggest that even these highly predicted helical sequences can form a multitude of secondary structures and nonnative trapped structures en route to their stable folded structures.
A Helix Stabilizes the Postfusion Structure.
Melting simulations starting from the postfusion structure corroborated the experimental finding that addition of the A helix stabilizes the coiled-coil structure (5). Two melting simulations were started from the postfusion structure, one with S2 + S3 and the other S1 + S2 + S3. Addition of the A helix shifted the melting temperature up by 50 K (Fig. 4B). Interestingly, the melting curves showed an intermediate that had the C-terminal half of the B loop in a coiled-coil structure that resembled the structural ensemble from the thermodynamic simulations (SI Appendix, Fig. S10). This provides additional evidence that the C-terminal core of the B loop is more stable than the N-terminal core.
Discussion and Conclusion
The transition of the B loop is of particular interest in the study of HA because the full coiled-coil transition of the B loop and A helix would extend the FPs of toward the endosomal membrane. This spring-loaded process is attractive because it provides a simple explanation for one of the necessary functions of HA: facilitating the burial of FPs in the host membrane (5, 8). Direct experimental observation of the dynamical features of the B-loop transition and HA intermediates in general are difficult due to the complicated bimembrane system. Thus, molecular simulations offer another avenue to understanding the conformational transitions of HA. Here, the free-energy profile generated for the B loop calls into question the description of the B loop as a simple loaded spring. The result that the post-fusion-like ensemble is significantly less stable than a half-formed coiled coil may be surprising, but it is not at odds with the full postfusion structure being the lowest free-energy configuration. In the context of the postfusion structure, the S1 coiled coil and the contacts with S5 can provide additional stability to the B-loop coiled coil.
The simulation results we have presented are compatible with previous in vitro experiments (5, 30) that focused on a 36-residue B-loop construct. An early experiment concluded from circular dichroism (CD) that below pH 5, the B loop formed a stable trimeric coiled coil that showed 90% helicity (5). More recent experiments indicated that the helicity of the Loop36 monomer was very low and insensitive to pH (30), and, thus, suggest that forming the trimer is important for the observation of a highly helical Loop36. This is in line with our simulations of a B-loop monomer that showed 3% helicity and 20% -character (SI Appendix, Fig. S8). Our simulations of the B-loop trimer show that an ensemble , with roughly half of the B-loop coiled coil formed, is most thermodynamically stable. Analyzing the helicity for the same residues as in Loop36 (Arg54 Ile89), which additionally contains 16 residues of S3, show contains 80% helicity and contains 90% helicity. Although the simulated ensemble appears to be slightly less helical than the Loop36 trimer, absolute quantification of secondary structure with CD is difficult and typically involves uncertainties of 10% (44). Thus, the behavior of our simulated B loop is a viable interpretation of the available experimental data.
The sequence patterns of coiled coils are able to encode a wide range of stabilities. Interestingly, hydrophilic residues at buried positions a and d occur with low frequency [15–20% (45–47)], and mutational studies have indicated that the positions and identities of these residues can alter properties such as parallel vs. antiparallel arrangement and the degree of multimerization (48–50). Buried hydrophilic residues destabilize coiled coils relative to an ideal hydrophobic heptad pattern (47), but by doing so can promote structural specificity through encouraging the hydrophilic residues to localize together. Thus, their placement can be important for protein regions undergoing functional rearrangements. The group 2 H3 HA studied here contains one buried hydrophilic residue in its B loop, Thr59 at heptad position d. There is a stutter in the B loop of HA, and its position is conserved in most class I (-helical) and class III (mixed /) viral fusion proteins (51). The functional significance of heptad repeat stutters remains unclear, but it has been shown that removal of the stutter in the B loop leads to supercoiling by one third turn in the B loop (52). The sequence Thr59–Asn60–Glu61–Lys62 in the B loop contains the two abnormalities, the buried hydrophilic Thr59 and the heptad stutter.
It is important to consider that our results are for H3, a group 2 HA, and that the sequence differences in other HA subtypes may lead to different B-loop behavior. The conservation of position 59, which strictly contains Thr59 in group 2 HA and Met59 in group 1 HA, suggests functional importance. We showed that Thr59 disrupts the hydrophobic core of the H3 B loop and that mutation to hydrophobic residues, Thr59Met or Thr59Val, created a dry hydrophobic core (Fig. 3B) and stabilized the B loop to thermal unfolding (Fig. 4A). It remains to be investigated, with a methionine at position 59, whether group 1 HAs have a more stable B-loop postfusion coiled coil and behave more closely to spring-loaded refolding or a B loop with a comparable stability due to destabilization at other positions.
In conclusion, free-energy profiles of the loop-to-coiled-coil transition describe a B loop that stably folds half of the postfusion coiled coil in tens of microseconds, but the full coiled coil is unstable. These results are compatible with previous experiments on the B loop, and the time scale is consistent with folding of a tethered leucine zipper. Thermal unfolding simulations provide indirect evidence that adding the A helix stabilizes the full B loop. Thus, it may be that the B loop is only fully stabilized by the eventual docking of the A-helix trimer or the final packing of S5. The burial of an N-terminal threonine triplet is shown to be the likely cause of the unstable full B-loop coiled-coil structure, and, thus, the sequence divergence at this position may signal a difference in the behavior of group 1 and 2 HAs, at least in the B-loop transition. Since the B-loop behavior can be influenced by the whole B-loop sequence, B-loop studies of several HA2 subtypes will be enlightening. Time-resolved pH-jump experiments on membrane-bound proteins show great promise for capturing these conformational changes in HA (53). A slower transition of the B loop and a long-lived intermediate may provide functional benefits by providing additional free-energy drive for membrane fusion and contributing extra time to the association among multiple HAs (54). We can speculate that this intermediate state is followed by the final rearrangement of S4 and S5, providing sufficient free energy to stabilize the final structure and possibly bringing the viral and cell membranes together.
Materials and Methods
The behavior of the B loop is the focus of this work, and the simulations were performed with truncated subdomains of . We were specifically exploring to what extent the structural switch of the B loop can drive the overall conformational rearrangement of . Four sets of simulations were performed (Table 1). The first set of simulations used an S2 + S3 construct with a combination of unbiased and umbrella-biased simulations that used continuous simulated tempering [CST (55, 56)] for an increased rate of thermodynamic convergence. This first set was used to generate the free-energy profile (Fig. 2) and consumed the majority of the computing cost. The second set of simulations was unbiased constant temperature kinetic simulations on the same S2 + S3 system started from a prefusion-like configurating. The third set of simulations was the same as the second set, except that the A helix was included (S1 + S2 + S3). The fourth set of simulations was melting simulations used to roughly determine relative stability between different B-loop constructs.
Table 1.
Summary of all simulations in this paper
| Set | Mutant | System | Length (s) | Temperature, K | MD simulation type |
| 1 | WT* | S2† + S3‡ | 23.0 | 300–600 | CST |
| 1 | WT | S2 + S3 | 8.0 | 300–550 | CST + Umbrella |
| 1 | WT | S2 + S3 | 7.0 | 300–550 | CST + Umbrella |
| 2 | WT | S2 + S3 | 1.0 | 350 | Unbiased |
| 2 | WT | S2 + S3 | 3.0 | 350 | Unbiased |
| 2 | WT | S2 + S3 | 7.2 | 350 | Unbiased |
| 3 | WT | S1§ + S2 + S3 | 6.0 | 350 | Unbiased |
| 3 | WT | S1 + S2 + S3 | 7.5 | 350 | Unbiased |
| 4 | WT | S2 + S3 | 0.5 | 300 600 | Thermal unfolding |
| 4 | WT | S1 + S2 + S3 | 0.5 | 300 600 | Thermal unfolding |
| 4 | Thr59Met | S2 + S3 | 0.5 | 300 600 | Thermal unfolding |
| 4 | Thr59Val | S2 + S3 | 0.5 | 300 600 | Thermal unfolding |
Group 2 H3 HA, sequence from ref. 2.
B loop (residues 54–75 of HA2).
Unchanged region between prefusion and postfusion HA structures (residues 76–105 of HA2).
A helix (residue 38–53 of HA2).
We first discuss parameters common to all of the simulations. The sequence of group 2 H3 HA was used for simulation because it is the only sequence for which both prefusion (2) and postfusion (4) B-loop structures exist (sequence: LKSTQAAIDQINGKLNRVIEKTNEKFHQIEKEFSEVEGRIQDLEKYVEDTKIDLWSYNAELLVALENQ). All simulations were performed with the CHARMM36 force field (57) and TIP3P water, which gives a balanced treatment of protein secondary structures (58). The N termini were capped by ACE (acetyl group) and C termini by NME (methylamine). The simulations used a time step of 2.0 fs, were neutralized by 24 ions and contained an ionic concentration of NaCl similar to endosomes of 0.15 M. The simulations were performed in the NVT ensemble because of the CST enhanced sampling protocol.
An important consideration for the rearrangement is its pH sensitivity. Several regions of HA are suggested to respond to lowered pH, including dissociation of (59), destabilization of the fusion peptide burial pocket (54, 60), and stability of the B-loop trimeric coiled coil (5). Interestingly, isolated folds into the postfusion structure at both neutral and low pH (61), suggesting a limited role for pH in . Nonetheless, since there is experimental evidence for pH sensitivity of the isolated B-loop fragment considered here [most stable below pH 5 (5)], we modeled the effect of pH in the simulations. To create the most stable environment for the B-loop coiled coil, we protonated the titratable residues of the B loop as though at pH 4. This had the beneficial side-effect of simplifying the computation because this pH is low enough that all titratable residues will be protonated with high probability for the entire simulation. Although methods for simulating a system in a constant-pH environment have been developed, both for coarse-grained systems (62, 63) and explicit solvent simulations (64), these methods for explicit solvent simulations still prove to be too computationally expensive for the size and time scales of interest for the B-loop transition. There were a total of three Asp residues (zero in the B loop), 10 Glu residues (six in the B loop), and one His residue (one in the B loop) in each monomer of the simulation system. Calculation of the pKa values for titratable residues was done with PROPKA (65) for the prefusion and postfusion structures of the isolated S2 + S3 construct (SI Appendix, Table S2). The results show that any residues with a pKa < 4.0 were located between the C-terminal and Glu74, while in the B loop, residues should be protonated at pH 4.0. We additionally protonated even the few residues with pKa < 4.0 in S3, because we reasoned that these negative charges would lead to trapping of the now positively charged B loop near prefusion-like configurations. Thus, this change to the system should only stabilize the postfusion structure.
The pKa values of titratable residues in the postfusion B-loop structure shared the same pattern as the prefusion structure, except for one residue, Glu67, which had a pKa < 4.0 in the final state due to the formation of a salt-bridge interaction with Lys62. Glu67 is located in the middle of the B loop, so the recovery of its charge state could either stabilize the basin D or G in our free-energy plot (Fig. 2). Because it is intractable to change the protonation state of this residue during the simulation, we performed a free-energy perturbation (FEP) calculation (66) after the simulation was completed. Our FEP analysis (SI Appendix, Fig. S4) suggested that adding a negative charge to Glu67 did not change the free energy of basin D relative to basin G, but instead would likely stabilize the prefusion state even further. Therefore, the protonation of this residue does not affect the main conclusion from our thermodynamic sampling. In sum, our protonation scheme, while below the range of pHs probed by experiments, is set up in favor of stabilizing the postfusion B-loop structure. Fig. 2 demonstrates that even in this situation, the B loop is unstable by itself in the postfusion state.
CST Simulations.
Simulation set 1 used CST (55, 56) as a method to accelerate the sampling of protein conformations. CST continuously changes the temperature of a single simulation copy while maintaining a generalized canonical ensemble. This method has been used to study the folding of proteins (56). A brief description of the method can be found in SI Appendix. The simulated construct is very similar to the Loop36 protein studied experimentally (5), but was extended to include the entire S3. The simulated system (truncated system of S2 + S3; Fig. 1C) was placed in a dodecahedral box of length 102 Å with 74,587 atoms. To fix the orientation of the molecule in the box, the atoms of S3 were restrained to their crystallographic positions by using isotropic harmonic position restraints. In this way, we were only investigating the conditional thermodynamic landscape of the B loop in the presence of S3 near its crystallographic position. Since the S3 coiled coil is conserved during the overall rearrangement of (the preconfigurations and postconfigurations have a rmsd Å), restraining S3 should not affect the results. To reduce the possibility for the N termini of S2 to interact with the C termini of S3, an unphysical configuration in a complete HA, a 1-nm radius excluded volume interaction was applied between the atoms of the terminal residues. The simulations were performed with an in-house version of Gromacs (Version 4.6.3) (67, 68) edited to include CST and PLUMED (69) for umbrella sampling.
During 23 s of unbiased CST sampling, the postfusion ensemble was not reached, so additional umbrella sampling based on the number of -helical hydrogen bonds in the B loop, , was used to ensure that configurations resembling the postfusion state were sampled. The umbrella potential was
| (1) |
where was either 55 or 60 and kJ/mol. is defined in Eq. 2. The umbrella simulations were started from a basin D structure, and only the portion of the trajectory after the protein left basin D for the first time was used in the free-energy calculation. This should have eliminated any bias on the starting structure (70). The unbiased sampling (i.e., ) and the umbrella sampling were combined with the weighted histogram analysis method (71). The reweighted free-energy profiles were consistent and explained why umbrella sampling was necessary, because the postfusion ensemble was less stable by 8 , and thus unlikely to be sampled.
Kinetic Simulations.
In simulation set 2, we performed conventional NPT simulations for the same system (system S2 + S3) as set 1. The simulations were initialized from the prefusion configuration of . These simulations were performed on the Anton1 supercomputer (42) with a rectangular box of 114 99 99 Å containing 110,141 atoms. Since we found in the CST simulations that the free-energy landscape of the B-loop transition at 350 K was similar to that at 310 K (SI Appendix, Fig. S2A), we ran the kinetic simulations at 350 K for the enhanced diffusion rate. Harmonic position restraints were applied to the atom of residue 80 in S3 to maintain the orientation of the simulated system.
In simulation set 3, the A helix was added (Fig. 1C). These simulations were designed to explore possible interactions between the A helix and the B loop during the conformational rearrangement. The 6-s simulation started from the prefusion configuration, and the 7-s simulation started with the A helix slightly extended and making no contacts with S3. As above, these simulations were performed on the Anton1 supercomputer (42) with a rectangular box of 119 119 138 Å (a total of 191,717 atoms). Again, residue 80 of S3 was restrained.
Melting Simulations.
In simulation set 4, we used thermal unfolding trajectories to estimate the relative stability of various B-loop configurations. Each simulation was run for 500 ns and repeated three times. The setup of the simulation system was the same as in set 1.
Order Parameters for Free-Energy Calculation and Umbrella Sampling.
Two order parameters were used throughout our analysis. counts the number of hydrogen bonds formed in the B-loop helices, and measures the similarity of the B loop to the postfusion state. Since we wanted to avoid any precise structural bias from the existing postfusion crystal structure in our thermodynamic simulations, we used for umbrella sampling. In the postsimulation analyses, we used both and . The equation for was taken from PLUMED (69): , where
| (2) |
and = 8, = 12, and = 2.5 Å (72, 73). and enumerated the hydrogen and oxygen atoms forming the backbone hydrogen bonds of an -helix. defined the length of a well-formed hydrogen bond. This choice for and made close to a step function and differentiable. quantified the similarity of the B loop to the postfusion crystal structure by counting the number of native atomic contacts formed in a protein configuration. The native contacts were defined as those atom pairs that were close together in the postfusion structure of the B loop, as calculated by the Shadow contact map (74). Small asymmetries in the homotrimeric contact map created by small asymmetries in the crystal structure were removed. In total, 441 native atomic contacts were obtained.
First Passage Times and Diffusion Coefficients.
The kinetics of the B-loop transition can be estimated from a free-energy profile along a collective coordinate by using the following formula (38):
| (3) |
where and refer to the number of -helical hydrogen bonds at the starting and ending states of the B-loop transition. is the free energy and is the diffusion coefficient.
With CST, the kinetic information of the protein dynamics at a specific temperature is lost, due to the changing simulation temperatures. Thus, to estimate , we performed additional constant temperature simulations at each basin identified from the free-energy profile. Three trajectories of 300 ns each were computed for each basin. The three initial structures for each basin’s simulations were determined by clustering the CST trajectories in each basin and taking the central structure from the top three clusters in each basin. The mean square deviation of the value scaled approximately linearly with time when is large, which is one indicator of diffusive behavior (Appendix, Fig. S7). The following formula relates the mean squared deviation with the diffusion coefficient,
| (4) |
and in practice means determining the slope of a linear fit to vs. at sufficiently large . The calculated diffusion coefficients are listed in SI Appendix, Table S1. There was a large variation in the three computed diffusion coefficients for each basin, and, thus, it did not seem meaningful to use these coefficients in a basin-dependent manner in Eq. 3. Thus, a constant diffusion coefficient for the whole profile was estimated by averaging at each over all of the 300-ns simulations. A constant value of 16.5 s was used in Eq. 3 to determine the first passage times in Fig. 2.
Folding rates are dependent on temperature through changes in either the free-energy profile or the diffusion coefficient. We also calculated the free-energy and diffusion coefficients at 350 K. The free-energy profile at higher temperature was very similar (SI Appendix, Fig. S2, Left), while the diffusion coefficients were larger (SI Appendix, Table S1).
Analysis of HA Sequences.
HA sequences were retrieved from the Influenza Research Database (75). We used all HA sequences up to now (a total of 103,091 sequences including partial sequences). Multiple sequence alignment was conducted by using the program MAFFT (76). To classify HA into two groups according to their subtypes, we used results from previous studies (77). Hellinger distance was used to capture the difference in sequence position probability distributions between group 1 and 2 HAs:
| (5) |
where and are the probability of each of the 20 amino acids in group 1 and 2 HAs. To compare the distribution of residues of the B loop in these two groups, only positions with 1- were selected for visualization (Fig. S1).
Supplementary Material
Acknowledgments
This work was supported by the Center for Theoretical Biological Physics sponsored by NSF Grant PHY-1427654 and also by NSF Division of Chemistry Grant 1614101 and Welch Foundation Grant C-1792. J.K.N. is a Humboldt Postdoctoral Fellow. X.L. was partially supported by National Institute of Health Grant R01-GM110310 at the early states of this work. J.M. is supported by National Institutes of Health Grants R01-GM067801, R01-GM116280, and R01-GM127628, National Science Foundation Grant MCB-0818353, and Welch Foundation Grant Q-1512. Q.W. is supported by the National Institutes of Health Grants R01-AI067839, R01-GM116280, and R01-GM127628, and Welch Foundation Grant Q-1826. Anton computer time (Grant PSCA14037P) was provided by the Pittsburgh Supercomputing Center (PSC) through National Institutes of Health Grant R01-GM116961. The Anton machine at PSC was generously made available by D. E. Shaw Research. This work used the Extreme Science and Engineering Discovery Environment through allocation TG-MCB140274, which is supported by National Science Foundation Grant ACI-1548562.
Footnotes
The authors declare no conflict of interest.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1805442115/-/DCSupplemental.
References
- 1.Skehel JJ, Wiley DC. Receptor binding and membrane fusion in virus entry: The influenza hemagglutinin. Annu Rev Biochem. 2000;69:531–569. doi: 10.1146/annurev.biochem.69.1.531. [DOI] [PubMed] [Google Scholar]
- 2.Wilson IA, Skehel JJ, Wiley DC. Structure of the haemagglutinin membrane glycoprotein of influenza virus at 3 Å resolution. Nature. 1981;289:366–373. doi: 10.1038/289366a0. [DOI] [PubMed] [Google Scholar]
- 3.Bullough PA, Hughson FM, Skehel JJ, Wiley DC. Structure of influenza haemagglutinin at the pH of membrane fusion. Nature. 1994;371:37–43. doi: 10.1038/371037a0. [DOI] [PubMed] [Google Scholar]
- 4.Chen J, Skehel JJ, Wiley DC. N- and C-terminal residues combine in the fusion-pH influenza hemagglutinin HA(2) subunit to form an N cap that terminates the triple-stranded coiled coil. Proc Natl Acad Sci USA. 1999;96:8967–8972. doi: 10.1073/pnas.96.16.8967. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Carr CM, Kim PS. A spring-loaded mechanism for the conformational change of influenza hemagglutinin. Cell. 1993;73:823–832. doi: 10.1016/0092-8674(93)90260-w. [DOI] [PubMed] [Google Scholar]
- 6.Weber T, et al. Evidence for H(+)-induced insertion of influenza hemagglutinin HA2 N-terminal segment into viral membrane. J Biol Chem. 1994;269:18353–18358. [PubMed] [Google Scholar]
- 7.Wharton SA, et al. Electron microscopy of antibody complexes of influenza virus haemagglutinin in the fusion pH conformation. EMBO J. 1995;14:240–246. doi: 10.1002/j.1460-2075.1995.tb06997.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Carr CM, Chaudhry C, Kim PS. Influenza hemagglutinin is spring-loaded by a metastable native conformation. Proc Natl Acad Sci USA. 1997;94:14306–14313. doi: 10.1073/pnas.94.26.14306. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Lin X, et al. Order and disorder control the functional rearrangement of influenza hemagglutinin. Proc Natl Acad Sci USA. 2014;111:12049–12054. doi: 10.1073/pnas.1412849111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Ivanovic T, Harrison SC. Distinct functional determinants of influenza hemagglutinin-mediated membrane fusion. eLife. 2015;4:e11009. doi: 10.7554/eLife.11009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Murzin AG. BIOCHEMISTRY: Metamorphic proteins. Science. 2008;320:1725–1726. doi: 10.1126/science.1158868. [DOI] [PubMed] [Google Scholar]
- 12.Ramírez-Sarmiento CA, Noel JK, Valenzuela SL, Artsimovitch I. Interdomain contacts control native state switching of RfaH on a dual-funneled landscape. PLoS Comput Biol. 2015;11:e1004379. doi: 10.1371/journal.pcbi.1004379. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Giri Rao VVH, Desikan R, Ayappa KG, Gosavi S. Capturing the membrane-triggered conformational transition of an -helical pore-forming toxin. J Phys Chem B. 2016;120:12064–12078. doi: 10.1021/acs.jpcb.6b09400. [DOI] [PubMed] [Google Scholar]
- 14.Panchenko AR, Luthey-Schulten Z, Wolynes PG. Foldons, protein structural modules, and exons. Proc Natl Acad Sci USA. 1996;93:2008–2013. doi: 10.1073/pnas.93.5.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bryngelson JD, Wolynes PG. Spin glasses and the statistical mechanics of protein folding. Proc Natl Acad Sci USA. 1987;84:7524–7528. doi: 10.1073/pnas.84.21.7524. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Leopold PE, Montal M, Onuchic JN. Protein folding funnels: A kinetic approach to the sequence-structure relationship. Proc Natl Acad Sci USA. 1992;89:8721–8725. doi: 10.1073/pnas.89.18.8721. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Whitford PC, Sanbonmatsu KY, Onuchic JN. Biomolecular dynamics: Order—disorder transitions and energy landscapes. Rep Prog Phys. 2012;75:076601. doi: 10.1088/0034-4885/75/7/076601. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lupas AN, Gruber M. Advances in Protein Chemistry. Vol 70. Elsevier; 2005. The structure of -helical coiled coils; pp. 37–38. [DOI] [PubMed] [Google Scholar]
- 19.Mason JM, Arndt KM. Coiled coil domains: Stability, specificity, and biological implications. ChemBioChem. 2004;5:170–176. doi: 10.1002/cbic.200300781. [DOI] [PubMed] [Google Scholar]
- 20.Plotkin SS, Onuchic JN. Investigation of routes and funnels in protein folding by free energy functional methods. Proc Natl Acad Sci USA. 2000;97:6509–6514. doi: 10.1073/pnas.97.12.6509. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yang WY, Gruebele M. Folding at the speed limit. Nature. 2003;423:193–197. doi: 10.1038/nature01609. [DOI] [PubMed] [Google Scholar]
- 22.Zhu Y, et al. Ultrafast folding of 3d: A de novo designed three-helix bundle protein. Proc Natl Acad Sci USA. 2003;100:15486–15491. doi: 10.1073/pnas.2136623100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Dragan AI, Privalov PL. Unfolding of a leucine zipper is not a simple two-state transition. J Mol Biol. 2002;321:891–908. doi: 10.1016/s0022-2836(02)00699-x. [DOI] [PubMed] [Google Scholar]
- 24.Wang T, Lau WL, DeGrado WF, Gai F. T-jump infrared study of the folding mechanism of coiled-coil GCN4-p1. Biophysical J. 2005;89:4180–4187. doi: 10.1529/biophysj.105.068809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Donten ML, et al. pH-jump induced leucine zipper folding beyond the diffusion limit. J Phys Chem B. 2015;119:1425–1432. doi: 10.1021/jp511539c. [DOI] [PubMed] [Google Scholar]
- 26.Noel JK, et al. Mirror images as naturally competing conformations in protein folding. J Phys Chem B. 2012;116:6880–6888. doi: 10.1021/jp212623d. [DOI] [PubMed] [Google Scholar]
- 27.Levy Y, Cho SS, Shen T, Onuchic JN, Wolynes PG. Symmetry and frustration in protein energy landscapes: A near degeneracy resolves the Rop dimer-folding mystery. Proc Natl Acad Sci USA. 2005;102:2373–2378. doi: 10.1073/pnas.0409572102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Otterstrom JJ, et al. Relating influenza virus membrane fusion kinetics to stoichiometry of neutralizing antibodies at the single-particle level. Proc Natl Acad Sci USA. 2014;111:E5143–E5148. doi: 10.1073/pnas.1411755111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Buchan DWA, Minneci F, Nugent TCO, Bryson K, Jones DT. Scalable web services for the PSIPRED protein analysis workbench. Nucleic Acids Res. 2013;41:W349–W357. doi: 10.1093/nar/gkt381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Casali M, Banta S, Zambonelli C, Megeed Z, Yarmush ML. Site-directed mutagenesis of the hinge peptide from the hemagglutinin protein: Enhancement of the pH-responsive conformational change. Protein Eng Des Selection. 2008;21:395–404. doi: 10.1093/protein/gzn018. [DOI] [PubMed] [Google Scholar]
- 31.Huang Q, Opitz R, Knapp EW, Herrmann A. Protonation and stability of the globular domain of influenza virus hemagglutinin. Biophysical J. 2002;82:1050–1058. doi: 10.1016/S0006-3495(02)75464-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Hicks MR, Holberton DV, Kowalczyk C, Woolfson DN. Coiled-coil assembly by peptides with non-heptad sequence motifs. Folding Des. 1997;2:149–158. doi: 10.1016/S1359-0278(97)00021-7. [DOI] [PubMed] [Google Scholar]
- 33.Oshaben KM, Salari R, McCaslin DR, Chong LT, Horne WS. The native GCN4 leucine-zipper domain does not uniquely specify a dimeric oligomerization state. Biochemistry. 2012;51:9581–9591. doi: 10.1021/bi301132k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Medina RA, García-Sastre A. Influenza S viruses: New research developments. Nat Rev Microbiol. 2011;9:590–603. doi: 10.1038/nrmicro2613. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Burke DF, Smith DJ. A recommended numbering scheme for influenza A HA subtypes. PLoS ONE. 2014;9:e112302. doi: 10.1371/journal.pone.0112302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Kovácová A, Ruttkay-Nedecký G, Haverlík IK, Janecek S. Sequence similarities and evolutionary relationships of influenza virus A hemagglutinins. Virus Genes. 2002;24:57–63. doi: 10.1023/a:1014038120979. [DOI] [PubMed] [Google Scholar]
- 37.Suzuki Y, Nei M. Origin and evolution of influenza virus hemagglutinin genes. Mol Biol Evol. 2002;19:501–509. doi: 10.1093/oxfordjournals.molbev.a004105. [DOI] [PubMed] [Google Scholar]
- 38.Socci ND, Onuchic JN, Wolynes PG. Diffusive dynamics of the reaction coordinate for protein folding funnels. J Chem Phys. 1996;104:5860–5868. [Google Scholar]
- 39.Best RB, Hummer G, Eaton WA. Native contacts determine protein folding mechanisms in atomistic simulations. Proc Natl Acad Sci USA. 2013;110:17874–17879. doi: 10.1073/pnas.1311599110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Lindorff-Larsen K, Piana S, Dror RO, Shaw DE. How fast-folding proteins fold. Science. 2011;334:517–520. doi: 10.1126/science.1208351. [DOI] [PubMed] [Google Scholar]
- 41.Kubelka J, Hofrichter J, Eaton WA. The protein folding ‘speed limit’. Curr Opin Struct Biol. 2004;14:76–88. doi: 10.1016/j.sbi.2004.01.013. [DOI] [PubMed] [Google Scholar]
- 42.Shaw DE, et al. Millisecond-Scale Molecular Dynamics Simulations on Anton. ACM; New York: 2009. p. 1. [Google Scholar]
- 43.Jones DT. Protein secondary structure prediction based on position-specific scoring matrices. J Mol Biol. 1999;292:195–202. doi: 10.1006/jmbi.1999.3091. [DOI] [PubMed] [Google Scholar]
- 44.Wiedemann C, Bellstedt P, Görlach M. CAPITO—A web server-based analysis and plotting tool for circular dichroism data. Bioinformatics. 2013;29:1750–1757. doi: 10.1093/bioinformatics/btt278. [DOI] [PubMed] [Google Scholar]
- 45.Lupas A, Van Dyke M, Stock J. Predicting coiled coils from protein sequences. Science. 1991;252:1162–1164. doi: 10.1126/science.252.5009.1162. [DOI] [PubMed] [Google Scholar]
- 46.Woolfson DN, Alber T. Predicting oligomerization states of coiled coils. Protein Sci. 1995;4:1596–1607. doi: 10.1002/pro.5560040818. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Akey DL, Malashkevich VN, Kim PS. Buried polar residues in coiled-coil interfaces. Biochemistry. 2001;40:6352–6360. doi: 10.1021/bi002829w. [DOI] [PubMed] [Google Scholar]
- 48.Harbury PB, Zhang T, Kim PS, Alber T. A switch between two-, three-, and four-stranded coiled coils in GCN4 leucine zipper mutants. Science. 1993;262:1401–1407. doi: 10.1126/science.8248779. [DOI] [PubMed] [Google Scholar]
- 49.Lumb KJ, Kim PS. A buried polar interaction imparts structural uniqueness in a designed heterodimeric coiled coil. Biochemistry. 1995;34:8642–8648. doi: 10.1021/bi00027a013. [DOI] [PubMed] [Google Scholar]
- 50.Oakley MG, Kim PS. A buried polar interaction can direct the relative orientation of helices in a coiled coil †. Biochemistry. 1998;37:12603–12610. doi: 10.1021/bi981269m. [DOI] [PubMed] [Google Scholar]
- 51.Igonet S, et al. X-ray structure of the arenavirus glycoprotein GP2 in its postfusion hairpin conformation. Proc Natl Acad Sci USA. 2011;108:19967–19972. doi: 10.1073/pnas.1108910108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Higgins CD, Malashkevich VN, Almo SC, Lai JR. Influence of a heptad repeat stutter on the pH-dependent conformational behavior of the central coiled-coil from influenza hemagglutinin HA2: The heptad repeat stutter in influenza HA2. Proteins Struct Funct Bioinf. 2014;82:2220–2228. doi: 10.1002/prot.24585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Jeong BS, Dyer RB. Proton transport mechanism of M2 proton channel studied by laser-induced pH jump. J Am Chem Soc. 2017;139:6621–6628. doi: 10.1021/jacs.7b00617. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Lin X, Noel JK, Wang Q, Ma J, Onuchic JN. Lowered pH leads to fusion peptide release and a highly dynamic intermediate of influenza hemagglutinin. J Phys Chem B. 2016;120:9654–9660. doi: 10.1021/acs.jpcb.6b06775. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Zhang C, Ma J. Enhanced sampling and applications in protein folding in explicit solvent. J Chem Phys. 2010;132:244101. doi: 10.1063/1.3435332. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Zhang C, Ma J. Folding helical proteins in explicit solvent using dihedral-biased tempering. Proc Natl Acad Sci USA. 2012;109:8139–8144. doi: 10.1073/pnas.1112143109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Best RB, et al. Optimization of the additive CHARMM all-atom protein force field targeting improved sampling of the backbone , and side-chain and dihedral angles. J Chem Theor Comput. 2012;8:3257–3273. doi: 10.1021/ct300400x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Best RB, Buchete NV, Hummer G. Are current molecular dynamics force fields too helical? Biophys J. 2008;95:L07–L09. doi: 10.1529/biophysj.108.132696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Zhou Y, Wu C, Zhao L, Huang N. Exploring the early stages of the pH-induced conformational change of influenza hemagglutinin: pH sensing in influenza hemagglutinin. Proteins Struct Funct Bioinf. 2014;82:2412–2428. doi: 10.1002/prot.24606. [DOI] [PubMed] [Google Scholar]
- 60.Ivanovic T, Choi JL, Whelan SP, van Oijen AM, Harrison SC. Influenza-virus membrane fusion by cooperative fold-back of stochastically induced hemagglutinin intermediates. eLife. 2013;2:e00333. doi: 10.7554/eLife.00333. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Chen J, et al. A soluble domain of the membrane-anchoring chain of influenza virus hemagglutinin (HA2) folds in Escherichia coli into the low-pH-induced conformation. Proc Natl Acad Sci USA. 1995;92:12205–12209. doi: 10.1073/pnas.92.26.12205. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Lee MS, Salsbury FR, Brooks CL. Constant-pH molecular dynamics using continuous titration coordinates. Proteins. 2004;56:738–752. doi: 10.1002/prot.20128. [DOI] [PubMed] [Google Scholar]
- 63.O Brien EP, Brooks BR, Thirumalai D. Effects of pH on proteins: Predictions for ensemble and single-molecule pulling experiments. J Am Chem Soc. 2012;134:979–987. doi: 10.1021/ja206557y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Goh GB, Knight JL, Brooks CL. Constant pH molecular dynamics simulations of nucleic acids in explicit solvent. J Chem Theor Comput. 2012;8:36–46. doi: 10.1021/ct2006314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Li H, Robertson AD, Jensen JH. Very fast empirical prediction and rationalization of protein pKa values. Proteins Struct Funct Bioinf. 2005;61:704–721. doi: 10.1002/prot.20660. [DOI] [PubMed] [Google Scholar]
- 66.Zwanzig RW. High-temperature equation of state by a perturbation method. I. Nonpolar gases. J Chem Phys. 1954;22:1420–1426. [Google Scholar]
- 67.Zang T, Yu L, Zhang C, Ma J. Parallel continuous simulated tempering and its applications in large-scale molecular simulations. J Chem Phys. 2014;141:044113. doi: 10.1063/1.4890038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Páll S, Abraham MJ, Kutzner C, Hess B, Lindahl E. Tackling Exascale software challenges in molecular dynamics simulations with GROMACS. In: Markidis S, Laure E, editors. Solving Software Challenges for Exascale. Vol. 8759. Springer International; Cham, Switzerland: 2015. pp. 3–27. [Google Scholar]
- 69.Bonomi M, et al. Plumed: A portable plugin for free-energy calculations with molecular dynamics. Comput Phys Commun. 2009;180:1961–1972. [Google Scholar]
- 70.Rosta E, Hummer G. Free energies from dynamic weighted histogram analysis using unbiased Markov state model. J Chem Theor Comput. 2015;11:276–285. doi: 10.1021/ct500719p. [DOI] [PubMed] [Google Scholar]
- 71.Kumar S, Rosenberg JM, Bouzida D, Swendsen RH, Kollman PA. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J Comput Chem. 1992;13:1011–1021. [Google Scholar]
- 72.Baker EN, Hubbard RE. Hydrogen bonding in globular proteins. Prog Biophys Mol Biol. 1984;44:97–179. doi: 10.1016/0079-6107(84)90007-5. [DOI] [PubMed] [Google Scholar]
- 73.McDonald IK, Thornton JM. Satisfying hydrogen bonding potential in proteins. J Mol Biol. 1994;238:777–793. doi: 10.1006/jmbi.1994.1334. [DOI] [PubMed] [Google Scholar]
- 74.Noel JK, Whitford PC, Onuchic JN. The shadow map: A general contact definition for capturing the dynamics of biomolecular folding and function. J Phys Chem B. 2012;116:8692–8702. doi: 10.1021/jp300852d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Zhang Y, et al. Influenza research database: An integrated bioinformatics resource for influenza virus research. Nucleic Acids Res. 2017;45:D466–D474. doi: 10.1093/nar/gkw857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Katoh K. MAFFT: A novel method for rapid multiple sequence alignment based on fast Fourier transform. Nucleic Acids Res. 2002;30:3059–3066. doi: 10.1093/nar/gkf436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Air GM. Sequence relationships among the hemagglutinin genes of 12 subtypes of influenza A virus. Proc Natl Acad Sci USA. 1981;78:7639–7643. doi: 10.1073/pnas.78.12.7639. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.