Origin of Jupiter’s cloud-level zonal winds remains a puzzle even after Juno

Significance

How the Jovian cloud-level zonal winds are generated and maintained has been a major scientific puzzle for decades. There are two main contenders to explain the origin of the winds: (i) They are maintained and generated by deep thermal convection and extend deep into Jupiter’s interior and (ii) they are associated with horizontal temperature differences between belts and zones and confined to a very thin stably stratified weather layer below which there exists an unknown convective circulation. We show that the Juno gravitational measurements alone cannot discriminate between these two different scenarios. The origin of the winds is still a mystery.

Abstract

How far Jupiter’s cloud-level zonal winds penetrate into its interior, a question related to the origin of the winds, has long been a major puzzle about Jupiter. There exist two different views: the shallow scenario in which the cloud-level winds are confined within the thin weather layer at cloud top and the deep scenario in which the cloud-level winds manifest thermal convection in the deep interior. We interpret, using two different models corresponding to the two scenarios, the high-precision measurements of Jupiter’s equatorially antisymmetric gravitational field by the Juno spacecraft. We demonstrate, based on the thermal-gravitational wind equation, that both the shallow and deep cloud-level winds models are capable of explaining the measured odd gravitational coefficients within the measured uncertainties, reflecting the nonunique nature of the gravity inverse problem. We conclude that the high-precision Juno gravity measurements cannot provide an answer to the long-standing question about the origin of Jupiter’s cloud-level zonal winds.

Even though alternating cloud-level zonal winds on Jupiter have been accurately measured for several decades (1–3), their depth of penetration into its interior, a question closely linked with the origin of the winds, is still uncertain. Since an internal zonal flow with sufficiently large amplitude can generate an externally measurable gravitational signature by inducing substantial density anomalies (4–6), it was hoped that the high-precision measurements of Jupiter’s gravitational field by the Juno spacecraft (7–9) would provide an opportunity to answer this long-standing question (4, 10–12).

There are two profoundly different views on the origin of the cloud-level zonal winds of Jupiter, suggesting two different models for the interpretation of the gravitational coefficients provided by the Juno spacecraft (9). One view is that the cloud-level zonal winds are shallow and confined within a thin, stably stratified weather layer about 70 km thick at cloud top in which the winds are associated with horizontal temperature differences between belts and zones (13, 14) and there exists a thick convection layer (15–17) beneath the thin weather layer. In this scenario, the fast cloud-level winds do not penetrate into the deep interior and the thin weather layer contains less than $10^{-4}\%$ of Jupiter’s total mass so the weather-layer zonal flow cannot be responsible for the measured gravitational coefficients. We refer to the first scenario as the shallow cloud-level winds model in this paper, which is also referred to as the $1\frac{1}{2}$-layer model (16, 17) [the fast zonal winds with $\text{O}\left(100\right)$ m/s are confined in the thin, stably stratified weather layer (the 1 layer) while an unknown slow circulation of $\text{O}\left(10\right)$ m/s occupies the underlying thick convection layer (the $\frac{1}{2}$ layer); see, for example, the $1\frac{1}{2}$-layer model discussed by Thomson and McIntyre (17)]. The most significant feature of the shallow cloud-level winds model is that the cloud-level structure of the fast zonal winds does not extend into Jupiter’s interior and, hence, an a priori unknown slow circulation taking place in the underlying thick convection layer accounts for the measured gravitational signal. The shallow-layer concept has actually received support from Juno’s observations of clusters of cyclones in the polar regions (18). Shallow-layer theory predicts Jupiter’s low-latitude axisymmetric zones and belts and it also predicts that they give way to cyclonic activity at higher latitudes (19–22). The second view, the deep convection scenario, is that the cloud-level winds are generated and maintained by thermal convection in the deep interior and penetrate into the interior so that the profile of the deep zonal flow is revealed at cloud top (23–26). According to this scenario, the cloud-level winds are directly linked with the amplitude and structure of the deep flow that produces the measured gravitational signal. We refer to the second scenario as the deep cloud-level winds model in this paper. The most significant feature of the deep cloud-level winds model is that the cloud-level structure extends into Jupiter’s interior and, hence, the fast zonal winds whose deep structure reflects its cloud-level pattern account for the measured gravitational signal. It has been claimed that the Juno gravitational measurements confirm this scenario (12) although we show here that the model is only one possibility that cannot be said to be the real Jupiter.

The equatorially symmetric and antisymmetric components of Jupiter’s gravitational field contain different information about its interior. The equatorially symmetric gravitational field, represented by even gravitational coefficients $J_{2n},n=\mathrm{1,2,3},\cdots$, is affected by both the rotational distortion of the planet and its fast equatorially symmetric zonal flow (6). It is difficult to accurately isolate the zonal-flow–induced contribution to the gravitational field (which is usually quite small) from the rotational-distortion–induced (which is usually dominant) contribution. Since the rotational distortion, because of its equatorial symmetry, does not contribute to the equatorially antisymmetric gravitational field (odd gravitational coefficients), this part of the field provides a direct window into the structure and amplitude of the internal zonal flow (10–12). In this paper, we therefore focus on the interpretation of the equatorially antisymmetric components of the Jovian gravitational field measured by the Juno spacecraft (9).

Following the two profoundly different views discussed above, we construct two different models, shallow and deep, for interpreting the four nonzero odd gravitational coefficients. The shallow cloud-level winds model assumes that the cloud-level winds are confined in the thin weather layer and, hence, its contribution to the measured gravitational signal is negligible. We then determine an unknown zonal flow in the underlying convection region constrained by the measured equatorially antisymmetric gravitational field without making a priori assumptions about the nature and structure of the flow. The deep cloud-level winds model, according to the deep convection scenario, assumes that the cloud-level winds structure extends into Jupiter’s interior and, hence, is responsible for the measured gravitational signal. This assumption allows us to construct a parameterized zonal flow whose cloud-level and internal structure/amplitude is constrained by the cloud-level profile.

The problem of determining fluid flow in the interior of a planet from its externally measured physical fields, such as its magnetic and gravitational fields, is characteristically nonunique. A well-known example is the determination of the fluid flow at the top of the Earth’s core from the measured external geomagnetic field (27–29). The core flow inferred from the geomagnetic field is necessarily nonunique, although the ambiguity can be reduced by placing various restrictions, such as the frozen-flux hypothesis and the tangentially geostrophic approximation, on the permitted flow (28, 29). In this study, we demonstrate that fluid flow inferred from the externally measured gravitational field of Jupiter is also necessarily nonunique: Both the shallow and deep zonal winds models are able to fully interpret the odd gravitational coefficients $J_{2n+1},n=\mathrm{1,2,3,4}$ within the measured uncertainties. It follows that the long-standing question about the origin of cloud-level winds cannot be answered by the high-precision measurements of Jupiter’s equatorially antisymmetric gravitational field.

Governing Equations

We assume that the equatorially antisymmetric zonal flow of Jupiter is characterized by small Rossby number, viscous forces are much smaller than the Coriolis forces, and its compressible fluid is described by the polytropic equation of state with index unity (4, 6, 30, 31). We also assume that Jupiter is uniformly rotating about the symmetry $z$ axis with the angular velocity $\mathrm{\Omega }=1.75853241\times 10^{-4}{\mathrm{s}}^{-\mathrm{1}}$, the effect of the rotational distortion on the equatorially antisymmetric gravitational field can be neglected (10–12), and the zonal flow is in a statistically steady state. The above assumptions lead to the following governing equations in the rotating frame of reference,

$$\begin{array}{ccc}\hfill 2\mathrm{\Omega }\widehat{\mathbf{z}}\times \mathbf{u}\left(\mathbf{r}\right)& =\hfill & -\frac{1}{\rho \left(\mathbf{r}\right)}\nabla p\left(\mathbf{r}\right)+\mathbf{g}\left(\mathbf{r}\right)+\frac{{\mathrm{\Omega }}^2}{2}\nabla {\left|\widehat{\mathbf{z}}\times \mathbf{r}\right|}^2\hfill \\ \hfill & \hfill & +\frac{1}{\rho \left(\mathbf{r}\right)}\mathbf{J}\left(\mathbf{r}\right)\times \mathbf{B}\left(\mathbf{r}\right),\hfill \end{array}$$ (1)

$$\nabla \cdot \left[\mathbf{u}\left(\mathbf{r}\right)\rho \left(\mathbf{r}\right)\right]=0,$$ (2)

where $\mathbf{r}$ is the position vector with the origin at the center of the figure, $\mathbf{u}\left(\mathbf{r}\right)$ represents the velocity of the equatorially antisymmetric zonal flow, $p\left(\mathbf{r}\right)$ is the pressure, $\rho \left(\mathbf{r}\right)$ is the density, $\mathbf{J}\left(\mathbf{r}\right)$ is the electric current, and $\mathbf{B}\left(\mathbf{r}\right)$ is the magnetic field. We then expand the pressure $p$, the density $\rho$, and the gravity $\mathbf{g}$ as

$$\begin{array}{ccc}\hfill & \hfill & p=p_0\left(\mathbf{r}\right)+p\prime \left(\mathbf{r}\right),\rho \left(\mathbf{r}\right)={\rho }_0\left(\mathbf{r}\right)+\rho \prime \left(\mathbf{r}\right),\hfill \\ \hfill & \hfill & \mathbf{g}\left(\mathbf{r}\right)={\mathbf{g}}_0\left(\mathbf{r}\right)+\mathbf{g}\prime \left(\mathbf{r}\right),\hfill \end{array}$$

where the leading-order solution, ($p_0,{\rho }_0,{\mathbf{g}}_0$), represents the Jovian hydrostatic state, and $\left(p\prime ,\rho \prime ,\mathbf{g}\prime \right)$ denotes the perturbations arising from the effect of the antisymmetric zonal flow $\mathbf{u}$, which are governed by the equation

$$2{\rho }_0\left(\mathrm{\Omega }\widehat{\mathbf{z}}\times \mathbf{u}\right)=-\nabla p\prime +{\mathbf{g}}_0\rho \prime +\mathbf{g}\prime {\rho }_0+\mathbf{J}\times \mathbf{B}.$$ (3)

Physically, when $\rho \prime$ is induced by the antisymmetric flow $\mathbf{u}$, the hydrostatic gravitational force ${\mathbf{g}}_0$ must be also perturbed to yield the corresponding gravitational perturbation $\mathbf{g}\prime$ which must be retained. Mathematically, the two terms, ${\mathbf{g}}_0\rho \prime$ and $\mathbf{g}\prime {\rho }_0$ in Eq. 3, are generally of the same order of magnitude.

A further assumption is that the electric current $\mathbf{J}$ is sufficiently weak such that the Lorentz force $\mathbf{J}\times \mathbf{B}$ can be neglected. This assumption restricts the location of the flow $\mathbf{u}$ to the outer molecular envelope where the electrical conductivity of the fluid is sufficiently small. Eq. 3 then leads to the thermal-gravitational wind equation (32) describing a mathematical relationship between the equatorially antisymmetric zonal flow $U_{asym}=\widehat{\varphi }\cdot \mathbf{u}$ and the wind-induced density perturbation $\rho \prime$,

$$\begin{array}{ccc}\hfill & \hfill & \frac{\rho \prime \left(r,\theta \right)g_0\left(r\right)}{r}-\frac{2\pi G\left(\mathrm{d}{\rho }_0/\mathrm{d}r\right)}{r}{\int }_0^{\pi }{\int }_0^R\frac{{\tilde{r}}^2\rho \prime \left(\tilde{r},\tilde{\theta }\right)}{\left|\mathbf{r}-\tilde{\mathbf{r}}\right|}\sin \tilde{\theta }\mathrm{d}\tilde{r}\mathrm{d}\tilde{\theta }\hfill \\ \hfill & \hfill & =2\mathrm{\Omega }{\int }_{\pi /2}^{\theta }\left[\cos \tilde{\theta }\frac{\partial }{\partial r}-\frac{\sin \tilde{\theta }}{r}\frac{\partial }{\partial \tilde{\theta }}\right]\left[{\rho }_0\left(r\right)U_{asym}\left(r,\tilde{\theta }\right)\right]\mathrm{d}\tilde{\theta },\hfill \end{array}$$ (4)

where $\mathbf{r}=\mathbf{r}\left(r,\theta \right)$, $\tilde{\mathbf{r}}=\tilde{\mathbf{r}}\left(\tilde{r},\tilde{\theta }\right)$, and the second term on the left side, a 2D kernel integral with Green’s function in its integrand, represents the gravitational perturbation produced by the density perturbation $\rho \prime$. We have adopted spherical polar coordinates $\left(r,\theta ,\varphi \right)$ with $\theta =0$ at the axis of Jupiter’s rotation and the corresponding unit vectors $\left(\widehat{\mathbf{r}},\widehat{\theta },\widehat{\varphi }\right)$. It is Green’s function $1/\left|\mathbf{r}-\tilde{\mathbf{r}}\right|$ in its integrand that causes the difficulty in obtaining an accurate numerical solution of this integral equation. Two important features of Eq. 4 should be highlighted. First, the two terms on the left side of Eq. 4 are generally comparable in size and, hence, the integral term cannot be neglected. Second, the zonal flow $U_{asym}$ in the inhomogeneous integral Eq. 4 must satisfy the required solvability condition: Its solution exists if and only if its inhomogeneous term (the term on its right side) satisfies the solvability condition (11, 33). As in many physical problems governed by inhomogeneous differential or integral equations, it is the solvability condition that helps to select mathematically acceptable and physically relevant solutions.

It should be pointed out that the results of Kaspi (10) and Kaspi et al. (12) are based on the thermal wind equation,

$$\rho \prime \left(r,\theta \right)=\frac{2r\mathrm{\Omega }}{g_0}{\int }_{\pi /2}^{\theta }\left[\cos \tilde{\theta }\frac{\partial }{\partial r}-\frac{\sin \tilde{\theta }}{r}\frac{\partial }{\partial \tilde{\theta }}\right]\left({\rho }_0{U}_{asym}\right)\mathrm{d}\tilde{\theta },$$ (5)

which neglects the integral term on the left side of Eq. 4 and, hence, represents a diagnostic relation. A “solution” $\rho \prime \left(r,\theta \right)$ for Eq. 5 always exists for any given $U_{asym}\left(r,\theta \right)$ and, thus, the solution is not valid when the constructed flow $U_{asym}\left(r,\theta \right)$ violates the solvability condition. Even for a constructed flow $U_{asym}\left(r,\theta \right)$ that satisfies the solvability condition, there is a typically more than 100% difference (33) between the results of Eqs. 4 and 5, which will be discussed further.

Models and Methods

Our shallow model assumes that the cloud-level zonal winds are confined in the thin weather layer and, because it contains too little mass, cannot produce the measured gravitational signal. Since the nature of the zonal flow in the underlying convection layer that produces the gravitational signal is unknown (17), we cannot make a priori assumptions about the amplitude and structure of the flow. We thus expand, following the theory of spherical inertial eigenfunctions in rotating spheres—whose general explicit analytical expressions are available (34) and which are mathematically complete (35)—an equatorially antisymmetric zonal flow $U_{asym}\left(r,\theta \right)$ in the general form

$$U_{asym}\left(r,\theta \right)=\widehat{\varphi }\cdot \left\{\sum _{k=1}^K\sum _{n=1}^k\left[{\mathcal{A}}_{kn}{\mathbf{u}}_{nk}\left(r,\theta \right)+c.c.\right]\right\},$$ (6)

where ${\mathcal{A}}_{kn}$ are complex coefficients to be determined, $c.c.$ denotes the complex conjugate of the preceding term, and the inertial eigenfunctions ${\mathbf{u}}_{nk}\left(r,\theta \right)$ are given by the double polynomials

$$\begin{array}{ccc}\hfill \widehat{\mathbf{r}}\cdot {\mathbf{u}}_{nk}& =\hfill & -\frac{\text{i}}{2}\sum _{i=0}^k\sum _{j=0}^{k-i}{\mathcal{C}}_{kij}\left[{\sigma }_{nk}^2\left(2i+2j+1\right)-\left(2i+1\right)\right]\hfill \\ \hfill & \times \hfill & \left[r^{2\left(i+j\right)}{\sigma }_{nk}^{2i-1}{\left(1-{\sigma }_{nk}^2\right)}^{j-1}{\sin }^{2j}\theta {\cos }^{2i+1}\theta \right],\hfill \\ \hfill \widehat{\theta }\cdot {\mathbf{u}}_{nk}& =\hfill & -\frac{\text{i}}{2}\sum _{i=0}^k\sum _{j=0}^{k-i}{\mathcal{C}}_{kij}\left[2j{\sigma }_{nk}^2{\cos }^2\theta +\right.\hfill \\ \hfill & \hfill & \left.\left(2i+1\right)\left(1-{\sigma }_{nk}^2\right){\sin }^2\theta \right]\hfill \\ \hfill & \times \hfill & \left[r^{2\left(i+j\right)}{\sigma }_{nk}^{2i-1}{\left(1-{\sigma }_{nk}^2\right)}^{j-1}{\sin }^{2j-1}\theta {\cos }^{2i}\theta \right],\hfill \\ \hfill \widehat{\varphi }\cdot {\mathbf{u}}_{nk}& =\hfill & \frac{1}{2}\sum _{i=0}^k\sum _{j=0}^{k-i}{\mathcal{C}}_{kij}{r}^{2\left(i+j\right)}{\sigma }_{nk}^{2i}{\left(1-{\sigma }_{nk}^2\right)}^{j-1}\hfill \\ \hfill & \times \hfill & \left(2j\right){\sin }^{2j-1}\theta {\cos }^{2i+1}\theta ,\hfill \end{array}$$

with $k=\mathrm{1,2},\dots$, $\text{i}=\sqrt{-1}$, ${\mathcal{C}}_{kij}$ defined as

$${\mathcal{C}}_{kij}=\frac{{\left(-1\right)}^{i+j}\left[2\left(k+i+j\right)+1\right]‼}{2^{j+1}\left(2i+1\right)‼\left(k-i-j\right)!i!{\left(j!\right)}^2},$$

and the eigenvalues ${\sigma }_{nk}$ are solutions of

$$\sum _{j=0}^k\left\{\frac{{\left(-1\right)}^j\left[2\left(2k-j+1\right)\right]!}{j!\left[2\left(k-j\right)\right]!\left(2k-j+1\right)!}\right\}{\sigma }_{nk}^{2\left(k-j\right)}=0,$$ (7)

where $k$ varies over all positive integers. For each given $k$, Eq. 7 has $k$ real distinct positive eigenvalues within $0<{\sigma }_{nk}<1$ which are arranged according to the size of ${\sigma }_{nk}$, $0<{\sigma }_{1k}<{\sigma }_{2k}<{\sigma }_{3k},\dots .$ For instance, the simplest equatorially antisymmetric eigenfunction is given by $k=1$ and $n=1$ with its eigenvalue ${\sigma }_{11}=\sqrt{5}/5$ and the corresponding complex eigenfunction ${\mathbf{u}}_{11}$ given by

$$\begin{array}{ccc}\hfill {\mathbf{u}}_{11}\left(r,\theta \right)& =\hfill & \widehat{\mathbf{r}}\frac{\text{i}3\sqrt{5}}{4}\left(1-r^2\right)\cos \theta +\widehat{\theta }\frac{\text{i}3\sqrt{5}}{4}\left(2r^2-1\right)\sin \theta \hfill \\ \hfill & \hfill & -\widehat{\varphi }\frac{15}{8}{r}^2\sin 2\theta .\hfill \end{array}$$

The eigenfunctions ${\mathbf{u}}_{nk}$ have already captured some key dynamical features of rotating flow and, thus, are particularly suitable for this inverse problem searching for a rotating flow in Jupiter’s interior. It should be stressed that the expansion Eq. 6 can be used, because of the mathematical completeness of spherical inertial eigenfunctions, to represent an arbitrary equatorially antisymmetric zonal flow that is continuous and differentiable. We truncate the expansion Eq. 6 at $K=6$ (corresponding to all of the double polynomials up to the degree 12) for modeling the odd harmonics up to $J_{2n+1}$ with $n=4$ because the higher-degree polynomials cannot be constrained by the measured gravitational harmonics. Moreover, the equatorially antisymmetric flow $U_{asym}\left(r,\theta \right)$ given by Eq. 6 satisfies the solvability condition required for the inhomogeneous integral Eq. 4.

With the flow $U_{asym}\left(r,\theta \right)$ given by Eq. 6, we then solve the integral Eq. 4 numerically, using an extended spectral method together with a special set of $r-\theta$ grids in spherical geometry, a method discussed in detail by Zhang et al. (32). Constrained by the odd coefficients $J_{2n+1},n=\mathrm{1,2,3,4}$ measured by the Juno spacecraft (9), we use an iterative procedure, via the thermal-gravitational wind Eq. 4, between an equatorially antisymmetric zonal flow $U_{asym}\left(r,\theta \right)$ and the four odd gravitational coefficients to determine the flow $U_{asym}\left(r,\theta \right)$ that gives rise to the four odd coefficients within the measured uncertainties. This iterative process, performed on modern massively parallel computers, is computationally expensive and lengthy, a consequence of the integral Eq. 4 marked by a 2D kernel integral in the form of Green’s function. The zonal flow inferred from the four odd gravitational coefficients in this way is necessarily nonunique. But the ambiguity is largely removed by a further restriction that the Lorentz force $\mathbf{J}\times \mathbf{B}$ in the solution domain must be sufficiently weak and, hence, the flow $U_{asym}\left(r,\theta \right)$ must be located within the outermost region where both the electrical conductivity of the fluid and the Lorentz force are small.

Our second model follows the deep convection scenario by constructing a highly constrained zonal flow. The structure and amplitude of the flow at cloud level $U_{asym}\left(r=R,\theta \right)$ is prescribed, together with an assumption that its amplitude decreases with increasing depth. We parameterize the radial structure by introducing two parameters $H$ and $h$,

$$\begin{array}{ccc}\hfill U_{asym}\left(r,\theta \right)& =\hfill & U_0\left(r\sin \theta \right)\frac{|r\cos \theta |}{\sqrt{R^2-r^2{\sin }^2\theta }}\hfill \\ \hfill & \times \hfill & {\text{e}}^{\frac{1}{h}\left[1-\frac{H^2}{H^2-{\left(R-r\right)}^2}\right]},\hfill \end{array}$$ (8)

$$\begin{array}{ccc}\hfill & \hfill & \text{in}0\le \theta \le \frac{\pi }{2},\hfill \end{array}$$

where $\left(R-H\right)\le r\le R$, $U_0\left(R\sin \theta \right)$ represents the observed antisymmetric zonal winds at cloud level in the northern hemisphere, $U_0\left(R\sin \theta \right)=-U_0\left(R\sin \theta \right)$ in the southern hemisphere $\pi /2\le \theta \le \pi$ because of the equatorial antisymmetry, $H$ denotes the thickness of an outer spherical shell in which the zonal flow is confined, i.e., $U_{asym}\left(r\le \left(R-H\right),\theta \right)=0$, and $h$ is related to its decay rate with depth. The higher-order terms, such as those proportional to ${\left(r\cos \theta \right)}^3$ and ${\left(r\cos \theta \right)}^5$, are not included in the ansatz function 8 because the structure of a convective flow under the controlling influence of rapid rotation is expected to be dominated by weak variations along the rotation axis (23, 24). Since the cloud-level antisymmetric flow $U_0\left(R\sin \theta \right)$ is derived by subtracting the dominant symmetric component from the observed zonal winds, its speed at the sharp spike near latitude $20^{○}$ is highly sensitive to any inaccuracy in the observations (3). Moreover, since the $20^{○}$ spike may be significantly distorted by the Great Red Spot in the southern hemisphere, we choose the flow speed at the spike, $U_{spike}$, as an additional parameter. Note that the existing measurements (3) suggest $U_{spike}=61.8$ m/s at the $20^{○}$ spike latitude. For given values of $H$, $h$, and $U_{spike}$, an iterative procedure is then performed, via the thermal-gravitational wind Eq. 4, between the constructed flow given by Eq. 8 and the four odd gravitational coefficients (9) to determine the optimized values of $H$, $h$, and $U_{spike}$. In comparison with the shallow cloud-level winds model, the iterative process involving the three parameters is computationally inexpensive.

It should be noted that the zonal flow $U_{asym}\left(r,\theta \right)$, given by Eq. 6 or Eq. 8, is continuous and differentiable everywhere and satisfies the required solvability condition. Consequently, solutions of Eq. 4 exist and are numerically convergent. By contrast, the constructed zonal flow used by Kaspi et al. (12) (their equations 12–14) is discontinuous across the equatorial plane and violates the required solvability condition. When their constructed flow is used in solving Eq. 4, solutions of Eq. 4 would be numerically divergent, reflecting a key mathematical property of the inhomogeneous integral Eq. 4. The nonphysical effect of the equatorial discontinuity on solutions of the thermal wind Eq. 5 is discussed in detail in Kong et al. (36).

Results

The physical and mathematical principles of the problem are well understood (4, 11). If an equatorially antisymmetric zonal flow $U_{asym}$ exists somewhere in Jupiter’s interior, it will induce a density perturbation $\rho \prime$ and a concomitant gravitational perturbation $\mathbf{g}\prime$, both of which are equatorially antisymmetric. A relationship between the antisymmetric gravitational perturbation $\mathbf{g}\prime$, the antisymmetric density perturbation $\rho \prime$, and the antisymmetric zonal flow $U_{asym}$ in spherical geometry is mathematically described by Eq. 4. After obtaining $\rho \prime$ from Eq. 4 with a given $U_{asym}$, one can compute the odd zonal gravitational coefficients $J_{2n+1}$ by performing the 2D integration

$$\begin{array}{ccc}\hfill J_{2n+1}=& -\hfill & \frac{4\pi }{M_J{R}^{2n+1}}{\int }_0^{\pi /2}{\int }_0^R\rho \prime \left(r,\theta \right)P_{2n+1}\left(\cos \theta \right)\hfill \\ \hfill & \hfill & \times \sin \theta r^{2n+3}\mathrm{d}r\mathrm{d}\theta ,\hfill \end{array}$$ (9)

for $n=\mathrm{1,2,3,4}$, where $P_{2n+1}\left(\cos \theta \right)$ is the Legendre polynomial, $M_J=1.8983556\times 10^{27}\mathrm{k}\mathrm{g}$ is Jupiter’s mass, and $R=\mathrm{69,911}\mathrm{k}\mathrm{m}$ is the mean radius of Jupiter at the one-bar surface. The four zonal gravitational coefficients, $J_{2n+1},n=\mathrm{1,2,3,4}$ measured by the Juno spacecraft (9), are listed in Table 1. With the thermal-gravitational wind Eq. 4 (connecting the antisymmetric flow $U_{asym}$ to the density perturbation $\rho \prime$) and the above integral (connecting the density perturbation $\rho \prime$ to the odd coefficients $J_{2n+1},n=\mathrm{1,2,3,4}$ measured by the Juno spacecraft), we can invert the zonal flow $U_{asym}\left(r,\theta \right)$ for the two different models.

Table 1.

Three sets of the odd zonal gravitational coefficients $J_{2n+1},n=\mathrm{1,2,3,4}$: measured by the Juno spacecraft (9) and computed from both the shallow and deep cloud-level winds models using the thermal-gravitational wind Eq. 4

Odd coefficients	Measured	Deep model	Shallow model
$J_3/10^{-8}$	$-4.24\pm 0.91$	−3.54	−4.24
$J_5/10^{-8}$	$-6.89\pm 0.81$	−7.56	−6.83
$J_7/10^{-8}$	$12.39\pm 1.68$	12.62	12.33
$J_9/10^{-8}$	$-10.58\pm 4.35$	−9.28	−10.03

Both of our models are able to produce all of the four odd gravitational coefficients measured by the Juno spacecraft within the error bars.

We first discuss the results of the shallow cloud-level winds model, which are computationally much more challenging. Through an iterative procedure, via the thermal-gravitational wind Eq. 4, between the expansion coefficients and the measured odd gravitational coefficients, we are able to derive an antisymmetric zonal flow that not only produces the measured odd coefficients $J_{2n+1},n=\mathrm{1,2,3,4}$ but also is consistent with the known dynamics taking place in Jupiter’s interior. The meridional cross-section of the antisymmetric zonal flow derived from this shallow model is depicted in Fig. 1; the corresponding gravitational coefficients $J_{2n+1},n=\mathrm{1,2,3,4}$ produced by this flow are presented in Table 1. For quantifying the depth of the flow, we introduce the kinetic energy $Q\left(r\right)$ averaged on a spherical surface of radius $r$,

$$Q\left(r\right)=\frac{1}{8\pi }{\int }_0^{2\pi }{\int }_0^{\pi }{\left|U_{asym}\left(r,\theta \right)\right|}^2\sin \theta \mathrm{d}\theta \mathrm{d}\varphi ,$$ (10)

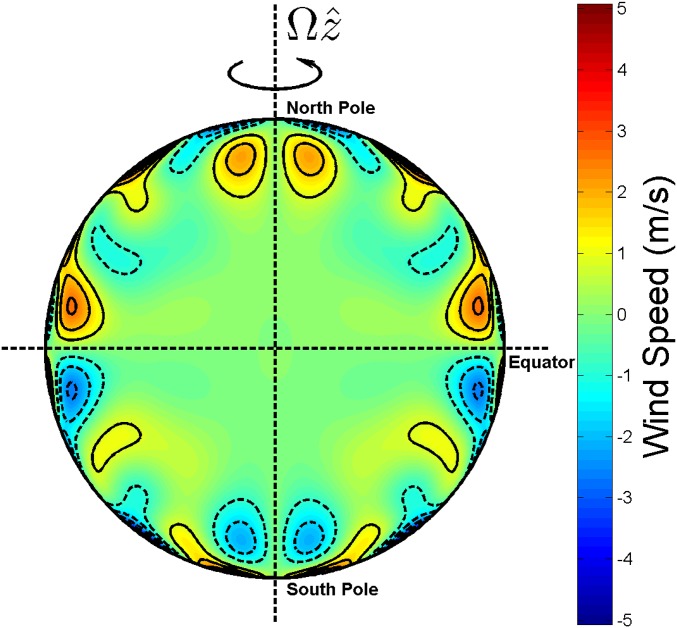
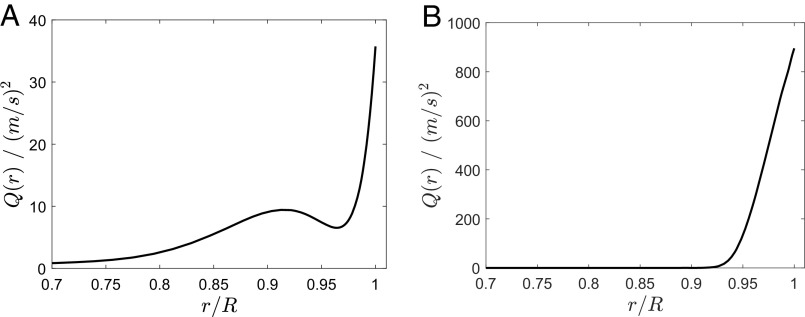
which is dimensional with the unit ${\left(\text{m/s}\right)}^2$. Three significant features of the results should be highlighted. First, the antisymmetric zonal flow in Fig. 1 derived from the shallow cloud-level winds model produces all of the four odd gravitational coefficients (9) measured by the Juno spacecraft within the error bars, as shown in Table 1. Second, the slow antisymmetric zonal flow in the underlying convection layer has an amplitude of $\text{O}\left(1\right)$ m/s which is much smaller than $\text{O}\left(100\right)$ m/s in the weather layer, being consistent with the picture of the shallow cloud-level winds model (16, 17). Third, the corresponding kinetic energy $Q\left(r\right)$, as shown in Fig. 2A, decreases rapidly from the outer surface and, then, extends slowly with a small amplitude to a depth of about $0.20R\sim 0.25R$, indicating that the underlying nonmagnetic convection layer has a thickness of about $0.20R\sim 0.25R$. These features are consistent with Jovian convective dynamo simulations showing that the transition zone between the dynamo and the molecular region is in the range from $0.7R$ to $0.9R$ (37, 38).

Fig. 1.

The meridional cross-section of the equatorially antisymmetric zonal flow, derived from the thermal-gravitational wind Eq. 4 and following the shallow scenario without making any a priori assumptions about its amplitude and structure, that gives rise to all of the odd gravitational coefficients measured by the Juno spacecraft within the error bars.

Fig. 2.

(A and B) The kinetic energy $Q\left(r\right)$ of the equatorially antisymmetric zonal flow derived from the shallow cloud-level winds model as a function of $r/R$ (A) and the profile of $Q\left(r\right)$ derived from the deep cloud-level winds model as a function of $r/R$ (B).

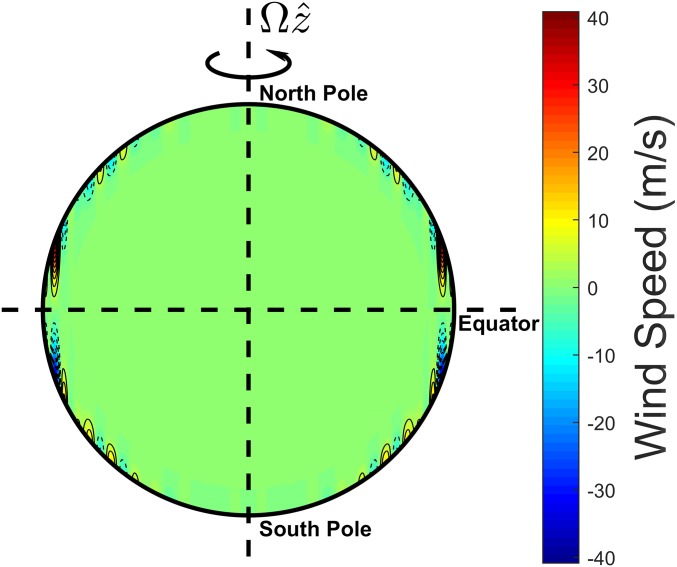
We now discuss the results of the deep cloud-level winds model, which, because it is highly constrained, is computationally much less challenging. For given values of $H$, $h$, and $U_{spike}$, an iterative procedure is performed, via the thermal-gravitational wind Eq. 4, between the constructed flow given by Eq. 8 and the four odd gravitational coefficients (9) to determine the optimized values of $H$, $h$, and $U_{spike}$. We found that the constructed flow given by Eq. 8 with $H=0.15R$, $h=0.22$, and $U_{spike}=43.2$ m/s produces the four odd coefficients $J_3,J_5,J_7,J_9$ within the error bars, which are presented in Table 1 along with the corresponding measured values. The meridional cross-section of the antisymmetric flow derived from this deep model is depicted in Fig. 3. The corresponding profile of $Q\left(r\right)$ is depicted in Fig. 2B, showing that $Q\left(r\right)$ decreases sharply from the outer surface to nearly zero at a depth of about $0.07R$. Although the spherical shell with $H=0.15R$ is relatively thick, the flow is primarily confined in the outermost part of the shell. It is noteworthy that even though the prescribed antisymmetric flow has large amplitude, a substantial penetration depth about $0.07R$ is still required to account for the four odd coefficients measured by the Juno spacecraft. This is because the large-amplitude flow is mainly restricted only to a narrow region near the red spot in the Jovian southern hemisphere and, hence, has a limited global gravitational contribution. In this deep model, the cloud-level zonal winds penetrate into the deep molecular region and, because of the Taylor–Proudman theorem, approximately align along the rotation axis of Jupiter.

Fig. 3.

The meridional cross-section of the equatorially antisymmetric zonal flow, derived from the thermal-gravitational wind Eq. 4 and following the deep scenario, that gives rise to all of the odd gravitational coefficients measured by the Juno spacecraft within the error bars.

Finally, we mention two significant points. First, while both our shallow and deep cloud-level winds models are able to produce the odd coefficients to within the stated uncertainties (9), we cannot rule out the existence of other models that are also able to fit the odd coefficients to within the uncertainties. Second, the reported uncertainties (9) are already an inflation by a factor of 3 of the formal uncertainties, indicating that ample freedom has already been given for a model to fit the data.

Conclusions and Remarks

A great mystery of our solar system is how deeply Jupiter’s cloud-level zonal winds penetrate into its interior, a question closely linked with the origin of the winds. We have constructed two profoundly different models, the shallow cloud-level winds model or the $1\frac{1}{2}$-layer model (the cloud-level structure of the fast zonal winds does not extend into Jupiter’s interior and an a priori unknown slow circulation in the underlying thick convection layer accounts for the measured gravitational signal) and the deep cloud-level winds model (the cloud-level structure extends into Jupiter’s interior and the fast zonal winds whose deep structure reflects its cloud-level pattern account for the measured gravitational signal) to successfully interpret the high-precision measurements of Jupiter’s equatorially antisymmetric gravitational field by the Juno spacecraft (9). We have demonstrated that the gravity inverse problem—determining the equatorially antisymmetric zonal flow from the four odd gravitational coefficients measured by the Juno spacecraft—is necessarily nonunique. Both of our models can be used to fully interpret the measured equatorially antisymmetric gravitational field of Jupiter by producing the four odd coefficients to within the measured uncertainties. We thus conclude that the question about the origin of Jupiter’s cloud-level winds, because of the nonunique nature of the problem, remains unanswered even after the high-precision Juno gravity measurements.

Our conclusion is based on solutions of the thermal-gravitational wind Eq. 4 in which the two terms on its left side are generally comparable in size. For example, using the flow shown in Fig. 1 which satisfies the required solvability condition, Eq. 4 gives $J_3=-4.24$ (Table 1), but neglecting the integral term on the left side of Eq. 4 [i.e., the thermal wind Eq. 5 used by Kaspi et al. (12)] yields $J_3=-0.97$, corresponding to nearly a 500% difference. This is why, in both our shallow and deep cloud-level winds models, we have adopted Eq. 4 even though its solution is computationally much more difficult and demanding. Some special profile $U_{asym}\left(r,\theta \right)$ might produce $\rho \prime \left(r,\theta \right)$ that has a special structure (for instance, an alternating positive and negative pattern leading to an average cancellation) such that the integral term on the left side of Eq. 4 is small compared with the first term and, thus, negligible. In this special case, however, the integral term can be neglected only a posteriori. There are no physical or mathematical reasons to justify the a priori neglect of the integral term in Eq. 4. We are also unable to obtain any numerically convergent solution of Eq. 4 when the constructed flow used by Kaspi et al. (12) is adopted, a consequence of the violation of the solvability condition by their constructed flow.

Since the rotational distortion of Jupiter, because of its equatorial symmetry, does not contribute to the odd coefficients, the four odd coefficients measured by the Juno spacecraft directly reflect, although nonuniquely, the structure and amplitude of the equatorially antisymmetric zonal flow taking place in the interior of Jupiter. Since the equatorially antisymmetric zonal flow is usually produced by the instabilities of an equatorially symmetric zonal flow (25, 26, 39), the structure and amplitude of the equatorially symmetric zonal flow in the Jovian interior are closely coupled with the equatorially antisymmetric flow.

What do we learn about the Jovian interior from our two different models that are constrained by the equatorially antisymmetric gravitational field measured by the Juno spacecraft? Our shallow cloud-level winds model paints the following picture. In the outermost stably stratified weather layer about 70 km thick, there are fast zonal winds of $\text{O}\left(100\right)$ m/s associated with horizontal temperature differences between belts and zones which do not account for the measured gravitational signal; the underlying convection layer about $0.20R\sim 0.25R$ thick with a zonal flow of the amplitude $\text{O}\left(1\right)$ m/s is required to account for the measured gravitational signal; and, hence, according to this model, the Jovian dynamo [which is marked by the strong magnetohydrodynamic braking effect (40) and, thus, by a small-amplitude zonal flow (37, 38) ($\ll \text{O}\left(1\right)$ m/s)] is likely to operate in the region $0.1R<r\le 0.75R\sim 0.80R$, where the radius of the solid core is assumed to be $0.1R$. Our deep cloud-level winds model paints a profoundly different picture of the Jovian interior. In the outer region $0.93R\le r\le R$, nonmagnetic thermal convection generates and maintains fast alternating zonal flows with an amplitude $\text{O}\left(100\right)$ m/s whereas the cloud-level winds, owing to the Taylor–Proudman theorem, just manifest the structure and amplitude of the deep convection. Consequently, the Jovian dynamo is likely to operate in the region $0.1R<r\le 0.93R$ which is significantly larger than that predicted by the shallow cloud-level winds model. The Juno gravitational measurements alone are incapable of discriminating between the shallow and deep cloud-level winds models discussed in this study. If the accurate magnetic field measurements are able to precisely locate the Jovian dynamo operating region, the question on the origin of Jupiter’s cloud-level winds may be answered by the help of additional constraints imposed by its magnetic field.