Noise cancellation for a whole-head magnetometer-based MEG system in hospital environment

Abstract

We describe a strategy of removing magnetic field interference for a whole-head pediatric magnetoencephalography (MEG) system (“babyMEG”) installed in a hospital. The 375-channel sensor array of babyMEG consists entirely of magnetometers in two layers to maximize the sensitivity for detecting MEG signals from infants, toddlers, and young children. It is equipped with a continuously operating closed-cycle helium recycler to reduce the operating costs. These two features pose special challenges for noise cancellation. Our strategy uses a combination of several methods. The system is installed in a light-weight, magnetically shielded room (MSR) equipped with an active external shielding. In addition we employ two software-based techniques - a signal space projection (SSP) technique and a synthetic gradiometer (SG) method – for removing the environmental magnetic noise in real time and displaying the output online. The shielding effects are: passive shielding – 36 dB, active shielding – 12 dB, SSP – 40 dB and SG – 40 dB, for a combined maximum shielding of about 90 dB at 0.1 Hz. We evaluated the performance of the babyMEG after applying the noise cancellation techniques. The dipole localization errors were <3 mm after averaging 50 epochs with empty room noise in a simulation study for dipoles >10 nAm, which is in the low range of empirically observed dipole moments. In a phantom study with realistic environmental noise, we could clearly recover an evoked cortical magnetic field produced by a 20 nAm dipole after averaging 50 epochs. The localization error was ~6 mm after averaging 20 epochs. In infants, we could clearly detect a somatic evoked field after averaging ~20 responses. The unique two-layer sensor design combined with the SSP or SG provides effective noise suppression for a magnetometer-based pediatric MEG system in hospital environment with the closed-cycle helium recycler operating continuously during MEG measurements.

1. Introduction

We have recently developed a 375-channel whole-head pediatric MEG system (“babyMEG”) (Okada et al 2016). This system has been fully operational since 2016 in an MEG facility of Boston Children’s Hospital, located on the 7^th floor next to a 3T MR scanner and the NICU (Neonatal Intensive Care Unit). We had several design targets in developing this system. First, the sensor array was designed to maximize the MEG signals from children with a wide range of head sizes younger than 3–4 years of age so that the instrument could be used as a noninvasive neuroimaging tool in advancing our understanding of the early electrophysiological development of the human brain. The helmet containing the sensor array is fixed in size and shape. Therefore, the gap between the sensor array and the head may be quite large when the head is much smaller than the helmet. To maximize the signal strength even for smaller heads, we used a sensor array consisting solely of magnetometers since they are more sensitive to distant sources than gradiometers. However, magnetometers also detect more environmental noises than gradiometers because magnetometers can sense both the uniform fields and the rapidly changing fields while gradiometers are insensitive to the uniform fields. Technically, the axial gradiometers are only sensitive to the spatial gradient of the field and the planer gradiometers are only sensitive to the gradient of the perpendicularly oriented magnetic fields but in a direction parallel to the plane of the coils (Cheyne and Papanicolaou, 2017). Second, we designed the babyMEG to operate in a lightly magnetically shielded room (MSR). This, however, required us to design the noise cancellation method with a large shielding factor (SF) to compensate for the relatively poor SF of the MSR. The SF can be generally defined as the ratio of the magnetic fields in the center of a room with and without a shielding method. Third, we designed the system to operate with a closed-cycle helium recycler in order to reduce the overall operating costs (Wang et al 2015). We required that this can be operated continuously without degradation of MEG signal quality. These specific goals created unique challenges for noise suppression.

This report describes the set of methods we have developed for operating the magnetometer-based whole-head babyMEG in a lightly shielded MSR in a hospital. We have reported empirical results earlier that the noise can be reduced to clearly detect spontaneous and evoked brain activity using the babyMEG (Okada et al 2016). However we have not described the method of each component in detail. This report provides a comprehensive description of the entire noise rejection strategy. We also describe the performance of the babyMEG after applying the noise cancellation method using (i) simulated data, (ii) phantom measurements, and (iii) recordings from infants. We show that our noise cancellation approach enables the babyMEG consisting entirely of magnetometers to operate fully even in a lightly shielded room with the helium recycler operating continuously.

2. Methods

2.1. Brief description of the babyMEG

Our 375-channel pediatric babyMEG system is similar to the conventional MEG systems based on the superconducting quantum interference device (SQUID) technology operating near the liquid helium temperature (4.2 Kelvin). Unlike most of the MEG systems, however, the sensors are located in the vacuum space of the cryostat, instead of in a liquid helium reservoir inside the cryostat. With this arrangement, the gap between the detection coils and outside of the helmet can be minimized to maximize the signal strength. The sensor array has a unique two-layer design (see Fig. 3 in Okada et al., 2016) with 270 magnetometers in the inner layer at a mean distance of 8.5 mm from the outer helmet surface. The outer layer is 4 cm away from the inner layer with 35 sets of three-axis magnetometers evenly distributed over the helmet. The sensitivity is 7.5 fT/√Hz for the inner layer and 4.9 fT/√Hz for the outer layer at 400–450 Hz; these noise levels are higher than for the adult MEG systems because the diameter of the magnetometer coils are smaller than in an adult system: 10 mm for the inner and 20 mm for the outer layer, respectively. The small inner-layer coils allowed us to achieve a high channel density with an average distance of ~15 mm between adjacent coils. One of the design targets of the MEG system was to achieve high sensitivity and spatial resolution for measuring MEG signals in the pediatric population below 3–4 years of age.

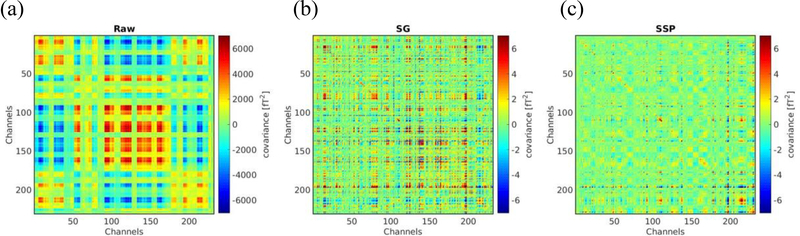
Fig. 3.

Reduction of empty room noise in different frequency bands. Each map shows the ratio of the powers in each frequency band with and without applying the SG or SSP compared to the raw data.

The use of magnetometers raised concern as to whether the babyMEG system can detect brain signals without being interfered by external noise sources. We employed the magnetometer array in our earlier simulation analysis (Nurminen et al 2008, 2010), which showed that it should be possible to achieve the necessary level of noise cancellation with a magnetometer-based system. Specifically, we evaluated how well the external noise can be removed by using a technique called signal space separation (SSS) (Taulu et al 2004, 2006, and 2014) for different sensor arrays. Magnetometers sense the magnetic field with a circular or square loop of coil. Gradiometers sense the magnetic field with a pair of such loops along the planar direction (planar gradiometer) or along the axial direction (axial gradiometer). The imbalance in gradiometers is due to differences in the loop areas. Nurminen et al (2008) found that the performance of SSS in noise cancellation deteriorates significantly when the imbalance is 1% or more, which is commonly the case for mechanically wound gradiometers. The magnetometer design eliminates this problem.

Nurminen et al (2010) then showed that a two-layer magnetometer array can achieve a SF of more than 800. The performance of SSS is 2–3x better using a two-layer array than a single-layer array. Furthermore, the value of SF is more than twice when the outer layer has 3-axis magnetometers instead of radially oriented magnetometers. We thus concluded that this additional shielding combined with conventional methods should be able to provide the shielding level sufficient for fully operating the magnetometer-based babyMEG.

2.2. Passive shielding achieved by a magnetically shielded room (MSR)

Basic noise cancellation was achieved using the conventional passive shielding method provided by an MSR. The “Vacoshield Basic +” was purchased from Vacuumschmelze, Hanau, Germany. It is installed in the new MEG facility on the 7^th floor of a new building in the main hospital of Boston Children’s Hospital (BCH). The MSR is a two-layer structure made of hypermalloy with a gap of 4.3 cm. There is an aluminum sheet (thickness 6 mm) touching each hypermalloy sheet (Vacoperm 70, thickness 1 mm); the aluminum layers face each other, separated by a pressed wood. Its dimensions are 3976 mm (W) x 2458 mm (H) x 3008 mm (D) exterior and 3856 mm (W) x 2338 m (H) x 2888 mm (D) interior. The design minimizes the amount of hypermalloy to reduce the cost. Compared to a standard Vacoshield Advance MSR (7.5 metric tons) and a standard Vacoshield Premium MSR (10.0 metric tons), our MSR only weights 4.5 metric tons. This relatively small weight of the room allows for installation in any ordinary room in a hospital or a research laboratory, even on an upper floor level as is the case at BCH. The sheets are prefabricated in a modular form for reducing the assembly cost. The MSR sits on a 10-cm deep well. The floor has a 9 mm high ramp to achieve a rise of 16 mm from the floor of the MEG facility. This “zero lip” is important for facilitating the transportation of the patient in and out of the MSR in case of emergencies. Vacuumschmelze has measured the shielding performance of this MSR as described in Results.

2.3. External active shielding

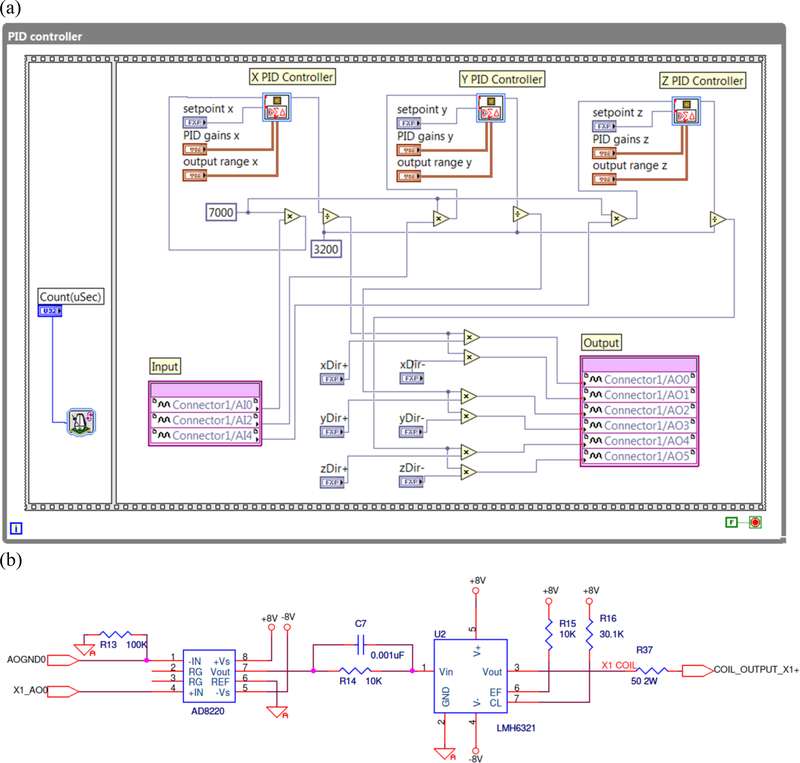
We developed an external active shielding (EAS) method to reduce the low frequency noise in the MSR. It uses three one-axis fluxgate magnetometers (StefanMeyer Instruments, Germany, model MK3-HM¹) as the null detectors in a feedback circuit. The EAS uses a one-axis fluxgate sensor attached to each of the three orthogonal external faces of the MSR for sensing the magnetic field along the three axes. A proportional-integral-derivative (PID) controller with a current driver is used to feed the currents based on the outputs of the fluxgate magnetometers to the external coils, which are pairs of square coils preinstalled on the opposite outside faces of the MSR, until the fluctuations sensed by the fluxgates are minimized. The PID controller (Bandwidth: 0–10 Hz) is implemented on a multifunction reconfigurable I/O device (NI-USB-7855R, National Instruments, Austin, TX) based on Kintex-7 70T Field Programmable Gate Arrays (FPGA). The feature of high speed control makes this device suitable for real time processing. The PID control program (Fig. 1a) is written with LabVIEW graphical language and downloaded to this hardware via LabVIEW project management tool. Three analog inputs are used to receive the outputs of the three orthogonal fluxgate magnetometers and three pairs of analog outputs are used to control the current fed to the external coils. The strengths of currents going through each analog output in a pair are identical and the directions can be flexibly configured depending on the configuration of each pair of coils. Inside the PID control program, three fix-point PID VIs provided by LabVIEW are directly called and executed in parallel. The PID tuning parameters are predefined and saved on the flash memory on board. There are six current source parts in the current control box (Tristan Technologies Inc., San Diego, USA). Each of them (Fig. 1b) is connected to an external coil installed on one outer surface of MSR individually. The current source part includes a pre-amplifier (AD8220, Analog Devices) with gain=1 and a voltage follower (LMH6321, Texas Instruments) with the 50Ω load. With this setup, the voltage follower can drive the output current ±300 mA continuously.

Fig. 1.

(a) LabVIEW Code for PID Controller downloaded to NI-USB-7855R and (b) Electrical diagram of the current source part for one output. It shows the connection from the analog output (X1_AO0) of NI-USB-7855R to the current input (COIL_OUTPUT_X1+) of one coil installed on the outer surface of MSR.

2.4. Environmental noises

The power line noise (60Hz and its harmonic) is significant. The vibration noise from the recycler (1.4Hz and its harmonic) can not be avoided but has been greatly reduced due to the vibration isolation techniques (Wang et al., 2016). The noise caused by the mechanical vibrations of the whole building is obvious due to the poorly magnetic shielded room. A residual magnetic field within MSR is consistently observed and varied with time (For a random selected channel (MEG001), significant spectral peaks can be observed around 17 Hz with −70 dB, 26 Hz with −80 dB, 30 Hz with −84 dB, 52 Hz with −84 dB, 68 Hz with −96 dB, 114 Hz with −98 dB, 147 Hz with −84 dB, … before software noise cancellation applied; decibel values are computed using the root-mean-square (RMS) averaged power spectrum density), which is thus a straightforward reason for the induced currents in the sensors (Tal and Abeles, 2013). In a hospital environment, especially in a higher floor (the 7^th floor in our case), environmental noises are usually stronger, contributed by a quite complicated combination of remote magnetic dipoles (e.g. the elevators, ventilation, air conditioners, traffic, etc.). Inside the dewar, noises from eddy currents arising from the aluminum sections and thermal effect related to the metallic components can be sensed too. Additionally, lab door opened/closed, and wheel chair movements may suddenly interfere with the MEG signals.

2.5. Signal space projection (SSP) method

The signal space projection (SSP) method (Uusitalo and Ilmoniemi 1997) is an optional method to be used for noise cancellation in our real-time software. This method decomposes any measured magnetic field across a number of channels into the signal and noise subspaces and removes the noise based on an orthogonal projection. In practice we remove the first 8 components in our open-source real-time software (Dinh et al 2013; Sun et al 2017; Esch et al 2018). The first three components approximately correspond to the three homogeneous magnetic field components as seen by the sensor array whereas the next five components correspond approximately to the five independent spatial derivatives of the magnetic field.

The SSP method is closely related to SSS discussed in a simulation paper (Nurminen et al 2010). In both methods, one selects a noise subspace to be suppressed. But, in SSS, the noise subspace is theoretically calculated from the magnetic multipole expansion whereas in SSP it is experimentally determined. Although SSS is an efficient general purpose interference and noise reduction method, the existence of sensor calibration uncertainty limits the performance of SSS. Any sensor calibration inaccuracy will result in a mismatch between the measured field and its SSS reconstruction. Therefore, a fine-tuned method based on SSS might be needed (Chella et al, 2012). Unlike SSS, SSP does not require precise calibration of the sensors, determination of their cross talk and geometry of the sensor array and SSP can often achieve the same degree of noise suppression with fewer dimensions in the noise subspace than SSS.

2.6. Synthetic gradiometer (SG) method

In addition to SSP we are employing a noise cancellation method using synthetic gradiometers (SGs) either by itself or together with the SSP. Each SG is constructed from the output of a specific magnetometer in the inner layer (primary sensor) and a weighted linear sum of the outputs of the channels in the outer layer. This is different from previous SG techniques that have combined the output of each of the primary sensors with outputs of a small number of distant reference channels (Vrba and Robinson 2001a, 2001b; Adachi et al 2001). Nurminen et al (2010) showed SF rapidly increases as the number of outer layer channels increases to about 40 and then the SF continues to increase as the number of outer layer channels increases to >100. The babyMEG thus has 105 channels in the outer layer as a compromise between the maximum noise rejection performance and the cost of additional channels. We use all good channels available in the outer layer for the construction of the SGs.

The weights of the SG channels are determined by linear regression. Let Y and X be the 270 × n_t and 150 × n_t matrices containing the n_t-sample recordings of noise from the inner and outer layer channels of the babyMEG without a subject present. We then find a 270 × 105weight matrix $\widehat{W}$ to predict the output of the inner-layer channels from the outer layer. In other words, we seek for a W which minimizes the Frobenius norm of the differences between the predicted and measured inner-layer signals $\Vert \mathit{Y}-\mathit{W}\mathit{X}{\Vert }_F^2={\Vert {\mathit{Y}}^T-{\mathit{X}}^T{\mathit{W}}^T\Vert }_F^2$. The well-known solution is $\widehat{W}=Y{X}^{+}$, where the superscript + denotes the pseudoinverse of a matrix. In practice, we employ a weight matrix, W_a, which is an average of weight matrices computed from 400 non-overlapped data segments (each 1 second long) extracted from 7 minutes recorded data sampled with 1024Hz. The W_a matrix needs to be estimated before normally recording a real subject and will not be updated during the whole recording. During a measurement noise reduction is then achieved by transforming the data according to:

$$\left(\begin{array}{c}{\mathit{Y}}^{\prime }\\ {\mathit{X}}^{\prime }\end{array}\right)=\mathit{T}\left(\begin{array}{l}\mathit{Y}\hfill \\ \mathit{X}\hfill \end{array}\right)=\left(\begin{array}{ll}\mathit{I}\hfill & -{\mathit{W}}_{\mathit{a}}\hfill \\ \mathbf{0}\hfill & \mathit{I}\hfill \end{array}\right)\left(\begin{array}{l}\mathit{Y}\hfill \\ \mathit{X}\hfill \end{array}\right).$$

Remarkably,

$${\mathit{T}}^{-1}=\left(\begin{array}{ll}\mathit{I}\hfill & {\mathit{W}}_{\mathit{a}}\hfill \\ \mathbf{0}\hfill & \mathit{I}\hfill \end{array}\right),$$

which means that as long as the SG weight matrix employed is saved together with all measurement channels and information whether the noise cancellation was applied or not, the SG approach can be easily switched on and off during the analysis. In source estimation, the effect of the synthetic gradiometer transformation needs to be taken into by transforming the forward solution accordingly. A similar approach is employed in adult MEG systems employing compensation sensors. However, in these systems, the compensation sensors are far away from the primary sensor array and thus detect only a small fraction of the actual MEG signals. The effect is thus minor for the forward solution. However, in the babyMEG, due to the proximity of the compensation (second layer) sensors, this correction of the forward solution is essential.

The SG method can be used for online and offline data analysis. When SG is to be used for online analysis, the weighting matrix is estimated from the empty room. For off-line analysis, if necessary, the weighting matrix can be recomputed. Before applying the SG method, all outer layer channels are calibrated and channels with large noise levels are excluded. Unlike in SSP, the transformation T does not make linear combinations of the inner-layer channels. SG can be used with an identical T even when some of the inner layer channels show transient noise.

3. Results

3.1. Passive shielding

The shielding performance is measured by SF. The measured values of SF are 27 @ 0.01 Hz, 67 @ 0.1 Hz, 470 @ 1 Hz, 4253 @10 Hz and 29,900 @100 Hz (Okada et al 2016). The performance of this two-layer Vacuumschmelze MSR at BCH is significantly worse than full-sized two- or three-layer MSRs installed in most of the MEG sites in the world because of the small separation between the two layers and the thinner layers of hypermalloy saving about half the weight of hypermalloy.

3.2. External active shielding

The performance of the EAS has been described previously in Okada et al (2016) in the form of a noise amplitude spectrum before and after applying the EAS. The EAS reduced the noise by a factor of 10 @ 0.01 Hz, 7 @ 0.1 Hz and 4 @ 0.5 Hz with some cancellation up to about 2 Hz visible in the noise spectrum. In practice, the EAS is very helpful to limit the total signal range of the SQUID amplifiers input, which can avoid saturation when using the larger gain in SQUID electronics. Of course, the 24 bit DAQ definitely offers a larger dynamic range based on a bit resolution in the single digit fT range than 12 or 16 bit DAQs. In our case, the least significant bit for 24 bit DAQ is ~ 3.6 fT (+/−10V; Gain 20; coefficient of unit conversion 6.0e-8 T/V).

3.3. Noise cancellation using SSP and Synthetic Gradiometers

We recorded data inside the MSR void of a subject. The maximum peak to peak amplitude averaged over all inner layer magnetometers was estimated with a 200-second data individually with EAS off (994.59 pT), EAS on (542.14 pT), EAS on with SG applied (29.85 pT), and EAS on with SSP applied (8.07 pT). We used another 5-minute data to determine the covariance matrix of the noise across all the channels of the inner layer, excluding those not working or exhibiting excessive instrumental noise. Figure 2A shows the covariance across pairs of good inner layer channels. The SG and SSP were then applied to the raw data individually. Each type of noise cancellation method significantly reduced the covariance. Note the scaling factor is increased by a factor of 1000 in displaying the results for the SG and SSP. The results demonstrate that both methods can significantly reduce both the empty room and device-originated noise and as well as its correlations across channels.

Fig. 2.

Covariance maps for empty room data: (a) raw data, (b) with SG and (c) with SSP.

The attenuation performance depends on the noise power in each frequency band. The ambient noise is mostly dominated by low frequency noise below a few Hz. But the frequency range of interest in brain research is mostly between 1–100 Hz for spontaneous brain activity. Figure 3 shows how the SG and SSP reduce the noise in the empty MSR in this frequency range: Delta (1–3.9Hz), Theta (4–7Hz), Alpha (8–15 Hz), Beta (16–30 Hz), Low Gamma (31–60 Hz), and High Gamma (61–120 Hz). The ratio of the power in the amplitude spectrum is approximately 100 across all the frequency bands for the SG, but the shielding effect is limited to the frequency bands up to the beta band for the SSP. This difference in attenuation ratio across the frequency bands reflects a basic difference in these two techniques. The SG removes all the noise across all the frequencies that are temporally correlated across the inner and outer layer channels separated by 4 cm. The SSP on the other hand removes spatially coherent components. Here we removed the first 8 spatial components, which approximately remove the three homogeneous field components and their five independent spatial derivatives. We also found both methods had the similar effects in the low frequency bands. The possible reason might be that the environmental noise is both temporally correlated across the inner and outer layers and spatially coherent over the inner layer.

The noise in the gamma range is evidently due to fields with non-uniform spatial gradients that had a significant linear component over the distance of 4 cm for the SG to reject. The same explanation can be used to explain the findings we have reported earlier that the SG removes the magnetic noise from the recycler located above the roof of the MSR and the magnetic noise generated by the vibration of the MSR walls (Okada et al 2016). However, this property is not a fundamental limitation of the SSP as the non-uniform gradient noise can be removed if one includes higher number of spatial components in the SSP vector construction.

3.4. Performance of the babyMEG after applying the noise cancellation techniques

We tested the performance of the BabyMEG system after applying noise cancellation with three types of data: (i) a simulated data set, (ii) recordings from a phantom, and (iii) human data from an infant.

3.4.1. Simulated data

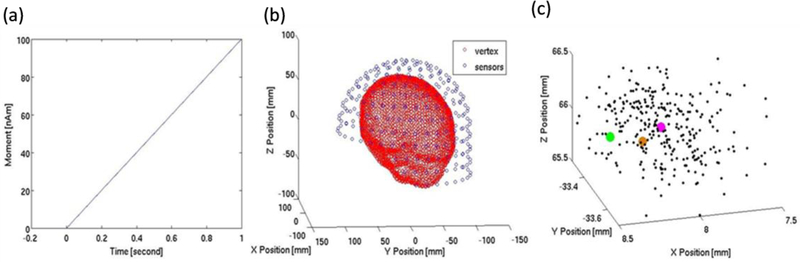
In the simulation study, a single current dipole was placed at a vertex of the cortical surface created from a realistic structural MRI images embedded inside the babyMEG helmet. A sphere model with origin at [0, 0, 0] for the dipole fitting was used in MNE software. The dipole moment Q was increased linearly in each repeated cycle of the simulation, see Fig. 4A. The simulation was carried out for the babyMEG inner-layer sensor array around the head (Fig. 4B). The Q directed along the +x axis (medial-lateral axis passing through the preauricular points) was located at a fixed coordinate (x = 8.43 mm, y = −33.81 mm, z = 66.44 mm). Then, the measured noise in the empty MSR after applying the SG was added to this field. Lastly, the magnetic field with residual noise was averaged across 500 replications to estimate the maximum performance possible. Figure 4C shows the cloud of estimated dipole locations for 300 sets of simulations based on the bootstrap resampling technique (Darvas et al 2005). The dipole fitting routine available in the MNE platform gave a goodness of fit of 99.8%. The mean of the dipole estimates was at x = 8.01 mm, y = −33.38 mm, z = 65.86 mm at the time when the dipole strength was 20 nAm. The error in each direction is <0.6 mm.

Fig. 4.

Dipole localization accuracy for a simulated data set. (a) Time course of the linearly increasing dipole moment over 1 s. (b) MRI- reconstructed head inside the babyMEG helmet. (c) Estimated dipole locations across 300 simulations obtained with bootstrap resampling computation (Noise is reduced with SG). Magenta dot is the mean of the cluster; green dot is the estimated dipole location from the noise free simulated data set; orange dot is the actual dipole location.

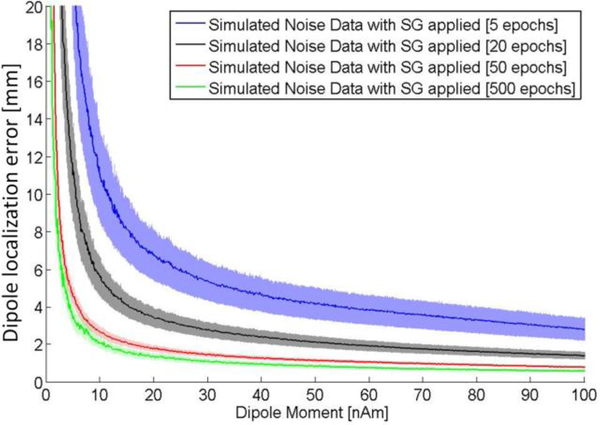
The use of the ramp with a linearly varying dipole strength enables us to quickly estimate the dependence of dipole localization error on dipole strength. Figure 5 shows this function for the entire range of dipole strength from 0 to 100 nAm. In addition we evaluated how the dipole localization error depends on number of averages. The estimates were obtained using 100 different dipole locations and orientations randomly selected. Bootstrap resampling was used to create the simulated field averaged over 5–500 epochs based on the empty room data with SG applied. The error decreases rapidly as the dipole moment increases from 0 to about 20 nAm. The dipole moments in human MEG studies range between about 10 and 100 nAm (Hämäläinen et al 1993; Konn et al., 2003; Cheyne and Papanicolaou, 2017). The errors are <3 mm for a current dipole with a relatively weak moment of 10 nAm after averaging 50 epochs.

Fig. 5.

Dipole localization error for the simulated MEG data: dipole strengths and epochs. Shades represent the standard error of the mean.

3.4.2. Phantom data

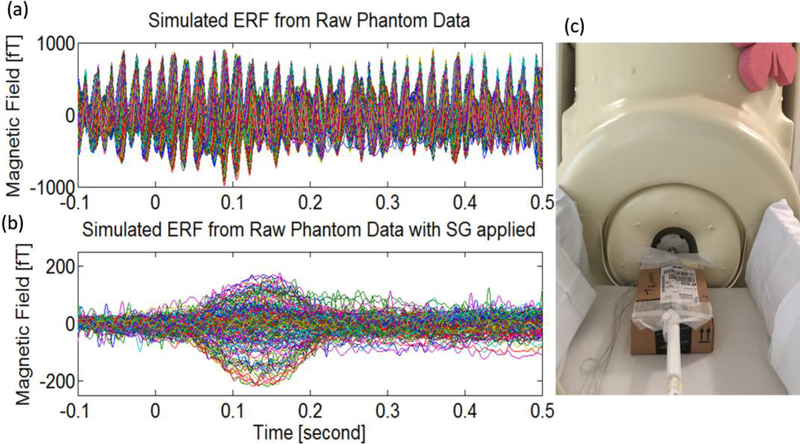
The magnetic field was created by dipoles in an Elekta phantom specifically designed to fit the babyMEG helmet. The Elekta phantom is a current phantom obtained from Elekta Oy of Helsinki, Finland. It generally includes 32 dipoles and four head position indicator coils. Each dipole is equal to a tangential current dipole which can create the equivalent magnetic field distributions (Omar et al., 2015). Our phantom only has 24 dipoles due to the smaller size. The phantom was placed in the center of the babyMEG helmet (Fig. 6c). A half sine wave pulse is outputted from the signal generator per each trigger and feeds into one phantom dipole which is serially connected with a 5KΩ resistor. The dipole length was 5 mm and the maximal output voltages were 2, 0.2, and 0.02V for three independent sets of measurements, corresponding to dipole moments Q of 2000, 200, and 20nAm, respectively at the same location (x = −6.40 mm, y = −39.72 mm, and z = 34.08 mm). The transient field was presented 50 times with an interstimulus interval of 1.8 to 2.2 s. Figure 6a shows the signal averaged over 50 epochs from the raw phantom data without any noise reduction except the passive shielding and external active shielding. Figure 6b is the same data but after applying the SG method. The event-related field produced by the phantom dipole was recovered clearly after applying the SG method.

Fig. 6.

Event-related field (ERF) produced by the phantom dipole (average of 50 epochs, dipole moment = 20 nAm) (Raw data, (b) Same but with the SG applied, and (c) Elekta phantom inside helmet.

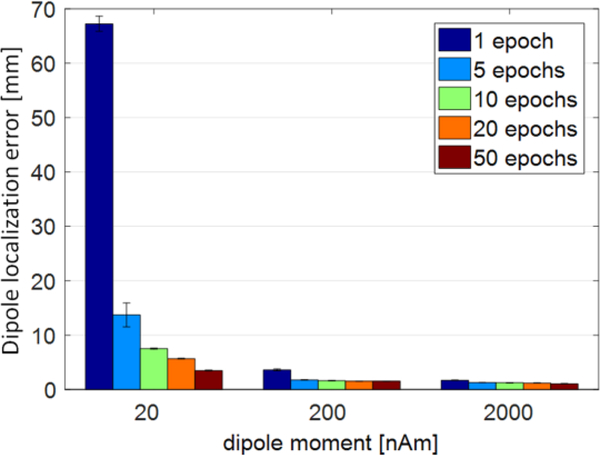
Dipole location was computed with the MNE dipole fitting routine at time 0.14 s after the trigger onset. As shown in Fig. 7, the localization error decreased with dipole strength and number of epochs averaged. The localization with errors ~6 mm can be obtained after averaging as few as 20 epochs even for the relatively weak moment of 20 nAm. The results are consistent with those for the simulated data.

Fig. 7.

Dipole localization error as a function of dipole strength and number of epochs averaged.

3.4.3. Human data

In addition to the simulated and phantom data, we evaluated the performance by analyzing MEG signals from an infant. One healthy 25 months male baby without any history of neurological disorders participated in this study. Informed consent was obtained from the participant’s family. The study was conducted under a human research protocol approved by the Institutional Review Board (IRB) of Boston Children’s Hospital. The subject’s brain imaging was performed on a 3T Magnetom Tim Trio (Siemens Healthcare, Germany). A high-resolution anatomical MRI data was acquired with magnetization prepared rapid acquisition gradient-echo (MPRAGE; TE 3.37ms, TR 2000 ms, voxel size 1×1×1 mm and FOV 22 cm). An infrared-based device (FastSCAN II, Polhemus Corp., Colchester, VT) was used for the digitization of the head shape, four head position indicator (HPI) coils, and three fiducial points at the nasion and 1 cm anterior to the tragus of the left and right ear. The baby was lying in the supine position with the head in the helmet. The head position and orientation with respect to the sensor array were determined by four HPI coils. After recording, the MEG and MRI data were coregistrated according to the locations of HPI coils and fiducial points. Tactile stimuli were delivered to the tip of the left middle finger through a piezo-electrical Braille cell which had two rows with four pins each (Metec AG, Stuttgart, Germany). The stimulator was connected to an in-house controller made with Arduino UNO and DC-DC converter. A computer was connected to Arduino board via USB port and controlled the Braille stimulator to mechanically stimulate at 2.1 Hz with a home-made LabVIEW application software. A set of 200 stimuli was presented. The subject was not required to perform any stimulus-related task and was sleeping during the MEG recording in the MSR. MEG data and the trigger signal were sampled at 1024 Hz after filtering the signals with a 0.16 high-pass filter and a 512 Hz low-pass filter. The environmental noise was removed by the SG method. Noisy or non-working channels were removed from the analysis. The epoch duration was 0.6 s (0.1 s pre-stimulus, 0.5 s post-stimulus periods). Some epochs with significant movements or eye movements/blinks artefacts detected by fieldtrip² software were discarded. The heart beat artefacts are ignored in the research of the evoke response due to the less influence after averaging (Sun et al., 2016). The SEF was averaged across varying number of epochs from 20 to 199. Each set of ERF data was baseline corrected by subtracting the mean value in the 50 ms pre-stimulus interval (−50 ms - 0 ms) and filtered by a band pass filter with cutoff frequencies of 2 and 40 Hz.

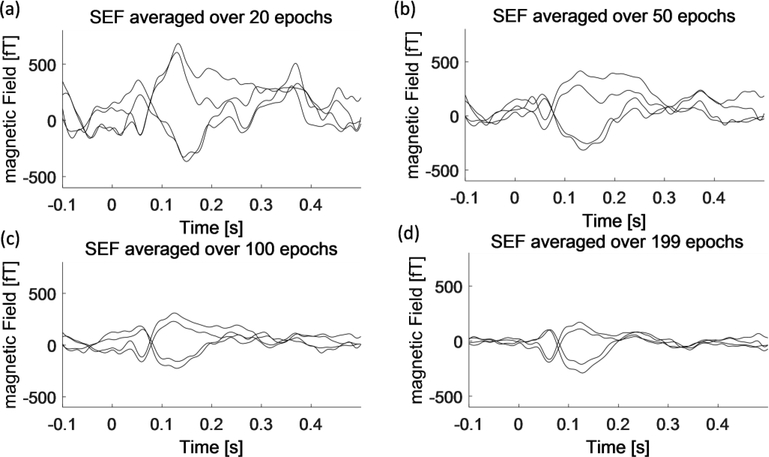
Figure 8 shows the time waveform of the SEF as a function of number of epochs averaged. It was possible to obtain SEFs after averaging as few as 20 responses with a waveform showing the components seen with larger numbers of averages (N = 100 and 199). The response amplitudes are larger for smaller number of averages due to selection bias. The mean amplitude was independent of number of averages when the data with a specific number of responses was randomly selected from the entire dataset.

Fig.8.

SEF time waveforms at the sensor level as a function of number of epochs averaged over 20 epochs (a), 50 epochs (b), 100 epochs (c) and 199 epochs (d) after applying the SG filter.

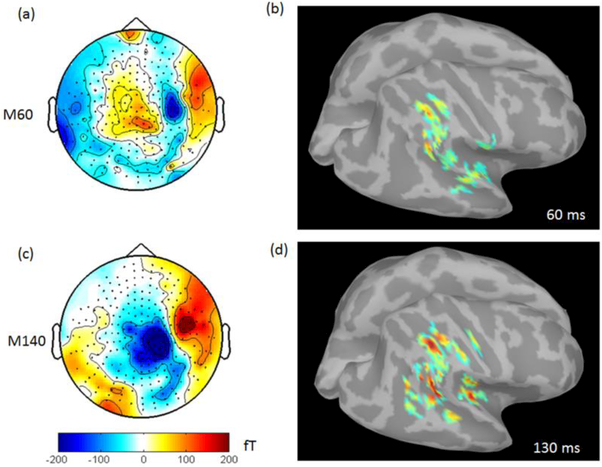
Figure 9 presents magnetic field patterns as well as source localizations for the two prominent somatosensory responses: M60 (55 −65 ms) and M140 (120 −150 ms). In Figure 9, the SEF averaged over 199 epochs (Fig. 8d) was used to estimate the averaged topographies for M60 and M140 and source localizations at 60 ms and at 130 ms individually. From the magnetic field patterns, clearly, M60 shows the identifiable contralateral response from the primary somatosensory cortices (SI). Comparably, M140 shows the bilateral responses from the second somatosensory cortices (SII) and it is much stronger in the right hemisphere. The source localization was implemented with dSPM in Brainstorm³ with the corrected forward model based on the main peak which occurred in each of components (60 ms for M60 and 130 ms for M140) respectively. The significant brain activity was found around the area of somatosensory cortices. The dipole fitting method was also implemented for estimating the current moment at 60 ms and 130 ms. The dipole moment at 60 ms is 2.5nAm with the MRI coordinate (X 178.9 mm, Y 93.0 mm, Z 175.3 mm) and goodness of fit (GOF) 32.23%. The dipole moment at 130 ms is 12.7 nAm with the MRI coordinate (X 172.7 mm, Y 103.8 mm, Z 156.4 mm) and GOF 79.47%.

Fig.9.

Topographies of M60 (a) and M140 (c) and source imaging with dSPM at 60 ms (b) and 122 ms (d).

4. Discussion

We demonstrated that it is possible to operate a whole-head MEG system consisting entirely of magnetometers installed in a lightly shielded MSR with a closed-cycle helium recycler above its roof operating continuously. The environmental magnetic noise was reduced to the instrumentation noise level. This was possible by using a combination of conventional and new noise cancellation schemes including a lightly shielded MSR, EAS, complemented by the new online SSP and/or SG. The EAS system is customized with the FPGA based NI device in combination of current sources. With the 16 bits ADC and the high sampling rate (1 MS/s) as well as the LabVIEW programming, the PID controller is very powerful, not only in providing the large current but also in tuning the PID through a graphical user-friendly interface. The shielding effects achieved by using these methods were: passive shielding – 36 dB, active shielding – 12 dB, and SSP – 40 dB or SG – 40 dB, for a combined maximum value of about 90 dB at 0.1 Hz (decibel values are computed using the power spectrum density). The use of SSP or SG alone was sufficient to reduce the noise to a level sufficiently low for measuring brain signals.

The SSP removes the dominant components of the environmental noise by projecting out the corresponding spatial patterns constituting the noise subspace. It does not require the two-layer sensor design and can remove most of the environmental noise using the inner layer only. The SG takes advantage of the two-layer sensor design. It removes the environmental noise that is temporally correlated across the inner and outer layer magnetometers. The similar SG method like ours has been implemented by others (Vrba and Robinson, 2001b; Adachi et al, 2001). But, unlike our SG method, the reference channels used in their methods are few and farther away from the primary sensors. Although such a setup is still dominated in the up-to-date MEG system (e.g., CTF system, Elekta Neuromag, York MEGSCAN, Neuroscan Orion Lifespan MEG system, etc.), it has the deficit of handling the rapid changed noise or weak noises such as the thermal noise close to the primary sensors. Our design provides a solution to suppress both the remote noises such as cars, elevators, etc. and nearby noises such as the recycler noise whose temporal correlation can be well captured by the inner and outer layers as well as the power line noise. The number of channels and the use of the vector magnetometers are based on the previous simulation analysis (Nurminen et al 2008, 2010), which has showed that an array of vector magnetometers is superior to an array of single-axis magnetometers for noise rejection. The SF increased rapidly as the number of outer layer channels increased to about 40, but it continued to improve with larger numbers of magnetometers. The number of channels (105) used in the babyMEG is the optimal value on the trade-off curve between the performance and cost. Notably, the previous results are based on the simulation. Our MEG system is the first in the real world to proof that the two layer structure, a large number of reference channels, and SG method can suppress environmental noise efficiently.

The babyMEG can operate using either the SSP or SG alone or using both together (using SG first and then SSP). Both remove the temporally coherent components of the environmental noise as shown in Fig. 2. The SG appears to be more effective than SSP in reducing the environmental noise generated locally by nearby sources such as the recycler. However, this difference is apparent, not fundamental, since the SSP can be constructed to cover a noise subspace with dimension k > 8 and can then dampen locally generated noise sources. Even though the SG can remove the recycler noise, it may attenuate brain signals since the outer layer is 4 cm away from the inner layer. This baseline of 4 cm increasingly reduces brain signals generated at locations farther than 4 cm away from the inner layer. Since the mean gap between the inner layer magnetometers and the outer helmet surface is 8.5 mm, the SG increasingly reduces the brain signals generated at locations deeper than about 3 cm from the scalp. The SG appears to be capable to removing the environmental noise in the gamma band better than the SSP (Fig. 3). However, this difference again depends on how the SSP is implemented. The SSP projector can include more than the eight components to remove the components above the beta band if they are generated by noise sources with more complex spatial patterns.

What is important for practical considerations is that these two methods (SSP and SG) can be implemented for online real time operation even for a magnetometer-based MEG system. This feature is important for increasing the versatility of the MEG technology. This online capability made it possible to monitor the spontaneous brain activity without being interfered by the environmental noise and activity in the cerebral cortex evoked by external stimuli which can be detected clearly after averaging as few as 20 responses or less. The reduction in number of responses needed for evoked response analysis greatly increases the usefulness of an MEG system for pediatric research since it is often very difficult to measure the brain signals for long periods of time.

A systematic validation of noise cancellation is estimated by the single dipole fitting method which is not the best but the simplest and efficient. However, the quality of signals is critical for this method. The noisy channels and problematic channels can seriously bias the dipole location especially after SSP (Nolte and Curio, 1999). Thus, carefully eliminating these bad channels is prerequisite. This step is also important for the SG method. In our system, we found 11 bad channels in the outer layer and 26 bad channels in the inner layer. The dipole accuracy is verified by the simulation (<3 mm; 10 nAm, averaging 50 epochs) and the phantom ( ~ 6 mm; 20 nAm, averaging 20 epochs). The simulation experiment can avoid measurement errors such as digitization and the phantom experiment can avoid disturbances related to the human such as spontaneous activity, eye movements/blinks, head movements, and so on. Those experiments can thus provide us the solid results with a simple and convinced approach. Although it is impossible to estimate the dipole localization error for the subjects due to the unknown locations of neural generators, we indeed found the significant neural activity related to the somatosensory response components at or around the primary somatosensory cortices.

The last point we want to illustrate is that the recycler eliminates the cost of helium liquid and the maintenance for helium refilling. The operating costs are thus comparable to the cost of operating an EEG facility in any clinic or a hospital.

5. Conclusion

We have shown that a whole-head MEG system based entirely on magnetometers installed in a hospital can operate in a light-weight MSR in the presence of a continuously operating closed-cycle helium recycler, which completely eliminates the helium refilling and reduces the operating costs to a level comparable for a clinical EEG facility. A combination of a passive shielding, an external active shielding, and a signal space projection technique or a synthetic gradiometer approach makes the real-time online operation possible. This greatly increased the versatility of the MEG technology. The noise cancellation strategy is validated with the satisfied dipole accuracy by the simulation and the phantom. The babyMEG system demonstrates its value with the human experiment which presents the tactile response in the somatosensory cortices.

Abbreviations:

MEG

Magnetoencephalography

SSP

Signal space projection

SG

Synthetic gradiometer

SF

Shielding factor

SEF

Somatic evoked magnetic field