Comparative Approach of MRI-Based Brain Tumor Segmentation and Classification Using Genetic Algorithm

Abstract

The detection of a brain tumor and its classification from modern imaging modalities is a primary concern, but a time-consuming and tedious work was performed by radiologists or clinical supervisors. The accuracy of detection and classification of tumor stages performed by radiologists is depended on their experience only, so the computer-aided technology is very important to aid with the diagnosis accuracy. In this study, to improve the performance of tumor detection, we investigated comparative approach of different segmentation techniques and selected the best one by comparing their segmentation score. Further, to improve the classification accuracy, the genetic algorithm is employed for the automatic classification of tumor stage. The decision of classification stage is supported by extracting relevant features and area calculation. The experimental results of proposed technique are evaluated and validated for performance and quality analysis on magnetic resonance brain images, based on segmentation score, accuracy, sensitivity, specificity, and dice similarity index coefficient. The experimental results achieved 92.03% accuracy, 91.42% specificity, 92.36% sensitivity, and an average segmentation score between 0.82 and 0.93 demonstrating the effectiveness of the proposed technique for identifying normal and abnormal tissues from brain MR images. The experimental results also obtained an average of 93.79% dice similarity index coefficient, which indicates better overlap between the automated extracted tumor regions with manually extracted tumor region by radiologists.

Introduction

The introduction of information technology and advancement in the e-health care system in the medical field helps clinical supervisors to provide better health care to the patient. This study addresses the problems of segmentation of normal and abnormal brain tissues such as gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF), from magnetic resonance (MR) image using feature extraction technique and classification based on genetic algorithm (GA) classifier [1, 2].

The tumor is basically an abnormal or uncontrolled growth of cancerous cells in the body, whereas brain tumor is classified as abnormal growth of cancerous cells in the brain. A brain tumor can be benign or malignant. A benign brain tumor has similarity in a structure called homogeneous structure and does not contain cancer cells, whereas malignant brain tumor has a non-similarity in a structure called heterogeneous structure and contains cancerous cells. The World Health Organization and American Brain Tumor Association [3] have initiated grading mechanism for tumor stages into grade I to grade IV to classify benign and malignant tumor types. On that scale, grades I and II are also called low-grade brain tumors and classified as benign tumor types, whereas grades III and IV are called high-grade brain tumors and classified as malignant brain tumors. The low-grade brain tumors possess a slow growth in comparison with high-grade brain tumors which possesses rapid growth.

If the low-grade brain tumor is left untreated, then it is likely to develop into high-grade brain tumors and hence, early detection and diagnosis of the brain tumor is primary concern by the radiology department [3]. The summary of benign and malignant tumors are shown in Table 1. Patients with grade II Gliomas require serial monitoring and observations by magnetic resonance imaging (MRI), computed tomography (CT) or by other modern imaging modalities scan in every 6 to 12 months [3].

Table 1.

Differences between benign and malignant tumors

Benign tumors	Malignant tumors
Non-cancerous	Cancerous
Abnormal cells incapable of spreading	Abnormal cells capable of spreading
Cells multiply slowly	Cells multiply rapidly
Grades I and II	Grades III and IV
Easier to remove and does not recur after excision	Difficult to remove and recurs after excision
Mass is mobile	Mass is fixed
Homogeneous in structure	Heterogeneous in structure
Surgical excursion is considered to be curative	Surgery, radiotherapy, chemotherapy, or combination thereof is needed

Segmentation is a process of separating an image into the similar class of properties such as color, contrast, brightness, and gray level into blocks or regions. Brain tumor segmentation is employed in medical imaging such as magnetic resonance (MR) images or other modern imaging modalities in order to separate the tumor tissues such as edema and necrosis (dead cells) from normal brain tissues, such as WM, GM, and CSF [4–8]. To detect tumor tissues from medical imaging modalities, segmentation is employed and depending on the evaluations performed using advanced medical imaging modalities, specialized patient care is provided to patients with a brain tumor [9].

The detection of a brain tumor at an early stage is a key issue for providing improved treatment to the patient. Once a brain tumor is clinically suspected, radiological evaluation is required to determine its location, size, and impact on the surrounding areas. It is evident that the chances of survival of a tumor contaminated patient can be increased significantly if the tumor is detected accurately in its early stage [10]. As a result, the study of brain tumors using imaging modalities has gained importance in the radiology department.

The rest of the paper is organized as follows: the “3” section presents the related works, the “3” section presents the steps used in the proposed technique, the “Results and Discussion” section presents the results and discussion, and finally, the “3” section contains the conclusions and future work.

Related Works

The tumor is a life-threatening disease for the human being and so the early diagnosis with the highest accuracy to offer a better treatment is a primary concern. In last one decade, many types of research are produced for the diagnosis evaluation of brain tumor based on different imaging modalities, in spite of that, it is not fully imperative to adopt, and so still encourages many researchers to investigate more advanced, technically acclaim diagnosis system. Many techniques have been proposed from the number of researchers for classification of brain tumors in MR images, most notably, fuzzy clustering means (FCM), support vector machine (SVM), artificial neural network (ANN), genetic algorithm (GA), self-organizing map (SOM), knowledge-based techniques, and expectation-maximization (EM) algorithm technique. An overview and findings of some of the recent researches with sound diagnosis accuracy in the area are presented here and is shown in Table 2.

Table 2.

Summary of related works

Authors	Technique used	Findings
Aneja and Rawat [11]	Fuzzy clustering means (FCM)	Proposes the algorithm of segmentation that works against the noise using FCM clustering. Segmentation performance is analyzed on the basis of cluster validity functions, execution time and convergence rate and obtained misclassifiction error of 0.537% using Intuitionistic Fuzzy C-Means (IFCM) technique.
Zhao et al. [12]	Multiobjective spatial FCM	Experimented on noisy images, the proposed method evolve the number of clusters automatically.
Kumar et al. [13]	Fuzzy-neuro logic segmentation algorithm	Develop an improved method of segmentation using fuzzy- neuro logic to detect various tissues like white matter, gray matter; cerebral spinal fluid and tumor for a given magnetic resonance image data set.
Wang et al. [14]	Fuzzy Kohonen clustering network based on high dimension fuzzy character	The algorithm developed by Wang et al. has two steps for the operation on image segmentation, in the first step fuzzification of the pixels is done and in the second step is about to construct 3-Dimensional feature vector of redundant images and their original images and then cluster the feature vector through RFKCN
Maoguo et al. [15]	Improved FCM algorithm	Extended the use of tradeoff weighted fuzzy factor and a kernel metric, the tradeoff weighted fuzzy factor depends on the space distance of all neighboring pixels and their gray level difference simultaneously and a kernel distance measure employed to enhances its robustness to noise and outliers.
Damodharan and Raghavan [16]	Neural network	Effectively segmented and separated normal brain tissues, such as WM, GM, and CSF from tumor region. They also give a comparison of accuracy, specificity, and sensitivity obtained from the classifier techniques based on K-Nearest Neighbors (K-NN), Bayesian algorithm and their proposed technique based on neural network, and obtained an accuracy of 83% using neural network based classifier.
Yang et al. [17]	Discrete wavelet transform (DWT)	Have proposed a technique for brain tumor clustering to cluster single voxel MR slices and obtained an accuracy of 94.2% with a balance error rate of 7.8%.
Demirhan et al. [4]	Self-organizing map (SOM), wavelet and neural networks	This method obtained an average dice similarity indexes for different tissue classes separately and achieve 91% for WM, 87% for GM, 96% for CSF, 61% for tumor, and 77% for edema.
Ahmed et al. [18]	Kullback-Leibler divergence (KLD)	Have presented a technique for posterior-fossa tumor clustering based on MR image. In this technique, relevant features for classification is selected using Kullback-Leibler divergence (KLD) measure, which is obtained using expectation maximization algorithm.
Torheim et al. [19]	Support vector machine (SVM)	Used texture-based analysis and SVM’s algorithm for effective classification of dynamic contrast-enhanced MR images and claims better predictions and improved clinical factors, tumor volumes and stage in comparison with first order statistical features.
Guo et al. [1]	One-class immune feature weighted SVM	Handle the non-linear distribution of real data without using any prior knowledge.
Maulik [20]	Genetic algorithm (GA)	Address the problems caused by poor image contrast, and other artifact that results in missing boundaries
Bahadure et al. [21]	Watershed segmentation and FCM	Addresses the problems of segmentation and proved superiority of FCM based segmentation using histogram equalization.
Jainy Sachdeva et al. [22]	Artificial neural network	Presented a multiclass brain tumor classification, segmentation, and feature extraction using a dataset of 428 MR images and obtained classification accuracy from 77 to 91%.

The literature review discussed in Table 2 has presented techniques for segmentation and detection, or for classification of the tumor type or for a combination of detection and classification. It is also observed that the selection of prominent features or only features required to judge the tumor type by the classifier is missing. To solve this problem, we investigated comparative approach of segmentation techniques based on segmentation score and select the segmented image based on the best segmentation score (maximum score) for further analysis. Further, to improve the accuracy of the classifier for the classification of tumor type, only relevant and useful features are needed to ensure by feature selection process and this is done very effectively using the Genetic algorithm.

In this study, to improve diagnostic accuracy, we perform a combination of watershed segmentation (WS), fuzzy clustering means (FCM) segmentation, discrete cosine transformation (DCT)-based segmentation, and Berkeley wavelet transform (BWT)-based segmentation and select the best one by comparing segmentation score. The purpose of this study is to extract relevant information from the segmented tumor region and classify healthy and infected tumor tissues for a large database of medical images. The classification with feature selection of the tumor region can be performed by using a genetic algorithm (GA) based classifier. The results of this research are helpful for classifying benign and malignant tumors, fast and accurately and thus, improving the diagnosis of tumor slices.

Dataset

To validate the performance of our algorithm, we used sample images of 15 patients with 9 slices for each patient. These test images were acquired using a 3 Tesla Siemens Magnetom Spectra MR machine. The total numbers of slices for all channels were 15, which leads to total 135 images at 9 slices per patient with a field of view of 200 mm, slice thickness of 5 mm, interslice gap of 1 mm, and voxel of size 0.78 mm × 0.78 mm × 0.5 mm. This dataset had ground truth images that helped to compare the results of our method with the manual analysis of radiologists. For the purpose of the analysis, we also considered 22 images from the Digital Imaging and Communications in Medicine (DICOM) dataset [23], all of which included are tumor infected brain tissues and 44 images from Brain Web dataset [24]. This research was approved by the Research Advisory Committee of the institute. Also, all of the processes and experimental analysis performed during the image acquisition comply with the ethical standards of the diagnosis center from which the images were taken.

Proposed Method

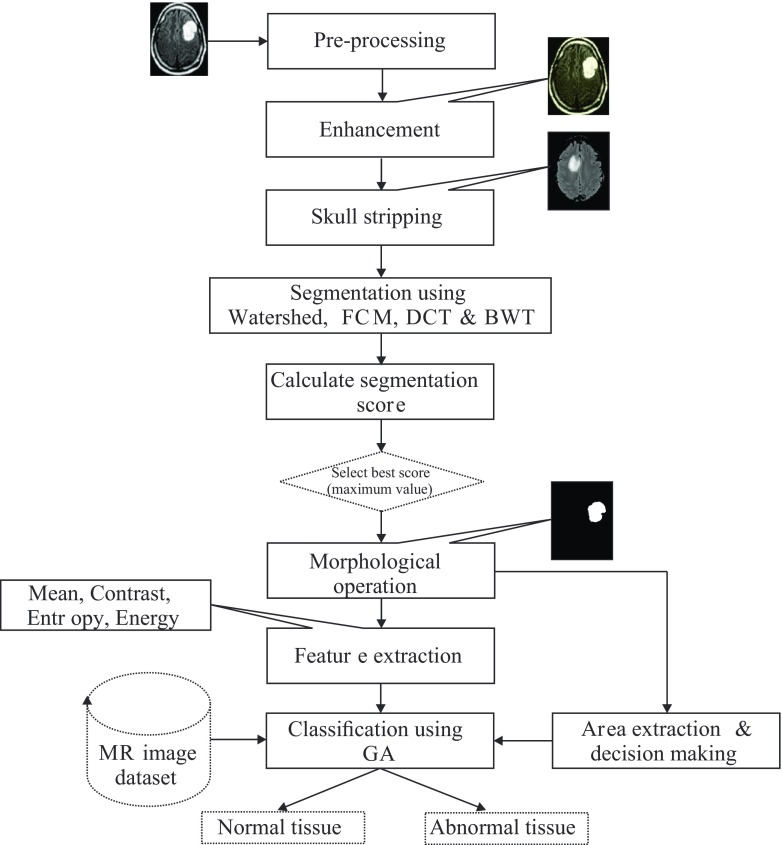
Figure 1 provides the flow diagram of the algorithm. It is developed to assist radiologists or clinical supervisors in classifying brain tumors on MR images. The proposed system utilizes major steps, which includes pre-processing of brain MR images, improvement in contrast and brightness using image enhancement, skull stripping operation, segmentation, extraction of features, selection of relevant features, and classification based on genetic algorithm. The following sections discuss the implementation of the algorithm.

Fig. 1.

Steps used in proposed algorithm

Pre-processing and Enhancement

The quality of the raw MR images is improved using pre-processing stage. In addition, pre-processing helps to improve certain parameters of MR images such as improving the signal-to-noise ratio, removing the irrelevant noise and undesired parts in the background, smoothing the inner part of the region and preserving its edges [4]. In our proposed system, to improve the signal-to-noise ratio, and thus the clarity of the raw MR images, we applied Adaptive Contrast Enhancement Based on modified Sigmoid Function [25]. The experimental result for the proposed enhancement technique in comparison with the other techniques is shown in Fig. 2.

Fig. 2.

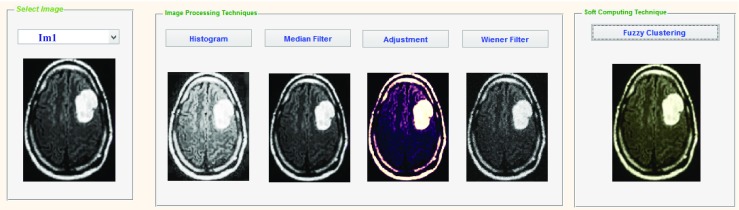
Enhancement of MR image

Skull-stripping

Additional cerebral tissues such as fat, skin, and skull in the brain images are affecting the segmentation result and therefore should be removed using the process called skull-stripping operation [26]. There are several techniques available to perform skull stripping, notably, some of them are, (1) automatic skull stripping using image contour, (2) skull stripping based on region growing and morphological operation, and (3) skull stripping based on the histogram analysis or a threshold value. The algorithm used in our proposed system is based on a threshold operation and is described in Algorithm 1

Segmentation and Morphological Operation

In this study, different segmentation schemes based on watershed segmentation, FCM segmentation, DCT segmentation, and BWT segmentation are considered for the segmentation and the best one is selected on the basis of segmentation score. The different segmentation schemes are discussed below:

Watershed Segmentation

In the watershed-based segmentation technique, when the watershed algorithm is applied, it will generate extensive watershed lines for the segmentation, so as to reduce the effect of rigidness, marker technique is applied, this operation is called post processing operation of watershed segmentation [27, 28]. Watershed-based segmentation epitomizes various concepts of three techniques, namely threshold-based, edge-based, and region-based segmentation. The deterministic concept of the watershed method used for the image segmentation is to find the watershed lines and then the transformation is done by dividing the image into the different regions.

Fuzzy Clustering Means

The fuzzy clustering means (FCM)-based clustering algorithm divides the entire data set into many smaller groups [29, 30]. The FCM algorithm simplifies the hard C-means (K-means) clustering to allow one data point to partially belong to multiple clusters [21, 31]. Hence, we used the FCM algorithm to effectively create soft boundaries for the given datasets, in addition to that we have also extended the objective function J₁ of the hard C–means clustering in the many ways [29] like fuzzy membership degrees in the cluster was submerged into an Eq. 1 and then an additional element w was introduced as an indicative of the weight exponent used in the fuzzy system.

$$J(F,V)=\sum _{j=1}^C\sum _{X_i𝜖C_j}|y_i-z_j{|}^2$$ 1

where V denotes the vector of a cluster and F denotes the function of separating the data set y into clusters C₁,C₂........C_k. The prolonged objective function, denoted as J_w is

$$J_w(F,V)=\sum _{j=1}^C\sum _{X_i𝜖C_j}{\left(\mu c_i\right(y_k\left)\right)}^w|y_i-z_j{|}^2$$ 2

The element w used in Eq. 2 is the weight exponent. The weight exponent is used to decide the factor at which partial members of a cluster affect the clustering result [31]. It was also shown that similar to the hard C-means method, the FCM technique also attempts to perform effective separation by searching the prototypes z_i that minimize the prolonged objective function J_w. However, both hard C-means and FCM techniques require to identifying the extended membership μc_i that minimizes J_w.

If the conditions given in the Eqs. 3 and 4 are satisfied, then on the fuzzy partition of clusters C₁,C₂........C_k can be a local minimum of prolonged objective function J_w otherwise not [31].

$$\mu c_i\left(y\right)=\frac{1}{{\sum }_{j=0}^{k-1}{\left(\frac{|y-z_i{|}^2}{|y-z_j{|}^2}\right)}^{\frac{1}{w-1}}}$$ 3

$$z_i=\frac{{\sum }_{\mathrm{y𝜖X}}{\left(\mu c_i\right(y\left)\right)}^{w}y}{{\sum }_{\mathrm{y𝜖X}}^n{\left(\mu c_i\right(y\left)\right)}^w}$$ 4

Based on Eqs. 3 and 4, the FCM repetitively updates the prototype and the membership function until a criterion of convergence is reached [31].

Discrete Cosine Transformation

The discrete cosine transform (DCT) helps to divide the image into sections of varying importance with respect to the images visual quality and this leads to effective segmentation [32]. The region wise dividing ability of discrete cosine transformation is used to segment any image according to their visual significance and quality. The discrete cosine transform is referred to be similar to Discrete Fourier transform because of its ability to transform a signal or image from the spatial domain to the frequency domain. The general equation for the one-dimensional DCT is defined as shown in Eq. 5 and the corresponding inverse one-dimensional DCT is shown in Eq. 6.

$$F(x,y)={\left(\frac{2}{N}\right)}^{\frac{1}{2}}\sum _{i=0}^{N-1}\delta (x,y)cos\left[\frac{\mathrm{\pi \mu }}{2N}\left(2\right(i,j)+1)\right]f(i,j)$$ 5

$$F^{-1}(x,y)=\left\{\begin{array}{ll}\delta (i,j)=\frac{1}{\sqrt{2}}& \text{for}𝜖=0\\ \delta (i,j)=1,& \text{otherwise}\end{array}\right.$$ 6

where N is the number of rows in the input image and f(i,j) is the intensity of the pixel in i^th row and j^th column of the image.

Berkeley Wavelet Transformation

In this study, the effectiveness of Berkeley wavelet transformation (BWT) is employed for effective segmentation of brain MR image. In fact, it is the first kind of its study to use BWT for segmentation of brain MR images. The wavelet transformation technique is emphasized to develop functions, operators, data or information into components of different frequency, which enables studying each component separately. All wavelets are generated from a basic wavelet Ψ(t), also referred to as a mother wavelet, because it is the point of origin for other wavelets and is defined by Eq. 7.

$${\mathrm{\Psi }}_{s,\tau }=\frac{1}{\sqrt{s}}\mathrm{\Psi }\left(\frac{t-\tau }{s}\right)$$ 7

where s and τ are the scale and translation factors, respectively.

The Berkeley wavelet transform (BWT) is described as a two-dimensional triadic wavelet transforms and can be used to process the signal or image. The seed point requires the selection and mark of the threshold are easily located in BWT transformation. The BWT presents an effective way of representation of image transformation and it is a complete orthonormal, and therefore it is best for segmentation of MR images involves complexity. The wavelet transformation forms a complete, orthonormal basis in two-dimensions by the operation of translation and scaling of the entire set with a single constant term of the wavelet. The mother wavelet transformation ${\beta }_x^{\phi }$ are piecewise constant function [33, 34]. The substitute wavelets from the mother wavelet ${\beta }_x^{\phi }$ are produced at various pixels positions in the two-dimensional plane through scaling and translation of the mother wavelet and it is shown in Eq. 8.

$${\beta }_x^{\phi }\left(\tau ,s\right)=\frac{1}{s^2}{\beta }_x^{\phi }\left(3^s\left(x-i\right),3^s\left(y-j\right)\right)$$ 8

Where τ and s are translation and scale parameter of the wavelet transformation respectively and ${\beta }_x^{\phi }$ is the transforming function, and it is called the mother wavelet of Berkeley wavelet transformation. The algorithm implemented for the brain tumor segmentation using BWT is described in Algorithm 2.

The morphological operation is used for the extraction of the boundary areas of the brain images. In the morphological operation, the pixel values greater than the selected threshold is mapped to white, while others are marked as black, due to this two different regions are formed around the infected tumor tissues, which is to be cropped out. Then, in order to eliminate white pixel, a morphological erosion operation is executed. Finally, the eroded region and the original image are both divided into two equal regions and the black pixel region extracted from the erode operation are counted as a brain MR image mask.

To evaluate and prove the performance of our proposed segmentation algorithm based on watershed segmentation, FCM, DCT and BWT, segmentation algorithms are evaluated on the basis of segmentation score S [15, 35]. The best segmentation score (maximum value) is selected and thus select the corresponding segmented image for further evaluation. Generally, segmentation score is calculated to prove the effectiveness of the segmentation or clustering operation. In fact, the clustering result is judged on the value of S, and the larger the value of S is, the better the clustering is. Mathematically it is represented as follows,

$$S=\sum _{n=1}^K\frac{f{(x,y)}_n\bigcap f{(x,y)}_{\mathrm{re}{f}_n}}{f{(x,y)}_n\bigcup f{(x,y)}_{\mathrm{re}{f}_n}}$$ 9

where f(x,y)_n represents the set of pixels to the nth class obtained by the algorithm, while f(x,y)_n represents the set of the pixels to the nth class in the reference or ground truth segmented image.

Table 3 gives a comparative analysis of the quantitative score. The experimental results for the watershed, FCM, DCT and BWT segmentation techniques are shown in Fig. 3.

Table 3.

Comparative analysis of segmentation score

Images	Tissue	WS	FCM	DCT	BWT
Image 1	WM	0.57	0.81	0.84	0.91
1	GM	0.48	0.68	0.79	0.85
	CSF	0.42	0.59	0.63	0.79
	Tumor	0.75	0.81	0.89	0.90
Average score		0.55	0.72	0.78	0.86
Average time (in seconds)		0.89	1.15	1.23	1.05
Image 2	WM	0.65	0.79	0.83	0.89
2	GM	0.71	0.73	0.73	0.83
	CSF	0.52	0.62	0.67	0.69
	Tumor	0.77	0.82	0.88	0.89
Average score		0.66	0.74	0.77	0.82
Average time (in seconds)		0.75	1.10	1.18	0.95
Image 3	WM	0.70	0.83	0.88	0.91
3	GM	0.71	0.79	0.91	0.90
	CSF	0.53	0.67	0.83	0.79
	Tumor	0.69	0.85	0.89	0.87
Average score		0.67	0.78	0.87	0.86
Average time (in seconds)		0.80	1.32	1.38	1.10
Image 4	WM	0.60	0.84	0.75	0.97
4	GM	0.57	0.82	0.84	0.93
	CSF	0.49	0.69	0.77	0.85
	Tumor	0.51	0.87	0.91	0.98
Average score		0.54	0.80	0.81	0.93
Average time (in seconds)		0.98	1.40	1.39	1.15
Image 5	WM	0.77	0.84	0.91	0.97
5	GM	0.71	0.83	0.81	0.93
	CSF	0.51	0.70	0.77	0.89
	Tumor	0.44	0.78	0.81	0.96
Average score		0.60	0.78	0.82	0.93
Average time (in seconds)		0.78	0.96	1.17	0.86

Fig. 3.

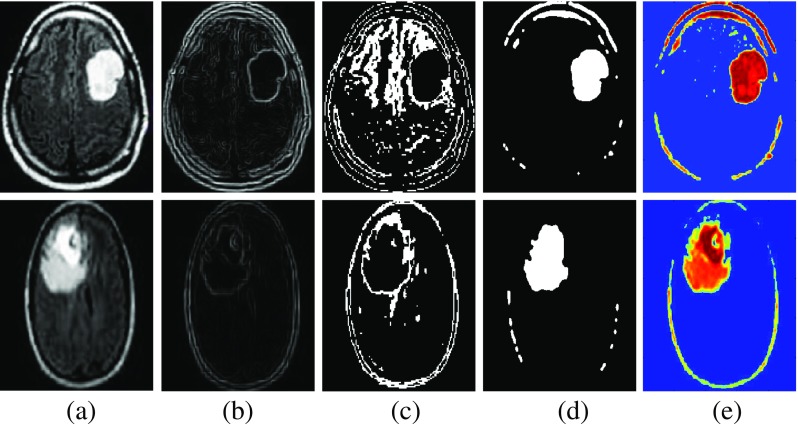
Experimental results of segmentation a original image b watershed segmentation c FCM segmentation (d) DCT segmentation e BWT segmentation

Feature Extraction

Feature Extraction is the process of bringing more preciseness and clearness in the image which in-turn defines the color, texture, size and edges of the body. Haralick et al. [36] introduced one of the most widely used image analysis application of Gray Level Co-ocurrence Matrix (GLCM) and texture feature. Feature extraction is a key area used for reducing the complexity of the classifier to classify characteristics of an image. Some of the useful features under the classification of gray level co-ocurrence matrix, segmentation based fractal texture analysis, and intensity-based features are listed in Table 4.

Table 4.

Performance matrices for segmented image and features

Metrics	Formulae
Mean (M)	M = $\left(\frac{1}{n\times m}\right){\sum }_0^{n-1}{\sum }_0^{m-1}f(n,m)$
	where n and m are image size. A lower value indicates good amount of noise elimination from the image.
Standard deviation (SD)	SD = $\sqrt{\left(\frac{1}{n\times m}{\sum }_0^{n-1}{\sum }_0^{m-1}{\left(f\right(n,m)-M)}^2\right)}$
	A higher value indicates better intensity level and high contrast among edges of an image.
Mean square error (MSE)	MSE = $\frac{1}{m\times n}\sum \sum {\left(f\right(n,m)-f^R(n,m\left)\right)}^2$
	where f(n,m) and fR(n,m) indicates original and reconstructed images, respectively
Entropy (E)	E = $-\sum _{m=0}^{m-1}\sum _{n=0}^{n-1}f(n,m)\underset{2}{log}f(n,m)$
	Higher value of entropy indicates more information contents and also indicates better imperceptibility.
Skewness (Sk)	Sk = $\left(\frac{1}{m\times n}\right)\frac{\sum \left|{\left(f\right(n,m)-M)}^3\right|}{S{D}^3}$
	Skewness is a measure of symmetry or the lack of symmetry
Kurtosis (Kurt)	Kurt = $\left(\frac{1}{m\times n}\right)\frac{\sum {\left(f\right(n,m)-M)}^4|}{S{D}^4}$
	The shape of a random variable’s probability distribution is describe by the parameter called Kurtosis
Energy (En)	En = $\sqrt{\sum _{x=0}^{m-1}\sum _{y=0}^{n-1}{f}^2(x,y)}$
	Energy is a parameter to measure the similarity of an image. If the image consists of very similar pixels, then its energy value will be large.
Contrast (Con)	Con = $\sum _{x=0}^{m-1}\sum _{y=0}^{n-1}{(x-y)}^{2}f(x,y)$
	Contrast is a measure of the intensity of a pixel and its neighbor over the image.
Homogeneity (H)	H =$\sum _{x=0}^{m-1}\sum _{y=0}^{n-1}\frac{1}{1+{(x-y)}^2}f(x,y)$
	Homogeneity may have a single or a range of values so as to determine whether the image is textured or non-textured.
Coarseness (Cness)	Cness = $\frac{1}{2^{m+n}}\sum _{x=0}^{m-1}\sum _{y=0}^{n-1}f(x,y)$
	Coarseness is a measure of roughness in the textural analysis of an image.

Area calculation: Apart from the discussed feature vectors shown in Table 4, we studied that, the area of the tumor is also used to classify the tumor type. So, to make better conclusion and decision on the tumor type, area calculation is also included as one of the feature vectors.

To calculate the size of tumor we convert the extracted image to binary form. The white pixels show the tumor area and are used to calculate the size of the tumor, as described below.

W=number of white pixels

where 1 pixel = 0.264 mm²

so, the size of the tumor in mm² is calculated as

$$\text{the size of the tumor in}m{m}^2=\left[\sqrt{W}\right]\ast 0.264$$ 10

In this study, it is assumed that if the area of the tumor is less than 8 mm² then it is benign or no tumor, otherwise malignant. Figure 4 shows the plot of some of the prominent features for randomly selected 10 images.

Fig. 4.

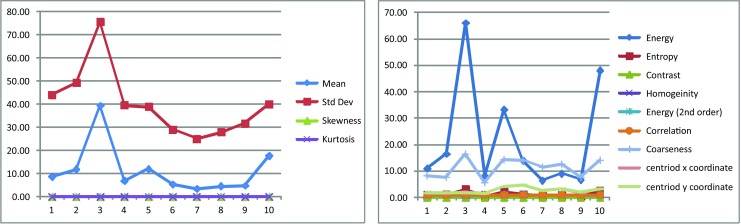
Plot of some prominent features

Classification

Genetic algorithm (GA) has been investigated for the numbers of applications which includes: image formation and reconstruction, image enhancement, image compression, image visualization, image segmentation and image matching [20]. In this study, GA has been investigated for feature optimization technique and classification. A Genetic algorithm is a method commonly used to solve search problems and optimization problems for both constrained and unconstrained data based on biological evolution such as mutation, crossover, and selection.

Feature extraction generates the number of features and all the features are not relevant for the classifier to classify the tumor type. The GA is employed to randomly select individual features from the current set of the feature vector and uses them for classification of tumor type. The algorithm used to select best features and then to classify them are described in Algorithm 3.

Results and Discussion

This section presents the results of our proposed image segmentation technique, which are obtained by brain MR images. The proposed algorithm was carried out using Matlab 7.12.0 (R2011a), which runs on the Windows 8 operating system and has an Intel core i3 processor and a 4GB RAM. The experimental results obtained are given in the next subsections.

Experimental Results

The proposed algorithm performs comparative approach of segmentation and selected the best segmentation result based on segmentation score. Further, to classify the tumor type, features are extracted and relevant features are optimized and classified using the genetic algorithm. The sample experimental results obtained from the proposed technique is depicted in Fig. 5 which shows the original image along with enhanced image, skull-stripped image, watershed segmented image, FCM segmented image, DCT segmented image, BWT segmented image, dice overlap image, and the tumor region with extracted area mark.

Fig. 5.

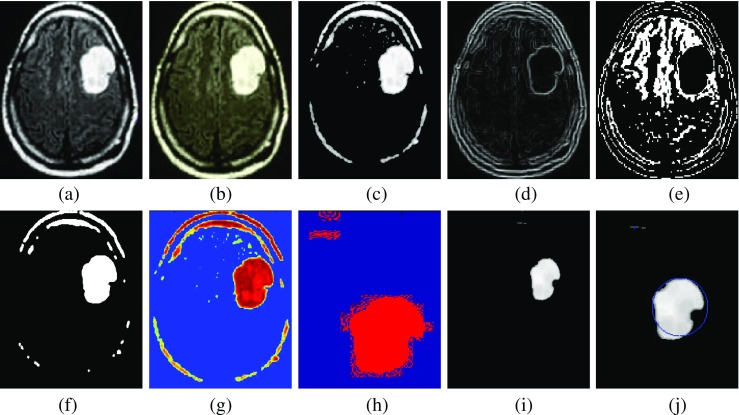
Experimental results. a Original image. b Enhance image. c Skull stripped image. d Watershed segmentation. e FCM segmentation. f DCT segmentation. g BWT segmentation. h Dice similarity image. i Extracted image (morphology operation). j Area-extracted tumor region

Performance Evaluation Metrics

The proposed algorithm performance can be evaluated in terms of accuracy, sensitivity, and specificity. The confusion matrix defining the terms TP, TN, FP, and FN from the expected outcome and ground truth result for the calculation of accuracy, sensitivity, and specificity are shown in Table 5.

Table 5.

Confusion matrix defining the terms TP, TN, FP, and FN

Expected outcome	Ground truth		Row total
	Positive	Negative
Positive	TP	FP	TP+FP
Negative	FN	TN	FN+TN
Column total	TP+FN	FP+TN	TP+FP+FN+TN

Where TP is the number of true positives, TN is the number of true negatives, FP is the number of false positive, and FN is the number of false negatives. Table 6 shows the formulas to calculate accuracy, sensitivity, specificity, and average dice similarity coefficient.

Table 6.

Accuracy, sensitivity, specificity, and average dice coefficient calculation

Quality parameter	Formula
Accuracy	$\frac{TP+\mathrm{TN}}{TP+\mathrm{TN}+FP+FN}$
Sensitivity	$\frac{TP}{TP+FN}$
Specificity	$\frac{\mathrm{TN}}{\mathrm{TN}+FP}$
Average dice coefficient index	$\frac{2TP}{2TP+FP+FN}$

The test performance of the GA classifier determined by the computation of the statistical parameters such as sensitivity, specificity, and accuracy in comparison with different classifier techniques such as an adaptive neuro-fuzzy inference system (ANFIS) and K-Nearest Neighbors (K-NN) is shown in Table 7.

Table 7.

Comparison of accuracies in different classifiers

Number of test images (normal = 67, abnormal= 134)
Evaluation parameter	ANFIS	GA	K-NN
		(proposed classifier)
True negative	60	64	61
False positive	9	6	12
True positive	118	121	114
False negative	14	10	14
Specificity (%)	86.95	91.42	83.56
Sensitivity (%)	89.39	92.36	89.06
Accuracy (%)	88.55	92.03	87.06
Average dice coefficient
index (%)	91.11	93.79	89.76

Conclusions and Future Work

In this study, we segmented brain tissues into normal tissues such as white matter, gray matter, cerebrospinal fluid (background), and tumor-infected tissues. We used pre-processing to reduce the effect of unwanted noise captured during the acquisition of MR images and employed enhancement based on our proposed auto-enhance FCM technique to improve the quality of raw MR images. The undesired cerebral tissues such as fat and skin are removed using skull stripping based on threshold technique. Further, to get the best possible segmentation results, we develop the comparative approach for comparing four segmentation techniques based on watershed, FCM, DCT, and BWT and select the best by comparing their segmentation score. To improve the accuracy for classification of the tumor stage, feature vector is extracted and also optimize and classified using the genetic algorithm. Our experimental results show that the proposed approach can aid in the accurate, and timely detection of brain tumor along with the identification of its exact location. Thus, the proposed approach is significant for brain tumor detection from MR images.

The experimental results achieved 92.03% accuracy, 93.79% average dice coefficient index, and 0.82 to 0.93 segmentation score using BWT-based segmentation demonstrating the effectiveness of the proposed technique for identifying normal and abnormal tissues from MR images. Our results is suitable to integrate clinical decision support systems for primary screening and diagnosis by the radiologists or clinical experts.

In the future work, to improve the accuracy and dice coefficient index of the present work, we are planning to investigate the more robust mechanism for the large database of medical images and selective scheme of the classifier by combining more than one classifier.