Comparison of Shallow and Deep Learning Methods on Classifying the Regional Pattern of Diffuse Lung Disease

Abstract

This study aimed to compare shallow and deep learning of classifying the patterns of interstitial lung diseases (ILDs). Using high-resolution computed tomography images, two experienced radiologists marked 1200 regions of interest (ROIs), in which 600 ROIs were each acquired using a GE or Siemens scanner and each group of 600 ROIs consisted of 100 ROIs for subregions that included normal and five regional pulmonary disease patterns (ground-glass opacity, consolidation, reticular opacity, emphysema, and honeycombing). We employed the convolution neural network (CNN) with six learnable layers that consisted of four convolution layers and two fully connected layers. The classification results were compared with the results classified by a shallow learning of a support vector machine (SVM). The CNN classifier showed significantly better performance for accuracy compared with that of the SVM classifier by 6–9%. As the convolution layer increases, the classification accuracy of the CNN showed better performance from 81.27 to 95.12%. Especially in the cases showing pathological ambiguity such as between normal and emphysema cases or between honeycombing and reticular opacity cases, the increment of the convolution layer greatly drops the misclassification rate between each case. Conclusively, the CNN classifier showed significantly greater accuracy than the SVM classifier, and the results implied structural characteristics that are inherent to the specific ILD patterns.

Introduction

Interstitial lung diseases (ILDs) represent a major cause of morbidity and mortality [1]. High-resolution computed tomography (HRCT) has become critical to characterize the imaging patterns of ILD [2, 3], but this approach remains vulnerable to inter- and intra-observer variation. To overcome human variation, automated techniques have been applied for differentiating a variety of obstructive lung diseases based on the features of a density histogram [4–7] and texture analyses [8–12] and for making ILD diagnoses based on the features of texture analysis [13–18]. Although the quantification and classification performances of these approaches for ILD remain unsatisfactory, automated schemes that provide a quantitative measurement of the affected lung or the probability of a certain disease with perfect reproducibility would be useful, as even experienced chest radiologists frequently struggle with differential diagnoses [8].

Generally, an automated scheme involves two main steps of quantification that analyze histogram, texture, and so on, along with classification using a machine learning mechanism. Therefore, the success of this scheme depends on identifying the most significant features to solve the classification problem and choosing which learning algorithm to use. Recently, deep learning methods have attracted considerable attention from various fields because of their remarkable performance enhancement [19–21]. Using a deep architecture to mimic the natural neuromorphic multi-layer network, these methods can automatically and adaptively learn a hierarchical representation of patterns from low- to high-level features and subsequently identify the most significant features for a given task. Compared to the conventional machine learning methods, a point of difference in deep learning should be that the quantification step of extracting features is omitted. Some recent reports on medical image analyses using deep learning algorithms have been introduced for basal-cell carcinoma cancer detection [22], multi-atlas segmentation of cardiac magnetic resonance images [23], and brain segmentation [24]. Neuromorphic networks have been applied to studies of ILDs [25], but a simple shallow architecture was employed in this study. Some studies have used neuromorphic networks with a deep architecture [26–29], but they employed different schemes in ILD subregions compared with our current approach and the present study focuses on the structural characteristics inherent to the specific ILD.

Materials and Methods

Subjects

Both of Asan Medical Center (AMC) and National Jewish Health Center institutional review board for human investigations approved the study protocol, removed all patient identifiers, and waived informed consent requirements because of the retrospective design of this study. From AMC (Seoul, Republic of Korea), where a Siemens CT scanner (Sensation 16, Siemens Medical Solutions, Forchheim, Germany) was used for examining the subjects, HRCT images were selected from a collection of images of 106 patients including 14 healthy subjects, 16 patients with emphysema, 35 patients with cryptogenic organizing pneumonia, 36 patients with usual interstitial pneumonia, 4 patients with pneumonia, and 1 patient with acute interstitial pneumonia. From the National Jewish Health Center (Denver, CO, USA), where a GE CT scanner (GE Lightspeed 16, GE Healthcare, Milwaukee, WI) was used, HRCT images of 212 patients including 39 patients with emphysema, 70 patients with cryptogenic organizing pneumonia, 72 patients with usual interstitial pneumonia, 18 patients with pneumonia, and 13 patient with acute interstitial pneumonia were selected. All the images were obtained using typical HRCT protocol parameters, including 220 mAs and 120–140 kVp with patients. Images were reconstructed at a slice thickness of 1 mm and intervals of 10 mm using an enhancing reconstruction kernel (B70f in the Siemens scanner and a sharp kernel in the GE scanner). CT image was scanned with breath-holding at full inspiration by radiographer’s instruction.

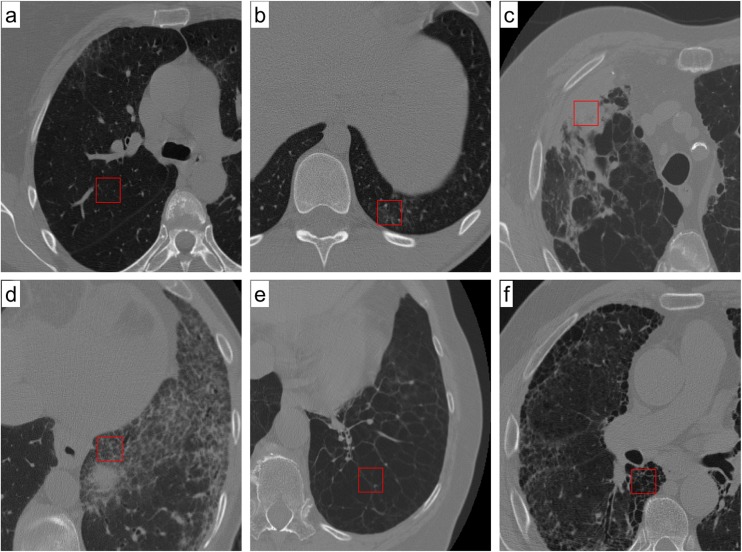
The following six types of image characteristics were examined: normal (Fig. 1a), ground-glass opacity (Fig. 1b), consolidation (Fig. 1c), reticular opacity (Fig. 1d), emphysema (Fig. 1e), and honeycombing (Fig. 1f). Ground-glass opacity is an abnormally hazy focus in the lungs that is not associated with obscured underlying vessels. A similar finding that is associated with obscured underlying vessels is defined as consolidation. Increased reticular lung opacity is the product of a thickened interstitial fiber network of the lung resulting from fluid, fibrous tissue, or cellular infiltration. In emphysema, there are focal areas of very low attenuation that can be easily contrasted with the surrounding higher attenuation of the normal parenchyma. Emphysema can typically be distinguished from honeycombing based on areas of emphysematous destruction that lack a visible wall, whereas honeycomb cysts have thick walls of fibrous tissue. Honeycombing is also characterized by extensive fibrosis with lung destruction, which results in a cystic, reticular appearance. However, a problematic middle area still exists in which more than two regional characteristics are simultaneously shown or when a regional characteristic is too ambiguous for radiologists to arrive at a consensus.

Fig. 1.

Images from high-resolution CT scans of the chest are shown. Each image shows the ROI that is a typical of each particular condition: a normal lung parenchyma, b ground-glass opacity, c consolidation, d reticular opacity, e emphysema, and f honeycombing

Image Representation

Two expert radiologists, who each had more than 20 years of experience, were asked to select rectangular regions of interest (ROIs) of 30 × 30 pixels on CT images from each scanner, which were categorized independently into one of five disease regional patterns or as a normal regional pattern excluding the airway, vessel, and pleura. The radiologists selected the 2D ROIs using 3D information. To reduce selection bias, only one ROI was selected per lobe. Subsequently, the two radiologists reached a consensus on the classification for each given ROI. For each scanner, the radiologists chose 100 ROIs for each class, resulting in the consideration of a total of 600 ROIs for each scanner.

The location of the ROI set used in the present study is the same with the ROIs used in our previous work [18], in which two shallow learning methodologies of Bayesian and SVM classifiers were compared and evaluated. The only difference was that 30 × 30 pixels of ROIs instead of 20 × 20 pixels of ROI were used. The reason for enlarging the ROI is to use data augmentation for the convolutional neural network (CNN) which is a widely used technique to improve the generalization performance of CNN [19–21].

Research Design

To classify each ROI into one of six subregions, the CNN, which is a representative classifier of a deep architecture, was used. Without pre-training, CNN enables supervised learning using back-propagation processes and interpixel data for an image. For various visual classification issues, this method is known to show a better performance compared with conventional shallow learning methodologies [19, 21, 30]. To evaluate the effects of different scanners on the accuracy of the classification of regional disease patterns, the following three study designs were employed: intrascanner, interscanner, and integrated scanner. In the intrascanner experiment, the training and test sets were obtained from the same scanner. In the interscanner experiment, the training and test sets were acquired from the other scanner. Finally, in the integrated scanner experiment, data from the two scanners were first merged and then were split into separate training and test sets. These three experimental designs are presented in Table 1.

Table 1.

Study design for assessments of automatic quantification

Notation	Study set	Study design	Training set (N)	Test set (N)
intra.G	Intrascanner study	GE	GE (480)	GE (120)
intra.S		Siemens	Siemens (480)	Siemens (120)
integ	Integrated scanner study	Integrated set	GE + Siemens (960)	GE + Siemens (240)
inter.G2S	Interscanner study	GE to Siemens	GE (480)	Siemens (120)
inter.S2G		Siemens to GE	Siemens (480)	GE (120)

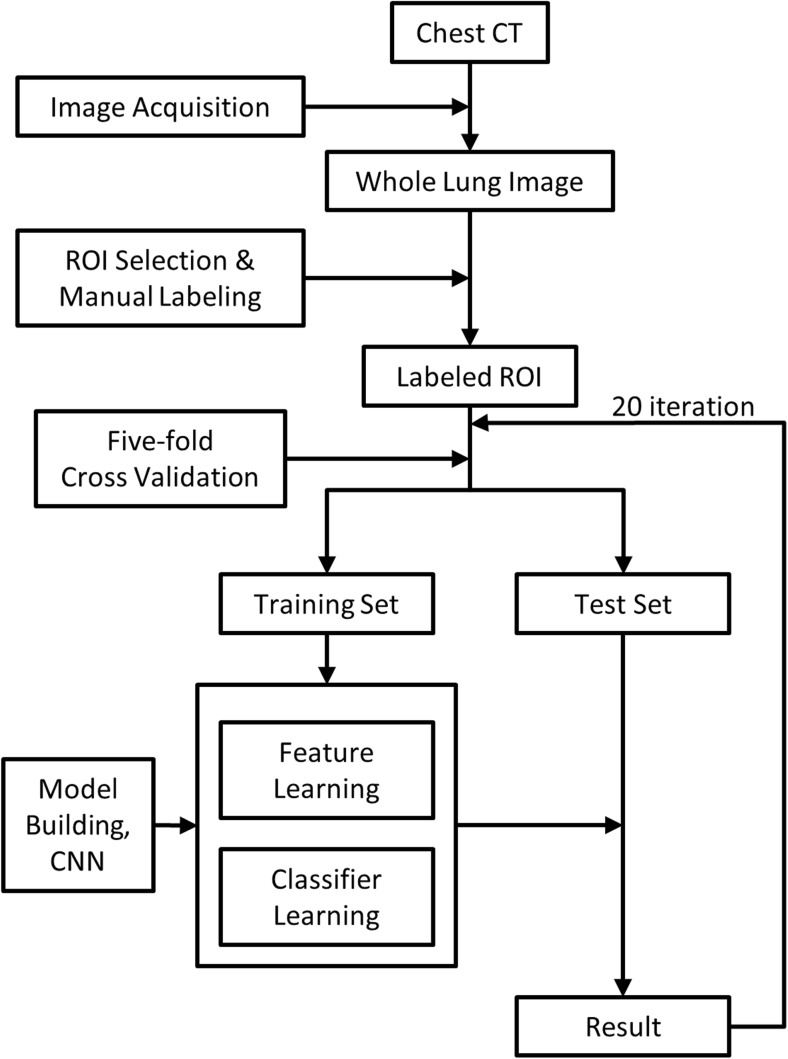
In each experiment, we performed fivefold cross-validations to evaluate the performance of the model. Specifically, we randomly split data into five folds and used four of these as a training set and the remainder as a test set for validation. This resulted in a training set of 480 samples and a test set of 120 samples from each scanner for intrascanner cases. For integrated scanner cases, we merged data from each scanner into a single set and performed random sampling for cross-validation, which resulted in a training set of 960 samples and a test set of 240 samples. Chang et al. [18] previously evaluated the effect of increasing the sample size from 600 to 1200 using an identical integrated data set approach and reported that there was no significant difference between the accuracy results based on the sample size variation. For interscanner cases, we randomly split the data set into five subsets and used four of them from one scanner as the training set, while one subset from the other scanner was used as a validation set. We repeated fivefold cross-validations 20 times for each case. Figure 2 summarizes the procedures used in the proposed automatic classification system.

Fig. 2.

Flow diagram of the automated classification system used in the CNN

Automated Classification

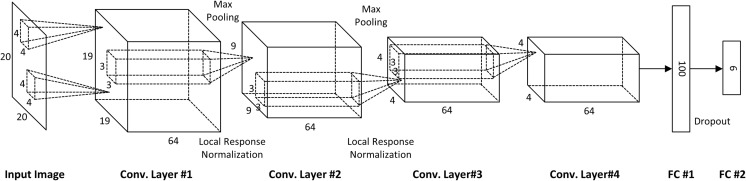
The overall CNN architecture used to train the network is described in Fig. 3. The network includes six learnable layers that consist of four convolution layers and two fully connected layers. To feed data into the input layer, we performed two basic data augmentation approaches to supplement the relatively small number of training data sets and reduce overfitting. The first form was random cropping and flipping. From the original 30 × 30 image pixels, 20 × 20 pixels of ROI patches were randomly cropped and an image with a probability of 0.5 was horizontally flipped. A second form of augmentation, which applies mean centering and random noise to all input pixels, was also applied. Specifically, the mean and standard deviation of all training pixel values and the mean value from all pixels of the training image were subtracted. Additionally, random noise was added, which was sampled from a Gaussian distribution with a mean of zero and standard deviation and was used based on one tenth of the value of the standard deviation of all pixel values. In every iteration, these two forms of data augmentation were applied to each mini-batch of samples.

Fig. 3.

Overall architecture for training the CNN network

In this study, the same 30 × 30 pixels of ROI were employed in both of the SVM and CNN approaches. For getting each best performance, however, the CNN adopted the data augmentation above and the SVM did not. To verify the effect of data augmentation, in another experiment, the same augmented data set of 20 × 20 pixel ROI patches cropped from the original 30 × 30 pixel ROI were applied to both of the classifiers and the classification accuracy results were compared.

The first convolutional layer learned 64 filters with a size 4 × 4 pixels and a stride of 1. The size of the first feature map became 19 × 19 because we used zero-padding for the input image. Additionally, local response normalization and max pooling, which leads to significant gains in performance, were applied. The size of pooling kernel is 3 × 3 with stride 2. Although it is optional to use local response normalization for general 8-bit image data sets, such as ImageNet or MINIST, local response normalization is critical to analyze 12-bit medical images to prevent activation of the upper layers, which are dominated by a set of high-input pixel values that reduce overfitting. The 64 filters with a 3 × 3 pixel size for the second convolution layer with a stride of 1 were used, and both local response normalization and maximum pooling were again applied. The third and fourth convolution layers were 64 filters with a 3 × 3 pixel size and a stride of 1 without local response normalization or pooling. The fourth convolutional layer was connected to the first fully connected layer with 100 nodes. The number of neurons in the first fully connected layer was chosen by cross-validation with 50, 100, and 200, in which 100 showed the best performance. The number of output classes was 6. Additionally, dropout with a ratio of 0.5 in the first fully connected layer was used to reduce overfitting. The output layer consisted of six nodes with softmax activation. The network was trained by minimizing cross-entropy loss between this softmax output and one hot-coded true label. Finally, for all layers in the architecture, rectified linear unit (ReLU) activation was used. The only data-dependent hyper-parameter was standard deviation of Gaussian random noise. The other hyper-parameters such as momentum, weight decay, learning rate, and number of training epochs were chosen by fivefold cross-validation. We did not use learning rate scheduling since the speed of convergence was fast and the performance was not highly sensitive to the value of learning rate.

The network was trained with stochastic gradient descent and a batch size of 20 samples, a momentum of 0.9, and a weight decay of 0.001. All weights and biases were initialized from a Gaussian distribution with a mean of zero and a standard deviation of 0.01, except for the first convolutional layer that had a standard deviation of 0.001. The CNN has been developed in-house, for all ROIs were processed with 12 bits per pixel. We used Nvidia Titan Black GPU with 6-GB memory for the present experiment.

For imaging features, the 22-dimensional features used by SVM are quantitative values from histogram, gradient, run-length, gray level co-occurrence matrix, low-attenuation area cluster, and top-hat transformation descriptors [18]. For CNN, the features are automatically learned from the raw training ROI patch images while maximizing the classification performance. We used 100-dimensional features obtained from the fully connected layer when we feed the ROI patches through the CNN.

Statistical Analysis

Accuracy was measured to compare the classification performance of the CNN and SVM classifiers for intrascanner, interscanner, and integrated scanner data. The classification accuracy of a classifier ‘Γ’ was defined as follows:

$$\text{Accuracy}=\frac{1}{n}\sum _{i=1}^n\mathrm{\Gamma }\left(R_i\right)\times 100\left(\%\right)$$

where

$$\mathrm{\Gamma }\left(R_i\right)=\left\{\begin{array}{c}1,\text{if}\text{correctly classifies}{R}_i\text{into}\mathrm{one}\text{of the}\mathrm{six}\text{classes}\\ 0.\text{otherwise},\end{array}\right.$$

Here, R _i is the i-th ROI of the test data in a trial of fivefold cross-validation and n is the number of ROIs in the test data. When the classifier Γ correctly classifies the ROI, R _i, into one of six classes (normal, ground glass opacity, consolidation, reticular opacity, emphysema, or honeycombing), the classification accuracy increases. To compare the accuracy performance between classifiers or between experimental sets, an unpaired t test was applied in all cases because each two data sets of the accuracy-tested groups were obtained independently. Here, the p value was calculated with the classification performance of all the fivefold cross-validations and their 20 replicates, which meant that unpaired the t test was done with 100 values for each set. For each fivefold cross-validation, we kept the indices of each fold and synchronized these indices for two classifiers.

Results

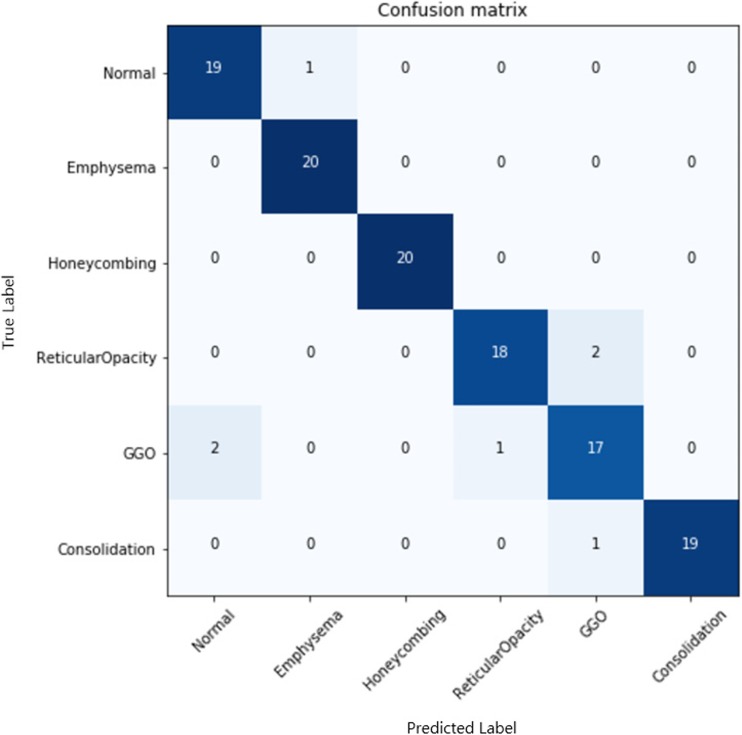
For the SVM and CNN classifiers, the mean and standard deviation of the classification accuracy were evaluated in three experimental designs to evaluate the intrascanner, integrated scanner, and interscanner data sets (Table 2). In all experiments, the CNN classifier showed better overall performance in accuracy (p value < 0.001) than the SVM classifier by 6–9%. In another data set in which the same condition of image augmentation was equally applied to exclude augmentation issue, our findings also showed a similar tendency for a better accuracy of the CNN by 4–11% (Appendix Table 4). Confusion matrix of subclasses in the case of training Siemens data and testing Siemens data was shown in Appendix Fig. 4. This finding establishes the significantly better performance of the classifier with a deep architecture compared with those with a shallow architecture, even in diagnostic images of regional patterns of ILD. Both classifiers showed accuracy degradation according to interscanner variation from intra- to integrated and then interscanner set. The degree of the accuracy degradation rates between the SVM and CNN were similar, but the CNN showed slightly lower degradation rates than the SVM with a statistical significance (Appendix Table 5).

Table 2.

Comparisons of classification-based accuracy between the SVM and CNN classifiers for six subregions of ILD

Study	Classification accuracy (%)		p value
	SVM	CNN
intra.G	90.06 ± 1.99	96.06 ± 1.61	< 0.001
intra.S	89.01 ± 2.20	96.11 ± 1.19	< 0.001
integ	88.07 ± 1.63	95.12 ± 1.91	< 0.001
inter.G2S	77.26 ± 3.08	86.13 ± 2.28	< 0.001
inter.S2G	77.03 ± 3.42	85.04 ± 1.91	< 0.001

Table 4.

Comparisons of classification-based accuracy between the SVM and CNN classifiers for six subregions of ILD with the same augmented data set. From each original 30 × 30 ROI patch, 10 ROI patches of 20 × 20 pixels were cropped from the five fixed positions (top-left, top-right, center, bottom-left, and bottom-right) and all the cropped patches were horizontally flipped. Both of the classifiers used the same data set augmented 10 times

Study	Classification accuracy (%)		p value
	SVM	CNN
intra.G	88.93 ± 1.19	95.86 ± 1.29	< 0.001
intra.S	90.31 ± 1.00	95.21 ± 1.60	< 0.001
Integ	86.81 ± 0.84	94.89 ± 1.60	< 0.001
inter.G2S	75.90 ± 1.57	86.04 ± 2.22	< 0.001
inter.S2G	73.11 ± 1.49	84.67 ± 2.50	< 0.001

Fig. 4.

Confusion matrix of subclasses in the case of training Siemens data and testing Siemens data

Table 5.

Classification-based accuracy comparisons between experimental sets. The scheme for calculating the accuracy for each classifier was the same as that indicated in Table 2

Study	Classification accuracy (%)				Improvement (%)	Accuracy degradation rate (%)
	SVM	p value	CNN	p value		SVM	CNN	p value
intrascanner set	89.53 ± 2.15	< 0.001	96.09 ± 1.41	< 0.001	6.56	1.61 ± 6.04	0.99 ± 5.40	0.03
integrated scanner set	88.07 ± 1.63		95.12 ± 1.91		7.05
		< 0.001		< 0.001		12.37 ± 9.51	9.98 ± 6.76	< 0.001
interscanner set	77.14 ± 3.25		85.59 ± 2.17		8.45

In the pathological point of view, there exists the subregional ambiguity between normal case and emphysema or between honeycombing and reticular opacity. To quantitatively evaluate differences in the rates of progress between these specific subregions, the classification error rates from normal case (or reticular opacity) to emphysema (or honeycombing) classifications and the reverse comparisons were determined with the convolution layer increment (Table 3). As the number of the convolution layer increased, the overall classification accuracy showed better performance from 81.27 to 95.12%, in which it became nearly saturated at the stage of four convolution layers from the classifiers with two convolution layers. The increment of the convolution layer greatly drops the misclassification rate between subregions. The classification error rates of the normal case (emphysema) with emphysema (normal case) dropped to 0.48% (1.21%), and those of honeycombing (reticular opacity) to reticular opacity (honeycombing) dropped to 2.12% (4.91%).

Table 3.

Classification error rates based on the CNN between subregions with increasing numbers of convolution layers

Study set	No. of convolution layers	Classification accuracy (%)	Error rate (%)
			N > Ea	E > Nb	H > Rc	R > Hd
Integrated set	1	81.27 ± 1.57	14.92	22.81	14.71	17.11
	2	90.67 ± 1.02	5.44	7.69	8.46	7.29
	3	93.73 ± 0.71	2.50	1.46	7.14	6.13
	4	95.12 ± 0.52	0.48	1.21	2.12	4.91

^aNormal case was misclassified as an emphysema case

^bEmphysema case was misclassified as a normal case

^cHoneycombing case was misclassified as a reticular opacity case

^dReticular opacity case was misclassified as a honeycombing case

Discussion

Automated schemes for classifying or diagnosing diseases have generally involved two steps for the quantification of features and classification of conventional classifiers with a shallow architecture, e.g., the SVM. However, deep learning methods have recently been found to show remarkable performance enhancement without extracting features or feature optimization [19–21]. Using a CNN classifier having a deep architecture, in the present study, we could achieve better accuracy compared to the SVM by 6–9% in all experiments for the intrascanner, integrated scanner, and interscanner tests. This finding establishes that the better performance of deep learning methods could also be applied to diagnostic images of ILD. We also could estimate a degree of similarity or relationship among subregions, which it might explain the relative distance of the structural characteristics that are inherent to each subregion of ILD. For example, the increment of convolution layer in the CNN shows the processes of differentiating among ILD subregions. The degree of the remaining mixture between subregions, e.g., reticular opacity and honeycombing, can be quantitatively calculated based on the error rate for misclassification. It may help to elucidate a degree of similarity between specific subregions and to understand the differentiation process among ILD subregions and to provide clinicians with findings to discuss and to help determine the number of subregions or provide standards in diagnosing a subregion.

Deep learning approach has been considered to be robust in many application domains because it does not use pre-defined features for training classifiers. Instead, deep learning models learn and extract features automatically from the data. In the condition of the different scanner’s data getting mixed, therefore, the SVM took the fixed pre-defined feature extraction and the CNN extracted features automatically with learning. In this study, since the top two layers of CNN is essentially a simple nonlinear classifier, we concluded that the difference in performance between the two methods was mostly due to the way their features are extracted. Especially in this ILD classification application, their subtypes of ground-glass opacity, consolidation, reticular opacity, emphysema, honeycombing, and normal pattern have very vague and abstract boundaries to define each other. Therefore, it has been thought that the deep learning method as a data-driven method has better performance rather than the conventional feature-based method does. Of course, both of the pre-defined features in SVM and the automatically learned features in CNN must be dependent on the scanner or the filter.

Although achieving better performance accuracy in classifying ILD subregions can be acquired using the CNN, several limitations still exist in this study. Even with data augmentation being employed, the data samples used in the present study were too small in typical deep learning structures. In medical applications, actually, it seems to be difficult to prepare a large image data set with the gold standard qualified by the radiologist. It is believed that a larger data set could give us higher and more robust classifying performance in accuracy. For this limited number of data, nevertheless, the performance of the CNN with feature learning was shown to be significantly better than the SVM with feature engineering in this study. We also wanted to try the developed machine to apply public data, but ILD data set, which is well classified and is proper to the present approach, seems to be rarely found. Unfortunately, NLST is also not an ILD cohort but lung cancer cohort (https://www.cancer.gov/types/lung/research/nlst). In fact, the present study was able to be performed because we already have the well-prepared ILD data set due to the previous study. In addition, the present ROI-based study design is an important limitation in real clinical applications because whole lung quantification data obtained using an automation tool would be needed to assist radiologists in real clinical situations as a computer-aided diagnosis (CAD). Our methodology has attempted to take whole lung quantification into account (Appendix Fig. 5). However, it does not address the totally independent issue of avoiding misclassifications by airways, vessels, and lung boundaries. Another requirement for a better lung CAD must be to use 3D information [9, 13, 29]. In general, however, clinical HRCT of ILD images consists of the repetition of a 1-mm axial image with a 10-mm interval on the Z-axis. Therefore, it scans a 3D human body (the lung in this study), but images do not have continuity along the Z-axis. Volumetric CT scan which has been used recently in a real clinical environment would enable a 3D CAD in the near future.

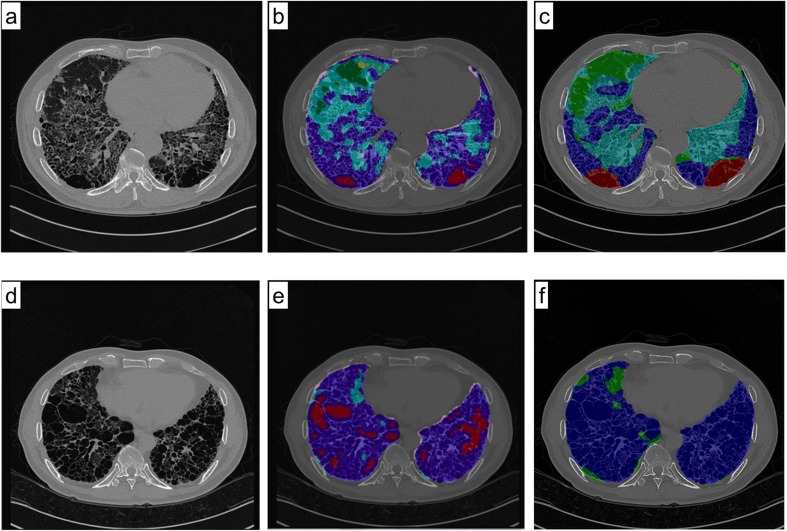
Fig. 5.

Comparison of whole lung quantification data using the golden standard by a radiologist (two cases). Each pixel was coded by the classification result, which is indicated by a semi-transparent color (normal, green; ground-glass opacity, yellow; reticular opacity, cyan; honeycombing, blue; emphysema, red; and consolidation, pink). a, d Original scanned images. b, e CNN classifier results. c, f Golden standard obtained by a radiologist. The colored areas beyond the lung were removed using a separately prepared lung mask

Conclusions

In our present study, the performance of a CNN classifier with a deep architecture was tested for subregion-demarked parenchymal lung disease of ILD. In all the interscanner variations, the CNN showed a better performance, as indicated by increased accuracy compared with the SVM with a shallow architecture. From the classification error rates between subregions, we could evaluate quantitative information as objective criteria to help radiologists arrive at a consensus when diagnosing subregions of ILD.