Quantitative Volumetric K-Means Cluster Segmentation of Fibroglandular Tissue and Skin in Breast MRI

Abstract

Mammographic breast density (MBD) is the most commonly used method to assess the volume of fibroglandular tissue (FGT). However, MRI could provide a clinically feasible and more accurate alternative. There were three aims in this study: (1) to evaluate a clinically feasible method to quantify FGT with MRI, (2) to assess the inter-rater agreement of MRI-based volumetric measurements and (3) to compare them to measurements acquired using digital mammography and 3D tomosynthesis. This retrospective study examined 72 women (mean age 52.4 ± 12.3 years) with 105 disease-free breasts undergoing diagnostic 3.0-T breast MRI and either digital mammography or tomosynthesis. Two observers analyzed MRI images for breast and FGT volumes and FGT-% from T1-weighted images (0.7-, 2.0-, and 4.0-mm-thick slices) using K-means clustering, data from histogram, and active contour algorithms. Reference values were obtained with Quantra software. Inter-rater agreement for MRI measurements made with 2-mm-thick slices was excellent: for FGT-%, r = 0.994 (95% CI 0.990–0.997); for breast volume, r = 0.985 (95% CI 0.934–0.994); and for FGT volume, r = 0.979 (95% CI 0.958–0.989). MRI-based FGT-% correlated strongly with MBD in mammography (r = 0.819–0.904, P < 0.001) and moderately to high with MBD in tomosynthesis (r = 0.630–0.738, P < 0.001). K-means clustering-based assessments of the proportion of the fibroglandular tissue in the breast at MRI are highly reproducible. In the future, quantitative assessment of FGT-% to complement visual estimation of FGT should be performed on a more regular basis as it provides a component which can be incorporated into the individual’s breast cancer risk stratification.

Introduction

The amount of fibroglandular tissue (FGT) including epithelial and stromal elements is an independent marker of breast cancer risk in conjunction with age, body mass index, and genetic predisposition [1, 2]. Traditionally, the amount of FGT has been evaluated visually from mammograms in which mammographic breast density (MBD) describes the proportion of FGT to fatty tissue. The Breast Imaging Reporting and Data System (BI-RADS®) 4th edition subdivided mammographic breast density (BD) into four quartiles [3]. However, the agreement between radiologists is only moderate and is especially challenging in the middle two density categories [4]. The new BI-RADS® 5th edition still categorizes MBD into four subgroups, i.e., almost entirely fatty, scattered areas of fibroglandular density, heterogeneously dense, or extremely dense [5]. Nevertheless, it is acknowledged that there is a clear need for further research into volume-based, reproducible percentage cutoff points.

Quantitative assessment of the percentage area of FGT in mammograms has been shown to associate more strongly to the individual’s breast cancer risk than can be achieved by its visual assessment [6, 7]. Automated quantitative MBD measurement methods have recently been developed [8] and two clinically applied software programs [9, 10] are now approved by the US Food and Drug Administration. The two-dimensional methods may suffer from tissue overlap [11]. Tomosynthesis, in which multiple low-dose images are used to reconstruct a 3D model, has been postulated to define more accurately tissue structures [12]. In addition to the breast cancer risk, the MBD may be a prognostic factor in patients with newly diagnosed breast cancer, i.e., one study suggested that patients with breast densities lower than 10% MBD have higher mortality rates than patients with denser breasts [13].

Magnetic resonance imaging (MRI) of the breast is being increasingly exploited in clinical practice with a wide range of clinical and screening indications [14]. Therefore, an accurate assessment of FGT as an adjunct to clinical breast MRI would be clinically valuable. The excellent soft tissue contrast in MRI provides clear distinguishing between fibroglandular and fatty tissues and allows a three-dimensional characterization of FGT volume without tissue compression or radiation exposure [15]. As a three-dimensional imaging modality, MRI is not limited by tissue overlap and could thus help to estimate breast cancer risk in high-risk populations [16]. The revised fifth edition of the BI-RADS® includes a recommendation to include a visual estimation of FGT with breast MRI. The categories for assessing the amount of FGT of breasts from MRI parallel those applied in MBD, i.e., almost entirely fat, scattered FGT, heterogeneous FGT, and extreme FGT. However, subjective visual estimation of FGT with MRI has revealed only moderate intra-/inter-rater agreement [17, 18].

Automated observer-independent quantitative measurements of FGT are therefore needed also in MRI if we are to achieve a more standardized risk evaluation. Although quantitative measurements are currently under extensive research, there is however no consensus on the optimal method to quantify FGT in MRI, with several automatic and semi-automatic algorithms now available [19–26]. Additionally, no consensus exists on the optimal sequence from which FGT volumes are to be determined. Dixon sequences were reported to show the highest correlation and reproducibility, yet T1 sequences reported comparable accuracies [27]. Nevertheless, observed proportions of FGT in MRI have often been inconsistent when compared to those of MBD and the reproducibility has varied, depending on which parameters are being determined [28–30]. The aim of the present study was to develop a clinically feasible and highly reproducible method to quantify FGT with MRI and to correlate these values to automatically acquired measurements from digital mammography and tomosynthesis.

Materials and Methods

Study Design and Patients

Patients from local screening centers, two district hospitals, and tertiary care centers are referred to our university hospital for management of clinically or mammographically detected breast lesions. All images are re-evaluated on routine basis by specialized breast radiologists before any further management. The study population consisted of consecutive patients admitted to our hospital between August 2014 and May 2017 and referred for diagnostic 3.0-T breast MRI and having undergone either additional full-field digital mammography or tomosynthesis at our hospital. The additional inclusion criteria were that at least one breast was proven to be healthy and had not been surgically operated.

The proportion of FGT measured from clinical MRI exams was compared to MBD assessed from either mammograms or breast tomosynthesis. Volumetric breast density was determined using a K-means clustering segmentation method on MRI and the Quantra method on mammography or tomosynthesis. The Institutional Ethics Board approved this retrospective study; the Chair of the Hospital District waived the need for written informed consent from the patients.

Full-Field Digital Mammography and Digital Breast Tomosynthesis

Mammograms were acquired on Selenia Dimensions (Hologic Inc., Bedford, MA, USA) full-field digital mammography system; the same system was used to acquire the tomosynthesis images. Quantra (version 2.1.0, Hologic Inc., Bedford, MA), commercially available fully automated software, was used for the estimation of volumetric breast density from raw format mammography and tomosynthesis images [9].

The slice thickness used in the tomosynthesis images was 1 mm. The volume of the FGT is determined by referencing each pixel’s attenuation to the attenuation of pixels that are considered as entirely adipose tissue and the estimated MBD is then obtained as a percentage of the FGT from the total breast volume [30].

Breast MRI

MRI examinations were performed in the prone position with a 7-element-phased-array coil dedicated to breast imaging (Philips Achieva 3.0-T TX, Philips N.V., Eindhoven, The Netherlands). The clinical structural breast MRI protocol consists of T2-weighted and non-contrast and contrast-enhanced three-dimensional T1-weighted sequences and diffusion-weighted imaging as described previously [31]. Non-contrast 3D-T1-weighted MRI sequence (TR = 4.57; TE = 2.3 ms; in-plane resolution 0.48 mm × 0.48 mm; 257 slices; slice thickness 0.7 mm; scanning time 6 min 11 s) was chosen for this study based on the good contrast between adipose and fibroglandular tissues after initial tests conducted on T1- and T2-weighted images.

Quantitative Analysis of MRI-Based Fibroglandular Tissue Volume

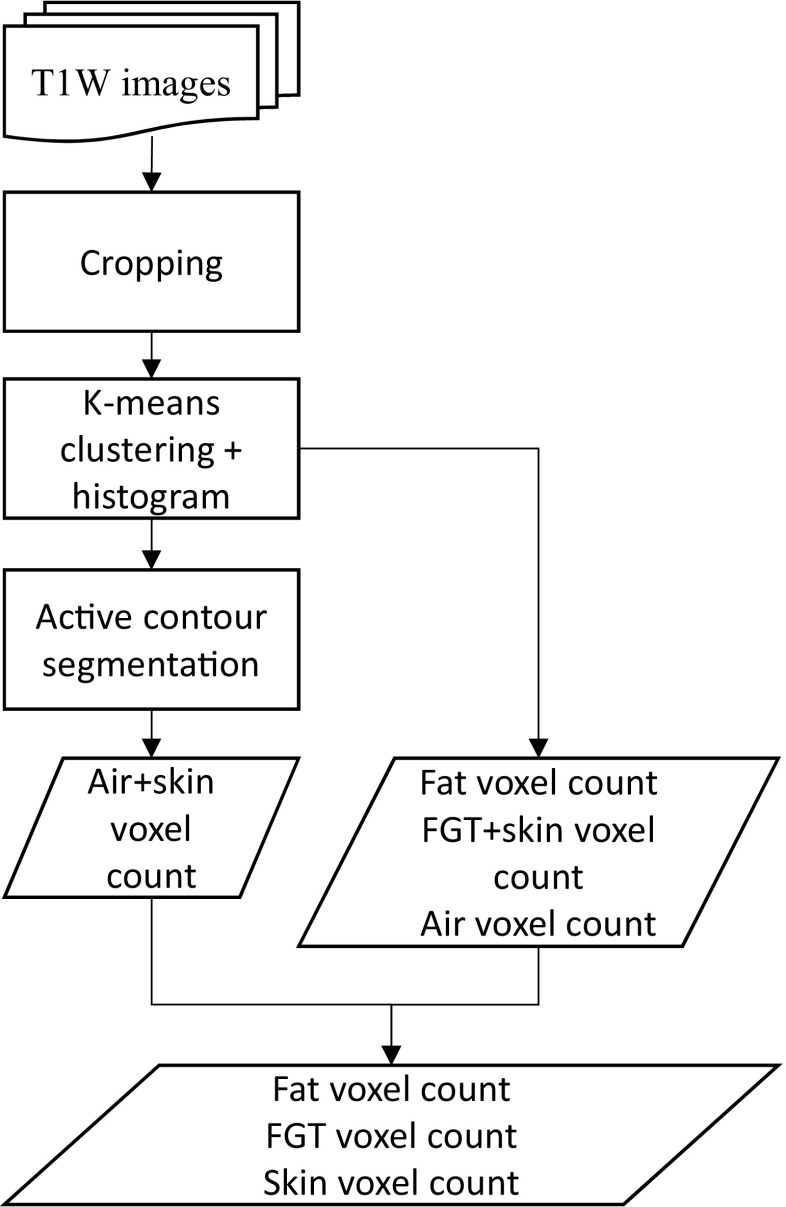
T1 slices were reconstructed at different slice thicknesses from the 3D T1-weighted dataset. The effect of slice thickness on FGT measurements was assessed with three different slice thicknesses, i.e., 0.7 mm (257 slices), 2 mm (90 slices), and 4 mm (45 slices). A flowchart of methods to determine the breast volume (BV) and FGT is presented in Fig. 1. Two observers blindly and independently analyzed all cases following the steps described. First, the image stack was cropped by delineation of breasts from the thoracic wall as suggested by Moon et al. [32] and was conducted as follows: the medial edge was set at the middle of the sternum and the posterior edge was set at the highest point of the pectoral muscle. Then, the K-means clustering technique (subsequently described) was used to classify the T1-weighted images into three clusters. In the presence of noise in the clustered images due to intensity inhomogeneity, four clusters were used. Volumes of fat, air, and the combined volume of skin and FGT were derived from the histogram of the clustered image stack representing the number of pixels with different gray scale tones. Skin and FGT volumes were distinguished by measuring the volume of the skin and the air surrounding breast with an active contour method. Since the volume of air was known, skin volume could be calculated by subtracting air volume from the measured volume of the skin and air. Finally, FGT volume was determined by subtracting skin volume from the volume of skin + FGT cluster. FGT-%, analogous to mammographic density, is the percentage ratio between FGT volume and total BV. The time needed to cluster and segment one breast is heavily dependent on the capabilities of the hardware and somewhat affected by the size of the breast. Processing time with our method is feasible for clinical purposes and similar to those reported in studies using fully automated algorithms [22, 23].

Fig. 1.

Flowchart of presented method

K-Means Clustering Method

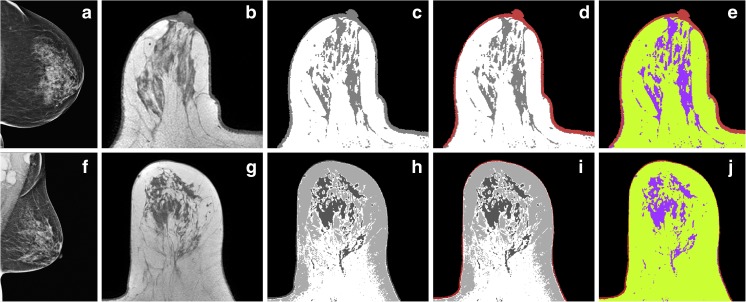
K-means segmentation technique [33] was used initially to label all MR voxels by using the ImageJ (version 1.47, Wayne Rasband, National Institutes of Health, Bethesda, MD, USA) with a K-means clustering plug-in (ij-Plugins Toolkit), thus segmenting breasts into three or four clusters depending on the amount of signal intensity inhomogeneity in MR images [34, 35]. This method is an unsupervised algorithm that assigns each voxel to a cluster (e.g., adipose tissue) based on its grayscale intensity (Fig. 2c, h). MRI image stack slices were interpreted as a 3D image. This process translates the partial volume effects in the image, which occurs when multiple tissues contribute to a single voxel, making it difficult to distinguish tissue edges. The clustering plug-in is based on a validated K-means++ algorithm [36]. However, this type of clustering cannot differentiate between skin and fibroglandular tissue as those share similar grayscale intensities and are therefore assigned to the same cluster. This problem was circumvented using active contour segmentation after initial K-means clustering.

Fig. 2.

Breast imaged with different modalities and in different steps of workflow. Mammogram from FFDM (CC view) (a), T1-W image (b), K-means clustered image (3 clusters) (c), active contours segmented image (d), Representation of different tissues measured (e), mammogram from DBT (MLO view) (f), T1-W image (g), K-means clustered image (4 clusters) (h), active contours segmented image (i), representation of different tissues measured (j)

Active Contour Method

Differentiation of the skin and FGT clusters was accomplished using the ITK-SnAP 3.2 software [37]. The separation of the skin and FGT is crucial, as the amount of skin can be substantial [38]. In our study, the FGT-% without skin exclusion was two times bigger (median = 2.06, range 1.19–6.60) than FGT-% with skin exclusion. This software displays structural images simultaneously in three different planes and allows semi-automatic segmentation and volume rendering of 3D medical images using an active contour algorithm (Fig. 2d, i). The algorithm implements two extensively applied 3D active contour segmentation methods (geodesic active contours and region competition contours) that derive an estimate of the structure of interest and represent it by one or more contours. After the K-means clustering, the intensity values of clusters can be thresholded instead of image intensities. When measuring the desired cluster volume, an upper threshold of 1.0070 was set so that the intensity (1.000) of the cluster consisting of the skin and FGT was below the threshold. Due to this threshold, the algorithm would segment all structures with intensity below 1.0070, the whole air cluster (intensity 0.000) and the neighboring cluster consisting of the skin and FGT. FGT would not be segmented, because adipose tissue acts as a barrier due to its intensity (2.000) that exceeds the threshold. Therefore, only volume of air with skin is segmented. Air volume is already known from histogram and skin volume can be calculated as (air + skin volume) − (air volume). The same threshold value was used for every case in order to avoid observer-related biases. All the cases had identical outcome after clustering; therefore, air was always assigned in black cluster, skin, and FGT in gray cluster and fat in white cluster. All clustering outcomes where fat cluster’s intensity is not between air cluster’s and skin + FGT cluster’s intensity could be used in segmenting, then the threshold is set so that the fat cluster is not segmented. The computers used for this study were equipped with Intel Core i7-4770 3.40-GHz CPUs, NVIDIA Quadro K2000 GPUs, and 16 GB of RAM.

Statistical Analysis

Continuous variables are presented as means ± standard deviations (SD) and categorical variables as absolute values and percentages. The information from the MRI volumetric measurements of both the observers was used to assess the interobserver agreement. The interobserver agreement was tested using the intra-class correlation (ICC) test. Otherwise, only the data from one randomly assigned observer was used. The Spearman correlation coefficient was used to analyze the correlation of breast and FGT volumes in the MRI and MBD measurements in mammography and tomosynthesis. The effect of slice thickness on MRI volumetric measurements was evaluated via the Spearman correlation coefficient. Statistical significance was set at p < 0.05. Data was analyzed using SPSS software (IBM SPSS Statistics for Windows, Version 22.0. Armonk, NY: IBM Corp).

Results

A total of 72 women (mean age 52.4 ± 12.3) were included in this study. All MRI examinations (n = 72) were performed within 4 months of the mammography or the tomosynthesis assessment. Twenty-nine patients (39 breasts) underwent tomosynthesis and 43 patients (66 breasts) underwent digital mammography. Unilateral breast malignancies were diagnosed in 39 patients.

Inter-rater agreement was tested using 2-mm-thick slices and proved to be excellent for MRI-based BVs (ICC 0.985, 95% CI 0.934–0.994), FGT volumes (ICC 0.979, 95% CI 0.958–0.989), and FGT-% values (ICC 0.994, 95% CI 0.990–0.997). Processing time varied from 6 to 13 min depending on slice thickness and breast size.

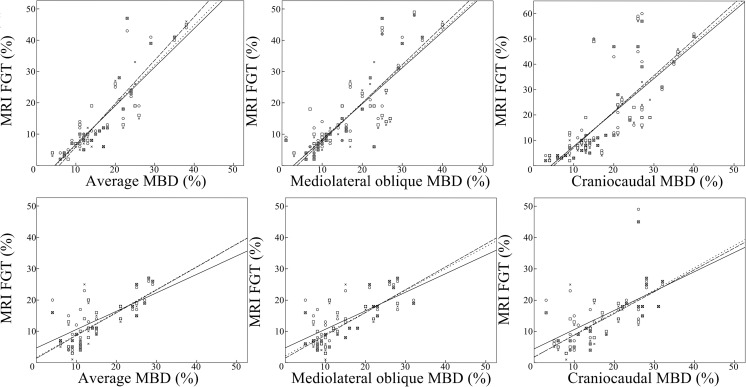
Intertechnique reproducibility is shown in Tables 1, 2, 3, and 4 and in Fig. 3. Moderate to excellent correlations (r = 0.659–0.967, P < 0.001) were achieved between MRI-based measurements and digital mammography for all parameters. When the MRI-based measurements were compared to tomosynthesis, the BVs showed excellent correlations (r = 0.866–0.959, P < 0.001). Regarding the FGT-%s and volumes, correlations were moderate to high (r = 0.528–0.778, P < 0.001). Comparison of earlier and present study is presented in Table 5.

Table 1.

Fibroglandular tissue volumes, total breast volumes, fibroglandular tissue percentages, and breast densities (mean ± standard deviation) measured from patients (n = 43, 66 breasts) imaged with 3D digital mammography and T1-weighted 3D MRI (3.0-T, Philips Achieva TX)

	FGT volume (cm3)	Total breast volume (cm3)	Mammographic breast density or FGT-% (%)
MRI (N = 66)
4-mm slice	88 ± 60	742 ± 402	17.3 ± 15.7
2-mm slice	87 ± 65	755 ± 402	17.0 ± 15.9
0.7-mm slice	88 ± 60	741 ± 400	17.1 ± 15.5
Mammography
MLO (N = 55)	112 ± 71	801 ± 456	16.9 ± 8.9
CC (N = 49)	111 ± 67	747 ± 365	16.2 ± 9.0
AVG (N = 38)	107 ± 69	740 ± 392	16.3 ± 8.0

MLO, mediolateral oblique view; CC, craniocaudal view; AVG, averaged measurements; FGT, fibroglandular tissue; FGT-%, fibroglandular tissue percentage

Table 2.

Intertechnique reproducibility between 3D mammography and MRI with different slice thicknesses as estimated by Spearman correlation coefficients and P values between fibroglandular tissue volumes, total breast volumes, fibroglandular tissue percentages, and breast densities

	FGT volume (r (95% CI))	Total breast volume (r (95% CI))	Mammographic breast density or FGT-% (r (95% CI))
MRI 4-mm slice vs:
MLO (N = 55)	0.682* (0.509–0.802)	0.936* (0.893–0.962)	0.864* (0.777–0.918)
CC (N = 49)	0.777* (0.635–0.868)	0.900* (0.829–0.951)	0.819* (0.699–0.894)
AVG (N = 38)	0.807* (0.657–0.895)	0.967* (0.937–0.982)	0.873* (0.768–0.932)
MRI 2-mm slice vs:
MLO (N = 55)	0.659* (0.478–0.786)	0.928* (0.880–0.957)	0.884* (0.809–0.930)
CC (N = 49)	0.753* (0.599–0.853)	0.861* (0.766–0.919)	0.863* (0.769–0.920)
AVG (N = 38)	0.761* (0.584–0.869)	0.933* (0.874–0.964)	0.904* (0.822–0.949)
MRI 0.7-mm slice vs:
MLO (N = 55)	0.674* (0.498–0.796)	0.939* (0.898–0.964)	0.868* (0.784–0.921)
CC (N = 49)	0.811* (0.687–0.889)	0.894* (0.819–0.939)	0.856* (0.758–0.916)
AVG (N = 38)	0.793* (0.635–0.887)	0.964* (0.932–0.981)	0.871* (0.765–0.931)

MLO, mediolateral oblique view; CC, craniocaudal view; AVG, averaged measurements; FGT, fibroglandular tissue; FGT-%, fibroglandular tissue percentage

*P < 0.001

Table 3.

Fibroglandular tissue volumes, total breast volumes, fibroglandular tissue percentages, and breast densities (mean ± standard deviation) measured from patients (n = 29, 39 breasts) imaged with tomosynthesis and MRI with different slice thicknesses

	FGT volume (cm3)	Total breast volume (cm3)	Mammographic breast density or FGT-% (%)
MRI (N = 39)
4-mm slice	86 ± 60	756 ± 425	13.4 ± 8.4
2-mm slice	80 ± 60	707 ± 426	13.1 ± 8.9
0.7-mm slice	94 ± 66	740 ± 418	14.4 ± 8.6
Tomosynthesis
MLO (N = 35)	126 ± 92	862 ± 506	16.6 ± 8.2
CC (N = 36)	106 ± 76	821 ± 438	14.6 ± 7.6
AVG (N = 33)	119 ± 83	862 ± 464	15.0 ± 7.4

MLO, mediolateral oblique view; CC, craniocaudal view; AVG, averaged measurements; FGT, fibroglandular tissue; FGT-%, fibroglandular tissue percentage

Table 4.

Intertechnique reproducibility between tomosynthesis and MRI with different slice thicknesses as estimated by Spearman correlation coefficients and P values of total breast volumes, fibroglandular tissue volumes, fibroglandular tissue percentages, and breast densities

	FGT volume (r (95% CI))	Total breast volume (r (95% CI))	Mammographic breast density or FGT-% (r (95% CI))
MRI 4-mm slice vs:
MLO (N = 35)	0.630* (0.376–0.796)	0.948* (0.899–0.973)	0.738* (0.537–0.859)
CC (N = 36)	0.778* (0.604–0.881)	0.936* (0.878–0.967)	0.719* (0.512–0.847)
AVG (N = 33)	0.736* (0.526–0.861)	0.945* (0.891–0.972)	0.752* (0.551–0.870)
MRI 2-mm slice vs:
MLO (N = 35)	0.528* (0.506–0.848)	0.904* (0.817–0.950)	0.685* (0.456–0.829)
CC (N = 36)	0.718* (0.510–0.846)	0.866* (0.752–0.929)	0.712* (0.501–0.843)
AVG (N = 33)	0.683* (0.444–0.831)	0.885* (0.779–0.942)	0.723* (0.506–0.854)
MRI 0.7-mm slice vs:
MLO (N = 35)	0.570* (0.293–0.759)	0.959* (0.920–0.979)	0.655* (0.412–0.811)
CC (N = 36)	0.695* (0.475–0.833)	0.926* (0.859–0.961)	0.630* (0.381–0.794)
AVG (N = 33)	0.680* (0.440–0.829)	0.940* (0.881–0.970)	0.650* (0.395–0.812)

MLO, mediolateral oblique view; CC, craniocaudal view; AVG, averaged measurements; FGT, fibroglandular tissue; FGT-%, fibroglandular tissue percentage

*P < 0.001

Fig. 3.

Scatterplots of FGT-%s and mammographic breast densities measured with mammography and tomosynthesis. In upper row, MRI FGT-% vs MBD from mammography. In lower row, MRI FGT-% vs MBD from tomosynthesis. Square, measurement with 4.0-mm slices; cross, measurement with 2.0-mm slices; circle, measurement with 0.7-mm slices; dotted line, regression line for 4.0-mm slices; dashed line, regression line for 2.0-mm slices; straight line, regression line for 0.7-mm slices

Table 5.

Performance of MRI-based methods to measure fibroglandular tissue percentages compared to mammographic breast density measurements. A review of the literature

	Pertuz et al. [28]	Nayeem et al. [29]	Wang et al. [30]	Tagliafico et al. [41]	Engeland et al. [25]	Petridou et al. [18]	Present study
N of patients (breasts)	68 (136)	137 (137)	99 (99)	48 (48)	22 (44)	40 (80)	72 (105)
Mean age (years)	52	35.9	47.2	41	NA	NA	52.4
MRI field strength, sequence	1.5-T, non-enhanced T1-W without fat suppression	1.5 T, 3DGRE and STIR	1.5-T and 3-T, T1-W non-contrast fat-saturated	3 T, ideal	1.5-T, T1-W FLASH-3D	3-T, spoiled gradient echo	3-T, T1-W fast field echo
Mammography device	FFDM and DBT	FFDM	FFDM	FFDM and DBT	FFDM	FFDM	FFDM and DBT
MRI slice (mm)	2.4–3.5	1.5 [3DGRE], 2 [STIR]	2	NA	1.5	1.8	0.7–4.0
MRI analysis method	Atlas-aided fuzzy C-means method	Curve-fitting algorithm (PeakFit 4.0)	Fuzzy C-means method	Semi-automatic maximum entropy thresholding	Semi-automatic thresholding and segmenting	Automatic segmentation with AMRA sequence	Semi-automatic K-means method with active contour segmentation
Mammography analysis method	DBT: fully automated algorithm; FFDM: Volpara 1.5	Histogram segmentation method (HSM), mathematical algorithm based on DICOM headers (MATH)	Single-energy X-ray absorptiometry (SXA), Quantra 3.2, Volpara 1.4.3	Semi-automatic maximum entropy thresholding	Calculation based on DICOM headers and empirical data from literature	Visual evaluation, four-quartile BI-RADS scale	Quantra 2.1.0
Agreement between MRI and mammography:
Breast volume	DBT: r = 0.95 FFDM: r = 0.96	3DGRE: r = 0.94 STIR: r = 0.99	SXA: R 2 = 0.91 Quantra: R 2 = 0.91 Volpara: R 2 = 0.91	NA	NA	NA	FFDM: r = 0.861–0.967
Fibroglandular tissue percentage	DBT: r = 0.88 FFDM: r = 0.84	3DGRE: r = 0.84–0.89 STIR: r = 0.83–0.86	SXA: R 2 = 0.51 Quantra: R 2 = 0.51 Volpara: R 2 = 0.73	DBT: r = 0.95 FFDM: r = 0.87	r = 0.94	r = 0.73–0.75	FFDM: r = 0.819–0.904
Fibroglandular tissue volume	DBT: r = 0.67 FFDM: r = 0.61	3DGRE: r = 0.71–0.91 STIR: r = 0.72–0.87	SXA: R 2 = 0.55* Quantra: R 2 = 0.40* Volpara: R 2 = 0.63*	NA	r = 0.97	NA	FFDM: r = 0.659–0.811

MRI, magnetic resonance imaging; FFDM, full-field digital mammography; DBT, digital breast tomosynthesis; AMRA, advanced MR analytics; Quantra, automated software to assess breast density; Volpara, automated software to assess breast density; SXA, single-energy X-ray absorptiometry

*For logarithmic fibroglandular volume

We evaluated our method using three different slice thicknesses: 0.7 mm (257 slices), 2 mm (90 slices), and 4 mm (45 slices). Measures correlated strongly with each other; r = 0.962–0.994 for BVs, r = 0.916–0.932 for FGT volumes, and r = 0.942–0.968 for FGT-%. The possibility of loss of fine structures of breasts by examining thicker slices proved to have no impact or only a minor effect on the measurements.

For MRI, the skin volumes were separately measured and the ratios between skin volumes and total breast volumes were calculated. The percentage of skin volume ranged between 2.74 and 35.2% with a mean value of 9.3%.

Discussion

The key finding of the present study was that our MRI-based method to assess FGT volumes and proportions achieved high interobserver reproducibility and convincing correlations to mammographic breast density measurements when using 4-mm-thick MRI slices. Our method also represents a novel way to measure skin as an independent tissue type, which may lead to a more accurate assessment of breast composition and this, in our opinion, reflects a more reliable volumetric measurement. To the best of our knowledge, no results concerning volumetric skin segmentation using active contour segmentation have been published.

At present, there is no consensus on the best technique to perform a quantitative breast tissue analysis with MRI. Compared to automatic programs, manual segmentation is more time-consuming, requires training, and is subject to observer-biased interpretation. The clinical feasibility of quantitative semi-automatic MRI techniques depends on the accuracy and robustness of the breast segmentation. Accordingly, a wide variety of MRI segmentation techniques exist and several methods have been proposed as being best for the assessment of breast volume and FGT volume. Klifa et al. and Wang et al. have evaluated a fuzzy c-means (FCM)-based method [15, 30], and Kang et al. have used a K-means clustering method [21] while Nie et al. proposed a two-step method, firstly locating the skin border and lungs by a FCM algorithm and subsequently applying an adaptive FCM algorithm to extract the FGT [20]. A deep-learning method has also been developed for breast and FGT segmenting from MRI in order to outperform existing methods relying on atlases, template matching, or edge and surface detection [39]. The thickness of MR image slices varies between studies and could be a factor contributing to different results. In our study, high agreement of FGT-%, BV, and FGT between slice thicknesses was noted. Due to faster active contour segmenting, thicker slices may be advocated over thin slice thicknesses.

Even though our study had a small sample size, statistically significant results regarding inter-rater agreement were achieved. Our method proved to have a high inter-rater correlation between all measurements (ICC 0.979–0.997). Van der Waal et al. compared visual agreement of BI-RADS assessment between readers and agreement between automated MBD software. Agreement of visual evaluation of BI-RADS categories from mammograms (kappa score 0.80–0.84) has slightly lower reliability than that of our method. Differences between commercial automatic MBD assessing software Quantra and Volpara are even greater with ICC of 0.64 (95% CI − 0.07–0.88) and 0.55 (95% CI 0.24–0.72) when comparing estimates of percent dense volume and absolute dense volume, respectively [40].

Previously, the various MRI segmentation methods have been compared to the performance of mammography and tomosynthesis in the assessment of quantitative breast factors (Table 5). Although different procedures (e.g., segmenting) are mostly done using computer algorithms, some operator inputs are still required, such as delineating breast from the image or selection of seed points for the region growing tool. However, even though there has been extensive research conducted on the intertechnique reproducibility between MRI, mammography, and tomosynthesis, the inter-rater agreements have rarely been reported (Table 5). In one publication, 11 cases were evaluated with an FCM-based segmentation algorithm and the average standard deviation of MRI-FGT-% between observers was reported to be 3.9% [20]. In another study, the breasts were imaged and segmented automatically before and after the administration of intravenous contrast medium. The correlation between these pre- and post-contrast breast density quantifications ranged between r = 0.98 and 0.99 [18]. Our results demonstrate that the MRI-based breast volumes, FGT volumes, and FGT-% values are highly reproducible. Even though the suggested semi-automatic method requires user input, its influence on the results is minimal.

We observed an excellent correlation between MRI and full-field digital mammography in agreement with previously published data (Table 5). In the earlier studies comparing MRI-based and mammographic measurements, correlations between FGT-% and MBD were in the range 0.71–0.94, between breast volumes 0.94–0.99 and between FGT volumes, they varied between 0.61–0.91 (Table 5). However, we noted that our correlations between tomosynthesis and MRI were slightly lower than those of between mammography and MRI. This contrasts with the studies of Tagliafico et al. and Pertuz et al. who achieved better correlations between tomosynthesis and MRI than between digital mammography and MRI [28, 41]. The difference between MBD from standard dose and synthetic mammograms was evaluated by Conant et al., and an average of 1.7% higher breast density was noted for synthetic mammograms over normal dose mammograms [42].

Differences in qualitative breast factors can be in part caused by the skin. The skin and FGT have similar signal intensities in MRI which complicates reliable FGT-% measurements. Only few studies have reported results of skin segmentation. Nie et al. studied the effect of skin removal on breast density measurement and suggested that the percentage of the skin volume ranged between 5.0 and 15.2% [38]. In our study, a range of 2.7–35.2% (mean 9.3%) was found. The method applied here could measure the skin separately by using active contour segmentation without any significant skin volume leakage into the FGT volume through the nipple area. In many other studies, the skin has been directly segmented as a part of “breast” or adipose tissue, but not separately segmented [22, 23, 41]. Mammographic density measurement software compensates routinely for the penetration through the skin in order to eliminate the impact that the skin has on the estimate of fibroglandular tissue volume and therefore we believe that future developments in volumetric measurements should always include skin segmentation protocol. We obtained excellent reproducibility and significant correlations with digital mammography and thus our results emphasize the importance of excluding skin reliably from FGT. Differences between the mammographic and MRI measurements may be due to difficulties in delineating the breast from subcutaneous fat tissue in the chest wall at MRI or in positioning of the breasts in mammograms [11].

The difference between the mammographic, tomosynthesis, and MRI-based FGT measurements may also be related to differences in breast content especially in mammographically dense breasts, where the projected results of mammography are more dependent on parenchymal patterns than on volume and therefore do not reflect the composition of tissue as well as MRI [16, 19]. Also, mammography is a two-dimensional imaging modality, and therefore suffers from tissue-overlapping and cannot accurately differentiate between overlapping fatty and fibroglandular tissues. The position of the patient and the degree of compression may increase the inaccuracies [43]. Klifa et al. (2010) speculated that breasts with very little FGT (i.e., fatty breasts) display a greater tendency to under- or over-estimate real fibroglandular regions due to the difficulty of segmenting very thin fibroglandular regions within the adipose tissue [16]. In our study population, the majority of patients had low or very low density breasts which may have exerted some influence on our correlations.

Our study has several limitations. First, our patient population is relatively small. Being a tertiary referral hospital, most of the patients were referred with the complete mammographic evaluation already done at other institutions. Our study population consists chiefly of patients who had to undergo repeated examinations according to the recommendation of specialized breast radiologists to re-evaluate additional mammographic findings. The patient sample consists of symptomatic patients with relatively non-dense breasts and is not representative of a normal screening population. Second, the lack of a golden standard as a reference for breast density and FGT volume analysis hinders the detection of systematic errors. According to our clinical practice, the patients underwent either digital mammography or tomosynthesis, but not both, in order to minimize their exposure to radiation. Nevertheless, our results achieved statistical significance, indicating that the hypothesis is applicable and tested method is feasible.

In conclusion, the MRI-based assessment of the proportion of fibroglandular tissue of the breast, including skin segmentation described in the present study, is highly reproducible and has potential to be utilized in assessment of FGT-% in clinical practice and scientific studies. In the future, a quantitative assessment of FGT-% to complement the visual estimation of FGT should be performed on a more regular basis since this technique reveals a component which can be included in the individual patient’s breast cancer risk stratification.

Compliance with Ethical Standards

The Institutional Ethics Board approved this retrospective study; the Chair of the Hospital District waived the need for written informed consent from the patients.