Warming of the interior Arctic Ocean linked to sea ice losses at the basin margins

Reduced sea ice cover opens a conduit for solar-heated water to reach the interior Arctic Basin halocline.

Abstract

Arctic Ocean measurements reveal a near doubling of ocean heat content relative to the freezing temperature in the Beaufort Gyre halocline over the past three decades (1987–2017). This warming is linked to anomalous solar heating of surface waters in the northern Chukchi Sea, a main entryway for halocline waters to join the interior Beaufort Gyre. Summer solar heat absorption by the surface waters has increased fivefold over the same time period, chiefly because of reduced sea ice coverage. It is shown that the solar heating, considered together with subduction rates of surface water in this region, is sufficient to account for the observed halocline warming. Heat absorption at the basin margins and its subsequent accumulation in the ocean interior, therefore, have consequences for Beaufort Gyre sea ice beyond the summer season.

INTRODUCTION

The dynamic Beaufort Gyre (BG) is a dominant circulation feature centered over the Arctic’s Canada Basin (Fig. 1). Prevailing anticyclonic winds over the sea ice–ocean system drive this upper-ocean anticyclonic circulation as well as the accumulation and storage of both heat and fresh water, processes that influence climate in the Arctic and beyond [for example, (1–3)]. Relatively fresh surface ocean layers ensure a strong BG halocline that, below the mixed layer, is composed of ocean layers characterized by temperatures up to a few degrees warmer than the local freezing temperatures persist throughout the year. The halocline stratification strongly inhibits vertical heat fluxes from these warm layers (4). However, the fate of sea ice is acutely sensitive to changes in ocean heat flux of as little as 1 W m⁻² (5).

Fig. 1. Temperature and salinity in the BG.

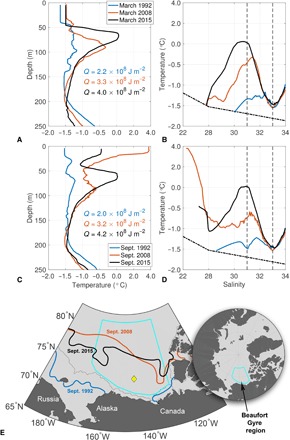
(A) Temperature and depth profiles in March 1992, 2008, and 2015 and (B) the same profiles on the temperature-salinity plane. The dashed-dotted black line indicates the freezing temperature at zero pressure, and the vertical dashed lines mark S = 31 and S = 33. (C) and (D) are the same, with the profiles being from September 1992, 2008, and 2015. Heat content (Q, J m⁻²) relative to the freezing temperature integrated between the isohalines S = 31 and S = 33 is shown in (A) and (C) for the profiles plotted. All profiles are in the vicinity of the diamond shown in the regional map (E), which was free of sea ice in September 2008 and 2015, and ice covered for the other profiles (contours indicate the monthly sea ice edge; 15% concentration); the cyan boundary delineates the BG region.

The upper water column structure of the BG is as follows. Immediately beneath the summer BG mixed layer, a local temperature maximum is often observed, believed the result of locally absorbed solar heat (4, 6, 7). This layer is subject to strong seasonal variability. Below, at depths between roughly 50 and 150 m, is a second layer of relatively warm water within a large vertical salinity gradient (Fig. 1). These warm halocline waters, believed to originate from the Pacific Ocean via the Chukchi Sea and Alaskan Coastal Current (8), exhibit little seasonal variability (they are too deep to be influenced by local penetrative solar radiation) but significant interannual change (Fig. 1) (9). In a region of the central Canada Basin, observations indicate a twofold increase in halocline heat content per unit area between 2003 and 2013 (9). These observations were assimilated in a numerical modeling study spanning 1992–2015, which showed a general increase in average temperatures of the central Canada Basin warm halocline over this period (10). Here, we examine ocean observations spanning the entire BG region to document and quantify a buildup of ocean heat content in the warm halocline over the past 30 years (1987–2017).

Focus is on the waters with salinity S in the range 31 ≤ S ≤ 33. The upper boundary of the warm halocline layer within the BG exhibits interannual variability, but is never saltier than S = 31; in recent years, the upper boundary has become fresher, but we do not consider S < 31 waters in our analysis of the time series to avoid the complicating influence of seasonally varying upper layers (9). The S = 33 isohaline lies within a local temperature minimum in depth, thus naturally defining the base of the warm halocline waters. Cryo-relevant heat content of the warm halocline waters in the BG region (hereafter referred to as heat content) was estimated by vertically integrating potential temperature profiles relative to the local freezing temperature (and scaling by density and specific heat) between these bounding isohalines. Temperature and salinity profiles from all available sources were grouped in 4- to 5-year intervals to produce mapped estimates of halocline heat content (Fig. 2).

Fig. 2. Maps of heat content in the BG warm halocline.

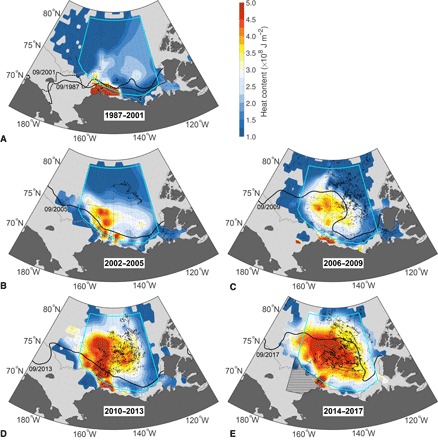
(A to E) Heat content (J m⁻²) relative to the freezing temperature integrated between the isohalines S = 31 and S = 33 for all data (including all seasons) in the periods (A) 1987–2001, (B) 2002–2005, (C) 2006–2009, (D) 2010–2013, and (E) 2014–2017. The hatched region in (E) is the NCS region of strongest subduction (see text). The cyan boundary delineates the BG region considered in the time series calculations. The gray bathymetric contour marks the 100-m isobath, and black dots indicate temperature-salinity profile locations. Black contours on each panel indicate the monthly sea ice edge (15% concentration) for the month labeled.

RESULTS

Ocean heat in the Beaufort Gyre

Before the 2000s, typical BG halocline heat content per unit area was around 2 × 10⁸ J m⁻² (Fig. 2A). Since that time, there has been a sustained increase in heat content per unit area (local values reach beyond 4 × 10⁸ J m⁻² in the 2014–2017 time period), with maximal values centered over the Canada Basin coincident with the climatological BG center (Fig. 2) (1). Over the period 1987–2017, total warm halocline heat content integrated horizontally over a region encompassing the BG has nearly doubled (Fig. 3A). It is instructive to set the resulting heat content increases in context alongside sea ice. The capacity for sea ice melt of the additional heat content (the increase of ~2 × 10⁸ J m⁻² over 30 years) equates to a change of about 0.8 m in thickness, taking the latent heat of melting to be 2.67 × 10⁵ J kg⁻¹ and the density of sea ice to be 900 kg m⁻³.

Fig. 3. BG warm halocline time series.

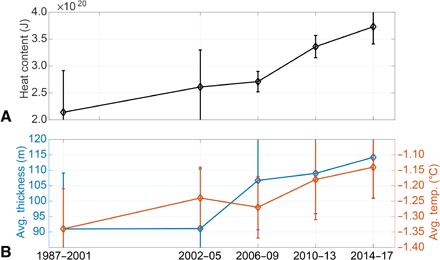
(A) Time series of total heat content (J) relative to the freezing temperature integrated between the isohalines S = 31 and S = 33 in the BG region delineated by the cyan line in Fig. 2. (B) Time series of average thickness (m) (left y axis) and layer-averaged temperature (°C) (right y axis) of the layer bounded by S = 31 and S = 33 over the BG region.

Both increased temperatures and a thickening of the warm halocline layer [associated with spin-up of the BG and accumulation of freshwater; see (1)] contribute to the observed heat content increase (Fig. 3B). The contributions to changes that result from either layer thickness h change (of the 31 ≤ S ≤ 33 layer) or layer-averaged temperature change may be examined by writing the change in heat content ΔQ = Q_f − Q_i (subscripts i and f denote initial and final, respectively) as ΔQ = [Q_i(h_f/h_i − 1)] + [Q_f − (h_f/h_i)Q_i], where the first term in square brackets is the contribution due to layer thickness change (from h_i to h_f), and the second term is the contribution due to temperature change. There is interannual variability in which contribution has a bigger influence on the overall heat content change, but neither of these presents as the dominant factor (not shown).

ACCUMULATION OF HEAT

Halocline ventilation

The source of the increased halocline heat content can be understood by first considering how the BG halocline is ventilated. The northern Chukchi Sea (NCS) region exerts major influence on the interior structure of the halocline; here, water masses with the salinity range of the warm halocline outcrop at the surface (11). In this region, which we define to be within 70°N to 75°N and 150°W to 170°W, and south of the 300-m isobath (Fig. 2E), water is pumped down from the surface (via the Ekman transport convergence as a result of the prevailing anticyclonic wind stress gradients) and transported laterally by the BG geostrophic flow into the interior gyre (9, 11). Observations suggest that the NCS is characterized by the strongest time-mean Ekman downwelling in the entire Canada Basin, with downwelling rates averaging around 20 m year⁻¹, which corresponds to a vertical Ekman flux of around 0.05 Sv (1 Sv = 10⁶ m³ s⁻¹) for the region (12). This strong downwelling, associated with the region of maximum strength of the prevailing easterlies, takes place year-round with some interannual variability, but no significant trend over 2003–2014 [see Figs. 4 to 6 in (12)].

A major oceanographic feature of relevance in the NCS is a surface front in the vicinity of the Chukchi slope. The front marks the lateral transition between relatively warm (in summer/fall) and salty surface waters (and a deeper mixed layer) to the south, and cool and fresh surface waters (and a shallower mixed layer) to the north, toward the interior of the BG freshwater center. Water at the surface on the south side of the front is transferred below the mixed layer and into the interior halocline by subduction: vertical Ekman pumping plus lateral induction. It should be noted that there are likely other physical mechanisms at play in this important region that depend on the details of surface buoyancy forcing and sea ice state [for example, (13, 14)], local winds, and properties, dynamics, and stability of regional boundary currents [for example, (8, 15–17)]. The ventilation rate from this region (combination of Ekman downwelling and lateral induction) is estimated to be around 0.2 Sv (11). The cause of the warming halocline can be discerned by examining surface ocean temperatures over this region of maximum subduction, the portal for halocline ventilation.

Sea ice decline and surface warming in the NCS

Cumulative net heat flux to the surface ocean in the NCS for July to September has a main component of surface solar absorption, taking into account the fractional area of open water (with net longwave, sensible, and latent heat exchanges being of secondary importance). On the basis of reanalysis products (see Materials and Methods), the cumulative net summertime (July to September) heat input to the NCS [this is the region of net positive subduction (11); Fig. 4] increased from around 100 to around 500 MJ m⁻² over the three decades between 1987 and 2017. The increase is primarily due to loss of sea ice area (Fig. 4), which allowed more solar absorption by the surface ocean.

Fig. 4. Time series in the NCS.

Time series of cumulative heat input (MJ m⁻²) for the months of July to September into the NCS (see Fig. 2E). Shading indicates 1 SD based on variance over the region. Fractional sea ice concentration (note inverted axis) and SST (°C) averaged over the same area for the same months are also shown.

The excess cumulative heat input for July to September is more than sufficient to account for the observed sea surface temperature (SST) increase in the NCS (Fig. 4). The change in temperature of a mixed layer of thickness D may be estimated in terms of the net heat flux F across the air-sea interface as ∂T/∂t = F/(ρc_pD), where ρ and c_p are density and specific heat capacity of the seawater, respectively. Taking D ≈ 20 m, and considering the influence of fluxes of the order 400 MJ m⁻² (the amount that summertime cumulative flux has increased over the three decades) over 3 months (July to September), we estimate that late-summer SSTs should be around 5°C warmer in recent years compared to three decades ago. Observed summertime SSTs are around 3°C warmer in recent years (Fig. 4), suggesting that some of the heat entering the NCS surface layer may be mixed to deeper levels. It remains a possibility that some of the NCS warming could be attributed to increased heat flux through the Bering Strait (18) [warm inflows through the Bering Strait have, at least, been shown to be essential in initiating the positive ice-albedo feedback (19)]. Uncertainties in the past decades’ record of heat influx through the Bering Strait (particularly the lack of measurements in the top 20 m) preclude us from ruling this out. Nevertheless, SST increases in the subduction region can be entirely accounted for by sea ice losses and increased local solar absorption; a warming contribution from the lateral advection of heat is not necessary to explain the observed NCS SST increases. How do these SST increases relate to a warmer halocline?

Heat entering the halocline

An estimate of heat entering the halocline from the main subduction region can be obtained by computing the energy (heat content) density in this region and multiplying it by the estimated volume flux into the halocline. Heat content per unit volume relative to the freezing temperature for a given summer may be inferred by the mean summer SST in the region (assumed constant over some mixed layer; Fig. 4) as ρc_p[SST − T_f], where T_f is the freezing temperature. For this estimate, we assume that the volume flux into the halocline is ~0.2 Sv (11) and is steady over the period from July to September. This amounts to a volume influx of 1.6 × 10¹² m³. In this way, from the time series of observed, area-averaged summer SST (Fig. 4), we estimate a cumulative heat input to the interior BG halocline of about 4 × 10²⁰ J. This is an upper bound, assuming all of the waters being subducted in the NCS region ventilate the BG halocline. Over this period, we observe a BG halocline heat content increase of around 1.5 × 10²⁰ J, less than the upper-bound estimate from the NCS subduction, which would allow for some heat loss via mixing (for example).

While vertical heat fluxes from the warm halocline are inhibited by the halocline stratification (that is, diapycnal diffusion is weak), reasonable estimates for heat lost vertically from the warm halocline may be obtained by considering the range of turbulent diffusivities estimated from observations in the central Canada Basin halocline: ~10⁻⁷ to 10⁻⁶ m² s⁻¹ (20). Heat loss is only considered across the top boundary of the layer. The range of diffusivities acting on the vertical temperature gradient centered around S = 31 (the top of the warm halocline) gives rise to upward heat fluxes in the range of 0.03 to 0.3 W m⁻². Taking the heat content in the layer to be ~4 × 10⁸ J m⁻², these fluxes suggest a time scale for diffusive removal of the anomalous layer heat of between 40 and 400 years. Therefore, we cannot rule out that some fraction of the subducted summer heat is lost from the layer by vertical diffusion. Note that eddy fluxes may also be responsible for transporting heat laterally out of the BG region in a dynamical response to the wind-energy input (21).

Role of BG intensification

Thus far, we have only described BG halocline heat content increases as they relate to sea ice losses and associated warmer SSTs in the Chukchi Sea region. Layer heat content change may also be induced by an increase in layer thickness (that is, volume influxes of waters characterized by 31 ≤ S ≤ 33). For example, the cumulative heat input to the BG halocline that would arise from fixed source-water SSTs (at pre-2000s values of about −0.5°C) and a steady 0.2-Sv summertime influx would be about 2 × 10²⁰ J over the three decades. This influx would correspond to a layer thickness increase (over three decades) of around 150 m (taking the area of the BG region to be about 1 × 10¹² m²), much larger than the ~25 m observed. While eddy equilibration of the BG also plays a role in regulating its spin-up and accumulation of fresh water and heat (21–23), it is clear that changes in source-water properties (that is, warmer NCS waters) are required to explain the observed interior halocline changes.

DISCUSSION

Implications and outlook

The doubling of BG halocline heat content over the past three decades appears attributable to a warming of the source waters that ventilate the layer, where this warming is due to sea ice losses in the Chukchi Sea that leave the surface ocean more exposed to incoming solar radiation in summer. The effects of an efficient local ice-albedo feedback are thus not confined to the surface ocean/sea ice heat budget but, in addition, lead to increased heat accumulation in the ocean interior that has consequences far beyond the summer season. Strong stratification and weak mechanical mixing in the BG halocline ensure that significant summertime heat remains in the halocline through the winter.

With continued sea ice losses in the Chukchi Sea, additional heat may continue to be archived in the warm halocline. This underscores the far-reaching implications of changes to the dynamical ice-ocean system in the Chukchi Sea region. However, there is a limit to this: Once the source waters for the halocline become warm enough that their buoyancy is affected, ventilation can be shut off. Efficient summertime subduction relies on the lateral surface front in the NCS region between warm, salty water that is denser to the south and cooler, fresher water that is less dense to the north. For longer-duration solar warming (that is, longer-duration ice-free conditions in the region), SSTs on the south side of the front may become warm enough (around 13°C, under the assumption of a 1.5-month ice-free period dominated by solar absorption) that the lateral density gradient is eliminated [see (24)]. It remains to be seen how continued sea ice losses will fundamentally change the water column structure and dynamics of the Arctic halocline. In the coming years, however, excess BG halocline heat will give rise to enhanced upward heat fluxes year-round, creating compound effects on the system by slowing winter sea ice growth.

MATERIALS AND METHODS

Ocean temperature and salinity

Water column measurements were provided by Ice-Tethered Profilers (ITPs) (25, 26), ship-based hydrographic data collected under the Beaufort Gyre Exploration Project (BGEP) (1), and CTD (conductivity-temperature-depth) data archived in the World Ocean Database 2013 (WOD13). The total number of profiles in each of the time periods considered is as follows: 819 (1987–2001), 2567 (2002–2005), 10,817 (2006–2009), 9924 (2010–2013), and 16,101 (2014–2017). Profiles were used to quantify the cryo-relevant heat content in the warm halocline, defined as the layer bounded by isohalines S = 31 and S = 33 at depths d₃₁ and d₃₃, respectively. Total heat content relative to the freezing temperature at a given location was computed by $\mathit{Q}={\int }_{{\mathit{d}}_{31}}^{{\mathit{d}}_{33}}\mathrm{\rho }(\mathit{z}){\mathit{c}}_{\mathrm{p}}(\mathit{z})[\mathit{T}(\mathit{z})-{\mathit{T}}_{\mathrm{f}}(\mathit{z})]\mathit{d}\mathit{z}$, where ρ and c_p are the density and the specific heat capacity of the seawater, respectively, T is the potential temperature referenced to zero pressure, and T_f is the freezing temperature at zero pressure, a function of salinity. SST data were from the National Oceanic and Atmospheric Administration (NOAA) Optimum Interpolation (OI) SST version 2 product (OISSTv2), which is a blend of in situ and satellite measurements (27).

Sea ice information

Monthly sea ice extent and ice edge data were from the National Snow and Ice Data Center (NSIDC) Sea Ice Index, version 3 (28).

Atmospheric fluxes

Estimates of air-sea heat flux were obtained from the European Centre For Medium-Range Weather Forecasts (ECMWF) Atmospheric Reanalysis (ERA) Interim reanalysis twice-daily product obtained from the ECMWF data server (http://apps.ecmwf.int/datasets/), with spatial resolution of 0.75° (29). ERA-Interim reanalyses of surface radiative fluxes showed good comparisons with observations (30); summer shortwave and longwave flux biases were consistently less than a few percentage. Cumulative heat input to the surface ocean was estimated as the sum of surface net longwave thermal radiation, surface sensible heat flux, surface latent heat flux, and surface solar radiation to the ocean. The last term F_i was estimated from the surface downward solar irradiance F_s, the albedo of the ocean α_w ≈ 0.07, and the fractional area of open water A_w as F_i = F_s(1 − α_w)A_w. This neglected solar penetration through thin ice. Lateral advection of ocean heat was neglected.

Data mapping and uncertainty estimates

Spatial maps (on a 0.5° × 1° latitude-longitude grid) were constructed using the Data-Interpolating Variational Analysis (DIVA) software (31); this procedure is similar to Optimal Interpolation used previously for mapping properties in the BG region (1). The regional integration of heat content was done on the mapped data. To estimate the uncertainty on the integral heat content estimates, a delete-d Jackknife analysis (32) that involved randomly subsampling the data in any given time interval (leaving out d observations at a time) and deriving the standard error of the mean of Jackknife samples was performed.