Abstract
Nanocrystalline InP quantum dots (QDs) hold promise for heavy-metal-free optoelectronic applications due to their bright and size-tunable emission in the visible range. Photochemical stability and high photoluminescence (PL) quantum yield are obtained by a diversity of epitaxial shells around the InP core. To understand and optimize the emission line shapes, the exciton fine structure of InP core/shell QD systems needs be investigated. Here, we study the exciton fine structure of InP/ZnSe core/shell QDs with core diameters ranging from 2.9 to 3.6 nm (PL peak from 2.3 to 1.95 eV at 4 K). PL decay measurements as a function of temperature in the 10 mK to 300 K range show that the lowest exciton fine structure state is a dark state, from which radiative recombination is assisted by coupling to confined acoustic phonons with energies ranging from 4 to 7 meV, depending on the core diameter. Circularly polarized fluorescence line-narrowing (FLN) spectroscopy at 4 K under high magnetic fields (up to 30 T) demonstrates that radiative recombination from the dark F = ±2 state involves acoustic and optical phonons, from both the InP core and the ZnSe shell. Our data indicate that the highest intensity FLN peak is an acoustic phonon replica rather than a zero-phonon line, implying that the energy separation observed between the F = ±1 state and the highest intensity peak in the FLN spectra (6 to 16 meV, depending on the InP core size) is larger than the splitting between the dark and bright fine structure exciton states.
Keywords: exciton fine structure, InP/ZnSe core/shell quantum dots, acoustic and optical phonons, high magnetic field
After nearly three decades of research, colloidal nanocrystalline quantum dots (QDs), especially from the Cd-chalcogenide and Pb-chalcogenide families, have reached a high level of maturity. Core/shell QDs that are based on a CdSe core and a variety of shells are already applied in LEDs for monitors and TV screens.1−5 However, there is a strong desire in society to replace these systems by Cd-free QDs, which, ideally, should show the same performance. In the visible spectral range for which CdSe QDs are the most famous, InP QDs form one of the most promising heavy-metal-free alternatives. The optical properties, though, are not yet optimal for optoelectrical applications. First of all, bare InP cores have a low photoluminescence (PL) quantum efficiency.6−14 To solve this problem, shells of ZnS, ZnSe, and (Zn,Cd)Se have been developed for InP-based core/shell systems with promising PL quantum efficiencies up to 70%.13−21 Second, optical absorption and luminescence spectroscopy showed that InP QDs have a broader PL peak than their CdSe analogues.21−23 The emission line width of an ensemble of QDs is mostly related to inhomogeneous broadening,24,25 but also to the exciton fine structure that fractionates the 8-fold degenerate 1Sh1Se exciton into several states with strongly varying oscillator strength, spread in energy. Finally, InP QDs also show a considerable global Stokes shift (on the order of 100–300 meV)10−13,19−21,26−32 between the absorption peak related to the band-edge exciton (1Sh1Se) and the corresponding PL peak of QD ensembles. Although the global Stokes shift in other QD systems (PbS, CdSe, CdTe) has been shown to be largely determined by inter-QD energy transfer within the ensemble and the size dependence of the oscillator strengths,33,34 the nature of the global Stokes shift of InP QDs is as yet unclear and may be (partially) related to the exciton fine structure.
Both the synthesis of InP QDs from inexpensive precursors21 and the characterization of the optoelectronic properties are currently under rapid development. However, up to now, not much attention has been devoted to the exciton fine structure of InP QDs, despite its fundamental scientific relevance and importance in InP-based optoelectronics. Theoretically, the exciton fine structure of zinc blende QDs has been investigated on the basis of k·p35 and atomistic theories.36,37 The exciton fine structure is determined by a combination of the electron–hole exchange, the crystal field splitting, and the possible shape anisotropy of the nanocrystals (prolate or oblate). For prolate-shaped zinc blende nanocrystals, the fine structure consists of five levels where the magnitude of the energy splitting between the levels increases fast with decreasing size, reaching tens of meV for sufficiently small QDs (on the order of 3 nm diameter).35,38 The lowest energy state has a total angular momentum projection along the nanocrystal axis F = +2 or −2, which means that its optical generation from the ground state and radiative decay back to the ground state are forbidden within the electric-dipole approximation (i.e., it is a “dark” state). The next higher energy state has F = +1 or −1, and thus there is an allowed electric-dipole optical transition between this state and the ground state (i.e., it is a “bright” state). Furthermore, in the core/shell geometry, which in the end will be the geometry of practical importance, asymmetric strain induced by the shell heteroepitaxy15,39 may also affect the fine structure energy levels.40 Experimentally, the fine structure of InP/ZnS core/shell QD systems has only been studied by time-resolved PL spectroscopy.41 It was found that there were two bright states above the dark state and that the energy separation between the dark F = ±2 state and the lowest bright F = ±1 state was in the 5–10 meV range, increasing with decreasing InP core size. The latter effect is directly related to the size dependence of the electron–hole exchange energy.35,36
Here, we present a thorough study of the exciton fine structure of InP/ZnSe core/shell QD systems. We focus on thick ZnSe shells because they lead to QDs with high photochemical stability and high photoluminescence quantum yields. These systems were synthesized using inexpensive precursors, and their production is amenable to upscaling.21 The QDs, with InP core size ranging from 3.6 to 2.9 nm, emit in the visible range (1.8–2.3 eV) with a PL quantum yield around 40%. We study their exciton fine structure with several techniques. PL decay at varying temperatures reveals an energy separation between the dark F = ±2 state and a higher energy bright state of about 4–7 meV, depending on the core diameter, with the energy difference increasing with decreasing core size. The Raman spectra of the InP/ZnSe core/shell QDs show longitudinal-optical (LO) and transverse-optical (TO) phonons from both the InP core and the ZnSe shell. These phonon modes are involved in the radiative recombination of the dark F = ±2 exciton state, as we show using fluorescence line-narrowing (FLN) spectroscopy at 4 K under high magnetic fields (up to 30 T) and circularly polarized excitation and detection. In fact, our results indicate that the most intense FLN peak is a Stokes acoustic phonon replica rather than a zero-phonon line. This implies that the energy separation observed between the F = ±1 state and the highest intensity peak in the FLN spectra (6–16 meV, depending on the InP core size) is larger than the splitting between the dark and bright fine structure exciton states, which can then be estimated to range from approximately 2 to 9 meV for the samples investigated in this work.
Results and Discussion
Structural and Chemical Characterization
The InP/ZnSe core/shell QDs were synthesized as described in ref (21). Most of the results discussed below were obtained on three samples with different InP core diameters (sample 1 with 2.9 nm, sample 2 with 3.1 nm, and sample 3 with 3.6 nm mean core diameter). Four other InP/ZnSe QD samples (referred to as samples 4–7) with different core diameters and a sample of bare InP QDs (referred to in the remainder of this paper as “core-only”) were used for complementary measurements. The core-only QDs were passivated with Cd-oleate to improve their chemical stability and thereby prevent surface oxidation. The core sizes were estimated from the lowest energy exciton peak position in the absorption and emission spectra (see below for a discussion of the optical spectra).42 Individual core/shell QDs were structurally characterized by high angle annular dark field scanning transmission electron microscopy (HAADF-STEM) and energy dispersive X-ray spectroscopy (EDX), as shown in Figure 1. The InP/ZnSe core/shell QDs are fairly monodisperse in size and shape. The zinc blende ZnSe shell grows around the InP core, yielding a truncated tetrahedral shape of 3–4 nm edge length. The EDX maps confirm that In and P form the core, and Zn and Se the shell. However, alloying of the core/shell interface cannot be excluded. Chemical-element analysis yields an estimated elemental ratio of In:P:Zn:Se = 3:4:49:44 (Figure 1c,d).
Figure 1.
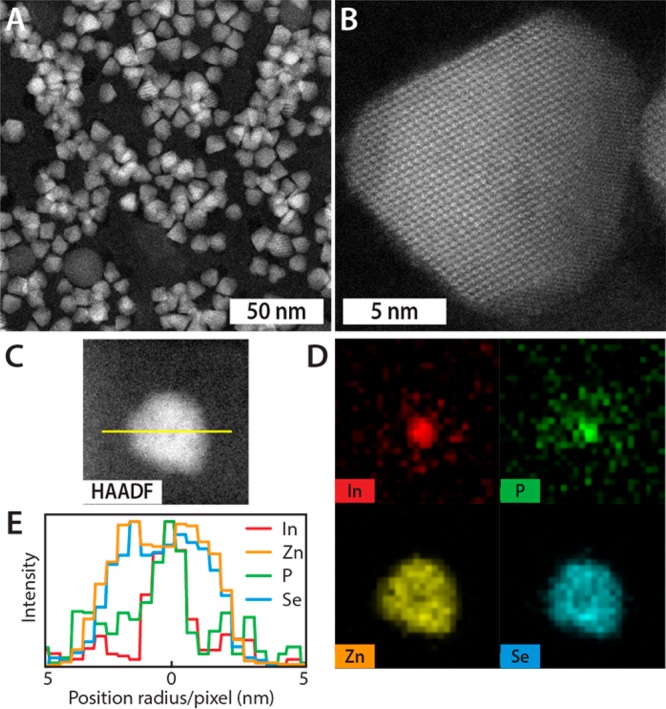
Chemical and structural characterization of InP/ZnSe core/shell QDs. (a and b) HAADF-STEM images of InP/ZnSe core/shell QDs, with an average InP core diameter of 2.9 nm and a total core/shell diameter of 9.6 ± 1.1 nm (mean ± standard deviation), at (a) low and (b) high magnification. The high magnification depicts the ZnSe crystal along the [110] direction. (c and d) HAADF-STEM image of a single InP/ZnSe QD and corresponding EDX maps providing evidence for an InP core diameter of approximately 3 nm and a ZnSe shell of 3–4 nm. (e) Elemental line scan along the yellow line through the InP/ZnSe QD shown in panel c. The core/shell structure of the QD is clearly resolved, since In and P are present primarily in the center of the nanocrystal, while Zn and Se are distributed throughout the QD. The diffuse and weaker background signal of P is ascribed to trioctylphosphine (TOP), which acts as a ligand.
Basic Optical Characterization
The samples were characterized by their absorption and PL spectra (Supporting Information, Figures S1 and S2). The absorption spectrum at room temperature of sample 1 shows a defined peak at 2.18 eV due to the 1Sh–1Se transition. The 1Sh–1Se PL peak is red-shifted by 120 meV with respect to the 1Sh–1Se absorption transition and has a full width at half-maximum of 170 meV. The PL peak of our InP-based QDs is considerably broader than for instance that of CdSe QDs emitting in the same spectral region (100 meV at the ensemble level).23,43 The PL peak of sample 1 (Supporting Information, Figure S1b) shows a considerable red-shift when the temperature is increased from 4 K (peak maximum at 2.137 eV) to room temperature (peak maximum at 2.03 eV), due to expansion of the crystal lattice with increasing temperature.44Figure S1c shows the PL spectra for the three samples investigated in this work with a red-shift of the 1Sh–1Se exciton transition with increasing InP core size due to reduced quantum confinement. We have measured the fine structure of the 1Sh–1Se exciton for the three different core sizes. In the following, we will show the results obtained with the smallest core size (sample 1), of which the structural characterization is shown in Figure 1. Additional data for the other core sizes are provided in the Supporting Information (Figures S2–S11).
Study of the Exciton Fine Structure by Photoluminescence Decay Measurements at Variable Temperature
Previous studies on the PL decay dynamics of the 1Sh1Se exciton in InP QDs showed that the PL decay becomes faster with increasing temperature.41 This thermally activated PL decay reflects the presence of a lowest energy dark state that dominates radiative decay at low temperatures and a higher energy brighter state that is thermally populated at elevated temperatures. To better understand the energy level structure involved in this thermally activated PL, we performed a detailed study of the PL decay dynamics of the three InP/ZnSe core/shell QDs as a function of the temperature.
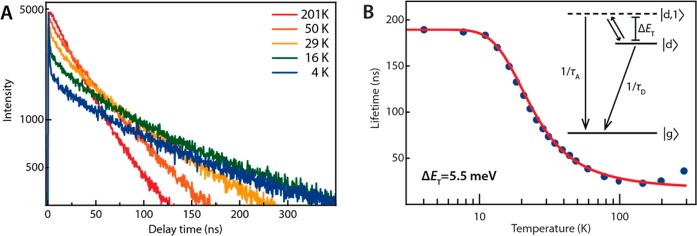
Figure 2a shows the PL decay transients for sample 1 (the full data set of the PL decay can be found in the Supporting Information, Figures S2–S5). At low temperatures (<10 K), the decay is biexponential with a slower lifetime component that becomes considerably faster with increasing temperature (from 190 ns at T ≤ 9 K to ∼30 ns at 300 K, Figure 2b). Similar results are obtained for the larger core diameters (Figure S2). We propose here that the long lifetime component in our measurements reflects radiative recombination from a thermal equilibrium between a thermally activated brighter state |d,1⟩ and the lowest dark state |d⟩. In this model the initial fast lifetime component (at t < 10 ns) of the biexponential PL decay is ascribed to emission from higher energy levels shortly after the laser pulse and prior to thermalization. The decay rate of the system at thermal equilibrium (Γtot) as a function of temperature is given by
| 1 |
where kB is the Boltzmann constant, ΔET is the energy difference between the dark state |d⟩ and the brighter state |d,1⟩, and τD and τA are the lifetimes of the lower energy dark and the higher energy “brighter” state, respectively (see inset in Figure 2b).
Figure 2.
Thermally activated PL decay at zero magnetic field for the InP/ZnSe core/shell QDs (sample 1). (a) PL decay measured at the PL peak maximum (which depends on temperature; see Figure S1b), at various temperatures from 4 K (blue) to 200 K (dark red). (b) Plot of the lifetime of the long component of the decay curves versus the temperature. The fitting (red line) is based on the thermal-occupation model (eq 1) with a thermal activation energy ΔET between the dark state |d⟩ and an optically active state |d,1⟩ of 5.5 meV. Inset: Schematic representation of the three-level scheme, with the dark state and thermally activated state with a higher oscillator strength.
Figure 2b shows the evolution of the long lifetime component as a function of temperature. From 10 mK to 8 K (Figure S5) the lifetime stays constant (similar behavior in samples 2 and 3; Figures S3–S5). The lifetime becomes gradually shorter as the temperature is increased above 8 K until a plateau is reached at around 100 K (Figure 2b). The results were fitted with eq 1, with ΔET, τd, and τA as fitting parameters (red line in Figure 2b; see Methods section below for details on the fitting procedure). The results are well described by eq 1, yielding an energy difference ΔET between the optically active state |d,1⟩ and the dark state |d⟩ of 5.5 meV. The PL decay dynamics of samples 2 and 3 are also well described by eq 1, with energy separations between the dark and thermally activated “brighter” state of respectively 4.9 and 4.3 meV (Supporting Information, Figure S4). These energies are slightly smaller than the 5–7 meV found in ref (41) for InP/ZnS of similar core size.
This analysis was repeated with four extra samples with different core sizes (samples 4–7). The results clearly show that the energy difference ΔET between the |d⟩ and |d,1⟩ excited levels increases with decreasing QD size (Supporting Information, Figure S6). The energy separation ΔET between the |d⟩ and |d,1⟩ levels obtained from the temperature dependence (T-dependence) of the PL decays and the microscopic nature of these levels will be discussed in more detail in the final section of this paper.
Fluorescence Line-Narrowing Spectroscopy
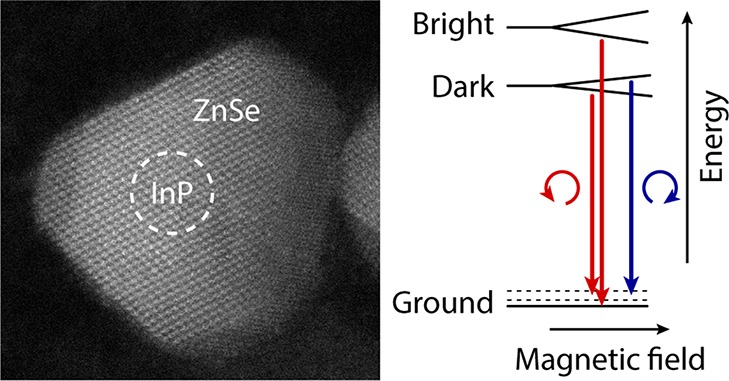
We performed size-selective spectroscopy using FLN experiments at 4 K to reduce the inhomogeneous line broadening of the observed nanocrystals. Using monochromatic laser light with photon energy matching the low-energy side of the lowest energy absorption peak, a small subensemble of the sample, with a certain core size, is excited. The optical transition is from the ground state to a fine structure state of the 1Se1Sh exciton with high oscillator strength, thus necessarily the bright F = ±1 state. By applying an external high magnetic field between 0 and 30 T, it is possible to induce a sizable Zeeman splitting of spin-degenerate states, which, combined with circularly polarized excitation, allows us to predominantly excite either the F = −1 or +1 states and therefore to resolve unambiguously the nature of the states.
Figure 3 presents the results obtained for excitation with σ+ circularly polarized light, predominantly exciting the upper F = +1 state (marked in red in the scheme shown in Figure 3c), and detection of the σ– circularly polarized emission. Figure 3a shows the FLN spectra, excited at 590 nm (2.1 eV). The FLN spectra are referenced to the energy of the laser excitation, or in other words, the bright F = +1 state is set at energy zero. At 0 T, three intense peaks are resolved, red-shifted with respect to this reference: the first at −11 meV, the second at −34 meV, and the third at −49 meV. Upon applying the magnetic field, the three peaks gradually shift to lower energies with respect to the reference. Interestingly, the magnitude of the shift is the same for all three peaks (viz., 3 meV at 30 T), which implies that they are due to optical transitions from the same F = −2 state (Figure 3c). We conclude that these three peaks differ in terms of coupling to different phonons. This assignment is corroborated by our Raman spectroscopic study presented below (Raman Spectroscopy section).
Figure 3.
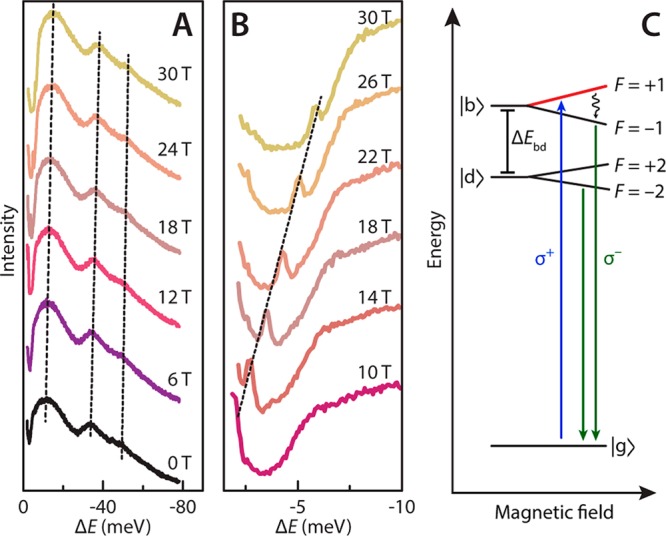
Fluorescence line-narrowing (FLN) spectroscopy at 4 K upon excitation of the bright F = +1 state with σ+ light of 2.1 eV. (a) FLN spectra showing the σ– emission at variable magnetic fields. The excited state at 2.1 eV (the excitation laser energy) is taken as reference and set to 0 meV. The main peak is related to emission from the dark state coupled to an acoustic phonon; the lower energy peaks are related to optical phonon replicas. (b) Zoom-in of the spectra at small ΔE, showing σ– emission from the F = −1 bright state, shifting to lower energy due to the Zeeman effect (panel c). All spectra are vertically shifted for clarity. (c) Energy level scheme showing the bright F = +1 state (marked in red) that is excited (blue arrow) and the σ– emissions from the bright F = −1 and dark F = −2 states (green arrows). The phonon states are omitted for clarity.
In essence, the temperature dependence of the exciton PL decay time and the magnetic field dependence of both the FLN and the degree of circular polarization (DCP) of the PL (Supporting Information, Figure S7) are similar to those of CdSe QDs35,45−47 that have an F = ±2 ground state, which indicates that the InP/ZnSe QDs studied here also have a F = ±2 ground state.
A second feature becomes evident from 10 T and up: a sharp optical transition that originates from zero ΔE shifts rapidly to lower energies with respect to the F = +1 state (the reference) with increasing field (Figure 3b). This optical transition must reflect emission from the bright F = −1 state (as has been observed for CdSe QDs),45,46 shifting to lower energy with respect to the reference because of the Zeeman splitting, ΔE = gμBJ·B, where g is the Landé gyromagnetic factor (g-factor), μB is the Bohr magneton (μB = 5.79 × 10–2 meV T–1), and J = L + S is the total angular momentum with L the orbital angular momentum and S the intrinsic spin (angular) momentum. From this linear Zeeman splitting, we deduce a Landé gyromagnetic factor g = 3.48 for the F = ±1 state. Similar results are obtained for the other two samples (Supporting Information, Figures S8–S10).
To understand the line widths of the bright and dark exciton emission in our FLN measurements, we note that the bright exciton emission in our FLN measurements in magnetic fields is shifted with respect to excitation due to the Zeeman effect. The splitting energy is only dependent on the g-factor, which is not strongly dependent on QD size (see Figures S8–S10). The bright exciton FLN peak is therefore sharp. The dark exciton, on the other hand, emits by coupling to acoustic phonons, as we will show in more detail below. The acoustic phonon energy depends on QD size. The FLN peak from the dark exciton is therefore inhomogeneously broadened.
Figure 4 presents the results obtained for excitation of the bright state with σ– circularly polarized light and detection of the σ+ circularly polarized emission. In this case, the F = −1 level is predominantly excited, and it will therefore be the reference state in the spectra (marked in red in Figure 4b). In Figure 4a, again three broad peaks are observed. Note that in this configuration, with increasing magnetic field, the Zeeman splitting between the F = +1 state to the F = −1 cannot be observed since with this polarization the F = +1 state cannot be excited. Instead the first intense peak (−11 meV at 0 T) shows the presence of two components, one at almost constant energy with respect to the reference (F = −1 state) and a second smaller component (a shoulder of the highest energy peak, emphasized in Figure 4a with the black arrow in the 30 T spectrum) shifting to higher energy with increasing magnetic field. This smaller component is related to the relaxation (after the photoexcitation into the optically bright F = −1 state) and the subsequent recombination from the dark F = +2 state, which occurs prior to the total relaxation of the system to the lowest F = −2 state. The component at constant ΔE is instead related to the recombination from the lowest energy dark level F = −2. This level only emits purely σ–-polarized light for QDs with their anisotropic axis parallel to the field, whereas QDs aligned perpendicularly to the field emit unpolarized light.47 As a result, within an ensemble of randomly oriented QDs the F = −2 levels also partly emit σ+-polarized light. This explains why the integrated emission intensity in this experiment (detecting σ+-polarized light; Figure 4) is lower by a factor 2 than when detecting σ–-polarized light (Figure 3).
Figure 4.
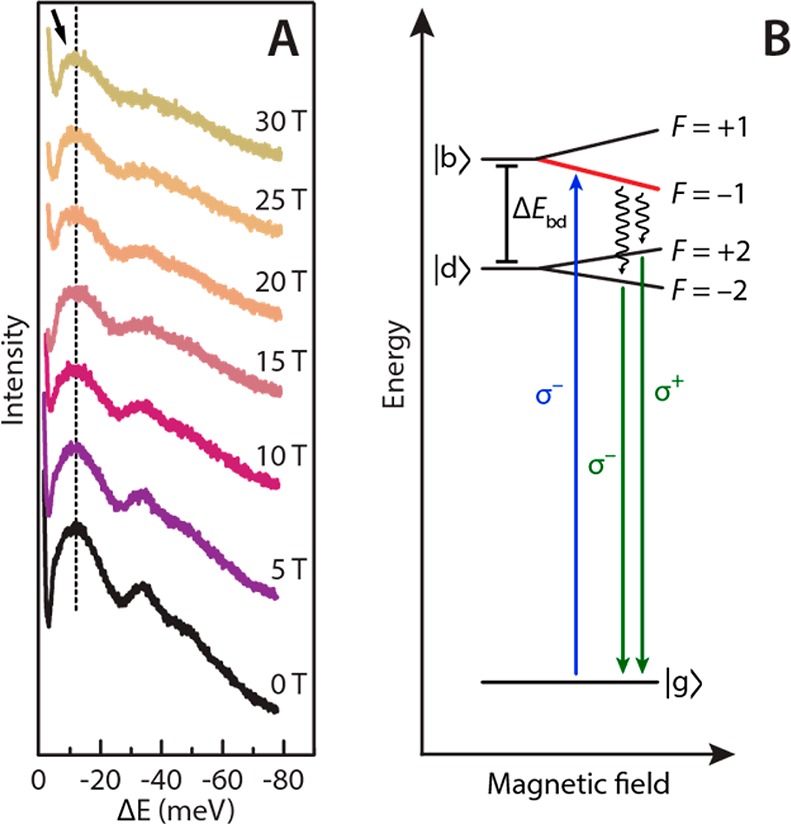
Fluorescence line-narrowing (FLN) spectroscopy at 4 K upon excitation of the bright F = −1 state with σ– light of 2.1 eV. (a) FLN spectra showing the σ+ emission peaks at variable magnetic field. The state at 2.1 eV (the excitation laser energy) is taken as reference and set to 0 meV. The main peak (marked by the dashed line) is due to emission from the F = ±2 states coupled to an acoustic phonon; the other two peaks are related to optical phonon replicas. (b) Energy level scheme showing the bright F = −1 state (marked in red) that is excited (blue arrow) and the emissions from the dark F = ±2 states (green arrows).
In Figure 4a it is also evident that the second (34 meV at 0 T) and the third peak (49 meV at 0 T) become broader with increasing magnetic field, following the same trend as the highest energy peak. We conclude again that the three peaks are emissions from the same exciton fine structure states (F = ±2) but involving coupling to different phonons. We will provide evidence below that the highest intensity peak is in fact an acoustic phonon replica originating from the coupling of the dark exciton state with a confined acoustic phonon mode.
Raman Spectroscopy
In order to study the phonon modes involved in the FLN process we carried out Raman scattering measurements on both InP/ZnSe QDs (sample 1) and core-only InP QDs of comparable size. Figure 5a presents the Raman spectra of both InP/ZnSe and core-only InP QD samples. For both samples, the sharp peak at approximately 520 cm–1 originates from the crystalline silicon substrate.48 The Raman spectrum of the core-only InP QDs (in blue) shows two well-defined peaks at 311 and 342 cm–1 (fitting in Figure 5b), which can be assigned to the TO and LO phonon modes of InP, as reported for bulk InP49 and InP core-only QDs.50
Figure 5.
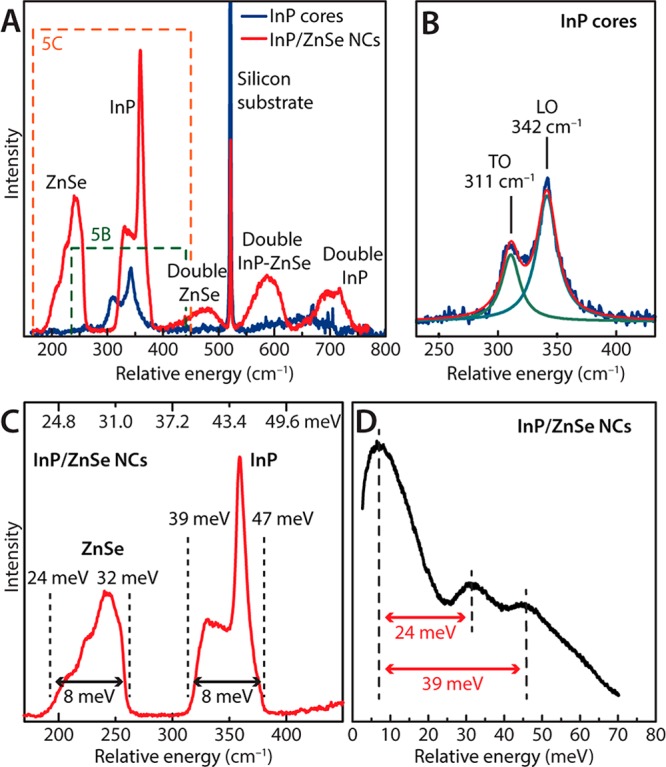
Raman and FLN spectra recorded at 4 K for InP cores and InP core/shell QDs with a mean core diameter of 2.9 nm. (a) Raman spectra, obtained with a 488 nm laser line, of InP QDs (blue) and InP/ZnSe core/shell QDs (red). The peaks in the 300–400 cm–1 range are assigned to the LO and TO phonon modes of the InP QDs and the InP core in the InP/ZnSe core/shell QDs. The group of peaks around 190–260 cm–1 is assigned to the ZnSe phonon modes. Two of them are LO and TO modes. (b) Lorentzian fits of the LO and TO phonons of the InP QDs. (c) Zoom-in of the first two Raman peaks related to the ZnSe and InP optical phonons of the InP/ZnSe core/shell QD sample. The dashed lines indicate energies that are relevant for comparison with the FLN spectra. (d) FLN spectrum of the same InP/ZnSe core/shell QD sample.
In the Raman spectrum of the InP/ZnSe core/shell QDs (in red), we identify directly the LO and TO phonon modes of the InP lattice (315–380 cm–1), which are shifted to higher energy due to the compressive strain imposed by the ZnSe heteroepitaxial shell (the lattice parameter of zinc-blende ZnSe is smaller than that of InP, viz., 5.668 and 5.869 Å, respectively). A second intense group of peaks is found between 200 and 260 cm–1. These peaks are present only in the Raman spectrum of the InP/ZnSe core/shell QDs; we therefore assign them to ZnSe phonons. According to the literature, two of these peaks are the LO and TO phonon modes of bulk ZnSe.51 This multiple-peak structure around 220 cm–1 in the ZnSe Raman spectrum might originate from a splitting of the LO and TO modes due to the strain. Double Raman processes of the InP and ZnSe phonons are also visible at higher energy in the Raman spectra (>400 cm–1).
The zoom-in of the first two groups of peaks of the InP cores and InP core/shell QDs (respectively Figure 5b and c) highlights the complex shape of the Raman peaks, which is rather broad likely due to the complexity of the QDs. Indeed defects in the crystal structure of InP and ZnSe can introduce perturbations in the system, resulting in a back-folding of the dispersion curve toward Γ and a concomitant increase of the density of phonon states.52 The broadening can also be enhanced by double-phonon processes, more likely around 100 cm–1 in ZnSe and 100–200 cm–1 in InP due to the high density of the states at these energies at the edge of the Brillouin zone.49,51,53 Another contribution to broadening of the Raman peaks is a distribution of phonon energies in the QD ensemble. Indeed, phonon energies can be influenced by interfacial strain, possible alloying in the InP–ZnSe core/shell heterointerface, and also the shape54 and size50 of the QDs.
Understanding the Role of the Phonons in the Radiative Recombination of Excitons in InP QDs
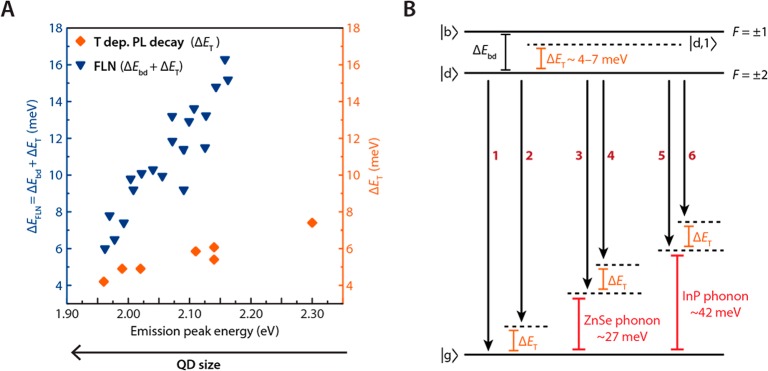
In Figure 6, we compare the energy splittings obtained from the T-dependent PL decay measurements (see also Figure 2) with those obtained from the FLN spectra. The former experiments provide a thermal excitation energy ΔET for emission, which is plotted in Figure 6a as a function of the PL peak energy. The latter experiments give the energy difference ΔEFLN between the excitation energy (i.e., the position of the bright F = ±1 state) and the highest intensity peak in the FLN spectra, which we plot also as a function of the FLN peak emission energy. ΔEFLN would correspond to the dark–bright splitting ΔEbd under the assumption that the highest intensity FLN peak is a zero-phonon line. However, we will show below that this assumption is inconsistent with our observations and that this transition is in fact an acoustic phonon replica.
Figure 6.
Comparison of the thermal activation energies obtained from PL decay measurements and the dark–bright splitting obtained from the FLN spectra. (a) Comparison of the results of the activation energy obtained from the time-resolved PL decay at varying T (orange diamonds) and the energy splitting obtained from the fluorescence line-narrowing (blue triangles). The x-axis displays the monitored PL emission peak energy or the emission energy in FLN, both at 4 K. (b) Overview of all possible recombination processes in InP/ZnSe QDs.
The energy splitting ΔEFLN from FLN measurements decreases from 16 meV to 6 meV with decreasing absolute peak emission energy, hence with increasing size of the InP core. The energy separation ΔET obtained from the T-dependent decay measurements also decreases with increasing size of the InP core, but over a much smaller range from 7 to 4 meV. This remarkable difference implies that these two energy scales have different origins, which will be discussed in detail below. The energy ΔET is ascribed to coupling of the dark state |d⟩ with thermally activated confined acoustic phonon modes (state |d,1⟩).55 We calculated the energy of the confined acoustic phonon modes as a function of the InP QD radius using Lamb theory56,57 and found an agreement with our experimental ΔET values (Supporting Information, Figure S11). This is in line with recent work on other QDs (CdSe, CdTe, PbSe, InAs,55,58 ZnSe,59 and CdTe/CdSe core/shell heteronanocrystals60). We note that acoustic phonon replicas have also been directly observed recently in the FLN spectra of self-assembled, vertically aligned arrays of CdSe/CdS dot-in-rod nanorods.61 Nevertheless, the mechanism behind the acoustic phonon-mediated brightening of the dark exciton state is not yet well understood. A possible mechanism is that the deformation potential arising from coherent confined acoustic phonon modes elastically distorts the nanocrystals, resulting in a transient mixing between bright and dark states, which enhances the radiative recombination rates.59,60,62,63
To understand the nature of the ΔEFLN splitting, it is necessary to consider the phonon modes available in the InP/ZnSe core/shell QDs studied here and their role in promoting optical transitions. Figure 5c and d show that the phonon modes of the ZnSe shell (24–32 meV) and InP core (39–47 meV), observed in the Raman spectra, nearly agree with the phonon energies obtained from the phonon replicas observed in FLN spectra (respectively 24 and 39 meV, mean value). Clearly, the phonon energies observed in the FLN spectra are slightly smaller (by 3–4 meV) than the mean value of the peaks in the Raman spectra. We explain these small energy differences in terms of the confined acoustic phonon modes observed also in the T-dependent PL decay. The complete process involved in the radiative recombination monitored in the FLN spectra (Figure 5d) can be understood assuming an energy scheme as shown in Figure 6b. The scheme is composed of a ground state |g⟩ and the two lowest excited states: a lowest energy dark state |d⟩ with projection of total angular momentum F = ±2, followed by a higher energy bright state |b⟩ with projection of total angular momentum F = ±1. Several phonon modes involved in the transitions are also represented in the scheme: ZnSe optical phonons (centered at 27 meV), InP optical phonons (centered at 42 meV), and confined acoustic phonon modes of the QDs having an estimated energy of 4–7 meV, depending on the core diameter.
In our FLN experiment, the resonant excitation brings the QDs in the bright state |b⟩ with F = ±1. Since the experiment is performed at 4 K (equivalent to 0.3 meV), the recombination of excitons that have decayed to the dark state F = ±2 should take place only from this dark state. All possible recombination processes are labeled in Figure 6b with the dark red numbers. Transition 1 from the dark state is formally forbidden within the effective mass and the electric-dipole approximations,35 but can be activated by coupling with phonon modes. Transition 2 corresponds to a transition assisted by coupling to a confined acoustic phonon mode (i.e., an acoustic phonon replica), which appears as the highest intensity line in the FLN spectra. This interpretation implies that ΔEFLN corresponds to ΔEbd plus the energy of the acoustic phonon mode that is coupled to the dark F = ±2 state. We assume that this phonon mode is the same one responsible for the thermal activation involved in the T-dependence of the PL decay dynamics. The difference between the two processes is that the acoustic phonon replica observed in the FLN spectra is due to a Stokes process in which a phonon is created, while the T-dependence of the PL decay is due to an anti-Stokes process, in which phonons are annihilated.
The first allowed transition (2) occurs at an energy of −ΔET with respect to the energy of the dark F = ±2 state. Other possible transitions involve the excitation of optical phonons, either as a single-phonon process or with additional coupling to confined acoustic phonon modes: transitions 3 and 4 involve ZnSe optical modes, while 5 and 6 involve InP optical modes. The transitions 3 and 4 occur at energies −ΔEZnSe and −(ΔEZnSe + ΔET), while 5 and 6 occur at −ΔEInP and −(ΔEInP + ΔET) (where ΔEZnSe and ΔEInP are the optical-phonon energies in ZnSe and InP). Transitions 3 and 4 are separated by only ΔET, so they appear in the FLN experiment as a single broad peak with center energy −(ΔEZnSe + ΔET/2) with respect to the dark F = ±2 state. The same holds for transitions 5 and 6, which constitute an FLN peak at −(ΔEInP + ΔET/2). Hence, with respect to the highest intensity FLN peak (transition 2), coupling to optical phonons in ZnSe (transitions 3 and 4) results in a peak shifted by −(ΔEZnSe – ΔET/2) and coupling to InP phonons (transitions 5 and 6) in a peak shifted by −(ΔEInP – ΔET/2). This explains why the differences we observe between peak energies in FLN (Figure 5d) are slightly smaller (by ΔET/2 = 3–4 meV) than the optical-phonon energies that we observe in the Raman spectra (Figure 5c).
Conclusion
In conclusion, we presented a detailed study of the fine structure of InP/ZnSe core/shell QDs using FLN experiments in a varying magnetic field, combined with T-dependent PL decay and Raman spectroscopic analysis. We observe that the lowest energy fine structure exciton state is an F = ±2 dark state, from which radiative recombination is assisted by coupling to confined acoustic phonons with energy ranging from 4 to 7 meV, depending on the core diameter. The FLN spectra are explained by coupling of the dark exciton state to LO, TO, and confined acoustic phonon modes of the core/shell QDs. Our data indicate that the highest intensity FLN peak is an acoustic phonon replica rather than a zero-phonon line, implying that the splitting between the dark and bright fine structure exciton states (estimated around 2–9 meV, depending on the InP core size) is smaller than the energy separation observed between the F = ±1 state and the highest intensity peak in the FLN spectra (6–16 meV).
Methods
Sample Preparation
InP/ZnSe QDs with different core diameters were synthesized, following the method reported in ref (21). Core-only InP QDs were synthesized following the method of ref (64). The QD samples were washed by precipitation with methanol, isolated by centrifugation, and redispersed in toluene and 1-dodecanethiol. To achieve a QD film, the solution was deposited using a drop-cast method on a crystalline silicon substrate.
HAADF-STEM and Energy Dispersive X-ray Spectroscopy
High-resolution HAADF-STEM measurements were performed using an aberration-corrected cubed FEI Titan 60-300 electron microscope operated at 120 kV. Energy dispersive X-ray spectroscopy (EDS) measurements were performed on an FEI Osiris electron microscope operated at 200 kV. Acquisition time for EDS measurements was ∼500 s. To avoid contamination growth during the experiment, the TEM grid was kept at 80 degrees for 4 h and then transferred directly inside the microscope. In order to check whether the heat treatment changed the internal structure or not, diffraction patterns have been acquired before and after the treatment.
Temperature Dependence of the Time-Resolved Photoluminescence
The time-resolved PL measurements were performed on a set of QD ensemble samples. The excitation was provided by a pulsed diode laser, operating at 375 nm with a repetition rate of 100 kHz for all samples.
The time-resolved PL spectra were obtained by a time-correlated single photon counting detector where the average count rate was kept at 3% of the laser repetition rate. This low excitation fluence was used in order to maintain single-photon statistics and avoid multiexciton formation.
The time-resolved PL measurements were performed monitoring the PL peak wavelength. The PL peak wavelength was selected, at each temperature, based on PL measurements, and the signal was dispersed by a monochromator (1200 grooves/mm grating, blazed at 500 nm) and detected by a fast photomultiplier tube. For both PL and time-resolved PL measurements, the PL was filtered through a 460 nm long-pass filter to eliminate scattered laser light. The QD solutions were contained in a quartz cuvette and mounted in a continuous He-flow cryostat allowing for measurements down to 4 K. In addition, measurements down to 10 mK were performed on QD films (see sample preparation) using a Bluefors dilution refrigerator at KTH in Stockholm.
Magneto-optical Measurements in High Magnetic Fields
Optical experiments at low temperatures and high magnetic fields were performed at High Field Magnet Laboratory (Radboud University), using two spectroscopic techniques: polarized PL and FLN spectroscopy. For these experiments the samples used were QD films (see sample preparation). The samples were mounted in a titanium sample holder on top of a three-axis piezo-positioner. The laser beam was focused on the sample by a singlet lens (10 mm focal length). The same lens was used to collect the PL emission and direct it to the detection setup (backscattering geometry). The samples and optical probe were mounted inside a liquid-helium bath cryostat (4.2 K) inserted in a 50 mm bore Florida-Bitter electromagnet with a maximum field strength of 30 T. All optical experiments were performed in Faraday geometry, i.e., with both incident and scattered light parallel to the magnetic field direction.
Polarized PL measurements were performed in time-integrated and time-resolved configuration, using the same excitation source, in continuous or pulsed excitation mode. The excitation was circularly polarized with the use of a linear polarizer and a Babinet Soleil compensator.
The PL light was guided through a 0.3 m long single grating spectrometer (300 grooves/mm grating) and detected by a liquid nitrogen cooled charge couple device (CCD) for time-integrated measurements and by an avalanche photodiode connected to a single-photon counter (time-correlated single photon counting) in the time-resolved configuration. The emitted photons were detected in crossed and co-polarization relative to the laser polarization by using a linear polarizer and a lambda-quarter-wave plate. Cut-off optical filters were used in excitation and detection.
The FLN measurements were performed using a narrow excitation source, achieved by using a tunable jet-stream dye (rhodamine 6G) laser and a 0.3 m long single grating spectrometer (1200 grooves/mm grating). This monochromatic laser beam was circularly polarized by means of a linear polarizer and a Babinet-Soleil compensator.
High-resolution FLN emission was detected in crossed polarization mode relative to the laser polarization by using a linear polarizer and a lambda-quarter-wave plate. The resonant-PL emission was analyzed by a 0.5 m long triple-grating spectrometer (three 1800 grooves/mm holographic gratings) in subtractive mode, equipped with a liquid nitrogen cooled CCD camera (Symphony-Horiba).
Raman Spectroscopy Measurements
Raman scattering measurements on InP core and InP/ZnSe core/shell samples (see sample preparation above) have been performed at High Field Magnet Laboratory (Radboud University). To achieve low temperatures, samples were placed in high vacuum (10–6 mbar) inside an optical 4He cryostat (Microstat Oxford). Samples were probed in backscattering geometry with an incident laser line at 488 nm from a solid-state laser. To prevent both excessive laser heating and sample damages, a low laser power of 30 μW was used. The scattered light was filtered by a RazorEdge ultrasteep long-pass edge filter and analyzed by a 1 m long single grating (1200 grooves/mm) FHR-1000 Horiba spectrometer equipped with a nitrogen-cooled PyLoN CCD camera (Princeton Instruments). The resolution of our measurements was 1 cm–1.
Fitting Procedure of the Exciton PL Decay Curves at Variable Temperatures
The fitting procedure is outlined in the Supporting Information Figures S3–S5. If the long component of the PL decay curve is fitted with a biexponential (Figure S3, blue points), we observe that the slowest time constant decreases with the increasing of T from 4 to 20 K. At higher T the time constant starts to increase again as a function of T. This is attributed to T-activated multiple trapping/detrapping resulting in “delayed” emission.65 For this reason, we decided to use only a limited part of the PL decay curves, which should describe unperturbed exciton emission. It is shows in Figure S4, where we fitted single-exponential decay to the time range dominated by direct radiative decay. This time range, however, varies with temperature. The exact time range taken into consideration for each temperature and the criterion used to determine it are described in the Supporting Information (Figure S4).
Acknowledgments
We acknowledge the support of the HFML-RU/FOM, member of the European Magnetic Field Laboratory (EMFL). D.V. and Z.H. acknowledge support by the European Commission via the Marie-Sklodowska Curie action Phonsi (H2020-MSCA-ITN-642656) and the Marie Sklodowska-Curie Action Compass (H2020 MSCA-RISE-691185). Z.H. acknowledges the Research Foundation Flanders (project 17006602) and Ghent University (GOA no. 01G01513). Z.H. and S.B. acknowledge SIM vzw (SBO-QDOCCO). F.T.R. acknowledges financial support from The Netherlands Organisation for Scientific Research NWO (Gravitation program Multiscale Catalytic Energy Conversion and VENI grant number 722.017.002). This work was also supported by the Dutch NWO-Physics Program DDC13, ERC Advanced Grant 692691 “First step”, and ERC Starting Grant 335078 “COLOURATOM”.
Supporting Information Available
The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsphotonics.8b00615.
Additional data including optical characterization of samples with different InP core sizes, more details about the data analysis, and Lamb theory calculations (PDF)
Author Contributions
The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.
The authors declare no competing financial interest.
Supplementary Material
References
- Jang E.; Jun S.; Jang H.; Lim J.; Kim B.; Kim Y. White-Light-Emitting Diodes with Quantum Dot Color Converters for Display Backlights. Adv. Mater. 2010, 22, 3076–3080. 10.1002/adma.201000525. [DOI] [PubMed] [Google Scholar]
- Kim T.-H.; Jun S.; Cho K.-S.; Choi B. L.; Jang E. Bright and Stable Quantum Dots and Their Applications in Full-Color Displays. MRS Bull. 2013, 38, 712–720. 10.1557/mrs.2013.184. [DOI] [Google Scholar]
- Talapin D. V.; Steckel J. Quantum Dot Light-Emitting Devices. MRS Bull. 2013, 38, 685–691. 10.1557/mrs.2013.204. [DOI] [Google Scholar]
- Supran G. J.; Shirasaki Y.; Song K. W.; Caruge J.-M.; Kazlas P. T.; Coe-Sullivan S.; Andrew T. L.; Bawendi M. G.; Bulović V. QLEDs for Displays and Solid-State Lighting. MRS Bull. 2013, 38, 703–711. 10.1557/mrs.2013.181. [DOI] [Google Scholar]
- Steckel J. S.; Ho J.; Coe-Sullivan S. QDs Generate Light for Next-Generation Displays. Photonics Spectra 2014, 48, 55–61. [Google Scholar]
- Micic O. I.; Curtis C. J.; Jones K. M.; Sprague J. R.; Nozik A. J. Synthesis and Characterization of InP Quantum Dots. J. Phys. Chem. 1994, 98, 4966–4969. 10.1021/j100070a004. [DOI] [Google Scholar]
- Micic O. I.; Sprague J. R.; Curtis C. J.; Jones K. M.; Machol J. L.; Nozik A. J.; Giessen H.; Fluegel B.; Mohs G.; Peyghambarian N. Synthesis and Characterization of InP, GaP, and GaInP2 Quantum Dots. J. Phys. Chem. 1995, 99, 7754–7759. 10.1021/j100019a063. [DOI] [Google Scholar]
- Mićić O. I.; Ahrenkiel S. P.; Nozik A. J. Synthesis of Extremely Small InP Quantum Dots and Electronic Coupling in Their Disordered Solid Films. Appl. Phys. Lett. 2001, 78, 4022–4024. 10.1063/1.1379990. [DOI] [Google Scholar]
- Guzelian A. A.; Katari J. E. B.; Kadavanich A. V.; Banin U.; Hamad K.; Juban E.; Alivisatos A. P.; Wolters R. H.; Arnold C. C.; Heath J. R. Synthesis of Size-Selected, Surface-Passivated InP Nanocrystals. J. Phys. Chem. 1996, 100, 7212–7219. 10.1021/jp953719f. [DOI] [Google Scholar]
- Lucey D. W.; MacRae D. J.; Furis M.; Sahoo Y.; Cartwright A. N.; Prasad P. N. Monodispersed InP Quantum Dots Prepared by Colloidal Chemistry in a Noncoordinating Solvent. Chem. Mater. 2005, 17, 3754–3762. 10.1021/cm050110a. [DOI] [Google Scholar]
- Battaglia D.; Peng X. Formation of High Quality InP and InAs Nanocrystals in a Noncoordinating Solvent. Nano Lett. 2002, 2, 1027–1030. 10.1021/nl025687v. [DOI] [Google Scholar]
- Nozik A. J.; Mićić O. I. Colloidal Quantum Dots of III-V Semiconductors. MRS Bull. 1998, 23, 24–30. 10.1557/S0883769400031237. [DOI] [Google Scholar]
- Xie R.; Battaglia D.; Peng X. Colloidal InP Nanocrystals as Efficient Emitters Covering Blue to near-Infrared. J. Am. Chem. Soc. 2007, 129, 15432–15433. 10.1021/ja076363h. [DOI] [PubMed] [Google Scholar]
- Joung S.; Yoon S.; Han C.-S.; Kim Y.; Jeong S. Facile Synthesis of Uniform Large-Sized InP Nanocrystal Quantum Dots Using Tris(tert-Butyldimethylsilyl)phosphine. Nanoscale Res. Lett. 2012, 7, 93. 10.1186/1556-276X-7-93. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pietra F.; De Trizio L.; Hoekstra A. W.; Renaud N.; Prato M.; Grozema F. C.; Baesjou P. J.; Koole R.; Manna L.; Houtepen A. J. Tuning the Lattice Parameter of InXZnYP for Highly Luminescent Lattice-Matched Core/Shell Quantum Dots. ACS Nano 2016, 10, 4754–4762. 10.1021/acsnano.6b01266. [DOI] [PubMed] [Google Scholar]
- Dupont D.; Tessier M. D.; Smet P. F.; Hens Z. Indium Phosphide-Based Quantum Dots with Shell-Enhanced Absorption for Luminescent Down-Conversion. Adv. Mater. 2017, 29, 1700686. 10.1002/adma.201700686. [DOI] [PubMed] [Google Scholar]
- Song W. S.; Lee H. S.; Lee J. C.; Jang D. S.; Choi Y.; Choi M.; Yang H. Amine-Derived Synthetic Approach to Color-Tunable InP/ZnS Quantum Dots with High Fluorescent Qualities. J. Nanopart. Res. 2013, 15, 1750. 10.1007/s11051-013-1750-y. [DOI] [Google Scholar]
- Coropceanu I.; Bawendi M. G. Core/shell Quantum Dot Based Luminescent Solar Concentrators with Reduced Reabsorption and Enhanced Efficiency. Nano Lett. 2014, 14, 4097–4101. 10.1021/nl501627e. [DOI] [PubMed] [Google Scholar]
- Ryu E.; Kim S.; Jang E.; Jun S.; Jang H.; Kim B.; Kim S. W. Step-Wise Synthesis of InP/ZnS Core - Shell Quantum Dots and the Role of Zinc Acetate. Chem. Mater. 2009, 21, 573–575. 10.1021/cm803084p. [DOI] [Google Scholar]
- Li L.; Reiss P. One-Pot Synthesis of Highly Luminescent InP/ZnS Nanocrystals without Precursor Injection. J. Am. Chem. Soc. 2008, 130, 11588–11589. 10.1021/ja803687e. [DOI] [PubMed] [Google Scholar]
- Tessier M. D.; Dupont D.; De Nolf K.; De Roo J.; Hens Z. Economic and Size-Tunable Synthesis of InP/ZnE (E = S, Se) Colloidal Quantum Dots. Chem. Mater. 2015, 27, 4893–4898. 10.1021/acs.chemmater.5b02138. [DOI] [Google Scholar]
- Qu L.; Peng X. Control of Photoluminescence Properties of CdSe Nanocrystals in Growth. J. Am. Chem. Soc. 2002, 124, 2049–2055. 10.1021/ja017002j. [DOI] [PubMed] [Google Scholar]
- Chen O.; Zhao J.; Chauhan V. P.; Cui J.; Wong C.; Harris D. K.; Wei H.; Han H.-S.; Fukumura D.; Jain R. K.; et al. Compact High-Quality CdSe–CdS Core–shell Nanocrystals with Narrow Emission Linewidths and Suppressed Blinking. Nat. Mater. 2013, 12, 445–451. 10.1038/nmat3539. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cui J.; Beyler A. P.; Marshall L. F.; Chen O.; Harris D. K.; Wanger D. D.; Brokmann X.; Bawendi M. G. Direct Probe of Spectral Inhomogeneity Reveals Synthetic Tunability of Single-Nanocrystal Spectral Linewidths. Nat. Chem. 2013, 5, 602–606. 10.1038/nchem.1654. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chandrasekaran V.; Tessier M. D.; Dupont D.; Geiregat P.; Hens Z.; Brainis E. Nearly Blinking-Free, High-Purity Single-Photon Emission by Colloidal InP/ZnSe Quantum Dots. Nano Lett. 2017, 17, 6104–6109. 10.1021/acs.nanolett.7b02634. [DOI] [PubMed] [Google Scholar]
- Micic O. I.; Cheong H. M.; Fu H.; Zunger A.; Sprague J. R.; Mascarenhas A.; Nozik A. J. Size-Dependent Spectroscopy of InP Quantum Dots. J. Phys. Chem. B 1997, 101, 4904–4912. 10.1021/jp9704731. [DOI] [Google Scholar]
- Mushonga P.; Onani M. O.; Madiehe A. M.; Meyer M. Indium Phosphide-Based Semiconductor Nanocrystals and Their Applications. J. Nanomater. 2012, 2012, 1–11. 10.1155/2012/869284. [DOI] [Google Scholar]
- Narayanaswamy A.; Feiner L. F.; van der Zaag P. J. Temperature Dependence of the Photoluminescence of InP/ZnS Quantum Dots. J. Phys. Chem. C 2008, 3, 6775–6780. 10.1021/jp800339m. [DOI] [Google Scholar]
- Mićić O. I.; Sprague J.; Lu Z.; Nozik A. J. Highly Efficient Band-Edge Emission from InP Quantum Dots. Appl. Phys. Lett. 1996, 68, 3150–3152. 10.1063/1.115807. [DOI] [Google Scholar]
- Ahrenkiel S. P.; Mićić O. I.; Miedaner A.; Curtis C. J.; Nedeljković J. M.; Nozik A. J. Synthesis and Characterization of Colloidal InP Quantum Rods. Nano Lett. 2003, 3, 833–837. 10.1021/nl034152e. [DOI] [Google Scholar]
- Nedeljković J. M.; Mićić O. I.; Ahrenkiel S. P.; Miedaner A.; Nozik A. J. Growth of InP Nanostructures via Reaction of Indium Droplets with Phosphide Ions: Synthesis of InP Quantum Rods and InP-TiO2 Composites. J. Am. Chem. Soc. 2004, 126, 2632–2639. 10.1021/ja039311a. [DOI] [PubMed] [Google Scholar]
- Ellingson R. J.; Blackburn J. L.; Yu P.; Rumbles G.; Mićić O. I.; Nozik A. J. Excitation Energy Dependent Efficiency of Charge Carrier Relaxation and Photoluminescence in Colloidal InP Quantum Dots. J. Phys. Chem. B 2002, 106, 7758–7765. 10.1021/jp025666p. [DOI] [Google Scholar]
- Voznyy O.; Levina L.; Fan F.; Walters G.; Fan J. Z.; Kiani A.; Ip A. H.; Thon S. M.; Proppe A. H.; Liu M.; et al. Origins of Stokes Shift in PbS Nanocrystals. Nano Lett. 2017, 17, 7191–7195. 10.1021/acs.nanolett.7b01843. [DOI] [PubMed] [Google Scholar]
- De Mello Donegá C. Formation of Nanoscale Spatially Indirect Excitons: Evolution of the Type-II Optical Character of CdTe/CdSe Heteronanocrystals. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 81, 1–20. 10.1103/PhysRevB.81.165303. [DOI] [Google Scholar]
- Efros A.; Rosen M.; Kuno M.; Nirmal M.; Norris D.; Bawendi M. Band-Edge Exciton in Quantum Dots of Semiconductors with a Degenerate Valence Band: Dark and Bright Exciton States. Phys. Rev. B: Condens. Matter Mater. Phys. 1996, 54, 4843–4856. 10.1103/PhysRevB.54.4843. [DOI] [PubMed] [Google Scholar]
- Fu H.; Zunger A. InP Quantum Dots: Electronic Structure, Surface Effects, and the Redshifted Emission. Phys. Rev. B: Condens. Matter Mater. Phys. 1997, 56, 1496. 10.1103/PhysRevB.56.1496. [DOI] [Google Scholar]
- Fu H.; Wang L.-W.; Zunger A. Excitonic Exchange Splitting in Bulk Semiconductors. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 59, 5568–5574. 10.1103/PhysRevB.59.5568. [DOI] [Google Scholar]
- Blokland J. H.; Claessen V. I.; Wijnen F. J. P.; Groeneveld E.; de Mello Donegá C.; Vanmaekelbergh D.; Meijerink A.; Maan J. C.; Christianen P. C. M. Exciton Lifetimes of CdTe Nanocrystal Quantum Dots in High Magnetic Fields. Phys. Rev. B: Condens. Matter Mater. Phys. 2011, 83, 35304. 10.1103/PhysRevB.83.035304. [DOI] [Google Scholar]
- Rafipoor M.; Dupont D.; Tornatzky H.; Tessier M. D.; Maultzsch J.; Hens Z.; Lange H. Strain Engineering in InP/(Zn,Cd)Se Core/Shell Quantum Dots. Chem. Mater. 2018, 30, 4393–4400. 10.1021/acs.chemmater.8b01789. [DOI] [Google Scholar]
- Fan F.; Voznyy O.; Sabatini R. P.; Bicanic K. T.; Adachi M. M.; McBride J. R.; Reid K. R.; Park Y.-S.; Li X.; Jain A.; et al. Continuous-Wave Lasing in Colloidal Quantum Dot Solids Enabled by Facet-Selective Epitaxy. Nature 2017, 544, 75–79. 10.1038/nature21424. [DOI] [PubMed] [Google Scholar]
- Biadala L.; Siebers B.; Beyazit Y.; Tessier M. D.; Dupont D.; Hens Z.; Yakovlev D. R.; Bayer M. Band-Edge Exciton Fine Structure and Recombination Dynamics in InP/ZnS Colloidal Nanocrystals. ACS Nano 2016, 10, 3356–3364. 10.1021/acsnano.5b07065. [DOI] [PubMed] [Google Scholar]
- Ministro J.A Study on the Synthesis and the Optical Properties of InP-Based Quantum Dots, Master Thesis, Ghent University, 2014. [Google Scholar]
- Qu L.; Peng X. Control of Photoluminescence Properties of CdSe Nanocrystals in Growth. J. Am. Chem. Soc. 2002, 124, 2049–2055. 10.1021/ja017002j. [DOI] [PubMed] [Google Scholar]
- Haruna K.; Ohashi K.; Koike T.; Maeta H. The Thermal Expansion Coefficient and Gruneisen Parameter of Inp Crystal at Low Temperatures. J. Phys. C: Solid State Phys. 1987, 20, 5275–5279. 10.1088/0022-3719/20/32/013. [DOI] [Google Scholar]
- Furis M.; Htoon H.; Petruska M. A.; Klimov V. I.; Barrick T.; Crooker S. A. Bright-Exciton Fine Structure and Anisotropic Exchange in CdSe Nanocrystal Quantum Dots. Phys. Rev. B: Condens. Matter Mater. Phys. 2006, 73, 241313. 10.1103/PhysRevB.73.241313. [DOI] [Google Scholar]
- Wijnen F. J. P.; Blokland J. H.; Chin P. T. K.; Christianen P. C. M.; Maan J. C.. Competition between Zero-Phonon and Phonon-Assisted Luminescence in Colloidal CdSe Quantum Dots. Phys. Rev. B: Condens. Matter Mater. Phys. 2008, 78, 10.1103/PhysRevB.78.235318. [DOI] [Google Scholar]
- Granados del Águila A.; Pettinari G.; Groeneveld E.; de Mello Donegá C.; Vanmaekelbergh D.; Maan J. C.; Christianen P. C. M. Optical Spectroscopy of Dark and Bright Excitons in CdSe Nanocrystals in High Magnetic Fields. J. Phys. Chem. C 2017, 121, 23693–23704. 10.1021/acs.jpcc.7b06170. [DOI] [Google Scholar]
- Lu Z. Q.; Quinn T.; Reehal H. S. Polarization-Dependent Raman Spectra of Thin Crystalline Silicon Films. J. Appl. Phys. 2005, 97, 33512. 10.1063/1.1844613. [DOI] [Google Scholar]
- Hou H.-J.; Kong F.-J. Theoretical Investigation on the Structural, Dynamical, and Thermodynamic Properties of the Zinc-Blende InX (X = P, As, Sb). Phys. Status Solidi B 2011, 248, 1399–1404. 10.1002/pssb.201046479. [DOI] [Google Scholar]
- Seong M. J.; Mićić O. I.; Nozik A. J.; Mascarenhas A.; Cheong H. M. Size-Dependent Raman Study of InP Quantum Dots. Appl. Phys. Lett. 2003, 82, 185–187. 10.1063/1.1535272. [DOI] [Google Scholar]
- Rössler U.New Data and Updates for Several Semiconductors with Chalcopyrite Structure, for Several II-VI Compounds and Diluted Magnetic IV-VI Compounds; Springer: Berlin, Heidelberg, 2013. [Google Scholar]
- Gadret E. G.; de Lima M. M.; Madureira J. R.; Chiaramonte T.; Cotta M. A.; Iikawa F.; Cantarero A. Optical Phonon Modes of Wurtzite InP. Appl. Phys. Lett. 2013, 102, 122101. 10.1063/1.4798324. [DOI] [Google Scholar]
- Buhot J.; Gallais Y.; Cazayous M.; Sacuto A.; Piekarz P.; Lapertot G.; Aoki D.; Méasson M.-A. Raman Active High Energy Excitations in URu2Si2. Phys. B 2017, 506, 19–22. 10.1016/j.physb.2016.10.034. [DOI] [Google Scholar]
- Sun C. Q.; Pan L. K.; Li C. M.; Li S. Size-Induced Acoustic Hardening and Optic Softening of Phonons in InP, CeO2, SnO2, CdS, Ag, and Si Nanostructures. Phys. Rev. B: Condens. Matter Mater. Phys. 2005, 72, 134301. 10.1103/PhysRevB.72.134301. [DOI] [Google Scholar]
- Oron D.; Aharoni A.; de Mello Donega C.; van Rijssel J.; Meijerink A.; Banin U. Universal Role of Discrete Acoustic Phonons in the Low-Temperature Optical Emission of Colloidal Quantum Dots. Phys. Rev. Lett. 2009, 102, 177402. 10.1103/PhysRevLett.102.177402. [DOI] [PubMed] [Google Scholar]
- Takagahara T. Electron—phonon Interactions in Semiconductor Nanocrystals. J. Lumin. 1996, 70, 129–143. 10.1016/0022-2313(96)00050-6. [DOI] [PubMed] [Google Scholar]
- Lamb H. On the Vibrations of an Elastic Sphere. Proc. London Math. Soc. 1881, s1–13, 189–212. 10.1112/plms/s1-13.1.189. [DOI] [Google Scholar]
- Cerullo G.; De Silvestri S.; Banin U. Size-Dependent Dynamics of Coherent Acoustic Phonons in Nanocrystal Quantum Dots. Phys. Rev. B: Condens. Matter Mater. Phys. 1999, 60, 1928–1932. 10.1103/PhysRevB.60.1928. [DOI] [Google Scholar]
- Eilers J.; Van Hest J.; Meijerink A.; Donega C. D. M. Unravelling the Size and Temperature Dependence of Exciton Lifetimes in Colloidal ZnSe Quantum Dots. J. Phys. Chem. C 2014, 118, 23313–23319. 10.1021/jp5038238. [DOI] [Google Scholar]
- Granados del Águila A.; Groeneveld E.; Maan J. C.; de Mello Donegá C.; Christianen P. C. M. Effect of Electron–Hole Overlap and Exchange Interaction on Exciton Radiative Lifetimes of CdTe/CdSe Heteronanocrystals. ACS Nano 2016, 10, 4102–4110. 10.1021/acsnano.5b07158. [DOI] [PubMed] [Google Scholar]
- Granados del Águila A.; Jha B.; Pietra F.; Groeneveld E.; de Mello Donegá C.; Maan J. C.; Vanmaekelbergh D.; Christianen P. C. M. Observation of the Full Exciton and Phonon Fine Structure in CdSe/CdS Dot-in-Rod Heteronanocrystals. ACS Nano 2014, 8, 5921–5931. 10.1021/nn501026t. [DOI] [PubMed] [Google Scholar]
- Wong C. Y.; Kim J.; Nair P. S.; Nagy M. C.; Scholes G. D. Relaxation in the Exciton Fine Structure of Semiconductor Nanocrystals. J. Phys. Chem. C 2009, 113, 795–811. 10.1021/jp807128j. [DOI] [Google Scholar]
- Huxter V. M.; Scholes G. D. Acoustic Phonon Strain Induced Mixing of the Fine Structure Levels in Colloidal CdSe Quantum Dots Observed by a Polarization Grating Technique. J. Chem. Phys. 2010, 132, 104506. 10.1063/1.3350871. [DOI] [PubMed] [Google Scholar]
- Stein J. L.; Mader E. A.; Cossairt B. M. Luminescent InP Quantum Dots with Tunable Emission by Post-Synthetic Modification with Lewis Acids. J. Phys. Chem. Lett. 2016, 7, 1315–1320. 10.1021/acs.jpclett.6b00177. [DOI] [PubMed] [Google Scholar]
- Rabouw F. T.; Kamp M.; Van Dijk-Moes R. J. A.; Gamelin D. R.; Koenderink A. F.; Meijerink A.; Vanmaekelbergh D. Delayed Exciton Emission and Its Relation to Blinking in CdSe Quantum Dots. Nano Lett. 2015, 15, 7718–7725. 10.1021/acs.nanolett.5b03818. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.