Acceleration of CO₂ insertion into metal hydrides: ligand, Lewis acid, and solvent effects on reaction kinetics

Kinetic studies of CO₂ insertion into transition metal hydrides provide evidence about the nature of the rate-determining transition state.

Abstract

The insertion of CO₂ into metal hydrides and the microscopic reverse decarboxylation of metal formates are important elementary steps in catalytic cycles for both CO₂ hydrogenation to formic acid and methanol as well as formic acid and methanol dehydrogenation. Here, we use rapid mixing stopped-flow techniques to study the kinetics and mechanism of CO₂ insertion into transition metal hydrides. The investigation finds that the most effective method to accelerate the rate of CO₂ insertion into a metal hydride can be dependent on the nature of the rate-determining transition state (TS). We demonstrate that for an innersphere CO₂ insertion reaction, which is proposed to have a direct interaction between CO₂ and the metal in the rate-determining TS, the rate of insertion increases as the ancillary ligand becomes more electron rich or less sterically bulky. There is, however, no rate enhancement from Lewis acids (LA). In comparison, we establish that for an outersphere CO₂ insertion, proposed to proceed with no interaction between CO₂ and the metal in the rate-determining TS, there is a dramatic LA effect. Furthermore, for both inner- and outersphere reactions, we show that there is a small solvent effect on the rate of CO₂ insertion. Solvents that have higher acceptor numbers generally lead to faster CO₂ insertion. Our results provide an experimental method to determine the pathway for CO₂ insertion and offer guidance for rate enhancement in CO₂ reduction catalysis.

Introduction

CO₂ is an attractive feedstock for the sustainable synthesis of carbon-based commodity chemicals such as formic acid and methanol due to its abundance, low cost, and non-toxicity.1 A promising approach for the conversion of CO₂ into these chemicals is the utilization of homogeneous transition metal catalysts. Recently, numerous molecular catalysts for CO₂ reduction have been described, but further work is still required to develop practical systems.1 In many of these catalytic processes such as the hydrogenation of CO₂ to formic acid or methanol, CO₂ insertion into a metal hydride is proposed to be a key step.2 Similarly, in the dehydrogenation of methanol or formic acid to CO₂ and H₂,1f,3 it is postulated that the microscopic reverse reaction – the decarboxylation of a metal formate to generate a metal hydride and CO₂ – is a crucial step.4 However, despite the importance of both these reactions in catalysis, there are few systematic experimental studies exploring these elementary reactions.

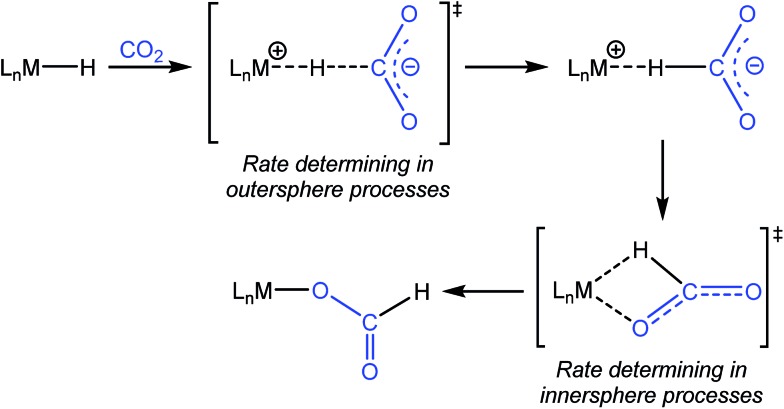
One of the most common pathways for CO₂ insertion into metal hydrides involves two steps: (i) nucleophilic attack of a metal hydride on the electrophilic CO₂ to form an H-bound formate and (ii) rearrangement of the H-bound formate to generate the O-bound formate product (Scheme 1).2b,5 Reactions in which the first step is rate-determining are considered outersphere, as there is no direct interaction between the CO₂ and the metal center in this transition state (TS), while reactions in which the second step is rate-determining are innersphere.5a,b,e An alternative concerted pathway involves a four-membered TS in which there is a direct interaction between CO₂ and the metal center.5a,e This is also referred to as an innersphere pathway, as the TS for the concerted process most resembles the TS for the rearrangement of the H-bound formate in stepwise CO₂ insertion.5a,b,e Information about the rate-determining TS for CO₂ insertion into a given metal hydride is generally obtained from computational rather than experimental studies, as these reactions typically occur within seconds at room temperature, making the measurement of kinetics challenging. As a consequence, there are only a few isolated measurements of the rates of CO₂ insertion into metal hydrides6 and little work comparing different metal systems or understanding the effects of the reaction environment.7,8 Furthermore, as part of studies on both catalytic CO₂ hydrogenation and formic acid dehydrogenation, it has been shown that LA co-catalysts can dramatically increase turnover number and turnover frequency.1f,2i,4c,9 One explanation for the improved performance is that the LA assists in the insertion of CO₂ into metal hydrides (or the decarboxylation of metal formates) by stabilizing the TS.4c,d Although previous work has demonstrated that LAs can accelerate the rate of CO₂ insertion into metal–alkyl bonds by stabilizing the TS,7a–c there is no quantitative evidence to substantiate this for metal hydrides. An improved understanding of these factors will facilitate the rational design of improved catalysts for reactions that involve either CO₂ insertion into metal hydrides or the decarboxylation of metal formates.

Scheme 1. Pathway for CO₂ insertion into transition metal hydrides.

Here, we use a stopped-flow instrument to measure the rates of CO₂ insertion into transition metal hydrides. Specifically, we compare the role of solvent and LAs on reactions that are proposed to proceed via an inner- or outersphere rate-determining TS. We show that LAs increase the rate of insertion for an outersphere system, but have no effect on the rate of CO₂ insertion for an innersphere system. Furthermore, we explore the impact of systematically modifying the ligand scaffold on the rate of insertion for an innersphere system. We demonstrate that decreased steric congestion around the metal hydride and/or the addition of an electron-donating substituent in the ligand scaffold increase the rate of CO₂ insertion. Our results also suggest that both inner- and outersphere systems exhibit similar solvent effects. This work represents the first quantitative study of LA effects on CO₂ insertion into transition metal hydrides.

Results and discussion

Solvent and Lewis acid effect for innersphere CO₂ insertion

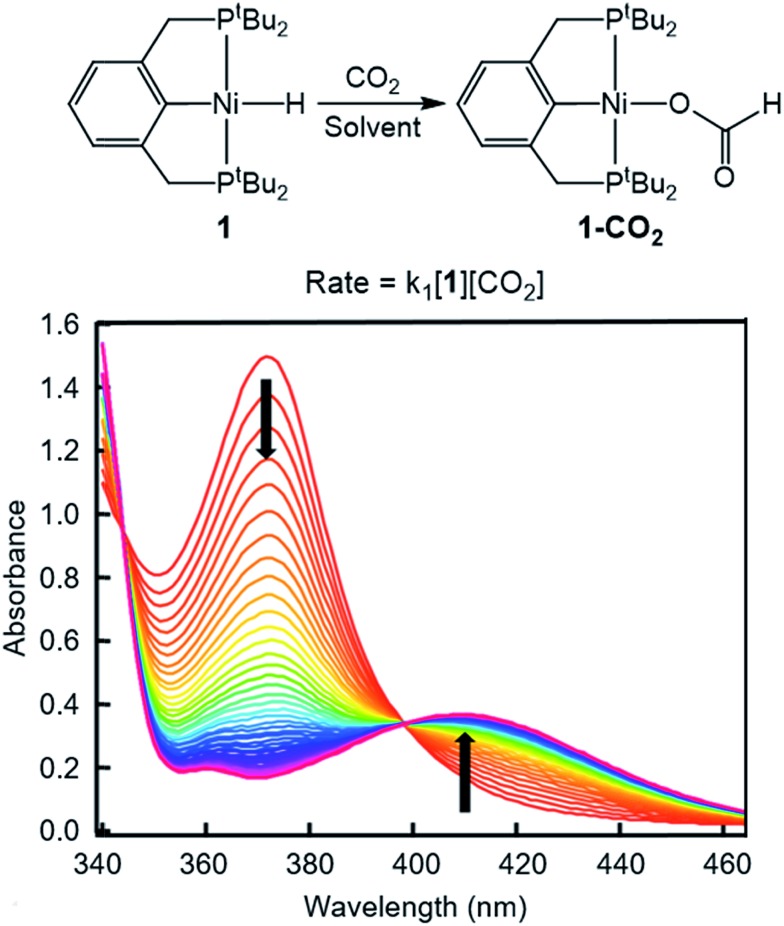
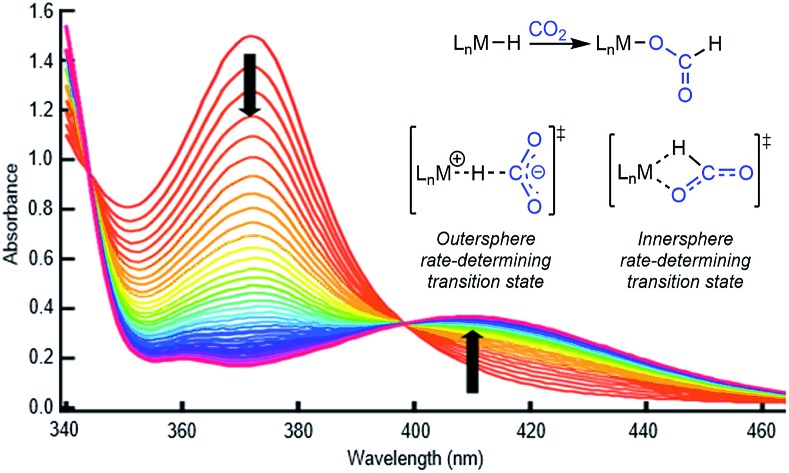
To probe solvent and/or LA effects for an innersphere CO₂ insertion reaction, the pincer-supported nickel hydride (^tBuPCP)NiH (^tBuPCP = 2,6-C₆H₃(CH₂P^tBu₂)₂) (1) was synthesized using literature methods.10 Previous DFT calculations on a model system show that the rate-determining TS for CO₂ insertion into 1 is a four-centered TS in which an oxygen atom from CO₂ directly interacts with the nickel center.5a Based on this, we regard 1 as a canonical example of systems that insert CO₂via an innersphere rate-determining TS. The kinetics of CO₂ insertion into 1 to form (^tBuPCP)Ni{OC(O)H} (1-CO₂) were measured using a rapid mixing stopped-flow instrument with a UV-Vis detector (Fig. 1). This allowed for the measurements of rates on a millisecond timescale at room temperature. Specifically, the reaction was followed spectroscopically from 340 to 560 nm using a ≥20-fold excess of CO₂. Globally fitting the data as a single exponential indicated that the reaction is first order in [1]. Subsequent experiments at different concentrations of CO₂ showed that the reaction is also first-order in [CO₂] (see ESI†), indicating that the overall rate law is k₁[1][CO₂].

Fig. 1. Representative stopped-flow data for CO₂ insertion into 1. Reaction conditions: [1] = 0.6 mM, [CO₂] = 45 mM, benzene, room temperature.

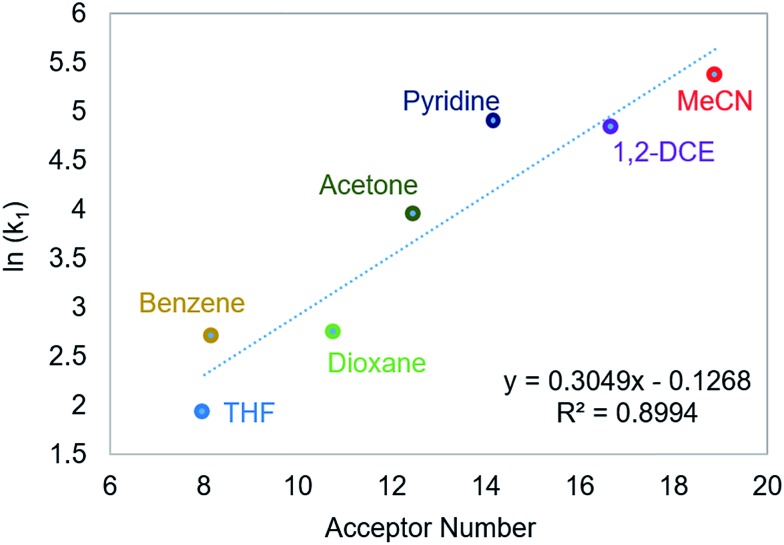
Using this methodology, we were able to determine k₁ under a range of conditions (Table 1). For CO₂ insertion into 1, there is excellent agreement between the experimental and computational activation parameters.5a As shown in Table 1, CO₂ insertion into 1 exhibits a small solvent effect. The rate of insertion increases by a factor of 32 between THF and MeCN (Table 1, entries 1a and 8). Analysis of the measured rate constants for insertion into 1 in a variety of solvents indicates that there is a poor correlation between the solvent dielectric constant and the rate of insertion (Fig. S23 in ESI†). The observed order of THF < benzene = dioxane < acetone < 1,2-DCE = DMI = pyridine < MeCN is instead predicted by increasing acceptor number (AN), a measure of the Lewis acidity of the solvent (Fig. 2).11 Both Konno et al. and Huang et al. have also demonstrated that there is relationship between the rate of CO₂ insertion into a metal hydride and the solvent AN, but for significantly higher polarity solvents.6b,e Although there is a solvent effect for CO₂ insertion into 1, the mechanism of insertion likely does not change as a function of solvent, as supported by the consistent activation parameters (Table 1, entries 1a and 8) and the similar isotope effects in THF and MeCN. Specifically, kinetic studies with (^tBuPCP)NiD revealed inverse isotope effects of 0.61 ± 0.15 in THF and 0.79 ± 0.18 in MeCN (see ESI†).

Table 1. Effect of solvent and LAs on the rate of CO₂ insertion into 1.

Entry	Solvent	k 1 (M–1 s–1) at RT	Rate increase	Activation parameters a
1a	THF	6.8 ± 0.7	—	ΔH‡ = 6.3 (3)
				ΔS‡ = –33 (1)
				ΔG‡298 K = 16.3 (4)
1b b	THF + LiPF6	6.6 ± 0.7	—	—
1c b , c	THF + NaBArF4	6.7 ± 0.7	—	—
2	Benzene	15 ± 2	2	—
3	1,4-Dioxane	15 ± 2	2	—
4	Acetone	51 ± 5	8	—
5	1,2-DCE d	1.2 (1) × 102	18	—
6	DMI e	1.3 (1) × 102	19	—
7	Pyridine	1.3 (1) × 102	19	—
8	MeCN	2.2 (2) × 102	32	ΔH‡ = 6.0 (3)
				ΔS‡ = –28 (1)
				ΔG‡298 K = 14.3 (3)

^aΔH^‡ and ΔG^‡ in kcal mol^–1 and ΔS^‡ in cal mol^–1 K^–1.

^b[LA] = 6.0 mM (20 equivalents with respect to 1).

^cNaBArF₄ = sodium tetrakis[3,5-bis(trifluoromethyl)phenyl]borate.

^d1,2-DCE = 1,2-dichloroethane.

^eDMI = 1,3-dimethyl-2-imidazolidinone.

Fig. 2. Relationship between the second-order rate constant k₁ for CO₂ insertion into 1 in various solvents and solvent AN.11.

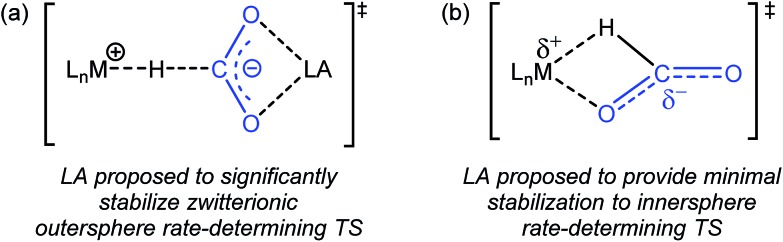
Previous studies on catalytic CO₂ hydrogenation and formic acid dehydrogenation have demonstrated that LA co-catalysts can dramatically increase both turnover number and turnover frequency.1f,2i,4c,9 This improved catalytic performance was proposed to result from a LA-assisted stabilization of charge in the rate-determining TS of the CO₂ insertion (or the microscopic reverse decarboxylation) step.4c,d Specifically, in these likely outersphere systems, it was suggested that the LA stabilizes the incipient negative charge on the carboxylate group in the rate-determining TS (Fig. 3a), as has been suggested in other systems.7a,b To probe the relevance of this hypothesis to an innersphere system, we measured the kinetics of CO₂ insertion into 1 in the presence of LAs (Table 1, entries 1a–1c). There is no LA effect for this reaction (see Table S3† for further information), as the addition of excess LiPF₆ or NaBArF₄ does not change the rate of insertion. Analyzing the charge separation in the postulated rate-determining TS for an innersphere CO₂ insertion allows us to rationalize this observation (Fig. 3b). In this case, there is proposed to be only a small amount of charge separation in the rate-determining TS, meaning that the LA can only provide minimal stabilization. This interpretation of our experimental finding suggests a more general conclusion that the rate of CO₂ insertion (or decarboxylation) reactions that proceed via an innersphere pathway will not be enhanced by the addition of LAs.

Fig. 3. (a) Proposed stabilization of the zwitterionic outersphere rate-determining TS in the presence of a LA. (b) Proposed structure of the innersphere rate-determining TS.

Steric and electronic ligand effect for innersphere CO₂ insertion

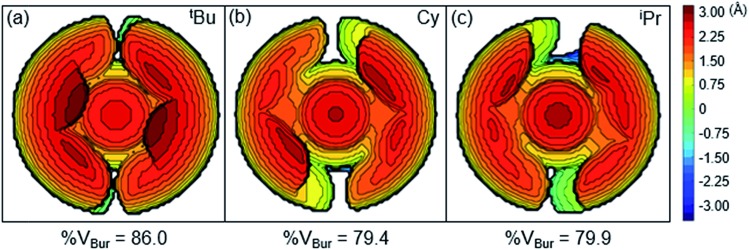
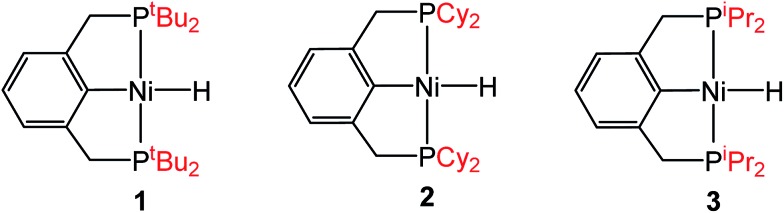
Although the insertion of CO₂ into 1 exhibits no rate enhancement from LAs and only a small solvent effect, altering the steric and electronic properties of the ancillary ligand may lead to larger changes in the reaction rate. Additionally, to date, systematic studies of the effects of modifying the ancillary ligand on the rate of CO₂ insertion in transition metal hydrides are rare,6a and therefore, it is difficult to rationally promote or inhibit the reaction by changing the supporting ligand. In order to determine how changing the steric properties of the ancillary ligand influences the rate of CO₂ insertion, we synthesized (^CyPCP)NiH (^CyPCP = 2,6-C₆H₃(CH₂PCy₂)₂) (2) and (^iPrPCP)NiH (^iPrPCP = 2,6-C₆H₃(CH₂PⁱPr₂)₂) (3) using literature methods.10 Under 1 atm CO₂, 2 and 3 cleanly generate (^CyPCP)Ni{OC(O)H} (2-CO₂) and (^iPrPCP)Ni{OC(O)H} (3-CO₂), respectively.5b The kinetics of these reactions were measured and directly compared to those obtained for 1. As shown in Table 2, changing the tert-butyl substituents in 1 to cyclohexyl or isopropyl groups led to a drastic enhancement of the reaction rate (500- and 647-fold, respectively). This substantial increase in the rate of CO₂ insertion is primarily attributed to the decreased steric congestion around the Ni–H bond in 2 and 3 as compared to 1. As a quantitative measure of the steric properties of the pincer ligands, the Salerno molecular buried volume calculation (SambVca) was used to calculate the percent buried volume (% V_Bur) of these nickel hydrides,12 based on their previously reported crystal structures.10,13 The calculated values are given in Table 2, and topographic maps illustrating the steric congestion in a qualitative manner are shown in Fig. 4. We propose that the significantly increased steric congestion around the Ni–H bond in 1 – as evidenced by the larger % V_Bur – makes it more difficult for CO₂ to approach the metal center and insert into the metal hydride bond, resulting in a much lower rate constant than that measured for 2 and 3.

Table 2. Effect of the phosphine substituents on the rate of CO₂ insertion into (^RPCP)NiH.

Entry	(RPCP)NiH	k 1 (M–1 s–1) at 298 K in THF	Rate increase	Calculated % VBur a
1	1	6.8 ± 0.7	—	86.0
2	2	3.4 (3) × 103	500	79.4
3	3	4.4 (4) × 103	647	79.9

^aSambVca parameters: 3.5 Å sphere radius with Ni atom defined as center, bond radii scaled by 1.17, H atoms included in calculation.12

Fig. 4. Topographic steric maps of (a) (^tBuPCP)NiH (1), (b) (^CyPCP)NiH (2), and (c) (^iPrPCP)NiH (3) as viewed down the H–Ni bond towards the plane defined by P–Ni–P.12.

The large ligand effect outlined above does, however, raise the following question: Is the small magnitude of the solvent effect as well as the lack of a LA effect observed for CO₂ insertion into 1 simply a result of increased steric congestion around the reaction center? To address this question, the kinetics of CO₂ insertion into 2 were measured in three different solvents and in the presence of LAs (Table 3). The rate of CO₂ insertion into 2 does not increase in the presence of a LA (entries 1a–1c). This indicates that the lack of a LA effect seen with 1 is, in fact, not an effect of increased steric congestion, but likely a function of a shared characteristic of the reaction pathways for 1 and 2. As the insertion of CO₂ into 2 is also proposed to proceed via an innersphere rate-determining TS, this result further supports our proposal that this TS does not involve a significant build-up of charge and, thus, is not stabilized by the addition of a LA even when the reaction center is less sterically crowded. Similarly, the solvent effect observed for CO₂ insertion into 2 is on the same order of magnitude as that measured for insertion into 1, again suggesting that there are strong mechanistic similarities between CO₂ insertion into these two complexes despite their steric differences.

Table 3. Effect of solvent and LAs on the rate of CO₂ insertion into 2.

Entry	Solvent	k 1 (M–1 s–1) at 273 K	Rate increase	Activation parameters a
1a	THF	1.8 (2) × 103	—	ΔH‡ = 4.4 (3)
				ΔS‡ = –28 (1)
				ΔG‡298 K = 12.6 (4)
1b b	THF + LiPF6	1.9 (2) × 103	—	—
1c b	THF + NaBArF4	1.9 (2) × 103	—	—
2	Benzene	3.7 (4) × 103	2	ΔH‡ = 3.0 (3)
				ΔS‡ = –31 (1)
				ΔG‡298 K = 12.3 (3)
3	Pyridine	7.9 (8) × 103	4	ΔH‡ = 4.7 (4)
				ΔS‡ = –23 (3)
				ΔG‡298 K = 11.6 (3)

^aΔH^‡ and ΔG^‡ in kcal mol^–1 and ΔS^‡ in cal mol^–1 K^–1.

^b[LA] = 6.0 mM (20 equivalents with respect to 2).

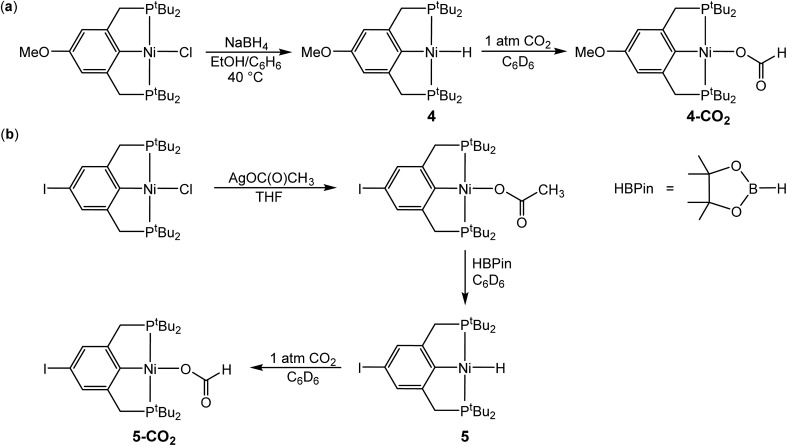
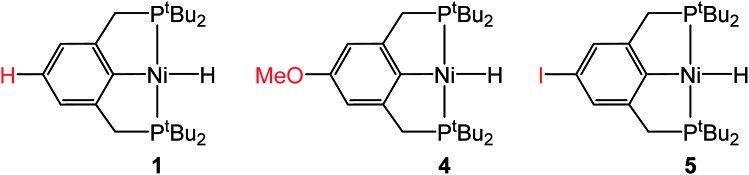
In the proposed innersphere rate-determining TS for CO₂ insertion, there is expected to be a small partial positive charge residing on the metal center (Fig. 3b). This suggests that increased electron density on the metal center may increase the rate of insertion by stabilizing the rate-determining TS, while decreased electron density may slow down the rate. To test this hypothesis, two novel substituted nickel hydrides were prepared – one with an electron-donating methoxy substituent and one with an electron-withdrawing iodo substituent in the para position of the ancillary ligand. The complexes (p-OMe-^tBuPCP)NiH (p-OMe-^tBuPCP = 4-OCH₃-2,6-(CH₂P^tBu₂)₂C₆H₂) (4) and (p-I-^tBuPCP)NiH (p-I-^tBuPCP = 4-I-2,6-(CH₂P^tBu₂)₂C₆H₂) (5) were synthesized. Scheme 2 outlines the preparation of the substituted nickel chloride precursors, which is based on previous literature methods.10,14 Complex 4 was then prepared from the corresponding nickel chloride using the same procedure as for 1 (Scheme 3a).10 To access 5, however, a different synthetic route was required (Scheme 3b), due to the tendency of the iodide on the ligand to react with nucleophilic hydride sources such as NaBH₄. Initially, a nickel acetate complex was synthesized from (p-I-^tBuPCP)NiCl using silver acetate to selectively abstract the chloride. Then pinacolborane (HBPin) was utilized as a transmetalling agent to substitute the acetate for a hydride while still maintaining the iodo substituent in the ligand backbone.

Scheme 2. Synthesis of (p-R-^tBuPCP)NiCl where R = OMe or I.

Scheme 3. (a) Synthesis of (p-OMe-^tBuPCP)NiH (4) and (p-OMe-^tBuPCP)Ni{OC(O)H} (4-CO₂). (b) Synthesis of (p-I-^tBuPCP)NiH (5) and (p-I-^tBuPCP)Ni{OC(O)H} (5-CO₂).

Complexes 4 and 5 both react with 1 atm CO₂ to cleanly form (p-OMe-^tBuPCP)Ni{OC(O)H} (4-CO₂) and (p-I-^tBuPCP)Ni{OC(O)H} (5-CO₂), respectively. The kinetics of these insertions were measured and directly compared to those obtained for 1 (Table 4). The incorporation of an electron-donating methoxy group in the para position of the ligand scaffold in 4 resulted in an almost doubling of the reaction rate as compared to the unsubstituted ligand. In contrast, the incorporation of an electron-withdrawing iodo group in 5 led to a 4-fold decrease in the reaction rate, again compared to the unsubstituted ligand. Given the larger magnitude of the Hammett σ_p⁺ parameter for the methoxy substituent (Table 4), it is rather surprising that the iodo substituent exhibits a more pronounced influence on the reaction rate. Our trends are in agreement with those elucidated for CO₂ insertion into fac-Re(4,4′-X₂-2,2′-bipy)(CO)₃H (X = H, Cl, Me, ^tBu, or OMe; bipy = bipyridine), which is the only other quantitative study exploring ligand effects on CO₂ insertion into transition metal hydrides.6a The electronic effect observed here supports our mechanism-based hypothesis and provides guidance on how to modify ancillary ligands to influence the rate of CO₂ insertion.

Table 4. Effect of the para-substituent on the rate of CO₂ insertion into (p-R-^tBuPCP)NiH.

Entry	(p-R-tBuPCP)NiH	k 1 (M–1 s–1) at RT in THF	Rate increase	σ p + a
1	5	1.6 ± 0.2	—	+0.13
2	1	6.8 ± 0.7	4	—
3	4	11.7 ± 1	7	–0.78

^aC. D. Ritchie and W. F. Sager, Prog. Phys. Org. Chem., 1964, 2, 323.

Solvent and Lewis acid effect for outersphere CO₂ insertion

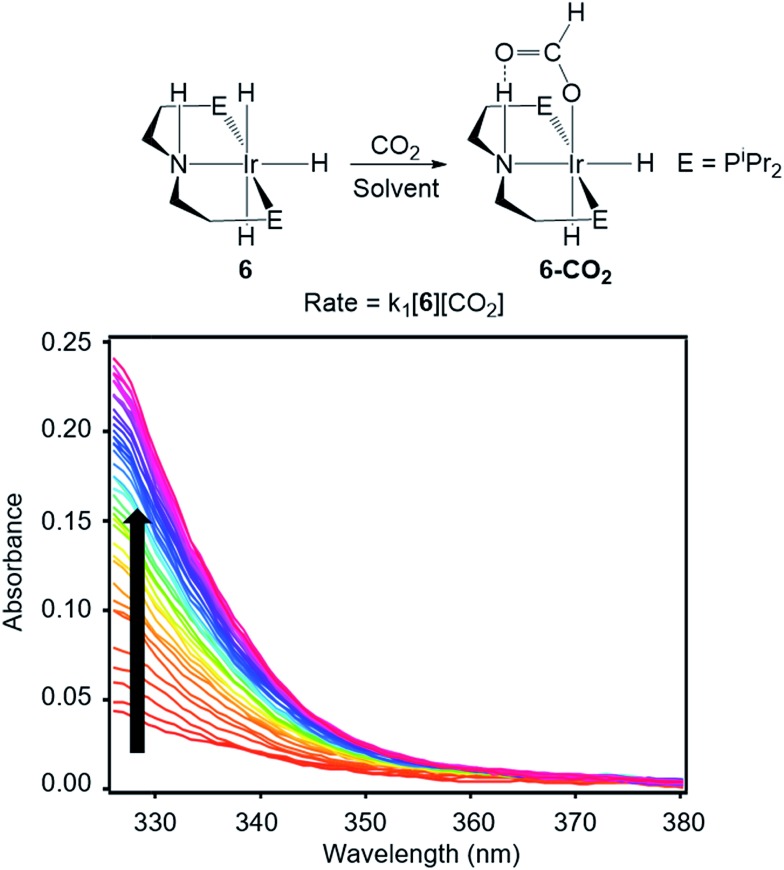
To directly compare inner- and outersphere CO₂ insertions, our initial goal was to perform the analogous solvent, LA, and ligand effect experiments with a metal hydride proposed to insert CO₂via an outersphere rate-determining TS. However, due to difficulties finding a suitable system that allowed for ligand effects to be readily probed, our studies with an outersphere system were limited to measuring a solvent and LA effect. Our model complex was the pincer-supported iridium trihydride (^iPrPN^HP)IrH₃ (^iPrPN^HP = HN{CH₂CH₂(PⁱPr₂)}₂) (6), which was synthesized using literature methods.15 Previous calculations on 6 suggest that CO₂ insertion proceeds via an outersphere rate-determining TS.2b The kinetics of CO₂ insertion into 6 to form (^iPrPN^HP)Ir(H)₂{OC(O)H} (6-CO₂) were also measured using a rapid mixing stopped-flow instrument with a UV-Vis detector (Fig. 5). The reaction was followed spectroscopically from 325 to 700 nm, and rates were measured under non pseudo-first order [CO₂] conditions to slow the reaction to observable timescales. The positive linear relationship between the measured initial rate and the concentration of CO₂ at various [CO₂] confirms that the reaction is first-order in [CO₂] (see Fig. S21 in ESI†). The elementary second-order rate constant k₁ for the insertion of CO₂ into 6 (Tables 5 and 6) was directly determined by globally fitting the data as a bimolecular reaction with rate law k₁[6][CO₂]. As with CO₂ insertion into 1, there is excellent agreement between the experimental and computational activation parameters for CO₂ insertion into 6.2b

Fig. 5. Representative stopped-flow data for CO₂ insertion into 6. Reaction conditions: [6] = 2 mM, [CO₂] = 11 mM, THF, 243 K.

Table 5. Effect of solvent on the rate of CO₂ insertion into 6.

Entry	Solvent	k 1 (M–1 s–1) at 298 K	Rate increase	Activation parameters a
1	Diethyl ether	70 ± 7	—	ΔH‡ = 6.8 (3)
				ΔS‡ = –27 (2)
				ΔG‡298 K = 14.9 (3)
2	THF	2.2 (2) × 102	3	ΔH‡ = 7.2 (3)
				ΔS‡ = –24 (1)
				ΔG‡298 K = 14.3 (3)
3	Glyme b	7.1 (7) × 102	10	ΔH‡ = 4.4 (3)
				ΔS‡ = –31 (1)
				ΔG‡298 K = 13.6 (3)
4	n-Hexane	7.6 (8) × 102	11	ΔH‡ = 3.6 (3)
				ΔS‡ = –33 (2)
				ΔG‡298 K = 13.5 (3)
5	1,4-Dioxane	9.5 (10) × 102	14	ΔH‡ = 8.2 (4)
				ΔS‡ = –18 (2)
				ΔG‡298 K = 13.4 (4)
6	Diglyme c	1.3 (1) × 103	19	ΔH‡ = 5.4 (3)
				ΔS‡ = –26 (1)
				ΔG‡298 K = 13.2 (3)
7	Benzene	2.0 (2) × 103	29	ΔH‡ = 11.1 (4)
				ΔS‡ = –6 (2)
				ΔG‡298 K = 12.9 (4)

^aΔH^‡ and ΔG^‡ in kcal mol^–1 and ΔS^‡ in cal mol^–1 K^–1.

^bGlyme = 1,2-dimethoxyethane.

^cDiglyme = diethylene glycol dimethyl ether.

Table 6. Effect of additives on the rate of CO₂ insertion into 6 in THF.

Entry	Additive	k 1 at 273 K a	Rate increase b	Activation parameters c
1	None	64 ± 6	—	ΔH‡ = 7.2 (4)
				ΔS‡ = –24 (2)
				ΔG‡298 K = 14.3 (5)
2	(nBu)4NPF6	4.0 (4) × 103	3	ΔH‡ = 6.7 (3)
				ΔS‡ = –17 (1)
				ΔG‡298 K = 11.7 (3)
3	LiOTf d	1.5 (2) × 104	9	ΔH‡ = 2.7 (3)
				ΔS‡ = –29 (1)
				ΔG‡298 K = 11.4 (4)
4	NaOTf	2.4 (2) × 104	15	ΔH‡ = 4.3 (3)
				ΔS‡ = –22 (1)
				ΔG‡298 K = 10.9 (3)
5	NaNTf2 e	3.0 (3) × 104	19	—
6	KNTf2	4.0 (4) × 104	25	—
7	LiPF6	4.9 (5) × 104	30	ΔH‡ = 1.8 (4)
				ΔS‡ = –30 (2)
				ΔG‡298 K = 10.7 (5)
8	LiNTf2	7.3 (7) × 104	46	—
9	LiBPh4·3DME f	1.2 (1) × 105	72	—
10	NaBPh4	1.3 (1) × 105	82	—
11	KB(C6F5)4	1.4 (1) × 105	88	—
12	NaBArF4	1.6 (2) × 105	100	ΔH‡ = 6.7 (3)
				ΔS‡ = –10 (1)
				ΔG‡298 K = 9.7 (3)

^aEntry 1 follows the second order rate law k₁[6][CO₂], where k₁ is in M^–1 s^–1; entries 2–12 are assumed to follow the third order rate law k₁[6][CO₂][LA], where k₁ is in M^–2 s^–1.

^bThe rate increase is based on the calculated rate of product formation (M s^–1) in the presence of 20 equivalents of LA (relative to [6]). This allows for the comparison of rates independent of overall reaction order. Due to the poor solubility of the LA, entries 9–12 were run with only 10 equivalents of LA and extrapolated to 20 equivalents. See ESI for further information.

^cΔH^‡ and ΔG^‡ in kcal mol^–1 and ΔS^‡ in cal mol^–1 K^–1.

^dOTF = trifluoromethanesulfonate.

^eNTf₂ = bis(trifluoromethane)sulfonamide.

^fLiBPh₄·3DME = lithium tetraphenylborate tris(1,2-dimethoxyethane).

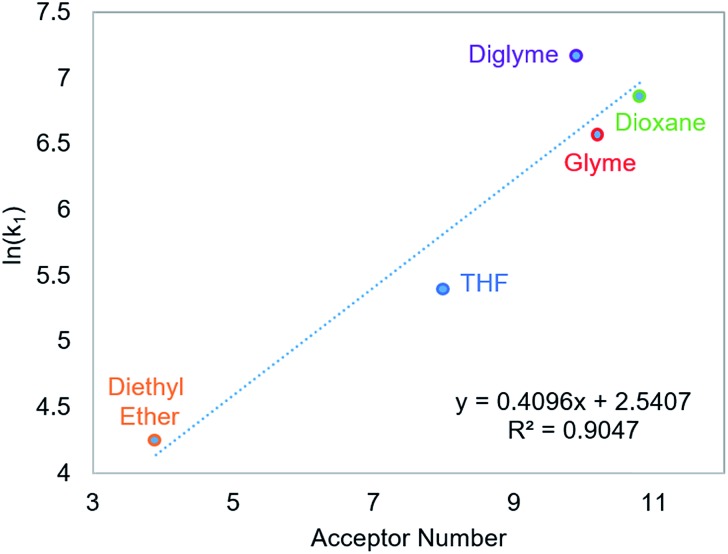
CO₂ insertion into 6 exhibits a small solvent effect on the same order of magnitude as that observed for CO₂ insertion into 1. The rate of insertion increases by a factor of 29 between diethyl ether (Table 5, entry 1) and benzene (Table 5, entry 7). Unfortunately, 6 is not stable in more polar solvents, and the rate of CO₂ insertion in these solvents, consequently, could not be measured. In contrast to the insertion of CO₂ into 1, there is no correlation between the solvent dielectric constant or AN and the rate of insertion for all seven solvents tested (see Fig. S24 and S25 in ESI†). The rate of CO₂ insertion into 6 does, however, strongly correlate with the solvent AN when the analysis is narrowed to only the five ethereal solvents used (Fig. 6). The unusual kinetics observed in n-hexane and benzene – highlighted by the lower enthalpy for n-hexane as well as the substantially higher enthalpy and less negative entropy of activation for benzene compared to the ethereal solvents – are not fully understood at the time. Regardless, our results indicate that there is not always correlation between AN and the rate of CO₂ insertion. Further work with more complexes is required to understand the generality of this relationship.

Fig. 6. Relationship between the second-order rate constant k₁ for CO₂ insertion into 6 in ethereal solvents and solvent acceptor number.11.

To probe the proposition that the presence of a LA increases the rate of an outersphere CO₂ insertion by stabilizing the incipient negative charge on the carboxylate group in the rate-determining TS (Fig. 3a),4c,d we measured the kinetics of CO₂ insertion into 6 in the presence of 10 different LAs. In contrast to the insertion of CO₂ into 1, the addition of LAs (≥10-fold excess with respect to 6) results in a substantial enhancement in the reaction rate (Table 6, entries 1 and 3–12). When the concentration of LiPF₆ was varied, a first-order dependence was observed (Fig. 7). This indicates that in the presence of LAs, there is an approximate third order rate law for CO₂ insertion k₁[6][CO₂][LA].16 Several control experiments were performed to confirm that the observed increase in rate was due to a LA effect. To explore the effect of increasing the ionic strength of the solution without adding a LA, the rate of CO₂ insertion into 6 was measured in the presence of (ⁿBu)₄NPF₆ (Table 6, entry 2). The rate of product formation for CO₂ insertion into 6 increases by only a factor of 3 in the presence of 20 equivalents of (ⁿBu)₄NPF₆ (see Table S4 in ESI†), indicating that while an increase in ionic strength may play a small role in the rate enhancement, the presence of the LA is a dominant factor. Furthermore, the activation enthalpy for CO₂ insertion in the presence of (ⁿBu)₄NPF₆ is similar to that measured with no additive, suggesting that (ⁿBu)₄NPF₆ does not change the mechanism of insertion (Table 6, entries 1 and 2). The activation enthalpy for CO₂ insertion in the presence of LiPF₆ is, however, markedly lower than that obtained with no additive (Table 6, entries 1 and 7), suggesting that the LA directly interacts with the metal complex in the rate-determining TS.17 Significant changes in the activation enthalpies were also observed with other LAs.

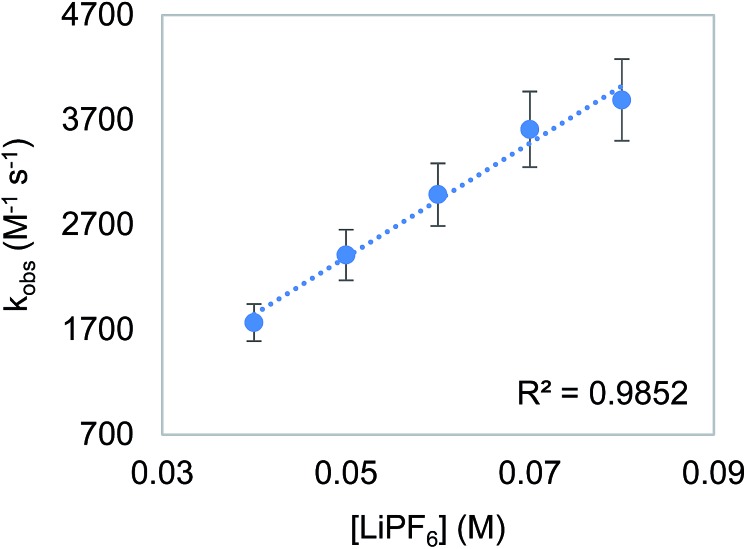
Fig. 7. Plot of observed rate constant (k_obs) versus [LiPF₆] for the insertion of CO₂ into 6. Reaction conditions: [6] = 2 mM, [CO₂] = 6.6 mM, [LiPF₆] = 40–80 mM, THF, 273 K.

Of the ten LAs tested, KB(C₆F₅)₄ and NaBArF₄ gave the most significant rate enhancements. In fact, extrapolation of our data suggests that with just 20 equivalents of NaBArF₄, a 100-fold rate enhancement would be obtained. Furthermore, given the first order dependence on [LA], this enhancement could in principle be increased even more dramatically by further increasing [LA]. Our data indicate that there is significant variation in the observed rate enhancements within a series of anions with the same cation (e.g. NaOTf, NaNTf₂, NaBPh₄, and NaBArF₄). We suggest that this is related to differences in ion-pairing, i.e. NaBArF₄ is more dissociated than NaOTf in THF, resulting in an increased effective concentration of Na⁺,18 as opposed to the anion having an explicit role in the reaction. Ion-pairing effects also potentially complicate direct comparison between cations. For example, the smaller rate enhancement seen with LiOTf as compared to NaOTf may be interpreted as LiOTf being less dissociated in THF rather than Na⁺ more effectively stabilizing a transition state than Li⁺. The results with LAs presented here are the first quantitative demonstration that these additives can directly increase the rate of CO₂ insertion into transition metal hydrides.

Conclusions

In this work, we have used stopped-flow kinetics to systematically probe both inner- and outersphere CO₂ insertion reactions. For the innersphere system, we have demonstrated that the rate of CO₂ insertion can be significantly changed by modifying the ancillary ligand. Both decreasing the steric congestion around the M–H bond and/or increasing the electron density on the metal center by, for example, incorporating an electron-donating substituent result in faster rates of CO₂ insertion. Additionally, both inner- and outersphere reactions show similar solvent effects that are loosely correlated with the solvent acceptor number, although the generality of this observation is not clear. Lastly, we have quantitatively shown that the rate of CO₂ insertion into 1 and 2, which are proposed to proceed via an innersphere pathway, does not increase in the presence of a LA, whereas the rate of CO₂ insertion into 6, proposed to proceed via an outersphere pathway, increases significantly in the presence of a LA. Although the effects of LAs on insertion into metal-element σ-bonds are well understood for substrates such as CO,19 they remain relatively unexplored for CO₂. While the effect of LAs on CO₂ insertion into metal–alkyl bonds has been studied,7a–c the work presented here is the first quantification of these effects for CO₂ insertion into metal hydrides. The effects and observations outlined here are rationalized by the proposed charge separation in the rate-determining TS in an inner- vs. outersphere insertion. The presence of a LA is expected to provide stabilization for the zwitterionic rate-determining TS in an outersphere CO₂ insertion, resulting in a rate increase. As this TS is not rate-determining in an innersphere insertion, the stabilization provided by the LA does not affect the rate of the reaction. In future work, we will utilize the experimental procedures we have developed here to establish whether these trends relating to LA and solvent effects are general to other metal hydrides that insert CO_2. We will also explore how these variables affect the insertion of CO₂ into other metal-element σ-bonds, such as M–OH, M–NH₂, and M–CH₃ bonds. It is expected that our current and future results will provide insight into how to optimize catalytic reactions involving CO₂ insertion into a metal-element σ-bonds or the microscopic reverse decarboxylation reaction as elementary steps.

Additional information

Full compound characterization, experimental procedures, and kinetics data are available via the Internet.

Conflicts of interest

The authors declare no competing financial interests.