Theoretical perspectives on active sensing

Abstract

A key component of interacting with the world is how to direct ones’ sensors so as to extract task-relevant information – a process referred to as active sensing. In this review, we present a framework for active sensing that forms a closed loop between an ideal observer, that extracts task-relevant information from a sequence of observations, and an ideal planner which specifies the actions that lead to the most informative observations. We discuss active sensing as an approximation to exploration in the wider framework of reinforcement learning, and conversely, discuss several sensory, perceptual, and motor processes as approximations to active sensing. Based on this framework, we introduce a taxonomy of sensing strategies, identify hallmarks of active sensing, and discuss recent advances in formalizing and quantifying active sensing.

Introduction

Skilled performance requires the efficient gathering and processing of sensory information relevant to the given task. The quality of sensory information depends on our actions, because what we see, hear and touch is influenced by our movements. For example, the motor system controls the eyes’ sensory stream by orienting the fovea to points of interest within the visual scene. Movements can therefore be used to efficiently gather information, a process termed active sensing. Active sensing involves two main processes: perception, by which we process sensory information and make inferences about the world, and action, by which we choose how to sample the world to obtain useful sensory information.

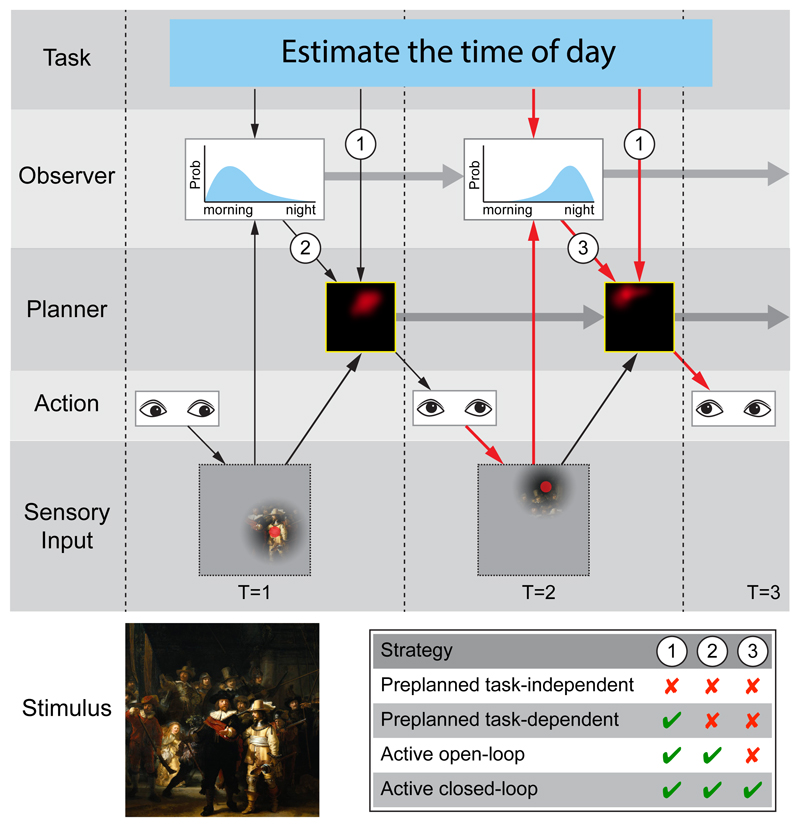
To illustrate the computational components of active sensing, we consider the task of trying to determine the time of day from a visual scene (Fig. 1). Because of the limited resolution of vision away from the fovea, sensory information at any point in time is determined by the fixation location (Fig. 1, red dot, Sensory Input). The perceptual process can be formalized in terms of an ideal observer model [1, 2] which makes task-relevant inferences. To do so, the observer uses the sensory input together with a knowledge of the properties of the task (Fig. 1, Task) and the world, as well as features of our sensors, such as the acuity falloff in peripheral vision [3, 4] and processing limitations, such as limited visual memory [5, 6]. Such observers are typically formulated within the Bayesian framework. For example, the observer could use luminance information to estimate the time of the day, in this case formalized as a posterior probability distribution (Fig. 1, Observer).

Figure 1. Active sensing framework and taxonomy.

An example of the temporal evolution of an active sensing strategy in which the task is to the estimate the time of day from an image (Stimulus: in this case the The Night Watch by Rembrandt). The gaze direction of the eye (Action) determines the fixation location (red dot in Sensory Input), and the Sensory Input is then limited by the typical fall-off of acuity with eccentricity (illustrated in Sensory Input). Given the Task and the Sensory Input, the Observer computes a probability distribution over the time of day. In this case the bright area fixated may suggest morning. Given the Task and the Observer’s inference, the Planner determines the expected value of moving the eyes to fixate different locations in the image (red intensity indicates value in the Planner). For example, the value could be the expected reduction in entropy in the Observer’s inference distribution. The eyes can then be moved to a location with high or maximum value (such as examining the sky). This leads to new Sensory Input which updates the Observer’s inference (to correctly suggest night). The larger gray arrows that link the Observer’s inference and the Planner’s action-objective map across time indicates that all the information from previous time steps are passed onto the current observer and planner. The red arrows in the figure highlights the components involved in a single loop of an active closed-loop strategy. The removal of specific sets of interactions (1, 2 & 3) leads to different sensing strategies (Table inset).

The process of selecting an action can be formalized as an ideal planner which uses both the observer’s inferences and knowledge of the task to determine the next movement, in this case where to orient the eyes (Fig. 1, Planner). Ultimately, the objective for the ideal planner is to improve task performance, but often it can be formalized as reducing uncertainty in task-relevant variables, such as the entropy of the distribution over the time of day. The plan is then executed, resulting in an action that leads to new sensory input (Fig. 1, Action). This closes the loop of perception and action that defines active sensing (Fig. 1, red arrow path). Although we describe these processes in discrete steps with a static stimulus and fixed task, in general, active sensing can be considered in real time with the stimulus and task changing continuously.

Active sensing as a form of exploration

As observer models have been extensively studied and reviewed [1, 2], we primarily focus here on the ideal planner which is the other key process in active sensing. In general, truly optimal planning is computationally intractable and we, therefore, need to consider approximations and heuristics. In fact, active sensing itself can be seen as emerging from such an approximation (see Box 1: Exploration, exploitation, and the value of information). The ultimate objective of behavior can be formalized as maximizing the total rewards that can be obtained in the long term [7]. This, in principle, requires considering the consequences of future actions, not only in terms of the rewards to which they lead, but also in terms of how they contribute to additional knowledge about the environment, which can be beneficial when planning actions in the more distant future. For example, when foraging for food, animals should choose actions that not only take them closer to known food sources but also yield information about potential new sources [8]. As this recursion is radically intractable, the most common approximation is to distinguish between actions that exploit current knowledge and seek to maximize future rewards, and actions that instead explore to improve knowledge of the environment [9].

Box 1. Exploration, exploitation, and the value of information.

The ideal observer performs inference, using Bayes’ rule, about several variables characterizing the state of the environment simultaneously, x (e.g. what objects are present in the scene, their configuration, features, etc.), given the sensory inputs up to the current moment, z_0:t, and an internal model of the environment and its sensory apparatus, M:

$$\mathbb{P}(\mathbf{\text{x}}|z_{0:t},\text{M})\propto \mathbb{P}(z_{0:t}|\mathbf{\text{x}},\text{M})\mathbb{P}(\mathbf{\text{x}}|\text{M})$$ (1)

A task defines a reward function over actions, a, that depends on the true state of the environment, $𝓡(a,\mathbf{x})$. There are two aspects of the reward function that make it task-dependent. First, it typically depends only on a subset of state variables, x_T (e.g. defining whether it is the time of day, or the age of the people in the picture of Fig. 1 that you want to estimate), and second, it has a particular functional form (e.g. determining how much under- or overestimating the time of day matters).

In general, an agent navigating the environment cannot use the reward function directly to select actions for two reasons. First, it does not directly observe the true state of the environment, so it must base its decisions on its beliefs about it as given by the ideal observer (Eq. 1). Second, its objective is to maximize total reward in the long run, and so the consequences of its actions in terms of how they change environmental states (or, more precisely, the agent’s beliefs about them) must also be taken into account. Thus, we can write the value of an action, $𝒬$, as the sum of its immediate and future values, each depending on the agent’s current beliefs:

$$\mathcal{Q}(a,\mathbb{P}(\mathbf{\text{x}}|z_{0:t},\text{M}))={\mathcal{Q}}_{\text{now}}(a,\mathbb{P}(\mathbf{\text{x}}|z_{0:t},\text{M}))+{\mathcal{Q}}_{\text{future}}(a,\mathbb{P}(\mathbf{\text{x}}|z_{0:t},\text{M}))$$ (2)

This equation is the well-known Bellman optimality equation [76] but, rather than expressing values directly for the states of the environment x, as typically done, here it is applied to the belief “states” of the agent, ℙ(x|z_0:t, M), i.e. the beliefs it holds about those states [77].

The immediate value ${𝒬}_{\text{now}}(a,\mathbb{P}({\mathbf{x}\text{|z}}_{0:t},\text{M}\left)\right)$ can be computed as the reward expected under the current posterior distribution provided by the ideal observer (“expected” gain in Bayesian decision theory [78]):

$${\mathcal{Q}}_{\text{now}}(a)={\displaystyle \sum _{\mathbf{\text{x}}}ℛ(a,\mathbf{\text{x}})\mathbb{P}(\mathbf{\text{x}}|z_{0:t},\text{M})}$$ (3)

The future value ${𝒬}_{\text{future}}(a,\mathbb{P}({\mathbf{x}\text{|z}}_{0:t},\text{M}\left)\right)$ has a more complicated form that is generally computationally intractable, but can be shown to depend on two factors: 1. the way the action leads to future rewards by steering the agent into future environmental states, and 2. the way it leads to new observations based on which the ideal observer can update its beliefs so that its uncertainty decreases, allowing better informed decisions and therefore higher rewards in the future. These two factors are commonly referred to as “exploitation” and “exploration”, respectively, and are often treated separately due to the intractability of ${𝒬}_{\text{future}}(a,\mathbb{P}({\mathbf{x}\text{|z}}_{0:t},\text{M}\left)\right)$, but as we see from Eq. 2 they both factor into the same greater objective of maximizing value (i.e. “exploitation”) in terms of belief states. Importantly, evaluating both factors requires recursion into the future so they are each intractable even when treated separately.

Just as exploitation can be optimized to yield maximal rewards, so can exploration be optimized to yield maximal information about the environment. Exploration, thus optimized, is known as “active learning” [10, 11, 12]. In general, a huge variety of actions can be used for active learning, from turning your head towards a sound source to opening your browser to check on the meaning of an unknown phrase (such as ‘epistemic disclosure’ [13]). Indeed, the way participants choose queries in categorization tasks [14, 15], locate a region of interest in a variant of the game of battleship [16], or choose questions in a 20-questions-like situation [17] has been shown to be optimized for learning about task-relevant information. Active sensing, more specifically, can be regarded as the realm of active learning which involves actions that direct your sensors to gain information about quantities that change on relatively fast time scales roughly corresponding to the time scale of single trials in laboratory-based tasks (see Box 2: Information maximization).

Box 2. Information maximization.

A useful proxy for the explorational value of an action, a (see Box 1), is the information that one expects to gain about environmental state, x, by taking that action. The (Shannon) information exactly expresses the expected reduction in uncertainty about x:

$$ℐ(\mathbf{\text{x}},z_{t+1}|a)=\mathscr{H}(\mathbf{\text{x}}|z_{0:t},\text{M})-{\langle {\langle \mathscr{H}(\mathbf{\text{x}}|z_{0:t+1},\text{M})\rangle }_{\mathbb{P}(z_{t+1}|a,\mathbf{\text{x}},\text{M})}\rangle }_{\mathbb{P}(\mathbf{\text{x}}|z_{0:t},\text{M})}$$ (4)

where 〈·〉 denotes an average according to the specific distribution given by the subscript, and

$$\mathscr{H}(\mathbf{\text{x}})=-{\langle \text{log}\mathbb{P}(\mathbf{\text{x}})\rangle }_{\mathbb{P}(\mathbf{\text{x}})}=-{\displaystyle \sum _{\mathbf{\text{x}}}\mathbb{P}(\mathbf{\text{x}})\text{log}\mathbb{P}(\mathbf{\text{x}})}$$ (5)

is the entropy of ℙ(x) quantifying uncertainty about x. The first term of Eq. 4 expresses the uncertainty about the state of the environment, x, under the current posterior, ℙ(x|z_0:t, M), while the second term expresses the average expected uncertainty for an updated posterior, ℙ(x|z_0:t+1, M), once we make a new observation, z_t+1, upon executing action a. The information we gain by this action is thus the reduction of uncertainty as we go from the current posterior to a fictitious new posterior, and an information maximizing ideal planner simply chooses the action a which maximizes this information:

$$a_{t+1}=\underset{a}{\text{argmax}}ℐ(\mathbf{\text{x}},z_{t+1}|a)$$ (6)

There are two ways in which Eq. 4 is merely an approximation to explorational value. First, it only considers the next action without performing the full recursion for future belief states and actions (hence is “greedy” or “myopic”). Second, explorational value typically depends on a task-specific reward function (because it is derived from Eq. 2) and thus it might favor gathering information about particular aspects (dimensions or regions) of x to which the reward function is particularly sensitive, while Eq. 4 treats all aspects of x equal and is thus agnostic as to the reward function. Nevertheless, when the reward function only depends on a subset of the variables in x, x_T (Box 1), as it usually does in most everyday and laboratory tasks, this aspect of the reward function can be taken into account by simply computing entropies over x_T rather than the full x. In this case, the resulting active sensing strategy is still task-dependent. However, when even this aspect of the current task is ignored, and so information is computed for a predetermined set of variables, or the average information for different sets of variables (corresponding to different potential tasks) is computed, the strategy becomes task-independent. This kind of task-independent strategy can also be thought of as curiosity-driven. When the posterior is updated based on observations one expects a priori, rather than on actual observations, the strategy becomes preplanned. (See Figure 1 for the different strategies.)

Even in its approximate form, Eq. 4 is computationally prohibitive. This is because for each action, a, it requires computing (the entropy of) an updated posterior, ℋ(x|z_0:t+1, M), for all possible fictitious observations, z_t+1, for each state of the world, x, that is thought possible according to the current posterior, ℙ(x|z_0:t, M). Fortunately, using the property that Shannon information is symmetric, it can be shown that Eq. 4 can be rewritten in a different, though mathematically equivalent form (for full derivation, see Ref. 71), which does not require fictitious posterior updates:

$$ℐ(\mathbf{\text{x}},z_{t+1}|a)=\mathscr{H}(z_{t+1}|a,z_{0:t},\text{M})-{\langle \mathscr{H}(z_{t+1}|a,\mathbf{\text{x}})\rangle }_{\mathbb{P}(\mathbf{\text{x}}|z_{0:t},\text{M})}$$ (7)

The terms in this form also have intuitive meaning: the first term formalizes the planner’s total uncertainty about what the next observation, z_t+1, might be, including uncertainty due to the fact that we are also uncertain about the state of the environment, x, whereas the second term expresses the average uncertainty we would have about z_t+1 if we knew what x was. In other words, the informational value is high for actions for which the main source of uncertainty about their consequent observation is the uncertainty about x (ie. their uncertainty is potentially reducible) and not because these observations are just more inherently noisy (which implies irreducible uncertainty). In contrast, an alternative approach, called maximum entropy, would only care about total uncertainty, ℋ(z_t+1|a, z_0:t, M), and therefore ignores this distinction between reducible and irreducible uncertainty.

Common approximations in active sensing strategies

Task-related active sensing, our main focus here, makes the further approximation of breaking up “life” into discrete, known tasks. In contrast, curiosity-driven forms of information seeking [13, 18, 19] may be understood as optimized for improving an internal model for whatever task may come our way. While laboratory tasks for studying task-related active sensing are usually designed to minimize the trade off between exploration and exploitation, such that rewards only depend on task-relevant information [3, 20], curiosity-driven information seeking is often demonstrated in tasks that do have an information-independent reward structure, such that participants can be shown to actively forego these rewards for additional information [21].

Even exploration or exploitation by themselves are still intractable due to the exponential explosion of future possibilities that need to be considered. For example, maximal exploitation in the game of chess would require considering a very large number of future sequences of movement to maximize task success. Therefore, several simpler heuristics have been proposed to describe behavior. The simplest heuristic considers only the consequence of the next action, and hence is termed greedy or myopic. Thus, in the context of exploration, ideal planners are typically formalized in a way that they seek the single action that will maximize information gain or an equivalent objective (See Box 2), without considering the possibility that an action leading to suboptimal immediate information gain may allow other actions later with which total information gain would eventually become larger [3, 22, 20]. Interestingly, the strategy of greedily seeking task-relevant information has been successful in describing both human eye movements [22, 20] and the foraging trajectories of moths [23] and worms [24]. However, for some tasks it has been shown that several future actions [25, 26] are considered when planning and that there can be a trade-off between the depth of planning and the number of plans considered when there are time constraints on planning [27].

Taxonomy of efficient sensing strategies

Active sensing can also be considered as part of a spectrum of strategies that organisms have developed to improve the efficiency of their sensory processing. Within this context we can consider restricted versions of the full active sensing strategy based on the extent to which the observer and planner form a full closed loop (Fig. 1, table). If the dependence on the observer is removed for all but the initial sensory input, the strategy becomes open-loop because all future actions are planned at the first time step and not updated. Examples of this sensing strategy include face recognition [28] and texture identification [29], in which the first observation is used to identify and prioritize regions of interest, and subsequent saccades follow the planned sequence without needing to update the plan.

If observer dependence is completely removed, the sensing strategy becomes entirely preplanned. Note that this may still allow the planner to depend on the sensory input, e.g. through the bottom-up salience of different visual features [30, 31]. A preplanned strategy can be task-dependent or independent. An example of the former is the method developed for a ship to search for a submerged submarine in which a logarithmic spiral search was shown to be optimal and successfully employed [32]. An example of a task-independent preplanned strategy is a Lévy flight that mimics certain summary statistics of human eye movement under many different scenarios [33]. In a Bayesian framework, an optimal preplanned task-independent strategy could be obtained by averaging over a prior probability distribution that specifies which tasks are more probable than others (as well as the relative importance of the tasks).

Active and preplanned strategies are not mutually exclusive in that actual patterns of sensor movements seem to be influenced by some mixture of them. For example, eye movements have been found to be best predicted by a combination of several bottom-up (such as saliency) and top-down (such as reward) factors [34, 35, 36] where the contribution of these different factors can depend on the timing requirement of the task and the time course and type of eye movement [37, 38, 39, 40, 41].

Generalized efficient sensing

We can use the same taxonomy we have developed to consider active sensing beyond simply generating actions to move our sensory apparatus. This allows us to consider the more general problem of allocating our limited perceptual processing resources and, thereby, place apparently disparate aspects of sensory and perceptual processing within our unifying framework.

The design principles underlying the organization of many sensory systems both at the morphological and the neural level have often been argued to be optimized for efficient information gathering. For example, predators that need accurate depth vision for catching their prey often have forward-looking eyes and vertical pupils, while preys that need to be able to avoid predators from as wide a range of directions as possible often have laterally placed eyes with horizontal pupils [42]. Moreover, our sensors are distributed so as to increase resolution at strategic regions (e.g. fingertips and foveas). At the neural level, classical forms of efficient coding include the optimization of receptor and sensory neuron tuning curves and receptive fields based on the statistics of inputs (“natural stimulus statistics”) [43]. Although these preplanned strategies are arguably optimized over an evolutionary time scale according to the tasks that animals have to achieve, we can think of these as corresponding to a task-independent strategy as they do not depend on the particular task the animal is pursuing at any one moment.

There are also aspects of perceptual processing that can be considered task-independent preplanned strategies that nevertheless depend on the stimulus. At the perceptual level, bottom-up saliency may indicate how much an image feature is informationally optimal “on average” and may thus serve as a proxy for the “real” information value that would be determined by top-down (task-dependent) processes [44]. At the sensory level, stimulus statistics can vary both spatially and temporally, and efficient coding has been successfully applied to account for the spatio-temporal context-dependence of receptive field properties [45]. Moreover, there exists mechanisms for the early filtering of sensory information to remove its predictable components based on the current action (for example, [46, 47]), presumably to save resources for processing unpredictable sensory inputs which thus have higher information content. While these processes are still task-independent, their stimulus-dependence increases information efficiency and, in that regard, takes them closer to fully task-dependent active sensing.

Finally, attention can dynamically change receptive fields and the allocation of perceptual processing resources in a task-dependent manner, thus corresponding to a task-dependent strategy. One example of how the brain filters out task-irrelevant information in purely perceptual tasks is the phenomenon of inattentional blindness, in which people fail to notice prominent stimuli in the visual scene that are irrelevant to the task that they are performing [48]. Similarly, in motor tasks, subjects are often only aware of large sensory input changes that have a bearing on the task at the precise time of the change, and are unaware of such changes otherwise [49]. Rather than just filtering out irrelevant information, the perceptual system can also adapt more finely in a task-dependent manner how it distributes resources to processing stimuli. In an object localization task, while fixation locations did not seem to be adaptively chosen, participants’ functional field of view doubled through learning [50]. Thus, participants still seem to have adopted an active sensing strategy in this more general sense, but one which did not include changing the ways in which they overtly moved their sensors (eyes). In contrast, in a face identification task allowing a single fixation, improvement was brought about by a mixture of overt (eye movement, 43%) and covert (improved processing, 57%) active sensing strategies [51]. Attention can also be updated moment-by-moment depending on sensory evidence. For example, subjects can solve a visual maze while fixating and presumably using attention to search for the exit [52]. Such continuous updating of attention is equivalent to a form of closed-loop active sensing.

Optimal stopping as active sensing

A particularly interesting aspect of active sensing, that is often treated formally but separately from other aspects, is the “optimal stopping problem” in sequential sampling. This problem involves choosing the duration (rather than the location) of sensory sampling, which is relevant as directing sensors to the same place longer usually yields more information. There is a trade-off however, as longer sampling of the same place usually entails an opportunity cost, losing out on other, potentially more informative locations, or more rewarding actions altogether. This is sometimes explicitly enforced in a task by time constraints on a final decision. While in higher level cognitive domains, “stopping decisions” are typically suboptimal (e.g. solving the “secretary problem” [53]), perceptual stopping has been shown to be near optimal in a task that was specifically designed to provide a slow accumulation of information [54]. Perceptual stopping also forms the basis of one of the key windows into infant cognition, where a standard experimental design measures looking times for different stimuli [55, 56]. Interestingly, information is rarely quantified explicitly in these experiments, and when there has been an effort made to quantify it, total entropy rather than information has been used with mixed results [57]. This may be because in active sensing, maximising total entropy rather than information (Box 2) can be greatly suboptimal in information efficiency, as has been shown in the context of object categorisation [20]. In visual search, the duration and location of fixations has been studied in an integrated framework, using a control-theoretic approach, in which the objective function included costs on time and effort, such that there was a trade-off between the information that increases with the fixation duration and the cost of the prolongation of the task time [58].

Hallmarks of active sensing

We can use the taxonomy developed above to define the hallmarks of active sensing. A necessary, but not sufficient, condition to determine whether sensing is active is that the actions should be task-dependent. Yarbus, in his pioneering work in vision, showed that even when viewing the same image, humans employed distinctively different eye movements when required to make different inferences about the image [59]. Recent studies confirmed such task dependence by showing that it was possible to predict the task simply from the recording of an individual’s eye movements in the Yarbus setting [60, 61], or the target they were looking for in a search task [62], or the moment-by-moment goal they were trying to achieve in a game setting [63].

Another requirement for active sensing is that different sensor and actuator properties should lead to different planning behaviors for a given task. Sensor dependence of eye movements has been demonstrated by showing that in conditions in which foveal vision is impaired (such as at low light levels, or with an artificially induced scotoma) the pattern of eye movements adapts such that it becomes fundamentally different from that in normal vision [64, 65] and near-optimal under the changed conditions [65]. Similarly, for motor dependence, patients with a cerebellar movement disorder were shown to employe eye movements that were consistent with an optimal strategy based on a higher motor cost compared to normal [66]. Indeed, several studies have suggested that motor costs may affect the active sensing strategy if participants trade-off informativeness for movement effort [58, 6].

A more stringent condition for evidence of active sensing is that actions should depend both on the task and the observations already made in the task. In their seminal work, Najemnik and Geisler [3] formalized such an active sensing strategy for a visual search task and demonstrated that several features of human eye movements are consistent with the model’s behavior, including inhibition of return, the tendency not to return to a recently fixated region. More direct evidence comes from studies that quantify the informativeness of potential fixation locations and show that humans choose locations with high information value. For example, recent studies have shown that humans can direct their eyes to locations that are judged informative [67, 20] and that they make faster eye movements to such locations [68, 69].

Formalizing and quantifying active sensing

Establishing conclusive evidence for active sensing ultimately requires constructing explicit models of what a theoretically optimal active sensor would do under the same conditions that are used to test experimental participants, and having quantifiable measures of the degree of match between the model and participants’ behavior. Visual search has become a major paradigm in the study of active sensing as it typically allows a straightforward observer model which simply represents the posterior probability of the target over the potential locations. The planner then selects the fixation location that leads to the greatest probability of correctly identifying the target location – which may not be the one closest to the predicted target location [3, 70]. The use of visual search tasks is also attractive as their analysis is amenable to using simple measures of performance such as the number of eye movements to find the target [3].

However, more complex, naturalistic tasks such as categorization and object recognition, do not map directly onto visual search and require more sophisticated models. In such cases, a direct generalisation of the information maximisation objective is prohibitive, because it requires the planner to run “mental simulations” for all possible outcomes of all putative actions, and in each case compute the corresponding update to the posterior over a potentially high-dimensional and complex hypothesis space, and finally compute the entropy of each posterior. For example, when planning the next saccade, the informativeness of several putative fixation locations needs to be compared. As we don’t yet know what we will see at those locations, a range of possible visual inputs need to be considered for each, and for each of these inputs the resulting posterior needs to be computed. Fortunately, it can be shown that information can be computed in a simpler (though mathematically equivalent) form that does not require simulated updates of the posterior (See Box 2), and only needs to compute entropy in the space of observations (e.g. the colour of an object seen at the fovea), which is typically much lower dimensional than the space of hypotheses (all possible object classes) [71, 20]. This not only makes modelling the information maximizing active sensor practical, but may also offer a more plausible algorithmic view on how the brain implements the active sensor. Such an approach has been successfully applied to a visual categorization task using an observer that combined information from multiple fixations to maintain a posterior over possible categories of a stimulus and a planner that selected the most informative location given that posterior [20].

Several other model objectives that the active planner is trying to optimise have also been proposed. For example, the visual search task of Najemnik and Geisler [3] used the objective of maximizing probability gain (or task performance) and in a binary categorization task in which participants could reveal one of two possible features, this objective was also better at describing their behavior than information gain [72]. Moreover, in a task in which subjects were required to perform ternary categorization, their queries were best described by a max-margin objective, where each query was optimized to resolve uncertainty between two categories at a time rather than all three simultaneously [73]. Furthermore, action objectives have been shown to adapt to task demands, with simple hypothesis-testing performed under time pressure and information maximization when temporal demands were relaxed [74]. These studies leave open the possibility that the objectives underlying different modalities of active sensing (such as eye movement or cognitive choices) may be fundamentally different (maximizing information or performance directly).

Measuring performance in naturalistic tasks also presents challenges. Classical measures of eye movements typically rely on the geometric features of performance (scan paths, direction, number of fixations to target) [3, 22]. More recently, ideal observers have not only been used to model the task but also to obtain a fixation-by-fixation measure of performance. For example, for an information maximizing active sensor, the ideal observer model could be used to quantify the amount of information accumulated about image category with each fixation within a trial [20]. This information-based measure of performance was more robust than directly measuring distances between optimal and actual scan paths because multiple locations are often (nearly) equally informative when planning the next saccade. This means that fixation locations that are far away from the optimal fixation location, and would therefore be deemed highly suboptimal by geometric measures, can nevertheless be close to optimal in terms of information content. For example, examining the sky or the ground for cast shadows could be almost equally informative as to the time of day in the picture shown in Fig. 1, yet, these regions of the image are far away. Thus, looking at the ground may appear geometrically very suboptimal, while informationally it is near-optimal. When such information-based measures were used, the efficiency in the planning of each eye movement was shown to be around 70% [20].

Conclusion

The use of the ideal observer-planner framework has allowed both qualitative and quantitative description of human sensing behaviors and thus offers insights into the computational principles behind actions and sensing. The next big challenge is to construct a flexible representation that connects sensory inputs to large classes of high-level natural tasks, such as estimating the wealthiness, age or intent of a person [59], and feed this construction into an ideal observer-planner model. Although constructing such algorithms is far from trivial, as Bayesian inference algorithms using structured probabilistic representations become increasingly sophisticated and powerful in matching human-level cognition [75], their integration into the active sensing framework will provide practical solutions for modeling such tasks. This advance will not only allow comparison with experiments on more natural tasks for a richer understanding of the active sensing process, but will also be a step towards applying such theories to improve learning in real-world situations.