Alkali Cation Effects on Redox-Active Formazanate Ligands in Iron Chemistry

Abstract

Non-covalent interactions of organic moieties with Lewis acidic alkali cations can greatly affect structure and reactivity. Herein, we describe the effects of interactions with alkali metal cations within a series of reduced iron complexes bearing a redox-active formazanate ligand, in terms of structures, magnetism, spectroscopy, and reaction rates. In the absence of a crown ether to sequester the alkali cation, dimeric complexes are isolated wherein the formazanate has rearranged to form a five-membered metallacycle. The dissociation of these dimers is dependent on the binding mode and size of the alkali cation. In the dimers, the formazanate ligands are radical dianions, as shown by X-ray absorption spectroscopy, Mössbauer spectroscopy, and analysis of metrical parameters. These experimental measures are complemented by DFT calculations that show the spin density on the bridging ligands.

Synopsis

Cation-π interactions in reduced iron complexes bearing formazanate radical dianions induce a ligand rearrangement that results in the formation of dimeric complexes. The nature of the alkali cation affects both the structure and reactivity of the dimers.

Introduction

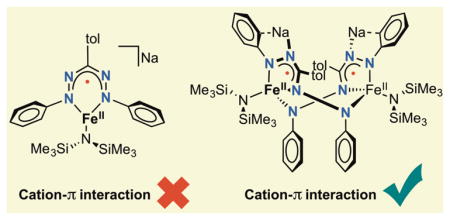
Alkali metal cations play essential roles in both biological chemistry¹ and synthetic chemistry² where they stabilize complex structures or act as cofactors in (bio)catalytic transformations. Detailed studies have shown that non-covalent interactions of organic moieties with redox-inactive metal cations can result in changes in electronic structure that affect geometry,³ redox potentials,⁴ N₂ cleavage⁵, reaction rates⁶ and selectivity of chemical transformations.⁷ The nature of the interaction with s-block cations is greatly influenced by their charge (z) : size (r) ratio. Cations with a high z/r ratio have the capacity for bond polarization, inducing bond covalency.⁸ When descending the s-block metal groups, the radii of the metals significantly increase,⁹ resulting in predominantly ionic bonding and an increased tendency for ion dissociation. Noncovalent interactions in the form of cation-π contacts are weaker than covalent interactions but can play a significant role in metal cation association. The electrostatic nature of cation-π contacts causes the strength of this interaction to rise with increasing z/r ratio.⁸ Typically, these interactions are observed when the distance is below the sum of the van der Waals radii of the independent elements.¹⁰ In the absence of neutral co-ligands such as THF, Et₂O or HMPA, aggregates can form resulting in low solubility or concentration dependent solution speciation. Multidentate ligands such as DME, TMEDA and crown ethers can sequester/stabilize the cation, thereby preventing aggregate formation, and at times drastically affect reactivity.¹¹ The right cation and crown ether or cryptand combination can give rise to fully separated ion pairs, which is often used to facilitate crystallization. However, allowing cation-π interactions to persist could be a useful strategy to tune the electronic structure and corresponding reactivity of transition metal complexes.

In many examples where alkali metal cations are involved in homogeneous catalysis and activating strong chemical bonds, the alkali metal cations result from using the corresponding zerovalent alkali and alkaline earth metals for reductive activation of pre-catalysts.¹² In addition to classical metal-centered reduction, electrons can be stored in redox-active ligands. These ligands have been shown to facilitate multi-electron processes in systems where the transition metal changes oxidation states by less than two electrons,¹³ and enable the formation of substrate-centered radicals.¹⁴ Given the increasing popularity of redox-active ligands¹⁵ that is demonstrated in this Forum, it is important to consider whether the reducing electron from the alkali metal goes into a metal- or ligand-centered orbital. Since redox-active ligands often contain extended π-systems and/or multiple heteroatoms that are potentially capable of Coulomb interactions with alkali cations, it is evident that cation-π interactions must be considered when evaluating redox-active ligands, especially in reductive reactions. Indeed, cation-π interactions have been observed for well recognized redox-active ligands, including catecholates,¹⁶ amidophenolates,¹⁷ o-phenylenediamides,¹⁸ salophens,¹⁹ dithiolenes²⁰ and bis(imino)pyridines.²¹ Despite this link, there have been few systematic studies into the interplay of cation-π interactions and redox-active ligands. A recent example that demonstrates the effect that different alkali cations can have was reported by Mazzanti and coworkers, who showed that one-electron reduction of a (salophen)cobalt(II) complex results in either metal or ligand-centered reduction, depending on the identity of the alkali metal.²²

As part of our interest in redox-active ligands and low-coordinate iron chemistry, we recently reported that Fe[N(SiMe₃)₂]₂²³ gives access to low-coordinate iron formazanate complexes that undergo ligand-centered reduction at the formazanate ligand (Scheme 1).²⁴ Formazanates have been established as good one-electron acceptors, particularly from the work of Otten and coworkers, who demonstrated ligand-centered reduction in various formazanates bound to redox-inert boron²⁵ or zinc.²⁶ Interestingly, a recently reported homoleptic formazanate iron(II) complex adopted a low spin iron(I) configuration upon one-electron reduction rather than generating a ligand-centered radical.²⁷ We found that one-electron reduction of complex 1 gives a complex with a formazanate radical dianion (S = ¹/₂) that is strongly antiferromagnetically coupled to a high-spin iron(II) (S = 2) to give an overall S = ³/₂ electronic configuration. When Na was used as the reductant in the presence of two equivalents of 12-crown-4, a mononuclear anionic iron complex 2 with a sequestered sodium cation was obtained. Herein, we report that one-electron reduction of 1 with alkali metals in the absence of a crown ether forms dimeric complexes in which alkali cation binding is connected to an isomerization of the formazanate into an unprecedented bridging mode, which changes the electron localization. Importantly, we show that the choice of alkali metal cation has a substantial effect on the structure and reactivity of these dimeric complexes.

Scheme 1.

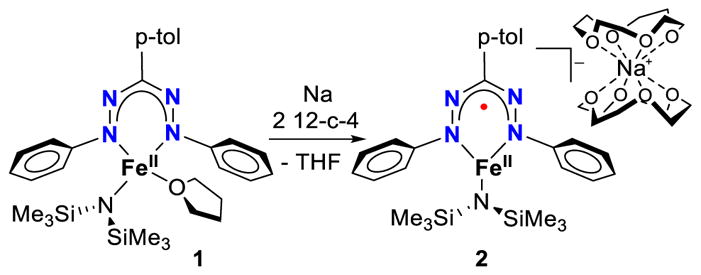
Previously reported ligand centered reduction of complex 1.

Results

The addition of Na sand to a purple THF solution of 1 at −78 °C gives a dark green solution upon warming to room temperature, similar to what is observed in the synthesis of complex 2. However, concentrating the mixture and addition of pentane, followed by cooling to −40 °C affords a differently colored complex 3-Na, which is a black crystalline solid in 71% yield (Scheme 2).

Scheme 2.

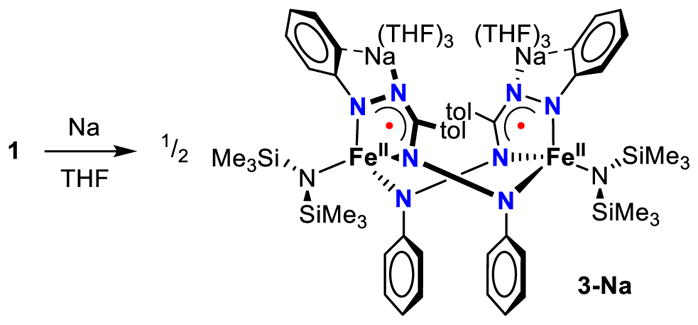
Reduction of complex 1 in the absence of 12-crown-4 to form dimer 3-Na.

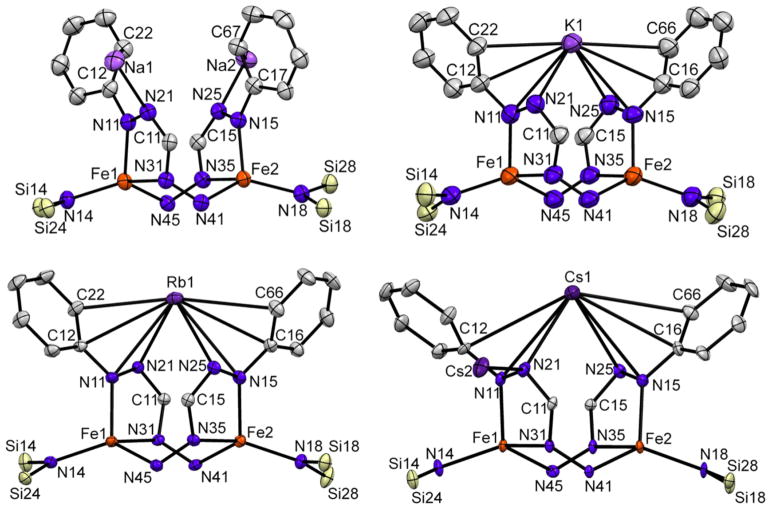
Crystals suitable for single crystal X-ray diffraction were obtained by cooling a solution of 3-Na in a THF/pentane mixture to −40 °C. The solid state structure of 3-Na (Figure 1) revealed a dimeric structure wherein the formazanate ligand has rearranged to coordinate through N1 and N3 to form a five-membered chelate. The exocyclic nitrogen (N4) coordinates to the other iron center in the dimer. Ligand rearrangements to bind N1 and N3 have been observed in non-reduced formazanates bound to boron²⁵ and zinc,²⁶ but we are not aware of any previous examples where the exocyclic N4 atom coordinates to another metal. The two [Na(THF)₃]⁺ ions have interactions with the internal N2 atoms of the five membered chelates and with nearby phenyl groups. The N–Na distances of 2.373(3) Å and 2.372(3) Å are comparable to those observed for non-isomerized formazanates bound to B (2.35 – 2.39 Å)²⁸ and Zn (2.41 – 2.52 Å)²⁹. The formazanate Fe–N bond lengths (2.006(3) – 2.067(3) Å) are all elongated compared to the solid state structure of 2 (1.935(5) – 1.958(5) Å), consistent with the higher coordination number of iron in 3-Na, which is four-coordinate in contrast to three-coordinate 2.

Figure 1.

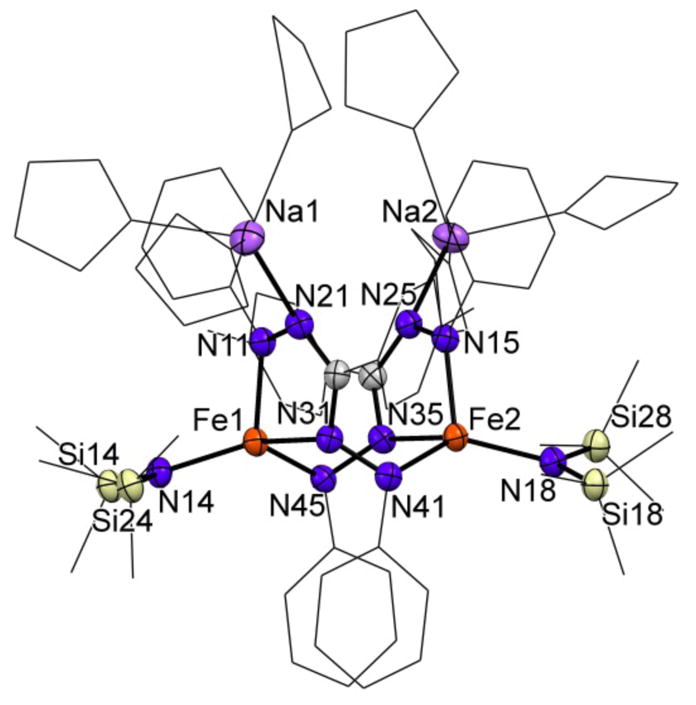
Displacement ellipsoid plot (50% probability) of complex 3-Na. Hydrogen atoms and a THF molecule have been omitted, and part of the structure is depicted as a wireframe for clarity. See Tables 1 and 2 for metrical parameters.

Metal complexes with multiple redox-active ligands can display ligand-based mixed valence, which is often reflected in distinct differences in intraligand metric parameters.^29,30 Although the two formazanate ligands in 3-Na are not crystallographically related, there are no significant differences in bond lengths and angles (Table 1), indicating that both ligands are in the same oxidation state. Analysis of the intraligand bond lengths of the formazanate core shows an elongation of the N–N bonds (1.372(4) – 1.393(4) Å) compared to 1 (1.317(2) – 1.325(2) Å), similar but more pronounced to what is observed in 2 (1.377(6) and 1.345(6) Å), suggestive of a ligand-centered reduction (Chart 1). The C–N bonds within the formazanate core of complex 2 (1.343(7) and 1.339(8) Å) show no significant changes when compared to 1 (1.339(2) – 1.350(2) Å). However, in 3-Na a contraction of the N2–C1 bonds (both 1.323(5) Å) and an elongation of the C1–N3 bonds (1.370(5) and 1.363(5) Å) are observed, indicating more localized double bond character for the N2–C1 bond. A comparable observation was made for a similarly rearranged but non-reduced formazanate bound to Zn, which showed double bond localization for N2–C1 and N3–N4.²⁶ In contrast, the N3–N4 bonds in 3 are significantly longer (1.393(4) and 1.378(4) Å), and are comparable to the N1–N2 bonds (1.372(4) and 1.375(4) Å), indicating that there is no double bond character for the N3–N4 bond as was observed for the non-reduced formazanate bound to Zn. The relative bond distances within the rearranged formazanate in 3-Na are very similar to DFT calculated values for a diamidoborane complex – formed upon intramolecular hydride reduction of the formazanate in a boron dihydride complex – with an identical binding mode as in 3-Na, yet protonated at N4.^25a The possibility of ligand-centered reduction is further supported by reported examples of five-membered metallacycles consisting of isothiosemicarbazide π-radical anions bound to nickel(II)³¹ and iron(III)³² with the same N-N-C-N motive as in 3-Na. In these examples elongation of the N-N bonds and contraction of the C-N bonds was also observed upon reduction of a neutral ligand to the corresponding radical monoanion. The mononanionic radical form of these ligands is characterized by intraligand bond distances of 1.333(1) – 1.350(1) Å for the N–N bond. This is significantly elongated compared to N–N bond in the neutral form of the ligand (1.254(7) – 1.267(2) Å), similar to the difference between 1 and 3-Na. However, in the reported isothiosemicarbazide π-radical anions both C–N bonds are comparable (1.322(1) – 1.355(1) Å), and less localized than in 3-Na. Overall, the metrical analysis implies that the rearranged formazanate ligands in 3-Na bind iron as radical dianions.

Table 1.

Selected bond lengths (Å) for the dimers.

	3-Na	3-K	3-Rb	3-Cs
Fe1–N14	1.993(3)	1.987(4)	1.9910(2)	1.985(5)
Fe2–N18	1.981(3)	1.991(4)	1.984(2)	1.983(5)
Fe1–N11	2.014(3)	2.051(3)	2.043(2)	2.025(5)
Fe2–N15	2.006(3)	2.046(3)	2.040(2)	2.028(4)
Fe1–N31	2.067(3)	2.053(4)	2.055(2)	2.051(4)
Fe2–N35	2.063(3)	2.055(4)	2.044(2)	2.066(4)
Fe1–N45	2.032(3)	2.055(3)	2.053(2)	2.030(5)
Fe2–N41	2.031(3)	2.047(3)	2.046(2)	2.039(5)
N11–N21	1.372(4)	1.384(5)	1.380(2)	1.377(6)
N15–N25	1.375(4)	1.387(5)	1.380(2)	1.367(6)
N21–C11	1.323(5)	1.329(5)	1.317(2)	1.324(7)
N25–C15	1.323(5)	1.313(5)	1.323(3)	1.332(7)
C11–N31	1.370(5)	1.377(5)	1.369(2)	1.370(7)
C15–N35	1.363(5)	1.378(5)	1.359(2)	1.358(7)
N31–N41	1.378(4)	1.390(5)	1.382(2)	1.369(6)
N35–N45	1.393(4)	1.384(5)	1.389(2)	1.365(6)
	M = Na	M = K	M = Rb	M = Cs
N21–M	2.373(3)	2.767(3)	2.924(2)	3.117(5)
N25–M	2.372(3)	2.766(3)	2.889(2)	3.092(5)

Chart 1.

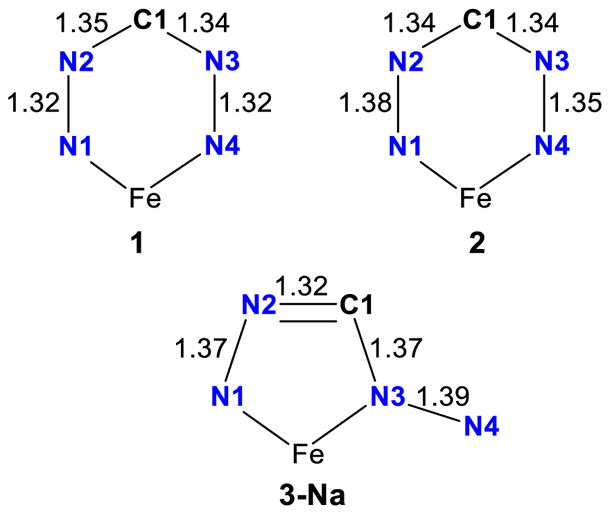
Averaged metrical details of the formazanate ligands in complexes 1, 2 and 3-Na. The average error of a given bond distance is ± 0.01 Å (3σ).

The zero-field Mössbauer spectrum of a solid sample of 3-Na at 80 K shows a slightly asymmetric doublet with isomer shift δ = 0.74 mm s⁻¹ and quadrupole splitting |ΔE_Q| = 2.30 mm s⁻¹ (Figure 2). The observation of only one doublet indicates identical electronic structures and environments for the two iron sites in 3-Na. The observed isomer shift of 3-Na is similar to that of complex 1 (δ = 0.71 mm s⁻¹), suggesting that the oxidation state at iron is the same in both cases. For additional insight, 3-Na was also analyzed by X-ray absorption spectroscopy at the Fe K-edge. The spectra of 1, 2 and 3-Na overlaid in Figure 3 are characterized by electric dipole forbidden but quadrupole-allowed 1s → 3d pre-edge transitions that appear at the base of the dipole-allowed 1s → np rising-edge that dominates a K-edge spectrum. Since the ligand field typically increases with increasing oxidation state for a given ligand set, the pre-edge energy often provides a useful marker for oxidation state.³³ The centers of mass for pre-edge peaks in spectra obtained for 1, 2 and 3-Na are identical within experimental error at 7112.2 ± 0.1 eV. Moreover the pre- and rising-edge spectral profile for 1 and 3 are almost superimposable, clearly indicating the same effective nuclear charge and coordination geometry (tetrahedral) about the Fe ions in these complexes. Thus, both Mössbauer and XAS analysis indicate that 1, 2, and 3-Na have the same oxidation state at iron. Since 1 is clearly iron(II), this suggests an iron(II) oxidation state in 3-Na, which in turn implies that the formazanates are reduced to radical dianions - in agreement with the metrical analysis described above.

Figure 2.

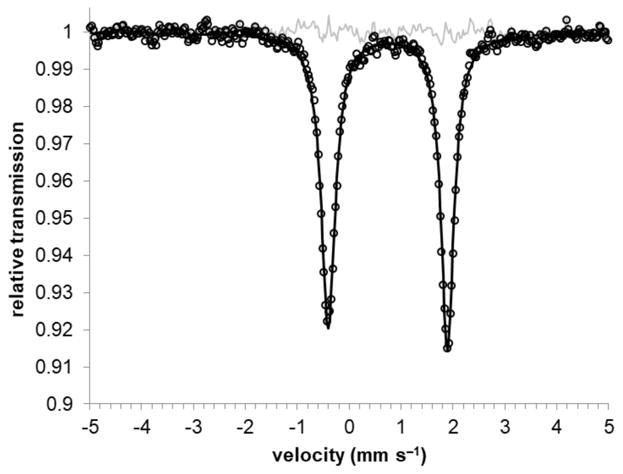
Zero-field Mössbauer spectrum of a solid sample of 3-Na at 80 K. The black circles are the data, the black line is a fit with two Lorentzians of equal intensity but slightly different line widths (γ_L = 0.328 and γ_R 0.304); the thin grey line is the residual from the fit.

Figure 3.

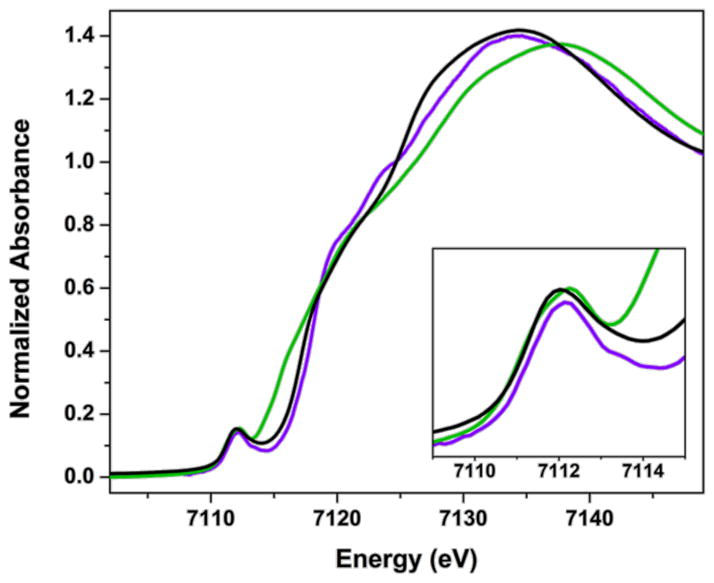
Overlay of the normalized Fe K-edge XAS spectra of 1 (violet), 2 (green), and 3-Na (black) at 10 K. Inset shows expansion of the pre-edge region.

The room temperature magnetic moment (μ_eff) in THF-d₈ solution using the Evans method was 6.95 ± 0.3 μ_B, which is comparable to the value obtained from SQUID measurements of a solid sample in the temperature range 50–300 K, μ_eff = 7.6 μ_B (Figure S19). The experimental values are close to the spin-only (s.o.) value for four uncoupled spin centers, two S_Fe = 2 and two ligand radicals S_rad = ¹/₂, namely μ_{eff, s.o.} = g_e√[2(2 + 1) + 2(2 + 1) + ¹/₂(¹/₂ + 1) + ¹/₂(¹/₂ + 1)] = 7.3 μ_B. The temperature independence of μ_eff(T) in this temperature range indicates is consistent with this model requires that the various pair exchange coupling constants |J_ij| between the four spins would need to be less than a few wavenumbers (Figure S19). Unfortunately, the low-temperature magnetic data are severely obscured by steep overshooting of μ_eff(T) below 50 K, presumably due to intermolecular interactions, which prevented us from further characterizing J values or zero-field splitting. Qualitative, rough fits (adopting g_rad = g_e for the radicals) suggest weak to moderate zero-field splitting for iron, iron-radical coupling of |J_Fe-rad| < 5 cm⁻¹ (Ĥ_ex = −2J S₁·S₂), and g_Fe = 2.07.

It is not a priori clear why exchange coupling between iron(II) centers and their coordinated ligand radicals in 3-Na should be weak, whereas the monomeric ferrous compound 2 shows strong local spin coupling.²⁴ We presume that the reason is small overlap and near-orthogonality of magnetic orbitals in the quasi-tetrahedral coordination. We also considered a model of very strong antiferromagnetic exchange coupling between each iron(II) centers and the ligand radical coordinated to it (as in 2), but weak coupling between the two sides. This model is made up of two local site spins S′= ³/₂, and predicts a spin-only magnetic moment of μ_{eff, s.o.} = g_e√[³/₂(³/₂ + 1) + ³/₂(³/₂ + 1)] = 5.5 μ_B, much lower than observed. Thus, the iron g-value would have to be g_Fe = 2.64 to match the experimental magnetic data. Since this value is far above the (geometrically averaged) g-value for 2 obtained from EPR simulations (g_av = 2.35),²⁴ this model of strong iron-radical coupling for 3-Na is not defensible, particularly as the corresponding large zero-field splitting of 2 (D = 16 cm⁻¹) is not consistent with the magnetic data of 3-Na (Figure S19).

The ¹H NMR spectrum of 3-Na in THF-d₈ shows resonances in the range from +160 to −70 ppm, and the number and integration of the peaks indicates that the two SiMe₃ groups are chemically inequivalent (Figure S1). Several protons on the formazanate are also split into pairs, suggesting that the dinuclear structure, with its lowered symmetry, is retained in solution. However, over time it fully converts to a new species (Figure S2), which has a similar ¹H NMR spectrum and green color as complex 2 (Figure S3), consistent with dissociation of the dimer to a mononuclear species (4-Na, Scheme 3). The rate of the dissociation of 3-Na to 4-Na in THF-d₈ was monitored between 273–313 K by ¹H NMR spectroscopy (Figure 4), and the concentrations followed an exponential time dependence indicating a rate law rate = k_obs[3-Na] (see SI for more details). Fitting the decay curves using Eq. 1 afforded rate constants, which were used to generate an Eyring plot (Figure S10) that gave the activation parameters ΔH^‡ = 28.0 ± 1.1 kcal mol⁻¹ and ΔS^‡ = −14.8 ± 3.7 cal mol⁻¹ K⁻¹. The loss in entropy in the transition state indicates an ordered early transition state that could involve binding of exogenous THF molecules to the Na atoms. This is consistent with the observation that the addition of two equiv of 12-crown-4 to complex 3-Na significantly increased the rate of dimer dissociation, and gives mononuclear complex 2 as previously reported. Moreover, in the solid state structure of the K analogue of 4-Na (see below) four THF molecules are bound to K, supporting the idea that incorporation of an additional THF molecule is feasible.

Scheme 3.

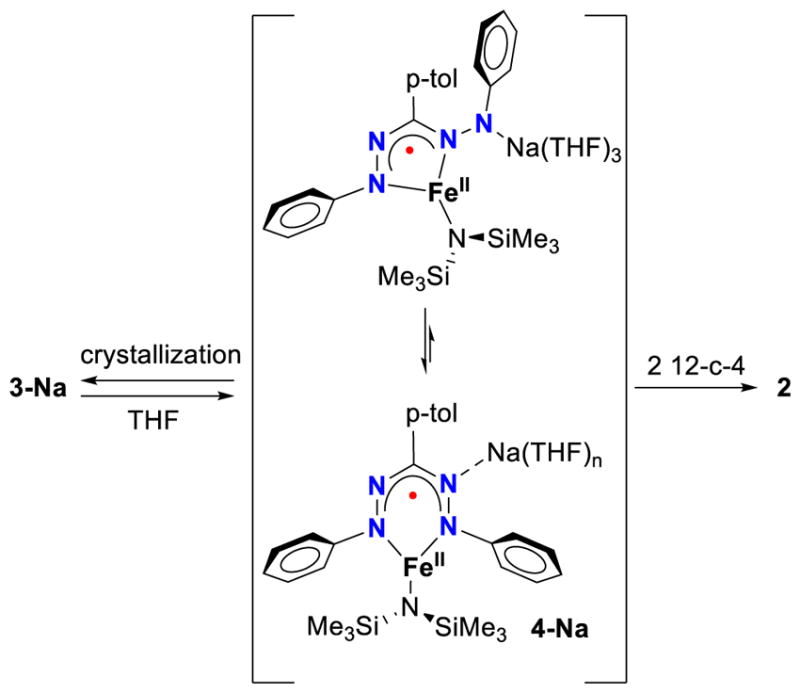
Dissociation of complex 3-Na in solution into a monomeric complex 4-Na in which the different formazanate binding modes are in equilibrium, and irreversible conversion into 2 by addition of a crown ether.

Figure 4.

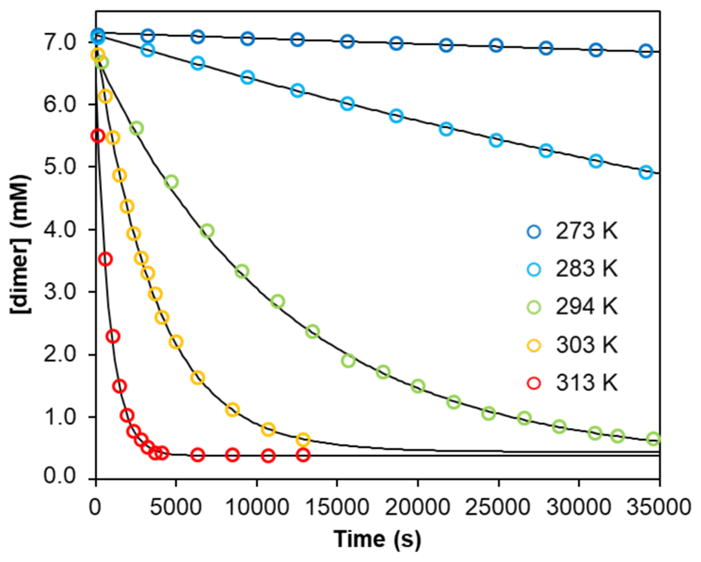
Concentration of dimer 3-Na vs time in THF solution at various temperatures. Open circles are data points and solid lines are fitted curves. Log plots of the data are in the Supporting Information (Fig. S11–S16).

$${[\mathbf{3}\mathbf{-Na}]}_t-{[\mathbf{3}\mathbf{-Na}]}_{\mathit{final}}={[\mathbf{3}\mathbf{-Na}]}_0{e}^{-kt}$$ (1)

Cooling mixtures of dissociated 4-Na gives no increase in dimer concentration as judged by ¹H NMR spectroscopy, indicating that the dissociation of the dimer is irreversible in dilute solution. However, crystallization from THF/pentane mixtures where 3-Na has fully converted to 4-Na affords solely black crystals of the dimer 3-Na. Analysis of a frozen THF solution of 3-Na that has partially dissociated into 4-Na by Mössbauer spectroscopy showed two signals that have isomer shift and quadrupole splitting parameters within the error margin of those for pure samples of 2 and 3-Na (Figure S17). Although dissociation of the dimer is irreversible in THF solution, we propose that an equilibrium involving the different coordination modes of the formazanate is present that enables crystallization as a dimer (Scheme 3). The room-temperature ¹H NMR spectra of 2 and 4-Na in THF-d₈ both show a single species with a number of peaks indicating idealized C_2v symmetry. However, the observed resonances broaden and start to deviate from Curie behavior below −50 °C (Figure S6 and S7), which could be due to intermediate exchange between formazanate binding modes on the NMR time scale. However, we were unable to resolve details because the spectra remained difficult to interpret at −90 °C, which was the lower temperature limit of the NMR spectrometer.

Intrigued by the change in formazanate binding mode induced by a coordinating Na cation, we investigated the effect of using different alkali metal reductants. The addition of MC₈ (M = K, Rb or Cs) to a THF solution of 1 at −78 °C gives a dark green solutions upon warming to room temperature. Addition of pentane and cooling to −40 °C gave complexes 3-K, 3-Rb and 3-Cs as dark crystalline solids (Scheme 4). Interestingly, rapid crystallization of 3-K from a THF/pentane mixture afforded two different crystal morphologies. ¹H NMR spectroscopy in THF-d₈ and Mössbauer spectroscopy of the obtained solids, and single crystal X-ray diffraction revealed a mixture of dimer 3-K (see below) and monomer 4-K. Although monomer 4-K was a minor component in the mixture, its solid state structure can be analyzed (Figure 5). The FeN and intraligand bond lengths in 4-K are within the uncertainty limits of the solid state structure of complex 2. A notable difference is that the potassium cation is bound to N21, three THF molecules and has close contacts to C22 and C31. Crystallization of 5 from a THF solution with less pentane at −40 °C, thereby slowing down the crystallization process, gives a crystalline material comprising >95% 4-K based on ¹H NMR and Mössbauer spectroscopies.

Scheme 4.

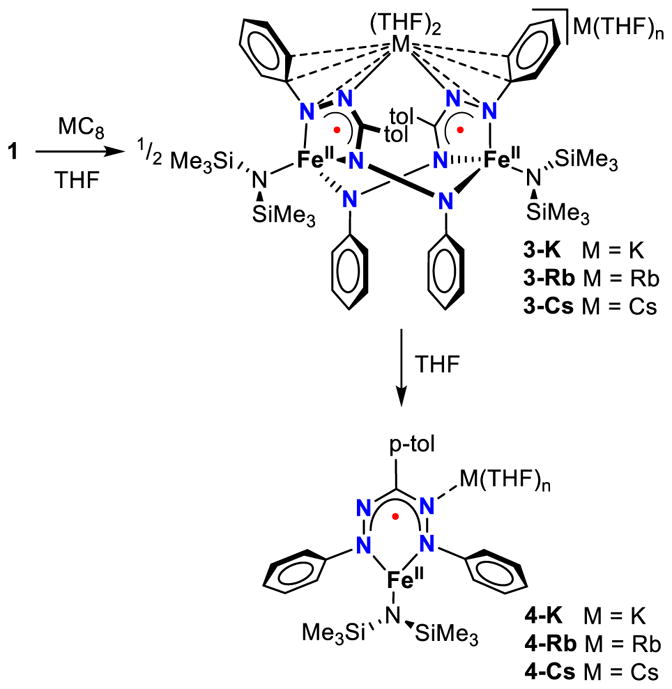
Synthesis of complexes 3-K, 3-Rb and 3-Cs and their decay to monomers in THF solution.

Figure 5.

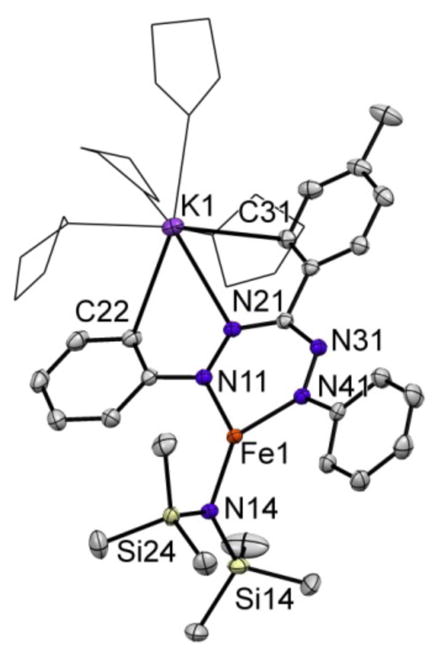
Displacement ellipsoid plot (50% probability) of 4-K. Hydrogen atoms are omitted and THF molecules are depicted in wireframe for clarity. Selected bond lengths (Å) and angles (°): Fe1–N11 1.933(1); Fe1–N41 1.937(1); Fe1–N14 1.944(1); N11–N21 1.362(2); N31–N41 1.358(2); N21–K1 2.865(1); C22–K1 3.344(1); C31–K1 3.213(1); N11–Fe1–N41 96.78(5); N11–Fe1–N14 133.75(5); N41–Fe1–N14 129.46(5).

Although we obtained crystals of 3-K, 3-Rb and 3-Cs suitable for single crystal X-ray diffraction, the rapid desolvation of the crystalline material, when transferred from the mother liquor to the immersion oil, resulted in poorly diffracting crystals. Fortunately, handling at temperatures below −40 °C in combination with cryo-mounting of the crystals (see SI for more details), led to solid state structures of all dimers (Figure 6). In agreement with the observed rapid desolvation of the crystals, several solvent molecules are in the asymmetric units. The quality of the structures of 3-K and 3-Cs was of lower quality than the other dimers (3-K diffracted weakly, and 3-Cs appears to have whole molecule disorder; see SI for details), so the structural detail is limited. Overall, it is clear that all complexes have a similar dimeric core structure as 3-Na where the formazanate has isomerized. No significant deviations in Fe-ligand bond distances are observed between the four dimers (Table 1). However, the manner in which the alkali cations are bound varies greatly. Whereas each formazanate in complex 3-Na is bound to a single Na cation, in 3-K, 3-Rb and 3-Cs one alkali cation bridges between the N21 and N25 of two separate formazanates. Close interactions with several other atoms in the N-phenyl substituent are also observed, which is in agreement with the softer nature of the larger cations favoring interaction with delocalized π systems over the harder N atom.³⁴ The other alkali cation is separated from the dimer and has only THF solvent molecules coordinated in the solid state structures of 3-K and 3-Rb. Interestingly, in the solid state structure of complex 3-Cs the second Cs cation is also bound to the N21 and N25 to yield a repeating polymeric structure (Figure S18).

Figure 6.

Displacement ellipsoid plots (50% probability) of the complexes 3-Na, 3-K, 3-Rb and 3-Cs showing the core structures. Hydrogen atoms, select organic fragments and solvent molecules are omitted for clarity.

The zero-field Mössbauer spectra of 3-K, 3-Rb and 3-Cs show doublets with isomer shifts that are indistinguishable from that of 3-Na (Table 3, Figure S8). The observed quadrupole splittings of 3-K, 3-Rb and 3-Cs range from 2.16 – 2.18 mm s⁻¹, which is slightly different from the quadrupole splitting of solid 3-Na. This is likely due to the different binding mode of the alkali cations, which is also reflected N–Fe–N bond angles of the dimers (Table 2).

Table 3.

Mössbauer parameters for solid samples of 3; experimental uncertainty is ±0.02 mm s⁻¹.

Complex	δ (mm s−1)	|ΔEQ| (mm s−1)
3-Na	0.74	2.30
3-K	0.72	2.16
3-Rb	0.71	2.17
3-Cs	0.72	2.18

Table 2.

Selected bond angles (°) for the dimers.

	3-Na	3-K	3-Rb	3-Cs
N14–Fe1–N45	124.8(1)	122.6(1)	122.8(1)	121.2(2)
N18–Fe2–N41	122.7(1)	123.0(1)	123.2(1)	120.5(2)
N14–Fe1–N11	110.1(1)	108.4(1)	107.9 (1)	107.2(2)
N18–Fe2–N15	109.4(1)	108.6(1)	107.9 (1)	108.1(2)
N11–Fe1–N45	116.1(1)	121.4(1)	121.1(1)	124.4(2)
N15–Fe2–N41	117.3(1)	120.5(1)	121.2 (1)	123.8(2)
N45–Fe1–N31	90.9(1)	89.7 (1)	89.5 (1)	88.9(2)
N41–Fe2–N35	90.3(1)	89.5(1)	89.5(1)	88.7(2)
N14–Fe1–N31	128.4(1)	130.0(1)	130.9(1)	131.4(2)
N18–Fe2–N35	132.2(1)	130.2(1)	130.1(1)	132.8(2)
N11–Fe1–N31	77.2(1)	77.1(1)	77.2(1)	77.5(2)
N15–Fe2–N35	77.4(1)	77.3(1)	77.1(1)	77.1(2)

The ¹H NMR spectra and solution magnetic moments of 3-K, 3-Rb and 3-Cs in THF-d₈ are similar to that of 3-Na in THF-d₈, indicating that the dimeric structures are retained in solution. Similarly, 3-K, 3-Rb and 3-Cs also convert to the corresponding monomers as judged by ¹H NMR spectroscopy. However, the rate at which the dimer breaks up in solution is highly dependent on the cation that is present (Figure 7). Complex 3-Cs is the most rapid (k_obs = 5.89 ± 0.03 × 10⁻⁴ s⁻¹) after 3-Rb (k_obs = 1.66 ± 0.01 × 10⁻⁴ s⁻¹) and 3-K (k_obs = 6.37 ± 0.04 × 10⁻⁵ s⁻¹). Though these follow a trend where the heavier alkali metal cation is fastest, the decay rate of 3-K is slower than that of 3-Na (k_obs = 8.50 ± 0.08 × 10⁻⁵ s⁻¹), breaking the periodic trend.

Figure 7.

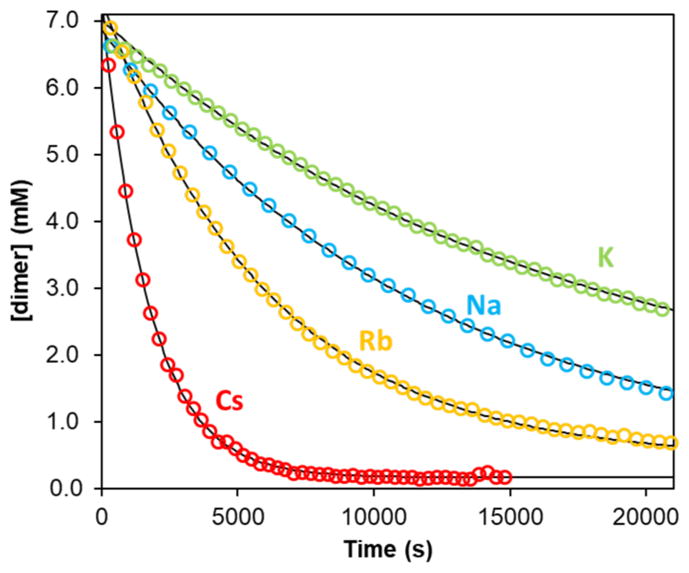
Concentration of dimers 3-Na, 3-K, 3-Rb and 3-Cs vs time in d₈-THF at 21 °C. Open circles are data points and solid lines are fitted curves.

Discussion

Interaction of Alkali Metals with Reduced Formazanate-Iron Complexes: Influences on Structure and Dynamics

The reduction of complex 1 in THF solution by different alkali metals gives dimeric complexes (3) featuring a rearranged formazanate. The formazanate binding mode in the dimeric complexes is stabilized by cation-π interactions with alkali metal cations. Although the different cations do not significantly alter the intraligand bond lengths of the rearranged formazanate, the interplanar angle (θ) and centroid-centroid distance (ζ) between the five-membered metallacycles significantly increases with the larger cations (Table 4). This trend is consistent with increasing ionic radii of the corresponding alkali cations, and likely results in the observed differences in the N–Fe–N bond angles (Table 2).

Table 4.

Distances and angles between the 5-membered metallacycles and N4 atoms in of 3.

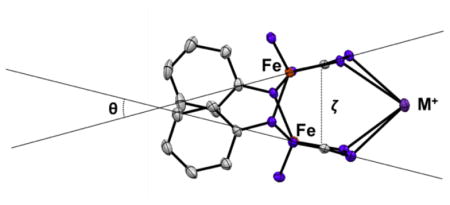
Complex	Angle θ (°)	Distance ζ (Å)	N4-N4 (Å)
3-Na	18.3	3.11	3.046(4)
3-K	23.3	3.21	2.999(5)
3-Rb	25.9	3.23	2.998(2)
3-Cs	33.7	3.37	2.989(5)

Although the dimeric nature is retained in solution as judged by initial ¹H NMR spectra, each dimer converts completely into the corresponding monomeric species in THF solution. Interestingly, the rate at which this process occurs varies greatly between the dimers. The slow rate of dissociation of 3-K shows that the energy barrier for dimer/monomer interconversion is higher than for the other complexes. This could explain why 4-K was the only one that could be crystallized as a monomer, because the higher barrier would also slow the reverse reaction, dimerization upon crystallization.

A periodic trend for the rates of monomer formation is observed with K < Rb < Cs, which correlates with weaker cation-π interactions as the z/r ratio of the cations decreases. This may arise from a stronger cation-π interaction with smaller alkali cations, which stabilizes the isomerized binding mode of the formazanate, and increases the activation energy for isomerization and splitting of the dimer. The deviation of the periodic trend for the Na analogue could be ascribed to the different binding of the alkali cations in 3-Na, where each rearranged formazanate has an interaction with a separate alkali cation in contrast with the bridging alkali cation observed in 3-K, 3-Rb and 3-Cs. The difference in 3-Na also influences the iron center, as judged by the subtly different quadrupole splitting in the Mössbauer spectrum of 3-Na in comparison to 3-K, 3-Rb and 3-Cs. The rate of dimer cleavage is faster for 3-Na than expected from the periodic trend, suggesting that the Na cations hold the core into the dimeric structure more weakly, which is consistent with the more central position of the alkali metal cations in 3-K, 3-Rb and 3-Cs. Alternatively, the relative rates of monomer formation could be due to the need for THF to access the alkali metal cation, which is suggested by the negative activation entropy for 3-Na going to 4-Na. In this alternative explanation, the faster rates for the larger cations would result from the larger size and faster expected exchange rate for solvent.

Analysis of the chemical shifts in the ¹H NMR spectra of the dimers shows another trend between the chemical shift with the size of the alkali metal for 3-K, 3-Rb and 3-Cs, but the trend does not fit well for all resonances of 3-Na (Figure S4), suggesting that the structural differences noted above are also retained in solution. After dissociation into the monomeric complexes, the chemical shifts in the ¹H NMR spectra also vary greatly by alkali cation (Figure 8). Comparison of the chemical shifts with complex 2, which has a fully separated ion pair in solution, shows that the chemical shifts move towards a narrower range going from 2 to 4-Na, 4-K, 4-Rb and 4-Cs. In this case the Na monomer does fit the periodic trend. Assuming that in solution the Na cation is fully sequestered by the crown ethers for 2, this trend in chemical shifts could be interpreted by a strengthening cation-π interaction between the formazanate and alkali cation in the series 4-Na, to 4-K, to 4-Rb to 4-Cs. However, this would be opposite to the typical trend in magnitudes of cation-π interactions, which are known to become weaker as the ion becomes larger.⁸ Therefore, a more likely explanation is that the alkali cation and THF ligands (Figure 5) perturb the geometry of the monomeric complex in solution to accommodate the cation-π interaction. This effect would be more pronounced with increasing alkali cation size, as observed in the solid state structures of dimers 3-K, 3-Rb and 3-Cs, in agreement with the biggest change in chemical shifts between 2 and 4-Cs.

Figure 8.

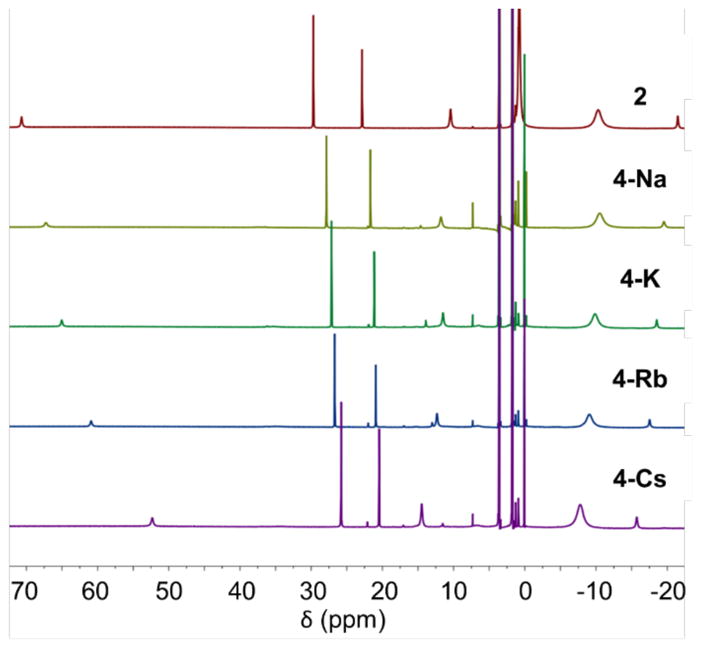
Stacked ¹H NMR spectra of complex 2 (top) and dissociated complexes 4-Na, 4-K, 4-Rb and 4-Cs, showing the trends in chemical shifts upon binding of alkali cations.

Electronic structure of 3-Na

Mössbauer and X-ray absorption spectra show experimentally that two high-spin iron(II) centers are present in 3, which implies that the two formazanate ligands are not in their usual closed-shell state but rather are reduced, open-shell radicals. The intraligand distances are distorted from that in conventional iron(II)-formazanate complexes, further supporting the assignment of a reduced formazanate.

The magnetic susceptibility data for 3-Na indicate very little magnetic coupling between the radical ligands and the iron(II) centers. It is notable that there is a short distance between the two N4 atoms of each formazanate ligand in 3 (2.989(5) – 3.046(4) Å, Table 4). In addition, the two five-membered metallacyles are parallel alignment and are separated by only 3.11 – 3.37 Å in this series, indicating a π-π interaction like those that have been reported for several chelating π radical ligands.³⁵ For example, two o-diiminosemiquinonate ligand radicals coordinated to zirconium(IV) are aligned parallel, and the short interligand separation of 3.42 Å gives rise to intramolecularly antiferromatic coupling between this two spin centers in this complex.³⁶ Moreover, in the previous forum on redox-active ligands, Scarborough and Wieghardt described a similar intramolecular π•-π• antiferromagnetic interaction in a dimeric complex between two bipyridine radicals.³⁷ In the system described here, details of weak coupling were obscured by low-temperature deviations in the SQUID magnetometry data, so we were unable to glean further experimental evidence.

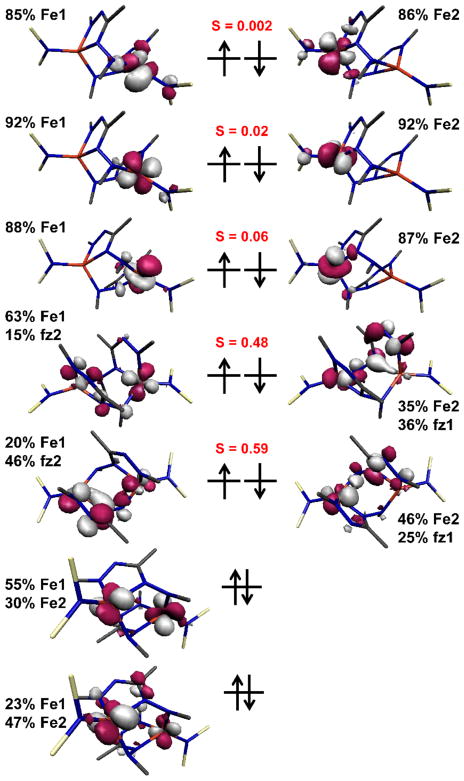
To gain insight into the electronic structure of the dimeric complexes, the ground state electronic structure of 3-Na was calculated using DFT calculations at the B3LYP/ZORA level of theory, using the broken symmetry (BS) formalism to give localized spins in an overall singlet state (M_S = 0). The electronic structure derived from a BS(5,5) calculation has five pairs of magnetic orbitals (the members of each pair are related to the other half of the dimer by symmetry), which are antiferromagnetically coupled to give the singlet ground state (Figure 9). The high-spin M_S = 5 solution is 15.9 kcal mol⁻¹ less favored than the BS solution.

Figure 9.

Qualitative MO scheme for 3-Na as derived from broken symmetry DFT calculations (B3LYP/ZORA). The Fe and formazanate (fz) content and spatial overlaps of the corresponding pairs of magnetic orbitals are given.

The DFT methodology is limited because BS calculations can only partition a molecule into two orbital fragments, one with spin-up electrons (α-spin) and the other spin-down electrons (β-spin). Of the five pairs of magnetic orbitals, three can be described as Fe-based d_xz, d_yz, d_z² orbitals of one Fe ion in the α-spin manifold that are antiferromagnetically coupled to the corresponding β-spin of matching symmetry on the other Fe ion. The computed overlap integrals (S) between these d orbitals in 3-Na are all very small, underscoring the essentially non-existent coupling between these well-separated spin centers. The highest doubly-occupied MOs are based on the d_x²-y² orbital for each Fe ion. The remaining two pairs of magnetic orbitals share Fe and formazanate character. The remaining d orbital (d_xy) has the correct symmetry to overlap with the highest ligand-based π* orbital (two N–N π* interactions) previously assigned with a₂ symmetry for the formazanate ligand.²⁴ The bonds between the d_xy and formazanate are highly polarized, giving rise to an antiferromagnetic interaction between this symmetry-matched pair. The most unusual aspect comes from the exocyclic nitrogen (N4), which has a bonding interaction with the other Fe d_xy orbital that is visible in the lowest magnetic orbital with S = 0.59 (Figure 9). This four-spin ensemble is challenging to compute because of the aforementioned limitations of BS-DFT, and the result here is one where the calculation mixes two pairs of SOMOs that are very close in energy, with polarized metal-ligand bonds at one end and covalent bonds at the other. The most appropriate description is that the first pair are predominantly ligand-centered with significant Fe d_xy content that produces a large overlap integral. The second pair can be considered almost exclusively the d_xy orbital of each Fe ion, who have a significantly smaller overlap integral (Figure 9).

This description is consistent with the Mössbauer and Fe K-edge data that diagnose two high-spin iron(II) (S = 2) ions, which are each coordinated by a dianionic formazanate radical (S = ¹/₂). This description is supported by the Mulliken spin population analysis, where 3.6 spins are found on each Fe with significant spin of the opposing sign on the coordinated dianionic formazanate radical ligands (Figure 10). This value is lower than four spins for each high-spin iron(II) center as a result of the covalent interaction with the exocyclic nitrogen that distributes some spin (of the same sign) on to the formazanate ligand. Though the calculations predict stronger antiferromagnetic coupling than we observe in the magnetic data, we ascribe the difference to the limitations of the BS formalism in a four-spin system as described above.

Figure 10.

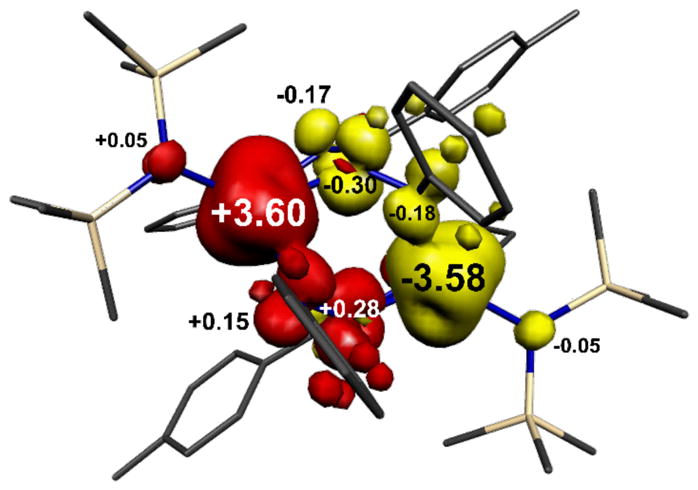
Mulliken spin population analysis for 3-Na (red: α-spin; yellow: β-spin). Counterions and solvents have been removed for clarity.

Overall, the resonance structures in Scheme 5 best describe the electronic structure of the rearranged formazanate radical dianions in 3 as they are in agreement with the presence two high-spin Fe centers, and reflect the intra- and interligand bond distances and computational data. The dimerization that is facilitated by the ligand rearrangement produces a pair of strongly coupled magnetic orbitals that are predominantly ligand in character though have a sizeable metal content by virtue of a bonding interaction between the exocyclic nitrogen and the other iron center. The net result is two high-spin iron(II) ions characterized by four highly localized magnetic orbitals that are weakly coupled on account of their large spatial separation. This general electronic structure description accurately reflects the physical characterization data despite the limitations of the BS-DFT calculations in reproducing the magnetic coupling. Moreover, it is unique among these iron-formazanate complexes, as the monometallic species 2 and 4 present a more common electronic configuration, that of a π-radical ligand (S_L = ¹/₂) strongly antiferromagnetically coupled to a paramagnetic metal ion (S_Fe = 2) to give an S = ³/₂ spin ground state.

Scheme 5.

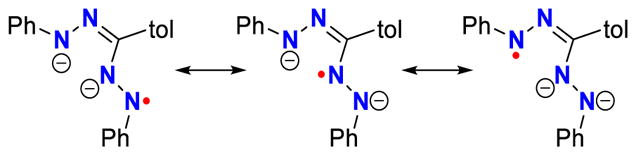
Limiting resonance forms for the rearranged formazanate radical dianion in dimers 3.

These studies show the significant effect that cation-π interactions can have on metal complexes with redox-active ligands. The observed rearranged formazanate binding mode is stabilized to different extent by the various alkali cations, which is reflected in the different solid state structures and observed decay rates for the dimers. The results show that cation-π interactions not necessarily only affect the electronic structure according to periodic trends but that the difference in size can also change result in different chemical structure.

Conclusion

In the absence of a crown ether, one-electron reduction of complex 1 by alkali metals results in the formation of dimeric complexes wherein the formazanate ligand has rearranged to form a five-membered metallacycle that is coordinated to the alkali cation. The electronic structure has two uncoupled high spin iron(II) centers and two ligand radicals as shown by Mössbauer, XAS, and DFT. Different alkali cations not only result in different orientations of the rearranged formazanate ligand but also affects how these dimers are converted to monomeric species in solution. Moreover, the difference in how the alkali cation is bound in the sodium dimer is shown to transcend periodic trends in terms of reactivity. This work demonstrates the considerable effect that Lewis-acidic cations can have on systems containing redox-active ligands, and shows the possibilities for tuning of structure and reactivity by choice of cation.