Mathematical models of HIV latency

Abstract

Viral latency is a major barrier to curing HIV infection with antiretroviral therapy, and consequently, to eliminating the disease globally. The establishment, maintenance, and potential clearance of latent infection are complex dynamic processes and can be best understood and described with the help of mathematical models. Here we review the use of viral dynamics models for HIV, with a focus on applications to the latent reservoir. Such models have been used to explain the multi-phasic decay of viral load during antiretroviral therapy, the early seeding of the latent reservoir during acute infection and the limited inflow during treatment, the dynamics of viral blips, and the phenomenon of post-treatment control. In addition, mathematical models have been used to predict the efficacy of potential HIV cure strategies, such as latency-reversing agents, early treatment initiation, or gene therapies, and to provide guidance for designing trials of these novel interventions.

1 History of mathematical modeling for HIV

The first models for HIV infection within individual people were developed in the late 1980s, quickly after the discovery of the virus itself. These models were inspired by the bread-and-butter models of mathematical epidemiologists, such as the SIS and SIR models introduced by Kendrick and McCormack in the early 1900s, which are used widely to describe the spread of infections between individuals in a population [64, 14, 4]. In contrast, “viral dynamics” models were developed to describe the spread of virus between infected cells within a single individual’s body [83]. These models have since been used to describe many other human virus infections, such as Hepatitis B [85, 91, 35] and C [82, 20], influenza [80], dengue [87, 27], and herpes simplex virus [116].

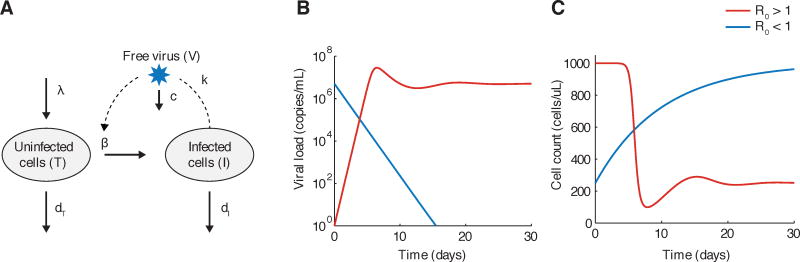
A description of the most basic version of the virus dynamic model is known in Box 1 and Figure 1. Despite its apparent simplicity, this model has provided tremendous insight into HIV dynamics. It predicted a viral load time-course similar to what was observed for acute HIV infection: an initial exponential increase, followed by a peak and then decline to steady state (Fig. 1B, C). The model demonstrated that it was not necessary to have the onset of an adaptive immune response to explain the post-peak decline: the fact that target cells turn over slower than infected cells and had a limited production rate were enough to explain this drop [97]. When it became possible to identify patients early in infection and follow them frequently, longitudinal data on viral load and CD4⁺ T cell count of sufficient quality to fit to the model were generated, allowing for estimation of the parameters governing viral dynamics [124, 17]. As a result, it was later determined that the post-peak drop in viral load was larger than could be explained by target cell limitation alone, and the effect of the adaptive immune response could be quantified.

Box 1. The basic viral dynamics model.

The basic viral dynamics model (Figure 1) tracks uninfected target cells of the virus (T), infected cells (I), and free virus (V). Target cells are produced at a rate λ, and die with rate constant d_T. Infected cells are produced by contact between target cells and free virus at a rate β, and die at rate d_I. Free virus is produced by infected cells at rate k and is cleared at rate c. The model is generally formulated as a system of ordinary differential equations:

$$\begin{gathered} \stackrel{.}{T}=\lambda -\beta TV-d_{T}T \\ \stackrel{.}{I}=\beta TV-d_{I}I \\ \stackrel{.}{V}=kI-cV \end{gathered}$$ (1)

The basic reproductive ratio, which describes the average number of virions produced from in a single round of infection when one virion is introduced into an otherwise uninfected host, can be calculated for this model as

$$R_0=\frac{\lambda \beta k}{d_T{d}_{I}c}$$ (2)

It represents a transcritical bifurcation in the system. When R₀ < 1, the only stable equilibrium is one with no virus or infected cells (I = V = 0). When inoculated from any size, the infection will decline towards eventual extinction. However, when R₀ > 1, infection levels will eventually reach a stable steady state level from any non-zero initial condition.

Fig. 1.

The basic viral dynamics model. A) Flow diagram of processes that are tracked in the model, as described in Box 1. B)–C) Example trajectory of viral load (V) and uninfected target cells (CD4⁺ T cells, T) when R₀ > 1 (red) and R₀ < 1 (blue). Graphs were generated by numerically integrating Equation 2 with parameters λ = 100 cells/uL, β = 10⁻⁷ or 0/day/(virus/mL), k = 1000 virus/cell, d_T = 0.1/day, d_I = 1/day, c = 25/day.

Mathematical analysis of the viral dynamics model demonstrates that it displays threshold behavior, similar to epidemiological models [37, 83]. It is possible to define a single composite quantity that depends on all the parameters of the system, and the value of this quantity alone determines the qualitative behavior of the system. One such quantity is R₀, the basic reproductive ratio. This value describes the average number of secondary infected cells produced by a single infected cell over the course of its lifetime, in a population of otherwise susceptible target cells. When the basic reproductive ratio is greater than one (R₀ > 1), an infection starting from a small size can grow and eventually establish a chronic state. When the basic reproductive ratio is less than one (R₀ < 1), an infection starting from any size will decline and eventually be cleared. R₀ could be estimated from studies of acute infection, and its value falls anywhere in the range of 2–25 (averaging around 8) in patients [105]. This gave a benchmark for the required efficacy of drugs to inhibit infection. Similar to the vaccination threshold in epidemiology [44], the required drug efficacy ε, which describes the fraction of infections inhibited by the drug, must satisfy ε > 1 − 1/R₀ to achieve viral suppression within an individual.

The standard formulation of the viral dynamics model (Fig. 1 and Eq. 2) assumes that virus and cells are well-mixed throughout the entire anatomical region of interest (for HIV, usually the plasma and lymph), and that they are present at high enough levels so that understanding the average (deterministic) behavior of the system is sufficient. However, the model can also be be simulated stochastically to account for small population sizes, chance extinction, and events that occur rarely. There are multiple related stochastic formulations of the model which are equivalent to the same time-average deterministic representation but have different levels of fluctuations around the average. Generally, in the model, the target cells of the virus are assumed to be all CD4⁺ T cells, though some versions of the model consider only activated cells in this class. Many other details of infection can be added to the model, such as a delay between infection and virion production, tracking anti-viral immune responses, viral latency, multiple-classes of infected cells, or the impact of drug treatments [83].

As described in the next section, the altered viral load trajectories observed once potent antiretroviral treatment is initiated allow for estimation of the rate of turnover of actively infected cells. When these observations were first made in the mid 1990s, they demonstrated that despite the slow-progressing clinical nature of chronic HIV infection, infected cells turned over on the order of a day, meaning that the rate of new infections and the virion production were extremely high [127, 56]. This fundamentally changed the view of HIV from a slow-moving to a dynamic infection.

When antiretroviral drugs were first used as monotherapy in patients, temporary declines in viremia were followed by resurgence to high (though slightly below pre-treatment) levels. Along with genotypic testing, models demonstrated that the appearance of drug-resistant strains and subsequent competition with wild-type strains could explain these dynamics [79, 47]. Parametrized viral dynamics models were able to show that pre-existing resistance at the time of therapy initiation was more likely than newly-emerging mutations once treatment was started [11, 12]. Importantly, these models, along with estimates for the mutation rate of HIV, suggested that at least three drugs would likely be needed to prevent rapid failure via drug resistance [104, 29].

Adaptations of the basic viral dynamics model which took into account interactions with the immune system (both immune control of virus and viral-mediated immune toxicity) were developed early on in the epidemic to understand the mechanism of pathogenesis and progression to AIDS. These models demonstrated the difficulty in explaining the long period of asymptomatic infection before the onset of AIDS and the slow decline of CD4⁺ T cells [5, 103, 133] with simple mechanisms. An early model proposed a “diversity threshold”, whereby continual immune escape eventually lead to a critical level of antigenic diversity in the viral population which prevented control of the infection at a level where progressive immune destruction was held at bay [84, 102]. To date, the mechanism of HIV pathogenesis remains unclear and no single model is fully supported by observations.

2 Models to interpret the decay of viremia during antiretroviral therapy

The viral dynamics model can be used to interpret changes in viremia when antiretroviral therapy begins. For a fully-effective drug which prevents productive infection of new cells (such as entry inhibitors, reverse transcriptase inhibitors, and integrase inhibitors), treatment can be modeled as β → 0 in the viral dynamics model. Viral load is expected to decay exponentially at a rate determined by the half-life of actively infected cells, after a short shoulder phase [56, 127] (Fig. 1B). This shoulder phase is determined by the clearance rate of free virus in the plasma, which is quite fast (free virus half life of around an hour)[99], and therefore creates only a short lag before exponential decay. In reality, the shoulder phase could be longer due to the delay required for drug absorption into the plasma and diffusion into the cell. This insight from models, along with frequently-sampled viral load values from patients on the first antiretroviral drugs, resulted in an estimated infected cell lifespan of around 2.5 days (half-life of 1.6 days in Perelson et al [92] and 1.8 days in Wei et al [127]). Later, when more potent drugs were developed and eventually used in combination, this estimate was adjusted to ≈ 1 day (half-life of 0.7 days in Markowitz et al [77]). As mentioned above, this finding consolidated the understanding of HIV as a very dynamic infection, since at steady-state viral loads, each infected cell that dies must be replaced by a newly infected one.

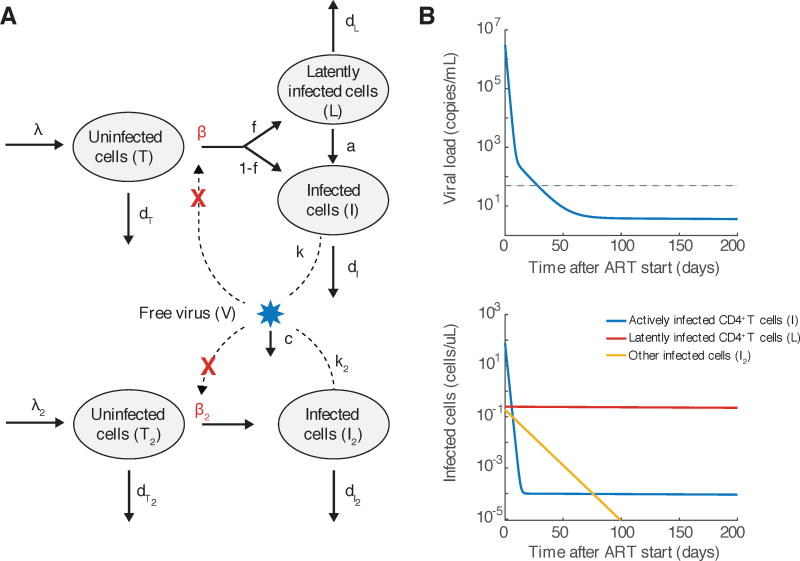
When more sensitive assays of viral load were developed and drug combinations which prevented the rapid evolution of resistance were used, it became apparent that viral load decline did not follow a simple exponential decay. Instead, it could best be fit by a multi-phasic decay pattern. Models were developed to explain this pattern in terms of different populations of infected cells with different death rates, and used to generate hypotheses about the nature of the cells responsible for each phase of decay (Figure 2 and Box 2).

Fig. 2.

An augmented model of viral dynamics that takes into account multiple populations of infected cells. A) Flow diagram of processes that occur in the model, as described in Box 2. Adapted from Perelson et al [93]. B) Multiphasic decay of viral load predicted by the model. C) Decay of individual populations of infected cells predicted by the model. Graphs were generated by numerically integrating Equation 5 with parameters approximately consistent with those estimated in Andrade et al [6]. We assumed that other target cells (I₂) live 10x longer with or without infection, exist at 1000x lower level before infection, produce virus at 10x slower rate, and are infected at the same rate. 1 in 10,000 infections result in latency, and that latently infected cells (L) live 10,000 times longer than actively infected cells. Parameters are λ = 100 cells/uL, β = 10⁻⁷ or 0/day/(virus/mL), k = 1000 virus/cell, d_T = 0.1/day, d_I = 1/day, λ₂ = 0.01 cells/uL, β₂ = 10⁻⁷ or 0/day/(virus/mL), k₂ = 100 virus/cell, d_T2 = 0.01/day, d_I2 = 0.1/day, c = 25/day, f = 10⁻⁴, a = 4 × 10⁻⁴/day, d_L = 10⁻⁴/day.

First, a second phase decay, thought to represent a population of virus-producing cells with a half-life of 14 days, was discovered [93, 6]. Based on this decay rate and an estimated total body infected cell population size of at maximum 10¹², it was estimated that it would take no more than 3 years to eradicate all virus from the body [93]. However, later studies using assays that could quantify viral loads down to 1 copy per mL of plasma identified a third phase of decay (half-life of 40–60 weeks, in Palmer et al [88], Andrade et al [6]), and perhaps a subsequent stable level of viremia [88]. Along with the discovery of latent infection in the form of provirus integrated into resting CD4⁺ T cells [24, 45, 120] and the observation of rebound upon ART interruption [36, 114], these findings quelled hopes of a cure for HIV via ART.

To this day, the identity of the later phases of viral decay are not completely known. The second phase remains particularly elusive. It could represent a longer-lived population of cells infected with HIV, such as monocytes, macrophages, partially-activated T cells, or cells with unintegrated HIV DNA. The third/fourth phase is likely due to reactivation of infection in long-lived latently infected cells.

Mathematical models have provided insight into this issue, in particular by interpreting the changes in decay kinetics observed in clinical trials when integrase inhibitors are used instead of reverse transcriptase inhibitors. Spivak et al [123] have used this approach to suggest that macrophages are not a likely candidate for second phase decay, and Andrade et al [6] have similarly suggested that pre-integration latency is an unlikely cause for the third phase decay.

Models have also suggested alternative hypotheses for the mechanism behind the decelerating decay. Arnaout et al [8] suggested that as viral loads declined after ART initiation, so would antigenic stimulation of cytotoxic T cell (CTL) levels. Lower CTLs would result in less killing of productively infected cells, and hence an apparent decrease in viral load decay rate. Kim and Perelson [66] hypothesized that viremia during the later phases was due to reactivation from latently infected memory CD4⁺ T cells, and that infected cells specific to more common antigens would be reactivated early on. The latent pool would then be comprised of cells specific for rare antigens which appear infrequently, resulting in deccelerating decay over time. Zhang and Perelson [134] suggested that the third phase of viral load decline could be explained by very slow release of virus bound to the surface of follicular dendritic cells, due to the complex multi-valent binding kinetics.

Box 2. Modeling HIV dynamics under antiretroviral therapy.

Antiretroviral therapy acts to block the production of new infected cells, effectively reducing β in the viral dynamics model (Fig. 1, Eq. 2). Assuming fully-effective treatment (a good approximation for combination therapy or monotherapy with some newer highly potent drugs), β → 0, and the basic viral dynamics model predicts [92, 127]) that viral load decays following

$$V(t)=V(0)\frac{(c{e}^{-d_{I}t}-d_I{e}^{-ct})}{c-d_I}$$ (3)

While this equation describes the first week of viral decay well (e.g. [77]), longer follow-up periods show that the decay slows over time. More realistic models that incorporate multiple populations of infected cells have been developed to help explain these dynamics (Fig. 2, adapted from Perelson et al [93]). A fraction f of new infections of target cells (T, CD4⁺ T cells) result in latency. Latently infected cells (L, generally representing resting memory CD4⁺ T cells) do not produce virus and are extremely long-lived. Occasionally (at rate a), these cells reactivate and produce virus. An alternative population of target cells (biological origin still debated) turns over more slowly and produces virus at a lower rate. The resulting equations are

$$\begin{gathered} \stackrel{.}{T}=\lambda -\beta TV-d_{T}T \\ {\stackrel{.}{T}}_2={\lambda }_2-{\beta }_2{T}_{2}V-d_{T_2}{T}_2 \\ \stackrel{.}{I}=(1-f)\beta TV-d_{I}I+aL \\ \stackrel{.}{L}=f\beta TV-d_{L}L-aL \\ {\stackrel{.}{I}}_2={\beta }_2{T}_{2}V-d_{I_2}{I}_2 \\ \stackrel{.}{V}=kI+k_2{I}_2-cV \end{gathered}$$ (4)

When fully-effective therapy is given (β, β₂ → 0), viral load decays as

$$V(t)=V(0)[A{e}^{-d_{I}t}+B{e}^{-(a+d_L)t}+C{e}^{-d_{I_2}t}+(1-A-B-C)e^{-ct}]$$ (5)

where T₀ is the CD4⁺ T cell level at the time of treatment start and

$$\begin{gathered} A=\frac{k\beta T_0}{(c-d_I)d_I}\left(1-\frac{(d_I-d_L)f}{(d_I-d_L-a)}\right) \\ B=\frac{\mathit{afk}\beta T_0}{(a+d_L)(d_I-a-d_L)(c-a-d_L)} \\ C=\frac{c-\frac{k\beta T_0}{d_I}\left(1-\frac{d_{L}f}{(a+d_L)}\right)}{c-d_{I_2}} \end{gathered}$$

3 Mechanisms of latent reservoir persistence

Plasma viral loads dramatically decrease during combination antiretroviral therapy, but ultra-sensitive assays find that some residual viremia persists at very low levels (≈1 viral RNA copy per mL of plasma) indefinitely during treatment [42]. Understanding the source of this persistent infection has been a major goal of HIV research for the past 20 years. The discovery of HIV latency has contributed to our understanding of the disease process, but also introduced new questions that remain unanswered to this day. Throughout this period, mathematical models have been an important tool to test the many competing hypotheses about HIV persistence.

HIV integrates into host cell genomes as a part of its normal lifecycle, and CD4⁺ T cells with resting, memory phenotypes can be isolated that contain proviral DNA [23]. Many of these cells can be induced to produce infectious virus when isolated, activated, and cultured ex vivo [24, 45, 120]. The term “HIV latency” refers to this process, and the pool of long-lived cells that contain provirus in a quiescent state is referred to as the “latent reservoir”. Latently infected cells can be found early on in the infection, and after therapy has begun [24, 45, 10, 3]. One of the most important questions about the latent reservoir has been how quickly it decays during therapy - if it decays at all. Longitudinal samples of inducible virus in resting memory CD+ T cells can be analyzed similarly to plasma viral loads, using models of exponential decay. Initial studies using single-exponential models beginning at timepoints immediately after ART initiation estimated a 6-month half-life of latent cells, implying 10 years of therapy would be needed to clear the estimated 10⁶ latently infected cells [24]. Later work that with a broader range and density of timepoints demonstrated multi-phase decay: This source of virus initially drops around 1,000-fold once ART is started, with a half-life on the order of weeks, likely due to resting cells with unintegrated virus that did not complete the transition to latent infection [10]. Then, after about 6 months of treatment, a more stable underlying population is revealed at a frequency of about 1 in a million, which decays extremely slowly, with a median half-life of 44 months [46, 120, 34]. This finding consolidated the realization that the duration of therapy needed at achieve a cure (≈70 years) was too long to have any practical value, and that antiretroviral therapy would need to be continued for life. This was supported by observations of universal and rapid rebound in viremia to pre-treatment levels when therapy was stopped [36, 114].

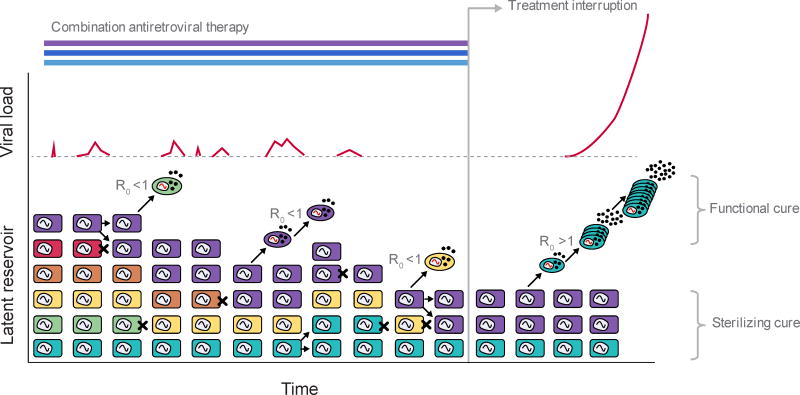
Once it was established that both latent HIV and residual plasma viremia persist almost indefinitely despite therapy, the major question became the mechanism for this persistence (Figure 3). One hypothesis is that the latent infection is maintained by the same mechanisms as immunologic memory, and the occasional reactivation of latent cells is responsible for residual viremia [9, 120]. Another theory is that ART is not completely effective in stopping viral replication (R₀ > 1), and that continual rounds of infection cause persistent viremia or persistent latent infection, or both [33, 78].

Fig. 3.

Schematic of latent reservoir dynamics. Long-lived resting memory CD4⁺ T cells (squares) may contain integrated HIV provirus - these cells comprise the latent reservoir. The majority of evidence suggests that during combination antiretroviral therapy in most patients, viral replication is subcritical (R₀ < 1) and so the persistence of virus represents the maintenance of the latent reservoir. Latently infected cells may occasionally die (black X), proliferate, or reactivate. The relative contribution of slow death vs proliferation to stability of the reservoir is still being worked out. A large contribution of proliferation would result in the virus in the reservoir becoming less diverse over time. Reactivated latent cells (ovals) can produce virus which can contribute to observed levels of residual viremia. New infections may occasionally occur but continuous chains of replication and evolution cannot occur when R₀ < 1. When treatment is interrupted (R₀ > 1), reactivated cells can produce virus that infects other cells, which, if it escapes stochastic extinction, can lead to eventual viral rebound. Research into curative interventions for HIV aim to prevent viral rebound by one of two mechanisms: either clearing enough latent virus or blocking reactivation to an extent that there is insufficient reactivation to seed rebound (“sterilizing cure”), or, by equipping the body with the ability to control the infection even in the face of reactivating virus (“functional cure”). Examples of potential sterilizing cures involve latency reversing agents or bone marrow transplants, and examples of functional cures involve therapeutic vaccination or CCR5-knockout gene therapies.

A large body of modeling work has investigated the relationship between the dynamics of latently infected cells and plasma viremia during ART [66, 60, 117, 107, 30, 32]. The most important insight from these studies is that as long as ART is marginally effective, the persistence of latent virus is dominantly influenced by the longevity of infected lymphocytes and the rate at which they reactivate, and not by any ongoing replication that continually seeds the reservoir. Models predict that low amounts of ongoing replication (0 < R₀ < 1) may influence the level of detectable plasma virus, but that these levels of replication are highly unlikely to allow for long-term sequence evolution of this virus (for example, the development of drug resistance)[66, 117, 107, 32]. Various clinical studies have shown that residual plasma virus levels during ART may fluctuate over time, occasionally producing higher “blips” in viral RNA, and models suggest that the size, duration, and frequency of these blips can be explained by occasional antigen-driven reactivation of latent cells [66, 60, 107, 30].

Experimental work backs up many of these modeling predictions. Ex vivo quantifications of antiretroviral efficacy suggest multi-log reduction in viral replication [119, 59]. Long-term studies of low-level plasma virus sequences show a lack of evolution, including a lack of development of drug resistance [65, 61]. “Treatment intensification” studies add a fourth or fifth antiretroviral drug to existing combination therapy, and show no change in residual viremia levels, suggesting that viral replication is optimally suppressed [38, 48]. The size of the latent reservoir is highly correlated with the level of plasma viremia during ART [7]. A study that tracked the movement of particular unique viral genetic sequences between plasma virus and resting memory CD4⁺ T cells was able to put an upper limit on the number of new latent cells produced each day (≈100), and show that this had a negligible impact on reservoir persistence [118].

While most evidence from models and experiments points towards ART being highly effective and the latent reservoir persisting due to intrinsic memory T cell longevity, some findings appear to conflict with this theory. When treatment intensification studies were done by adding the integrase inhibitor raltegravir to patients taking three drugs from other classes, some studies tracked not only plasma viral RNA but also levels of a type of circularized viral DNA (“2-LTR circle”) that forms in cells when virus is unable to complete the integration step. Similar to other studies, treatment intensification did not influence plasma viremia, but 2-LTR levels showed a transient increase in some patients [18, 50]. Modeling work by Luo et al [72] showed that these kinetics could not be explained the dynamics of latent and actively infected cells under fully-effective ART (R₀ < 1 everywhere), but instead were highly suggestive of at least a small compartment in the body where viral replication continued (R₀ > 1) despite ART. However, this effect was only observed in about 1 in 6 patients, and model conclusions were sensitive to the (noisy) experimental data, and so the clinical significance is still being debated.

Even if the persistence of residual viremia can be explained completely by occasional reactivation of latent cells, and if the slow decay of the latent reservoir is purely a product of memory T cell maintenance, the dynamics of latency itself remain opaque. In the absence of any re-seeding, the total decay rate of the reservoir is the net effect of cell death, cell reactivation, and cell proliferation. Various combinations of each of these processes could lead to the same observed net decay. For example, if latent cells lived on average 5.5 years, reactivated on average every 70 years, and never proliferated, then the reservoir would decay at a rate of 0.2/years, equivalent to a 44 month half-life. The same net decay would occur if cells instead lived only 4 months and proliferated every 114 days. Some researchers initially assumed that latently infected CD4⁺ T cells could not undergo proliferation without reactivating viral gene expression and succumbing to viral cytopathic effects or cytolytic immune responses. However, multiple lines of evidence now suggest that latently infected cells can indeed divide and expand without reactivating, including studies of cell-surface markers and cytokines indicative of proliferation in virally-suppressed individuals [21], repeated occurrences of an exact viral integration site or full-length genetic sequence [28, 76, 121], or ex vivo culture experiments [57]. Even before this evidence existed, various mathematical models included the possibility of all three changes to reservoir size, but parameter values have simply been educated guesses and to date the relative contribution of each process to reservoir stability remains unknown [66, 106, 22]. The efficacy of hypothetical interventions to speed up killing of latently infected cells or inhibit their proliferation can only be estimated if quantitative values can be determined for these processes.

4 Strategies to clear the reservoir and cure HIV infection

The persistence of latent HIV prevents combination antiretroviral therapy from being curative. If therapy is stopped, viral load rebounds in approximately 2 weeks and rapidly reaches high levels similar to acute infection [36, 114] (Figure 3). This rebound occurs in patients treated early in infection [108, 62], in primate models of HIV (SIV-infected rhesus macaques) treated within a few days of infection [129], and in individuals in whom the reservoir size is reduced by multiple orders of magnitude compared to typical infected people [25, 51, 73]. Consequently, it is now accepted that achieving a cure in most patients will require either a method to augment immunity or complete clearance of the latent reservoir [115, 2].

The observed decay rate of the reservoir during ART suggests that 60+ years of therapy would likely be needed to clear all latently infected cells (around 10⁶ cells with a 44 month half life), and even a 1,000-fold smaller than average reservoir size would take ≈30 years to clear on its own. These calculations optimistically assume that the reservoir is homogeneous and the decay rate is constant, while in reality decay may slow over time, for example, if cells specific to more common antigens reactivate and are cleared sooner [66]. Even if some low-level, subcritical replication persists during ART that allows occasional entry of new cells into the latent pool, the body of modeling work cited in the previous section concludes that complete elimination of replication would have an insignificant impact on the rate of reservoir decay [66, 117, 107, 32]. Clearly, eradicating the latent reservoir will require the development of new interventions.

The important question posed to modelers in regards to disrupting HIV latency is “How much must the latent reservoir be reduced to delay or prevent viral rebound once ART is stopped?”. Stochastic models of the latent reservoir and low-level infection are required to answer this question. Hill et al [52] estimated used such a model to estimate that reservoir reductions of 2 to 3 logs are required to delay rebound for a few months, while > 4-log reductions may be required for cure in most patients. They predicted that patients may rebound even after experiencing several years off treatment without detectable viremia, which was later observed [51, 73]. Additionally, their model demonstrated that large inter-patient variation in times to rebound is expected when reservoir sizes were reduced - simply due to the stochastic nature of reactivation from latency and infection dynamics at low population sizes. Overall, this work suggested that reservoir clearance must be nearly complete to have any significant clinical benefit, and that designing and interpreting clinical trials for reservoir-reducing strategies would be complex. Pinkevych et al [98] developed a similar model to address the same questions, but their conclusions were much more optimistic: they suggested that a 50-fold reduction in the reservoir size could result in a 1 year remission.

The main difference between these modeling approaches, and the main source of uncertainty in the predictions of any given model, are the parameter values. Hill et al [52] examined a large class of stochastic viral dynamics models analytically and numerically and determined that the predictions for rebound time depend only on a small number of composite parameters. Two of these parameters can be estimated from clinical data relatively easily: the half-life of the pool of latently infected cells is estimated from studies of LR decay [120, 34], and the viral growth rate can be estimated from studies of supervised cART interruption [71, 114]. A third parameter is the rate at which latently infected cells reactivate (or, framed another way, the number of cells that reactivate daily from typical reservoir sizes), and different methods to estimate this rate are the major source of discrepancy between different models. Many earlier models that tracked latent infection during ART but were not specifically designed to be used to model reservoir clearance estimated this rate based on the cellular activation required to explain the observed levels of residual viremia (≈ 1 HIV RNA/ml), getting values on the order of 1000 cells/day in the whole body [117, 66, 107, 30, 109, 31, 32]. Other work by Luo et al [71] estimated this rate based on the timing of viral rebound upon ART cessation (≈0.03 viral RNA/mL/day or 60 cells/day). Hill et al [52] used this value, but also needed to estimate a fourth composite parameter: the probability that a single activated cell manages to establish a growing infection. This quantity can only be indirectly estimated from in vitro [122, 15] and population-genetic studies [110, 89, 90] (reviewed in Rouzine et al [112]), and remains quite uncertain.

Pinkevych et al [98] used a simplified, approximate model in which viral growth occurs deterministically once a cell that is fated to establish a growing infection exits the reservoir. Consequently, they only estimated the product of the reservoir exit rate and the establishment probability. To do this, they assumed that all variation in rebound time between different patients was caused by different timing of viral reactivation. Since rebound times vary by up to a week between patients with (assumed) identical reservoir sizes, they concluded that the effective activation rate was low, and therefore therefore that any reservoir reduction would significantly delay rebound. Hill et al [54] have argued that varying rebound times are better explained by inter-patient variation in parameter values, and that the lack of variation in typical rebound times despite the 2–3 orders of magnitude variation in typical reservoir sizes is more consistent with their estimate of multiple effective reactivations per day vs rare reactivation (≈4/day vs ≈1/6 days). Additional experimental work will be needed to resolve this issue and narrow down estimates for these important rates.

Both Pinkevych and Hill have developed methods to use model predictions to interpret treatment interruption trials. They demonstrate that large trial sizes will be needed to estimate the reservoir reduction achieved by a particular therapy from the timing of rebound [98, 53]. They offer estimates for the reservoir size in the Boston patients [51] and Mississippi baby [73] based on rebound delay, and suggest ways to design the frequency of viral load sampling during interruption trials. These activities demonstrate how mathematical models can be used to design the most informative and cost-effective clinical trials and optimally interpret the findings in the context of prior knowledge.

These modeling conclusions are agnostic to how the latent reservoir is reduced, which could be accomplished by a variety of means. Much experimental work has focused on identifying drug candidates which can reactivate latent infection, with the hope that cells that are rapidly reactivated will then die to to viral cytopathic effects of cytolytic immune responses, without reverting back to latency. Many such compounds, called “latency reversing agents (LRA)” have been identified (see next chapter), but their efficacy so far in vitro [16] or in vivo [40, 41, 100, 126] has been relatively limited. Mathematical modelers have evaluated the expected dynamics of latent infection, active infection, and viremia under latency reversing treatment [96, 55]. Petravic et al [96] have outlined a method to relate the observed dynamics of cells expressing HIV during ART+LRA to an expectation for reservoir reduction, and used it to interpret recent clinical trials of two LRAs [40, 100]. Hill et al [55] have suggested that under most realistic conditions, LRA which significantly reduce the latent reservoir should cause relatively large, detectable blips in plasma viremia. The shape and size of these blips may be used to estimate parameters related to LRA-activated cells and reservoir reduction. However both sets of authors concluded that the expected levels of HIV transcription or viremia are dependent on the lifespan and burst size of LRA-reactivated cells, which may differ from naturally activated cells, complicating interpretation.

Other work has focused on understanding when - in the course of infection and treatment - is the ideal time to administer latency reversing treatment. Petravic et al [95] suggest that because the turnover of the latent reservoir in resting CD4 T cells is higher when viral loads are higher, it would be most effective to administer latency reversing drugs immediately following ART initiation. This is in contrast to the common practice in existing trials of latency reversing agents, where only patients who have been ART for many years with fully suppressed viral loads are included.

Instead of trying to reduce the size of the latent reservoir once it’s formed, other work has focused on preventing seeding of the latent reservoir in the first place. The question is then how early ART must be initiated to result in small enough reservoir sizes to delay or prevent viral rebound when ART is later stopped. Archin et al [7] used paired measurements of viral load and CD4 count pre-treatment along with reservoir size post-treatment to estimate the rate at which the latent reservoir is seeded. They compared the observed data to a mathematical model in which some fraction of new infected cells become latent, as opposed to actively producing virus. In agreement with predictions of this model, the reservoir size was highly correlated with the area-under-the-curve of the product of viral load and CD4 count during acute infection, and they were able to estimate the fraction of cells that became latent. This work suggested that the vast majority of reservoir seeding happens during peak viremia in acute infection, and very early ART would be needed to substantially limit seeding. In a primate model of infection, there was a similarly strong relationship between pre-treatment viral burden and reservoir size that was well-described by simple models, and even ART initiated 3 days after infection did not prevent viral rebound when treatment was stopped [129]. Similarly, case studies of immediate post-partum treatment of neonates infected during gestation showed that reservoir sizes could be limited to extremely small levels and rebound delayed for months to years, but not be prevented all together [73]. Therefore, it is now clear that for the majority of patients even extremely early ART initiation is unlikely to make a cure possible.

There are a subset of patients in whom early treatment seems to have a disproportionately beneficial effect. Multiple cohort studies have retrospectively identified a group of “post-treatment controllers”, who had high viremia during acute infection, but do not rebound, or rebound only to very low levels, following ART interruption [49, 70, 125, 26, 75, 43]. The mechanisms of this effect are still unknown. Most models of HIV infection do not display this behavior [83]. Early work by Wodarz et al [132, 131] suggested that the dynamics of memory CD8⁺ T cells (i.e. cytotoxic T lymphocytes, CTL) – in particular their dependence on CD4 help and their persistence during ART – could lead to control after ART interruption, a phenomenon that had been observed in the SIV system as early as 2000 by Lifson et al [67, 68]. More recently, Conway and Perelson [31] have explored the potential basis of post-treatment control using a viral dynamics models that track latent and active infection, and cytolytic immune responses which expand in the presence of viral antigen but may also become exhausted from antigen exposure. They found that this model yields bistability: Even for identical parameter values, different initial conditions can make the difference between establishment of a high setpoint viral load, or control of viral load to a low level. This implies that the size of the latent reservoir at the time of ART interruption (the “initial condition”) could determine which state the infection ends up in. Their work suggests that early treatment initiation either a) in a subset of patients with relatively effective immune responses, or, b) in combination with an immune-boosting intervention, could be used to induce indefinite post-treatment control. Such a curative intervention would be termed a “functional cure” – meaning that latent cells would remain and occasionally reactivate but high-level rebound would be avoided – as opposed to a “sterilizing cure” in which latent cells would be cleared. However, this work currently remains speculative, because the observation of bistability in models is sensitive to the model structure and to values of pararameters, and, because we do not know the immunological basis of post-treatment control and do not know how to identify patients who may benefit from it.

The conclusion of this body of modeling work is that clearing the latent reservoir to a low enough level to significantly delay or prevent viral rebound upon ART cessation is likely impossible in most patients. Instead, curative interventions will likely need to instead limit the ability of reactivated virus to re-start full-blown infection. One approach is to administer immunotherapy or therapeutic vaccination along with ART or after ART cessation, to reduce the fitness of reactivated virus. Recent studies in SIV-infected primates have highlighted the potential promise of this approach [69, 13, 19]. In these studies, viral rebound was delayed, reached lower peak levels, and was eventually controlled (suppressed below the detection limit) in a subset of animals, and modeling work suggested that the dominant mechanism for this control was based on the immunologic effect, and not the reservoir reduction.

5 HIV latency and viral evolution

The rapid evolution of HIV is known to play a major role in pathogenesis, and is also responsible for viral adaptation to humans after crossing over from primates 1̃00 years ago. Researchers have used mathematical models to investigate the role that latent infection plays in the rate and direction of HIV evolution within and between hosts. Other work has theorized about whether latency is itself an evolved trait of HIV, as opposed to simply a byproduct of the lifecycle of the lymphocytes the virus infects.

The long-lived nature of latently infected cells compared to those actively producing virus means that the latent reservoir serves as an archive of viral strains present at earlier time points in infection. Most virus produced in the bloodstream is from cells that were recently infected, and so will contain the most recently evolved strains, whereas the provirus contained in latently infected cells – which may occasionally reactivate and produce virions – may contain more ancestral virus that is more genetically similar to the transmitted strain. Genetic sequencing of plasma viral RNA and proviral DNA in cells that remain after long-term therapy has confirmed this hypothesis, showing that archived strains means that wildtype virus can persist despite years of antiretroviral therapy and drug resistant strains can persist after therapy has stopped [94, 113, 65, 86, 130].

Mathematical models of viral evolution which take into account this strain archiving have suggested that it has multiple effects on infection dynamics. Within an individual patient, the rate of intra-host evolution may be decreased relative to the case without latency [63, 39], drug resistant mutations may appear in the absence of ongoing replication from pre-existing strains the reservoir [109], and recombination could occur between strains which dominated the viral population at very different times during infection [58]. At a population level, strain archiving resulting in selective transmission of ancestral virus may explain the paradoxically slow rate of between-host HIV evolution [1, 74], by allowing transmission of strains similar to those which initiated the infection despite years of diversification during chronic infection, and could theoretically change the evolutionarily optimal set-point viral load [39]. The relative magnitude of these effects is more uncertain, as it depends strongly on the fraction of infections that become latent, the turnover of the latent reservoir, and the effective population size of active infection, which are all difficult to quantify.

Given that the presence of viral latency alters HIV dynamics, a natural question is whether latency itself is an adaptive trait that the virus has evolved to increase some aspect of fitness. While most experimental evidence is consistent with latency as a byproduct of the natural lifecycle of activated T cells [81], some cell-culture work on latency also supports the idea that viral gene expression can be switched off by a virally-encoded, transcription-factor mediated feedback loop [128, 101]. Inspired by that work, a mathematical modeling study showed that if latency enhances trafficking of infected cells across the musoca after inoculation, viral latency could increase transmission rates and be evolutionarily favored [111]. However, some predictions of this model – such as the high fraction of cells reverting to latency during early infection and the potential for a long delay between inoculation and establishment of infection – continue to be debated.