Study of biological networks using graph theory

Abstract

As an effective modeling, analysis and computational tool, graph theory is widely used in biological mathematics to deal with various biology problems. In the field of microbiology, graph can express the molecular structure, where cell, gene or protein can be denoted as a vertex, and the connect element can be regarded as an edge. In this way, the biological activity characteristic can be measured via topological index computing in the corresponding graphs. In our article, we mainly study the biology features of biological networks in terms of eccentric topological indices computation. By means of graph structure analysis and distance calculating, the exact expression of several important eccentric related indices of hypertree network and X-tree are determined. The conclusions we get in this paper illustrate that the bioengineering has the promising application prospects.

1. Introduction

In mathematical biology, mathematical methods are applied to biology to deal with various modeling and calculation problems. In the microscopic field of biology, DNA and other protein molecular structure can be represented as a graph, and thus as a mathematical tool, graph theory is introduced to the analysis and calculation of molecular topology.

1.1. Example 1. DNA graphs

The study of DNA sequence is the most important issue in biology science, and there are lots of contributions on DNA analysis and computation from mathematical and algorithmic point of view (Rastgou et al., 2017, Shoaib et al., 2017) pointed out that Hartree-Fock exchange percentage of density functional has a key factor in getting the structure electronic properties. The notable features sequencing platform based on a mathematical framework and it working mechanism has some characteristics, such as: optimizing cost, implement, and sensitivity analysis to different parameters (O'Reilly et al., 2016). The demography and reproductive success and by means of coalescent theory to compute mitochondrial DNA sequences from the Japanese sardine (Niwa et al., 2016, F.J. Khan et al., 2017, H.U. Khan et al., 2017, Samina and Khan, 2017). The DNA storage channel and modeled the read process considering profile vectors. They raised new asymmetric coding tricks to combat the effects of sequencing noise and synthesis, and an asymptotic analysis of the number of profile vectors was also presented. At last, two families of codes for this channel model were constructed. To effectively store FASTQ files raised by big DNA sequencers, Chlopkowski et al. (2016) determined a specialized compressor designing. The ionization potential with single and double excitations was estimated by means of equation of motion coupled cluster trick, and VIEs is estimated in terms of density functional theory with dispersion corrected omega B97x-D (Chakraborty and Ghosh, 2016). A studied on how to build independent spanning trees on hypercubes and how to use them to predict mitochondrial DNA sequence parts through paths on the hypercube (da Silva and Pedrini, 2016). An alignment-free technology for DNA sequence similarity analysis based on graph theory concepts and genetic codes (Jafarzadeh and Iranmanesh, 2016a, Jafarzadeh and Iranmanesh, 2016b). The new approach to test the DNA sequences using optical joint Fourier transform (Alqallaf and Cherri, 2016). Theoretically studied the transverse electron transport through all four DNA nucleotide bases by electron propagator theory (Kletsov et al., 2015).

Let $k⩾2$ be an integer. The DNA graph is defined by Wang et al. (2008), and it said that a directed graph $D=(V(D)\text{,}E(D))$ is DNA graph whether it can assign a label $(l_1(x)\text{,}{l}_2(x)\text{,}\dots \text{,}{l}_k(x))$ of length k to each vertex $x\in V(D)$ as follows:

• (1)$l_i(x)\in \{\text{A,C,T,G}\}$ where $i\in \{1\text{,}\dots \text{,}k\}$;
• (2)$(l_1(x)\text{,}{l}_2(x)\text{,}\dots \text{,}{l}_k(x))\ne (l_1(y)\text{,}{l}_2(y)\text{,}\dots \text{,}{l}_k(y))$ if $x\ne y$;
• (3)$(x\text{,}y)\in E(D)$ if an only if $(l_2(x)\text{,}\dots \text{,}{l}_k(x))=(l_1(y)\text{,}\dots \text{,}{l}_{k-1}(y))$.

For a multiset consists of oligonucleotides with length k, a DNA graph can be constructed as follows: set each oligonucleotide with length k from the multiset as a vertex; add an arc between two vertices if the $k-1$ rightmost nucleotides of first vertex overlap with the $k-1$ leftmost nucleotides of the second one. Several contributions on DNA graph and DNA mathematical expression (Aram and Iranmanesh, 2012, Pesek and Zerovnik, 2008, Jafarzadeh and Iranmanesh, 2012, Bokhari and Sauer, 2005, Blazewicz et al., 1999, Sa-Ardyen et al., 2003, Pendavingh et al., 2003, Blazewicz et al., 2009, Pevzner et al., 2001, Jafarzadeh and Iranmanesh, 2013, F.J. Khan et al., 2017, H.U. Khan et al., 2017, Shah and Bushnaq, 2017).

1.2. Example 2. Biological networks

The main task of microorganism science is to study the viruses, protozoa, bacteria, euglena, opalinia, fungi, paramecium and amoeba et al. All living organisms consist of cells which are basic structure of life and can be expressed as vertex in the graph model. As an important biology computation model, biological networks are used to deal with biology problems in which its vertex represent cells, genes or proteins, and its edges are expressed as the potential connection between these components. For instance, the mathematical framework of protein interaction, gene expression, carrier transfer information and metabolic networks can be regarded as biological networks. The topological index defined on biological networks can be considered as a numeric function which maps the given structure to a real number, and thus measure its physical, chemical and biological characters. Some contributions on biological networks and other graph applications in biology science can refer to (Jafarzadeh and Iranmanesh, 2016a, Jafarzadeh and Iranmanesh, 2016b, Nandagopal and Elowitz, 2011, Rajan et al., 2015, Alexander, 2013, Banerjee and Jost, 2007, Ma'ayan, 2008, Mason and Verwoerd, 2006, Lesne, 2006, Eckman and Brown, 2006, Aittokallio and Schwikowski, 2006, El-Ghoul et al., 2006).

In this paper, we focus on the biochemical properties of biological networks via topological index computation. The structure of the rest of this paper is stated as follows: we first give the information about the setting of topological index defined on biological networks; then, the main results and their detailed proofs are presented in Section 3; at last, we discuss the future projects in this filed.

2. Setting

In what follows, let G = $(V(G)\text{,}E(G))$ be a undirected molecular graph with vertex set $V(G)$ and edge set $E(G)$, where each vertex expresses a cell, gene or protein, and each edge is presented as the connection between two components. A topological index can be a function f: $G\to {\mathbb{R}}^{+}$ which can map each molecular graph to a positive real number. Several degree-based or distance-based topological indices like Wiener index, atom-bond connectivity index, harmonic index, sum connectivity index and others are defined to test the chemical, physical, pharmaceutical and biological properties. Furthermore, there are some mention-able work on distance-based and degree-based topological indices of special structures which can be referred to Basavanagoud et al., 2017, Gao et al., 2016a, Gao et al., 2016b, Gao et al., 2016c, Gao et al., 2016d, Gao et al., 2017a, Gao et al., 2017b, Gao and Siddiqui, 2017, Gao and Wang, 2015, Gao and Wang, 2016.

The distance $d(u\text{,}v)$ between two vertices u and v in a connected graph is denoted as the length of the shortest path between them. For any vertex $v\in V(G)$, the eccentricity of v is defined as $\mathit{ec}(v)=\max \{d(v\text{,}u)|u\in V(G)\}$.

Ghorbani and Khaki (2010) introduced the eccentric version of geometric-arithmetic index as fourth geometric-arithmetic eccentricity index which is stated as

$${\mathit{GA}}_4(G)={\displaystyle \sum _{\mathit{uv}\in E(G)}}\frac{2\sqrt{\mathit{ec}(u)\mathit{ec}(v)}}{\mathit{ec}(u)+\mathit{ec}(v)}\text{.}$$

The fourth Zagreb index is defined by Farahani and Kanna (2015) as

$${\mathit{Zg}}_4(G)={\displaystyle \sum _{\mathit{uv}\in E(G)}}(\mathit{ec}(u)+\mathit{ec}(v))\text{.}$$

Its multiplicative version, named as the fourth multiplicative Zagreb index, is stated by

$${\mathrm{\Pi }}_4^{\ast }(G)={\displaystyle \prod _{\mathit{uv}\in E(G)}}(\mathit{ec}(u)+\mathit{ec}(v))\text{.}$$

Analogously, the sixth Zagreb index is described as

$${\mathit{Zg}}_6(G)={\displaystyle \sum _{\mathit{uv}\in E(G)}}\mathit{ec}(u)\mathit{ec}(v)\text{.}$$

And, the multiplicative version, named as sixth multiplicative Zagreb index is defined by

$${\mathrm{\Pi }}_6^{\ast }(G)={\displaystyle \prod _{\mathit{uv}\in E(G)}}\mathit{ec}(u)\mathit{ec}(v)\text{.}$$

Correspondingly, the fourth Zagreb polynomial and the sixth Zagreb polynomial are defined as

$${\mathit{Zg}}_4(G\text{,}x)={\displaystyle \sum _{\mathit{uv}\in E(G)}}{x}^{\mathit{ec}(u)+\mathit{ec}(v)}$$

and

$${\mathit{Zg}}_6(G\text{,}x)={\displaystyle \sum _{\mathit{uv}\in E(G)}}{x}^{\mathit{ec}(u)\mathit{ec}(v)}\text{,}$$

respectively.

Motivated by Kulli (2016) who introduced the multiplicative version of first atom bond connectivity index, we defined the fifth multiplicative atom bond connectivity index

$${\mathit{ABC}}_5\prod (G)={\displaystyle \prod _{\mathit{uv}\in E(G)}}\sqrt{\frac{\mathit{ec}(u)+\mathit{ec}(v)-2}{\mathit{ec}(u)\mathit{ec}(v)}}\text{.}$$

The traditional tree pattern of a tree which is a connected cyclic graph, is usually a binary tree where is composed with vertices, and there are a left reference, a right reference and a data element existing in it. We name the top most vertex root. There are three fields in the vertex of the binary tree. To illustrate, the data are denoted in one field, and the information of left and right sons of the vertex is located in the other two fields. The binary tree can meet the requirements to be a complete binary tree (described in Fig. 1), if there are just two descendants in every internal vertex.

Fig. 1.

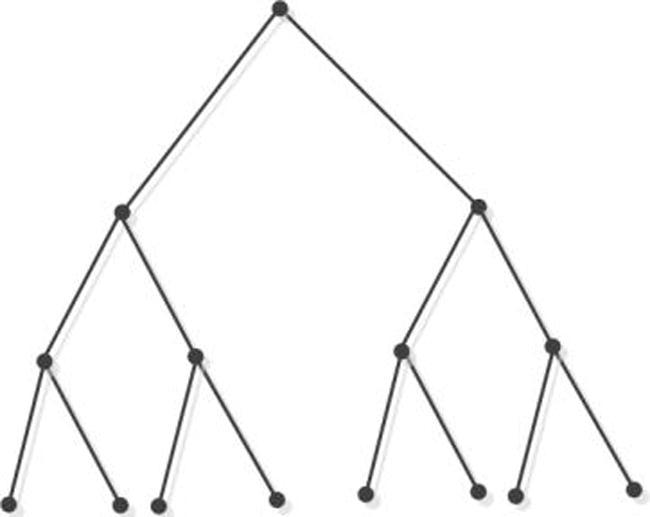
Binary tree.

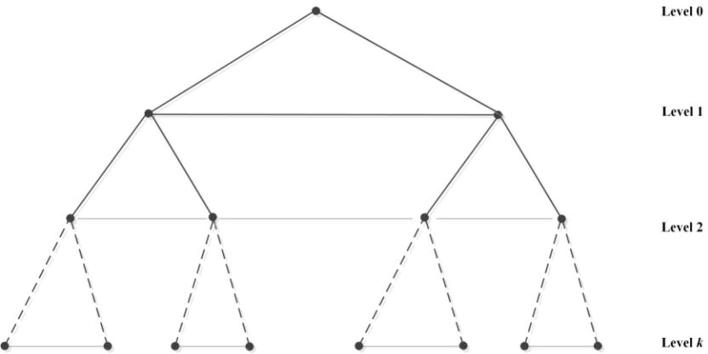
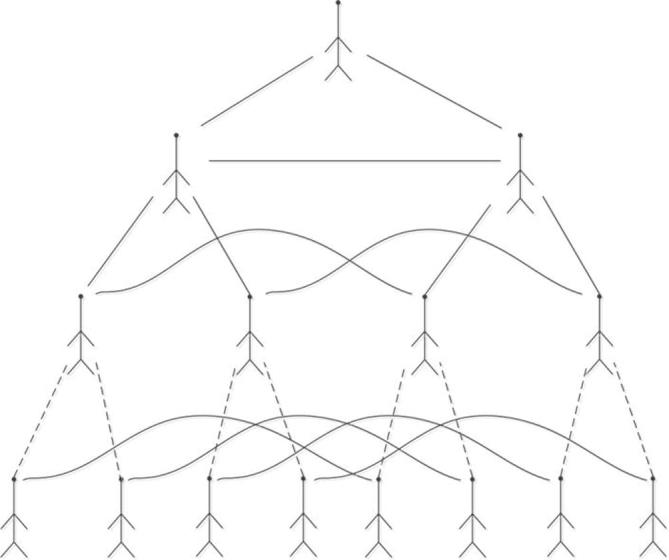
The fundamental structure of hypertree k-level is easy to be confirmed as a complete binary tree $\mathit{HT}(k)$. The root vertex of the tree is marked by label 1 and its root is at level 0. If 0 and 1 are added to the labels of the parent vertex separately, we can obtain the labels of left and right children. Then we can denote the children of the vertex x into 2x and 2x + 1. Moreover, other links of hypertree are horizontal and when the label difference of the vertices is $2^{i-2}$, the two vertices which share the same level of the tree are joined. As a result, if we add edges (sibling edges) between left and right children of the same parent vertex, we will get the 1-rooted sibling tree ${\mathit{ST}}_k^1$ (described in Fig. 2) from the 1-rooted tree $T_k^1$.

Fig. 2.

1-rooted sibling tree network ${\mathit{ST}}_k^1$.

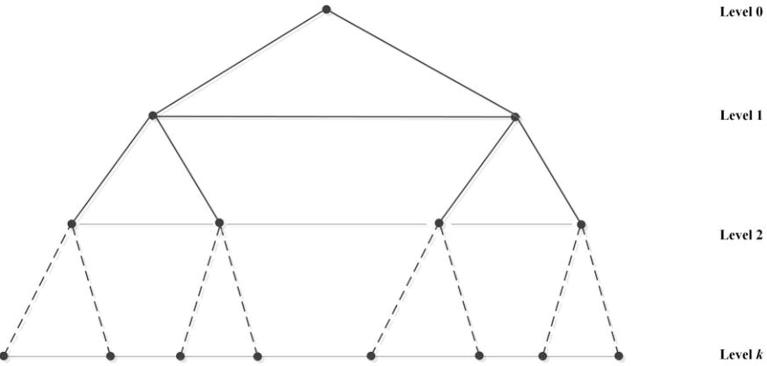
We also obtain the X-tree $\mathit{XT}(k)$ whose structure is described in Fig. 3 from complete binary tree on $2^{k+1}-1$ vertices of height $2^i-1$ and adding paths $P_i$ left to right by all the vertices at level i with $i\in \{1\text{,}\dots \text{,}k\}$.

Fig. 3.

k-level X-tree network $\mathit{XT}(k)$.

3. Main results and proofs

This section mainly aims to calculate a closed result of eccentric related indices. Besides, the result of two kinds of eccentric version Zagreb polynomials for hyper binary trees, and for k-level networks is also aimed to be achieved. Meanwhile, with the purpose to explore the biological properties and activities, this section will borrow the networks to biological networks. There are numerous micro livings such as bacteria, viruses and others in our everyday life, which could be a problem of our life and also a good thing for our health. In terms of the structure of bacteria, they are single celled without true nucleus. The bacteria reproduce quickly and productively by conducting binary fission. During the process, a parental cell is splited into two daughter cells. Sometimes, bacteria and viruses could be dangerous in our life, for they may cause disease or make the disease more serious. With the help of replication, the action of copying, we start the reproduction procedure of viruses. Some diseases like Tuberculosis, cholera, typhoid, influenza, HIV (AIDS), chicken pox might be fatal if they are not considered seriously in time.

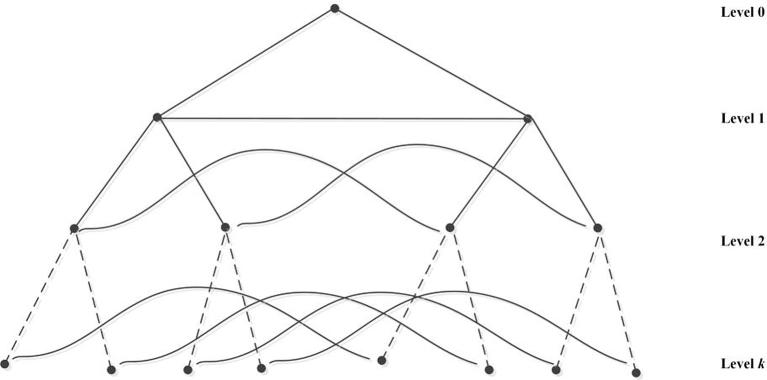
In the process, it’s the infected person that serves as the media to spread diseases. For example, a person who gets cold and fever will spread the bacteria and viruses whenever they get touch with other people. They can spread by sneezing or by touching/shaking hands with others. Usually, the body fluids play a necessary role in transferring bacteria and viruses among people. We can regard the hypertree network as hypertree biological network. Hence, the parental vertex is considered as the ill person who carries bacteria and viruses, which is shown in Fig. 4. The bacteria reproduce quickly and productively by conducting binary fission, so we can suppose two persons that are infected by an ill person. Their interaction and communications will help to increase the disease level. Maybe one patient is weaker than another one for his immunological deficiency, which arouses the increase in this kind of disease. What we practice in reality to deal with the problem is to take anti-infection medicine. In the below, we obtain a closed result of eccentric related indices and polynomials for hypertree k level $\mathit{HT}(k)$ which is presented in Fig. 5.

Fig. 4.

Hypertree biological network.

Fig. 5.

k-level hypertree network $\mathit{HT}(k)$.

Let $\delta =\min \{\mathit{ec}(v)|v\in V(G)\}$ and $\mathrm{\Delta }=\max \{\mathit{ec}(v)|v\in V(G)\}$. The edge set E(G) and vertex set V (G) can be classed into the following subsets:

• •for any i with $\delta \le i\le \mathit{Delta}$, let $D_i$ = {u ∈ V(G)|$\mathit{ec}(v)$ = i} and $d_i=|D_i|$;
• •for any i, j meet $\delta$ ≤ i, j ≤ Δ, let $E_{i\text{,}j}$ = {e = uv ∈ E(G)|$\mathit{ec}(u)$ = i, and $\mathit{ec}(v)$ = j} and $n_{\mathit{ij}}=|E_{i\text{,}j}|$.

Theorem 1

Let $\mathit{HT}(k)$ be the k-level hypertree network. We have

$${\mathit{GA}}_4(\mathit{HT}(k))=3+{\displaystyle \sum _{i=1}^{k-1}}{\displaystyle \sum _{p=k}^{2k-2}}{2}^i\left(\frac{4\sqrt{p(p+1)}}{2p+1}+1\right)\text{,}$$

$${\mathit{Zg}}_4(\mathit{HT}(k))=6k+(9k-2)(2^k-2)(k-1)\text{,}$$

$${\mathrm{\Pi }}_4^{\ast }(\mathit{HT}(k))=6k{\displaystyle \prod _{i=1}^{k-1}}{\displaystyle \prod _{p=k}^{2k-2}}{2}^{2i}(4p+2)(2p+2)\text{,}$$

$${\mathit{Zg}}_6(\mathit{HT}(k))=3k^2+\frac{7k(2^k-2)(2k^2-3k+1)}{2}\text{,}$$

$${\mathrm{\Pi }}_6^{\ast }(\mathit{HT}(k))=3k^2{\displaystyle \prod _{i=1}^{k-1}}{\displaystyle \prod _{p=k}^{2k-2}}{2}^{2i+1}p{(p+1)}^3\text{,}$$

$${\mathit{Zg}}_4(\mathit{HT}(k)\text{,}x)=3x^{2k}+{\displaystyle \sum _{i=1}^{k-1}}{\displaystyle \sum _{p=k}^{2k-2}}(2^{i+1}{x}^{2p+1}+2^i{x}^{2p+2})\text{,}$$

$${\mathit{Zg}}_6(\mathit{HT}(k)\text{,}x)=3x^{k^2}+{\displaystyle \sum _{i=1}^{k-1}}{\displaystyle \sum _{p=k}^{2k-2}}(2^{i+1}{x}^{p(p+1)}+2^i{x}^{{(p+1)}^2})\text{,}$$

$${\mathit{ABC}}_5\prod (\mathit{HT}(k))=\frac{3\sqrt{2k-2}}{k}{\displaystyle \prod _{i=1}^{k-1}}{\displaystyle \prod _{p=k}^{2k-2}}\frac{2^{2i+1}}{p+1}\sqrt{\frac{4p-2}{p+1}}\text{.}$$

Proof of Theorem 1

We prove the result based on the structure analysis and edge dividing technology.

By analyzing the structure of $\mathit{HT}(k)$ and compute the distances from vertices, it’s edge set $E(\mathit{HT}(k))$ can be divided into three partitions according to the eccentricities of associated vertices:

• •$E_{p\text{,}p}=\{e=\mathit{uv}\in E(G)|\mathit{ec}(u)=\mathit{ec}(v)=p\}$ and $n_{\mathit{pp}}=3·2^i$, where i = 0 and p = k;
• •$E_{p\text{,}p+1}=\{e=\mathit{uv}\in E(G)|\mathit{ec}(u)=p$ and $\mathit{ec}(v)=p+1$} and $n_{p(p+1)}=2·2^i$, where $i\in \{1\text{,}\dots \text{,}k-1\}$ and $p\in \{k\text{,}\dots \text{,}2k-2\}$;
• •$E_{p+1\text{,}p+1}=\{e=\mathit{uv}\in E(G)|\mathit{ec}(u)=\mathit{ec}(v)=p+1$} and $n_{(p+1)(p+1)}=2^i\text{,}$

where $i\in \{1\text{,}\dots \text{,}k-1\}$ and $p\in \{k\text{,}\dots \text{,}2k-2\}$.

Form the definitions of eccentric version indices, we get

$${\mathit{GA}}_4(\mathit{HT}(k))={\displaystyle \sum _{i=0}}3·2^i{\displaystyle \sum _{p=k}}\frac{2\sqrt{p^2}}{p+p}+{\displaystyle \sum _{i=1}^{k-1}}2·2^i{\displaystyle \sum _{p=k}^{2k-2}}\frac{2\sqrt{p(p+1)}}{p+p+1}+{\displaystyle \sum _{i=1}^{k-1}}{2}^i{\displaystyle \sum _{p=k}^{2k-2}}\frac{2\sqrt{(p+1)(p+1)}}{p+1+p+1}=3+{\displaystyle \sum _{i=1}^{k-1}}{\displaystyle \sum _{p=k}^{2k-2}}{2}^i\left(\frac{4\sqrt{p(p+1)}}{2p+1}+1\right)\text{,}$$

$${\mathit{Zg}}_4(\mathit{HT}(k))={\displaystyle \sum _{i=0}}3·2^i{\displaystyle \sum _{p=k}}(p+p)+{\displaystyle \sum _{i=1}^{k-1}}2·2^i{\displaystyle \sum _{p=k}^{2k-2}}(p+p+1)+{\displaystyle \sum _{i=1}^{k-1}}{2}^i{\displaystyle \sum _{p=k}^{2k-2}}(p+1+p+1)=6k+{\displaystyle \sum _{i=1}^{k-1}}{\displaystyle \sum _{p=k}^{2k-2}}{2}^i(6p+4)=6k+(9k-2)(2^k-2)(k-1)\text{,}$$

$${\mathrm{\Pi }}_4^{\ast }(\mathit{HT}(k))={\displaystyle \prod _{i=0}}3·2^i{\displaystyle \prod _{p=k}}(p+p)\times {\displaystyle \prod _{i=1}^{k-1}}2·2^i{\displaystyle \prod _{p=k}^{2k-2}}(p+p+1)\times {\displaystyle \prod _{i=1}^{k-1}}{2}^i{\displaystyle \prod _{p=k}^{2k-2}}(p+1+p+1)=6k{\displaystyle \prod _{i=1}^{k-1}}{\displaystyle \prod _{p=k}^{2k-2}}{2}^{2i}(4p+2)(2p+2)\text{,}$$

$${\mathit{Zg}}_6(\mathit{HT}(k))={\displaystyle \sum _{i=0}}3·2^i{\displaystyle \sum _{p=k}}(p·p)+{\displaystyle \sum _{i=1}^{k-1}}2·2^i{\displaystyle \sum _{p=k}^{2k-2}}(p·(p+1))+{\displaystyle \sum _{i=1}^{k-1}}{2}^i{\displaystyle \sum _{p=k}^{2k-2}}{(p+1)}^2=3k^2+{\displaystyle \sum _{i=1}^{k-1}}{\displaystyle \sum _{p=k}^{2k-2}}{2}^i(3p^2+4p+1)=3k^2+\frac{7k(2^k-2)(2k^2-3k+1)}{2}\text{,}$$

$${\mathrm{\Pi }}_6^{\ast }(\mathit{HT}(k))={\displaystyle \prod _{i=0}}3·2^i{\displaystyle \prod _{p=k}}{p}^2\times {\displaystyle \prod _{i=1}^{k-1}}2·2^i{\displaystyle \prod _{p=k}^{2k-2}}(p(p+1))\times {\displaystyle \prod _{i=1}^{k-1}}{2}^i{\displaystyle \prod _{p=k}^{2k-2}}{(p+1)}^2=3k^2{\displaystyle \prod _{i=1}^{k-1}}{\displaystyle \prod _{p=k}^{2k-2}}{2}^{2i+1}p{(p+1)}^3\text{,}$$

$${\mathit{Zg}}_4(\mathit{HT}(k)\text{,}x)={\displaystyle \sum _{i=0}}3·2^i{\displaystyle \sum _{p=k}}{x}^{p+p}+{\displaystyle \sum _{i=1}^{k-1}}2·2^i{\displaystyle \sum _{p=k}^{2k-2}}{x}^{p+p+1}+{\displaystyle \sum _{i=1}^{k-1}}{2}^i{\displaystyle \sum _{p=k}^{2k-2}}{x}^{p+1+p+1}=3x^{2k}+{\displaystyle \sum _{i=1}^{k-1}}{\displaystyle \sum _{p=k}^{2k-2}}(2^{i+1}{x}^{2p+1}+2^i{x}^{2p+2})\text{,}$$

$${\mathit{Zg}}_6(\mathit{HT}(k)\text{,}x)={\displaystyle \sum _{i=0}}3·2^i{\displaystyle \sum _{p=k}}{x}^{p^2}+{\displaystyle \sum _{i=1}^{k-1}}2·2^i{\displaystyle \sum _{p=k}^{2k-2}}{x}^{p·(p+1)}+{\displaystyle \sum _{i=1}^{k-1}}{2}^i{\displaystyle \sum _{p=k}^{2k-2}}{x}^{{(p+1)}^2}=3x^{k^2}+{\displaystyle \sum _{i=1}^{k-1}}{\displaystyle \sum _{p=k}^{2k-2}}(2^{i+1}{x}^{p(p+1)}+2^i{x}^{{(p+1)}^2})\text{,}$$

$${\mathit{ABC}}_5\prod (\mathit{HT}(k))={\displaystyle \prod _{i=0}}3·2^i{\displaystyle \prod _{p=k}}\sqrt{\frac{p+p-2}{p·p}}\times {\displaystyle \prod _{i=1}^{k-1}}2·2^i{\displaystyle \prod _{p=k}^{2k-2}}\sqrt{\frac{p+1+p-2}{p·(p+1)}}\times {\displaystyle \prod _{i=1}^{k-1}}{2}^i{\displaystyle \prod _{p=k}^{2k-2}}\sqrt{\frac{p+1+p+1-2}{(p+1)·(p+1)}}=\frac{3\sqrt{2k-2}}{k}{\displaystyle \prod _{i=1}^{k-1}}{\displaystyle \prod _{p=k}^{2k-2}}\frac{2^{2i+1}}{p+1}\sqrt{\frac{4p-2}{p+1}}\text{.}$$

Thus, the desired results are obtained.

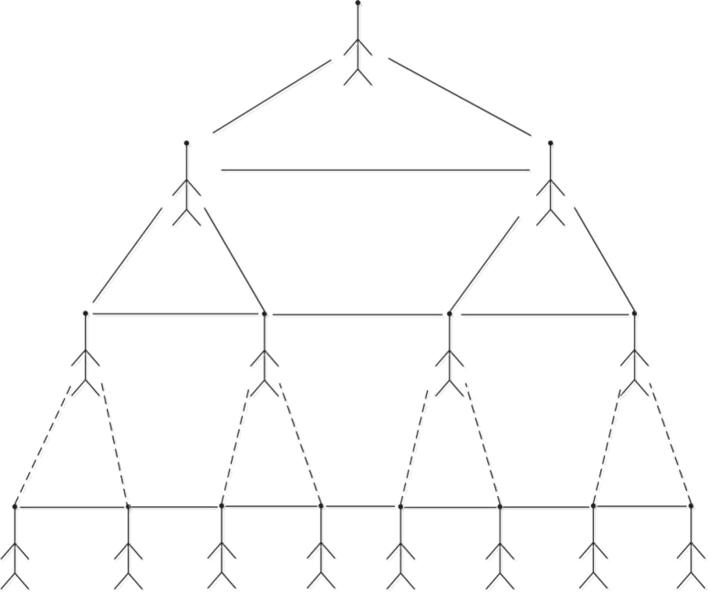
In one word, due to people’s social activity, the infected diseases could spread among people directly or indirectly. As a biological network, the X-tree is another form of binary hypertree network. We can regard the parental vertex of X-tree network as the victim, and it will spread the bacteria and viruses among people through the contact with others in in hypertree biological network. We can see that there is a strong relationship among the whole infected persons at each level X-tree in biological network, which is represented in Fig. 6. In contrast, the relevance between two infected persons and the reasons of abundant infections are dealt. As a result, the infections will increase at much higher level than hypertree biological network.

Theorem 2

Let XT(k) be the k-level X-tree with $k⩾3$. We get

$${\mathit{GA}}_4(\mathit{XT}(k))=(3k-5)2^{k-1}-3k^2+6k+4+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k}^{2k-3}}(6·2^i+12)\frac{\sqrt{p(p+1)}}{2p+1}+4(2^{k-2}+1)\frac{\sqrt{(2k-2)(2k-1)}}{4k-3}\text{,}$$

$${\mathit{Zg}}_4(\mathit{XT}(k))=174k-37k·2^{k-1}+13·2^{k-1}-81k^2+9k^3+9k^2{2}^k-74\text{,}$$

$${\mathrm{\Pi }}_4^{\ast }(\mathit{XT}(k))=6k(4k-3)(2^{2k}-16)(2k-1)\times {\displaystyle \prod _{i=1}^{k-2}}{\displaystyle \prod _{p=k+1}^{2k-2}}6p(2^i-1)\times {\displaystyle \prod _{i=1}^{k-2}}{\displaystyle \prod _{p=k}^{2k-3}}(3·2^i+6)(2p+1)\text{,}$$

$${\mathit{Zg}}_6(\mathit{XT}(k))=51k{2}^{k-2}-151k-3·2^k+\frac{367}{2}{k}^2-\frac{141k^3}{2}+7k^4-71k^2{2}^{k-2}+7k^3{2}^k+38\text{,}$$

$${\mathrm{\Pi }}_6^{\ast }(\mathit{XT}(k))=6k^2(2k-2){(2k-1)}^3(2^{2k-2}-4){\displaystyle \prod _{i=1}^{k-2}}{\displaystyle \prod _{p=k+1}^{2k-2}}3p^2(2^i-1)\times {\displaystyle \prod _{i=1}^{k-2}}{\displaystyle \prod _{p=k}^{2k-3}}3p(p+1)(2^i+2)\text{,}$$

$${\mathit{Zg}}_4(\mathit{XT}(k)\text{,}x)=6x^{2k}+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k+1}^{2k-2}}(3·2^i-3)x^{2p}+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k}^{2k-3}}(3·2^i+6)x^{2p+1}+(2^{k-1}+2)x^{4k-3}+(2^{k-1}-2)x^{4k-2}\text{,}$$

$${\mathit{Zg}}_6(\mathit{XT}(k)\text{,}x)=6x^{k^2}+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k+1}^{2k-2}}(3·2^i-3)x^{p^2}+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k}^{2k-3}}(3·2^i+6)x^{p(p+1)}+(2^{k-1}+2)x^{(2k-2)(2k-1)}+(2^{k-1}-2)x^{{(2k-1)}^2}\text{,}$$

$${\mathit{ABC}}_5\prod (\mathit{XT}(k))=\frac{3(2^{2k}-16)}{k(2k-1)}\sqrt{\frac{(4k-5)(k-1)}{2k-1}}\times {\displaystyle \prod _{i=1}^{k-2}}{\displaystyle \prod _{p=k+1}^{2k-2}}\frac{(3·2^i-3)\sqrt{2p-2}}{p}\times {\displaystyle \prod _{i=1}^{k-2}}{\displaystyle \prod _{p=k}^{2k-3}}(3·2^i+6)\sqrt{\frac{2p-1}{p(p+1)}}\text{.}$$

Proof of Theorem 2

Again, we prove the conclusions in light of the structure analysis and edge dividing technology.

By analyzing the structure of $\mathit{XT}(k)$ and compute the distances from vertices, it’s edge set $E(\mathit{XT}(k))$ can be cut into four subsets by using the eccentricities of associated vertices:

• •$E_{p\text{,}p}$ = {e = uv ∈ E(G)|$\mathit{ec}(u)$ = ec(v) = p}: $n_{\mathit{pp}}^1=6·2^i$, where $i=0$ and $p=k$; $n_{\mathit{pp}}^2=3·2^i-3$, where $i\in \{1\text{,}\dots \text{,}k-2\}$ and $p\in \{k+1\text{,}\dots \text{,}2k-2\}$. Thus, $n_{\mathit{pp}}=n_{\mathit{pp}}^1+n_{\mathit{pp}}^2$.
• •$E_{p\text{,}p+1}$ = {e = uv ∈ E(G)|$\mathit{ec}(u)=p$ and $\mathit{ec}(v)=p+1$} and $n_{p(p+1)}=3·2^i+6$, where $i\in \{1\text{,}\dots \text{,}k-2\}$ and $p\in \{k\text{,}\dots \text{,}2k-3\}$;
• •$E_{2p-2\text{,}2p-1}$ = {e = uv ∈ E(G)|$\mathit{ec}(u)=2p-2$ and $\mathit{ec}(v)=2p-1$ } and $n_{(2p-2)(2p-1)}=2·2^i+2$, where $i=k-2$ and p = k;
• •$E_{2p-1\text{,}2p-1}$ = {e = uv ∈ E(G)|$\mathit{ec}(u)=\mathit{ec}(v)=2p-1$} and $n_{(2p-1)(2p-1)}=2·2^i-2\text{,}$ where $i=k-2$ and p = k.

Fig. 6.

X-tree biological network.

Form the definitions of eccentric version indices, we get

$${\mathit{GA}}_4(\mathit{XT}(k))={\displaystyle \sum _{i=0}}6·2^i{\displaystyle \sum _{p=k}}\frac{2\sqrt{p^2}}{p+p}+{\displaystyle \sum _{i=1}^{k-2}}(3·2^i-3){\displaystyle \sum _{p=k+1}^{2k-2}}\frac{2\sqrt{p^2}}{p+p}+{\displaystyle \sum _{i=1}^{k-2}}(3·2^i+6){\displaystyle \sum _{p=k}^{2k-3}}\frac{2\sqrt{p(p+1)}}{p+p+1}+{\displaystyle \sum _{i=k-2}}(2·2^i+2){\displaystyle \sum _{p=k}}\frac{2\sqrt{(2p-2)(2p-1)}}{2p-2+2p-1}+{\displaystyle \sum _{i=k-2}}(2·2^i-2){\displaystyle \sum _{p=k}}\frac{2\sqrt{(2p-1)(2p-1)}}{2p-1+2p-1}=6+(k-2){\displaystyle \sum _{i=1}^{k-2}}(3·2^i-3)+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k}^{2k-3}}(6·2^i+12)\frac{\sqrt{p(p+1)}}{2p+1}+(2·2^{k-2}+2)\frac{2\sqrt{(2k-2)(2k-1)}}{4k-3}+(2·2^{k-2}-2)=(3k-5)2^{k-1}-3k^2+6k+4+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k}^{2k-3}}(6·2^i+12)\frac{\sqrt{p(p+1)}}{2p+1}+(2·2^{k-2}+2)\frac{2\sqrt{(2k-2)(2k-1)}}{4k-3}\text{,}$$

$${\mathit{Zg}}_4(\mathit{XT}(k))={\displaystyle \sum _{i=0}}6·2^i{\displaystyle \sum _{p=k}}(p+p)+{\displaystyle \sum _{i=1}^{k-2}}(3·2^i-3){\displaystyle \sum _{p=k+1}^{2k-2}}(p+p)+{\displaystyle \sum _{i=1}^{k-2}}(3·2^i+6){\displaystyle \sum _{p=k}^{2k-3}}(p+p+1)+{\displaystyle \sum _{i=k-2}}(2·2^i+2){\displaystyle \sum _{p=k}}(2p-2+2p-1)+{\displaystyle \sum _{i=k-2}}(2·2^i-2){\displaystyle \sum _{p=k}}(2p-1+2p-1)=12k+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k+1}^{2k-2}}6p(2^i-1)+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k}^{2k-3}}(3·2^i+6)(2p+1)+(4k-3)(2^{k-1}+2)+(2k-1)(2^k-4)=174k-37k·2^{k-1}+13·2^{k-1}-81k^2+9k^3+9k^2{2}^k-74\text{,}$$

$${\mathrm{\Pi }}_4^{\ast }(\mathit{XT}(k))={\displaystyle \prod _{i=0}}6·2^i{\displaystyle \prod _{p=k}}(p+p)\times {\displaystyle \prod _{i=1}^{k-2}}(3·2^i-3){\displaystyle \prod _{p=k+1}^{2k-2}}(p+p)\times {\displaystyle \prod _{i=1}^{k-2}}(3·2^i+6){\displaystyle \prod _{p=k}^{2k-3}}(p+p+1)\times {\displaystyle \prod _{i=k-2}}(2·2^i+2){\displaystyle \prod _{p=k}}(2p-2+2p-1)\times {\displaystyle \prod _{i=k-2}}(2·2^i-2){\displaystyle \prod _{p=k}}(2p-1+2p-1)=6k(2^k+4)(4k-3)(2^k-4)(2k-1)\times {\displaystyle \prod _{i=1}^{k-2}}{\displaystyle \prod _{p=k+1}^{2k-2}}6p(2^i-1)\times {\displaystyle \prod _{i=1}^{k-2}}{\displaystyle \prod _{p=k}^{2k-3}}(3·2^i+6)(2p+1)\text{,}$$

$${\mathit{Zg}}_6(\mathit{XT}(k))={\displaystyle \sum _{i=0}}6·2^i{\displaystyle \sum _{p=k}}(p·p)+{\displaystyle \sum _{i=1}^{k-2}}(3·2^i-3){\displaystyle \sum _{p=k+1}^{2k-2}}(p·p)+{\displaystyle \sum _{i=1}^{k-2}}(3·2^i+6){\displaystyle \sum _{p=k}^{2k-3}}(p·(p+1))+{\displaystyle \sum _{i=k-2}}(2·2^i+2){\displaystyle \sum _{p=k}}(2p-2)·(2p-1)+{\displaystyle \sum _{i=k-2}}(2·2^i-2){\displaystyle \sum _{p=k}}(2p-1)·(2p-1)=6k^2+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k+1}^{2k-2}}3p^2(2^i-1)+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k}^{2k-3}}p(p+1)(3·2^i+6)+(2^{k-1}+2)(2k-2)(2k-1)+(2^{k-1}-2){(2k-1)}^2=51k{2}^{k-2}-151k-3·2^k+\frac{367}{2}{k}^2-\frac{141k^3}{2}+7k^4-71k^2{2}^{k-2}+7k^3{2}^k+38\text{,}$$

$${\mathrm{\Pi }}_6^{\ast }(\mathit{XT}(k))={\displaystyle \prod _{i=0}}6·2^i{\displaystyle \prod _{p=k}}(p·p)\times {\displaystyle \prod _{i=1}^{k-2}}(3·2^i-3){\displaystyle \prod _{p=k+1}^{2k-2}}(p·p)\times {\displaystyle \prod _{i=1}^{k-2}}(3·2^i+6){\displaystyle \prod _{p=k}^{2k-3}}(p·(p+1))\times {\displaystyle \prod _{i=k-2}}(2·2^i+2){\displaystyle \prod _{p=k}}((2p-2)·(2p-1))\times {\displaystyle \prod _{i=k-2}}(2·2^i-2){\displaystyle \prod _{p=k}}((2p-1)·(2p-1))=6k^2(2k-2){(2k-1)}^3(2^{2k-2}-4){\displaystyle \prod _{i=1}^{k-2}}{\displaystyle \prod _{p=k+1}^{2k-2}}3p^2(2^i-1)\times {\displaystyle \prod _{i=1}^{k-2}}{\displaystyle \prod _{p=k}^{2k-3}}3p(p+1)(2^i+2)\text{,}$$

$${\mathit{Zg}}_4(\mathit{XT}(k)\text{,}x)={\displaystyle \sum _{i=0}}6·2^i{\displaystyle \sum _{p=k}}{x}^{p+p}+{\displaystyle \sum _{i=1}^{k-2}}(3·2^i-3){\displaystyle \sum _{p=k+1}^{2k-2}}{x}^{p+p}+{\displaystyle \sum _{i=1}^{k-2}}(3·2^i+6){\displaystyle \sum _{p=k}^{2k-3}}{x}^{p+p+1}+{\displaystyle \sum _{i=k-2}}(2·2^i+2){\displaystyle \sum _{p=k}}{x}^{2p-2+2p-1}+{\displaystyle \sum _{i=k-2}}(2·2^i-2){\displaystyle \sum _{p=k}}{x}^{2p-1+2p-1}=6x^{2k}+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k+1}^{2k-2}}(3·2^i-3)x^{2p}+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k}^{2k-3}}(3·2^i+6)x^{2p+1}+(2·2^{k-2}+2)x^{4k-3}+(2·2^{k-2}-2)x^{4k-2}\text{,}$$

$${\mathit{Zg}}_6(\mathit{XT}(k)\text{,}x)={\displaystyle \sum _{i=0}}6·2^i{\displaystyle \sum _{p=k}}{x}^{p·p}+{\displaystyle \sum _{i=1}^{k-2}}(3·2^i-3){\displaystyle \sum _{p=k+1}^{2k-2}}{x}^{p·p}+{\displaystyle \sum _{i=1}^{k-2}}(3·2^i+6){\displaystyle \sum _{p=k}^{2k-3}}{x}^{p·(p+1)}+{\displaystyle \sum _{i=k-2}}(2·2^i+2){\displaystyle \sum _{p=k}}{x}^{(2p-2)·(2p-1)}+{\displaystyle \sum _{i=k-2}}(2·2^i-2){\displaystyle \sum _{p=k}}{x}^{(2p-1)·(2p-1)}=6x^{k^2}+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k+1}^{2k-2}}(3·2^i-3)x^{p^2}+{\displaystyle \sum _{i=1}^{k-2}}{\displaystyle \sum _{p=k}^{2k-3}}(3·2^i+6)x^{p(p+1)}+(2·2^{k-2}+2)x^{(2k-2)(2k-1)}+(2·2^{k-2}-2)x^{{(2k-1)}^2}\text{,}$$

$${\mathit{ABC}}_5\prod (\mathit{XT}(k))={\displaystyle \prod _{i=0}}6·2^i{\displaystyle \prod _{p=k}}\sqrt{\frac{p+p-2}{p·p}}\times {\displaystyle \prod _{i=1}^{k-2}}(3·2^i-3){\displaystyle \prod _{p=k+1}^{2k-2}}\sqrt{\frac{p+p-2}{p·p}}\times {\displaystyle \prod _{i=1}^{k-2}}(3·2^i+6){\displaystyle \prod _{p=k}^{2k-3}}\sqrt{\frac{p+p+1-2}{p(p+1)}}\times {\displaystyle \prod _{i=k-2}}(2·2^i+2){\displaystyle \prod _{p=k}}\sqrt{\frac{2p-2+2p-1-2}{(2p-2)(2p-1)}}\times {\displaystyle \prod _{i=k-2}}(2·2^i-2){\displaystyle \prod _{p=k}}\sqrt{\frac{2p-1+2p-1-2}{(2p-1)(2p-1)}}=\frac{6\sqrt{2k-2}}{k}\frac{2^{2k-2}-4}{2k-1}\sqrt{\frac{8k-10}{2k-1}}\times {\displaystyle \prod _{i=1}^{k-2}}{\displaystyle \prod _{p=k+1}^{2k-2}}\frac{(3·2^i-3)\sqrt{2p-2}}{p}\times {\displaystyle \prod _{i=1}^{k-2}}{\displaystyle \prod _{p=k}^{2k-3}}(3·2^i+6)\sqrt{\frac{2p-1}{p(p+1)}}\text{.}$$

Hence, we yield the expected conclusions.

4. Conclusions and future problems

In this paper, we discuss the theoretical topics in some biology problems, and finally determine the eccentric topological indices of biological networks in view of structure analysis, distance calculating and mathematical derivation. Since the biological networks can help the researchers better understand how infectious diseases fast increase through infected persons, the theoretical results have the wide and promising application prospects in biological, medical and pharmacy engineering.

The following topics can be considered as the future work:

• •How to structure a kind of graph to express the microstructure under more biology problems.
• •Design an algorithm with low computational complexity to express the complex DNA gene structure and apply it in gene mutation.
• •How to put the known theoretical results into biological reverse engineering.

Conflict of interests

The authors declare that there is no conflict of interests regarding the publication of this paper.