Abstract
Ligand-gated ion channels bind agonists with higher affinity in the open than in the closed state. The kinetic basis of this increased affinity has remained unknown, because even though the rate constants of agonist association to and dissociation from closed receptors can be estimated with reasonable certainty, the kinetics of the binding steps in open receptors have proven to be elusive. To be able to measure the agonist-dissociation rate constant from open muscle nicotinic receptors, we increased the probability of ligand unbinding from the open state by engineering a number of mutations that speed up opening and slow down closing but leave the ligand-binding properties unchanged. Single-channel patch-clamp recordings from the wild-type and mutant constructs were performed at very low concentrations of acetylcholine (ACh). The durations of individual channel activations were analyzed assuming that “bursts” of fully liganded (diliganded) receptor openings can be terminated by ligand dissociation from the closed or open state (followed by fast closure) or by desensitization. This analysis revealed that ACh dissociates from diliganded open receptors at ≈24 s−1, that is, ≈2,500 times more slowly than from diliganded closed receptors. This change alone without a concomitant change in the association rate constant to the open state quantitatively accounts for the increased equilibrium affinity of the open channel for ACh. Also, the results predict that both desensitization and ACh dissociation from the open state frequently terminate bursts of openings in naturally occurring gain-of-function mutants (which cause slow-channel congenital myasthenia) and therefore would contribute significantly to the time course of the endplate current decay in these disease conditions.
The muscle acetylcholine (ACh) receptor channel (AChR) mediates fast synaptic transmission at the vertebrate neuromuscular junction. The dynamic behavior of this ion channel can be regarded as the independent combination of conformational changes (gating and desensitization) and two ligand-binding steps in the form of cyclic reaction schemes (refs. 1–4; Fig. 1).
Figure 1.
A Monod–Wyman–Changeux type of model (1) for the muscle AChR. C, O, and D denote the closed, open, and desensitized conformations, respectively, and A denotes the agonist concentration. Under equilibrium conditions, the net free-energy change around a “thermodynamic cycle” is zero. Therefore, the product of the equilibrium constants around each loop in this model is constrained to be unity (principle of detailed balance). This leads to the calculation that the affinity of the open state (j+/j−) is larger than that of the closed state (k+/k−) by a factor of 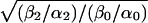 . In the case of the wild-type AChR and all the mutant constructs having wild-type ligand-binding properties, this factor is ≈1,500–5,000 in the presence of ACh. The model is appropriate as far as gating (occurring as a one-step reaction) and desensitization of diliganded receptors (proceeding from the open state) are concerned. It is clear, however, that there is more than one desensitized state (Fig. 4 and refs. 5 and 6), and it is not known whether the mono- and unliganded D states are connected directly to the open, closed, or both states (hence, the dashed arrows; ref. 7). Nevertheless, none of these uncertainties and simplifications compromise the conclusions of this work. Once the channel reaches the OA2 state (from CA2, OA, or DA2), it can close and reopen repeatedly (OA2 ⇋ CA2). If the concentration of ligand is sufficiently low and the rate constant of the DA2 → OA2 transition is much slower than that of DA2 → DA, these bursts of openings will continue until the ligand dissociates from CA2 or OA2 (followed by closure) or until the channel desensitizes. We refer to the mean number of sojourns in OA2 per burst as the “number of openings per burst.” The five rate constants that determine the time constant of the slowest component of the burst-length distribution at very low concentrations of agonist (Eq. 2), and thus that would shape the time course of the endplate current decay (8, 9), are indicated in bold.
. In the case of the wild-type AChR and all the mutant constructs having wild-type ligand-binding properties, this factor is ≈1,500–5,000 in the presence of ACh. The model is appropriate as far as gating (occurring as a one-step reaction) and desensitization of diliganded receptors (proceeding from the open state) are concerned. It is clear, however, that there is more than one desensitized state (Fig. 4 and refs. 5 and 6), and it is not known whether the mono- and unliganded D states are connected directly to the open, closed, or both states (hence, the dashed arrows; ref. 7). Nevertheless, none of these uncertainties and simplifications compromise the conclusions of this work. Once the channel reaches the OA2 state (from CA2, OA, or DA2), it can close and reopen repeatedly (OA2 ⇋ CA2). If the concentration of ligand is sufficiently low and the rate constant of the DA2 → OA2 transition is much slower than that of DA2 → DA, these bursts of openings will continue until the ligand dissociates from CA2 or OA2 (followed by closure) or until the channel desensitizes. We refer to the mean number of sojourns in OA2 per burst as the “number of openings per burst.” The five rate constants that determine the time constant of the slowest component of the burst-length distribution at very low concentrations of agonist (Eq. 2), and thus that would shape the time course of the endplate current decay (8, 9), are indicated in bold.
Consistent with its physiological role, the closed ⇋ open reaction (“gating”) of the diliganded AChR is much more favorable (Keq = β2/α2 ≅ 25; Fig. 1; ref. 10) than that of the unliganded receptor (Keq = β0/α0 ≅ 10−5–10−6; Fig. 1; refs. 11–13). From the thermodynamic principle of detailed balance, which constrains the product of the equilibrium constants around each loop in Fig. 1 to be unity, it follows that the affinity of the AChR for ACh has to be ≈1,500–5,000-fold higher in the open than in the closed conformation (see Fig. 1 legend). Along these lines, the different efficacies displayed by different ligands can be interpreted as arising from the differences in their respective excess binding energies to the open versus the closed conformation. Although the kinetics of ACh association to and dissociation from closed AChRs have been known for several years now, those corresponding to open AChRs have not.
Because the different conformations of the muscle AChR interconvert and the ACh-association/dissociation rate constants are exceedingly fast, there is no prospect of being able to measure directly (that is, with binding assays) the kinetics of the agonist-binding steps in a conformation-specific manner. A reasonable alternative is to postulate an appropriate kinetic model and to estimate the agonist-association/dissociation rate constants from single-channel recordings. It is precisely this approach that has revealed that ACh associates to (adult mouse muscle) closed unliganded AChRs with a rate constant of ≈3 × 108 M−1⋅s−1 and dissociates from closed diliganded receptors at ≈50,000 s−1 (10, 14, 15). Single-channel kinetic analysis, however, had not been exploited thus far to elucidate the open-channel agonist-binding kinetics.
In this paper, we estimated the rate at which ACh dissociates from open AChRs by measuring the effect that this phenomenon has on the duration of single-channel activations. Although the data were analyzed in the framework of a particular model (Fig. 1), the conclusions are valid in the context of any kinetic scheme that features a single-step closed ⇋ open reaction (16), desensitization of diliganded receptors predominantly from the open state (7, 17), and ligand dissociation from both the closed and open conformations (4).
We conclude that the increase in ACh affinity that drives ion channel opening is largely, if not entirely, caused by a decrease in the ACh-dissociation rate constant from the open state with little change in the kinetics of ACh association. Also, the results allow us to predict that, unlike the situation during normal neuromuscular synaptic transmission, both desensitization and ACh dissociation from the open state significantly contribute to the time course of the endplate current decay in patients with congenital myasthenic syndrome.
Materials and Methods
Recording and Analysis of Single-Channel Currents.
Single-channel currents from adult mouse muscle AChRs (α2βδɛ) were recorded by using the cell-attached configuration of the patch-clamp technique (18) on transiently transfected HEK-293 cells (13). The recordings were digitized (100 kHz), visualized, and idealized (dc to 20 kHz bandwidth) by using the QUB software for kinetic analysis (www.qub.buffalo.edu; ref. 19). Time constants and areas of the various components of the dwell-time distributions were estimated by using maximum likelihood methods. A minimum resolvable duration of 25 μs was imposed retrospectively on both open and shut intervals. To establish the validity of Eq. 2, Q-matrix eigenvalues were solved numerically (20, 21) by using MAPLE 6 (Waterloo Maple, Ontario, Canada).
The Burst-Length Distribution.
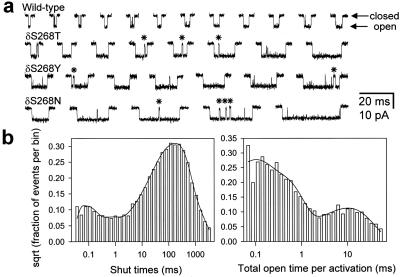
Open periods recorded at very low concentrations of ACh were interrupted frequently by brief but well defined shut intervals (mean lifetime ≈0.5–1.0 ms; Fig. 2a). Most likely, these “gaps” correspond to sojourns in a short lived desensitized state from which recovery is fast, rather than to sojourns in the much shorter CA2 (mean lifetime <10 μs). To simplify the analysis and be able to interpret the data in the framework of a model in which entry into desensitized states terminates bursts (Fig. 1), all shut intervals shorter than a critical time (tcrit) were deleted, and the flanking open intervals were concatenated. To calculate tcrit, one of the components of the shut-time distribution (usually the second shortest; Fig. 2b) was interpreted as the longest gap that interrupts series of consecutive openings arising from the same diliganded channel (indicated with asterisks in Fig. 2a). A value of tcrit was calculated for each patch between this component (τ2 or “gap component”) and the immediately longest (τ3) by solving numerically for t in the expression exp(−t/τ2) = [1 − exp(−t/τ3)] (ref. 22) by using MAPLE 6. The average values of τ2, τ3, and tcrit were 0.585 ± 0.376, 137.4 ± 90.7, and 2.1 ± 1.3 ms, respectively, for all the constructs used in this study (mean ± SD, 11 constructs, 44 patches). The average probability of having misclassified a shut interval as being within, when it was actually between, series of consecutive openings from the same channel (and vice versa) was ≈0.03. We refer to the duration of these extended openings as “total open time per activation” and to the time constant of the slowest component of the corresponding distribution as “τburst.” Because of these gaps (not predicted by Fig. 1), the slowest time constant of the endplate current decay through these channels would actually be slightly longer than the experimental values of τburst.
Figure 2.
Single-channel activations and the estimation of τburst values. (a) Bursts of openings excised from continuous single-channel recordings elicited by low concentrations of ACh (5 μM for the wild-type and 100 nM for the other three constructs) at ≈ −100 mV in the cell-attached configuration. Some of the open periods were interrupted by short but well defined gaps (0.355-ms component in the example shut-time histogram of b), some of which are indicated with asterisks. These, and other less well defined shut intervals also present in the figure (48-μs component in the example below) most likely correspond to dwellings in nonconductive diliganded states other than the very brief CA2 (mean lifetime < 10 μs). Sojourns in these “extra” states were ignored by concatenating the flanking open intervals (see Materials and Methods). Display bandwidth, dc to 6 kHz. Openings are downward deflections. (b) Dwell-time histograms of an example patch of a cell expressing the δS268N mutant. The shut-time histogram, which includes all the shut intervals in the record, was best fitted (maximum likelihood method) with a mixture of five exponential densities with means of 48 μs (5%), 0.355 ms (3%), 32.1 ms (21%), 141 ms (60%), and 430 ms (11%); 5,543 events were included in the fit. The total-open-time-per-activation histogram (see Materials and Methods) was best fitted with a mixture of three exponential densities with means of 60 μs (41%), 0.276 ms (51%), and 14.9 ms (8%); 5,051 events were included in the fit. We refer to the time constant of the slowest component of this distribution as τburst. The intermediate and fastest components correspond, to a very good approximation, to isolated monoliganded and unliganded openings, respectively.
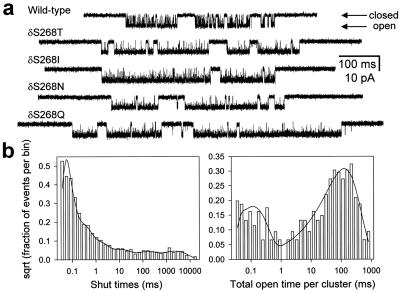
The Rate of Entry into Desensitization.
In the presence of a saturating concentration of ACh, binding is so fast that single-channel currents consist of openings and closings in quick succession interrupted only by entry into desensitized states (that is, Fig. 1 reduces to CA2 ⇋ OA2 ⇋ DA2). Because at saturating concentrations of ACh there also is blockade by the agonist itself (which complicates the kinetics), we used a concentration of 100 μM, at which binding is still fast, but blockade is not significant (Fig. 4). To estimate the net rate of entry into desensitization (k+D), the recordings obtained at 100 μM ACh were analyzed in a similar way to that used for recordings at low ACh concentrations. A tcrit value was calculated for each patch (2.0 ± 0.55 ms on average, mean ± SD, 4 constructs, 15 patches) based on the time constants of the corresponding shut-time distributions. The average values of the two time constants used for this calculation were 0.935 ± 0.202 and 16.7 ± 6.8 ms (mean ± SD, 4 constructs, 15 patches), which correspond to the gap component (usually the third shortest at 100 μM ACh) and the immediately longest, respectively (Fig. 4b). The average misclassification probability (see above) was ≈0.125. All shut intervals shorter than tcrit were deleted, and the flanking openings were concatenated. We refer to the duration of these extended openings as “total open time per cluster” and to the reciprocal of the time constant of the longest component of the corresponding distribution as the “rate of entry into desensitization” (k+D).
Figure 4.
The rate of entry into desensitization. (a) Clusters of single-channel activity recorded at 100 μM ACh and ≈ −100 mV were used to estimate the rate of entry into desensitization, k+D (as defined in Materials and Methods). At this high concentration of ACh, binding is so fast that sojourns in the closed state are very short lived. Hence, most of the longer lived shut intervals correspond to visits to a number of desensitized states. The average value for the tested constructs (Thr, Ile, Asn, and Gln mutants) was k+D = 14.8 ± 6.0 s−1 (mean ± SD, 4 constructs, 15 patches). The wild-type's data were not included in this calculation, because the longer lived closures at 100 μM ACh (see traces) precluded a clear identification of the gap component (see Materials and Methods). The kinetics of entry into desensitization were not affected greatly in the outlier construct δS→Q (k+D = 11.4 ± 3.2 s−1, mean ± SD, 5 patches) suggesting that this mutation most likely affects the ligand-binding properties of the channel. Display bandwidth, dc to 6 kHz. Openings are downwards. (b) Dwell-time histograms of an example patch of a cell expressing the δS268Q mutant. The shut-time histogram, which includes all of the shut intervals in the record, was best fitted (maximum likelihood method) with a mixture of six exponential densities with means of 20 μs (70%), 0.134 ms (20%), 0.711 ms (6%), 6.3 ms (2%), 88 ms (1%), and 1.5 s (1%). 8,750 events were included in the fit. The total-open-time-per-cluster histogram (see Materials and Methods) was best fitted with a mixture of two exponential densities with means of 82 μs (20%) and 92 ms (80%); 458 events were included in the fit. The reciprocal of the time constant of the longest component gives the k+D value. The short lived component corresponds to isolated openings present even at concentrations as high as 100 μM ACh.
Results and Discussion
The rate constants of muscle AChR gating are such that openings of mono- and unliganded receptors occur mostly as isolated events, whereas those of diliganded receptors occur as “bursts” of openings in quick succession (22, 23). According to the standard linear model C ⇋ CA ⇋ CA2 ⇋ OA2 (see Fig. 1 for symbol definition), the slowest component of the burst-length distribution measured at very low concentrations of agonist (τburst) is well approximated by Eq. 1 as long as the open probability within bursts of openings is ≈1:
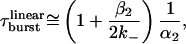 |
1 |
where β2 and α2 are the opening and closing rate constants of diliganded receptors, respectively, and 2k− is the agonist-dissociation rate constant from diliganded closed receptors (23). The linear model ignores ligand dissociation from the open state and desensitization, which as far as τburst is concerned is justified in the case of wild-type receptors (see below). However, this is not the case of “gain-of-function” mutants. According to the cyclic scheme shown in Fig. 1, the larger the diliganded-gating equilibrium constant (β2/α2), the higher the chances of desensitization and ligand dissociation from the open state cutting a burst short. Although the exact expression for τburst according to the cyclic scheme is unwieldy (it is given by the reciprocal of the smallest eigenvalue of the Q matrix partition that includes the very short lived closed state CA2 and the open states OA2, OA, and O), we found that Eq. 2 is an excellent approximation as long as the open probability within bursts is ≈1:
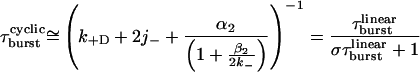 |
2 |
where σ = 2j− + k+D (Fig. 1).
As is generally the case with time constants of complex models, τ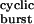 cannot be given a simple physical interpretation. However, this time constant is related closely to the duration of an average burst of diliganded openings, which consists of a series of OA2 ⇋ CA2 transitions that can be terminated by entry into desensitization, ligand dissociation from the closed state, or ligand dissociation from the open state followed by fast closure (see Fig. 1 legend). From the synaptic physiology perspective, it is interesting to note that τ
cannot be given a simple physical interpretation. However, this time constant is related closely to the duration of an average burst of diliganded openings, which consists of a series of OA2 ⇋ CA2 transitions that can be terminated by entry into desensitization, ligand dissociation from the closed state, or ligand dissociation from the open state followed by fast closure (see Fig. 1 legend). From the synaptic physiology perspective, it is interesting to note that τ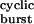 also is the predicted value of the time constant of the endplate current decay. Because Eq. 2 is a function of 2j−, this expression provides a tool to estimate the kinetics of ligand unbinding from the open state. The problem reduces to estimating the burst durations at very low concentrations of agonist (to minimize rebinding) of receptors with different gating kinetics (that is, different β2 and α2 values) but with wild-type ligand-binding and desensitization properties.
also is the predicted value of the time constant of the endplate current decay. Because Eq. 2 is a function of 2j−, this expression provides a tool to estimate the kinetics of ligand unbinding from the open state. The problem reduces to estimating the burst durations at very low concentrations of agonist (to minimize rebinding) of receptors with different gating kinetics (that is, different β2 and α2 values) but with wild-type ligand-binding and desensitization properties.
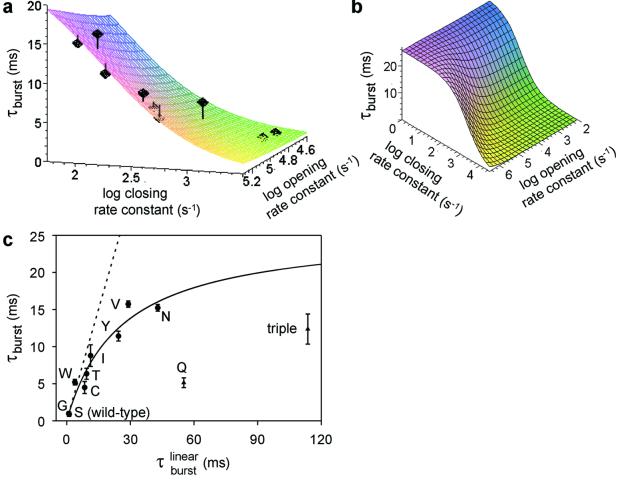
In our previous work (13, 16) we found that point mutations at the 12′ position of the second transmembrane segment (M2) of the δ subunit (Ser-268) affect the kinetics of gating in a graded manner and that at least the Ser → Thr mutation does not affect the equilibrium binding properties of the closed and open conformations. Because the gating kinetics of the various M2 12′ mutants in the presence of ACh are too fast for these rates to be estimated reliably, the corresponding opening and closing rate constants were calculated from their counterparts measured in the presence of the weak agonist choline (Table 1). τburst values for the wild-type and mutant AChRs were estimated from single-channel patch-clamp recordings by using ACh as the agonist (Fig. 2) and were fitted with Eq. 2 as a function of two variables, β2 and α2 (Fig. 3 a and b). The δS→Q and the triple βΤ→S + δS→T + ɛT→S mutants were excluded from the fit, because the corresponding τburst values were much shorter than expected based on their gating equilibrium constants (Table 1 and Fig. 3c).
Table 1.
Rate and time constants of gating in wild-type and M2 12′ mutant AChRs
| Construct | β2 ACh, s−1 | α2 ACh, s−1 | (β2/α2)ACh | τ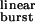 , ms , ms |
τburst, ms | [ACh], μM | No. of patches |
|---|---|---|---|---|---|---|---|
| Wild-type | 50,000 | 2,000 | 25 | 0.94 | 0.99 ± 0.23 | 5 | 4 |
| δS→G | 60,700 | 1,807 | 34 | 1.14 | 0.89 ± 0.29 | 1 | 4 |
| δS→W | 66,537 | 564 | 118 | 3.84 | 5.21 ± 0.38 | 1 | 3 |
| δS→C | 108,950 | 346 | 315 | 8.44 | 4.49 ± 0.81 | 0.1 | 4 |
| δS→T | 129,770 | 351 | 370 | 9.35 | 6.34 ± 0.74 | 0.1–1 | 6 |
| δS→I | 161,480 | 342 | 472 | 11.24 | 8.79 ± 1.46 | 0.1 | 5 |
| δS→Y | 185,020 | 174 | 1,063 | 24.39 | 11.42 ± 0.66 | 0.1 | 4 |
| δS→V | 149,030 | 125 | 1,192 | 29.02 | 15.73 ± 0.42 | 0.1 | 4 |
| δS→N | 192,410 | 102 | 1,886 | 42.92 | 15.23 ± 0.45 | 0.1 | 3 |
| δS→Q | 188,910 | 78 | 2,422 | 55.18 | 5.14 ± 0.66 | 0.1 | 4 |
| βT→S + δS→T + ɛT→S | 921,790 | 151 | 6,105 | 113.67 | 12.37 ± 2.03 | 0.1 | 3 |
The opening and closing rate constants of wild-type diliganded AChRs in the presence of ACh (β2 ACh and α2 ACh) were taken as 50,000 s−1 and 2,000 s−1, respectively, according to previously published values (10). The corresponding values for the mutants were calculated from the rate-constant estimates in the presence of choline (16) by applying the relation kmutant ACh/kwild-type ACh = kmutant choline/kwild-type choline, where k is either the opening or closing rate constant (13). For the calculation of τ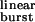 (Eq. 1), the values of β2 ACh and α2 ACh were taken from this table, and 2k− was taken as 56,870 s−1, as estimated from the fit of τburst with Eq. 2 (Fig. 3). τburst values (mean ± SD) were determined experimentally from single-channel recordings as described in Materials and Methods, at the indicated concentration of ACh, and in the indicated number of patches.
(Eq. 1), the values of β2 ACh and α2 ACh were taken from this table, and 2k− was taken as 56,870 s−1, as estimated from the fit of τburst with Eq. 2 (Fig. 3). τburst values (mean ± SD) were determined experimentally from single-channel recordings as described in Materials and Methods, at the indicated concentration of ACh, and in the indicated number of patches.
Figure 3.
σ value estimation. (a) Plot of experimental τburst values as a function of the opening and closing rate constants. The values of τburst, β2, and α2 for each construct in the presence of ACh are shown in Table 1. The fit with Eq. 2 (least squares method) yielded estimates of 2k− = 56,870 ± 17,310 s−1 and σ = 39 ± 9 s−1 (mean ± SD). The vertical lines denote the distance between each experimental point and the fitted surface. The points corresponding to the δS→Q and the βT→S + δS→T + ɛT→S mutants are not displayed. (b) A lower magnification version of the plot in a. (c) Plot of τburst (mean ± SD) as a function of τ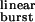 . τ
. τ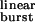 values (Eq. 1) were calculated for each construct by using the values of β2 and α2 in Table 1 and the estimated 2k− value of 56,870 s−1. The fit with Eq. 2 (least squares method) yielded σ = 39 ± 4 s−1 (mean ± SD). This fit predicts a maximum τburst value of 1/σ = 25.6 ms. The δS→Q and βT→S + δS→T + ɛT→S (“triple”) mutants were deemed outliers and were excluded from the fit. Most likely, the affinities for ACh in the closed and/or open states are altered in these two constructs (Fig. 4). The dashed straight line is the prediction of models that ignore desensitization and ligand dissociation from the open state (e.g., refs. 10, 24, and 25). That is, from Eq. 2, if σ = 0, then τ
values (Eq. 1) were calculated for each construct by using the values of β2 and α2 in Table 1 and the estimated 2k− value of 56,870 s−1. The fit with Eq. 2 (least squares method) yielded σ = 39 ± 4 s−1 (mean ± SD). This fit predicts a maximum τburst value of 1/σ = 25.6 ms. The δS→Q and βT→S + δS→T + ɛT→S (“triple”) mutants were deemed outliers and were excluded from the fit. Most likely, the affinities for ACh in the closed and/or open states are altered in these two constructs (Fig. 4). The dashed straight line is the prediction of models that ignore desensitization and ligand dissociation from the open state (e.g., refs. 10, 24, and 25). That is, from Eq. 2, if σ = 0, then τ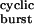 = τ
= τ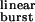 . Because σ is actually different from zero, desensitization and ligand dissociation from the open state can cut bursts short and thus can shape the time course of the endplate current decay.
. Because σ is actually different from zero, desensitization and ligand dissociation from the open state can cut bursts short and thus can shape the time course of the endplate current decay.
The best-fit estimates of the two unknown parameters were 2k− = 56,870 ± 17,310 s−1 and σ = 39 ± 9 s−1 (mean ± SD, least squares method). The former is in remarkable agreement with the wild-type receptor estimate obtained by simultaneous fitting of entire sequences of (apparent) open and shut times recorded at different ACh concentrations, a completely unrelated method (50,534 s−1 in ref. 10, 43,800 s−1 in ref. 14, and 57,400 s−1 in ref. 15). This is compelling evidence that, with the exception of the two outliers, the engineered mutations do not affect the kinetics of ACh dissociation from the closed state. To better appreciate the goodness of this fit, Fig. 3c plots the measured τburst values as a function of a single variable, τ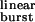 . The close fit to the rectangular hyperbola predicted by Eq. 2 strongly suggests that the agonist indeed can dissociate from both the closed and open conformations, that the calculation of gating rate constants in the presence of ACh from those measured in the presence of the weak agonist choline (Table 1) is valid, and that the kinetics of ACh dissociation from the open state as well are unaffected by the mutations in question.
. The close fit to the rectangular hyperbola predicted by Eq. 2 strongly suggests that the agonist indeed can dissociate from both the closed and open conformations, that the calculation of gating rate constants in the presence of ACh from those measured in the presence of the weak agonist choline (Table 1) is valid, and that the kinetics of ACh dissociation from the open state as well are unaffected by the mutations in question.
To obtain the open-channel dissociation rate constant from the σ value estimate (σ = 2j− + k+D), the net rate of entry into desensitization was measured at a high concentration of ACh for a number of constructs (Fig. 4). A mean value of 14.8 ± 6.0 s−1 was obtained for k+D (mean ± SD, 4 constructs, 15 patches). Therefore, 2j− = σ − k+D ≅ 24 s−1. In other words, in the hypothetical case of no channel isomerization, it would take an average of 42 ms for an ACh molecule to fall off of a diliganded-open AChR but only an average of 20 μs to fall off of a diliganded-closed AChR. We conclude that 2j− can be estimated reliably by a combination of single-channel measurements and mutagenesis.
From the estimates above, we calculate that ACh dissociates 2,370 times more slowly from open- than from closed-diliganded receptors (2k−/2j− = 56,870/24). Also, from thermodynamic considerations, we estimate that the equilibrium affinity for ACh increases by a factor of 1,500–5,000 after opening (Fig. 1). Hence, the increase in ACh affinity that drives opening is largely if not entirely caused by the decrease in the ACh-dissociation rate constant with little change in the kinetics of association. For other allosteric proteins this situation is different. In hemoglobin (to the best of our knowledge, the only other allosteric protein for which the kinetics of ligand binding/unbinding to/from the different conformations have been estimated; ref. 26), the O2-association rate constant increases by a factor of ≈9, and the dissociation rate constant decreases by a factor of ≈24 after the T→R transition (at pH 7.4 and averaging α and β subunits). In the case of carbon monoxide, the CO-association rate constant increases by a factor of ≈72, and the dissociation rate constant decreases by a factor of ≈23.
Assuming an ACh-association rate constant of 1.5 × 108 M−1⋅s−1 to each open-channel binding site (the same as that to the closed channel), we can calculate that the ACh-dissociation equilibrium constant in the open state (j−/j+) is ≈80 nM. Interestingly, the ACh-dissociation equilibrium constant in the (proadifen-induced) desensitized state was measured to be ≈40 nM in the same preparation (27). Taken together, these results support the previous suggestion (4, 28) that the ACh affinity of the open state is very similar or even identical to that of the desensitized state(s).
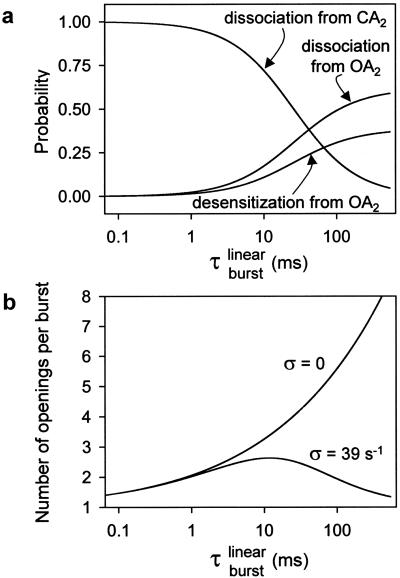
Fig. 5 illustrates some properties of bursts of diliganded openings calculated in the context of the kinetic model in Fig. 1; these are displayed most conveniently as a function of τ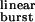 (Eq. 1). Fig. 5a shows that in wild-type receptors (τ
(Eq. 1). Fig. 5a shows that in wild-type receptors (τ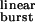 = 0.94 ms; Table 1), ≈96% of the diliganded bursts are predicted to be terminated by ACh dissociation from the closed state with only ≈4% being terminated by ACh dissociation from the open state or desensitization. This explains: (i) the adequacy of linear schemes like C ⇋ CA ⇋ CA2 ⇋ OA2 (ref. 23) as models of the wild type's diliganded activity (29), (ii) the fact that 2j− cannot be estimated from wild-type recordings, and (iii) the negligible contribution of desensitization (8) and ACh dissociation from the open state to the time course of the endplate current decay in normal, wild-type receptors. However, as τ
= 0.94 ms; Table 1), ≈96% of the diliganded bursts are predicted to be terminated by ACh dissociation from the closed state with only ≈4% being terminated by ACh dissociation from the open state or desensitization. This explains: (i) the adequacy of linear schemes like C ⇋ CA ⇋ CA2 ⇋ OA2 (ref. 23) as models of the wild type's diliganded activity (29), (ii) the fact that 2j− cannot be estimated from wild-type recordings, and (iii) the negligible contribution of desensitization (8) and ACh dissociation from the open state to the time course of the endplate current decay in normal, wild-type receptors. However, as τ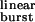 is increased by mutations that speed up opening and slow-down closing, the probability of a burst terminating from the closed state decreases, and the chances of the AChR entering the desensitized state or of ACh dissociating from the open state increase. Fig. 5b shows the predicted number of openings per burst for the δ12′-mutant series calculated as if neither desensitization nor ligand dissociation from the open state occurred (that is, with σ = 0) and with the estimated value of σ = 39 s−1. Because the contribution of desensitization and open-channel dissociation to the termination of a burst is negligible at low τ
is increased by mutations that speed up opening and slow-down closing, the probability of a burst terminating from the closed state decreases, and the chances of the AChR entering the desensitized state or of ACh dissociating from the open state increase. Fig. 5b shows the predicted number of openings per burst for the δ12′-mutant series calculated as if neither desensitization nor ligand dissociation from the open state occurred (that is, with σ = 0) and with the estimated value of σ = 39 s−1. Because the contribution of desensitization and open-channel dissociation to the termination of a burst is negligible at low τ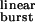 values, the predicted number of openings per burst for the wild-type AChR is the same (≅ 1.9) regardless of whether these alternative pathways are taken into account or not. However, the differences between the predictions of a model with σ = 0 and the model in Fig. 1 are very pronounced at prolonged τ
values, the predicted number of openings per burst for the wild-type AChR is the same (≅ 1.9) regardless of whether these alternative pathways are taken into account or not. However, the differences between the predictions of a model with σ = 0 and the model in Fig. 1 are very pronounced at prolonged τ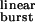 values, similar to those of numerous experimental and naturally occurring gain-of-function mutants (30). Table 1 shows the τ
values, similar to those of numerous experimental and naturally occurring gain-of-function mutants (30). Table 1 shows the τ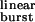 values corresponding to the wild-type and M2 12′ mutants studied here. Among congenital myasthenic syndrome AChRs, the αS269I receptor (31), for example, has a τ
values corresponding to the wild-type and M2 12′ mutants studied here. Among congenital myasthenic syndrome AChRs, the αS269I receptor (31), for example, has a τ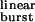 value of ≈40 ms (opening is ≈28 times faster, and closing is 3.3 times slower; ref. 32). The calculation in Fig. 5 thus predicts that only 39% of the bursts of αS269I AChRs are terminated by ACh dissociation from the closed state, as opposed to the value of 100% predicted by linear models. It follows that taking into account ligand dissociation from the open state, desensitization, and the previously unrecognized relationship given by Eq. 2 is essential for the correct interpretation of structure-function relationships and pathological synaptic transmission in nicotinic, and perhaps other, receptor channels.
value of ≈40 ms (opening is ≈28 times faster, and closing is 3.3 times slower; ref. 32). The calculation in Fig. 5 thus predicts that only 39% of the bursts of αS269I AChRs are terminated by ACh dissociation from the closed state, as opposed to the value of 100% predicted by linear models. It follows that taking into account ligand dissociation from the open state, desensitization, and the previously unrecognized relationship given by Eq. 2 is essential for the correct interpretation of structure-function relationships and pathological synaptic transmission in nicotinic, and perhaps other, receptor channels.
Figure 5.
Properties of bursts of diliganded openings. (a) The probability of a burst being terminated by ligand dissociation from the open state (followed by closure), desensitization, or ligand dissociation from the closed state were calculated as 2j−τ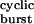 , k+Dτ
, k+Dτ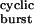 , and 1 − στ
, and 1 − στ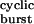 , respectively, where τ
, respectively, where τ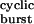 is given by Eq. 2, and σ = 2j− + k+D. The values of 2j− and k+D were taken as 24 and 25 s−1, respectively. (b) It is difficult, or even impossible, to count the number of openings per burst in constructs that open at wild type or even higher rates (>50,000 s−1), because sojourns in the closed diliganded state, CA2, are too short (<10 μs on average) to be fully detected. However, in the framework of the kinetic scheme in Fig. 1, this number can be calculated as (σ + α2)τ
is given by Eq. 2, and σ = 2j− + k+D. The values of 2j− and k+D were taken as 24 and 25 s−1, respectively. (b) It is difficult, or even impossible, to count the number of openings per burst in constructs that open at wild type or even higher rates (>50,000 s−1), because sojourns in the closed diliganded state, CA2, are too short (<10 μs on average) to be fully detected. However, in the framework of the kinetic scheme in Fig. 1, this number can be calculated as (σ + α2)τ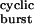 . For the δ12′ mutant series and in the hypothetical case of σ = 0, this number increases continuously. With σ = 39 s−1, however, this number goes through a maximum of ≈2.6 openings and tends to 1 at limiting large values of τ
. For the δ12′ mutant series and in the hypothetical case of σ = 0, this number increases continuously. With σ = 39 s−1, however, this number goes through a maximum of ≈2.6 openings and tends to 1 at limiting large values of τ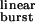 . These calculations are not heavily model-dependent; they are based only on the notion that AChRs can open and close, that desensitization of diliganded receptors proceeds predominantly from the open state, and that the ligand can dissociate from both the closed and open conformations.
. These calculations are not heavily model-dependent; they are based only on the notion that AChRs can open and close, that desensitization of diliganded receptors proceeds predominantly from the open state, and that the ligand can dissociate from both the closed and open conformations.
The dissociation rate constant of a ligand from a binding site is determined by both the energetics of the ligand-receptor contacts and the probability of the ligand escaping from the “encounter complex” (33, 34). The extent to which these two fundamentally different mechanisms change after opening to slow down the unbinding of ACh from open AChRs is far from clear. We hope that having learned how to measure the kinetics of ligand dissociation from the open state, along with the recently solved structure of an ACh-binding protein (35), will bring us closer.
Acknowledgments
We thank Dr. Asbed Keleshian for insightful discussions. This work was supported by an American Heart Association (New York State Affiliate) grant (to C.G.) and National Institutes of Health Grant NS 23513 (to A.A.).
Abbreviations
- ACh
acetylcholine
- AChR
ACh receptor channel
Footnotes
This paper was submitted directly (Track II) to the PNAS office.
References
- 1.Monod J, Wyman J, Changeux J P. J Mol Biol. 1965;12:88–118. doi: 10.1016/s0022-2836(65)80285-6. [DOI] [PubMed] [Google Scholar]
- 2.Karlin A. J Theor Biol. 1967;16:306–320. doi: 10.1016/0022-5193(67)90011-2. [DOI] [PubMed] [Google Scholar]
- 3.Jackson M B. In: The Nicotinic Acetylcholine Receptor: Current Views and Future Trends. Barrantes F, editor. Austin,TX: Landes Bioscience; 1997. pp. 61–84. [Google Scholar]
- 4.Edelstein S J, Changeux J P. Adv Protein Chem. 1998;51:121–184. doi: 10.1016/s0065-3233(08)60652-x. [DOI] [PubMed] [Google Scholar]
- 5.Reitstetter R, Lukas R J, Gruener R J. J Pharmacol Exp Ther. 1999;289:656–660. [PubMed] [Google Scholar]
- 6.Wilson G, Karlin A. Proc Natl Acad Sci USA. 2001;98:1241–1248. doi: 10.1073/pnas.031567798. . (First Published January 16, 2001; 10.1073/pnas.031567798) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Jackson M B. Adv Neurol. 1999;79:511–524. [PubMed] [Google Scholar]
- 8.Edmonds B, Gibb A J, Colquhoun D. Annu Rev Physiol. 1995;57:469–493. doi: 10.1146/annurev.ph.57.030195.002345. [DOI] [PubMed] [Google Scholar]
- 9.Wyllie D J, Behe P, Colquhoun D. J Physiol. 1998;510:1–18. doi: 10.1111/j.1469-7793.1998.001bz.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Salamone F N, Zhou M, Auerbach A. J Physiol. 1999;516:315–330. doi: 10.1111/j.1469-7793.1999.0315v.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Jackson M B. Biophys J. 1986;49:663–672. doi: 10.1016/S0006-3495(86)83693-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jackson M B. J Physiol. 1988;397:555–583. doi: 10.1113/jphysiol.1988.sp017019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Grosman C, Auerbach A. J Gen Physiol. 2000;115:621–635. doi: 10.1085/jgp.115.5.621. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Wang H L, Auerbach A, Bren N, Ohno K, Engel A G, Sine S M. J Gen Physiol. 1997;109:757–766. doi: 10.1085/jgp.109.6.757. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bouzat C, Barrantes F, Sine S. J Gen Physiol. 2000;115:663–672. doi: 10.1085/jgp.115.5.663. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Grosman C, Auerbach A. J Gen Physiol. 2000b;115:637–651. doi: 10.1085/jgp.115.5.637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Auerbach A, Akk G. J Gen Physiol. 1998;112:181–197. doi: 10.1085/jgp.112.2.181. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hamill O P, Marty A, Neher E, Sakmann B, Sigworth F J. Pflügers Arch. 1981;391:85–100. doi: 10.1007/BF00656997. [DOI] [PubMed] [Google Scholar]
- 19.Qin F, Auerbach A, Sachs F. Biophys J. 1996;70:264–280. doi: 10.1016/S0006-3495(96)79568-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Colquhoun D, Hawkes A G. In: Single-Channel Recording. Sakmann B, Neher E, editors. New York: Plenum; 1995. pp. 397–482. [Google Scholar]
- 21.Colquhoun D, Hawkes A G. In: Single-Channel Recording. Sakmann B, Neher E, editors. New York: Plenum; 1995b. pp. 589–633. [Google Scholar]
- 22.Colquhoun D, Sakmann B. J Physiol. 1985;369:501–557. doi: 10.1113/jphysiol.1985.sp015912. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Colquhoun D, Hawkes A G. Proc R Soc London Ser B. 1981;211:205–235. doi: 10.1098/rspb.1981.0003. [DOI] [PubMed] [Google Scholar]
- 24.Milone M, Wang H L, Ohno K, Fukudome T, Pruitt J N, Bren N, Sine S M, Engel A G. J Neurosci. 1997;17:5651–5665. doi: 10.1523/JNEUROSCI.17-15-05651.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Akk G, Zhou M, Auerbach A. Biophys J. 1999;76:207–218. doi: 10.1016/S0006-3495(99)77190-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Unzai S, Eich R, Shibayama N, Olson J S, Morimoto H. J Biol Chem. 1998;273:23150–23159. doi: 10.1074/jbc.273.36.23150. [DOI] [PubMed] [Google Scholar]
- 27.Sine S M, Ohno K, Bouzat C, Auerbach A, Milone M, Pruitt J N, Engel A G. Neuron. 1995;15:229–239. doi: 10.1016/0896-6273(95)90080-2. [DOI] [PubMed] [Google Scholar]
- 28.Edelstein S J, Schaad O, Henry H, Bertrand D, Changeux J-P. Biol Cybern. 1996;75:361–379. doi: 10.1007/s004220050302. [DOI] [PubMed] [Google Scholar]
- 29.Sine S M, Claudio T, Sigworth F J. J Gen Physiol. 1990;96:395–437. doi: 10.1085/jgp.96.2.395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Ashcroft F M. Ion Channels and Disease. New York: Academic; 2000. pp. 269–290. [Google Scholar]
- 31.Croxen R, Newland C, Beeson D, Oosterhuis H, Chauplannaz G, Vincent A, Newsom-Davis J. Hum Mol Genet. 1997;6:767–774. doi: 10.1093/hmg/6.5.767. [DOI] [PubMed] [Google Scholar]
- 32.Grosman C, Salamone F N, Sine S M, Auerbach A. J Gen Physiol. 2000;116:327–339. doi: 10.1085/jgp.116.3.327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Eigen M, Hammes G G. Adv Enzymol. 1963;25:1–38. doi: 10.1002/9780470122709.ch1. [DOI] [PubMed] [Google Scholar]
- 34.Shoup D, Szabo A. Biophys J. 1982;40:33–39. doi: 10.1016/S0006-3495(82)84455-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Brejc K, van Dijk W J, Klaassen R V, Schuurmans M, van Der Oost J, Smit A B, Sixma T K. Nature (London) 2001;411:269–276. doi: 10.1038/35077011. [DOI] [PubMed] [Google Scholar]