Skip to main content
PMC home page
ACS AuthorChoice logoLink to ACS AuthorChoice
. 2018 Aug 7;10(34):29107–29114. doi: 10.1021/acsami.8b08218

Cell Membrane Disruption by Vertical Micro-/Nanopillars: Role of Membrane Bending and Traction Forces

Rosario Capozza †, Valeria Caprettini †,‡, Carlo A Gonano †, Alessandro Bosca †, Fabio Moia †, Francesca Santoro §, Francesco De Angelis †,*
PMCID: PMC6117743  PMID: 30081625

Abstract

graphic file with name am-2018-08218x_0006.jpg

Gaining access to the cell interior is fundamental for many applications, such as electrical recording and drug and biomolecular delivery. A very promising technique consists of culturing cells on micro-/nanopillars. The tight adhesion and high local deformation of cells in contact with nanostructures can promote the permeabilization of lipids at the plasma membrane, providing access to the internal compartment. However, there is still much experimental controversy regarding when and how the intracellular environment is targeted and the role of the geometry and interactions with surfaces. Consequently, we investigated, by coarse-grained molecular dynamics simulations of the cell membrane, the mechanical properties of the lipid bilayer under high strain and bending conditions. We found out that a high curvature of the lipid bilayer dramatically lowers the traction force necessary to achieve membrane rupture. Afterward, we experimentally studied the permeabilization rate of the cell membrane by pillars with comparable aspect ratios but different sharpness values at the edges. The experimental data support the simulation results: even pillars with diameters in the micron range may cause local membrane disruption when their edges are sufficiently sharp. Therefore, the permeabilization likelihood is connected to the local geometric features of the pillars rather than diameter or aspect ratio. The present study can also provide significant contributions to the design of three-dimensional biointerfaces for tissue engineering and cellular growth.

Keywords: nanopillars, lipid bilayer, nanopore, membrane disruption, molecular dynamics, intracellular delivery

Introduction

Direct access to the intracellular compartment is an open challenge1 with many potential applications, such as gene transfection,2,3 biomolecule delivery,4 and electrical recording in electroactive cells.5,6 The main difficulties are related to the impermeability of the plasma membrane, which, after a billion years of evolutionary defenses, strictly controls the trafficking in and out of the cell. The most popular methods for intracellular delivery are electroporation,7 chemical transfection, and virus-mediated transduction, although novel methods have been considered recently.8−11 Among them, local membrane permeabilization through vertical nanopillars or other three-dimensional (3D) nanostructures is emerging as a robust approach.12−18 Essentially, the concept relies on arrays of vertical standing nanostructures in a fakir bedlike configuration. When cells are cultured on these arrays, the plasma membrane exhibits tight adhesion to the pillars or even engulfment-like events.19 These processes often lead to a spontaneous increase in membrane permeability20 that can be used to deliver molecules into the cytosol by bypassing the conventional biochemical pathways or to record intracellular electrical activity via the enhanced electrical coupling between the conductive pillar and the cell.5 In general, there is a wide interest in designing novel 3D biointerfaces for tissue engineering and cellular growth21 to investigate how cells interact and proliferate onto these types of geometries22−24 and which structures improve the cell viability.25 However, the exact mechanism enabling local permeabilization is still not fully understood, and many controversies still exist. Recent studies suggested that the internalization of molecules is not due to the temporary disruption of the plasma membrane in contact with the 3D nanostructures but is instead driven by membrane deformation26 or enhancement of the clathrin-mediated endocytosis process of the cell at the interface with sharp edges.27 On the contrary, a previous study, developing a simple but effective mechanical continuum model of elastic cell membranes,28 ascribes such complex behaviors to actual penetration of the plasma membrane. In that work, two main mechanisms at the interface are considered, namely “impaling”, where cells land on a bed of nanowires, and “adhesion-mediated” permeabilization, which occurs as cells spread on the substrate and generate adhesion force. In the former, the force leading to the membrane disruption is gravity, whereas in the latter mechanism, this force is the adhesion-force provided by membrane proteins. In both cases, membrane permeabilization occurs when the nanopillar generates sufficient tension to overcome a critical membrane tension value. However, the pillar is modeled as a cylindrical probe with a hemispherical tip, and the effect of local geometry (e.g., the sharpness of pillar edge) is not taken into account. Hence, only the diameter, the height, and the spacing between the pillars determine the penetration forces for a cell line of a given stiffness. This approach may explain the experimental reports of spontaneous poration observed in vertical nanostructures of small diameters on the order of 50–200 nm29−31 or below. Indeed, as we will subsequently show, we found experimentally that spontaneous permeabilization may occur even for much larger pillar diameters of approximately 2 μm. Such a finding is also confirmed by another study that recently reported spontaneous membrane disruption by pillars of 1 μm in diameter, even in the absence of adhesion with the substrate;32 hence, the models mentioned above cannot fully explain the membrane permeabilization. In other words, the reasons why these large micropillars/nanopillars can effectively permeabilize the membrane are still unclear, thus demanding a more complex scenario that includes not just gravity and adhesion but also traction forces, membrane deformations (bending), and local geometric features (sharp edges on the pillars). Obviously, biological mechanisms and surface properties also participate in the increase in cell internalization processes, but the present mechanical model will not take them into account.

Molecular dynamics simulation is a powerful tool that may elucidate the behavior of these systems. However, to the best of our knowledge, there are still few molecular dynamics (MD) studies investigating the mechanical properties of a membrane when in contact with a nanostructure.33 Furthermore, most MD studies tackle the problem only in the regime of small bending deformations,34−36 which is not applicable for this case of study.

In this work, we first undertake MD simulations in synergic combination with a mechanical model of the cell membrane that goes beyond the linear response approximation. We found that the bending of the membrane is characterized by an elastic regime at low bending angles, followed by a plastic one at higher angles.

We also included the local geometry of the pillar by investigating the role of curvature or edges at the pillar tip (different from the pillar diameter), and we found that a high curvature favors the rupture even at very low tensile strength.

Afterward, we show that simulation results are supported by experimental data, suggesting that when cells are cultured on pillars with diameters in the micrometric range, their permeabilization likelihood is strongly increased in the presence of sharp edges. We conclude that, under the given conditions, the local curvature may dramatically affect the lipid bilayer permeabilization to a greater extent than the effect of the pillar diameter.

Results and Discussion

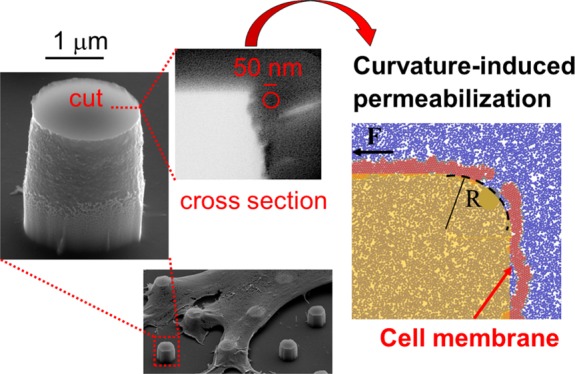
Figure 1 shows a SEM/FIB cross-sectional image of cell cultured on micropillars with a diameter of 2 μm and height of 1.5 μm, obtained by using a technique explained elsewhere.37 This image displays possible configurations of the cell/nanostructure interface and highlights the proximity of the cell membrane to the pillars: the cell can tightly wrap around the 3D pillar (b) or assume a “tentlike” configuration (a). In both cases, the cell membrane conforms to the pillar’s head geometry, where we assume most of the tensile strength is concentrated, via adhesion with the substrate and forces exerted through the cell body. Therefore, the membrane curvature is dictated by the pillar’s edge. Furthermore, the forces acting on the membrane can be oriented in any direction depending on the local configuration of the system, as sketched in panels (c,d) of Figure 1. Traction and bending cannot be considered separately, and they may cooperate to lower the threshold for local permeabilization or nanopore creation. For instance, when the traction force is mainly directed laterally (parallel to the substrate), the pillar may behave like a knife edge, meaning that only the size of the edge matters and the diameter plays a minor role.

Figure 1.

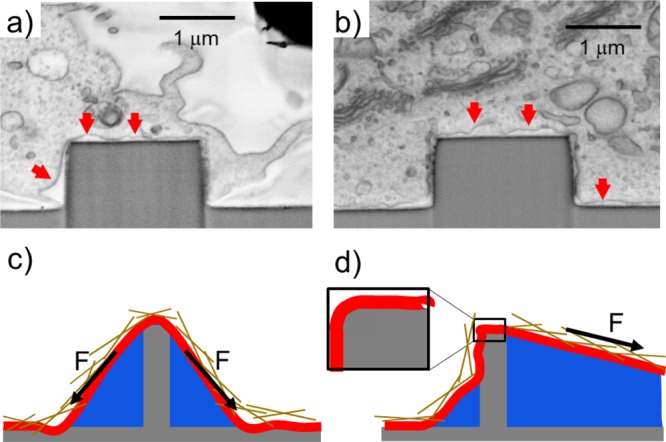
Figure 1

Open in a new tab

Scanning electron microscopy (SEM) images showing a focused ion beam (FIB) cross sections of a cell cultured on an array of 2 μm diameter pillars. The samples were fixed and stained following a recently developed ROTO protocol (see S2 for more details) and embedded in a thin film of epoxy resin. The cell membrane (indicated by red arrows) can assume a “tentlike” configuration (a) or be tightly wrapped around the pillars (b). (c) Adhesion-induced mechanism of permeabilization. (d) Traction-induced mechanism of permeabilization. Inset: the membrane’s bending is dictated by the local radius of curvature rather than by the micropillar/nanopillar diameter.

Simulation Model

We used a two-dimensional (2D) coarse-grained model of the cell membrane in which the lipid molecule is made of a hydrophilic Lennard-Jones (L-J) particle (the head) and a hydrophobic tail made of five L-J beads (Figure 2b). We included an additional harmonic interaction between the L-J beads of the tail. The water is simulated as a single L-J bead.38 First, we tested the validity of our system by simulating free lipid molecules randomly dispersed in water and checking that the lipids undergo a self-assembly process that leads to the formation of the lipid membrane. As expected, under the conditions we used, a bilayer is formed spontaneously with the hydrophilic heads pointing toward water and the tails clustering together, minimizing their interaction with water (see S2). The average distance between hydrophilic heads is 0.8 nm corresponding approximately to an average area per lipid39 of 0.67 nm2. The average area per lipid usually ranges40 between 0.6 and 0.75 nm2, so the chosen value is about in the middle of this range. We are aware that these parameters can impact the mechanical properties and permeabilization likelihood of a membrane in contact with the pillars, but we stress that our scope is to gain a qualitative understanding of some experimental results reported in the literature.32

Figure 2.

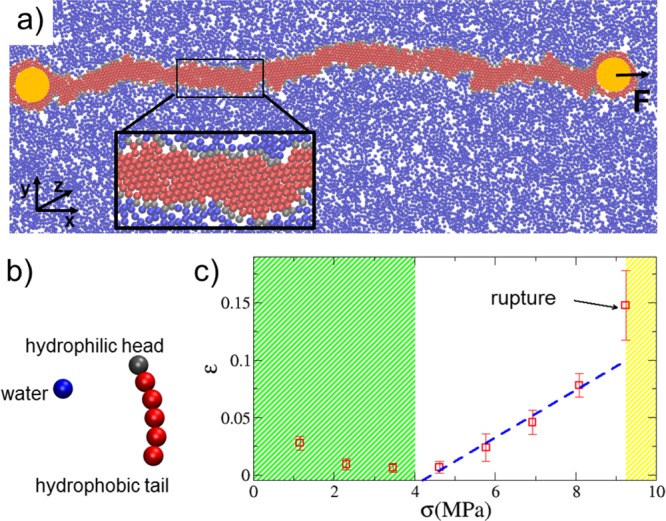
Figure 2

Open in a new tab

(a) Snapshot of a simulated segment of membrane subject to a horizontal traction force F. Two cylinders (yellow circles) are embedded into the membrane segment. One cylinder is kept fixed, while the other one applies a force F along the positive direction of the x axis. Here, water is indicated in blue, hydrophilic heads in gray, and hydrophobic tails in red. Inset: Blow-up of the simulated system showing the molecular arrangement in detail. (b) Coarse-grained model of water and the lipid molecule with a single bead for the hydrophilic head and five beads for the hydrophobic hydrocarbon tail. (c) Strain–stress curve showing three loading regimes: a thermally dominated regime (thermal noise larger than the applied stress), an elastic regime, and failure for F > 28 pN (corresponding to σ > 9.2 MPa).

Clearly, with a 2D model, we cannot reproduce all of the 3D phenomena, for example, the lipid diffusion through the membrane’s surface.

In addition, the MD model presented here considers just the lipid bilayer and not the cytoskeleton and membrane proteins that certainly affect the mechanical properties of the cell.

However, we carefully checked that our numerical simulations can qualitatively reproduce many real processes (self-assembly, bilayer, micelles, vesicles, etc.) that depend on the geometrical features of molecules.40 This method can be regarded as a good compromise between the computational cost and the accuracy of the mechanical analysis and allows a statistical analysis of results. After the bilayer formation, we replicate the structure to create a system size at will and set up the initial configuration (Figure 2a). The typical size of our system is on the order of 100 nm.

Modeling of the Plasma Membrane Mechanical Response

The mechanical properties of a material are often described by means of a mathematical relation linking the strain ε (ratio between a displacement and a rest length) to the applied stress σ (force per unit area). For an ideal linear material, the applied stress is given by σ = E·ε, where E is the Young’s modulus (see S3). The Young’s modulus E is a characteristic of the material, so it is an intensive parameter in the sense that it does not depend on extensive properties of the considered object (e.g., length and mass); however, membrane deformation is often described in terms of stiffness and applied forces.28,35,40 For example, the area stretch modulus KA (characterizing the rigidity of a membrane to traction force) and the bending stiffness Kbend (linking the curvature to the applied moment) are extensive parameters because they depend on the membrane’s length and thickness (see S4). We decided to calculate both intensive and extensive quantities. Because the cell membrane may undergo large deformation when in contact with nanostructures, the approximation of a linear material is no longer valid, and the membrane could also exhibit plastic behavior (hysteresis). In this case, the Young’s modulus can be interpreted as the derivative of the stress σ with respect to the strain ε, formally

graphic file with name am-2018-08218x_m001.jpg 1

More simply, extracting the strain–stress relation is a standard strategy for characterizing the elastic properties of a material. For that purpose, we simulated a cell membrane loaded by cylinders measuring the displacements and the applied forces, as shown in Figure 2a.

Afterward, we calculated the strain–stress curve through the classical Euler–Bernoulli beam model connecting the bending moment Mz to the deflection of the beam (the membrane) through the Young’s modulus E and a local linearization.

In the simple case of pure traction, we calculate the stress–strain curve by applying a traction force to the edges of the membrane (Figure 2a) and estimating the ultimate tensile strength as the force FTS we need to apply to break the membrane. After embedding two cylinders into the membrane segment, we keep one fixed, while the other one applies a force F along the positive direction of the x axis. The force is increased in steps ΔF = 3.5 pN and kept constant for a time interval Δt = 1.2 ns. During the step-wise increase in force, we monitored the strain ε of the membrane, and we found that the membrane ruptures at F = 28 pN (corresponding to an ultimate tensile stress σ = 9.2 MPa). Therefore, the value FTS = 28 pN represents the tensile strength of the membrane in the straight configuration.

The longitudinal strain εxx is the ratio between the displacement Δsx and the rest length lx = 92 nm.

graphic file with name am-2018-08218x_m002.jpg 2

The applied stress σxx here is simply the force on the membrane’s section

graphic file with name am-2018-08218x_m003.jpg 3

The plot of the strain–stress curve (Figure 2c) clearly shows three loading regimes

  • For 0 ≤ σ ≤ 4.5 MPa, the stress does not significantly affect the strain. The membrane fluctuates, and the thermal noise overwhelms the effects of the applied force.

  • For 4.5 MPa < σ < 9.2 MPa, the membrane responds elastically, and we estimate a Young’s modulus E = 50 MPa by linear regression (blue dashed curve in Figure 2c). This value is in the range of experimental measurements.40

  • For σ > 9.2 MPa, membrane rupture occurs.

From Young’s modulus E, we calculate the area-stretch modulus 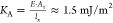Inline graphic. As expected, KA and FTS are approximately 2 orders of magnitude smaller than the ones calculated for typical free biological cell membranes, which range28,40 from 100 to 250 mJ/m2. In fact, our system is representative of a longitudinal section of a 3D membrane; thus, the domain’s depth must be taken into consideration.

In the following, we describe the calculation of the membrane bending stiffness Kbend. Previous approaches estimated Kbend by analyzing the height (spatial) fluctuation spectrum of a membrane.41−44 However, these methods present serious drawbacks because of the slow convergence of long wavelengths34,35 and assume a regime of small deformations. In contrast, a membrane in contact with micropillars/nanopillars could be strongly deformed. For this reason, we studied the bending invoking neither the hypothesis of small deformations nor the hypothesis of a linear material. Hence, the elastic parameters such as E and Kbend could depend on the strain.

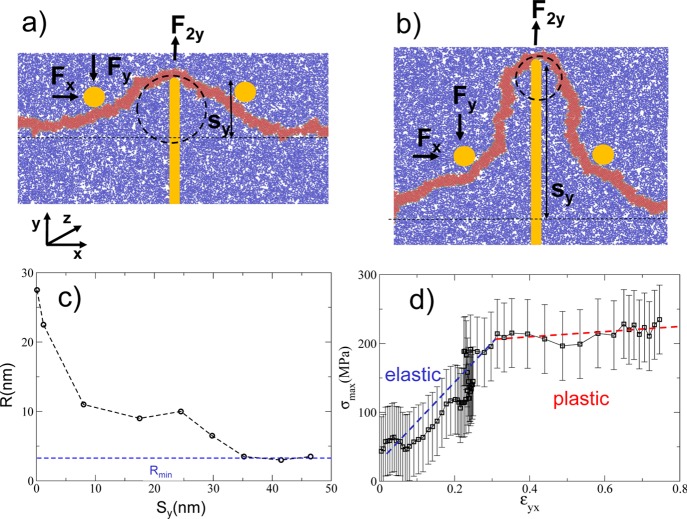
We employed a simulation setup similar to the one already used in the literature.34 A segment of membrane with free ends is pushed in the center through a nanopillar (with a hemispherical tip of radius rp ≈ 2 nm) moving upward and two immobile cylinders (Figure 3a,b) interacting just with the hydrophobic tails. The segment is free to flow under the lateral cylinders to avoid stretching and to study the mechanical response under pure bending. During the course of simulations, we measured the x and y components of the force on the cylinders and the pillar and the vertical displacement sy, and we estimate the local radius of curvature R as the best circle approximating the average membrane profile (Figure 3c). For small values of vertical displacement sy, R is independent on the pillar size, and it rapidly decreases reaching the plateau Rmin ≈ 4 nm at sy ≈ 35 nm (Figure 3c). The value Rmin represents the smallest possible radius of curvature considering the membrane thickness is ly ≈ 4.5 nm and corresponds to the membrane wrapping around the pillar’s tip. As explained in detail in S6 and S7, for a linear material, the stress σ and the local radius of curvature R are both proportional to the bending moment Mz. It is then possible to show that the stress–strain relation reads as

graphic file with name am-2018-08218x_m005.jpg 4

where ly ≈ 4.5 nm is the average membrane thickness. Because both σx and the curvature strain εxy can be obtained from the simulations, and even for a nonlinear material, the Young’s modulus can be estimated as 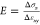Inline graphic.

Figure 3.

Figure 3

Open in a new tab

Configuration of the membrane in response to a small (a) and high (b) deformation sy. (c) Behavior of the estimated radius of curvature R as a function of the deformation sy. For sy > 35 nm, the radius of curvature R reaches the minimum Rmin, corresponding to the membrane wrapping around the pillar’s tip. (d) Stress–strain curve showing the elastic and plastic regimes.

The stress–strain curve is reported in Figure 3d. Two distinct regimes, elastic and plastic, can be clearly identified. In fact, for values of curvature strain εxy < 0.3, the membrane responds elastically, while for εxy > 0.3, it is plastically deformed. This latter regime, characterized by a smaller Young’s modulus, suggests a hysteretic behavior. In fact, upon retraction of the nanopillar, the membrane does not return to its initial straight configuration, at least in the time interval available to our simulations. Each point in Figure 3d is obtained from a statistical average over 10 different simulations. We fitted the points of the stress–strain curve (Figure 3d) with two lines, and we estimated the Young’s modulus for the elastic regime Eelas = (600 ± 150) MPa and plastic regime Eplas = (75 ± 25) MPa. Not surprisingly, the value of Eplas is (considering the error) equal to the E calculated for the pure stretching, indicating that for εxy > 0.3, the bending corresponds to an effective stretching of the outer membrane monolayer.

As shown in S5, the relation 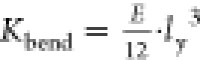Inline graphic allows us to estimate the bending stiffness in the elastic Kbendelas ≈ (4.5 ± 2.6) × 10–18 J and plastic regime Kbend ≈ (0.57 ± 0.37) × 10–18 J. The value of Kbendplast is of the same order of magnitude of the ones reported in the literature,40 while Kbend is 1 order of magnitude larger. This large value of Kbendelast can be attributed to the limits of our 2D modeling, which cannot correctly reproduce the interlayer diffusivity of lipid molecules. We stress that the estimation of Kbend is affected by a large uncertainty related to the dependency on the cube of membrane thickness ly (see S5) and the one related to Young’s modulus E.

Membrane Mechanical Response to Local Curvature

In the following, we investigate how curvature and bending affect the ultimate tensile strength FTS. In fact, the edges of 3D nanostructures in contact with the cell membrane could be very sharp, and their sharpness is usually very difficult to control experimentally. The lipid bilayer can adhere to the micropillar/nanopillar edge and, then, follow its curvature. Traction forces are on the order19 of 1 nN and in principle too small to promote spontaneous rupture of membrane.

What is the relation between the ultimate tensile strength FTS and the curvature?

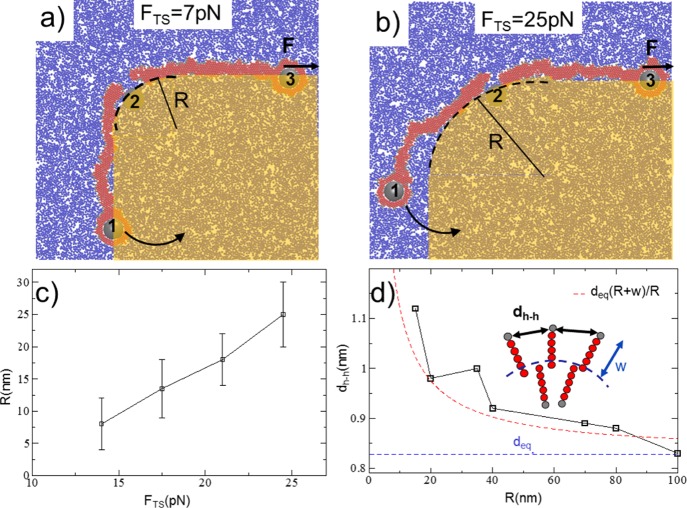
To clarify this point, we performed simulations by stretching and bending the membrane simultaneously. The three-cylinder configuration is shown in Figure 4a. Two cylinders (1 and 3) are embedded into the membrane, while cylinder 2 is kept fixed. Cylinder 3 applies a constant force F to the membrane along the positive direction of the x axis and lower than the membrane’s ultimate tensile strength, FTS = 28 pN.

Figure 4.

Figure 4

Open in a new tab

Three-cylinder simulation geometry used to calculate the effect of the local radius curvature R on the ultimate tensile strength FTS. Cylinder 3 applies a constant force F, and cylinder 1 rotates around cylinder 2 (at rest) (a,b). A smaller value of F corresponds to a smaller R needed to bring the membrane to the rupture. The yellow shaded area suggests a possible configuration of the membrane in contact with a micropillar/nanopillar. (c) Behavior of the critical radius of curvature R as a function of FTS. (d) Average distance between hydrophilic heads, dh–h, as a function of the bending radius R, as calculated in the segment where the membrane is bent. The blue dashed line is the equilibrium distance deq in the absence of bending, and the red dashed line shows the behavior of dh–h from an analytical model. Here, deq = 0.83 nm and w = ly/2 = 2.25 nm.

Cylinder 1 rotates the membrane around an axis passing through cylinder 2 and directed along z, imposing a curvature on the membrane. We found that the smaller F is, the higher is the curvature (the smaller R) needed to bring the membrane to the rupture, as reported in the snapshots of the system in Figure 4a,b. In Figure 4c, the local radius R is plotted as a function of FTS; each value of R was obtained from a statistical average over 10 different simulations. The behavior of the local radius of curvature R as a function of FTS clearly shows that even a tiny force can promote a rupture, provided that R is small, that is, the edge is sharp.

What is the reason for the curvature-induced membrane weakening?

Figure 4d shows the variation in the average distance between hydrophilic heads, dh–h, as a function of the bending radius R, calculated only in the segment where the membrane is bent. In the absence of bending, dh–h = deq = 0.83 nm (blue dashed line in Figure 4d), which is the equilibrium distance after the self-assembly process of the membrane (see S3). After the membrane is bent, dh–h deviates from the equilibrium and rapidly increases as the radius of curvature R decreases.

Let us consider an initially straight bar composed of n elements at distance deq and finite thickness ly (i.e., the average thickness of the membrane). When the bar is bent, the distance dh–h between the elements of its upper surface (see inset in Figure 4d) increases following the relation 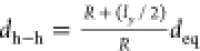Inline graphic (the red dashed line shown in Figure 4d). The values of dh–h versus R, calculated from the numerical simulations, follow approximately the theoretical red dashed line, suggesting that the membrane is effectively deformed like a bar composed of discrete elements.

When dh–h increases, the membrane is brought out of its equilibrium distance deq, and the probability of nanopore formation increases as well. In this situation, traction forces further increase the probability of defect formation (lowering the activation energy for nanopore formation) and favor breakdown.

Experiment

Investigation of Permeabilization on Sharp Pillars

To confirm the effect of the edge on the cell membrane permeabilization, we fabricated two sets of pillars, denoted as “sharp” and “smooth”; the pillars had an identical pitch of 5 μm, comparable diameter of approximately 2 μm, height of 2.5 and 1 μm, respectively, and their most important difference was the edge sharpness, as reported in Figure 5a,b (see S1 for more details on the fabrication process). We estimated their radius of curvature as Rsharp ≈ 20 ± 5 nm for the sharp case and Rsmooth ≈ 250 ± 20 nm for the smooth one from the cross sections of the pillars, as shown in the inset of Figure 5a. Afterward, we cultured NIH-3T3 cells on these arrays of pillars and administered the impermeable dye propidium iodide in solution together with the permeable calcein acetoxymethyl (AM) dye to verify the healthiness of the cells. Surprisingly and contrary to some previous literature results,28 we found that in the case of large but sharp pillars, the dye entered the cell body with a probability of approximately 70%, staining the cells red, as demonstrated by fluorescence images reported in Figure 5c (see Supporting Information for more details) maintaining their viability, confirmed by the green stain. These results have been acquired on 400 cells in 6 different cell cultures. In contrast, cells cultured on the smooth pillars showed no sign of dye internalization (no red color) and a green color indicating cell viability but no permeabilization (see Figure 5d).

Figure 5.

Figure 5

Open in a new tab

(a) SEM image of a “sharp” pillar with a diameter of 2 μm and a height of 2.5 μm. The inset highlights a cross section of the sharp edge, with an estimated radius of curvature of Rsharp ≈ 20 ± 5 nm (compare the approximating circle with the scale bar). (b) SEM image of a “smooth” pillar with a diameter of 2 μm and a height of 1 μm. The estimated radius of curvature is Rsmooth ≈ 250 ± 20 nm. (c) Fluorescence image of cells cultured on sharp pillars fabricated with a spacing of 5 μm (green spots) and treated with both permeable calcein AM (green) and impermeable dye propidium iodide (red) administrated in solution. Most of the cells present green and red staining, with a permeability likelihood very close to 70%. (d) Corresponding fluorescence image of cells cultured on smooth pillars and treated with the same dyes. In this case, only a limited number of cells contain propidium iodide and are hence stained in red, meaning that the cell membrane is successfully permeabilized in a few cases (see S2 for more details). A specific red staining is probably due to the fraction of death cells and DNA dispersed in the cell culture.

Although we were unable to study the effect of the curvature on pillars with identical aspect ratio (due to the difficulty in precisely controlling curvature and aspect ratio simultaneously), we consider these experimental results as a further support of our theoretical/computational investigation. In fact, the presence of shorter pillars ensures stronger adhesion with the substrate that, according to previous studies,28 is assumed to be one of the factors increasing the permeabilization probability. However, our fluorescence analysis of smooth pillars did not show such an increase, displaying permeabilization in very few cases that we have estimated to represent less than 10% (30 cells over 320 in 5 different cell cultures).

Additionally, these last results demonstrate that the overall geometry of pillar’s edge plays the most important role, while sharp local asperities present on the smooth pillars (displayed for clarity in Figure S1) are negligible in this configuration.

The radius of curvature of sharp pillars (Rsharp ≈ 20 ± 5 nm) falls in the range of values where, according to the simulation results reported in Figure 4c, we expect a significant decrease in tensile strength for rupture. This can explain the increase of permeabilization, as shown in Figure 5c by fluorescence images.

For sake of clarity, we remark that the novelty here is represented by the role of the sharp edge and not by fine tuning of the aspect ratio. Similar findings were also recently observed by another group that studied plasmid transfection driven by cells interfacing with 3D nanostructures.32

We consider these results of great importance in the field for two reasons: (i) cell membrane permeabilization is reported at pillar sizes, where permeabilization is not theoretically expected.28 (ii) The comparison between sharp and smooth pillars highlights the importance of membrane curvature and its role as a key player in the permeabilization processes.

Conclusions

In summary, we studied, through a 2D coarse-grained MD model, the mechanical behavior of a cell membrane interacting with micropillars/nanopillars. To identify the stress–strain relations and the rupture conditions, we performed simulations of a lipid bilayer subjected to different loading conditions: longitudinal traction, pure bending, and combined traction and bending. We have also proposed a simple mechanical model for estimating the main intensive elastic parameters, such as the Young’s modulus and the ultimate tensile stress, in a regime of large stress and deformation. Notably, we did not introduce any restrictive hypothesis on the constitutive relation for the membrane’s elasticity: actually, the stress–strain relation could be nonlinear. Moreover, we extracted the ultimate tensile loads from the simulations without postulating any value a priori. We found that the bending of a membrane is characterized by an elastic regime at low bending angles, followed by a plastic one at higher angles, namely, spatial configurations that are irreversible within the time window of the simulations.

Importantly, the simulation shows that bending of the membrane (e.g., at the pillar’s edge) dramatically lowers the rupture force.

To support these theoretical findings, we investigated experimentally the permeabilization of cells cultured on micropillars. Surprisingly, we found that spontaneous permeabilization events may occur on pillars of diameters in the micrometer range, which is much larger than previously observed. A comparison between cells cultured on pillars with a comparable aspect ratio but different sharpness at the edges suggests that the local curvature of the membrane could be responsible for the strong increase in permeabilization, with a probability that increases from 10% in the smooth case to the 70% in the sharp case.

Therefore, the simulation results suggest a direct interpretation of the experimental data. In principle, even step edges can cause local membrane disruption, provided that they are sharp enough.

The results obtained from our simulations could also be applied to the understanding of the internalization of substrate-free nanowires,45,46 because cellular traction forces exist in that situation as well. In fact, the internalization process often starts at the sharp tip of nanowires, where the curvature is higher. In conclusion, local geometric features at the cell–substrate interface can dramatically affect cell permeabilization to a greater extent than the effect of the pillar aspect ratio and spacing. These results may provide important information for the field of biointerfaces and tissue engineering, offering valuable insight into designing devices for gene transfection, intracellular delivery, and electrical recording.

Acknowledgments

This work was supported by the European Research Council under the European Union’s Seventh Framework Programme (FP/2007-2013)/ERC grant agreement no. (616213), CoG: Neuro-Plasmonics.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsami.8b08218.

  • Fabrication method; cell culture and imaging; MD simulation of membrane self-assembly; strain–stress curve; bending stiffness; maximum stress on the membrane’s section; and stress–strain relation for bent membrane (PDF)

Author Contributions

R.C. conceived and performed the MD simulations and the data analysis and wrote the manuscript. V.C. carried out the experiments and associated data analysis. C.A.G. performed the mechanical and mathematical analysis of simulation data. A.B. and F.M. fabricated the micropillars to be used for cell culture. F.S. assisted in the experimental analysis and imaging. F.D.A. conceived the experiment, supervised the work, and analyzed the data. All authors contributed to the preparation of the manuscript and have given approval to the final version.

The authors declare no competing financial interest.

Supplementary Material

am8b08218_si_001.pdf (3.6MB, pdf)

References

  1. Stewart M. P.; Sharei A.; Ding X.; Sahay G.; Langer R.; Jensen K. F. In vitro and ex vivo strategies for intracellular delivery. Nature 2016, 538, 183–192. 10.1038/nature19764. [DOI] [PubMed] [Google Scholar]
  2. Washbourne P.; McAllister A. K. Techniques for gene transfer into neurons. Curr. Opin. Neurobiol. 2002, 12, 566–573. 10.1016/s0959-4388(02)00365-3. [DOI] [PubMed] [Google Scholar]
  3. He G.; Chen H.-J.; Liu D.; Feng Y.; Yang C.; Hang T.; Wu J.; Cao Y.; Xie X. Fabrication of Various Structures of Nanostraw Arrays and Their Applications in Gene Delivery. Adv. Mater. Interfaces 2018, 5, 1701535. 10.1002/admi.201701535. [DOI] [Google Scholar]
  4. Ma Y.; Nolte R. J. M.; Cornelissen J. J. L. M. Virus-based nanocarriers for drug delivery. Adv. Drug Delivery Rev. 2012, 64, 811–825. 10.1016/j.addr.2012.01.005. [DOI] [PubMed] [Google Scholar]
  5. Xie C.; Lin Z.; Hanson L.; Cui Y.; Cui B. Intracellular recording of action potentials by nanopillar electroporation. Nat. Nanotechnol. 2012, 7, 185–190. 10.1038/nnano.2012.8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Dipalo M.; Amin H.; Lovato L.; Moia F.; Caprettini V.; Messina G. C.; Tantussi F.; Berdondini L.; De Angelis F. Intracellular and Extracellular Recording of Spontaneous Action Potentials in Mammalian Neurons and Cardiac Cells with 3D Plasmonic Nanoelectrodes. Nano Lett. 2017, 17, 3932–3939. 10.1021/acs.nanolett.7b01523. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Teissié J.; Eynard N.; Gabriel B.; Rols M. P. Electropermeabilization of cell membranes. Adv. Drug Delivery Rev. 1999, 35, 3–19. 10.1016/s0169-409x(98)00060-x. [DOI] [PubMed] [Google Scholar]
  8. Yoon S.; Kim M. G.; Chiu C. T.; Hwang J. Y.; Kim H. H.; Wang Y.; Shung K. K. Direct and sustained intracellular delivery of exogenous molecules using acoustic-transfection with high frequency ultrasound. Sci. Rep. 2016, 6, 20477–20488. 10.1038/srep20477. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Fan Q.; Hu W.; Ohta A. T. Efficient single-cell poration by microsecond laser pulses. Lab Chip 2015, 15, 581–588. 10.1039/c4lc00943f. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Xiong R.; Samal S. K.; Demeester J.; Skirtach A. G.; De Smedt S. C.; Braeckmans K. Laser-assisted photoporation: fundamentals, technological advances and applications. Adv. Phys.: X 2016, 1, 596–620. 10.1080/23746149.2016.1228476. [DOI] [Google Scholar]
  11. Saklayen N.; Huber M.; Madrid M.; Nuzzo V.; Vulis D. I.; Shen W.; Nelson J.; McClelland A. A.; Heisterkamp A.; Mazur E. Intracellular Delivery Using Nanosecond-Laser Excitation of Large-Area Plasmonic Substrates. ACS Nano 2017, 11, 3671–3680. 10.1021/acsnano.6b08162. [DOI] [PubMed] [Google Scholar]
  12. Durney A. R.; Frenette L. C.; Hodvedt E. C.; Krauss T. D.; Mukaibo H. Fabrication of Tapered Microtube Arrays and Their Application as a Microalgal Injection Platform. ACS Appl. Mater. Interfaces 2016, 8, 34198–34208. 10.1021/acsami.6b11062. [DOI] [PubMed] [Google Scholar]
  13. Chiappini C.; Martinez J. O.; De Rosa E.; Almeida C. S.; Tasciotti E.; Stevens M. M. Biodegradable Nanoneedles for Localized Delivery of Nanoparticles in Vivo: Exploring the Biointerface. ACS Nano 2015, 9, 5500–5509. 10.1021/acsnano.5b01490. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Chiappini C.; De Rosa E.; Martinez J. O.; Liu X.; Steele J.; Stevens M. M.; Tasciotti E. Biodegradable silicon nanoneedles delivering nucleic acids intracellularly induce localized in vivo neovascularization. Nat. Mater. 2015, 14, 532–539. 10.1038/nmat4249. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Hai A.; Shappir J.; Spira M. E. In-cell recordings by extracellular microelectrodes. Nat. Methods 2010, 7, 200–202. 10.1038/nmeth.1420. [DOI] [PubMed] [Google Scholar]
  16. Hai A.; Spira M. E. On-chip electroporation, membrane repair dynamics and transient in-cell recordings by arrays of gold mushroom-shaped microelectrodes. Lab Chip 2012, 12, 2865–2873. 10.1039/c2lc40091j. [DOI] [PubMed] [Google Scholar]
  17. Caprettini V.; Cerea A.; Melle G.; Lovato L.; Capozza R.; Huang J.-A.; Tantussi F.; Dipalo M.; De Angelis F. Soft electroporation for delivering molecules into tightly adherent mammalian cells through 3D hollow nanoelectrodes. Sci. Rep. 2017, 7, 8524–8532. 10.1038/s41598-017-08886-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Shalek A. K.; Robinson J. T.; Karp E. S.; Lee J. S.; Ahn D.-R.; Yoon M.-H.; Sutton A.; Jorgolli M.; Gertner R. S.; Gujral T. S.; MacBeath G.; Yang E. G.; Park H. Vertical silicon nanowires as a universal platform for delivering biomolecules into living cells. Proc. Natl. Acad. Sci. U.S.A. 2010, 107, 1870–1875. 10.1073/pnas.0909350107. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Xie X.; Aalipour A.; Gupta S. V.; Melosh N. A. Determining the Time Window for Dynamic Nanowire Cell Penetration Processes. ACS Nano 2015, 9, 11667–11677. 10.1021/acsnano.5b05498. [DOI] [PubMed] [Google Scholar]
  20. Lin Z. C.; Xie C.; Osakada Y.; Cui Y.; Cui B. Iridium oxide nanotube electrodes for sensitive and prolonged intracellular measurement of action potentials. Nat. Commun. 2014, 5, 3206–3216. 10.1038/ncomms4206. [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Stevens M. M.; George J. H. Exploring and Engineering the Cell Surface Interface. Science 2005, 310, 1135–1138. 10.1126/science.1106587. [DOI] [PubMed] [Google Scholar]
  22. Huang J.; Gräter S. V.; Corbellini F.; Rinck S.; Bock E.; Kemkemer R.; Kessler H.; Ding J.; Spatz J. P. Impact of Order and Disorder in RGD Nanopatterns on Cell Adhesion. Nano Lett. 2009, 9, 1111–1116. 10.1021/nl803548b. [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Persson H.; Li Z.; Tegenfeldt J. O.; Oredsson S.; Prinz C. N. From immobilized cells to motile cells on a bed-of-nails: effects of vertical nanowire array density on cell behaviour. Sci. Rep. 2015, 5, 18535–18547. 10.1038/srep18535. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Liu X.; Liu R.; Gu Y.; Ding J. Nonmonotonic Self-Deformation of Cell Nuclei on Topological Surfaces with Micropillar Array. ACS Appl. Mater. Interfaces 2017, 9, 18521–18530. 10.1021/acsami.7b04027. [DOI] [PubMed] [Google Scholar]
  25. Toma M.; Belu A.; Mayer D.; Offenhäusser A. Flexible Gold Nanocone Array Surfaces as a Tool for Regulating Neuronal Behavior. Small 2017, 13, 1700629–1700640. 10.1002/smll.201700629. [DOI] [PubMed] [Google Scholar]
  26. Sharei A.; Zoldan J.; Adamo A.; Sim W. Y.; Cho N.; Jackson E.; Mao S.; Schneider S.; Han M.-J.; Lytton-Jean A.; Basto P. A.; Jhunjhunwala S.; Lee J.; Heller D. A.; Kang J. W.; Hartoularos G. C.; Kim K.-S.; Anderson D. G.; Langer R.; Jensen K. F. A vector-free microfluidic platform for intracellular delivery. Proc. Natl. Acad. Sci. U.S.A. 2013, 110, 2082–2087. 10.1073/pnas.1218705110. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Zhao W.; Hanson L.; Lou H.-Y.; Akamatsu M.; Chowdary P. D.; Santoro F.; Marks J. R.; Grassart A.; Drubin D. G.; Cui Y.; Cui B. Nanoscale manipulation of membrane curvature for probing endocytosis in live cells. Nat. Nanotechnol. 2017, 12, 750–756. 10.1038/nnano.2017.98. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Xie X.; Xu A. M.; Angle M. R.; Tayebi N.; Verma P.; Melosh N. A. Mechanical Model of Vertical Nanowire Cell Penetration. Nano Lett. 2013, 13, 6002–6008. 10.1021/nl403201a. [DOI] [PubMed] [Google Scholar]
  29. Kim W.; Ng J. K.; Kunitake M. E.; Conklin B. R.; Yang P. Interfacing Silicon Nanowires with Mammalian Cells. J. Am. Chem. Soc. 2007, 129, 7228–7229. 10.1021/ja071456k. [DOI] [PubMed] [Google Scholar]
  30. Yan R.; Park J.-H.; Choi Y.; Heo C.-J.; Yang S.-M.; Lee L. P.; Yang P. Nanowire-based single-cell endoscopy. Nat. Nanotechnol. 2012, 7, 191–196. 10.1038/nnano.2011.226. [DOI] [PubMed] [Google Scholar]
  31. Singhal R.; Orynbayeva Z.; Sundaram R. V. K.; Niu J. J.; Bhattacharyya S.; Vitol E. A.; Schrlau M. G.; Papazoglou E. S.; Friedman G.; Gogotsi Y. Multifunctional carbon-nanotube cellular endoscopes. Nat. Nanotechnol. 2011, 6, 57–64. 10.1038/nnano.2010.241. [DOI] [PubMed] [Google Scholar]
  32. Harding F. J.; Surdo S.; Delalat B.; Cozzi C.; Elnathan R.; Gronthos S.; Voelcker N. H.; Barillaro G. Ordered Silicon Pillar Arrays Prepared by Electrochemical Micromachining: Substrates for High-Efficiency Cell Transfection. ACS Appl. Mater. Interfaces 2016, 8, 29197–29202. 10.1021/acsami.6b07850. [DOI] [PubMed] [Google Scholar]
  33. Huang C.-H.; Hsiao P.-Y.; Tseng F.-G.; Fan S.-K.; Fu C.-C.; Pan R.-L. Pore-Spanning Lipid Membrane under Indentation by a Probe Tip: a Molecular Dynamics Simulation Study. Langmuir 2011, 27, 11930–11942. 10.1021/la201977d. [DOI] [PubMed] [Google Scholar]
  34. Kawamoto S.; Nakamura T.; Nielsen S. O.; Shinoda W. A guiding potential method for evaluating the bending rigidity of tensionless lipid membranes from molecular simulation. J. Chem. Phys. 2013, 139, 034108–034118. 10.1063/1.4811677. [DOI] [PubMed] [Google Scholar]
  35. Diggins P.; Deserno M. Determining the bending modulus of a lipid membrane by simulating buckling. J. Chem. Phys. 2013, 138, 214110–214123. 10.1063/1.4808077. [DOI] [PubMed] [Google Scholar]
  36. Noguchi H. Anisotropic surface tension of buckled fluid membranes. Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys. 2011, 83, 061919–061925. 10.1103/physreve.83.061919. [DOI] [PubMed] [Google Scholar]
  37. Santoro F.; Zhao W.; Joubert L.-M.; Duan L.; Schnitker J.; van de Burgt Y.; Lou H.-Y.; Liu B.; Salleo A.; Cui L.; Cui Y.; Cui B. Revealing the Cell-Material Interface with Nanometer Resolution by Focused Ion Beam/Scanning Electron Microscopy. ACS Nano 2017, 11, 8320–8328. 10.1021/acsnano.7b03494. [DOI] [PMC free article] [PubMed] [Google Scholar]
  38. Venturoli M.; Sperotto M. M.; Kranenburg M.; Smit B. Mesoscopic models of biological membranes. Phys. Rep. 2006, 437, 1–54. 10.1016/j.physrep.2006.07.006. [DOI] [Google Scholar]
  39. Patra M.; Karttunen M.; Hyvönen M. T.; Falck E.; Lindqvist P.; Vattulainen I. Molecular Dynamics Simulations of Lipid Bilayers: Major Artifacts Due to Truncating Electrostatic Interactions. Biophys. J. 2003, 84, 3636–3645. 10.1016/s0006-3495(03)75094-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Israelachvili J. N.Intermolecular and Surface Forces; Academic Press: London, 2011. [Google Scholar]
  41. Goetz R.; Gompper G.; Lipowsky R. Mobility and Elasticity of Self-Assembled Membranes. Phys. Rev. Lett. 1999, 82, 221–224. 10.1103/physrevlett.82.221. [DOI] [Google Scholar]
  42. Lindahl E.; Edholm O. Mesoscopic Undulations and Thickness Fluctuations in Lipid Bilayers from Molecular Dynamics Simulations. Biophys. J. 2000, 79, 426–433. 10.1016/s0006-3495(00)76304-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Brannigan G.; Lin L. C.-L.; Brown F. L. H. Implicit solvent simulation models for biomembranes. Eur. Biophys. J. 2006, 35, 104–124. 10.1007/s00249-005-0013-y. [DOI] [PubMed] [Google Scholar]
  44. Marrink S. J.; Mark A. E. Effect of Undulations on Surface Tension in Simulated Bilayers. J. Phys. Chem. B 2001, 105, 6122–6127. 10.1021/jp0103474. [DOI] [Google Scholar]
  45. Zimmerman J. F.; Parameswaran R.; Murray G.; Wang Y.; Burke M.; Tian B. Cellular uptake and dynamics of unlabeled freestanding silicon nanowires. Sci. Adv. 2016, 2, 1601039–1601050. 10.1126/sciadv.1601039. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Lee J.-H.; Zhang A.; You S. S.; Lieber C. M. Spontaneous Internalization of Cell Penetrating Peptide-Modified Nanowires into Primary Neurons. Nano Lett. 2016, 16, 1509–1513. 10.1021/acs.nanolett.6b00020. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

am8b08218_si_001.pdf (3.6MB, pdf)

Articles from ACS Applied Materials & Interfaces are provided here courtesy of American Chemical Society

RESOURCES