Size-Dependent Band-Gap and Molar Absorption Coefficients of Colloidal CuInS₂ Quantum Dots

Abstract

The knowledge of the quantum dot (QD) concentration in a colloidal suspension and the quantitative understanding of the size-dependence of the band gap of QDs are of crucial importance from both applied and fundamental viewpoints. In this work, we investigate the size-dependence of the optical properties of nearly spherical wurtzite (wz) CuInS₂ (CIS) QDs in the 2.7 to 6.1 nm diameter range (polydispersity ≤10%). The QDs are synthesized by partial Cu⁺ for In³⁺ cation exchange in template Cu_2–xS nanocrystals, which yields CIS QDs with very small composition variations (In/Cu = 0.91 ± 0.11), regardless of their sizes. These well-defined QDs are used to investigate the size-dependence of the band gap of wz CIS QDs. A sizing curve is also constructed for chalcopyrite CIS QDs by collecting and reanalyzing literature data. We observe that both sizing curves follow primarily a 1/d dependence. Moreover, the molar absorption coefficients and the absorption cross-section per CIS formula unit, both at 3.1 eV and at the band gap, are analyzed. The results demonstrate that the molar absorption coefficients of CIS QDs follow a power law at the first exciton transition energy (ε_E1 = 5208d^2.45) and scale with the QD volume at 3.1 eV. This latter observation implies that the absorption cross-section per unit cell at 3.1 eV is size-independent and therefore can be estimated from bulk optical constants. These results also demonstrate that the molar absorption coefficients at 3.1 eV are more reliable for analytical purposes, since they are less sensitive to size and shape dispersion.

Colloidal semiconductor quantum dots (QDs) exhibit size-dependent optoelectronic properties, making them promising materials for many applications, such as solution-processed solar cells,¹⁻³ luminescent solar concentrators,¹ photodetectors,⁴ light-emitting devices,^1,5 optoelectronic devices,^1,6 and biomedical imaging.⁷⁻⁹ The successful development of these applications requires a precise control over both the size and the concentration of the QDs. Additionally, an accurate knowledge of the QD concentration is also crucial for the synthesis of heteronanocrystals (e.g., core/shell QDs),¹⁰⁻¹² preparation of QD superlattices,¹³⁻¹⁵ and fundamental studies of the nucleation and growth of nanoparticles.¹⁶ This has made the determination of the molar absorption coefficients ε of QDs an important endeavor, since optical absorption spectroscopy offers a very fast and convenient way to establish the concentration of colloidal suspensions of QDs. Moreover, the absorption cross-section of QDs is a relevant parameter for applications requiring the precise knowledge of the relationship between excitation fluence and exciton density per QD (e.g., lasers). The quantitative understanding of the size-dependence of the optical properties of QDs also allows the construction of empirical sizing curves correlating the lowest energy absorption peak with the QD size, which can in turn be used to verify the validity of theoretical models describing quantum confinement effects and the nature of the radiative recombination in semiconductor nanocrystals. Nevertheless, the quantitative study of the size-dependence of the optical properties of QDs has been to date primarily focused on binary compositions (Cd-, Pb-, and Ag-chalcogenides,¹⁷⁻³⁵ InP,³⁶ and InAs^37,38).

Ternary CuInS₂ (CIS) QDs have attracted increasing attention due to their nontoxicity, large absorption coefficients across a broad spectral range, and wide photoluminescence (PL) tunability through the visible to the NIR spectral window.³⁹⁻⁴¹ These QDs have been applied in light-emitting devices,⁴²⁻⁴⁴ luminescent solar concentrators,⁴⁵⁻⁴⁸ and biolabels.^49,50 However, despite the importance of these nanomaterials, there are at present only two reports on the size-dependence of the molar absorption coefficients of CIS QDs.^51,52 Intriguingly, the size dependence of the ε values at the first exciton transition energy (E₁) reported in these works is dramatically different: Qin etal.⁵¹ reported a power law with an exponent of 2.1, while Booth etal.⁵² found a power law with an exponent of 3.7. The latter work also reports that the ε values at higher energy (3.1 eV) scale with the diameter to the power of 3.8,⁵² which is far stronger than the cubic size dependence that is theoretically expected, and has been experimentally observed in several binary chalcogenides.^{23,25,28,34,38} Although the reasons for these discrepancies are as yet unclear, they may be attributed to the inherent difficulties associated with the determination of sizes, absorption peak positions, and concentrations of colloidal QDs. These experimental intricacies have in the past been responsible for large inconsistencies between results reported by different groups for the size-dependencies of the molar absorption coefficients and band gap of binary QDs, such as the prototypical CdSe.^{24,25,27,29,31−33} From this viewpoint, CIS QDs are even more challenging, since the synthesis of ternary nanocrystals (NCs) with well-controlled size, shape, and composition requires a strict balance between the reactivities of three different precursors, to prevent the formation of binary byproducts (e.g., Cu₂S and In₂S₃, rather than CIS) or hetero-NCs (e.g., Cu₂S–CIS).⁴⁰ Moreover, CIS QDs produced by direct synthesis are typically trigonal-pyramidal in shape,⁵²⁻⁵⁵ further complicating the determination of their sizes and introducing ambiguities, since “diameter” becomes an ill-defined quantity, leading different authors to use different metrics for the QD size (e.g., average edge length,⁵⁵ average diagonal length,⁵² Scherrer’s diameter determined from powder X-ray diffraction^51,56).

In this work, we circumvent these difficulties by using topotactic partial Cu⁺ for In³⁺ cation exchange to convert template Cu_2–xS NCs into nearly spherical and stoichiometric (In/Cu = 0.91 ± 0.11) wurtzite (wz) CIS QDs ranging from 2.7 to 6.8 nm in diameter (size dispersion ≤10%), which are ideally suited to investigate the size-dependence of the band gap and of the molar absorption coefficients at both the first exciton transition energy and far above the band gap (3.1 eV). We also address the size-dependence of the band gap of chalcopyrite (cp) CIS QDs by reanalyzing experimental data published by several groups.^{51,52,54−57} Our results demonstrate that the molar absorption coefficients of wz CIS QDs follow a power law with an exponent of 2.45 at first exciton transition energy and scale with the QD volume at 3.1 eV.

Results and Discussion

Size-Controlled CIS QDs via Partial Cation Exchange

Nearly spherical colloidal CIS QDs with small size dispersion (≤10%) were synthesized by partial, self-limited Cu⁺ for In³⁺ cation exchange (CE) in template high-chalcocite Cu_2–xS NCs, following previously reported procedures (Figure 1a).⁵⁸ The product CIS QDs inherit the shape, size, and polydispersity of the template Cu_2–xS NCs (Figure 1b,c). High-resolution transmission electron microscopy (HRTEM) (Figure 1c) and X-ray diffraction (XRD) [Supporting Information (SI), Figure S1] show that the product CIS QDs have the wurtzite crystal structure, demonstrating that the hexagonal sulfide sublattice of the template Cu_2-xS NCs is preserved in the product NCs, in agreement with previous reports.^58,59 This protocol is highly versatile and can be applied to obtain CIS QDs in the 2.7–6.8 nm diameter range by using suitable template Cu_2–xS NCs (SI, Table S1, Figure S2). The product CIS QDs have a nearly spherical shape and exhibit good TEM contrast, allowing the unambiguous determination of the QD diameters with good accuracy (SI, Figure S2).

Figure 1.

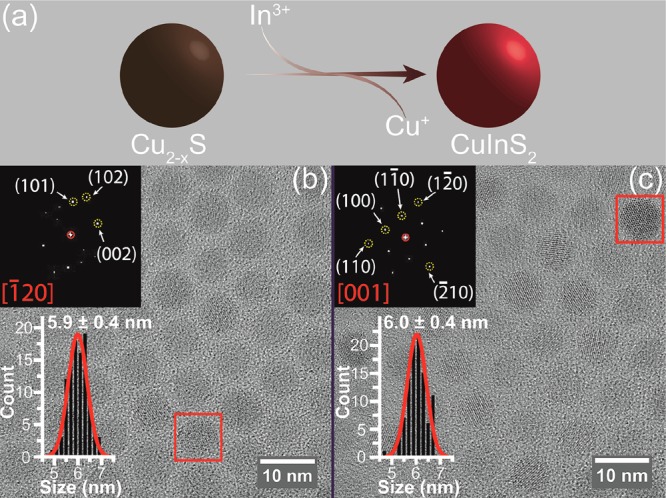
(a) Schematic diagram of partial Cu⁺ for In³⁺ cation exchange in template Cu_2–xS NCs. (b) High-resolution transmission electron microscopy (HRTEM) image and corresponding size histogram of 5.9 nm template Cu_2–xS NCs (polydispersity of 6.8%). The inset shows the Fourier transform (FT) analysis of a single Cu_2–xS NC indicated by a red rectangle, which can be indexed to [−120] axial projection of the high chalcocite Cu₂S. (c) HRTEM image and corresponding size histogram of CIS QDs obtained by cation exchange using the Cu_2–xS NCs shown in (b) as templates (see Methods for details). The size of the product CIS QDs is 6 nm with a polydispersity of 6.7%. The inset shows the FT analysis of a single CIS QD indicated by a red rectangle, which can be indexed to [001] axial projection of the wurtzite CIS. The size histograms are constructed by measuring over 200 NCs and are fitted to a Gaussian distribution function.

Composition and Concentration of the CIS QDs

The composition of the product CIS QDs was determined by inductively coupled plasma optical emission spectroscopy (ICP-OES) analysis and found to be nearly stoichiometric (In/Cu = 0.91 ± 0.11) in the 2.7–6.8 nm size range (Figure 2a). For simplicity, these nearly stoichiometric Cu_1.1In_0.9S₂ QDs will be hereafter referred to as “CIS”, without explicit reference to their exact composition, unless the composition is relevant to the point under discussion. To simplify the calculation of the QD concentration, we approximate the In/Cu molar ratio to 1 (see crystallographic model of a single wz CIS QD in Figure 2b). Given that Cu⁺ is taken as the reference, the CIS QD concentration can be expressed as follows (see SI, method 1 for details):

1

n_Cu⁺ denotes the molar concentration of Cu⁺ measured by ICP-OES analysis. V_QD is the volume of a single CIS QD, while V_uc represents the volume of the wz CIS unit cell (V_uc = 84.99 ų),⁶⁰ and N_Cu⁺/uc is the number of Cu⁺ ions per unit cell (N_Cu⁺/uc = 1).⁶⁰

Figure 2.

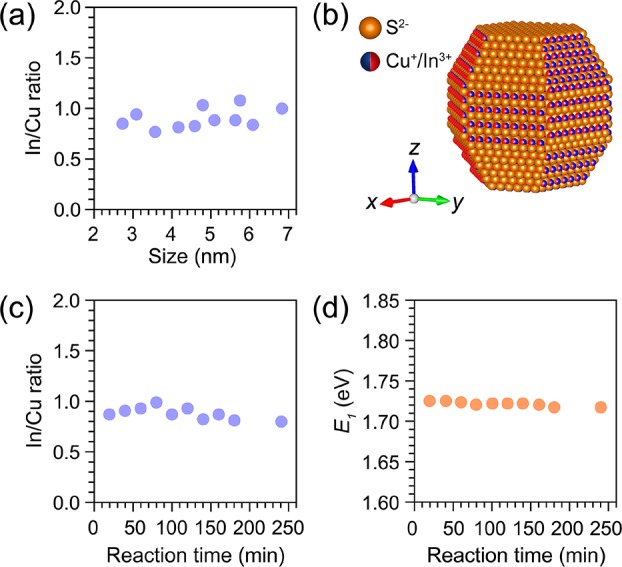
(a) In/Cu molar ratios of wz CIS QDs in a size range from 2.7 to 6.8 nm. (b) Perspective view of the single CIS QD model (Cu⁺ or In³⁺ has the same occupation probability). (c) In/Cu molar ratios of wz CIS QDs obtained from 5.5 nm template Cu_2–xS NCs. Ten parallel batches of cation exchange reactions were performed by using different reaction times (20–200 min) and In/Cu feeding ratios (1–5), while keeping all other parameters constant (see SI, Table S2 for details). (d) The first excitonic transition energies of the wz CIS QDs extracted from absorption spectra of the samples mentioned in (c).

To test the reproducibility and robustness of the synthesis protocol used in our work, 10 different CE reactions were performed using the same batch of 5.5 nm Cu_2–xS NCs as templates. The In/Cu feeding ratio was varied from 1 to 5, and the reaction time increased from 20 to 200 min, while keeping all other parameters constant (see SI, Table S2 for details). Interestingly, the In/Cu ratios of the product CIS QDs fluctuated only slightly (average 0.90 ± 0.09) (Figure 2c), regardless of the In/Cu feeding ratio and reaction times. This shows that the Cu⁺ for In³⁺ CE in Cu_2–xS NCs is self-limited under mild reaction conditions (≤130 °C), in agreement with the model proposed in ref (59), which attributes the self-limitation to the high activation energies required to reorganize the anionic sublattice from hexagonal close-packed in high-chalcocite Cu_2–xS and wz CIS to face-centered cubic in In₂S₃.⁵⁹ The partial and self-limited character of the Cu⁺ for In³⁺ CE in Cu_2–xS NCs thus makes the synthesis method developed in our work quite robust and reproducible.

The peak position of the lowest energy absorption transition (E₁) of these 10 CIS QD samples was extracted from the second derivative of their absorption spectra (Figure 2d and SI, Figure S3a) and found to be essentially the same (1.722 ± 0.003 eV), despite the slight composition fluctuations (In/Cu = 0.90 ± 0.09). In contrast, the PL peak positions randomly fluctuate from batch to batch (SI, Figures S3b and S4), probably due to the low photoluminescence quantum yields (PLQYs ≈ 1%) of the samples (SI, Figure S5). This observation implies that the PL peak positions are unreliable quantities to investigate the size dependence of the band gap of CIS QDs. It should be noted that the PL spectra of CIS QD samples with low PLQYs may not necessarily reflect the size, shape, and composition polydispersity of the ensemble, as will be discussed in detail below. The low PL QYs of the wz CIS QD samples investigated here are due to the extensive washing required to ensure that the product QDs were free of unreacted precursors, which resulted in a decrease of the PLQYs of the as-prepared QDs by 1 order of magnitude, likely due to defects induced by the excessive removal of surface ligands.

Size-Dependence of the Optical Transitions of CIS QDs

The absorption and PL spectra of the nearly stoichiometric wz CIS QDs prepared in this work shift to lower energies with increasing NC sizes (Figure 3 and SI, Figure S6), in agreement with previous reports on both cp and wz CIS QDs.^{40,41,51,52,55−58,61} However, it is as yet unclear whether the wide tunability of the optical properties of CIS NCs (and other ternary copper chalcogenides) can be attributed solely to quantum confinement effects, in striking contrast with the II–VI, IV–VI, and III–V binary analogues.⁴⁰ The foremost difference between ternary copper (and silver) chalcogenides (I–III–VI₂) and binary II–VI and IV–VI compounds is that the former can easily tolerate large deviations from stoichiometry, both in the I/III ratio and VI/(I + III) ratio, resulting in a rich defect chemistry.⁶²⁻⁶⁵ This has a dramatic impact on the optical properties of ternary copper chalcogenides, because the upper valence band in these materials is composed primarily of Cu 3d orbitals hybridized with the p orbitals of the chalcogen, while the conduction band consists of Cu 4s orbitals with some mixing of p character from the group VI element, which makes their band gap composition-dependent.⁶⁶ For example, band-gap reductions of up to 190 meV have been reported for bulk CIS upon decreasing the In/Cu ratio from 1.1 to 0.5, accompanied by the development of a low-energy tail extending up to 200 meV below the band gap.^62,63 The potential complications arising from a composition-dependent band gap become particularly relevant at the nanoscale, since CIS NCs are even more tolerant to off-stoichiometry than their bulk counterpart, being readily made with In/Cu ratios ranging from 0.34 to 3.33,⁶⁷ and also changing composition during the growth process (e.g., In/Cu ratio from 0.58 to 1.09 in the 3.6 to 7.6 nm size range⁵⁵). From this perspective, the small composition and size distributions of the nearly stoichiometric CIS QDs prepared in the present work (viz., In/Cu = 0.91 ± 0.11 and ≤10%, respectively) make them ideally suited to investigate the size-dependence of the optical properties of CIS QDs, without the confounding contribution of significant composition fluctuations. It should also be noted that the size-dependent trends observed in our work are likely also representative of fully stoichiometric wz CuInS₂ NCs, given that the deviation from stoichiometry of the investigated CIS QDs is small. The nearly stoichiometric character of the wz CIS QDs studied in the present work is also evidenced by the absence of localized surface plasmon resonance bands, which are typically associated with Cu-rich CIS NCs.⁴⁰

Figure 3.

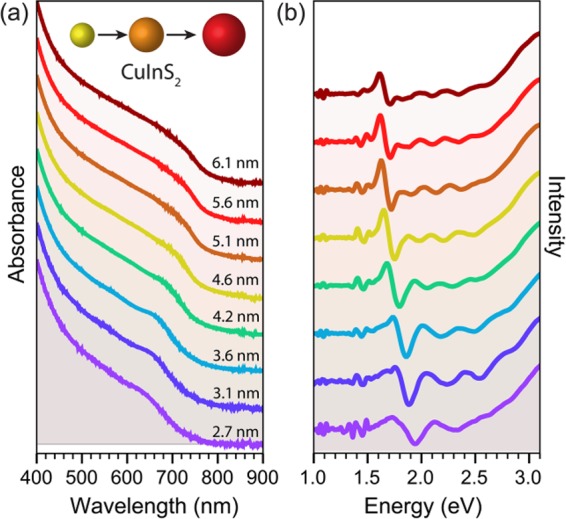
Absorption spectra (a) and corresponding second derivative spectra (b) of wz CIS QDs ranging from 2.7 to 6.1 nm in size.

However, as shown above, PL peak positions are less reliable metrics for the size dependence of the band gap of CIS QDs, since they vary significantly even under roughly constant QD size and composition (SI, Figure S4). Moreover, the PL quantum yields of bare CIS QDs are generally low (≤10%),^{40,41,54,57,58,61} and therefore the observed PL spectra may not necessarily reflect the size, shape, and composition polydispersity of the ensemble. The inadequacy of the PL peak positions for quantitative studies of the size-dependence of the band gap is further aggravated by the fact that the PL in CIS NCs (and other ternary Cu chalcogenides) is characterized by broad bandwidths [full width at half-maximum (fwhm), ∼200–400 meV] and large global Stokes shifts (Δ_ST ≈ 300–500 meV).^40,41,68 For these reasons, the size-dependence of the band gap of CIS QDs will be investigated here using only the peak position of the lowest energy absorption transition, which is more accurate because the absorption spectra are determined by the whole QD ensemble. This is however challenging, as the absorption spectra of CIS NCs are essentially featureless and do not show a sharp first absorption transition, even for QD ensembles with small size dispersion (≤10%), such as those prepared in the present work (Figure 3, SI, Figures S2 and S6). Nevertheless, the first absorption transition energy (E₁) can be reliably determined by locating the minimum of the second derivative of the absorption spectrum (Figure 3). It should be noted that the absorption spectra of colloidal QDs might be distorted by the presence of absorbing impurities. Therefore, the evaluation of the CIS QD purity prior to acquisition of the absorption spectra is essential (see Methods for details). As observed in Figure 3, the E₁ values are clearly size-dependent. This size-dependence will be quantitatively addressed below, after we have discussed the spectral characteristics of CIS QDs in more detail.

As mentioned above, the optical spectra of CIS NCs are characterized by broad features, in both absorption and PL.^{40,41,52,54,58,68} However, only the PL fwhm’s have been quantitatively discussed in the literature, probably because they can be readily obtained from the PL spectra. In contrast, the fwhm of the lowest energy absorption transition can only be extracted from the absorption spectra by fitting a Gaussian distribution function centered at the peak position determined from the second derivative of the spectra (SI, Figure S7). We performed this analysis for the wz CIS QDs prepared in our work and found that the fwhm of the lowest energy absorption transition varies from 180 to 320 meV, while that of the PL peak ranges from ∼300 to 420 meV (SI, Figure S8). For comparison, we also analyzed wz CIS QDs that had been investigated in our previous work.⁵⁸ These samples have similar compositions to those investigated in the present work (viz., In/Cu = 0.7 ± 0.1), but present higher PLQYs (22% to 3.4% in the 5.4 to 7.2 nm size range)⁵⁸ and therefore yield more reliable PL fwhm values. It can be seen that the fwhm values of these samples are comparable to those of the wz CIS QDs prepared in the present work, except for the PL fwhm of the QD samples with d ≥ 5 nm, which are significantly larger for the presently investigated samples (viz., 420–380 and 320–300 meV, respectively, SI, Figure S8). This difference can be attributed to the lower PLQYs of the samples investigated in the present work, which result in PL spectra with higher signal-to-noise ratios and therefore less reliable PL fwhm. Taken together, the data obtained from both groups of samples suggest that the PL fwhm is essentially size-independent (∼300–320 meV in the 2.7 to 7.2 nm diameter range, neglecting the values obtained for the QDs prepared in the present work with d ≥ 5 nm), while that of the lowest energy absorption peak decreases with size from ∼300 to ∼200 meV in the 2.7 to 7.2 nm diameter range. We have also determined the global Stokes shifts (Δ_ST) of the wz CIS QDs investigated in the present work and in our previous work⁵⁸ and established that they are size-independent (viz., 455 ± 27 meV in the 2.7 to 7.2 nm size range, SI, Figure S8). This is in contrast with the weakly size-dependent Δ_ST values (viz., 470 to 350 meV in the 2.5 to 5.1 nm size range) previously reported for cp CIS QDs.⁵² The discrepancy is unlikely to be due to the different crystal structures (wz and cp), since very similar Δ_ST values have been reported for similarly sized cp CIS QDs (viz., 460 meV for 2.2 nm NCs,⁵⁷ 436 meV for 2.5 nm NCs⁵⁴). The fwhm’s observed here for the PL peaks are also comparable to those previously reported for cp CIS NCs.^{40,41,52,54,68}

The characteristics of the PL of CIS NCs (viz., broad fwhm: 200–400 meV, large Δ_ST: ∼300–500 meV, and long radiative lifetimes τ: ∼200–400 ns)^40,41,68 are strikingly different from those of the 1S_h–1S_e band-edge PL of the prototypical II–VI NCs (e.g., fwhm: 150 to 80 meV,^69,70 Δ_ST: ∼21 ± 4 meV,⁶⁹ and τ: 18–40 ns,²⁵ for ensembles of CdSe QDs in the 2.6 to 8 nm size range with ≤10% size dispersion), indicating that the radiative recombination mechanisms in these two classes of materials are fundamentally dissimilar in nature. The origin of the PL of CIS (and other ternary Cu and Ag chalcogenides) NCs has been under intense debate⁴⁰ and likely involves the radiative recombination of a delocalized conduction band electron with a localized hole.^{54,58,71−73} The hole localization after photoexcitation occurs on subpicosecond time scales, probably on a Cu⁺ ion.^54,73 We note that the larger variability of the PL peak positions of CIS NCs with respect to the absorption transitions (see discussion above and SI, Figure S4) is consistent with this radiative recombination model and can be accounted for by the inherently stochastic nature of the hole localization process.

However, the radiative recombination model presented above cannot account for the broad bandwidths observed for the lowest energy absorption transition of CIS QDs (∼200–300 meV, which is twice as large as those observed for CdSe QDs^69,70 and ∼4 times larger than those reported for PbSe QDs⁷⁴), since the line widths of absorption transitions in semiconductor QDs cannot be affected by the localization of the photogenerated hole. A possible explanation can be found in a recent theoretical paper by Efros and co-workers,⁷⁵ which proposes that the PL of spherical cp CIS NCs originates from the 1S_h–1S_e exciton transition, similarly to the cases of the binary II–VI, IV–VI, and III–V QDs. The exciton radiative recombination in this model thus precludes the involvement of localized carriers. The characteristics of the PL of CIS QDs are attributed to the nature of the 1S_h–1S_e exciton fine-structure states, of which the lowest emitting state is nominally a dark exciton that hardly contributes to the absorption and is separated by a large size-dependent energy gap from three upper bright fine-structure states, which account for most of the absorption oscillator strength.⁷⁵ This model thus explains both the large Δ_ST values and long radiative lifetimes associated with the PL of CIS QDs and can also explain the broad (and size-dependent) line widths of the lowest energy absorption transition, as the energy separation between the highest and the lowest energy bright states varies from 100 to 30 meV in the 2 to 3.6 nm diameter range.⁷⁵ Nevertheless, this model also predicts a strongly size-dependent Stokes shift (viz., 300 to 100 meV in the 2 to 3.6 nm diameter range), in contrast to the size-independent Stokes shift (viz., 455 ± 27 meV in the 2.7 to 7.2 nm size range) observed in the present work. This model is also unable to explain the broad and (essentially) size-independent PL fwhm displayed by CIS QDs, which suggests that the emitting state is subject to a strong exciton–phonon coupling. We note that a strong exciton–phonon coupling could also explain the broad bandwidths of the lowest energy absorption transition of CIS QDs, but this explanation lacks as yet experimental and theoretical support. It is thus clear that the full understanding of the exciton transitions in both cp and wz CIS QDs requires further experimental and theoretical work.

Sizing Curves for wz and cp CIS QDs

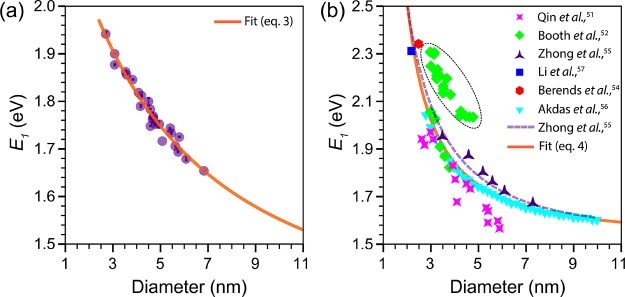
To shed light on the size-dependence of the band gap of CIS QDs, we constructed empirical sizing curves for both wz and cp CIS QDs (Figure 4). The peak positions of the lowest energy absorption transition (E₁) of wz CIS QDs were extracted from the second derivative of the absorption spectra of the nearly stoichiometric (In/Cu = 0.91 ± 0.11) CIS QDs prepared in our work (Figure 3), while the QD diameters were determined from TEM images (SI, Figure S2). The data points for cp CIS QDs were collected from previous reports^{51,52,54−57} and were mostly obtained from nearly stoichiometric QDs, with In/Cu ratios of 1.0 ± 0.1 (see Supporting Information, Table S3, for the reported composition of all the cp CIS QDs included in Figure 4b). The composition of the cp CIS QDs studied by Zhong etal. were reported to be size-dependent, changing from In/Cu = 0.42 to 0.88 in the 3.6 to 7.6 nm size range.⁵⁵ A modest size-dependence of the composition was also observed by Li etal. (In/Cu = 1.04 to 0.93 in the 2.2 to 3.3 nm size range).⁵⁷ It should be noted that the sizes and E₁ values for cp CIS QDs were not all determined in the same way. For instance, the effective QD diameter was taken to be the edge length of the pyramidal NCs by Zhong etal.,⁵⁵ while Booth etal.⁵² took their height (i.e., the diagonal length of the 2D TEM projections), and Qin etal.⁵¹ and Akdas etal.⁵⁶ used the Scherrer’s diameter determined from powder X-ray diffraction. The E₁ values were also determined by using different methods (e.g., extrapolation of Tauc plots in ref (55), double-tangent method in ref (51)). Nevertheless, as we will show below the uncertainties and systematic errors associated with individual reports, as well as the compositional variations between CIS QD samples investigated in different studies, are averaged out when the combined data set is analyzed as a whole.

Figure 4.

(a) Sizing curve of colloidal wz CIS QDs (In/Cu = 0.91 ± 0.11). The solid line is a fit based on a theoretical expression (eq 2) and is described by eq 3. (b) Sizing curve of colloidal cp CIS QDs. The symbols represent experimental data collected from previous reports.^{51,52,54−57} The In/Cu ratio of most samples is 1.0 ± 0.1 (see Supporting Information, Table S3, for the reported composition of all samples). The composition of the CIS QDs studied by Zhong etal.⁵⁵ and Li etal.⁵⁷ were reported to be size-dependent (In/Cu = 0.42 to 0.88 in the 3.6 to 7.6 nm size range⁵⁵ and 1.04 to 0.93 in the 2.2 to 3.3 nm size range,⁵⁷ respectively). The purple dashed line represents a calculation based on a finite depth-well effective mass approximation model.⁵⁵ The orange solid line is a fit based on a theoretical expression (eq 2) and is described by eq 4. The green data points circled by the dashed ellipsoidal line are derived from an empirical polynomial function reported by Booth etal. using their data⁵² and was not included in the fit (see text for further details). For convenience, sizing curves correlating the QD diameter with the wavelength of the first absorption peak are provided in the Supporting Information (Figure S9).

To fit the empirical size-dependent trends shown in Figure 4, we used an expression previously proposed by Allan and Delerue based on tight binding calculations:⁷⁶

2

where E_g(d) and E_g(∞) are the band gap (in eV) for a QD of diameter d (in nm) and for bulk, respectively, and a, b, and c are constants. Equation 2 has been successfully used to fit the empirical trends observed for PbSe,^28,76 PbS,²³ CdSe,²⁵ and CdTe²⁵ QDs. Fitting the experimental data for wz CIS QDs (Figure 4a) to eq 2 yields (χ² ≈ 0.9999):

3

Interestingly, the E_g(∞) value obtained from the fit (1.327) is very close to the bulk band gap of wz CIS calculated by Tomić and co-workers using hybrid density functional theory (DFT) (viz., 1.3 eV).⁷⁷ Bulk wz CIS is metastable at room temperature, and therefore experimental data on its band gap have only recently become available, owing to the development of synthesis methods yielding ensembles of large wz CIS nanoparticles.^60,78 The reported band-gap values, however, still carry a significant uncertainty and are spread over a wide range (viz., 1.10–1.23 eV in ref (60) and 1.42 eV for 20 nm NCs in ref (78)). Nevertheless, it is clear that the band gap of wz CIS is smaller than that of cp CIS, which explains why wz CIS QDs typically show PL at lower energies than similarly sized cp CIS QDs.^58,68 This is also consistent with the expression obtained by fitting the experimental data for cp CIS QDs (Figure 4b) to eq 2 (χ² ≈ 0.9997):

4

which yields a E_g(∞) value that agrees very well with the band gap reported for bulk cp CIS (viz., 1.535 eV at 300 K).⁷⁹ We note that some data points (indicated by the dashed ellipsoid in Figure 4b) were not included in the fit because they clearly deviated from the general trend evidenced by the other data points. The excluded data points were obtained from an empirical sizing curve reported by Booth and co-workers,⁵² which was constructed using PL peak positions. To make these E₁ values comparable to the values extracted from absorption data, we corrected them by using the size-dependent Stokes shifts reported in the same work.⁵² The evident discrepancy between this group of data points and the E₁ values extracted directly from absorption spectra (including the spectra reported by Booth and co-workers in ref (52)) clearly demonstrates the inadequacy of PL peak positions as metrics for the band gap, as discussed in detail above. A systematic error can also be identified in the data reported by Qin etal.⁵¹ for cp CIS QDs with diameters equal to or larger than 4 nm, probably due to the large uncertainties associated with the determination of E₁ by the double-tangent method in absorption spectra with broad and indistinct peaks.

The fitting results (eqs 3 and 4) show that the increase in band gap with the reduction of the CIS QD size is mainly determined by the 1/d term, for both wz and cp QDs. The contribution of the 1/d² term only becomes relevant for sufficiently small QDs. This is in striking contrast with the size-dependence of the band gap reported for CdSe and CdTe QDs, which is almost completely due to the 1/d² term,²⁵ but is analogous to that observed for PbSe and PbS QDs, which also varies mainly with 1/d.^23,28,76 The 1/d² term is typically associated with the quantum confinement contribution, since this is the dependence predicted based on the effective mass approximation (EMA), while the 1/d dependence reflects the Coulomb interaction contribution.⁸⁰ However, the contribution of the Coulomb interaction decreases with increasing dielectric constant ε⁸⁰ and should thus not be significant for CIS QDs (ε = 10).⁸¹ Therefore, the dominance of the 1/d term can be interpreted as evidence that, similarly to the Pb-chalcogenides, the energy dispersion is mostly linear around the band gap, being parabolic only in a very small region near the extrema (i.e., top of valence band and bottom of conduction band).⁷⁶ This implies that the hole and electron effective masses should not be relevant quantities to determine the extent of quantum confinement effects in CIS QDs. However, it is clear that the size-dependence of the band gap of cp CIS QDs is much stronger than that of wz CIS QDs (see Figure 4a and b and eqs 3 and 4). A possible explanation for this difference can be found in the electron and hole effective masses of the two materials, which are smaller for cp CIS (viz., m_e = 0.153 m₀, m_h = 0.958 m₀)⁷⁷ than for wz CIS (viz., m_e = 0.173 m₀, m_h = 2.181 m₀).⁷⁷ Since the experimental effective masses for wz CIS are not yet known, we compared theoretical values calculated by hybrid DFT for both wz and cp CIS.⁷⁷ However, it should be pointed out that the calculated values for cp CIS are slightly different from the experimental ones (viz., m_e = 0.16 m₀, m_h = 1.3 m₀).⁵⁵

We note that a model based on the EMA (viz., the finite depth-well EMA)⁸² has been successfully used by Zhong and co-workers⁵⁵ to describe the empirical size-dependence observed in their work for cp CIS QDs (3.6 to 7.3 nm; see dashed line in Figure 4b, parameters used: m_e= 0.16 m₀, m_h = 1.3 m₀; E_g(bulk) = 1.53 eV; E_g(cap) = 7 eV). This modified EMA model takes into account the fact that the confinement potential V₀ is finite and estimates it as being the difference between the HOMO–LUMO energy gap of the capping ligands and the band gap of the semiconductor (V₀ = [E_g(cap) – E_g(bulk)]/2).⁸² However, Figure 4 clearly shows that the fit based on eq 2 (i.e., eq 4 above) is more accurate over the whole QD size range analyzed than the calculations based on the modified EMA (dashed line). The sizing curves reported in the present work (Figure 4 and eqs 3 and 4) thus offer a convenient and accurate way of determining the sizes of both wz and cp CIS QDs directly from absorption spectroscopy measurements. For convenience, sizing curves directly correlating the QD diameter with the wavelength of the first absorption peak are provided in the Supporting Information (Figure S9).

Molar Absorption Coefficient of wz CIS QDs at the First Exciton Transition Energy

The molar absorption coefficients ε of CIS QDs can be obtained using the Beer–Lambert law:

5

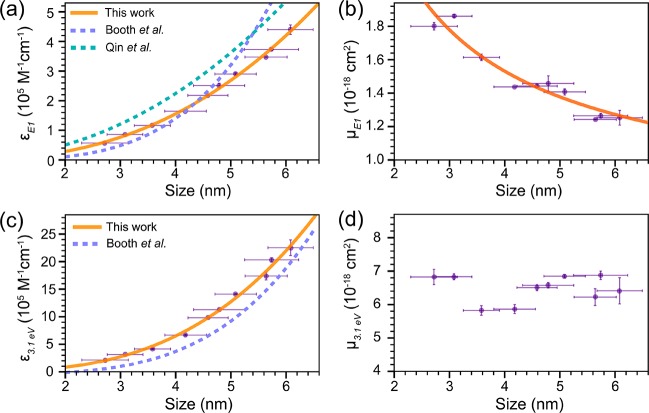
where A is the measured absorbance at the lowest energy absorption transition E₁ (i.e., the first exciton transition 1S_h–1S_e), c denotes the molar concentration of CIS QDs, and l is the optical path length. The concentration of CIS QDs is obtained as discussed above (see also SI, method 1, for details). The peak positions E₁ were extracted from the second derivative of the absorption spectra as described above. The size-dependent molar absorption coefficients at the first exciton transition energy (ε_E1 in 10⁵ M^–1·cm^–1) of CIS QDs can thus be readily obtained (Figure 5a). We observed that CIS QDs larger than 6.1 nm tend to lose their colloidal stability after extensive purification, which results in the formation of aggregates that introduce light-scattering contributions to the measured absorption spectra. This issue affects the accuracy of the determination of absorption coefficients; thus data concerning CIS QDs larger than 6.1 nm are not included in Figure 5.

Figure 5.

(a) Size-dependent molar absorption coefficients ε_E1 at the first exciton transition energy (E₁) of nearly spherical wz CIS QDs (In/Cu = 0.91 ± 0.11). The orange solid line is a fit to the data using a power law function (eq 6). Purple and green dashed lines denote the size-dependent trends reported in the literature for pyramidal cp CIS QDs (In/Cu = 0.91 and ∼1).^51,52 (b) Size-dependent absorption cross-section per formula unit at E₁(μ_E1) of wz CIS QDs (In/Cu = 0.91 ± 0.11). The orange solid line is a fit to the data using a power law function (eq 9). (c) Size-dependent molar absorption coefficients ε_3.1 eV at 3.1 eV of wz CIS QDs (In/Cu = 0.91 ± 0.11). The orange solid line is a fit to the data using a power law function (eq 11). The purple dashed line denotes the size-dependent trend reported in the literature for pyramidal cp CIS QDs (In/Cu = 0.91) by Booth etal.⁵² (d) Size-dependent absorption cross-section per formula unit at 3.1 eV (μ_3.1 eV) of wz CIS QDs (In/Cu = 0.91 ± 0.11).

Similarly to previous work on binary InAs,^37,38 Cd-chalcogenide,^{25,29,31−33} and Pb- chalcogenide QDs,^23,26,28,30 the data in Figure 5a can be fitted to a power law as follows (χ² = 0.999):

6

It is evident that the size-dependence observed in our work is significantly different from those reported by both Qin and co-workers (viz., 11430d^2.147)⁵¹ and Booth and co-workers (viz., (830 ± 660)d^3.7±0.6).⁵² Moreover, the absolute ε_E1 values in both reports are overestimated with respect to those presented here (in the case of Booth etal. only for d <4.5 nm). As discussed above, these discrepancies likely originate from the inherent experimental difficulties associated with the accurate determination of the effective diameter of trigonal-pyramidal NCs (which may or may not be truncated depending on the size), peak positions from broad and indistinct absorption spectra, and concentrations of ternary QDs that may have significant compositional polydispersity. The combined effect of these uncertainties may be very large, especially considering that the QD concentrations are affected by the uncertainties in both their size and composition. Moreover, colloidal stability issues may introduce additional errors due to light-scattering contributions, which may go unnoticed given the typically featureless aspect of the absorption spectra of CIS NCs.

The molar absorption coefficient ε is related to the absorption cross-section per QD σ by^25,30,33,38

7

where N_A is Avogadro’s constant. The absorption cross-section per formula unit μ is given by²⁵

8

where N_unit/QD denotes the number of unit cells per QD. The number of formula units per unit cell (Z = 1) can be obtained from the crystal lattice parameters of wz CIS QDs.⁶⁰ As shown in Figure 5b, the absorption cross-section per formula unit at the first exciton transition energy (μ_E1) of wz CIS QDs is size-dependent and can be described as (χ² = 0.998):

9

This size-dependence strongly deviates from the theoretically expected one, since a nearly size-independent oscillator strength per QD is predicted for the first exciton transition 1S_h–1S_e by several theoretical models (viz., k·p EMA,^80,83 tight-binding,⁸⁴ and effective bond-orbital model⁸⁵), which implies that μ_E1 should follow a 1/d³ dependence. Nevertheless, discrepancies between this theoretical prediction and empirical trends are commonly observed. For example, a 1/d² dependence has been reported for a number of colloidal QD systems (CdSe QDs with d = 1.5–8 nm,^25,33 CdTe QDs with d = 3.5–9 nm,²⁵ PbSe QDs with d = 3–8 nm,²⁸ and CdS QDs with d = 2.4–5.6 nm³⁵). To date, a 1/d³ dependence has only been reported for CdTe QDs with d = 2–4 nm^25,86 and CdS QDs with d = 1.3–2.4 nm.³⁵ The reasons for the divergence between the theoretical prediction and the experimental observations remain as yet unclear. Furthermore, it is important to note that the strong size-dependence of the absorption coefficient of the lowest energy absorption transition of colloidal QDs makes it less suitable as a tool to determine QD concentrations, since its accuracy may be strongly compromised by the size and shape polydispersity of the sample under consideration.

Molar Absorption Coefficient of CIS QDs at Energies Far above the Band-Edge

The molar absorption coefficient at higher energy (3.1 eV) of the wz CIS QDs prepared in this work can be obtained by

10

where A_3.1 eV and A_E1 are the absorbances at 3.1 eV and at the first exciton transition energy, respectively. The obtained data were plotted with respect to the CIS QD diameter (d) (Figure 5c) and fitted to a power function yielding (χ² = 0.998)

11

It is interesting to note that the ε_3.1 eV values scale with the volume of QDs, showing that the spectral density of states is no longer significantly affected by quantum confinement effects. This has been experimentally observed for a number of colloidal QD systems (CdSe,^24,25,33,87 CdTe,²⁵ PbSe,²⁸ InAs³⁸) and is consistent with theoretical predictions based on the EMA model.⁸⁷ In contrast, the size-dependence of ε_3.1 eV reported by Booth and co-workers for cp CIS QDs (viz., (2123 ± 1090)d^3.8±0.3)⁵² is far stronger than the theoretical expectation and the previous experimental observations. The reasons for the inconsistency between the present results and those previously reported in ref (52) are probably the same as already discussed above for the size-dependence of the ε_E1 values. The absorption cross-section per formula unit at 3.1 eV (μ_3.1 eV) can be determined by applying eq 8 above and is observed to be size-independent over the whole size range investigated in our work (Figure 5d). These results confirm that ε_3.1 eV scales with the volume of the CIS QDs and imply that ε_3.1 eV is a more reliable parameter to accurately determine the concentrations of colloidal suspensions of CIS QDs.

The fact that the absorption cross-sections per unit cell at sufficiently high energies above the band gap are size-independent implies that they can be estimated from bulk optical constants. This is indeed the case, as has been demonstrated for a number of materials (e.g., CdSe,^25,87 InAs³⁸). The absolute absorption cross-section per formula unit of both wz and cp CIS QDs at 3.1 eV can then be calculated based on the Bruggeman effective media theory,^25,33,88 which can be written as

12

where n_s and n are respectively the refractive indices of the solvent (1.5 for toluene) and the semiconductor at 3.1 eV (2.636 for wz CIS⁸⁹ and 2.795 for cp CIS⁷⁹). α_3.1 eV is the absorption coefficient of bulk CIS QDs at 3.1 eV (1.9 × 10⁵ cm^–1 for wz CIS and 2.55 × 10⁵ cm^–1 for cp CIS), which is calculated by⁹⁰

13

where λ is the wavelength of light in the vacuum. k denotes the extinction coefficient of bulk CIS at 3.1 eV (0.605 for wz CIS⁸⁹ and 0.813 for cp CIS⁷⁹).

The term f_LF in eq 12 is the local field correction factor, which is given by^25,33,88

14

m₁ (m₁ = n – ik) and m₂ are the complex refractive indices of the semiconductor and solvent, respectively. Since the absorption of toluene at 3.1 eV is negligible, m₂ can be replaced by n_s (viz., 1.5). The absolute absorption cross-section per formula unit of wz and cp CIS at 3.1 eV is thus calculated to be 9.7 × 10^–18 and 1.18 × 10^–17 cm², respectively. It should be noted that the bulk optical constants (n and k) used for wz CIS are theoretical values obtained by DFT calculations,⁸⁹ since experimental data are available only for bulk cp CIS. Nevertheless, the calculated μ_3.1 eV value of wz CIS is very close to that of cp CIS QDs, and they are both in good agreement with the value experimentally determined in our work for wz CIS QDs [μ_3.1 eV = (6.3 ± 0.4) × 10^–18 cm²]. This demonstrates that the absorption cross-section of CIS QDs at high energies can be indeed deduced from the bulk optical constants.

Conclusions

We have reported here a detailed study of the size-dependence of the optical properties of colloidal wz CIS QDs in the 2.7 to 6.1 nm diameter range, with emphasis on the energy of the first absorption transition (1S_e–1S_h) and its absorption coefficient ε_E1 and on the absorption coefficient at higher energy (3.1 eV). Nearly spherical wz CIS QDs with small size dispersion (≤10%) are synthesized by self-limited topotactic partial Cu⁺ for In³⁺ cation exchange in template Cu_2–xS NCs. This synthesis protocol is robust and highly reproducible, yielding nearly stoichiometric CIS QDs with very small composition variations (In/Cu = 0.91 ± 0.11), regardless of their sizes. The well-defined nearly spherical size and small composition and size distributions of the CIS QDs prepared in the present work make them ideally suited to this study. Our results show that the band gap of wz CIS QDs increases with decreasing QD size, following a trend that depends primarily on 1/d. A sizing curve is also constructed for cp CIS QDs by collecting and reanalyzing data published by several different groups.^{51,52,54−57} The size-dependence of the band gap of cp CIS QDs is observed to be slightly stronger than that of wz CIS QDs, but also follows primarily a 1/d dependence. These sizing curves provide a convenient and accurate way of determining the sizes of both wz and cp CIS QDs directly from absorption spectroscopy measurements. Moreover, we find that the experimental size dependence of the molar absorption coefficient ε_E1 of wz CIS QDs at the first exciton transition energy can be accurately fit by the expression ε_E1 = 5208d^2.45. Interestingly, we observe that the absorption coefficients of the wz CIS QDs at energies far above the band gap (i.e., 3.1 eV) scale directly with the QD volume, which implies that the absorption cross-sections per unit cell are size-independent and therefore can be estimated from bulk optical constants. Indeed, the absolute absorption cross-sections per formula unit calculated from the bulk optical constants of wz and cp CIS at 3.1 eV (viz., 9.7 × 10^–18 and 1.18 × 10^–17 cm², respectively) are in good agreement with the value experimentally determined in our work for wz CIS QDs [(6.3 ± 0.4) × 10^–18 cm²]. These results demonstrate that the absorption coefficients at 3.1 eV are better suited to determine the concentrations of colloidal suspensions of CIS QDs, since they are less sensitive to size and shape dispersion.

Methods

Materials

Copper(I) acetate (CuAc, 97%), indium acetate (In(Ac)₃, 99.99%), 1-dodecanethiol (DDT, ≥98%), trioctylphosphine (TOP, 90%), trioctylphosphine oxide (TOPO, 99%), 1-octadecene (ODE, 90%), nitric acid (HNO₃, 69.5%), anhydrous toluene, methanol, and butanol were purchased from Sigma-Aldrich. Multi-Element calibration standard 3 and Multi-Element calibration standard 5 (10 μg/mL of each element) were purchased from PerkinElmer. TOPO and ODE were degassed at 120 °C under vacuum overnight prior to synthesis. Other reagents were used as received. The chemicals were weighed and handled inside a glovebox.

Synthesis of Cu_2–xS NCs

Template Cu_2–xS NCs were synthesized in a standard Schlenk line according to previously reported procedures.⁵⁸ CuAc (1 mmol, 0.126 g) and TOPO (4.65 mmol, 1.834 g) were mixed with 10 mL of predegassed ODE in a 100 mL three-neck flask. The mixture was degassed at 100 °C for 1 h. Then, the flask was purged by N₂ and further heated to 210 °C. At 160 °C, 2.5 mL of DDT were swiftly injected accompanied by a sharp decrease of temperature to 147 °C. A change in solution color from dark green to brown indicates the nucleation and growth of Cu_2–xS NCs. These NCs were allowed to grow at 210 °C for 5–70 min, followed by naturally cooling to room temperature. The crude reaction products were washed using isometric butanol and methanol, followed by centrifugation at 3000 rpm for 10 min. The washing step was repeated twice to remove residual precursors. Finally, the purified Cu_2–xS NCs were dispersed into 5 mL of anhydrous toluene and stored in a glovebox for further use.

Synthesis of CIS QDs

The wz CIS QDs were prepared following previously published procedures.⁵⁸ A 1 mL amount of purified Cu_2–xS NCs was degassed to remove toluene and was then redispersed into a solution of DDT (0.5 mL) and ODE (1.5 mL). In the meantime, In(Ac)₃ (0.2 mmol, 0.0584 g), TOP (0.2 mmol, 100 μL), and 2 mL of ODE were mixed and degassed at 125 °C for 1 h. Subsequently, the reaction flask containing the In–TOP complex (In/TOP = 1) solution was refilled with N₂ and maintained at 125 °C. After that, the aforementioned Cu_2–xS NCs solution was swiftly injected into the In–TOP complex solution under N₂. The mixture was kept at 125 °C for a variable amount of time depending on the size of template Cu_2–xS NCs (see SI, Table S1 for details). The mixture was vigorously stirred, then naturally cooled to room temperature. The crude reaction mixture was directly centrifuged at 2500 rpm for 1 min to isolate unreacted precursors. The supernatant was collected and the product CIS QDs were isolated and extensively washed (at least three times), using the same purification procedure described above. Occasionally, the solution became a gel after cooling or during the washing, requiring the addition of a few drops of octylamine to redisperse the QDs and proceed with the washing cycles. Finally, the CIS QDs were dispersed into 4 mL of anhydrous toluene, well-sealed, and stored in a glovebox for further use.

Assessment of the Sample Purity

Prior to the ICP-OES analysis and absorption spectroscopy measurement, the purity of the CIS QDs was assessed by XRD after different steps of purification. Since the indium source in the CE reaction is In(Ac)₃, which is insoluble in nonpolar solvents, residual In(Ac)₃ may still be present after the reaction. To remove In(Ac)₃, the crude samples were directly centrifuged without adding any antisolvents, followed by collecting suspended QDs in supernatant. This step essentially removes unreacted In(Ac)₃, as evidenced by XRD measurements (SI, Figure S10). The suspended QDs in the supernatant were subsequently washed, using the same purification procedure described above, for at least three times to ensure complete removal of In(Ac)₃ and other byproducts. After this purification step, the CIS QDs were dispersed into anhydrous toluene and were stored in a glovebox.

Optical Spectroscopy

Prior to optical measurements, the quartz cuvettes were immersed in 69.5% nitric acid for 5 min, then thoroughly rinsed with Milli-Q water and absolute ethanol for a final rinse, and dried by compressed air flow. This step is crucial for reducing experimental error caused by contaminations from the cuvettes. Samples for optical measurements were prepared by dispersing CIS QDs into 3 mL of anhydrous toluene in precleaned sealable quartz cuvettes under N₂. To reduce inner filter effects, the optical density at the lowest energy transition was below 0.1. Absorption spectra were recorded on a double-beam PerkinElmer Lambda 950 UV/vis/NIR spectrometer (175–3300 nm). PL spectra were acquired using an Edinburgh Instruments FLS920 spectrofluorometer equipped with a 450 W Xe lamp as excitation source and double-grating monochromators for both the excitation and the emission. A Hamamatsu R928 photomultiplier tube (250–800 nm) and a liquid N₂ cooled Hamamatsu R5509-72 photomultiplier tube (750–1600 nm) were used as detectors for obtaining PL spectra.

Photoluminescence Quantum Yields

The PLQYs were measured using indocyanine green (ICG, PLQY = 12%) in DMSO as a standard.^58,91 To avoid inner filter effects, the absorbances of the QD and ICG solutions at and above the excitation wavelength (678 nm) were below 0.1.

X-ray Diffraction

XRD results were recorded on a Bruker D2 Phaser, equipped with a Co Kα X-ray source (1.790 26 Å). Samples were washed at least three times, dried under vacuum overnight, and uniformly dispersed on a silicon wafer prior to XRD measurements.

Transmission Electron Microscopy (TEM)

Conventional TEM images were acquired using a FEI Tecnai-20 microscope operating at 200 kV. HRTEM was performed on a FEI Talos F200X microscope operating at 200 kV. The lattice spacings of NCs were obtained by Fourier transform from the area of interest in HRTEM images. Samples for TEM imaging were prepared by drop-casting a toluene solution of purified NCs onto a carbon-coated 200 mesh copper TEM grid.

Inductively Coupled Plasma Optical Emission Spectroscopy

ICP measurements were performed on a PerkinElmer Optima 8300 ICP-OES spectrometer equipped with a high-performance segmented-array charge-coupled-device detector. Samples were carefully dried under vacuum overnight and then thoroughly dissolved in HNO₃ (69.5%), yielding clean yellow solutions. This solution was further diluted by 1000 times to reach the ppm ranges required for the measurement. In the meantime, Cu⁺ and In³⁺ calibration curves were prepared using Multi-Element calibration standard 3 (10 μg/mL of each element in 5% HNO₃) with trace concentrations ranging from 0 to 1 ppm. S^2– calibration curves were prepared using Multi-Element calibration standard 5 (10 μg/mL of each element in H₂O with a trace of HF) with trace concentrations ranging from 0 to 1 ppm. All the calibration curves were fitted to lines with R-values larger than 0.999. The relative standard deviation of Cu⁺ (324.752 nm) or In³⁺ (325.609 nm) concentration was less than 3%.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acsnano.8b03641.

• XRD patterns of template Cu_2–xS NCs and product CIS QDs; TEM images and corresponding size histograms of CIS QDs with a size range from 2.7 to 6.8 nm; PL spectra of product CIS QDs; detailed parameters for synthesizing CIS QDs via partial cation exchange in template Cu_2–xNCs; determination of CIS QD concentration; PL peak positions and second derivative of absorption spectra of 5.5 nm CIS QDs (PDF)

The authors declare no competing financial interest.