“Complete Streets” and Adult Bicyclist Fatalities: Applying G-Computation to Evaluate an Intervention That Affects the Size of a Population at Risk

Abstract

“Complete streets” policies require transportation engineers to make provisions for pedestrians, bicyclists, and mass transit users. These policies may make bicycling safer for individual cyclists while increasing the overall number of bicycle fatalities if more people cycle due to improved infrastructure. We merged county-level records of complete streets policies with Fatality Analysis Reporting System counts of cyclist fatalities occurring between January 2000 and December 2015. Because comprehensive county-level estimates of numbers of cyclists were not available, we used bicycle commuter estimates from the American Community Survey and the US Census as a proxy for the cycling population and limited analysis to 183 counties (accounting for over half of the US population) for which cycle commuting estimates were consistently nonzero. We used G-computation to estimate the effect of complete streets policies on overall numbers of cyclist fatalities while also accounting for potential policy effects on the size of the cycling population. Over a period of 16 years, 5,254 cyclists died in these counties, representing 34 fatalities per 100,000 cyclist-years. We estimated that complete streets policies made cycling safer, averting 0.6 fatalities per 100,000 cyclist-years (95% confidence interval: −1.0, −0.3) by encouraging a 2.4% increase in cycling but producing only a 0.7% increase in cyclist fatalities. G-computation is a useful tool for understanding the impact of policy on risk and exposure.

Bicycling is an economically efficient form of active transportation that promotes physical and mental health (1, 2). However, many American adults choose not to ride bicycles, owing to safety concerns (3, 4). Modifying the built environment to promote safe cycling—for example, by creating bike lanes (5, 6)—may encourage more cycling and prevent injury to cyclists. The dual health benefits of activity promotion and injury reduction are a key premise underlying “complete streets” initiatives (7). Complete streets initiatives are legislation, resolutions, internal memos, or executive orders which direct transportation planners to consider the safety of nonmotorized road users, including bicyclists, when planning street layouts (8). However, because improvements in bicycling safety may induce more people to ride bicycles more often, such policies may decrease the risk per cyclist while elevating the burden of cyclist fatalities by increasing the size of the population at risk (2).

The fact that complete streets policies may affect both the numerator and denominator of an injury rate poses a challenge for evaluating the public health consequences of such policies. Conventional policy evaluation techniques, such as difference-in-differences analysis, can estimate the change in the expected fatality count resulting from implementing a policy. However, these estimates may incorrectly assume that the size of the population at risk was not affected by the policy (1). Difference-in-differences analyses estimate the direct impact of policies on the size of the population at risk but do not account for changes in numbers of fatalities due to a change in the size of the population within the same analysis.

Epidemiologic methods developed to explicitly estimate outcomes or time-varying covariates that would have been observed had exposure been different may be helpful in this context. In particular, methods that use substitution estimators such as the G-computation algorithm (9) explicitly simulate the values of time-varying variables, including the denominator (e.g., size of the cycling population) and numerator (e.g., number of cyclist fatalities) that would be observed under counterfactual policy regimes (e.g., how many residents would have reported cycling in a county with a policy had that county actually not had a policy), thereby estimating the effect of both the activity promotion and injury prevention policy simultaneously. Such explicit counterfactual outcomes can make interpretation of results more intuitive (10).

In this study, we estimated the simultaneous impact of complete streets policies on the numbers of cyclists riding and the numbers of cyclists killed in traffic collisions using G-computation. Our work quantifies the substantive value of complete streets policies while providing a model for future use of G-computation in investigations of policy impact.

METHODS

Overview

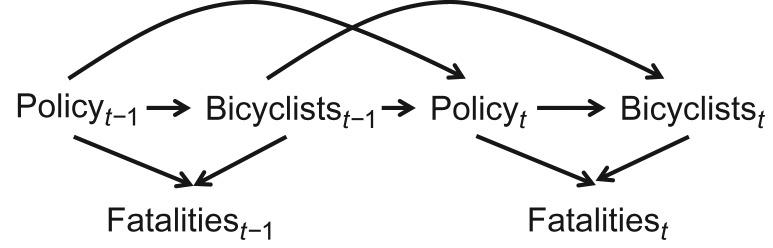
Figure 1 shows the theorized causal relationships between complete streets policies in some geographic unit, the number of bicyclists in that unit, and the number of bicyclist fatalities occurring in that unit. The fatality rate is the number of fatalities divided by the number of bicyclists over a set period of time; thus, estimating complete streets policies’ impact on safety requires estimating changes to both the numerator and the denominator of the rate.

Figure 1.

Hypothesized causal relationships between “complete streets” policies, numbers of bicyclists, and numbers of bicyclist fatalities. The count of bicyclists and the presence of a complete streets policy in a county are independent predictors of the number of fatalities among bicyclists in that county. The number of bicyclists predicts both the presence of a policy and the number of bicyclists in the next year, as does the presence of a complete streets policy. t, current year; t − 1, prior year.

Data

We used cyclist fatality records from the Fatality Analysis Reporting System (FARS) (11), a census of collisions occurring on US public roadways resulting in 1 or more fatalities (12). FARS data are collected for surveillance and research purposes and have been used extensively for scholarly analyses of driver, vehicle, and environmental influences on motor vehicle fatalities (13–16). Each incident listed in FARS includes 1) the date on which the collision occurred; 2) the location where the collision occurred, including a code for the county; and 3) the number of fatally injured people, categorized by type of road user (driver, passenger, cyclist, pedestrian, etc.). Using FARS records, we identified the number of cyclists killed in motor vehicle collisions in each county in the United States during the years 2000–2015. Though FARS includes records of incidents in which child cyclists were killed, we focused on adult cyclists for this analysis because no estimates of child cycling prevalence were available (see below for details on cycling prevalence estimates). We were unable to examine the impact of complete streets policies on injury severity (including fatal vs. nonfatal injuries) using FARS data, because FARS includes only incidents resulting in a fatality. We did not limit our analysis to collisions occurring on streets that had received improvements, because improvements encourage ridership (potentially resulting in fatalities) on unimproved streets in order to access the improved infrastructure (1).

We used records from Smart Growth America to identify the year in which the first complete streets policy became active in a state or county during the years 1971–2015 (17, 18). Smart Growth America is a 501(c)(3) organization focused on mixed residential and commercial development, sustainable transportation options, and other development principles (19). These records considered any legislation, executive order, resolution, tax, or Department of Transportation policy statement requiring planners to consider all street users to constitute a complete streets policy. We conducted this analysis with counties as the jurisdiction of interest; when state-level policies were implemented, we considered all counties in that state to have a policy. The Smart Growth America database also has records of policies enacted at the city or regional level; as detailed in the Discussion section, we did not consider the effects of these policies in this analysis, because no consistently assessed data on the prevalence of cycling were available for cities or regions. We did not analyze updates to existing policies, because updates were rare; we consider potential consequences of this decision in the Discussion.

There is substantial spatiotemporal variation in the prevalence of cycling in the United States (5). To estimate the effect of complete streets policies on numbers of cyclists at risk of fatality, we needed an estimate of the cycling population in each jurisdiction of interest in each year. Unfortunately, there were no validated estimates of the total number of cyclists in each county during this time period. As proxy estimates of the cycling population in each county, we used the 2000 US Census and 2007–2015 American Community Survey (ACS) 1-year estimates of the numbers of bicycle commuters in each county. Both the US Census and the ACS ask respondents who indicate that they worked for pay in the last week to specify the mode of travel used for the longest commuting distance to work during that time period. We selected 1-year ACS estimates rather than 5-year ACS estimates to avoid oversmoothing variation in cycle commuter counts between years. Because ACS 1-year estimates were not available for 2001–2006, we linearly interpolated estimated numbers of cycle commuters in each year from the 2000 estimate and the 2007 estimate.

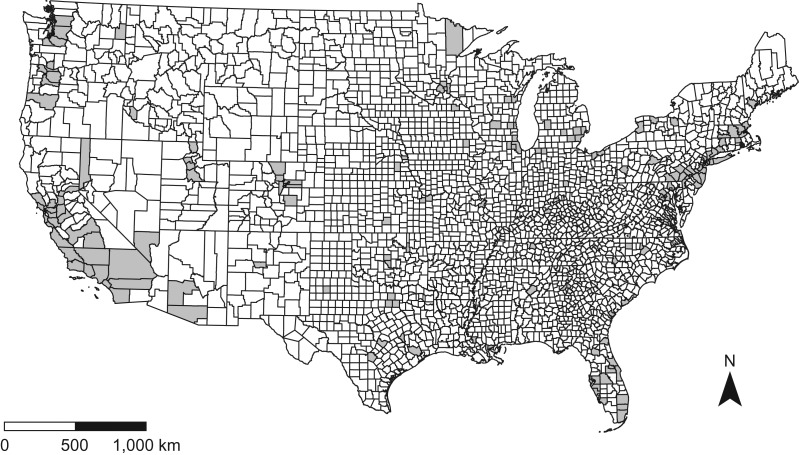
Because cycling was rare in many counties, we limited analysis to the 183 counties where the margin of error for the ACS count of cycle commuters excluded the possibility of zero (no cycle commuters) for all years from 2007 to 2015 (Table 1). As of the 2000 US Census, 52% of the total US population lived in these counties, which include the principal county in most of the country’s most populous metropolitan areas. Figure 2 shows a 2010 map of the United States; counties included in the analysis are indicated in gray.

Table 1.

Characteristics of the 183 Counties for Which the Prevalence of Bicycle Commuting Was Definitively Greater Than Zero in All American Community Survey 1-Year Estimates, United States, 2000–2015

Characteristic	Year(s)	Minimum	Median (IQR)	Maximum
Population, no. of persons	2000	91,861a	558,522 (349,048–880,921)	9,538,191b
Population growth, change in no. of persons	2000–2015	−292,451c	62,596 (34,845–119,596)	1,021,131d
Estimated no. of cyclists	2000	204e	1,758 (982–4,123)	48,030f
Increase in no. of cyclists	2000–2015	246e	2,031 (1,217–4,732)	58,395f

Abbreviation: IQR, interquartile range.

^a Cache County, Utah.

^b Los Angeles County, California.

^c Wayne County, Michigan.

^d Harris County, Texas.

^e Johnson County, Kansas.

^f Stanislaus County, California.

Figure 2.

Map of all counties in the continental United States in 2010, highlighting in gray all counties assumed to have bicycle commuters—that is, those in which American Community Survey estimates with a margin of error excluded the possibility that there were no county residents who commuted by bicycle. The highlighted counties were included in this analysis; all others were excluded.

Because Pucher et al. (20) found that 53% of cycle trips in urban areas are commuting trips and nearly all of the counties we analyzed are substantially urbanized, we estimated the total number of cyclists in each county-year period to be double the number of cycle commuters. Web Figure 1 (available at https://academic.oup.com/aje) shows estimated cycle counts for 5 randomly selected counties over the 16-year period of interest.

Primary analysis

In order to assess the joint impact of complete streets policies on the size of the bicyclist population and the number of bicyclist fatalities, we developed a model using the parametric G-formula (9, 21). The parametric G-formula has been described in detail elsewhere (22–24). Briefly, the approach consists of estimating an intervention-specific mean by simulating from parametric models for the final outcome of interest and any time-varying covariates affected by prior treatment, potentially including intervention status (see Web Appendix 1 (Web Tables 1 and 2) for details).

For this analysis, we used county and year fixed effects to control for time-invariant confounding by county and for county-invariant secular trends by year. We were concerned, however, that the size of the cycling population would be a predictor of passing a policy and would also be affected by the presence of a policy (25). We therefore treated the cyclist count as a time-varying covariate affected by the presence of a complete streets policy, taking advantage of G-computation’s ability to account for such effects (22). Specifically, we assumed that the cycling population at time t was determined by county-level fixed effects, policies in place at time t, a secular time trend, and the number of cyclists at time t − 1:

$$\begin{array}{c}{\text{Cyclist}\text{Count}}_{ij}={\mathrm{\beta }}_0{\mathrm{County}}_i+{\mathrm{\beta }}_2{\mathrm{Policy}}_{ij}+{\mathrm{\beta }}_3{\mathrm{Year}}_j\hfill \\ +{\mathrm{\beta }}_4{\text{Cyclist}\text{Count}}_{i(j-1)}+\mathrm{\epsilon }.\hfill \end{array}$$

Because complete streets policies target infrastructure changes rather than behavior changes, we hypothesized that increases in cycling and decreases in fatalities ultimately caused by the policies would not occur immediately after a policy was implemented. To account for this delay, our models assumed a 2-year implementation lag—we coded the policy variable as true if a complete streets policy had been in place for at least 2 years. We based the 2-year lag time on prior evidence indicating that a decrease in risk following allocation of funding for Safe Routes to School programs began after 2 years (26); however, we also tested this assumption using sensitivity analyses (detailed below).

Next, we fitted the following model to predict fatalities in each county, assuming a Poisson distribution for the outcome error:

$$\begin{array}{c}{\log (\text{Fatalities}}_{ij})={\mathrm{\beta }}_0{\mathrm{County}}_i+{\mathrm{\beta }}_1\log \left({\text{Cyclist}\text{Count}}_{ij}\right)\hfill \\ +{\mathrm{\beta }}_2{\mathrm{Policy}}_{ij}+{\mathrm{\beta }}_3{\mathrm{Year}}_j+\mathrm{\epsilon },\hfill \end{array}$$

where County_i is a dummy variable indicating the ith county, Cyclist Count_ij represents the estimated cyclist count in county i for year j, Policy_ij is a dummy variable indicating the presence of a complete streets policy in county i for year j (lagged 2 years to allow for infrastructure implementation of the policy change as in the cyclist count model), and Year_j indicates the jth year. Parameters are interpretable as follows: β₀ represents a county-level fixed effect accounting for all unmeasured time-fixed county-level confounding. β₁ represents the logarithm of the multiplicative increase in fatality risk indicated by an additional cyclist. We estimated β₁ rather than assume it to be invariant (i.e., an offset in the model) because of the “safety-in-numbers” phenomenon suggesting that the per-cyclist risk decreases as the number of cyclists increases (27–29). β₂ represents the estimated increase in the number of fatalities occurring per year after the complete streets policy was passed as compared with the prior period. β₃ represents the cumulative change in fatality risk from time-varying factors not related to complete streets policies, such as changes in driver and cyclist education, change in the prevalence of helmet-wearing, etc. We used conventional regression diagnostics to validate the predictive accuracy of this model. We tested a similar model including an interaction term between the presence of a policy and change over time, but model fit was not improved for this model (likelihood ratio test: P > 0.05). Model selection for model-based substitution estimators, including G-computation, is an area of active research (30–32).

Using these models, we simulated observations of cyclists and cyclist fatalities under 3 scenarios: 1) always treated (in which policy was always set to 1 for all counties), 2) never treated (in which policy was always set to 0 for all counties), and 3) natural course (in which the policy value was set at true if and only if it was true in the observed data). All simulations were conducted by sampling with replacement from the counties available for analysis, and point estimates and 95% confidence intervals were estimated from 5,000 simulations.

Secondary and sensitivity analyses

Though we believe that G-computation is a more appropriate technique for a context where the population at risk may be affected by treatment, we also conducted a conventional difference-in-differences analysis of the same data for comparison. This analysis is presented in Web Appendix 2 (Web Table 3); briefly, difference-in-differences analysis uses the observed data in units that received treatment at different times to estimate what would have been observed had those units received alternate treatment patterns.

We conducted 2 sensitivity analyses. First, to test robustness to the assumption of a 2-year lag, we reran the analyses after lagging the policy value 0 years and 5 years. Second, to test robustness to the county selection criteria, we reran the analyses with more stringent selection criteria (limiting counties to the 89 counties reporting more than 1,000 cycle commuters in 2000) and more lax selection criteria (analyzing the 242 counties reporting more than zero cycle commuters for every year of follow-up).

Software

We used Stata 13MP (StataCorp LLC, College Station, Texas) to compile the FARS data from 2000–2014 and to code the years of implementation of complete streets policies from Smart Growth America records. In all subsequent analyses, including incorporation of FARS data for 2015, all US Census and ACS data, and the G-computation analysis, we used R for Windows, version 3.3.1 (R Foundation for Statistical Computing, Vienna, Austria).

RESULTS

Policies, cyclists, and fatalities

Only 26 (14%) of the 183 counties in this analysis had complete streets policies in place in 1998. Over 16 years of observation, complete streets policies were implemented at the county or state level for all but 22 counties, meaning that a first policy was implemented in 74% of counties we observed (Web Figure 2). No policies were repealed or removed over this time period.

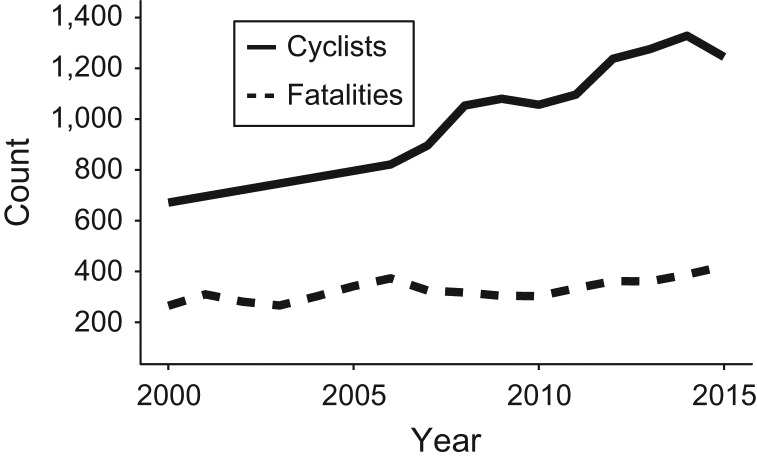
Between 2000 and 2015, there were 5,235 collisions between motor vehicles and cyclists that resulted in 5,254 adult cyclist fatalities recorded in FARS in study counties, corresponding to a rate of about 34 fatalities per 100,000 estimated adult cyclist-years. Yearly fatality totals ranged from as low as 265 (in 2000) to as high as 421 (in 2015) and showed a gradual rising trend (Figure 3).

Figure 3.

Observed yearly count of the total numbers of cyclists (in thousands) and cyclist fatalities in 183 counties in the United States, 2000–2015.

G-computation results

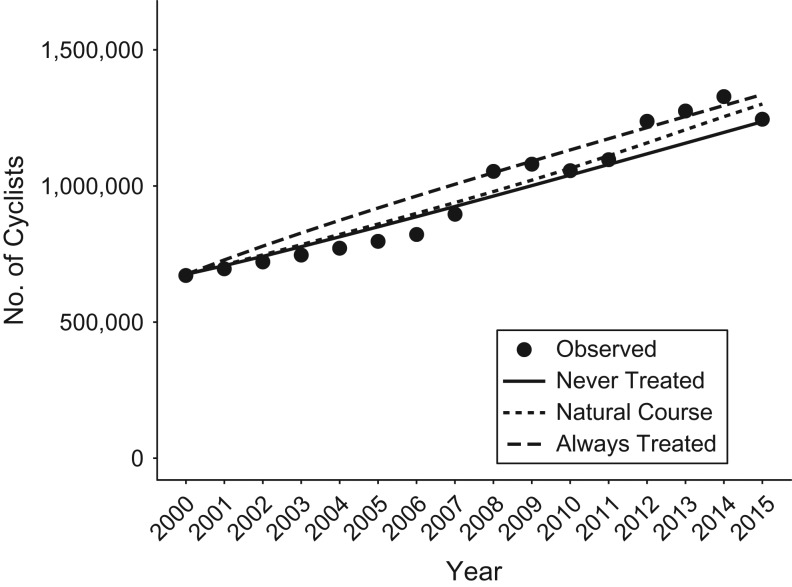
“Natural course” simulations, where counties were assigned policies in the same year (subject to the 2-year lag) as that in which the counties actually enacted policies in real life, replicated observed data closely (Table 2). Cyclist counts on a per-year basis were replicated with high fidelity (r = 0.91; Figure 4), and the observed fatality and cyclist totals consistently fell within the 95% confidence intervals for both total estimated number of cyclists and number of cyclist fatalities.

Table 2.

Estimates of the Effect of “Complete Streets” Policies on Numbers of Bicyclist Fatalities in 183 Counties, United States, 2000–2015

Scenario	No. of Cyclist-Years	Difference in No. of Cyclistsa	No. of Cyclist Fatalities	Difference in No. of Fatalitiesa	No. of Cyclist Fatalities per 100,000 Cyclist-Years	RDa	95% CI for RDb
Observed data	15,494,330		5,254		33.9
Never treatedc	15,012,706		5,211		34.7
Natural coursed	15,379,640	366, 934	5,246	35	34.1	−0.6	−1.0, −0.3
Always treatede	16,172,431	1,159,725	5,164	−47	31.9	−2.8	−3.7, −2.0

Abbreviations: CI, confidence interval; RD, rate difference.

^a Difference as compared with the never-treated scenario.

^b Nonparametric bootstrap from 5,000 simulations of each scenario.

^c No counties received complete streets policies.

^d Counties received complete streets policies for each year if they had a policy in that year in real life.

^e All counties received complete streets policies at the start of follow-up.

Figure 4.

Estimated numbers of cyclists per year in 183 US counties, 2000–2015. Lines indicate estimates simulated using the G-computation formula; dots indicate estimates calculated from US Census data. “Never treated” refers to the simulation in which no counties got “complete streets” policies; “natural course” refers to the simulation in which counties got complete streets policies in the simulation in the same simulated year as the year in which those counties actually received such policies in real life; and “always treated” refers to the simulation in which all counties got complete streets policies at baseline and kept them throughout the full simulation.

Observed data and results from all 3 simulation scenarios are presented in Table 2. Broadly, we estimated that the actual implementation of a complete streets policy resulted in a 2.4% increase in the cycling population over what would have been seen had no counties implemented such policies, and we estimated that there would have been a 6% increase in cyclist-years overall had all counties implemented complete streets policies for the full period of follow-up. Similarly, we estimated that complete streets policies prevented 0.6 fatalities per 100,000 cyclist-years (95% confidence interval (CI): −1.0, −0.3), or about a 2% decrease from the fatality rate that would have been observed had there been no complete streets policies. The potential causal effect estimate (i.e., the always-treated estimate minus the never-treated estimate) suggested that complete streets policies could have prevented 2.8 fatalities per 100,000 cyclist-years (95% CI: 2.0, 3.7) had such policies been implemented in all counties for all 16 years.

The practical cumulative impact of the countervailing 2% increase in cyclists and 0.6% reduction in risk of a fatal crash per 100,000 cyclist-years was a net average increase of 2.3 cyclist deaths per year, or 35 cyclist deaths in total.

Difference-in-differences and sensitivity analyses

From the difference-in-differences analysis, we estimated that on average complete streets policies could have prevented 1.2 cyclist fatalities per 100,000 cyclist-years (95% CI: −2.0, 4.5) had they been applied in all counties in the study in 2000. This analysis assumed that the size of the cycling population was a time-dependent covariate that was not affected by the presence of a complete streets policy. More details on the difference-in-differences analysis are available in Web Appendix 2.

Analyses using no lag rather than a 2-year lag showed a slightly stronger estimated protective effect of complete streets policies (natural course vs. never treated: rate difference (RD) = −2.8 fatalities per 100,000 cyclist-years (95% CI: −2.0, −3.6); always treated vs. never treated: RD = −5.5 fatalities per 100,000 cyclist-years (95% CI: −4.1, −6.9); Web Table 1). Analyses using a 5-year lag showed policies decreasing ridership while substantially increasing fatalities, resulting in an overall elevation of fatality risk (natural course vs. never treated: RD = 2.0 fatalities per 100,000 cyclist-years (95% CI: 1.4, 2.7); always treated vs. never treated: RD = 6.6 fatalities per 100,000 cyclist-years (95% CI: 5.4, 7.9); Web Table 2).

Analyses limited to the 89 counties with more than 1,000 cycle commuters in 2000 showed slightly stronger protective effect estimates than were found in the main analysis (natural course vs. never treated: RD = −1.2 fatalities per 100,000 cyclist-years (95% CI: −0.6, −1.7); always treated vs. never treated: RD = −2.9 fatalities per 100,000 cyclist-years (95% CI: −1.8, −4.0)). Analyses limited to the 242 counties wherein cycle commuter counts were present and greater than zero throughout the period of follow-up showed slightly stronger protective effect estimates than were found in the main analysis (natural course vs. never treated: RD = −1.0 fatalities per 100,000 cyclist-years (95% CI: −0.7, −1.3); always treated vs. never treated: RD = −2.8 fatalities per 100,000 cyclist-years (95% CI: −2.1, −3.5)).

DISCUSSION

In this study, we explored the impact of complete streets policies on fatal crash rates per 100,000 cyclist-years by estimating policy effects on both bicycle ridership and fatalities using G-computation. We found implementation of complete streets policies to be associated with a substantial increase in the cycling population and a smaller increase in the number of cyclist fatalities. Over a period of 16 years, complete streets policies did not appear to prevent cyclist fatalities at a population level but did appear to decrease per-cyclist risk by about 2%, or 0.6 fatalities per 100,000 cyclist-years.

This 2% reduction in bicycle fatality risk was consistent with the generally limited scope of infrastructure improvements expected under these policies. One prior analysis indicated that a statewide complete streets policy reduced Florida’s pedestrian fatality rate by about 0.5% (33) more than would have been expected by time trends alone. While prior research on cyclist infrastructure has broadly shown that cyclist-friendly environmental modifications substantially protect against cyclist injury (1, 34, 35), many cyclist injuries continue to occur on streets that have not received improvements (35). Our findings are also consistent with the safety-in-numbers effect frequently described in the transportation safety literature, wherein, within a given spatial unit, there are fewer pedestrian or cyclist injuries on a per-pedestrian or per-cyclist basis where there are more pedestrians or cyclists (27, 36, 37). Future research should focus on the role of microscale factors in cyclist injury (e.g., the safety impacts of adding protected cycling lanes or the transient risk elevation posed by road construction) after complete streets policy implementation to determine which improvements increase safety, potentially leveraging archived street imagery to explore these factors on a national scale (38).

Our analysis used G-computation to estimate the impact of complete streets policies on both the numerator and denominator of the cyclist fatality rate (23, 39). G-computation is a “substitution estimator” for the parametric G-formula, meaning that the estimate for the final causal effect is determined by simulating intermediate values and outcomes from fitted models (40, 41). To the best of our knowledge, our work illustrates a novel use of G-computation for policy analyses in which the policy might modify the per-unit risk as well as the size of the population at risk. In future analyses, investigators might explore the use of targeted maximum likelihood estimation (32, 42), an alternate substitution estimator which can support data-adaptive procedures to simulate counterfactuals, which might allow them to better account for potential time-varying determinants of the size of the population at risk.

While the novel use of causal inference techniques, a reliable and well-validated outcome measure, and a relatively long (16-year) period of follow-up constitute strengths of this analysis, our results must be considered in light of several important limitations. The primary limitation is that we did not have access to detailed person-time cycling data (i.e., the true time at risk) in each county. The only nationally available county-level cyclist data we had access to were numbers of people who reported cycling to work. However, since commuting accounts for only a portion of cycling time, our use of a constant estimate that half of people’s cycling time was spent commuting embedded the assumption that all effects of policies and time trends on cycling to work were proportionate to the true amount of person-time spent on bicycles within the county’s public roadways. Some cross-sectional studies have suggested that bike commuting is more strongly associated with infrastructure than is recreational cycling (43). If this cross-sectional association implies that improved infrastructure consequent to enactment of complete streets policies disproportionally induced commuter cycling, then we probably overestimated the impact of complete streets policies on increasing the cyclist population. However, a detailed study of cycling motivation suggests that sensitivity to infrastructure is present across patterns of cycling (e.g., utilitarian or recreational), which supports our assumption that the commuter cyclist count is a proxy for the total cycling population both before and after infrastructure improvements (44). Future studies should investigate the impact of infrastructure changes on the purpose of cycling trips and the risk profiles of cyclists who begin cycling in response to infrastructure changes. Such studies should address both location-based risk impacts (e.g., do new riders disproportionately use improved facilities?) and behavioral impacts (e.g., do new riders disproportionately wear helmets?).

Four other limitations of our work should be noted. First, because we did not have access to consistent data on cyclist injuries across the country over the 16-year study period, we focused on fatalities as an outcome. However, cyclist injury is much more common than cyclist fatality (45). Nationwide, there are nearly 500 cyclist injury emergency department visits for each cyclist fatality, and morbidity due to cycling injury is a substantial public health burden (46). Future analyses should focus on the impacts of complete streets policies on nonfatal injury. Second, because our sole estimate of the cycling population was limited to commuting-to-work data, we focused on adult cyclists. However, complete streets policies may additionally prevent injury and fatality among younger cyclists. Future research should focus on the effect complete streets policies may have on injuries among child and teenage cyclists. Third, cycling is a seasonal activity, with fair weather and daylight hours strongly affecting the number of riders in a given location (47). Because the ACS is conducted throughout the year and we used yearly fatality estimates, we do not expect that estimates were biased by seasonal variation. Nonetheless, because complete streets policies may induce more “fair weather” riders or offer better rider protection in inclement conditions, assessing seasonal effects of complete streets policies is a promising area for future work. Finally, for pragmatic reasons, our analysis focused on the impact of the first policy taking effect within a county; we did not consider city or regional policies, variations in policy specifics, implementation, enforcement, or impacts of subsequent complete streets policies. Future work should investigate policy variations using location-specific denominator estimates (e.g., as available from mobile cycling app providers like Strava (Strava, Inc., San Francisco, California)) in order to provide more precisely policy-relevant findings (48).

In conclusion, we estimated that complete streets policies increased the prevalence of cycling while holding the cyclist fatality count constant, resulting in a modest decrease in the cyclist fatality rate. The G-computation analytical approach allowed us to control for potential time-varying confounding by number of cyclists while yielding simultaneous insight into the potential impact of complete streets policies not only on incidence of an outcome of interest (e.g., cyclist fatalities) but also on the approximate size of the population at risk (e.g., cyclists). G-computation may be useful in other policy evaluation settings.

Abbreviations

ACS

American Community Survey

CI

confidence interval

FARS

Fatality Analysis Reporting System

RD

rate difference