Cluster-Randomized Test-Negative Design Trials: A Novel and Efficient Method to Assess the Efficacy of Community-Level Dengue Interventions

Abstract

Cluster-randomized controlled trials are the gold standard for assessing efficacy of community-level interventions, such as vector-control strategies against dengue. We describe a novel cluster-randomized trial methodology with a test-negative design (CR-TND), which offers advantages over traditional approaches. This method uses outcome-based sampling of patients presenting with a syndrome consistent with the disease of interest, who are subsequently classified as test-positive cases or test-negative controls on the basis of diagnostic testing. We used simulations of a cluster trial to demonstrate validity of efficacy estimates under the test-negative approach. We demonstrated that, provided study arms are balanced for both test-negative and test-positive illness at baseline and that other test-negative design assumptions are met, the efficacy estimates closely match true efficacy. Analytical considerations for an odds ratio–based effect estimate arising from clustered data and potential approaches to analysis are also discussed briefly. We concluded that application of the test-negative design to certain cluster-randomized trials could increase their efficiency and ease of implementation.

Cluster-randomized controlled trials are the gold standard for evaluating the efficacy of health interventions delivered at the community level, including vector control interventions to reduce transmission of arboviruses such as dengue and Zika. A recent literature review emphasized the need for high-quality randomized controlled trials to improve disease control strategies (1, 2). The importance of measuring impact on disease, not only on vector indices, has been specifically highlighted. However, it is widely accepted that trials using clinical endpoints can be resource intensive and logistically difficult to implement.

Cluster-randomized trials customarily randomly allocate an intervention to some predefined spatial units, and follow a cohort of “at risk” participants over time to measure the endpoint of interest in treated versus untreated clusters. When sufficient units are available, randomization results in groups comparable in all factors except for the intervention under study, and provides the basis for statistical inference (3). Such trials with epidemiologic endpoints are resource-intensive due to the requirement for active case surveillance. The nonindependence of individuals within each cluster and resultant statistical inefficiency necessitates inflation of the cluster-randomized trial sample size to achieve power equivalent to an individually randomized trial (3–6). Traditional cluster-randomized trials frequently require thousands of participants to generate sufficient events for hypothesis testing (7–12), particularly for interventions against uncommon events (e.g., clinically apparent dengue). This has significant cost, time, ethical, and logistical implications. These challenges may partly account for the small number of cluster-randomized trials and subsequent weak evidence base for vector-control interventions against arboviruses (1), limiting evidence-based decision making for disease control.

Considerable literature demonstrates that sampling participants on the basis of their outcome status (case-control design) rather than their exposure status (cohort design) increases efficiency of observational studies (13–17). We propose a cluster-randomized trial design with test-negative sampling (cluster-randomized test-negative design, or CR-TND), a form of outcome-based recruitment, as an efficient method to assess the efficacy of community-level interventions against dengue (such as introgression of Wolbachia into mosquito populations (18, 19)). The approach offers the advantage of being more efficient, cost-effective, and logistically simpler to achieve than a traditional cluster-randomized trial. We review the assumptions inherent to the test-negative design (TND) and how these relate to its application in the context of a cluster-randomized trial, use simulations to demonstrate the validity of estimates produced by a CR-TND study, and discuss potential approaches to analysis and interpretation of results.

ASSUMPTIONS OF THE TND AND APPLICATION TO CLUSTER-RANDOMIZED TRIALS

The TND is a modified case-cohort study in which symptomatic patients meeting predefined inclusion/exclusion criteria are enrolled and subsequently classified as test-positive “cases” or test-negative “controls” based on the results of definitive diagnostic testing. This design is frequently used for evaluating the effectiveness of seasonal influenza vaccination (20–25), and its internal validity has been explored in depth (20–23, 26–28). Briefly, validity depends primarily upon the avoidance of selection bias in the sampling of cases and controls, as well as the extent to which the exposure distribution among controls is representative of the exposure distribution among the source population that gives rise to cases. Key assumptions and their relevance to CR-TND trials are discussed below. For ease of discussion we refer to the illness in those testing positive for the pathogen of interest as “test-positive illness” and in those testing negative as “test-negative illness.”

Assumption 1: Test-negative illness is not associated with the intervention

A core assumption of the TND is that the test-negative illness is not affected by the intervention (21, 22, 26) (i.e., in the case of influenza vaccine-effectiveness studies, receipt of the influenza vaccine would not be expected to modify the incidence of noninfluenza acute respiratory illness). In randomized trials, random allocation of the intervention reduces the likelihood of any association between test-negative illness and the intervention. With an increasing number of clusters, the likelihood of test-negative illness occurring disproportionately in one study arm by chance is reduced. This may be particularly relevant where the test-negative illness is a communicable disease, as these tend to cluster in space and time. In cluster-randomized controlled trials with few allocation units, constrained randomization (29) can improve balance in factors potentially associated with test-positive or test-negative illness. Randomization thus represents a methodological advantage over influenza vaccine effectiveness studies in which self-selection may lead to an association between the intervention and outcome.

Assumption 2: The relative propensity of treated and untreated populations to seek health care is nondifferential for cases and controls

Haber et al. (26) suggested that the TND yields an unbiased estimate of effectiveness/efficacy even if the likelihood of seeking health care (and being enrolled) is associated with the intervention, provided this association exists for both test-positive and test-negative patients. Thus the TND may reduce bias due to intervention-driven changes to health-care–seeking behavior relative to traditional cohort designs, a feature that may be particularly appealing in cluster-randomized trials if blinding the community to intervention status is not feasible. A recent exploration of the theoretical basis of the TND in observational studies of influenza vaccine effectiveness (28) argued that the TND achieves a reduction in, rather than elimination of, bias due to health-care–seeking behavior, because health-care–seeking behavior represents a continuous propensity rather than a simple binary variable that can be conditioned upon. Such potential bias should be further reduced in the CR-TND, given that randomization of the intervention should achieve balance between study arms in individuals’ average propensity to seek health care. Constrained randomization can further enforce a balance between study arms in their baseline observed incidence of test-negative illness (that incorporates care-seeking propensity as well as true disease incidence).

Assumption 3: The efficacy of the intervention is not associated with health-care–seeking behavior

The external validity of the TND depends on the intervention being equally effective across groups with different health-care–seeking behavior, such that the effectiveness/efficacy estimate generated through a study of individuals presenting to clinics is generalizable to the broader population (21). A limitation to this assumption could arise in both TND and CR-TND studies if those more or less likely to seek care at a study clinic differ systematically in some factor associated with intervention effectiveness. For example, if socioeconomic status differs with health-care–seeking behavior, this may correlate with differences in housing, vector density, community uptake of the intervention, or other factors that might affect the effectiveness of a dengue vector control intervention. Tacitly, in extending effectiveness estimates to cases of all severity, we assume that the intervention does not modify the spectrum of disease outcomes.

Assumption 4: The test used to determine disease status is highly sensitive and specific

Several authors (23, 26, 30) have modeled the effects of imperfect diagnostic testing on the TND estimate under different scenarios, demonstrating that a test (or combination of tests) with imperfect sensitivity or specificity biases the estimate toward the null, with the greatest bias arising from imperfect specificity. This, of course, remains true with clustered participants because clustering affects variation and not bias. Thus TND or CR-TND studies that demonstrate effectiveness/efficacy even with imperfect test sensitivity and/or specificity will underestimate the true effect (23). Use of a consistent diagnostic algorithm and gold-standard diagnostic tests, with laboratory testing performed blind to exposure status, will minimize the potential for differential or nondifferential outcome misclassification to bias the estimates from a TND or CR-TND study, in the same way as for other designs.

Assumption 5: The sampling of controls is uncensored

The effect measure estimated from a retrospective study depends critically upon the criteria applied to the selection of controls (31, 32). If controls are drawn from all individuals in the population at risk, without exclusion of those who test positive at any other time during the study period (i.e., uncensored or inclusive sampling), then the exposure distribution in the controls can be assumed to reflect the exposure distribution in the source population. In that case, the study provides a direct estimate of the population relative risk, without dependence on the rare disease assumption (32, 33), and, in this regard, a TND most resembles a case-cohort design. If controls are sampled inclusively as above, and also longitudinally throughout the study period concurrently with cases (incidence-density or risk-set sampling), then their cumulative exposure distribution represents that of the source population at each point in time (“risk period”) that a case arose. If this temporal matching is accounted for in the analysis, then the odds ratio directly estimates a population incidence rate ratio (31, 33, 34).

In the case of a (cluster-randomized) TND study, patients presenting to participating clinics with a test-negative illness are assumed to represent a sample of the source population from which cases arise (i.e., the population who would present to these clinics and be enrolled as a case if they experienced a test-positive illness). Foppa et al. (25) have demonstrated that TND studies using incidence-density sampling produce valid estimates of effect even when the incidence of test-positive or test-negative illness varies temporally. Because calendar time may correlate also with the exposure distribution (e.g., influenza vaccination uptake), analyses of observational TND studies have often included adjustment for calendar time (21). In the analysis of a CR-TND study, a participant’s exposure to the intervention is considered fixed and non–time-varying for the purpose of the intention-to-treat analysis, as per the randomized allocation, in which case time adjustment is not warranted. A per-protocol analysis, however, may account for individuals’ time-varying exposure to the intervention and require adjustment for calendar time.

Assumption 6: Participants with test-negative illness are recruited only when test-positive illness is circulating

An extension of assumption 5 in the case of a seasonal illness is that, in order to achieve incidence-density sampling of test-positive and test-negative participants, recruitment should occur only during periods when test-positive illness is circulating (21). Outside the transmission season there is effectively no “population at risk” of test-positive illness, and therefore test-negative controls recruited during this period are not a valid sample of the source population from which test-positive cases arise. This principle holds also for CR-TND studies. In practice, if a study is to run over more than one transmission season it may be infeasible to stop and start patient recruitment, or the beginning and end of the transmission periods may not be easily predicted in advance. This criterion can still be met, while allowing continuous recruitment, by restricting the data set for analysis to include only those test-negative controls enrolled during periods in which there were also test-positive participants recruited.

Finally, we note that many of the concerns regarding the TND raised by careful consideration of biases (27, 28, 35) are mitigated, or removed, by exposure randomization in a CR-TND. For example, randomization essentially removes the impact of differential misclassification of disease outcome within levels of extraneous factors (28) because the latter are balanced across arms. In addition, in the case of an infectious disease where spatiotemporal heterogeneity could lead to differences in baseline risk of illness between clusters, randomization of a sufficient number of clusters will ensure that the overall risk of illness remains balanced between study arms. The causal diagrams relevant to TNDs (specifically directed acyclic graphs) (28) apply here directly but are simplified given that no arrows point into the (randomly assigned) intervention node; clustering of response does not affect a directed acyclic graph. Further, randomization of exposure removes bias from estimation of marginal odds ratio measures of association (27). The noncollapsibility of the odds ratio (27) applies here to the extent that an intervention’s effect at a cluster level may be greater than the population effect; however, this means that the latter measure will simply be conservative. Below, we show that basic estimation procedures for cluster-randomized trials and TNDs can be straightforwardly extended to CR-TND study data.

SIMULATIONS

We assessed the validity of efficacy estimates generated through a CR-TND using simulations and found that accurate and unbiased estimates were produced, provided the randomization achieved balance between study arms at baseline in both the outcome of interest and the test-negative illness, and other assumptions of the TND were met. We simulated scenarios to compare the CR-TND efficacy estimate against the true efficacy of a hypothetical preventive intervention against dengue (Web Figure 1, available at https://academic.oup.com/aje). Initially we assumed the intervention had no effect. Hypothetical study populations were generated, consisting of 20–100 clusters, each with a random population size drawn from a uniform distribution with a range of 5,000–25,000. Baseline dengue and test-negative illness incidence rates in each cluster were simulated based on independent beta distributions and were applied to cluster population sizes to yield case counts for each category (Web Figure 2). Parameter choices for test-negative illness incidence were selected to yield 2 distinct values of the intercluster coefficient of variation (k), k = 0.5 and 0.25; k was set at 0.5 for dengue incidence. The rate parameters were selected to mimic dengue case notification rates (36–38) and k values (39) from southeast Asian dengue endemic settings. Note that any covariation of dengue and test-negative case counts arises solely from common cluster population sizes.

We randomly allocated half the clusters to receive the intervention. We performed simple randomization plus 3 constrained randomizations in which we generated a large number of potential random allocations and accepted only those in which the baseline 1) dengue incidence, 2) test-negative illness incidence, or 3) both dengue and test-negative illness incidence were balanced between arms, defined as a difference of ≤10% in aggregate incidence.

We calculated the exposure odds ratio (OR) in dengue versus test-negative controls for each random allocation, using the standard formula:

$$\begin{array}{c}\mathrm{OR}=\frac{\text{dengue}\text{cases}\text{in}\text{intervention}\text{arm}}{\text{dengue}\text{cases}\text{in}\text{nonintervention}\text{arm}}\hfill \\ ÷\frac{\text{test}-\text{negative}\text{controls}\text{in}\text{intervention}\text{arm}}{\text{test}-\text{negative}\text{controls}\text{in}\text{nonintervention}\text{arm}}.\hfill \end{array}$$

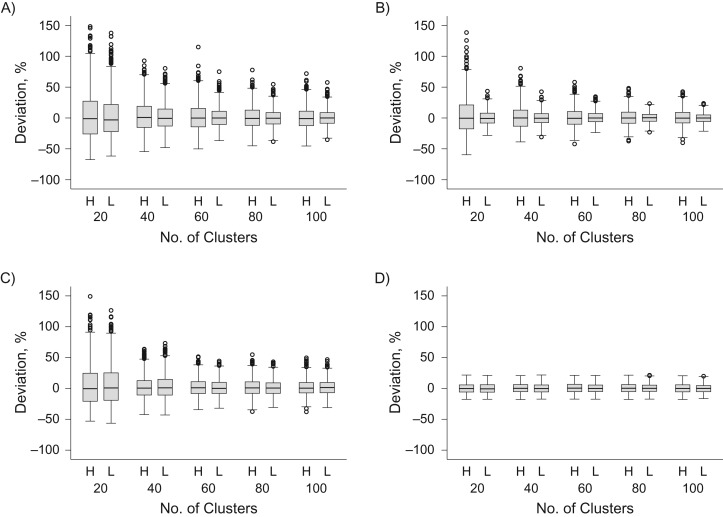
For simplicity, we assumed complete sampling of dengue (test-positive) cases and test-negative controls from both study arms, perfect diagnostic test sensitivity and specificity, and that all assumptions of the TND were met. Thus the only variation across simulations was in cluster intervention assignment. We repeated each simulation 1,000 times for each combination of the number of clusters and intercluster coefficient of variation. The percentage deviation from the expected null value (i.e., odds ratio = 1) was assessed for each simulation (Figure 1).

Figure 1.

Validity of odds ratio estimates from a simulated cluster-randomized test-negative design study, under the null hypothesis of no intervention effect. Box-and-whisker plots show the distribution of odds ratio estimates from 1,000 simulated cluster-randomized allocations of a hypothetical dengue preventive intervention, displayed as the % deviation from the expected odds ratio = 1, assuming that the true intervention efficacy is zero. The 10 different scenarios within each graph represent a variable number of clusters under study (20–100) and 2 scenarios of the intercluster coefficient of variation (k) in baseline test-negative illness incidence: high (H; k = 0.5) or low (L; k = 0.25). Intercluster variation in baseline dengue incidence was constant in all scenarios (k = 0.5). Random allocation of the intervention was either unconstrained (A) or constrained to ensure balance between the study arms (within 10%) in baseline dengue incidence (B), test-negative illness incidence (C), or both dengue and test-negative illness incidence (D). Note: 5 odds ratio estimates from panel A (4/1,000 simulations with 20 clusters and high k, and 1/1,000 simulation with 20 clusters and low k) and 2 odds ratio estimates in panel C (2/1,000 simulations with 20 clusters and low k) had a deviation value greater than 150% and are not shown on the graph.

Results demonstrated that the odds ratio estimated through a CR-TND study approximates the true null value. Random variation around the null was particularly reduced when study arms were balanced for both test-positive and test-negative illness baseline incidence. Such variation also decreased as the number of study clusters increased and at the lower value of intercluster heterogeneity for test-negative illness incidence. With balance on historical incidence of both dengue and test-negative outcomes, estimation was effective even with small numbers of clusters (Figure 1D).

We further investigated validity of the odds ratio estimates assuming a true intervention efficacy of 50%, by repeating the above steps while deterministically halving dengue incidence in each intervention cluster. The deviation of the simulation-derived odds ratio estimates from the expected “true” value was identical for an assumed efficacy of 50% (Web Figure 3) and at the null (Figure 1).

ANALYSIS OF CR-TND STUDIES

Community-level interventions introduce additional complexity into analysis of a CR-TND compared with an observational TND study, while allowing inference to be based on randomization. With TNDs, vaccine effectiveness is usually estimated through the odds ratio as defined above (21). Logistic regression models allow adjustment for potential confounders (20, 40) including calendar time. Common adjustments are time-matching using a conditional logistic regression model or, in an unconditional model, inclusion of calendar week as a categorical parameter using splines (40). For a CR-TND, however, any analysis needs to account for the clustering. We note 2 possible approaches that adapt procedures commonly used for cluster-randomized controlled trials.

Cluster-level summary data

We can simply use the estimated odds ratio based on data aggregated across all clusters, with the null hypothesis that the odds of being in the intervention arm are the same among test-positives as test-negatives. Inference can be based on the permutation distribution that considers all possible cluster intervention assignments. An approximate version of this test uses an estimate of the variance of the estimated odds ratio that accounts for the clustering using simple finite-population sampling ideas (41).

The aggregate odds ratio provides a consistent estimate of the relative risk, albeit at a population-averaged, or marginal, level (41). (This is in contrast to a cluster-specific odds ratio that is, in general, further from the null than the marginal version—see Hayes and Moulton (3); the difference is not of practical concern with rare outcomes.) Confidence intervals can either be based on inverting the permutation test or estimated via the approximate variance formula (41).

An alternative summary efficacy measure is based on the proportion of test-positive patients (among all tested individuals) in each cluster. At the null, the average of these proportions should be the same in both arms. For testing, the average of these proportions for the intervention clusters can then be compared with the same for control clusters via the t statistic, with inference based on a permutation test again, or on an approximate variance (41).

This approach also provides an estimate of the (cluster-specific) relative risk (RR). Specifically, with 2m clusters (m assigned to intervention), the expected proportion of test-positives in the intervention clusters is approximately $\frac{RR}{RR+\left(\frac{r}{2}\right)(1+RR)}$, and $\frac{1}{1+\left(\frac{r}{2}\right)(1+RR)}$ for the control clusters, where the ratio of sampled controls to cases is r. For example, if r = 1 and RR = 0.5, the average proportion of test-positives in a treated cluster is 2/5 (0.40) and 4/7 (0.57) in a control cluster. These calculations assume that the intervention effect is identical in all treated clusters. The difference in these average proportions of test-positives between intervention and control clusters yields an estimate of the relative risk given that we can substitute the estimated difference in the proportions, d, into the formula $d=\frac{1}{1+\left(\frac{r}{2}\right)(1+RR)}-\frac{RR}{RR+\left(\frac{r}{2}\right)(1+RR)}$, yielding a quadratic equation for RR. This yields an estimate of RR, along with an appropriately transformed confidence interval (from that for d) (41).

Note that estimates of the odds ratio from generalized estimating equations that use robust variances do not perform well in situations where there are relatively few clusters. On the other hand, random-effects logistic regression performs better and may provide a third alternative approach with sufficient clusters available (41).

Individual-level analysis

In the CR-TND a form of “per-protocol” analysis is likely of interest, to reduce the potential impact of exposure misclassification arising from the fact that some individuals in an intervention cluster may spend substantial time in a control cluster and vice versa. This “contamination” would necessarily reduce the observed effect of the intervention. Available measurements on such mobility contemporaneous to symptoms would then be included in an analysis that allows for individual-level covariates, in addition to calendar time, as previously discussed.

Modifications to the permutation distribution techniques used for either the odds ratio or the difference in average test-positive proportions across clusters may be developed by extending similar approaches for standard cluster-randomized trials (42–44). In addition, covariates can be introduced straightforwardly into a random-effects logistic regression model. Incorporating calendar time in this way effectively fits a proportional hazards frailty model if one assumes that the intervention effect is constant over time.

DISCUSSION

Public health strategies to control dengue and other arboviruses lack a robust evidence base due to the absence of well-powered cluster-randomized controlled trials of community-level interventions with disease endpoints (2). The absence of such trials might reflect the common belief that mosquito population suppression must inevitably lead to lower disease incidence, yet this relationship is poorly characterized and unlikely to be linear (45, 46). Additionally, there is a perception that cluster-randomized trials require fever surveillance of predefined cohorts of “at risk” individuals and that such efforts must always be logistically and financially demanding. Here we propose that cluster-randomized trials with TND sampling offer increased efficiency and validity by recruiting participants based on their outcome rather than exposure status. Advantages include a smaller total sample size and potentially single rather than repeat contact with study participants, as well as avoidance of potential biases that can arise in longitudinal studies from underascertainment of illness events or loss to follow-up. A primary advantage of the CR-TND approach over traditional TNDs is the randomization of the intervention that reduces confounding and provides a firm basis for inference. The CR-TND therefore represents an attractive novel design for trials of community-based interventions against acute infectious diseases such as dengue.

The key assumption underlying the validity of CR-TND effect estimates is that the ratio of exposed to unexposed patients with test-negative illness is an unbiased estimate of the ratio of exposed to unexposed persons in the source population who would seek health care if they developed the test-negative (or test-positive) illness. This assumption could be violated if an inappropriate test-negative illness was selected, upon which the intervention has a true effect. For example, in the case of a dengue vector-control intervention trial, another Aedes-borne pathogen such as Zika or chikungunya must be excluded from the classification of test-negative illness because the intervention could also feasibly modify the distribution of these diseases. Furthermore, small numbers of clusters limit the power of the design. Our simulations indicated that constrained randomization might be useful to increase precision, particularly when the number of clusters under study is small.

The outcome-based sampling in a CR-TND uses an odds ratio as the estimate of effect, the interpretation of which depends on the criteria applied in sampling test-negative controls. When controls are sampled concurrently with cases and without regard for past or future test-positive illness, as is proposed here, the odds ratio of exposure in test-positive versus test-negative patients yields a direct estimate of the relative risk in the source population. If the temporal matching of test-positives and test-negatives is accounted for in the analysis, then this becomes an unbiased estimate of the rate ratio, and thus the CR-TND can produce an equivalently intuitive and valid effect estimate as a traditional longitudinal cluster-randomized trial design but with potentially substantial savings in time and resources (41).

In addition to its efficiency benefits, the outcome-based sampling employed in the CR-TND also has a potential advantage over traditional study designs in reducing biases that can arise through longitudinal follow-up where the ascertainment of disease endpoints relies on passive case detection of study participants presenting to clinics when ill. Such designs carry a risk of misclassification bias, because any cohort members with the disease of interest who fail to present to a study clinic, or to be identified upon presentation, are falsely classified as disease-free (21). Loss-to-follow up that is differential between study arms and/or outcome status is another potential source of bias in traditional longitudinal designs, particularly when follow-up periods are long. The health-care–seeking behavior of the population, if differential between treatment arms (e.g., with a nonblinded intervention), can also confound the observed association between intervention and outcome (21). These biases are avoided in the CR-TND through the sampling of test-negative controls from the same patient population as the test-positive cases, and because of the random assignment of the intervention. Cluster-randomized trials of community interventions are susceptible to exposure misclassification if participants’ mobility patterns lead to contamination between intervention and control clusters. The CR-TND allows for inclusion of a per-protocol analysis employing more nuanced exposure classification based on recall of movements just prior to illness onset, which would not be possible in, for example, a prospective serological cohort with sampling at annual or 6-monthly intervals.

A key challenge to implementation of the CR-TND, compared with an observational TND, is adaptation of analytical methods to account adequately for clustering of participants with respect to their intervention allocation status. We have elsewhere proposed methods to accommodate clustering in group-level analysis of intervention effect, using a permutation approach to statistical inference (41). Published cluster-randomized trial formulas for sample-size calculations are inadequate for the CR-TND, and simulation studies based on baseline data, best estimates, or pilot studies are needed to assess the required sample size (41). Even for traditional cluster-randomized trials, sample-size calculations need preliminary estimates of design effects induced by the clustering—information that is often poorly reported.

The accuracy of sample size estimations, and the benefits conferred by constraining randomization to only those allocations in which balance is achieved in both test-negative and test-positive illness incidence, depend on the availability of reliable baseline data and the degree to which historical patterns are likely to reflect the future illness distribution. The spatial and temporal variability in many infectious diseases, and their propensity to cluster in space and time, could lead to a different distribution being observed during the study period compared with baseline. The incidence rate ratio of test-negative illness between treated and untreated arms during the study period should therefore be reported; this should approximate one if the assumption of no relationship between intervention and test-negative illness is upheld. Reestimation of power/sample size at an interim time point after study commencement—using the trial data from the control arm to determine intercluster heterogeneity of test-positive and test-negative illness—may also be advisable to affirm the estimates based on historical data.

The study design described here extends the test-negative design to cluster-randomized intervention trials. We have demonstrated that valid estimates of effect are produced by the CR-TND, even with a relatively small number of clusters, particularly when constrained randomization is employed to ensure balance in baseline test-positive and test-negative illness, and assuming the core assumptions of the TND are upheld. This design offers potential for improving the efficiency of cluster-randomized trials of preventive interventions, including for arboviral diseases such as dengue and Zika, through targeted clinic-based enrollment and testing of patients with a specified disease syndrome instead of longitudinal follow-up of large cohorts. Other public health applications in which the CR-TND could prove valuable include the evaluation of mass drug administration for parasitic infections and estimation of both the direct and indirect (“herd”) effects of vaccine-derived immunity in the context of vaccine trials or observational studies, subject to first establishing that the assumptions outlined here are upheld.

Further extensions to this work will refine the approaches to statistical inference and sample-size estimation and will aim to develop methods for individual-level analysis that allow adjustment for individual covariates such as time of recruitment or nonbinary exposure status due to mobility or heterogeneous coverage of the intervention. Extension to nonparallel randomized allocations will also be explored (e.g., where a community-level intervention is deployed using a stepped-wedge design). The first field implementation of the CR-TND, to our knowledge, is a cluster-randomized trial to assess the efficacy of Wolbachia-infected mosquito deployments against dengue in Yogyakarta, Indonesia (ClinicalTrials.Gov: NCT03055585 (47)). This will provide a valuable opportunity to test both the feasibility and validity of the design in practice, generating experience to inform improved design of trials to evaluate preventive interventions for vector-borne diseases and other public health priorities.

Abbreviations

CR-TND

cluster-randomized test-negative design

TND

test-negative design