Implications of the Propensity Score Matching Paradox in Pharmacoepidemiology

Abstract

Recent work has demonstrated that propensity score matching may lead to increased covariate imbalance, even with the corresponding decrease in propensity score distance between matched units. The extent to which this paradoxical phenomenon might harm causal inference in real epidemiologic studies has not been explored. We evaluated the effect of this phenomenon using insurance claims data from the Pharmaceutical Assistance Contract for the Elderly (1999–2002) and Medicaid Analytic eXtract (2000–2007) databases in the United States. For each data set, we created several 1:1 propensity-score–matched data sets by manipulating the size of the covariate set used to generate propensity scores, the index exposure prevalence in the prematched data set, and the matching algorithm. We matched all index units, then progressively pruned matched sets in order of decreasing propensity score distance, calculating covariate imbalance after each pruning. Although covariate imbalance sometimes increased after progressive pruning of matched sets, the application of commonly used propensity score calipers for defining an acceptable match stopped pruning near the lowest region of the imbalance trend and resulted in an improvement over the imbalance in the prematched data set. Thus, propensity score matching does not appear to induce increased covariate imbalance when standard propensity score calipers are applied in these types of pharmacoepidemiologic studies.

Propensity score matching (PSM) is a popular method to control for differences in propensity score distributions in observational research (1–3). Other methods, notably stratification by propensity score, may be preferable with respect to overall efficiency, but PSM remains popular, perhaps owing to its reduction of the matching process to one dimension (2, 4–6). With PSM, index units are matched to reference units with similar propensity score values, even though their underlying covariate profiles might be dissimilar. Even with this underlying dissimilarity, the distributions of observed covariates should be similar, on average, between index and reference units, conditional on the propensity score (5, 7). From a practical perspective, PSM is easily understood among researchers and is easily implemented with available algorithms (8).

King and Nielsen (9) recently argued that PSM should be avoided because of the potential for the “PSM paradox” to degrade causal inference. The paradox, in brief, is that, for data sets that already are well-balanced on measured covariates, pruning of matched sets with the largest propensity score distances between the index and reference units may lead to increased imbalance in the underlying covariate distributions between exposure groups and, thus, to increased bias in the effect estimate.

Because King and Nielsen demonstrated the paradox in data sets with fewer covariates and with better initial covariate balance than what typically is encountered in pharmacoepidemiology, the practical effect of the paradox in pharmacoepidemiologic analyses is not clear.

Here, we have presented a description of the paradox and the results of an analysis of the impact of the paradox in pharmacoepidemiologic applications using insurance claims data. We used methods similar to those used by King and Nielsen in order to track levels of imbalance produced by progressive pruning of matched pairs from data sets in which, initially, all index units are matched. We varied a number of key parameters in the matching process, generating multiple matched data sets. Our intent was to evaluate the practical implications of the theoretical findings of King and Nielsen.

THE PSM PARADOX

The standard approach to 1:1 PSM for a dichotomous exposure is: 1) generate propensity scores corresponding to the estimated probability of receiving the index exposure, conditional on observed covariates, for every unit in a data set (commonly via logistic regression); 2) match a reference unit to each index unit via some algorithm (e.g., nearest-neighbor matching (NNM)); 3) prune from the resulting data set the matched pairs with the largest propensity score distances in order to eliminate poorly matched units and to ensure balanced propensity score distributions (usually via application of a caliper as part of step 2); 4) compare (usually at the univariate level) pre- and postmatched covariate distributions to assess the improvement in covariate balance due to PSM; 5) estimate the effect parameter of interest in the matched data set (10). The key benefit of matching on the propensity score is the dimension reduction that allows for efficient matching on a scalar summary of a potentially large vector of covariates.

Let X be the vector of observed covariates that inform the propensity score model. PSM guarantees balance among the matched sets on the conditional probability of exposure, $\mathrm{Pr}(\mathrm{Exposure}|\mathbf{X})$, but it guarantees balance on X only asymptotically (11, 12). With asymptotic balance, any pruning of matched sets from the resulting data set is expected to be random with respect to underlying covariate balance. The reduction in study size resulting from random pruning could, by chance, increase the underlying X distance between matched units. Thus, although the intent of pruning propensity-score–matched sets is to increase covariate balance, this process could have the opposite effect. By extension, with better covariate balance prior to any matching or pruning, it becomes more likely that balance will begin to deteriorate after only a few prunings. If the same procedure of pruning the worst-matched units is applied in the context of matching on the actual components of X, rather than on the scalar propensity score, an increase in imbalance is not expected because distances between the original covariate values inform the matching and pruning decisions (13–17).

We present a simple example of this phenomenon using only 2 covariates in Table 1. In this population of 12, 4 are exposed to the index exposure and 8 to the reference exposure. The distributions of sex and race in this population are perfectly balanced between the 2 exposure groups. The propensity score for every unit is $\mathrm{Pr}(\mathrm{Index\; Exposure}|\text{Sex},\text{Race})=1/3$. If 1:1 PSM without replacement is performed, there should be no algorithmic preference to match any reference unit to any index unit, because all 12 units have the same propensity score value. There are 70 possible selections of 4 reference units from the pool of 8 reference units to build the matched cohort consisting of 8 total units. Only 16 of those selections will retain perfect covariate balance in the sex-race distribution. Thus, we expect that 77% of the time, covariate balance will be worse after the initial pruning of units via PSM, compared with the balance in the prematched data set. This phenomenon occurs even though the distribution of propensity scores will be perfectly balanced in any matched data set. If either of these 2 covariates is related to outcome, we expect the covariate imbalance to correspond to bias in the treatment effect estimate.

Table 1.

Simple Example of the Propensity Score Matching Paradox

Sex and Racea	Index Exposure (n = 4)	Reference Exposure (n = 8)	Total (n = 12)	Stratum PS
Male
White	1	2	3	0.3
Not white	1	2	3	0.3
Female
White	1	2	3	0.3
Not white	1	2	3	0.3

Abbreviation: PS, propensity score.

^a The example population represented in this table contains index and reference exposure groups that are perfectly balanced on sex and race. The propensity score values for all 12 units are equal. One-to-one propensity score matching without replacement would be expected to increase the underlying covariate imbalance in the matched data set, compared with the prematched data set.

Unlike our example data set, the typical pharmacoepidemiologic claims data set, which comprises a large number of patients and a large number of potential confounders of an association between a drug and health outcome (e.g., corresponding to concomitant medications and comorbidities), is not well-balanced on X before matching (18–20). Thus, we expected to observe a notable improvement in balance after PSM long before pruning could worsen balance.

METHODS

Description of data sets

Two retrospective cohorts were used in these analyses. The first was a cohort of 49,919 low-income Medicare beneficiaries, at least 65 years of age, who were enrolled in the Pharmaceutical Assistance Contract for the Elderly (PACE) database in New Jersey over the years 1999–2002 and who initiated nonselective nonsteroidal antiiinflammatory drugs (NSAIDs) or selective cyclooxygenase-2 (COX-2) inhibitors (21, 22). The PACE cohort was generated to perform an analysis of the effect of selective COX-2 inhibitors, compared with nonselective NSAIDs, on the risk of gastrointestinal complications. Approximately 60% of patients represented in this cohort were selective COX-2 inhibitor initiators. Approximately 2,000 cases of gastrointestinal complication were observed in this cohort.

The second cohort comprised information on 886,996 completed pregnancies and was generated from the Medicaid Analytic eXtract (MAX) over the years 2000–2007 (6, 23, 24). The MAX cohort was used to perform an analysis of the effect of statin use during the first trimester of pregnancy, compared with no use during the first trimester of pregnancy, on the risk of congenital malformation in the infant. Statin use was defined as the existence of at least 1 claim for a dispensed statin within the first trimester. Approximately 0.13% of women represented in this cohort filled a statin prescription during the first trimester. Approximately 30,000 congenital malformations were observed in this cohort.

Creation of matched data sets

We created multiple 1:1-matched data sets using propensity scores generated via logistic regression. In order to relax distributional assumptions for the propensity score models, all continuous variables were categorized. The propensity score models based on PACE predicted the probability of exposure to nonselective NSAIDs (there were fewer nonselective NSAID initiators than selective COX-2 inhibitor initiators), while the propensity score models based on MAX predicted the probability of exposure to statins. Each matched data set represented a different manipulation of: 1) the richness of the covariate set informing the propensity score model, 2) the prevalence of index exposure in the prematched data set, and 3) the matching algorithm.

Covariate set richness

To assess whether increasing the number of covariates in the propensity score model decreases the number of prunings required for covariate imbalance to increase, we used 3 PACE-based covariate sets. The first covariate set, “small,” comprised 19 covariates that were selected based on clinical importance. The second and third covariate sets (“standard” and “large,” respectively) comprised additional covariates (representing concomitant medications, comorbidities, and other medical encounters) selected by a high-dimensional propensity score (HDPS) algorithm (25), in addition to the 19 predetermined covariates. The 50 covariates with the highest bias-based HDPS ranks were included in the “standard” covariate set, and the 100 covariates with the highest bias-based HDPS ranks were included in the “large” covariate set. All models generated from MAX were based on one covariate set comprising 20 categorical covariates, which were selected based on clinical importance.

Prevalence of index exposure in the prematched data set

To determine how the size of the fully matched data set affects covariate balance during matched-set pruning, the index exposure prevalence values of PACE and MAX were varied, via simple random sampling with replacement, but the original data set sizes were retained. Matched data sets were generated from PACE, separately for each of the 3 covariate set scenarios, using the original index exposure prevalence, 50% of the original index exposure prevalence, and 20% of the original index exposure prevalence. Matched data sets were generated from MAX using the original index exposure prevalence, 400% of the original index exposure prevalence, and 700% of the original index exposure prevalence.

Matching algorithm

Because the matching quality may depend on the matching algorithm, we used two 1:1 PSM algorithms that have been used in previous pharmacoepidemiologic analyses: a variation of NNM and a variation of Parson’s digit-based greedy matching (DGM) (8). While the former algorithm attempts to minimize the overall propensity score distance among matched sets, the latter algorithm matches units on decreasing levels of precision, up to the fifth digit of the propensity score, without consideration of overall distance.

Because King et al. (9, 26) referred to Mahalanobis distance matching (MDM) as a potentially better option than PSM for maintaining covariate balance after matching, we also implemented MDM. Like the propensity score, the Mahalanobis distance is a scalar summary of the original covariate space. However, unlike the propensity score, it is a direct representation of distance between units in the actual covariate space, and has the following form:

$$\sqrt{\left[\left({\mathbf{X}}_i-{\mathbf{X}}_j\right)\prime {\sum _{\_}}^{-1}\left({\mathbf{X}}_i-{\mathbf{X}}_j\right)\right]},$$

where i indexes the exposed unit, j indexes the unexposed unit, X is the vector of covariates for a given unit, and $\sum _{\_}$ is the sample covariance matrix of the original data (11). We selected a nearest-neighbor matching algorithm to implement MDM given the popularity of this algorithm for MDM (27, 28).

We constructed 12 unique data sets (9 PACE data sets and 3 MAX data sets) and 36 unique matching scenarios for our analysis. Our manipulation strategy is summarized in Web Figure 1 (available at https://academic.oup.com/aje).

Pruning and assessment of imbalance

For each fully matched data set, matched pairs were ranked in order of decreasing absolute propensity score distance or Mahalanobis distance, and the matched pair with the largest distance was pruned from the data set. Covariate balance was assessed for the remaining data set, then the matched pair with the largest distance in the remaining data set was pruned, and covariate balance was assessed again. This process was repeated until only a single matched pair was left in the data set.

We used 2 metrics to summarize covariate imbalance: the Mahalanobis balance and the C statistic. The Mahalanobis balance is a type of Mahalanobis distance that represents the extent of covariate balance in the actual covariate space, and has the following form:

$$\sqrt{\left[\left({\overline{\mathbf{X}}}_{T1}-{\overline{\mathbf{X}}}_{T0}\right)\prime {\sum _{\_}}^{-1}\left({\overline{\mathbf{X}}}_{T1}-{\overline{\mathbf{X}}}_{T0}\right)\right]},$$

where ${\overline{\mathbf{X}}}_{TK}$ is the vector of covariate means in exposure group k, and $\sum _{\_}$ is the sample covariance matrix of the original data (29, 30). Higher Mahalanobis balance values indicate worse covariate balance. We used the C statistic to determine changes in the discriminatory power of the logistic model predicting index exposure in the matched data set (31, 32). Balance on the covariates in the matched data set should lead to poor ability of the corresponding logistic model to determine which units are exposed (i.e., C statistics near 0.5) (29). Thus, higher C statistic values (greater than 0.5) indicate worse covariate balance.

The points in the pruning process at which 3 absolute propensity-score distance calipers were achieved were marked both for the NNM and DGM scenarios. We selected our calipers from the common range (0.01–0.05) (33). We focused on a 0.05 caliper and then applied the more conservative calipers of 0.025 and 0.01 in order to determine whether the further loss of matched sets would correspond to increased covariate imbalance. Each caliper criterion was satisfied when the maximum propensity score distance between 2 units of a matched pair in a pruned data set was less than the caliper value.

Tracking changes in the effect estimate

We calculated and plotted a point estimate of effect after each pruning. For PACE, we calculated the relative risk estimate corresponding to the effect of nonselective NSAIDs, compared with COX-2 inhibitors, on the risk of gastrointestinal complications. For MAX, we calculated the relative risk estimate corresponding to the effect of statin use during the first trimester of pregnancy, compared with no use during the first trimester of pregnancy, on the risk of congenital malformation. Our goal in generating these graphs was to depict the pattern describing how the paradox might lead to bias in the effect estimate.

RESULTS

We display example covariate distributions for the prematched data set and for the fully matched data sets for PACE in Table 2 and for MAX in Table 3. These tables indicate that covariate balance in the prematched data set was far worse for MAX than for PACE. In both data sets, covariate balance improved after the creation of the fully matched data set. For PACE, improvement was more marked for NNM and DGM than for MDM (Table 2). For MAX, the opposite was true (Table 3). We also analyzed standardized differences and drew the same conclusions (Web Figures 2 and 3) (34).

Table 2.

Example Distributions of the Non–High-Dimensional Propensity Score Covariates in the Prematched Pharmaceutical Assistance Contract for the Elderly Data Set (United States, 1999–2002), “Standard” Covariate Set, Original Index Exposure Prevalence Data Set, and in the 3 Corresponding Fully Matched Data Sets

Covariate	Prematched (n = 49,653)				Full, NNM		Full, DGM		Full, MDM
	Nonselective NSAIDs (n = 17,611)a		Selective COX-2 Inhibitors (n = 32,042)		Selective COX-2 Inhibitors (n = 17,611)		Selective COX-2 Inhibitors (n = 17,611)		Selective COX-2 Inhibitors (n = 17,611)
	Mean (SD)	%	Mean (SD)	%	Mean (SD)	%	Mean (SD)	%	Mean (SD)	%
Age	77.79 (7.30)		79.76 (7.24)		78.15 (7.24)		78.16 (7.23)		78.95 (7.06)
No. of generics prescribed	7.43 (5.02)		8.41 (5.25)		7.56 (5.02)		7.60 (5.03)		6.75 (4.17)
No. of medical visits	7.74 (6.61)		8.60 (6.67)		7.86 (6.53)		7.90 (6.59)		6.96 (5.32)
Charlson Comorbidity Index score	1.85 (1.97)		2.05 (2.01)		1.85 (1.95)		1.87 (1.96)		1.47 (1.58)
Male sex		18.84		14.09		17.47		17.50		13.43
Race
White		89.76		95.45		92.94		92.86		94.61
Black		8.97		3.54		5.91		5.96		4.15
Other		1.27		1.02		1.15		1.19		1.24
Comorbidities
Bleeding		1.11		1.72		1.15		1.25		1.08
CHF		24.58		30.36		24.76		25.17		18.80
Coronary disease		14.78		16.43		14.89		14.87		9.60
Hypertension		70.20		72.82		70.18		70.29		70.82
Rheumatoid arthritis		2.70		5.00		3.02		2.84		2.54
Osteoarthritis		33.49		48.53		35.16		35.01		41.23
Ulcer		2.42		3.71		2.58		2.58		2.14
Hospitalization in prior year		26.07		30.60		26.47		26.90		17.86
Nursing home resident		5.66		8.34		6.18		6.23		3.64
Other medications
Corticosteroid		7.80		8.74		8.08		8.17		5.48
Other gastrointestinal medication		20.44		27.42		21.70		21.75		20.28
Warfarin		6.55		13.27		7.00		7.02		5.95
Year of exposure initiation
1999		48.79		41.68		47.09		47.11		43.21
2000		23.91		29.94		24.90		24.79		29.10
2001		20.00		21.28		20.49		20.73		21.08
2002		7.30		7.09		7.52		7.38		6.62

Abbreviations: CHF, congestive heart failure; COX-2, cyclooxygenase-2; DGM, digit-based greedy matching; MDM, Mahalanobis distance matching; NNM, nearest-neighbor matching; NSAID, nonsteroidal antiiinflammatory drug; SD, standard deviation.

^a The nonselective NSAIDs covariate distribution is shown only once, because this distribution was the same in each data set.

Table 3.

Example Distributions (Percentage) of All Covariates in the Prematched Medicaid Analytic eXtract Data Set (United States, 2000–2007), Original Index Exposure Prevalence Data Set, and in the 3 Corresponding Fully Matched Data Sets

Covariate	Prematched (n = 886,996)		Full, NNM	Full, DGM	Full, MDM
	Statins (n = 1,152)a	No Statins (n = 885,844)	No Statins (n = 1,152)	No Statins (n = 1,152)	No Statins (n = 1,152)
Age category, years
≤19	5.56	29.43	5.21	4.25	5.21
20–24	14.06	35.6	12.76	14.41	14.24
25–29	21.09	20.41	21.96	22.31	22.74
30–34	28.13	9.48	28.91	28.65	27.34
35–39	22.22	4.17	21.96	21.61	21.53
≥40	8.94	0.91	9.20	8.77	8.94
Race
Asian/other Pacific Islander	6.51	3.42	6.42	5.90	5.38
Black/African American	25.69	34.09	22.92	24.31	27.95
Hispanic/Latino	17.10	15.08	21.09	17.88	17.88
Other	5.73	4.74	6.08	7.47	4.86
Unknown	2.95	2.01	3.39	3.21	2.78
White	42.01	40.67	40.10	41.23	41.15
US region
Midwest	23.18	32.02	22.48	20.92	24.39
Northeast	21.27	14.97	20.57	22.83	18.75
South	26.04	26.07	24.13	26.13	26.48
West	29.51	26.94	32.81	30.12	30.38
No. of nonantihypertensive generics used
0	8.33	46.45	6.25	7.29	10.76
1–3	27.00	36.64	30.30	28.39	28.21
>3	64.67	16.91	63.45	64.32	61.02
No. of physician visits during the preindex period
0	27.08	52.07	25.78	25.52	25.87
1–3	49.91	39.52	51.82	51.48	53.39
>3	23.00	8.41	22.40	23.00	20.75
Year of delivery
2000	0.00	0.14	0.00	0.00	0.00
2001	4.17	9.65	4.51	4.25	3.39
2002	5.56	11.04	6.34	4.77	6.34
2003	10.42	14.59	10.33	9.72	10.33
2004	19.10	17.61	18.23	18.92	17.36
2005	20.14	16.88	20.23	20.23	20.31
2006	23.78	17.49	21.18	24.05	24.74
2007	16.84	12.60	19.18	18.06	17.53
Comorbidities
Hypertension	40.63	5.00	39.76	40.97	40.02
Diabetes	45.14	3.06	40.71	41.75	45.14
Renal disease	4.17	0.46	3.91	3.82	4.17
Obesity	23.35	5.31	23.87	25.26	23.35
Tobacco use	11.02	7.77	10.16	11.11	8.85
Alcohol abuse	3.99	2.61	4.60	4.69	3.13
Illicit drug use	6.42	5.33	6.60	6.68	5.38
Dyslipidemia	67.10	3.14	71.09	71.53	66.58
Multiple gestation	6.60	3.55	6.16	7.03	5.64
Multipara	88.80	75.69	88.02	88.54	92.01
Other medications
Insulin	30.47	1.24	26.30	25.95	30.47
Antidiabetic medication	38.80	1.27	33.94	34.29	38.80
Hypertension medication	53.73	6.65	52.52	50.95	52.78
Potentially teratogenic medication	31.68	3.63	29.08	28.47	30.30

Abbreviations: DGM, digit-based greedy matching; MDM, Mahalanobis distance matching; NNM, nearest-neighbor matching.

^a The statins covariate distribution is shown only once, because this distribution was the same in each data set.

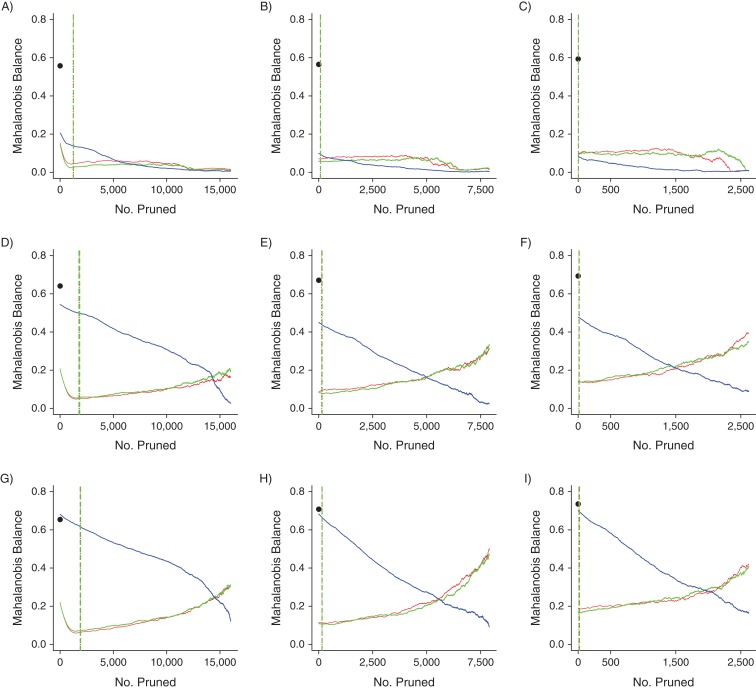
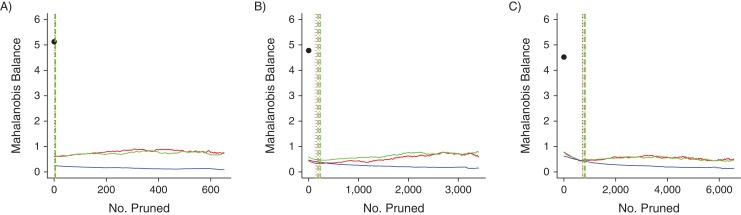
We display all Mahalanobis balance metric trend graphs for PACE and MAX in Figures 1 and 2, respectively. The C statistic metric trend graphs were similar and are displayed in Web Figures 4 and 5 for PACE and MAX, respectively. We also present zoomed-in versions of Figures 1 and 2 in Web Figures 6 and 7, respectively.

Figure 1.

Mahalanobis balance metric trends for the 9 data sets based on data from Pharmaceutical Assistance Contract for the Elderly, United States, 1999–2002. A) “Small” covariate set, original index exposure prevalence (IEP); B) “small” covariate set, 50% of IEP; C) “small” covariate set, 20% of IEP; D) “standard” covariate set, IEP; E) “standard” covariate set, 50% of IEP; F) “standard” covariate set, 20% of IEP; G) “large” covariate set, IEP; H) “large” covariate set, 50% of IEP; I) “large” covariate set, 20% of IEP. The black dots indicate the Mahalanobis balance values of the prematched data sets. Red lines indicate propensity-score nearest-neighbor matching trends; green lines indicate propensity-score digit-based greedy-matching trends; and blue lines indicate Mahalanobis-distance matching trends. The dotted and dashed vertical lines (for propensity-score nearest-neighbor matching and propensity-score digit-based greedy matching, respectively) mark the 6 points at which the propensity score matching trends first met the 0.05, 0.025, and 0.01 absolute propensity score distance caliper criteria (vertical line colors correspond to trend colors). The caliper criteria were always met in the order 0.05, 0.025, and 0.01 during the pruning process.

Figure 2.

Mahalanobis balance metric trends for the 3 data sets based on data from Medicaid Analytic eXtract, United States, 2000–2007. A) Original index exposure prevalence (IEP); B) 400% of IEP; C) 700% of IEP. The black dots indicate the Mahalanobis balance values of the prematched data sets. Red lines indicate propensity-score nearest-neighbor matching trends; green lines indicate propensity-score digit-based greedy-matching trends; and blue lines indicate Mahalanobis-distance matching trends. The dotted and dashed vertical lines (for propensity-score nearest-neighbor matching and propensity-score digit-based greedy matching, respectively) mark the 6 points at which the propensity score matching trends first met the 0.05, 0.025, and 0.01 absolute propensity score distance caliper criteria (vertical line colors correspond to trend colors). The caliper criteria were always met in the order 0.05, 0.025, and 0.01 during the pruning process.

In each panel of Figures 1 and 2, the fully matched data sets produced by NNM and by DGM had much better covariate balance than the corresponding prematched data set, although this was not always the case for MDM—in one case, balance actually was worse for MDM in the fully matched data set (Figure 1G). Moreover, the points at which the caliper criteria were met were always near the lowest regions of the NNM and DGM trend lines. These results indicate that if a typical caliper on the absolute propensity score scale in the range (0.01–0.05) had been required after NNM or DGM, before performing inference on these data, the covariate balance in the corresponding pruned data set would always have been near optimal (at least, as measured by the Mahalanobis balance). However, even though NNM and DGM always greatly improved covariate balance with respect to the prematched data sets after only a few prunings, covariate imbalance did eventually increase after further pruning in certain cases.

Covariate set richness

For the PACE NNM- and DGM-matched data sets, for a given index exposure prevalence, fewer prunings were required for covariate imbalance to increase as the number of covariates used to construct the corresponding propensity score model increased (Figure 1). This result is demonstrated by the fact that the imbalance trends increased more quickly during the pruning process as the number of covariates increased, by the fact that the Mahalanobis balance value of the fully matched data set increased as the number of covariates increased, or both. A similar trend occurred for the PACE MDM-matched data sets. As the number of covariates used to perform MDM increased, the Mahalanobis balance value of the fully matched data set increased. Finally, increasing the number of covariates used to construct the propensity score model generally increased the number of prunings required to achieve the caliper criteria (Web Figure 6).

Prevalence of index exposure in the prematched data set

No consistently strong trends in imbalance across index exposure prevalence levels were noted, although the largest index exposure prevalence scenarios for PACE and MAX always required more prunings to minimize imbalance. This relation was especially clear for PACE (Figure 1A, 1D, and 1G). Also, for a given covariate set size, lower index exposure prevalence values always corresponded to fewer prunings required to achieve the caliper criteria (Web Figures 6 and 7).

Matching algorithm

The differences between the performances of NNM and DGM in reducing imbalance were not substantial in any scenario. For MAX, MDM performed better overall than NNM and DGM with respect to maintaining low covariate imbalance (Figure 2). However, for PACE, as the number of covariates used to build the propensity score model increased, MDM performance became increasingly worse, as evidenced by the elevated MDM trend lines (Figure 1). Finally, all MDM imbalance trends were effectively monotonic decreasing, whereas the paradox was visible in some cases for the NNM and DGM trends.

Tracking changes in the effect estimate

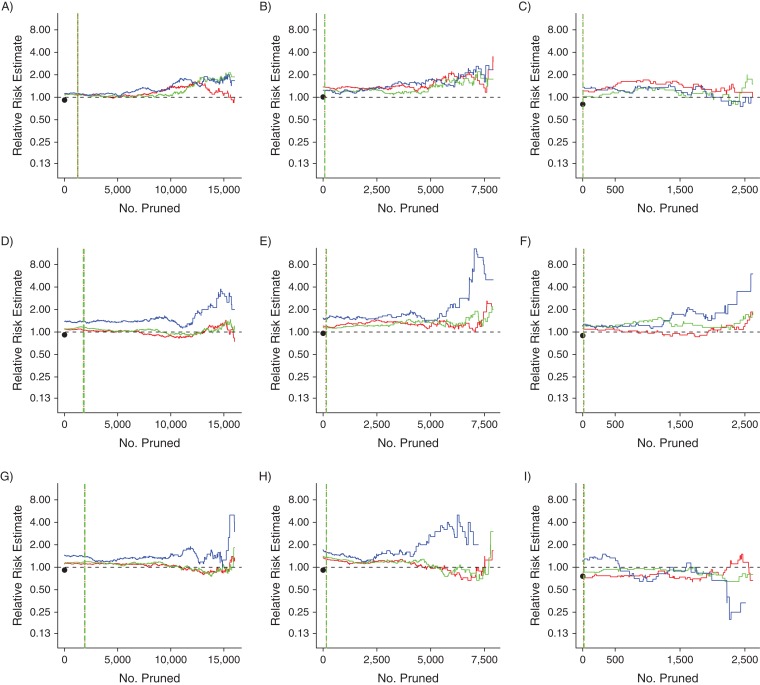
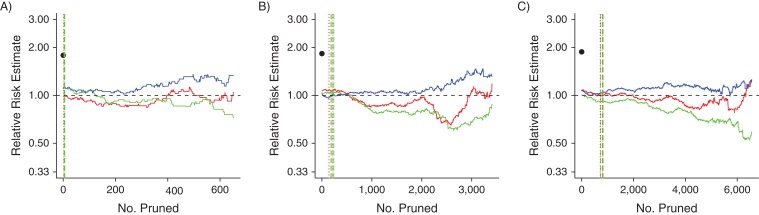
The relative risk estimate trends for PACE and MAX are displayed in Figures 3 and 4, respectively. We found that, in general, the NNM and DGM trends were similar, especially at the left-most portion of each panel (i.e., in the caliper regions). For PACE, in the larger covariate set scenarios, the MDM trends indicated relative risk estimates further from the null than did the NNM and DGM trends, whereas in the “small” PACE scenarios and in all MAX scenarios, all 3 algorithms produced similar relative risk estimates early in the pruning process. These findings corresponded to the findings regarding imbalance. Finally, in most cases, there was a clear difference between the prematched relative risk estimate and the relative risk estimates early in the pruning process. This difference also corresponded to the clear differences in imbalance among the data sets (e.g., compare Figure 4A with Figure 2A).

Figure 3.

Relative risk estimate trends for the 9 data sets based on data from Pharmaceutical Assistance Contract for the Elderly, United States, 1999–2002. A) “Small” covariate set, original index exposure prevalence (IEP); B) “small” covariate set, 50% of IEP; C) “small” covariate set, 20% of IEP; D) “standard” covariate set, IEP; E) “standard” covariate set, 50% of IEP; F) “standard” covariate set, 20% of IEP; G) “large” covariate set, IEP; H) “large” covariate set, 50% of IEP; I) “large” covariate set, 20% of IEP. A dashed horizontal black line at the relative risk estimate value of 1.00 is included for reference. The black dots indicate the relative risk estimates of the prematched data sets. Red lines indicate propensity-score nearest-neighbor matching trends; green lines indicate propensity-score digit-based greedy-matching trends; and blue lines indicate Mahalanobis-distance matching trends. The dotted and dashed vertical lines (for propensity-score nearest-neighbor matching and propensity-score digit-based greedy matching, respectively) mark the 6 points at which the propensity score matching trends first met the 0.05, 0.025 and 0.01 absolute propensity score distance caliper criteria (vertical line colors correspond to trend colors). The caliper criteria were always met in the order 0.05, 0.025, and 0.01 during the pruning process.

Figure 4.

Relative risk estimate trends for the 3 data sets based on data from Medicaid Analytic eXtract, United States, 2000–2007. A) Original index exposure prevalence (IEP); B) 400% of IEP; C) 700% of IEP. A dashed horizontal black line at the relative risk estimate value of 1.00 is included for reference. The black dots indicate the relative risk estimates of the prematched data sets. Red lines indicate propensity-score nearest-neighbor matching trends; green lines indicate propensity-score digit-based greedy-matching trends; and blue lines indicate Mahalanobis-distance matching trends. The dotted and dashed vertical lines (for propensity-score nearest-neighbor matching and propensity-score digit-based greedy matching, respectively) mark the 6 points at which the propensity score matching trends first met the 0.05, 0.025 and 0.01 absolute propensity score distance caliper criteria (vertical line colors correspond to trend colors). The caliper criteria were always met in the order 0.05, 0.025, and 0.01 during the pruning process.

DISCUSSION

PSM greatly improved covariate balance compared with balance in the prematched data set. The points at which our caliper criteria would have been met were always near the lowest points on the imbalance trends, indicating that matched data sets constructed from these data by many would have corresponded to excellent covariate balance. Although imbalance increased with further pruning when the propensity score model was based on a higher number of covariates, this phenomenon occurred only after pruning more matched sets than would have been required to achieve our caliper criteria. Moreover, although MDM led to near-monotonic decreasing imbalance trends, PSM achieved better covariate balance with fewer prunings and much larger matched data set sizes for the larger covariate set scenarios.

The fact that the paradox was clearer in the larger covariate set scenarios was not surprising. When more covariates are used to build the underlying propensity score model, there is a greater probability that different individuals with similar propensity score values will have more dissimilar underlying covariate profiles, thus increasing the chance that balance will deteriorate after only a few prunings (9). A similar logic applies to our finding that, in general, more prunings were required to achieve the caliper criteria when the underlying propensity score model was based on a larger vector of covariates. Even so, matching on the propensity score based on a larger vector of covariates always provided a great improvement in covariate balance in the caliper-matched data set compared with the prematched data set—more so than MDM.

We found that manipulation of the index exposure prevalence affected the balancing of propensity score distributions more than the balancing of the underlying covariate distributions. For both NNM and DGM, the fact that the caliper criteria were always achieved with fewer prunings as the index exposure prevalence decreased was not surprising when considered from the perspective of balancing propensity score distributions. Lower index exposure prevalence equates to a higher probability of a single index unit finding a good reference unit match on the propensity score simply because, for a given study size, the pool of reference units is relatively larger when the index exposure prevalence is lower. However, it was difficult to perceive a clear effect on the underlying covariate balance, as evinced by the fact that the imbalance trend shapes did not change much as the index exposure prevalence was altered.

For our analyses, the PSM algorithm was not an important indicator of the appearance of the paradox, although previous studies comparing NNM with DGM have suggested a preference for NNM over DGM with respect to bias (8).

The monotonicity of the MDM trends also was not surprising (26). The failure of MDM to achieve adequate covariate balance early in the pruning process with more covariates may be attributed to known issues with MDM (30, 35–37). It has been suggested that higher dimensions diminish the efficiency of MDM because, unlike the logit-based PSM, MDM attempts to match units while regarding all interactions in the covariate space as equally important. Thus, having more covariates equates to having more complicated interactions to balance. This phenomenon may explain our finding that certain covariates were balanced differently after MDM compared with NNM and DGM and that the relative risk estimates were usually different for MDM, compared with NNM and DGM, with larger covariate sets (Web Figures 2 and 3; Figures 3 and 4). Thus, PSM may be the better option for the high-dimensional matching scenarios that are common to pharmacoepidemiologic research.

During matching, only covariate distribution imbalance and study size may be controlled directly, although the bias-variance trade-off for effect estimation certainly may be affected by the imbalance-study size tradeoff (26). Thus, it is difficult to make strong statements regarding our effect estimate trends. Even so, in general there were no large differences between the relative risk estimates from NNM and DGM early in the pruning process, whereas MDM produced clearly different relative risk estimates when based on larger covariate set sizes.

We conclude that in our claims data, PSM in its conventional application would not have harmed covariate balance in the manner predicted based on King and Nielsen’s work. Although our findings conform to King and Nielsen’s description of the paradox, implementing either version of PSM in our data sets with any standard absolute propensity-score distance caliper resulted in very good balance and preservation of sample size. Conversely, the utility of MDM depended on the prematched data set and resulted in either excellent balance with few prunings or excellent balance only after pruning a very large portion of the matched data set.

Although we analyzed a limited set of conditions, we focused on data and techniques that are common in pharmacoepidemiology. Thus, our results bear important implications for applied researchers. Specifically, our results indicate that the paradox might not arise for situations in which the prematched data set has high covariate imbalance and in which a reasonable absolute propensity-score distance caliper is applied. We expect that the paradox should be a practical concern only when the prematched data set has very low covariate imbalance, such that covariate balance worsens either after the full match or after only a few prunings, as in our simple example, or in the unlikely scenario in which pruning is allowed to continue well beyond the point at which a reasonable absolute propensity-score distance caliper would stop the pruning process, as in our example studies. We stress the importance of checking covariate balance after PSM in order to identify any increase in covariate imbalance—at the very least, via a univariate comparison of the pre- and postmatched covariate distributions. Finally, existing algorithms may be used to explore imbalance trends in order to identify disagreements between propensity score distribution balance and covariate balance (38).

Abbreviations

COX-2

cyclooxygenase-2

DGM

digit-based greedy matching

MAX

Medicaid Analytic eXtract

MDM

Mahalanobis distance matching

NNM

nearest-neighbor matching

NSAID

nonsteroidal antiiinflammatory drug

PACE

Pharmaceutical Assistance Contract for the Elderly

PSM

propensity score matching