Abstract
The emergence of highly resistant bacteria is a serious threat to global public health. The host immune response is vital for clearing bacteria from the infected host; however, the current drug development paradigm does not take host‐pathogen interactions into consideration. Here, we used a systems‐based approach to develop a quantitative, mechanism‐based disease progression model to describe bacterial dynamics, host immune response, and lung injury in an immunocompetent rat pneumonia model. Previously, Long‐Evans rats were infected with Acinetobacter baumannii (A. baumannii) strain 307‐0294 at five different inocula and total lung bacteria, interleukin‐1beta (IL‐1β), tumor necrosis factor‐α (TNF‐α), cytokine‐induced neutrophil chemoattractant 1 (CINC‐1), neutrophil counts, and albumin were quantified. Model development was conducted in ADAPT5 version 5.0.54 using a pooled approach with maximum likelihood estimation; all data were co‐modeled. The final model characterized host‐pathogen interactions during the natural time course of bacterial pneumonia. Parameters were estimated with good precision. Our expandable model will integrate drug effects to aid in the design of optimized antibiotic regimens.
Study Highlights.
WHAT IS THE CURRENT KNOWLEDGE ON THE TOPIC?
☑ Previous studies have performed simulations using published literature values to describe host‐pathogen interactions. Modeling the time course of measured biomarkers of the infectious process using a systems‐based approach remains largely unexplored.
WHAT QUESTION DID THIS STUDY ADDRESS?
☑ Can we develop a mechanism‐based model to quantitatively describe the host‐pathogen interactions during the pathogenesis of bacterial pneumonia using an immunocompetent rat pneumonia model of infection in the absence of treatment?
WHAT DOES THIS STUDY ADD TO OUR KNOWLEDGE?
☑ The mechanism‐based disease progression model describes the time course of A. baumannii pneumonia and host‐pathogen interactions by characterizing the interplay among bacterial dynamics, host immune responses, and lung injury.
HOW MIGHT THIS CHANGE DRUG DISCOVERY, DEVELOPMENT, AND/OR THERAPEUTICS?
☑ The mechanism‐based model can be used to integrate the contribution of the host immune system for designing in vivo antibiotic PK/PD studies. The model can be expanded to incorporate additional mechanistic details providing an in‐depth understanding of the underlying biology of pneumonia and enabling the model‐based development of antibiotics and design of novel treatment regimens.
Lower respiratory tract infections are the third most common cause of death worldwide.1 Bacterial pneumonia is an acute lower respiratory tract infection caused by bacteria such as Acinetobacter baumannii (A. baumannii). The global emergence of multidrug resistant gram‐negative bacteria combined with a dwindling drug pipeline complicates the selection and design of effective antibiotic therapy.2 Current translational research primarily optimizes existing antibiotics against these hard‐to‐treat pathogens using in vitro and in vivo infection pharmacokinetic (PK) and pharmacodynamic (PD) models of drugs and bacteria. In vitro models of infection include static time‐kill, dynamic one‐compartment, and hollow‐fiber systems; in vivo infection models typically utilize neutropenic mice.3, 4
However, current preclinical translational designs and models fail to take the host immune response, which is key to initiating bacterial clearance and clinical outcome, into account. The interaction between the invading bacterial pathogen and host innate immune system is the principal pathway for elimination of virulent extracellular gram‐positive and gram‐negative pathogens from the lung, tipping the immune balance toward inflammation. Toll‐like receptor‐4, pattern recognition receptors present on host alveolar macrophages and bronchial epithelial cells, recognizes lipopolysaccharide, a pathogen‐associated molecular pattern present on the outer membrane of gram‐negative bacteria, and dictates the natural progression of bacterial pneumonia.5 This receptor‐mediated signaling plays a crucial role in the innate immune responses that ensue by activation of nuclear factor‐κB (NF‐κB). The NF‐κB signaling pathway in macrophages regulates the expression of pro‐inflammatory cytokines, such as tumor necrosis factor‐α (TNF‐α) and interleukin‐1β (IL‐1β), to initiate the inflammatory response, and the subsequent recruitment of polymorphonuclear leukocytes to the lungs.6, 7, 8 Resident alveolar macrophages and recruited neutrophils are essential in the host defense against bacterial pneumonia.9, 10
As the clinical outcome of patients with pneumonia depends on the interplay among bacterial virulence, drug effect, and host immune response, integrating host‐pathogen interactions into the design and optimization of antibiotic treatment regimens is important. Mathematical modeling provides a means to incorporate and evaluate the impact of the immune response on the evolution and resolution of bacterial infection. Previous mathematical models of infection have explored the role of the immune response in infection.11, 12, 13, 14, 15 However, given the complexity of the immune response and the lack of measured immune components, these studies are largely theoretical in nature.
High‐quality, quantified immune response time course data would facilitate the development of more mechanistic systems models.16 A quantitative systems‐based approach has the potential to provide a comprehensive mechanistic understanding of host‐pathogen interactions during the pathogenesis of bacterial pneumonia and assist in the design of therapeutic optimization studies. Thus, the objective of our study was to develop a mechanism‐based model to quantitatively describe the interactions among (i) bacterial dynamics, (ii) the host immune response, and (iii) lung injury in an immunocompetent rat pneumonia model of infection. This base model can be expanded to include the effects of antibiotics on the host‐pathogen interactions.
Methods
Pathogenesis data
We previously conducted bacterial pneumonia studies in immunocompetent rats.17 In brief, a clinical isolate of A. baumannii (strain 307‐0294) was introduced into the lungs of Long‐Evans rats via intratracheal instillation. Rats were challenged with five different initial inocula: 7.00 × 106, 5.76 × 107, 3.50 × 108, 4.32 × 108, and 7.65 × 109 colony forming units (cfu)/mL, with 18 animals per inoculum. During the time course of infection, terminal sampling was performed and rats were euthanized at 3, 6, 24, 48, 72, and 168 hours postinoculation for bronchoalveolar lavage fluid (BALF) and lung explants. Three animals were euthanized at each time point. The total lung bacterial burden was quantified as the sum of bacteria in the lung homogenate and BALF. The host immune response in the lung was quantified by measuring IL‐1β, TNF‐α, cytokine‐induced neutrophil chemoattractant‐1 (CINC‐1), and neutrophil counts in BALF (neutrophil counts not measured in the 7.65 × 109 cfu/mL inoculum group). Lung injury was assessed by measuring BALF albumin concentrations, which represent vascular leakage into the alveolar spaces.17, 18
Model development
A mechanism‐based disease progression model was developed to describe the time courses of:
Bacterial dynamics: bacterial replication, natural death, and clearance by neutrophils;
Host immune response: bacterial stimulation of pro‐inflammatory cytokines and stimulation of neutrophil recruitment by pro‐inflammatory cytokines; and
Lung injury: albumin leakage dependent on pro‐inflammatory cytokine expression.
The model was based on acute processes during the pathogenesis of bacterial pneumonia.
Modeling was performed using ADAPT5 version 5.0.54.19 The model was developed using a pooled approach (naïve pooled data module) with maximum likelihood estimation. Samples from multiple animals in each inoculum group were pooled, and all data were comodeled. Simultaneously modeled data included: five different inocula with six different disease progression biomarkers per inoculum; (i) bacterial burden; (ii) IL‐1β, (iii) TNF‐α, and (iv) CINC‐1 expression; (v) neutrophil recruitment; and (vi) albumin leakage. The residual variance models were defined as:
where is the error variance at the ith observation, and are variance model parameters, and is the fitted value of the observation. A separate variance model was used for each biomarker. For biomarkers in the logarithmic domain (bacterial burden and neutrophils), the variance models were defined as:
where is the error variance of the ith log(observation) and is a variance model parameter. A bottom‐up approach was used for model development where individual components were added one after another. Various mechanism‐based disease progression models were proposed, fitted, and compared. When transit compartments were included, the number of transit compartments was optimized by performing model discrimination after evaluating a range of one to five compartments. Selection criteria during model development were based on visual inspection of the fitted curves, goodness‐of‐fit plots, sum of squared residuals, the Akaike information criterion, and standard errors (SE%) of the estimated parameters. Overall r2 for each of the different inocula was calculated for each biomarker by pooling the observed vs. predicted values.19
Results
Model structure
The schematic of the mechanism‐based disease progression model is shown in Figure 1. Intra‐tracheal bacterial (CFU) challenge activates the NF‐κB pathway, which subsequently triggers a pro‐inflammatory immune response and production of IL‐1β and TNF‐α. Both pro‐inflammatory cytokines play a vital role in the recruitment of neutrophils (N) to the lungs. The TNF‐α recruits neutrophils by stimulating lung epithelial cells to secrete chemokines, such as CINC‐1. The pro‐inflammatory response is regulated by anti‐inflammatory cytokines (ACs). An overactive pro‐inflammatory response damages the lung epithelial‐endothelial permeability barrier resulting in BALF albumin (ALB), a measure of lung injury.
Figure 1.
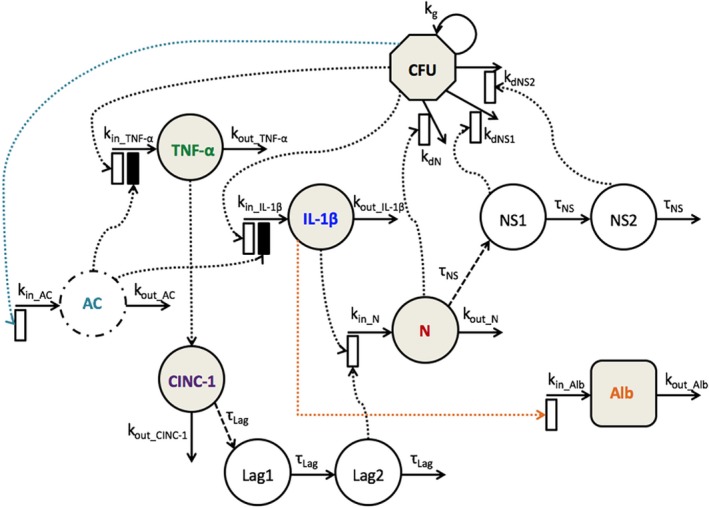
Schematic of the mechanism‐based disease progression model incorporating bacterial burden (CFU), proinflammatory cytokines (interleukin‐1beta (IL‐1β), tumor necrosis factor‐α (TNF‐α), and cytokine‐induced neutrophil chemoattractant 1 (CINC‐1)), an anti‐inflammatory cytokine (AC), neutrophils (N), neutrophil signaling (NS1 and NS2), and albumin (ALB). Shaded compartments indicate measured components. Open and solid boxes represent stimulatory and inhibitory effects. The model is described by Eqs. 1–11 with parameters defined in Table 1.
Bacterial dynamics
CFU dynamics were described by:
| (1) |
where is bacterial concentration in cfu/mL, is the first‐order rate constant for bacterial growth, is the number of neutrophils, and represent neutrophil signaling, is the second‐order rate constant for bacterial killing by neutrophils, and are second‐order rate constants for bacterial killing by neutrophil signaling, and is the initial bacterial burden.
Host immune response
IL‐1β and TNF‐α expression were described using indirect response models20 with capacity‐limited stimulation by bacterial burden (CFU). AC was included as an unobserved variable also characterized by an indirect response model with capacity‐limited stimulation by CFU. AC acts by inhibiting the rate of production of both IL‐1β and TNF‐α. The expression of these cytokines was described as:
| (2) |
| (3) |
| (4) |
where ‐ , ‐ , and are cytokine concentrations in pg/mL, is the zero‐order production rate constant of the cytokine, is the first‐order loss rate constant of the cytokine, is the maximum stimulatory effect of bacteria on cytokine expression (capacity constant), is the bacterial concentration at which half‐maximal effect is achieved (sensitivity constant), is the scaling factor for the inhibitory effect exerted by AC on the pro‐inflammatory cytokine expression, and ‐ , ‐ , and are cytokine concentrations at baseline. The system was assumed to be at steady‐state at time zero, yielding estimates of , , and (secondary parameters) as ‐ , ‐ , and , respectively.
CINC‐1 chemokine expression was described by:
| (5) |
where ‐ is the CINC‐1 concentration in pg/mL, is the scaling factor for the stimulatory effect of TNF‐α on CINC‐1 expression, is the first‐order loss rate constant of CINC‐1, and ‐ is the CINC‐1 concentration at baseline.
Neutrophil recruitment was described using an indirect response model with linear stimulation by IL‐1β and CINC‐1 on the rate of production of N. Transit compartments were included to capture the time delay between CINC‐1 expression and neutrophil recruitment. Neutrophil dynamics were described by:
| (6) |
| (7) |
| (8) |
where and are transit steps, is the first‐order transit rate between steps, ( is the mean transit time of each transit step), is the number of neutrophils, is the zero‐order production rate constant of neutrophils, is the first‐order loss rate constant of neutrophils, and are scaling factors for stimulatory effect of IL‐1β and CINC‐1 on neutrophil recruitment, and is the neutrophil count at baseline.
Neutrophil signaling was modeled using transit compartments and described by:
| (9) |
| (10) |
where and are transit compartments, and is the first‐order transit rate between steps ( is the mean transit time).
Lung injury
Albumin leakage was characterized using an indirect response model with linear stimulation by IL‐1β on rate of production, described as:
| (11) |
where is albumin concentration in mcg/mL, is the zero‐order production rate constant of albumin, is the first‐order loss rate constant of albumin, is the scaling factor for stimulatory effect of IL‐1β on albumin leakage, and is the baseline albumin concentration.
Baseline values of all disease progression biomarkers were fixed to experimental values (Table 1) and were comparable to previous studies performed in Long‐Evans rats.17, 21, 22 The initial bacterial burdens ( ) were fixed to the initial inocula (7.00 × 106, 5.76 × 107, 3.50 × 108, or 4.32 × 108) except for the 7.65 × 109 cfu/mL inoculum, which was fixed to 1.00 × 109 cfu/mL. This was based on the assumption that the high bacterial load introduced intratracheally did not completely seed, as suggested by the data (Figure 2 a (v); 0 and 3 hours). The variance parameters and were fixed to 0.01 and 0.10 for IL‐1β, TNF‐α, CINC‐1, and ALB residual variance models. For CFU and N residual variance models, was fixed to 0.30.
Table 1.
Parameter estimates for the mechanism‐based disease progression model
| Parameter | Description | Estimate | SE% | |
|---|---|---|---|---|
| Bacterial dynamics | ||||
| kg (h‐1) | Firstt order rate constant for net bacterial growth | 0.327 | 3.95 | |
| log ( (cells‐1 h‐1)) | Second order rate constant for bacterial killing by N | −7.71a | 0.05 | |
| log ( (cells‐1 h‐1)) | Second order rate constant for bacterial killing by NS1 | −7.48a | 0.06 | |
| log ( (cells‐1 h‐1)) | Second order rate constant for bacterial killing by NS2 | −7.00a | 0.33 | |
| (cfu/mL) | Initial bacterial burden | ‐b | Fixedc | |
| Host immune response | ||||
| (h‐1) | First order loss rate constant for IL‐1β | 0.122 | 3.68 | |
|
|
Capacity constant for CFU stimulating IL‐1β | 94.7 | 5.46 | |
| log ( (cfu/mL)) | Sensitivity constant for CFU stimulating IL‐1β (low/high inoc) | 7.21/8.89a | 0.43/0.35 | |
| (mL/pg) | Scaling factor for IL‐1β inhibition by AC | 6.48 × 10‐4 | 226 | |
| ‐ (pg/mL) | Baseline IL‐1β concentration | 48 | Fixedc | |
| (h‐1) | First order loss rate constant for TNF‐α | 0.205 | 6.14 | |
|
|
Capacity constant for CFU stimulating TNF‐α | 64.2 | 5.14 | |
| log ( (cfu/mL)) | Sensitivity constant for CFU stimulating TNF‐α (low/high inoc) | 8.06/8.20a | 0.27/0.43 | |
| (mL/pg) | Scaling factor for TNF‐α inhibition by AC | 0.02 | 0.007 | |
| ‐ (pg/mL) | Baseline TNF‐α concentration | 20 | Fixedc | |
| (h‐1) | First order loss rate constant for AC | 0.101 | 6.18 | |
|
|
Capacity constant for CFU stimulating AC | 57.9 | 6.08 | |
| log ( (cfu/mL)) | Sensitivity constant for CFU stimulating AC (low/high inoc) | 8.96/8.92a | 1.10/0.67 | |
| (pg/mL) | Baseline AC concentration | 48 | Fixedc | |
| (h‐1) | First order loss rate constant for CINC‐1 | 1.75 | 12.5 | |
| (h‐1) | Scaling factor for CINC‐1 stimulation by TNF‐α | 4.12 | 12.4 | |
| ‐ (pg/mL) | Baseline CINC‐1 concentration | 30 | Fixedc | |
| (h‐1) | First order transit rate for N recruitment delay by CINC‐1 | 0.044 | 4.80 | |
| (cells/h) | Production rate constant for N | 6.61 × 105 | 17.8 | |
| (h‐1) | First order loss rate constant for N | 1.12 | 16.3 | |
| (mL/pg) | Scaling factor for N stimulation by IL‐1β (low/high inoc) | 2.52 × 10‐2/6.51 × 10‐3 | 10.3/9.55 | |
| (mL/pg) | Scaling factor for N stimulation by CINC‐1 | 4.93 × 10‐4 | 11.3 | |
| (cells) | Baseline N count | 28,230 | Fixedc | |
| (h‐1) | First order transit rate for NS | 6.36 × 10‐3 | 6.3 | |
| Lung injury | ||||
| (mcg/mL/h) | Production rate constant for ALB | 1,012 | 7.9 | |
| (h‐1) | First order loss rate constant for ALB | 0.705 | 8.08 | |
| (mL/pg) | Scaling factor for ALB stimulation by IL‐1β | 9.77 × 10‐4 | 4.83 | |
| (mcg/mL) | Baseline ALB concentration | 125 | Fixedc | |
AC, anti‐inflammatory cytokine; ALB, albumin; high inoc, 3.50 × 108, 4.32 × 108, and 7.65 × 109 cfu/mL initial inocula; CFU, bacterial burden; CINC‐1, cytokine‐induced neutrophil chemoattractant‐1; IL‐1β, interleukin‐1β; low inoc, 7.00 × 106 and 5.76 × 107 cfu/mL initial inocula; N, neutrophil; NS, neutrophil signaling; TNF‐α, tumor necrosis factor‐α.
Parameter reported as log10 transformed estimate.
7.00 × 106, 5.76 × 107, 3.50 × 108, 4.32 × 108, or 1.00 × 109 cfu/mL.
Figure 2.
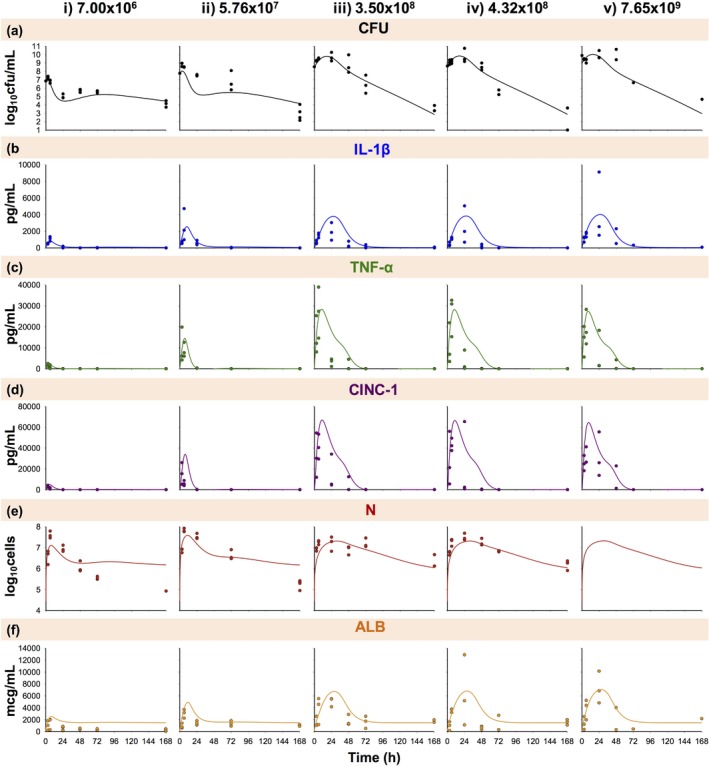
Disease progression time course of bacterial burden (a; CFU); interleukin‐1β (b; IL‐1β), tumor necrosis factor‐α (c; TNF‐α), and cytokine‐induced neutrophil chemoattractant‐1 (d; CINC‐1) expression; neutrophil recruitment (e; N); and albumin leakage (f; ALB) during A. baumannii pneumonia at an initial inoculum of 7.00 × 106 (i), 5.76 × 107 (ii), 3.50 × 108 (iii), 4.32 × 108 (iv), and 7.65 × 109 (v) cfu/mL. Symbols indicate observed pooled data (where each observed data point represents data quantified in the terminal sample obtained from a different animal), and lines indicate model fits based on the mechanism‐based disease progression model in Figure 1. N was unobserved for the 7.65 × 109 cfu/mL inoculum.
Model results
The schematic for the final model is shown in Figure 1; final parameter estimates are reported in Table 1. The observed pooled data and model fits are shown in Figure 2. Disease progression with an initial inocula of 7.00 × 106 and 5.76 × 107 cfu/mL (low inocula; Figure 2 a–f (i–ii) was markedly different from 3.50 × 108, 4.32 × 108, and 7.65 × 109 cfu/mL (high inocula; Figure 2 a–f (iii–v). Therefore, the sensitivity constants ( parameters) acting on stimulation of IL‐1β, TNF‐α, and AC by CFU were allowed to differ between low and high inocula.
Bacterial dynamics
Model fits of total lung bacterial burden are shown in Figure 2 a (overall r2 0.85). Time to maximum predicted CFU ranged from ∼3 to 6 hours for the low inocula (Figure 2 a (i‐ii)) and from ∼14 to 18 hours for the high inocula (Figure 2 a (iii–v)). All inoculum groups resulted in a trend toward bacterial eradication by 168 hours. The estimated bacterial growth rate constant was 0.327 h−1 (3.95% SE), and bacterial killing rates by neutrophils and neutrophil signaling, log10 , log10 , and log10 , were −7.71, −7.48, and −7.00 (0.05%, 0.06%, and 0.33% SE), respectively (Table 1).
Host immune response
Model fits for pro‐inflammatory cytokines IL‐1β and TNF‐α are shown in Figure 2 b,c (overall r2 0.48 and 0.60). As the initial bacterial inoculum increased, the expression of the pro‐inflammatory cytokines grew in magnitude and was prolonged. Maximal IL‐1β stimulation ranged from ∼5 to 11 hours for low inocula (Figure 2 b i–ii) and ∼22 to 30 hours for high inocula (Figure 2 b (iii–v)). IL‐1β concentrations returned to baseline values by ∼24 hours for low inocula and ∼72 hours for high inocula. The estimated was 94.7 (5.46% SE), and the log10 values were 7.21 and 8.89 (0.43% and 0.35% SE) for low and high inocula (Table 1). Maximal TNF‐α stimulation ranged from ∼4 to 10 hours and returned to baseline by ∼24 hours for low inocula (Figure 2 c (i–ii)) and ∼72 hours for high inocula (Figure 2 c (iii–v)). The estimated was 64.2 (5.14% SE), and the log10 values were 8.06 and 8.20 (0.27 and 0.43% SE) for low and high inocula (Table 1).
Figure 2 d shows the model fits of CINC‐1 chemokine expression (overall r2 0.57). Maximal CINC‐1 stimulation ranged from ∼5 to 11 hours and returned to baseline by ∼24 hours for low inocula (Figure 2 d (i–ii)) and ∼72 hours for high inocula (Figure 2 d (iii–v)). The estimated was 4.12 h−1 (12.4% SE).
The predicted time course of the anti‐inflammatory cytokine AC is shown in Figure 3. AC expression was predicted to increase with increasing inocula, and maximal stimulation ranged from ∼5 to 9 hours for low inocula (Figure 3 i–ii) and ∼24 to 32 hours for high inocula (Figure 3 iii‐v). AC concentrations returned to baseline by ∼24 hours for low inocula and ∼72 hours for high inocula. The estimated was 57.9 (6.08% SE) and the log10 values were 8.96 and 8.92 (1.10% and 0.67% SE) for low and high inocula (Table 1). AC inhibited IL‐1β and TNF‐α production with and estimates of 6.48 × 10−4 (226% SE) and 0.02 (0.01% SE) mL/pg.
Figure 3.
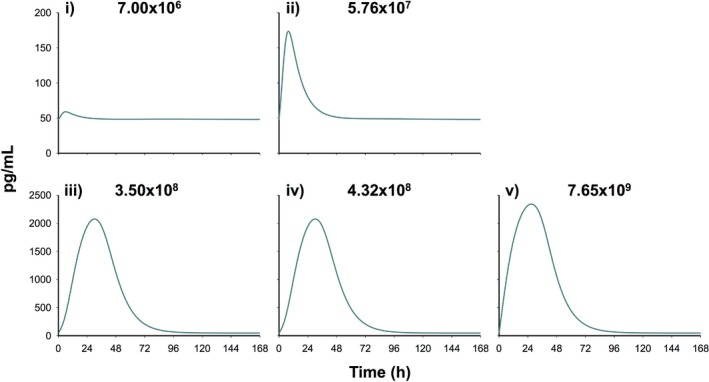
Model‐predicted time course of the empirical anti‐inflammatory cytokine (AC) compartment during A. baumannii pneumonia at an initial inoculum of 7.00 × 106 (i), 5.76 × 107 (ii), 3.50 × 108 (iii), 4.32 × 108 (iv), and 7.65 × 109 (v) cfu/mL.
Model fits of neutrophil counts are shown in Figure 2 e (overall r2 0.60). Neutrophils peaked between ∼6 and 11 hours for low inocula (Figure 2 e (i–ii)) and between ∼27 and 35 hours for high inocula (Figure 2 e (iii–v)). The magnitude was greater for low inocula; therefore, was allowed to differ between low and high inocula. The estimates were 2.52 × 10−2 and 6.51 × 10−3 mL/pg (10.3 and 9.55% SE) for low and high inocula. The estimated was 4.93 × 10−4 mL/pg (11.3% SE; Table 1).
Lung injury
Model fits of albumin are shown in Figure 2 f (overall r2 0.51). As the initial bacterial inoculum increased, the increased IL‐1β expression resulted in increased and prolonged albumin leakage. Albumin concentrations peaked from ∼7 to 12 hours for low inocula (Figure 2 f (i–ii)) and ∼25 to 30 hours for high inocula (Figure 2 f (iii–v)). Concentrations returned to a baseline of 1,504 mcg/mL beyond 24 hours for low inocula and 72 hours for high inocula, which was different from the initial baseline concentration (125 mcg/mL) as both and were estimated parameters (Table 1). Estimates of , , and were 1,012 mcg/mL/h (7.9% SE), 0.705 h−1 (8.08% SE), and 9.77 × 10−4 mL/pg (4.83% SE), respectively.
Discussion
Pneumonia caused by multidrug resistant gram‐negative pathogens has a higher propensity for lung injury, systemic dissemination, sepsis, and ultimately mortality.23 The development of pneumonia is the result of complex interactions between the infecting pathogen and host immune system that modulate the early and late innate immune responses and disease progression.24 Although antibiotics have been used for over 6 decades, the combined impact of the virulence factors of the invading pathogen, bacterial inoculum, and the innate pulmonary host defense system have been overlooked. The emerging discipline of quantitative systems pharmacology allows for the integration of experimentally measured host‐pathogen interaction data into current model‐based PK/PD approaches. Some current mathematical models describe the dynamic and continuous nature of interactions between the host immune system and invading pathogen as a network of discrete states with conditions for transition between these discrete states.25 These models are unable to capture the continuous dynamics of disease progression. A lack of quantitative time course immune data in the patient population of interest has necessitated the use of values published in the literature. Few models have attempted to evaluate host immune response to bacteria using in vivo data with published immune response data.15, 25 Modeling the time course of relevant biomarkers of host‐pathogen interactions evaluated in vivo using a systems‐based approach to understand the critical determinants of the underlying pathogenesis of pneumonia remains largely unexplored. Here, we have developed a mechanism‐based model that quantitatively describes the time course of interactions between bacterial dynamics, host innate immune response, and lung injury using an immunocompetent rat pneumonia model of infection.
In this model, in the absence of antimicrobial treatment, bacterial dynamics reflects the net effect of replication and host immune response mediated bactericidal activity. Neutrophils are largely responsible for bacterial killing via phagocytosis as well as signaling to recruit other immune cells, such as dendritic cells, natural killer cells, and macrophages.26, 27 Activated neutrophils also release extracellular traps, which contain antimicrobial proteins bound to a DNA scaffold.28 The model was able to describe bacterial dynamics based on these mechanisms. The estimated bacterial growth rate constant ( : 0.327 h−1; representing net replication) was comparable to previous studies modeling A. baumannii.29, 30 As neutrophils were the only measured immune cells, transit compartments were used to represent neutrophil signaling. Transit compartments serve as placeholders for these natural antibacterial processes to be quantified in future studies.16 Incorporation of bacterial killing processes by both neutrophils and neutrophil signaling allowed the model to capture the overall time course of bacterial burden. Smith et al.12 evaluated different models of innate immune response to pneumococcal pneumonia; model simulations of bacterial burden agreed better with the observed data after addition of monocyte‐derived macrophage recruitment compared to neutrophil response alone.
Activation of NF‐κB in alveolar macrophages results in increased expression of IL‐1β and TNF‐α. These early pro‐inflammatory cytokines stimulate production of chemokines, such as CINC‐1, that help recruit neutrophils to the lungs through chemotactic migration.31 Indirect response models have been previously used to capture pro‐inflammatory cytokine dynamics in inflammatory diseases.32, 33 In the current study, indirect response models with bacterial stimulation of cytokine production captured the early upregulation of IL‐1β and TNF‐α, characteristic of bacterial pneumonia. Expression of the chemokine CINC‐1 closely followed TNF‐α and was captured with direct stimulation by TNF‐α. An indirect response model adequately captured the resulting neutrophil recruitment with stimulation by IL‐1β and CINC‐1.
Anti‐inflammatory cytokines, such as IL‐10 regulate the inflammatory response to help prevent a “cytokine storm” and the related sequelae of acute lung injury, and sepsis as a consequence of pro‐inflammatory cytokine overproduction.34, 35, 36 Hence, an empirical anti‐inflammatory cytokine was introduced as an unobserved model component to help regulate the inflammatory responses by inhibiting the production of TNF‐α and IL‐1β. Although unmeasured, the model simulated profiles were close to reported IL‐10 BALF concentrations in Long‐Evans rats with pulmonary inflammation due to gastric aspiration.21, 22 Inclusion of the inhibitory effect on TNF‐α production was necessary to capture TNF‐α expression dynamics, and was estimated with good precision (0.007% SE). However, the anti‐inflammatory cytokine was predicted to have a lesser inhibitory effect on IL‐1β production ( : 6.48 × 10−4 mL/pg, : 0.02 mL/pg), and was imprecisely estimated (226% SE) as the anti‐inflammatory cytokine may not have had a significant impact on IL‐1β expression in our animal models. IL‐10 is known to regulate TNF‐α at multiple levels and may inhibit TNF‐α production more potently.37, 38 All other model parameters were estimated with good precision (Table 1).
The host immune response was distinctly different between low and high inocula. The time to maximum IL‐1β expression and return to baseline was delayed for high inocula infection burdens. The time to maximum TNF‐α and CINC‐1 expression was similar for low and high inocula; however, expression was prolonged for high inocula infections. Interestingly, neutrophil recruitment was earlier and in greater numbers for low inocula. Allowing the and model parameters to differ between high and low inocula enabled co‐modeling of the five different infection burdens. The observed differences and the need for an infection burden threshold may be due to the complexity of the immune system as there are multiple pattern recognition receptors and signaling cascades interconnected by crosstalk, redundancy, and feedback.39 Different inocula may produce host immune responses with differing magnitudes and temporal relationships between immune components or invoke alternative signaling pathways to those measured in the present study.40, 41 Gauthier et al.41 evaluated the effect of cyclosporine H, a neutrophil formyl peptide receptor antagonist, on neutrophil recruitment to the lungs during murine pneumococcal pneumonia. Neutrophil counts were significantly reduced in high (107 cfu) but not low (106 cfu) inoculum infections, suggesting the involvement of other chemo‐attractants that are activated by a low but not high bacterial burden. Conversely, chemokine‐neutralizing antibodies, anti‐keratinocyte chemoattractant, and anti‐macrophage‐inflammatory protein‐2, significantly reduced neutrophil counts in low but not high inoculum infections due to other pathways that are activated by higher bacterial burdens to compensate for the inhibited chemokines.41
High IL‐1β expression levels have been linked to acute lung injury.42, 43, 44 Using albumin as an indicator of increased pulmonary permeability and injury, our model successfully captured lung injury dynamics with an indirect response model stimulated by IL‐1β. As the bacterial burden increased, the pro‐inflammatory response was augmented, resulting in increased and prolonged lung injury. The predicted baseline albumin concentration after 7 days was ∼10‐fold greater compared to the initial concentration (1,504 vs. 125 mcg/mL), suggesting long‐term changes in lung pathology, which may be even more evident with higher bacterial inocula.
In the present study, anti‐inflammatory and neutrophil signaling variables were unobserved model components. Future studies that measure additional biomarkers, such as IL‐10, myeloperoxidase released by activated polymorphonuclear leukocytes,45 and macrophages would help validate these model components. Currently, the measurement of immune biomarkers at the site of infection (i.e., the lungs) requires terminal sampling; novel sampling techniques enabling longitudinal sample collection from the same animal in order to reduce variability in observations would help address this limitation. Another limitation of the rat infection model is that the bacterial pneumonia in this rodent species is self‐limiting even at the highest evaluated inoculum. Additionally, there are differences in lung physiology and disease progression biomarkers between rats and humans. Future studies using in vivo infection models that are more susceptible to human pathogens, with lung pathology similar to humans (i.e., guinea pigs), would better facilitate clinical translation.
As increased host‐pathogen interaction data becomes available with advances in “omics” technologies, systems biology approaches can aid in the parsimonious analysis of heterogeneous disease pathogenesis data by modeling the dynamics of these complex signaling networks to identify potential targets and predict behavior.46, 47, 48 Bacterial pathogens have evolved strategies to manipulate and dampen the host immune response. The growing interest in understanding the molecular and cellular mechanisms of infectious processes has presented the appropriate opportunity to bridge the gap between microbiology and immunology. Synergy between these fields will enable the design of new strategies to treat infectious processes like the discovery of new target antigens and development of novel adjuvant therapies.28 Development of immunomodulating therapies requires detailed mechanistic knowledge of the immune system and host‐pathogen interactions to elucidate which immune pathways to enhance and which to suppress.
To the best of our knowledge, this is the first mechanism‐based disease progression model describing the time course of host‐pathogen interactions during A. baumannii pneumonia using quantitative data on bacterial dynamics, host immune responses, and lung injury in the absence of treatment. This animal model can be extended by incorporating the PK/PD of antibiotics of interest and additional host‐pathogen interaction biomarkers. Quantitative systems pharmacology modeling can be performed using a step‐wise approach49 to characterize the interplay between bacterial dynamics, host immune responses, and lung injury. The resulting PK/PD/disease progression model incorporating mechanistic details will provide an in‐depth understanding of the underlying biology of pneumonia and truly enable the model‐based development of antibiotics and design of novel treatment regimens.
Source of Funding
No funding was received for this work.
Conflict of Interest
The authors declared no competing interests for this work.
Author Contributions
J.K.D. and G.G.R. wrote the manuscript. G.G.R. designed the research. J.K.D., T.A.R., and G.G.R. performed the research. J.K.D. and G.G.R. analyzed the data.
Supporting information
Acknowledgments
We thank Dr Alan Forrest and Dr Wojciech Krzyzanski for their input and insightful modeling discussions. This work was presented in part at the 7th American Conference on Pharmacometrics (ACoP7), Bellevue, Washington, USA October 23–26, 2016 (Abstract M‐29) and at the 26th Population Approach Group in Europe (PAGE2017), Budapest, Hungary, June 6–9, 2017. The National Institute of Allergy and Infectious Diseases of the National Institutes of Health provided support to G.G.R. via award number CTSA/NIH 4KL2TR001109. T.A.R. was supported in part by the Office of Research and Development, Medical Research Service, Department of Veterans Affairs (IBX000984A). The content is solely the responsibility of the authors and does not necessarily represent the official views of the National Institutes of Health.
References
- 1. GBD 2015 Mortality and Causes of Death Collaborators . Global, regional, and national life expectancy, all‐cause mortality, and cause‐specific mortality for 249 causes of death, 1980–2015: a systematic analysis for the Global Burden of Disease Study 2015. Lancet 388, 1459–1544 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2. Boucher, H.W. et al 10 x '20 Progress–development of new drugs active against gram‐negative bacilli: an update from the Infectious Diseases Society of America. Clin. Infect. Dis. 56, 1685–1694 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3. Diep, J.K. et al Polymyxin B in combination with rifampin and meropenem against polymyxin B‐resistant KPC‐producing Klebsiella pneumoniae. Antimicrob. Agents Chemother. 61, e02121–16 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4. Soon, R.L. et al Pharmacodynamic variability beyond that explained by MICs. Antimicrob. Agents Chemother. 57, 1730–1735 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5. Schurr, J.R. , Young, E. , Byrne, P. , Steele, C. , Shellito, J.E. & Kolls, J.K. Central role of toll‐like receptor 4 signaling and host defense in experimental pneumonia caused by Gram‐negative bacteria. Infect. Immun. 73, 532–545 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6. Mizgerd, J.P. Molecular mechanisms of neutrophil recruitment elicited by bacteria in the lungs. Semin. Immunol. 14, 123–132 (2002). [DOI] [PubMed] [Google Scholar]
- 7. Quinton, L.J. et al Functions and regulation of NF‐kappaB RelA during pneumococcal pneumonia. J. Immunol. 178, 1896–1903 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8. Standiford, T.J. , Strieter, R.M. , Greenberger, M.J. & Kunkel, S.L. Expression and regulation of chemokines in acute bacterial pneumonia. Biol. Signals 5, 203–208 (1996). [DOI] [PubMed] [Google Scholar]
- 9. Kolaczkowska, E. & Kubes, P. Neutrophil recruitment and function in health and inflammation. Nat. Rev. Immunol. 13, 159–175 (2013). [DOI] [PubMed] [Google Scholar]
- 10. Karaolis, D.K. et al Cyclic di‐GMP stimulates protective innate immunity in bacterial pneumonia. Infect. Immun. 75, 4942–4950 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Handel, A. , Margolis, E. & Levin, B.R. Exploring the role of the immune response in preventing antibiotic resistance. J. Theor. Biol. 256, 655–662 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Smith, A.M. , McCullers, J.A. & Adler, F.R. Mathematical model of a three‐stage innate immune response to a pneumococcal lung infection. J. Theor. Biol. 276, 106–116 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Mochan, E. , Swigon, D. , Ermentrout, G.B. , Lukens, S. & Clermont, G. A mathematical model of intrahost pneumococcal pneumonia infection dynamics in murine strains. J. Theor. Biol. 353, 44–54 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Gjini, E. & Brito, P.H. Integrating antimicrobial therapy with host immunity to fight drug‐resistant infections: classical vs. adaptive treatment. PLoS Comput. Biol. 12, e1004857 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Ankomah, P. & Levin, B.R. Exploring the collaboration between antibiotics and the immune response in the treatment of acute, self‐limiting infections. Proc. Natl. Acad. Sci. USA 111, 8331–8338 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Jusko, W.J. Moving from basic toward systems pharmacodynamic models. J. Pharm. Sci. 102, 2930–2940 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Russo, T.A. et al Rat pneumonia and soft‐tissue infection models for the study of Acinetobacter baumannii biology. Infect. Immun. 76, 3577–3586 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Matute‐Bello, G. et al An official American Thoracic Society workshop report: features and measurements of experimental acute lung injury in animals. Am. J. Respir. Cell Mol. Biol. 44, 725–738 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. D'Argenio, D.Z. , Schumitzky, A. & Wang, X. ADAPT 5 user's guide: pharmacokinetic/pharmacodynamic systems analysis software. BMSR Biomedical Simulations Resource. <bmsr.usc.edu/software/adapt/users‐guide/> (2009).
- 20. Sharma, A. & Jusko, W.J. Characteristics of indirect pharmacodynamic models and applications to clinical drug responses. Br. J. Clin. Pharmacol. 45, 229–239 (1998). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Raghavendran, K. et al Superimposed gastric aspiration increases the severity of inflammation and permeability injury in a rat model of lung contusion. J. Surg. Res. 155, 273–282 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Knight, P.R. et al Progressive, severe lung injury secondary to the interaction of insults in gastric aspiration. Exp. Lung Res. 30, 535–557 (2004). [DOI] [PubMed] [Google Scholar]
- 23. Gikas, A. et al Gram‐negative bacteremia in non‐neutropenic patients: a 3‐year review. Infection 26, 155–159 (1998). [DOI] [PubMed] [Google Scholar]
- 24. Berk, R.S. , Preston, M. , Montgomery, I.N. , Hazlett, L.D. & Tse, H.Y. Antibody hyporesponsiveness in resistant BALB/cJ mice intracorneally infected with Pseudomonas aeruginosa. Reg. Immunol. 3, 186–192 (1990). [PubMed] [Google Scholar]
- 25. Thakar, J. , Pilione, M. , Kirimanjeswara, G. , Harvill, E.T. & Albert, R. Modeling systems‐level regulation of host immune responses. PLoS Comput. Biol. 3, e109 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26. Mayadas, T.N. , Cullere, X. & Lowell, C.A. The multifaceted functions of neutrophils. Annu. Rev. Pathol. 9, 181–218 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Jaillon, S. , Galdiero, M.R. , Del Prete, D. , Cassatella, M.A. , Garlanda, C. & Mantovani, A. Neutrophils in innate and adaptive immunity. Semin. Immunopathol. 35, 377–394 (2013). [DOI] [PubMed] [Google Scholar]
- 28. Sansonetti, P.J. & Di Santo, J.P. Debugging how bacteria manipulate the immune response. Immunity 26, 149–161 (2007). [DOI] [PubMed] [Google Scholar]
- 29. Cheah, S.E. , Li, J. , Tsuji, B.T. , Forrest, A. , Bulitta, J.B. & Nation, R.L. Colistin and polymyxin B dosage regimens against Acinetobacter baumannii: differences in activity and the emergence of resistance. Antimicrob. Agents Chemother. 60, 3921–3933 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Rao, G.G. et al Polymyxin B in combination with doripenem against heteroresistant Acinetobacter baumannii: pharmacodynamics of new dosing strategies. J. Antimicrob. Chemother. 71, 3148–3156 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Handa, O. , Naito, Y. & Yoshikawa, T. Rat cytokine‐induced neutrophil chemoattractant‐1 (CINC‐1) in inflammation. J. Clin. Biochem. Nutr. 38, 51–58 (2006). [Google Scholar]
- 32. Earp, J.C. , Dubois, D.C. , Molano, D.S. , Pyszczynski, N.A. , Almon, R.R. & Jusko, W.J. Modeling corticosteroid effects in a rat model of rheumatoid arthritis II: mechanistic pharmacodynamic model for dexamethasone effects in Lewis rats with collagen‐induced arthritis. J. Pharmacol. Exp. Ther. 326, 546–554 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Lon, H.K. , DuBois, D.C. , Earp, J.C. , Almon, R.R. & Jusko, W.J. Modeling effects of dexamethasone on disease progression of bone mineral density in collagen‐induced arthritic rats. Pharmacol. Res. Perspect. 3, e00169 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34. Fiorentino, D.F. , Zlotnik, A. , Mosmann, T.R. , Howard, M. & O'Garra, A. Pillars Article: IL‐10 inhibits cytokine production by activated macrophages. J. Immunol. 1991. 147: 3815–3822. J. Immunol. 197, 1539–1546 (2016). [PubMed] [Google Scholar]
- 35. Moore, K.W. , de Waal Malefyt, R. , Coffman, R.L. & O'Garra, A. Interleukin‐10 and the interleukin‐10 receptor. Annu. Rev. Immunol. 19, 683–765 (2001). [DOI] [PubMed] [Google Scholar]
- 36. Tisoncik, J.R. , Korth, M.J. , Simmons, C.P. , Farrar, J. , Martin, T.R. & Katze, M.G. Into the eye of the cytokine storm. Microbiol. Mol. Biol. Rev. 76, 16–32 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Brennan, F.M. , Green, P. , Amjadi, P. , Robertshaw, H.J. , Alvarez‐Iglesias, M. & Takata, M. Interleukin‐10 regulates TNF‐alpha‐converting enzyme (TACE/ADAM‐17) involving a TIMP‐3 dependent and independent mechanism. Eur. J. Immunol. 38, 1106–1117 (2008). [DOI] [PubMed] [Google Scholar]
- 38. Williams, L.M. , Ricchetti, G. , Sarma, U. , Smallie, T. & Foxwell, B.M. Interleukin‐10 suppression of myeloid cell activation–a continuing puzzle. Immunology 113, 281–292 (2004). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39. Takeuchi, O. & Akira, S. Pattern recognition receptors and inflammation. Cell 140, 805–820 (2010). [DOI] [PubMed] [Google Scholar]
- 40. Morris, A.E. , Liggitt, H.D. , Hawn, T.R. & Skerrett, S.J. Role of toll‐like receptor 5 in the innate immune response to acute P. aeruginosa pneumonia. Am. J. Physiol. Lung Cell. Mol. Physiol. 297, L1112–L1119 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Gauthier, J.F. , Fortin, A. , Bergeron, Y. , Dumas, M.C. , Champagne, M.E. & Bergeron, M.G. Differential contribution of bacterial N‐formyl‐methionyl‐leucyl‐phenylalanine and host‐derived CXC chemokines to neutrophil infiltration into pulmonary alveoli during murine pneumococcal pneumonia. Infect. Immun. 75, 5361–5367 (2007). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42. Martínez‐Colón, G.J. , Taylor, Q.M. , Wilke, C.A. , Podsiad, A.B. & Moore, B.B. Elevated prostaglandin E2 post‐bone marrow transplant mediates interleukin‐1β‐related lung injury. Mucosal Immunol. 11, 319–332 (2018). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Wang, Y.X. , Ji, M.L. , Jiang, C.Y. & Qian, Z.B. Upregulation of ICAM‐1 and IL‐1β protein expression promotes lung injury in chronic obstructive pulmonary disease. Genet. Mol. Res. 15, 15037971 (2016). [DOI] [PubMed] [Google Scholar]
- 44. Seekamp, A. , Warren, J.S. , Remick, D.G. , Till, G.O. & Ward, P.A. Requirements for tumor necrosis factor‐alpha and interleukin‐1 in limb ischemia/reperfusion injury and associated lung injury. Am. J. Pathol. 143, 453–463 (1993). [PMC free article] [PubMed] [Google Scholar]
- 45. Lau, D. et al Myeloperoxidase mediates neutrophil activation by association with CD11b/CD18 integrins. Proc. Natl. Acad. Sci. USA 102, 431–436 (2005). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46. Ryall, K.A. & Tan, A.C. Systems biology approaches for advancing the discovery of effective drug combinations. J. Cheminform. 7, 7 (2015). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47. De Keersmaecker, S.C. , Thijs, I.M. , Vanderleyden, J. & Marchal, K. Integration of omics data: how well does it work for bacteria? Mol. Microbiol. 62, 1239–1250 (2006). [DOI] [PubMed] [Google Scholar]
- 48. Abu‐Asab, M.S. et al Biomarkers in the age of omics: time for a systems biology approach. OMICS 15, 105–112 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49. Miao, X. , Koch, G. , Ait‐Oudhia, S. , Straubinger, R.M. & Jusko, W.J. Pharmacodynamic modeling of cell cycle effects for gemcitabine and trabectedin combinations in pancreatic cancer cells. Front. Pharmacol. 7, 421 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials


