A physically grounded damped dispersion model with particle mesh Ewald summation

Abstract

Accurate modeling of dispersion is critical to the goal of predictive biomolecular simulations. To achieve this accuracy, a model must be able to correctly capture both the short-range and asymptotic behavior of dispersion interactions. We present here a damped dispersion model based on the overlap of charge densities that correctly captures both regimes. The overlap damped dispersion model represents a classical physical interpretation of dispersion: the interaction between the instantaneous induced dipoles of two distinct charge distributions. This model is shown to be an excellent fit with symmetry adapted perturbation theory dispersion energy calculations, yielding an RMS error on the S101x7 database of 0.5 kcal/mol. Moreover, the damping function used in this model is wholly derived and parameterized from the electrostatic dipole-dipole interaction, making it not only physically grounded but transferable as well.

I. INTRODUCTION

The range of possible problems for molecular mechanics models to solve is immense. For problems that are too large to solve with Schrodinger’s equation but too small to be observed experimentally, we rely on classical models to make predictions and generate hypotheses. This ability has made molecular mechanics force fields integral to the study of problems from RNA folding¹ to new alloy characterization.² Because they are classical approximations to quantum mechanical reality, the success of these models is entirely dependent on how accurate that approximation is on a wide variety of systems. To achieve this, most force fields split the interaction energies of interacting atoms into physically meaningful components. Among the most significant of these components is the dispersion interaction that arises from the correlation of instantaneous induced dipoles.

No force field can provide fully accurate predictions for every component of the total energy of a system. In current models, this has been typically handled by careful cancellation of errors between the various components (electrostatics, polarization, repulsion, dispersion, etc.). More recently, however, a new crop of next-generation force fields is emerging that aim to reduce this dependence on error cancellation by comparing directly to ab initio energy decomposition analysis (EDA) data.^3–10 We are working on a model with this same objective. Previously we have shown that it is possible to accurately model electrostatics (to within 1 kcal/mol) in regions where previously error cancellation had long been relied upon, the so-called “charge penetration” error.¹¹ In this work, we shall demonstrate that the same is possible for the dispersion interaction component. While this does not represent a complete force field capable of condensed phase simulations, it is an important step toward such a full model.

Accurately modeling dispersion in classical force fields is known to be important, particularly for biological systems. On a phenomenological level, dispersion is what causes neutral atoms and molecules to be weakly attracted to each other. This makes it essential to modeling simple Lennard-Jones fluids such as liquid argon, but it is also critically important to more complex systems. Dispersion has been shown to be an essential component of modeling nucleic acid structure,¹² where it contributes to the so-called stacking energy of nucleic acid bases. It is known to play a part in halogen bonding, supporting, along with electrostatics, the stabilization energy of the interaction.^13,14 Additionally, long-range dispersion is widely recognized to be important for the simulation of lipid bilayers.¹⁵ This broad spectrum of applications motivates the necessity of accurate dispersion models.

The history of dispersion models dates back to Fritz London, who first established the canonical 1/r⁶ dependence of the London dispersion energy. This model has been enormously influential. The vast majority of biological force fields in use today still use this simple model (Amber,¹⁶ CHARMM,¹⁷ etc.) or derivatives thereof such as the attractive part of Halgren’s buffered 14-7 potential¹⁸ used in the AMOEBA¹⁹ force field. It is well known, however, that the 1/rⁿ potential expansion breaks down for short-range interactions where charge distributions of interacting molecules overlap.²⁰ There is a long history of attempts to correct this divergence though the use of damping functions. An important early damped dispersion model was the empirical HFD (Hartree-Fock-Dispersion) scheme proposed by Scoles and co-workers.²¹ Another notable attempt to describe this phenomenon was undertaken by Tang and Toennies who introduced a damping function parameterized to account for the overlap in charge distributions.²² A comprehensive review of dispersion damping functions is beyond the scope of this work, but the original Tang and Toennies report provides a thorough overview of dispersion damping functions up to that point. These types of formalisms have seen the widest use as dispersion corrections to density functional theory (DFT) calculations.²³ DFT-D schemes have used the Tang-Toennies function, as well as various other damping functions proposed by Wu and Yang,²⁴ Chai and Head-Gordon,²⁵ and Johnson and Becke.²⁶ Despite wide use in the DFT community, damped dispersion functions have been taken up in decidedly fewer molecular mechanics models. Notably, the Effective Fragment Potential (EFP) model employs a dispersion model that utilizes an overlay-based parameter-free modification of the Tang-Toennies damping function.^27,28 And recently, Verma et al. proposed using the dispersion part of the DFT-D3 formulation of Grimme²³ as a molecular mechanics model.²⁹ However, while it has been shown that previous damping functions can effectively account for the change in dispersion upon charge overlap, they do so largely empirically. In the case of the Tang-Toennies damping function, for example, the form is based on a Born-Mayer potential described by an empirically fit width parameter.

In this paper, we propose a damped dispersion function similar in spirit to that of Tang and Toennies but rooted in a physical model of charge distribution overlap. In previous work, we have shown that a relatively simple model can capture the physical extent of atomic charge distributions that leads to the so-called charge penetration error in electrostatic interactions between molecules.¹¹ Here we will show that this same model can be used directly and without modification to create a dispersion model that is elegantly unified with the electrostatic model. This unification is possible because both the electrostatic and dispersion terms depend on the density. The electrostatic term is simply the interaction between two static densities, while the dispersion term arises from the interaction of densities associated with instantaneous induced dipoles. In this work, we will show that the same rough description of the density can be used in both cases to great effect. This will be done in five parts. First, we elucidate the theory that starts from dipole-dipole interactions and gives rise to this new damped dispersion function. Second, we describe the methods of the study. Third, we evaluate the performance of this function against benchmark Symmetry Adapted Perturbation Theory (SAPT) calculations. Fourth, we will describe how the model has been implemented with dispersion particle mesh Ewald (DPME) to boost its efficiency. And finally, we will discuss the implications of this work and some general conclusions.

II. THEORY

To present our new damped dispersion model, we shall first revisit a simple derivation of the original London dispersion model. We do so first and foremost because it forms the basis for our damped model, but also because it is instructive. One of the defining characteristics of a damped dispersion model, as we shall argue later in the paper, is that it has a straightforward physical interpretation. Dispersion is correctly said to be a fundamentally non-classical phenomenon, but the model we use to describe it need not to be so bound. We will show that an interpretable model of dispersion can be constructed from physical models of atomic polarizability and charge density.

A. London dispersion

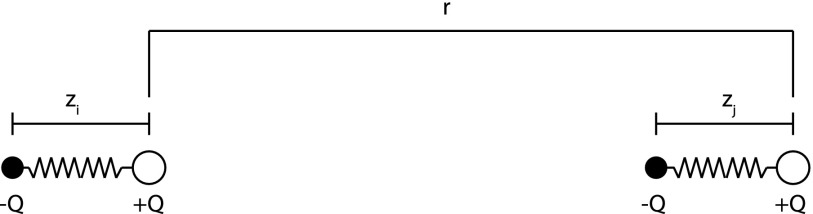
For our description of canonical London dispersion energy, we will follow that of Maitland et al.³⁰ The dispersion energy between two atoms arises from the interaction between instantaneous dipoles of these atoms. To model this system, we consider a simplified one-dimensional Drude oscillator model, as illustrated in Fig. 1.

FIG. 1.

Classical model of dispersion.

In this representation, each atom is represented by a fixed charge +Q bound by a spring with spring constant, k, and an equal and opposite charge −Q with mass, M. This model is crude, but it captures the essential elements of the dispersion interaction. At any point in time, each atom has a dipole moment, μ = Qz (dependent on the atomic polarizability determined by k) and those dipole moments are free to interact with each other.

When atom i and atom j are infinitely separated, the Schrödinger equation for each can be written as

$$\frac{1}{M}\frac{{\partial }^2{\mathrm{\Psi }}_i}{\partial z_i^2}+\frac{2}{{\hslash }^2}\left(E_i-\frac{1}{2}k{z}_i^2\right){\mathrm{\Psi }}_i=0,$$ (1)

where the potential energy term is merely the energy of a simple harmonic oscillator. The same can be written for atom j. The solutions to this equation can be found trivially, yielding ground state energies of

$$E_i=\frac{1}{2}\hslash {\omega }_0\text{\hspace{1em}and\hspace{1em}}{E}_j=\frac{1}{2}\hslash {\omega }_0,$$ (2)

where the frequency, ω₀, is

$${\omega }_0=\sqrt{\frac{k}{M}}.$$ (3)

In the complete non-interacting limit, the total energy of the system is

$$E\left(r\to \infty \right)=E_i+E_j=\hslash {\omega }_0.$$ (4)

This limit in itself is not useful, but if we consider what happens when the two atoms get closer, we shall see that it sets a useful reference for our potential energy function. If we bring the two atoms closer so that they do interact, but not so close that their charge distributions overlap, our Schrödinger equation is no longer trivially separable. The wave equation for two interacting atoms now includes the electrostatic interaction between the two dipoles and becomes

$$\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_i^2}+\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_j^2}+\frac{2}{{\hslash }^2}\left(E-\frac{1}{2}k{z}_i^2-\frac{1}{2}k{z}_j^2-U_{electrostatic}\right)\mathrm{\Psi }=0.$$ (5)

One can see that in addition to the simple harmonic oscillator terms, a new potential appears in Eq. (5). This is the potential energy at any given instant between the two interacting instantaneous multipole distributions. For the dipole-dipole interaction of the simple Drude model of Fig. 1, the form of this potential is easily obtained from simple electrostatics

$$U_{electrostatic}=U_{dipole-dipole}=\nabla \nabla U_{chg-chg}=\nabla \nabla \left(\frac{q_i{q}_j}{r}\right)=\frac{1}{r^3}\left({\overrightarrow{\mu }}_i\cdot {\overrightarrow{\mu }}_j-3\frac{\left({\overrightarrow{\mu }}_i\cdot {\overrightarrow{r}}_{ij}\right)\left({\overrightarrow{r}}_{ij}\cdot {\overrightarrow{\mu }}_j\right)}{r^2}\right).$$ (6)

If we plug in the Drude dipoles from Fig. 1, μ = Qz, Eq. (6) becomes

$$U_{dipole-dipole}=\frac{1}{r^3}\left({\mu }_i{\mu }_j-3\frac{\left({\mu }_{i}r\right)\left({\mu }_{j}r\right)}{r^2}\right)=-\frac{2{\mu }_i{\mu }_j}{r^3}.$$ (7)

This dipole-dipole energy is the source, as we shall show, of the canonical 1/r⁶ leading term dependence of the dispersion energy.

Combining Eq. (7) with Eq. (5) yields

$$\begin{array}{ccc}\hfill \frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_i^2}+\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_j^2}+\frac{2}{{\hslash }^2}\left(E-\frac{1}{2}k{z}_i^2-\frac{1}{2}k{z}_j^2-\frac{2{\mu }_i{\mu }_j}{r^3}\right)\mathrm{\Psi }=0.& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ (8)

Following the transformation of variables of Maitland, Rigby, Smith, and Wakeham, we define

$${\lambda }_1=\frac{z_i+z_j}{\sqrt{2}},{\lambda }_2=\frac{z_i-z_j}{\sqrt{2}}$$ (9)

and rewrite Eq. (8) as

$$\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_i^2}+\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_j^2}+\frac{2}{{\hslash }^2}\left(E-\frac{1}{2}{k}_1{\lambda }_i^2-\frac{1}{2}{k}_2{\lambda }_j^2\right)\mathrm{\Psi }=0,$$ (10)

where

$$k_1=k+\frac{2Q^2}{r^3},k_2=k-\frac{2Q^2}{r^3}.$$ (11)

Equation (10) is simply a transformed version of the original problem of two independent harmonic oscillators. It can be solved in the same manner giving

$$E\left(r\right)=\frac{1}{2}\hslash \left({\omega }_1+{\omega }_2\right),$$ (12)

where

$$\begin{array}{ccc}\hfill {\omega }_1=\sqrt{\frac{k_1}{M}}={\omega }_0\sqrt{1-\frac{2Q^2}{r^{3}k}},{\omega }_2=\sqrt{\frac{k_2}{M}}={\omega }_0\sqrt{1+\frac{2Q^2}{r^{3}k}}.& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ (13)

One can see that as r becomes large, ω₁ and ω₂ converge to ω₀ where we recover the independent oscillator solution. For small perturbations, ω₁ and ω₂ can be approximated with a binomial expansion

$$\sqrt{1+x}=1+1/2x-1/8x+\cdots ,$$ (14)

so the total energy becomes

$$E\left(r\right)=\hslash {\omega }_0-\frac{Q^4\hslash {\omega }_0}{2r^6{k}^2}+\cdots .$$ (15)

The final step is to subtract the energy of infinitely separated atoms. This gives the dispersion potential energy

$$U_{dispersion}=E\left(r\right)-E\left(\infty \right)=-\frac{Q^4\hslash {\omega }_0}{2k^2{r}^6}+\cdots ,$$ (16)

where the canonical r⁶ dependence arises from the first non-zero term from the application of the binomial expansion.

It should be noted that while the dipole-dipole interaction is the dominant electrostatic term of Eq. (5), there are terms arising from higher-order multipole interactions as well. The dipole-quadrupole and quadrupole-quadrupole interactions giving rise to the 1/r⁸ and 1/r¹⁰ potentials are derived in the Appendix. There are a number of models that use these terms, including EFP, SIBFA (Sum of Interactions Between Fragments Ab initio computed), and Misquitta and Stone’s model for small organic molecules.^27,31,32 For a perspective on the importance of these higher order terms for the case of the neon dimer, the reader is directed to the work of Bytautas and Ruedenberg.³³ The latter reference showed that even for this simple dimer, the 1/r⁸ and 1/r¹⁰ terms are nearly impossible to distinguish at reasonable separations. There are odd-power terms (1/r⁷, 1/r⁹, etc.) that can be included in the expansion as well. These arise from the mixing of the even order terms, are highly angularly dependent, and spherically average to zero at long range.³⁴ There has also been recent work on incorporating these terms into dispersion models,^35,36 where these higher-order terms give successively better approximations to the exact dispersion energy. As we will show, however, to reach the stated accuracy goal of <1 kcal/mol, only the leading term will be necessary.

For most systems, the perturbation of the dipole-dipole interaction energy is small compared to the energy holding the electrons to their respective atoms. This makes taking only the leading r⁶ term of Eq. (16) a good approximation for most long-range intermolecular interactions. In practice, this is done by introducing a parameter, C, to capture this dependence

$$U^{dispersion}=-\frac{C_6^i{C}_6^j}{r^6}.$$ (17)

This model will be referred to throughout the remainder of the paper as the London dispersion model. Unfortunately, this method of approximation starts to break down when the charge distributions of interacting atoms start to overlap. We will handle this situation through the introduction of short-range damping, but rather than relying on empiricism for the damping function, we look to the underlying electrostatics to provide a consistent model.

B. Short-range electrostatics

A long-standing problem in the modeling of electrostatics for molecular mechanics models is the so-called charge penetration error. The error arises when charge distributions of interacting atoms overlap, causing the true electrostatic energy of the interacting densities to diverge from the point charge or point multipole approximation. We have shown in previously published studies^11,37,38 that a simple hydrogen-like approximation of the Coulomb potential does a remarkably good job at correcting this error.

Why is this germane to a study of dispersion? Dispersion, as shown above, can be modeled as arising from a dipole-dipole interaction. In the context of the multipolar AMOEBA force field, we have shown that the hydrogen-like approximation to the Coulomb interaction can be extended to the interactions between higher-order multipole moments. In fact, including these corrections for charge-dipole, dipole-dipole, dipole-quadrupole, etc. interactions is essential to the transferability and accuracy of the model.¹¹ Here we show that the dipole-dipole interaction arising from this earlier model can be used directly to create a new damped dispersion model.

To illustrate where the dipole-dipole damping comes from, we follow a similar derivation to that of Ref. 11. The potential due to the electrons for this model is defined as

$$V\left(r\right)=\frac{q_i}{r}\left(1-e^{-{\alpha }_{i}r}\right),$$ (18)

where r is the distance from the center of the charge distribution and α is a parameter describing the width of the distribution. Application of Poisson’s equation,

$${\nabla }^{2}V=\frac{\rho }{{\epsilon }_0},$$ (19)

yields the corresponding density,

$$\rho \left(r\right)=\frac{q_i{\alpha }_i^2{\epsilon }_0}{r}{e}^{-{\alpha }_{i}r}.$$ (20)

These two quantities can be used to approximate the Coulomb interaction energy between two charge distributions,

$$\begin{array}{ccc}\hfill U_{electrostatic}^{chg-chg}& =\hfill & \int \int \frac{{\rho }_i\left({\mathbf{r}}_i\right){\rho }_j\left({\mathbf{r}}_j\right)}{{\mathbf{r}}_{ij}}d{\mathbf{r}}_{i}d{\mathbf{r}}_j\hfill \\ \hfill & =\hfill & \frac{1}{2}\left(\int {\rho }_i\left({\mathbf{r}}_i\right)V_j\left({\mathbf{r}}_j\right)d{\mathbf{r}}_i+\int {\rho }_j\left({\mathbf{r}}_j\right)V_i\left({\mathbf{r}}_i\right)d{\mathbf{r}}_j\right).\hfill \\ \hfill & \hfill & \hfill \end{array}$$ (21)

Application of the one-center integral method of Coulson³⁹ gives

$$\begin{array}{ccc}\hfill U_{electrostatic}^{chg-chg}=\frac{q_i{q}_j}{r}\left(1-\frac{{\alpha }_j^2}{\left({\alpha }_j^2-{\alpha }_i^2\right)}{e}^{-{\alpha }_{i}r}-\frac{{\alpha }_i^2}{\left({\alpha }_i^2-{\alpha }_j^2\right)}{e}^{-{\alpha }_{j}r}\right).& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ (22)

Equation (22) gives the charge-charge electrostatic energy. To get the dipole-dipole energy, recall that the full multipole energy of the i-j interaction can be written as

$$\begin{array}{ccc}\hfill U_{electrostatic}^{total}& =\hfill & U^{chg-chg}+U^{chg-dipole}+U^{dipole-chg}\hfill \\ \hfill & \hfill & +U^{dipole-dipole}+\cdots \hfill \\ \hfill & =\hfill & q_i{T}_{ij}{q}_j+q_i\nabla T_{ij}{\mu }_j-{\mu }_i\nabla T_{ij}{q}_j\hfill \\ \hfill & \hfill & +{\mu }_i\nabla \nabla T_{ij}{\mu }_j+\cdots .\hfill \end{array}$$ (23)

For a point-point interaction, T_ij is simply 1/r, but for our model, direct inspection of Eq. (22) yields

$$\begin{array}{ccc}\hfill T_{ij}=\frac{1}{r}\left(1-\frac{{\alpha }_j^2}{\left({\alpha }_j^2-{\alpha }_i^2\right)}{e}^{-{\alpha }_{i}r}-\frac{{\alpha }_i^2}{\left({\alpha }_i^2-{\alpha }_j^2\right)}{e}^{-{\alpha }_{j}r}\right)=\frac{1}{r}{f}_1^{damp}.& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ (24)

We can now apply this new relation for T_ij to the definition of the dipole-dipole energy from Eq. (23),

$$\begin{array}{ccc}\hfill U_{damp}^{dipole-dipole}& =\hfill & {\mu }_i\nabla \nabla T_{ij}{\mu }_j\hfill \\ \hfill & =\hfill & f_3^{damp}\frac{{\overrightarrow{\mu }}_i\cdot {\overrightarrow{\mu }}_j}{r^3}-f_5^{damp}\frac{3\left({\overrightarrow{\mu }}_i\cdot {\overrightarrow{r}}_{ij}\right)\left({\overrightarrow{r}}_{ij}\cdot {\overrightarrow{\mu }}_j\right)}{r^5},\hfill \end{array}$$ (25)

where f₃ and f₅ are the damping terms that come from the derivatives of the f₁^damp term of Eq. (24),

$$\begin{array}{c}{f}_3^{damp}=1-\frac{{\alpha }_j^2}{\left({\alpha }_j^2-{\alpha }_i^2\right)}\left(1+{\alpha }_{i}r\right)e^{-{\alpha }_{i}r}-\frac{{\alpha }_i^2}{\left({\alpha }_i^2-{\alpha }_j^2\right)}\left(1+{\alpha }_{j}r\right)e^{-{\alpha }_{j}r},\hfill \\ f_5^{damp}=1-\frac{{\alpha }_j^2}{\left({\alpha }_j^2-{\alpha }_i^2\right)}\left(1+{\alpha }_{i}r+\frac{1}{3}{\left({\alpha }_{i}r\right)}^2\right)e^{-{\alpha }_{i}r}-\frac{{\alpha }_i^2}{\left({\alpha }_i^2-{\alpha }_j^2\right)}\left(1+{\alpha }_{j}r+\frac{1}{3}{\left({\alpha }_{j}r\right)}^2\right)e^{-{\alpha }_{j}r}.\hfill \end{array}$$ (26)

Now let us compare Eqs. (25) and (6). Clearly the difference between the point dipole-dipole interaction and the new model’s dipole-dipole interaction is the damping terms that arise from the hydrogen-like model of charge density. For large separations, f₃ and f₅ approach one and we recover the point interaction. For small density overlaps, f₃ and f₅ represent a perturbation that damps the point dipole-dipole interaction.

C. Overlap damped dispersion

To derive our damped dispersion model, we start from the earlier derivation of London dispersion. Equations (1)–(5) remain the same, but instead of inserting the point dipole-dipole interaction energy into Eq. (5), we now substitute our damped dipole-dipole interaction from Eq. (25). Following our simple one-dimensional Drude model, we obtain

$$\begin{array}{ccc}\hfill \begin{array}{c}\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_i^2}+\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_j^2}+\frac{2}{{\hslash }^2}\left(E-\frac{1}{2}k{z}_i^2-\frac{1}{2}k{z}_j^2-U_{dipole-dipole}\right)\mathrm{\Psi }=0,\\ U_{damp}^{dipole-dipole}=f_3^{damp}\frac{{\overrightarrow{\mu }}_i\cdot {\overrightarrow{\mu }}_j}{r^3}-f_5^{damp}\frac{3\left({\overrightarrow{\mu }}_i\cdot {\overrightarrow{r}}_{ij}\right)\left({\overrightarrow{r}}_{ij}\cdot {\overrightarrow{\mu }}_j\right)}{r^5},\end{array}& \hfill & \hfill \end{array}$$ (27)

where U^{dipole-dipole} can be simplified to

$$U_{dipole-dipole}=f_3^{damp}\frac{{\mu }_i{\mu }_j}{r^3}-f_5^{damp}\frac{3\left({\mu }_{i}r\right)\left({\mu }_{j}r\right)}{r^5}.$$ (28)

Inserting this into the Schrödinger equation yields

$$\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_i^2}+\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_j^2}+\frac{2}{{\hslash }^2}\left(E-\frac{1}{2}k{z}_i^2-\frac{1}{2}k{z}_j^2-\left(3f_5^{damp}-f_3^{damp}\right)\frac{{\mu }_i{\mu }_j}{r^3}\right)\mathrm{\Psi }=0.$$ (29)

This can be solved by the same transformation as the non-damped case discussed earlier where

$$\begin{array}{c}{k}_1=k-\frac{2Q^2}{r^3}{f}_{dispersion}^{damp},k_2=k+\frac{2Q^2}{r^3}{f}_{dispersion}^{damp},\hfill \\ f_{dispersion}^{damp}=3f_5^{damp}-f_3^{damp}.\hfill \end{array}$$ (30)

This results in the solution

$$\begin{array}{c}E=\frac{1}{2}\hslash \left({\omega }_1+{\omega }_2\right),\hfill \\ {\omega }_1=\sqrt{\frac{k_1}{M}}={\omega }_0\sqrt{1-\frac{2Q^2}{r^{3}k}{f}_{dispersion}^{damp}},{\omega }_2=\sqrt{\frac{k_2}{M}}={\omega }_0\sqrt{1+\frac{2Q^2}{r^{3}k}{f}_{dispersion}^{damp}}.\hfill \end{array}$$ (31)

Applying the binomial expansion and subtracting the energy of infinitely separated atoms yield the damped dispersion energy

$$U_{dispersion}^{damp}=-\frac{Q^4\hslash {\omega }_0}{2k^2{r}^6}{\left(f_{dispersion}^{damp}\right)}^2+\cdots .$$ (32)

Just as before, for small density overlaps, the leading term of Eq. (32) dominates. To convert this into a parameterized molecular mechanics model, we again introduce C₆ parameters, giving our final model energy

$$U_{dispersion}^{damp}=-\frac{C_6^i{C}_6^j}{r^6}{\left(f_{dispersion}^{damp}\right)}_{ij}^2.$$ (33)

This model represents an elegant and simple unification of the electrostatics and dispersion models for molecular mechanics force fields. We will refer to this model throughout the remainder of the paper as the “overlap damped dispersion” model. It has some important features:

• 1.The model retains the canonical 1/r⁶ asymptotic behavior as f tends to unity at large separations.
• 2.The damping function has a straightforward physical interpretation: it is the integral of the overlap of between charge distributions on interacting atoms.
• 3.The damping function follows a similar exponential form as other previously proposed dispersion damping functions.
• 4.The damping function has no adjustable parameters. The parameters are fixed from the electrostatics charge penetration damping function.

As we will show in Sec. IV, this model, in addition to being theoretically compelling, produces good agreement with dispersion energies from ab initio energy decomposition analysis calculations.

III. METHODS

The damped dispersion model we propose requires the fitting of C₆ parameters. To obtain these parameters, validate their robustness, and assess the model’s accuracy, we set out a four-step protocol. First, we assemble a database of representative molecular interactions. Second, we perform benchmark ab initio reference calculations on that database. Third, we fit the parameters of our model to the reference ab initio data. Fourth, we assess the robustness of the fit by validation of the model on systems outside of the database.

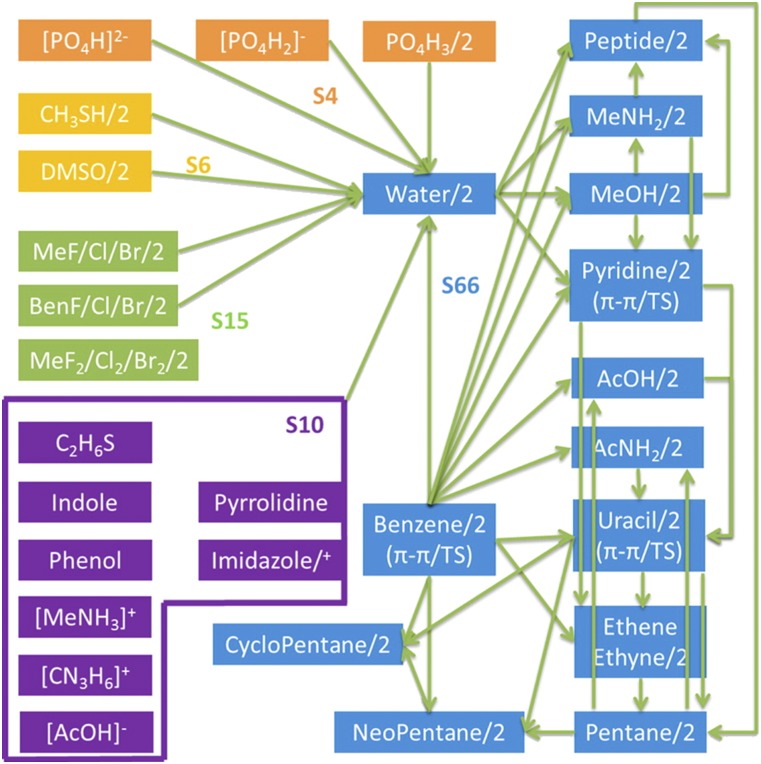
For the scope of this study, we intend to parameterize our model for the chemical space of biomolecules. To this end, we use the previously constructed S101x7 database⁴⁰ for fitting. This database consists of 101 distinct pairs of molecular dimers. For each of these dimers, seven points along the dissociation curve are established at 0.7, 0.8, 0.9, 0.95, 1.0, 1.05, and 1.1 times the equilibrium intermolecular distance. Details on how the structures were generated are available in Ref. 37. The dimers in this set represent a cross section of typical interactions found in protein and nucleic acid systems. We note that the points in the dataset at 0.7x the equilibrium distance are important despite the fact that they are rarely sampled in condensed phase simulations for most systems. These points are included to ensure that the shape of the potential at the closest sampled points (often 0.8x the equilibrium distance) is accurately captured. A summary of all the pair interactions is presented in Fig. 2.

FIG. 2.

Dimer pairs in the S101 database. Arrows indicate heterodimers, while “/2” indicates a homodimer. Reprinted with permission from Wang et al., J. Chem. Theory Comput. 11, 2609–2618 (2015). Copyright 2015 American Chemical Society.

In order to parameterize our model, a set of dispersion reference data is required. Because dispersion is not a physical observable, we must rely on an ab initio energy decomposition analysis (EDA) to generate our reference data. We have chosen Symmetry Adapted Perturbation Theory (SAPT)⁴¹ for this purpose. SAPT has a number of features that makes it a reasonable choice. First, SAPT is a perturbation theory approach that takes the electron density of monomers as its unperturbed state. This is an exact analogy to molecular mechanics models where distributed multipoles are calculated from monomer densities. Second, because of this correspondence, SAPT is the theory that was used to generate the parameterization of the electrostatic model referenced in Sec. II. Using SAPT here as well ensures a straightforwardly unified model. Finally, SAPT is a well-established theory with a proliferation of studies analyzing its accuracy with respect to various orders and basis sets. We use the SAPT2+ level of theory as defined by Sherrill et al.⁴² with Dunning correlation consistent basis sets^43,44 to estimate the complete basis set (CBS) limit⁴⁵ for the SAPT energy components. The SAPT2+ method with large augmented basis sets has been previously shown to give errors relative to coupled-cluster single, double and perturbative triple excitations [CCSD(T)]/CBS of about 0.3 kcal/mol. This was chosen over the cheaper to compute SAPT0 method, which gives errors of around 0.5 kcal/mol. In order to minimize the difference between our SAPT calculations and gold-standard CCSD(T), we evaluated the residual

$$R=\left|E_{total}^{CCSD\left(T\right)/CBS}-\left(E_{non-dispersion}^{SAPT2+/CBS}+c{E}_{dispersion}^{SAPT2+/CBS}\right)\right|,$$ (34)

where (E_{non-dispersion} + E_dispersion) represents the total SAPT2+ energy, with a scale factor, c, introduced as a parameter. Minimizing this residual with respect to c yielded a scale factor of c = 0.89 that is used to scale all dispersion energies. For further details on the construction of the reference data for S101x7, please see Ref. 37. The Psi4 program was used to perform all SAPT calculations.^46–48 All structures and reference data are available at the S101x7 online repository.⁴⁰

To obtain C₆ parameters, we performed a nonlinear least square fit of the SAPT dispersion reference data using a Levenberg-Marquardt algorithm implemented in the Tinker molecular mechanics software package. To test the robustness of this parameterization, we leave out some of the data points and repeat the fit. The model with the new parameters is then evaluated on the excluded points. As a validation test case, we also evaluate the performance of the model on previously published nucleic acid interaction data.⁴⁹

The last part of the study is the evaluation of the dispersion particle mesh Ewald (DPME) method. DPME has been implemented in a locally modified version of Tinker and is available through the Tinker GitHub site.⁵⁰ To evaluate the efficiency of this implementation, the DPME method is tested on a 36 Å periodic cube containing 1600 water molecules. The PME summation was performed with a ∼1 Å grid, 5th order B-splines, and an Ewald coefficient of 0.4. Timings are computed on a 6-core, 2.66 GHz Intel Xeon processor for 100 energy evaluations using standard (non-Ewald) and DPME overlap damped dispersion.

IV. RESULTS

A. Model accuracy

The question that we are attempting to answer in this study is whether or not a damped dispersion model that is consistent with an underlying electrostatic model is demonstrably more accurate relative to ab initio data than simpler counterparts. To test this question, we employed a two-step approach. First, we compared the pure London dispersion model with our new overlap damped dispersion model on the S101x7 database. Then we compared these models to recently published work fitting the S101x7 database with a buffered 14-7 potential function.

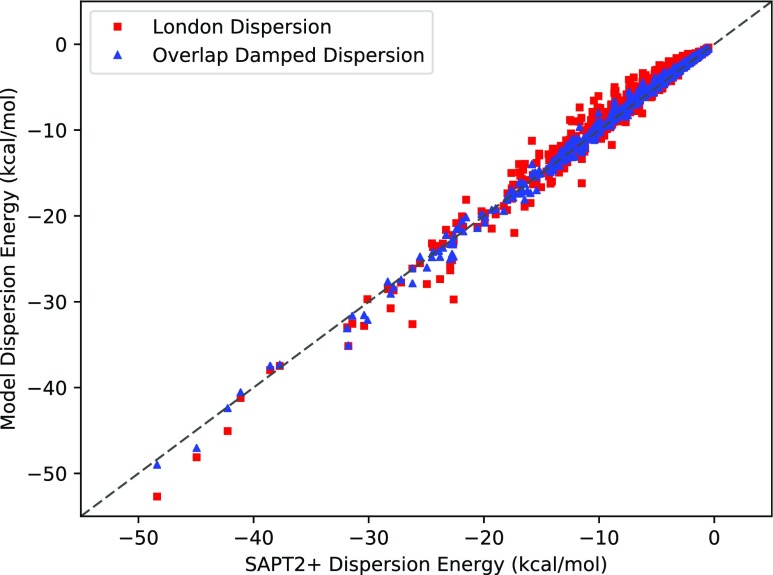
To compare the damped and non-damped 1/r⁶ dispersion potentials, we fit both to the SAPT2+ dispersion values from the S101x7 database. The results of these fits are presented in Table I and Fig. 3.

TABLE I.

Goodness of the fit on the S101x7 database (kcal/mol).

	London	Overlap damped
	dispersion	dispersion
Total root mean square error (RMSE)	1.19	0.52
Short-range RMSE (0.7–0.8× equil dist)	1.52	0.65
Long-range RMSE (0.9–1.1× equil dist)	1.04	0.46

FIG. 3.

Damped and undamped dispersion models against SAPT2+ dispersion energies. The diagonal y = x dashed line indicates perfect agreement. The overlap damped dispersion model produces a significantly improved fit.

Clearly the overlap damped dispersion potential performs better on this set of data, displaying a total root mean square error of 0.52 kcal/mol, as opposed to 1.2 kcal/mol for the pure London dispersion function. Figure 3 illustrates how the overlap damped dispersion model consistently fits the SAPT dispersion data better than the non-damped model over a range of interactions energies.

Moreover, the difference in fit quality between the short-range and long-range points shown in Table I is much smaller for the overlap damped dispersion model. This seems to indicate that the damping is having the short-range effect we hoped it might. This issue will be examined further in the robustness tests.

It is instructive to note exactly what is and is not being fit in these two models. For both models, the only parameters being fit are one C₆ coefficient per atom class. (Atom class definitions can be found in Table II. They are identical to those defined in Ref. 11.) It bears emphasizing that for the overlap damped dispersion model, the damping parameters [α_i in Eq. (26)] are not allowed to vary; they are fixed at the values determined in Ref. 11. These values, recapitulated here in Table II, describe the physical extent of an atom’s electron distribution. They were fit to the SAPT electrostatic energies of the same S101x7 database in the previous study. A comparison of the C₆ parameters between the damped and non-damped models in Table III shows that the damped dispersion model exhibits a smoother variation within classes.

TABLE II.

Fixed electrostatic damping parameters.

Element	Atom class	α (Å−1)
Hydrogen (H)	Non-polar	3.2484
	Aromatic	3.4437
	Polar, water	3.2632
Carbon (C)	sp3	3.5898
	Aromatic	3.2057
	sp2	3.1286
Nitrogen (N)	sp3	4.0135
	Aromatic	3.6358
	sp2	3.7071
Oxygen (O)	sp3, hydroxyl, water	4.1615
	Aromatic	4.3778
	sp2, carbonyl	3.7321
Phosphorous (P)	Phosphate	2.7476
Sulfur (S)	Sulfide	3.3112
	Sulfur IV	2.6247
Fluorine (F)	Organofluoride	4.4675
Chlorine (Cl)	Organochloride	3.4749
Bromine (Br)	Organobromide	3.6696

TABLE III.

Model C₆ parameters.

		London	Damped
	Atom	dispersion C6	dispersion C6
Element	class	(Å6 kcal/mol)	(Å6 kcal/mol)
Hydrogen (H)	Non-polar	3.4118	6.3960
	Aromatic	4.7993	5.7678
	Polar, water	0.9114	5.1133
Carbon (C)	sp3	28.5333	18.1732
	Aromatic	23.2125	23.3605
	sp2	26.1301	23.0103
Nitrogen (N)	sp3	33.6562	21.4927
	Aromatic	18.2114	19.7421
	sp2	30.6586	19.4543
Oxygen (O)	sp3, hydroxyl, water	25.5861	15.1656
	Aromatic	25.2794	14.8569
	sp2, carbonyl	23.1181	18.4344
Phosphorous (P)	Phosphate	46.4113	44.8658
Sulfur (S)	Sulfide	62.1844	52.8970
	Sulfur IV	39.0781	59.2558
Fluorine (F)	Organofluoride	15.0568	13.6549
Chlorine (Cl)	Organochloride	44.4420	45.7799
Bromine (Br)	Organobromide	59.9587	62.0655

The fact that a similar set of parameters produces a damped dispersion model that yields a fit that is 0.5 kcal/mol better than the non-damped model, despite having the exact same number of fitting parameters, is instructive. It shows us that the quality is not due to any extra flexibility in the fitting procedure. This hints that our model may be seizing some of the same physical reality captured in the electrostatics model.

The London dispersion model is widely used, but it is certainly not the only simple dispersion model used in molecular mechanics force fields. One alternative is Halgren’s buffered 14-7 potential.¹⁸ As discussed in Sec. II, the 1/r⁶ term is only the first term in the expansion of the dispersion energy. The buffered 14-7 potential,

$$\begin{array}{ccc}\hfill U_{vdW}=\sum _{vdw}\sum _{i\ne j}{\epsilon }_{ij}{\left(\frac{1+\delta }{{\rho }_{ij}+\delta }\right)}^7\left(\frac{1+\gamma }{{{\rho }_{ij}}^7+\gamma }-2\right),{\rho }_{ij}=\frac{r_{ij}}{{\sigma }_{ij}},& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ (35)

attempts to accommodate higher order terms by means of the buffered 1/r⁷ attractive term to describe dispersion. The buffered 14-7 van der Waals potential has been used in a number of force fields, including AMOEBA, for which a large amount of analysis involving the S101x7 database has already been done.

In a recent study, Qi, Wang, and Ren fit the buffered 14-7 van der Waals potential to the sum of the exchange-repulsion and dispersion data from the S101x7 database yielding a model they call “vdw2016.”⁵¹ Given the quality of the total van der Waals energy reported, we set out to see how the corresponding dispersion energies compared to 1/r⁶ derived functions.

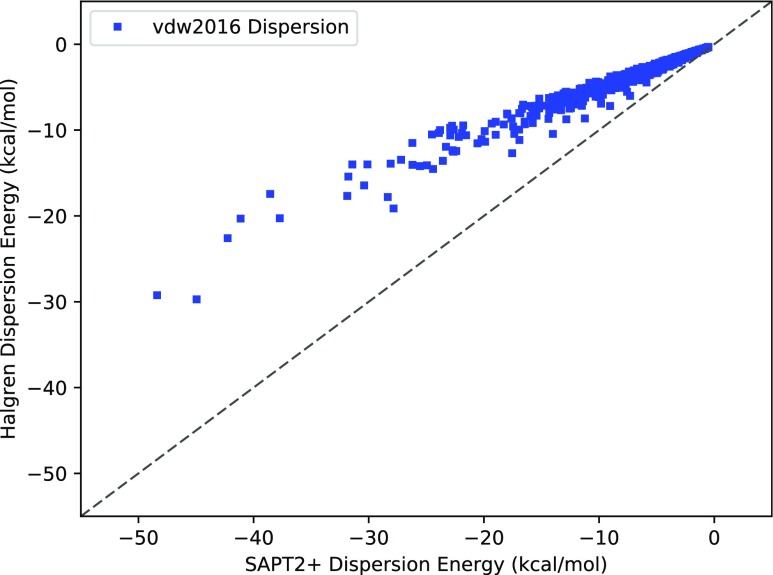
To assess the performance of the dispersion part of the vdw2016 model, we performed calculations using only the attractive part of the buffered 14-7 potential defined in Eq. (35). The vdw2016 model differs slightly from the damped and non-damped 1/r⁶ dispersion models in its number of atom classes. Where we define just 18 atom classes for the molecules in S101, Qi, Wang, and Ren found that they need 28 to accurately model the van der Waals energy. For each class, they allowed two parameters to vary: the well depth, ε, and radius, σ. Despite this greater flexibility in parameters, the vdw2016 model performs very poorly on predicting the dispersion part of the van der Waals energy. As is clearly seen in Fig. 4, it is not nearly attractive enough.

FIG. 4.

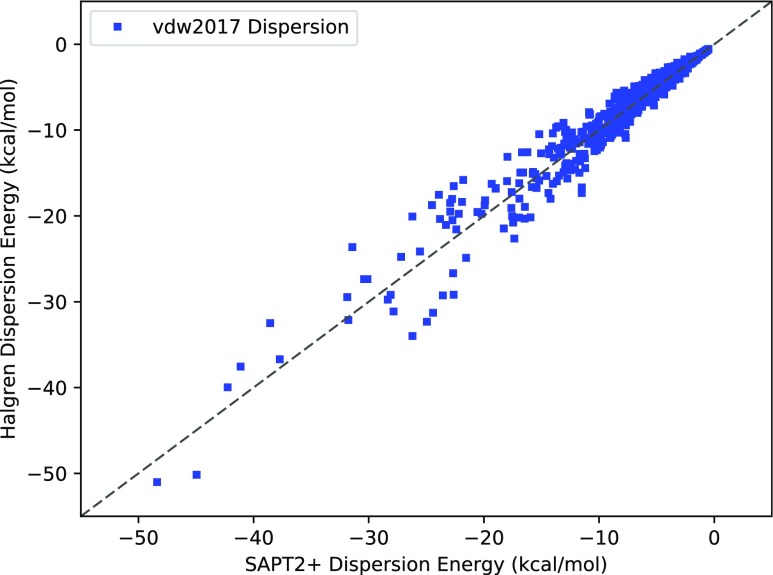
vdw2016 against SAPT2+ dispersion. The diagonal y = x dashed line indicates perfect agreement. The vdw2016 model systematically underestimates the magnitude of the dispersion energy.

This is unsurprising given the nature of the fit that was performed. Since the target data were the sum of the exchange-repulsion and dispersion energies, the fit is highly skewed by the exchange-repulsion energy. The exchange-repulsion can often be an order of magnitude large than dispersion, especially at short-range, and thus drives values obtained for the fit. This does not mean that vdw2016 does not make an adequate empirical total van der Waals model (indeed buffered 14-7 has almost always been used in its totality), but it does mean that this parameterization will not work as a stand-alone dispersion model if the goal is to reduce the cancellation of errors.

While the vdw2016 model has been shown to yield good van der Waals energies, it does so to the detriment of having a separate and interpretable dispersion model. To attempt to remedy this, we performed a second fit of the buffered 14-7 van der Waals form to the S101x7 dataset, vdw2017, where the exchange-repulsion and dispersion components were fit independently. The results of this fit are shown in Fig. 5.

FIG. 5.

vdw2017 dispersion against SAPT 2+ dispersion energies. The diagonal y = x dashed line indicates perfect agreement. The vdw2017 model RMS error is 1.6 kcal/mol.

One can see that the systematic deviation in dispersion that plagues the vdw2016 model is largely alleviated in the new fit. However, the root mean square error for vdw2107 dispersion remains at 1.6 kcal/mol. This occurs despite preserving the extra flexibility of having 28 atom classes. This seems to show that while the buffered 14-7 may have a fortunate cancellation of errors for the total van der Waals energy, a 1/r⁶ asymptotic function is a more natural fit to the pure dispersion interaction.

Comparing the overall fits of the Halgren dispersion potentials to the (damped or non-damped) London dispersion potentials, it is clear that the latter produce a better fit to the S101x7 dataset. Since the empirical buffered 14-7 potential seems to offer no advantage in accuracy for dispersion, there is no reason to further pursue it as a viable interpretable dispersion model for the purposes of this study. The next step is to assess whether the advantage in the accuracy of the damped dispersion model is worth the extra complexity and computational effort.

B. Model robustness

Although the overlap damped dispersion model shows a better fit to the S101x7 dispersion dataset, we would like to be sure that this advantage over the simpler London dispersion model is robust. To test this point, we employed two separate validation assessments. First, we interrogated the quality of the fit with regard to intermolecular distance. Here our aim was to ascertain which of the two functions is a more natural fit to the data. Second, we applied both models to cases outside of the S101 suite of dimers.

The S101x7 dataset contains sets of dimers arranged at seven different intermolecular distances (0.7, 0.8, 0.9, 0.95, 1.0, 1.05, and 1.1 times the equilibrium distance). Because this data set includes a good amount of information about close contact points, we want to be sure that our models fit the short-range points well without sacrificing asymptotic behavior. To judge the long-range fit, we excluded all of the 0.7 and 0.8 times equilibrium data points and then reoptimized the parameters. The results, presented in the “long-range” entries of Table IV, show that for this near-equilibrium regime, the London dispersion and overlap damped dispersion models give comparable fits.

TABLE IV.

Dispersion model robustness test (kcal/mol).

	London	Overlap damped
	dispersion	dispersion
Total root mean square error (RMSE)	3.12	0.67
Total mean signed error (MSE)	0.91	−0.31
Short-range RMSE (0.7–0.8× equil dist)	5.55	0.84
Long-range RMSE (0.9–1.1× equil dist)	1.15	0.59
Short-range MSE (0.7–0.8× equil dist)	2.71	−0.12
Long-range MSE (0.9–1.1× equil dist)	0.20	−0.38

The test of robustness is to then use the parameters that come out of the near-equilibrium fits and evaluate each model on the close-contact points that were left out of the fit. This shows how well the shape of the function matches the intrinsic shape of the dispersion dissociation curve at short range. As can be seen in Table IV, there is a difference between the London dispersion and overlap damped dispersion models.

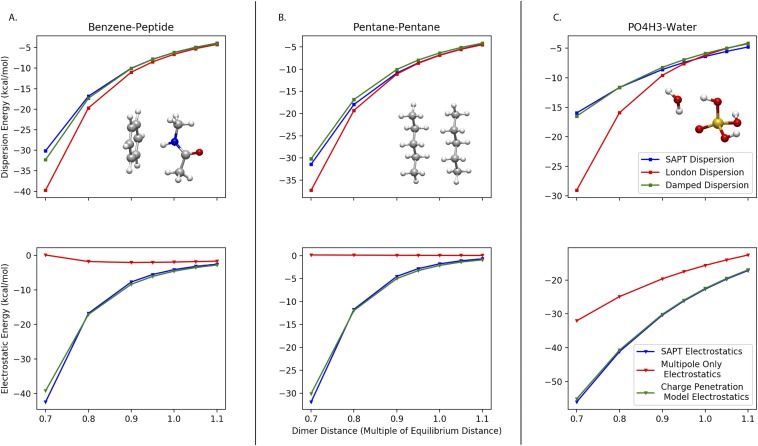
The total RMS error of the overlap damped dispersion model increases modestly when the close-contact points are included, as should be expected since these points were not included in the fit. The total RMS error of the non-damped London dispersion model, however, rises dramatically. While the long-range quality of the fit (those points that were included in the fit) is good for both models, the short-range quality (those points not included in the fit but included in the robustness test) is very different between the two models. The RMS error on the short-range test points with the overlap damped dispersion model is less than 1 kcal/mol, but the RMS error of the London dispersion model is over 5 kcal/mol. These errors are clearly caused by the inability of a simple 1/r⁶ function to adequately describe both the asymptotic and overlap regimes. Moreover, it is clear from Table IV that the overlap damped dispersion model is not sacrificing accuracy in the asymptotic regime, where it is actually slightly better than the London dispersion model. A handful of illustrative examples show how the London dispersion model fit to near-equilibrium points systematically predicts the dispersion energy to be too attractive. Figure 6 shows three examples where this effect is pronounced.

FIG. 6.

Examples of dispersion (top row) and electrostatic (bottom row) corrections for charge density overlap in (a) benzene-peptide, (b) pentane-pentane, and (c) water-PO₄H₃ interactions. The x-axis indicates dimer intermolecular distance as a fraction of each dimer’s equilibrium separation. In all three examples, the undamped “classical” model diverges from the ab initio result at short range, while the damped model follows the ab initio curve closely.

The pentane-pentane, benzene-peptide, and water-PO₄H₃ interactions are all examples of important component interactions in biology. They also exhibit the importance of damping the dispersion energy at short range for an ab inito-based force field. Clearly, including the damping function from the electrostatic model improves the agreement with SAPT dispersion data at the closest points.

We suggest that the effectiveness of this damping is fundamentally tied to the overlap in charge distributions. If we compare the non-damped London dispersion curves with their corresponding non-damped electrostatic curves (no charge penetration correction) in Fig. 6, we see that the divergence of non-damped energies from their SAPT counterparts occurs at roughly the same separation. This suggests that deviation from the 1/r⁶ asymptotic behavior in the dispersion energy at short-range is also attributable to the overlap in charge distributions. We know that the point multipole expansion model for electrostatic interactions is rigorously accurate until charge distributions begin to overlap. The fact the divergence in the point dipole derived dispersion energy occurs at a similar distance suggests that the same effect is driving this phenomenon. Moreover, the fact that the exact same parameters can be used to accommodate the change from the asymptotic behavior for both electrostatics and dispersion indicates that these are separate manifestations of the same physical reality.

Although the London dispersion model may be simpler and computationally less expensive than the overlap damped dispersion model, it is clear from this robustness test that the latter provides a much better description of the dispersion interaction that spans both the close contact and asymptotic regimes. For the S101x7 dataset, generally, the 0.8x points represent the closest intermolecular distance for liquids under ambient conditions. The robustness test shows that a force field using the overlap damped dispersion model will rely less on the cancellation of errors in this area than an undamped model. Importantly, we note that the overlap damped dispersion model retains the 1/r⁶ dependence at long range as the damping factor quickly approaches unity when charge distributions no longer overlap. This gives us confidence that the shape of the function is well suited to the intrinsic shape of the dispersion dissociation curve.

C. Model analysis and validation

Having established the capability of the overlap damped dispersion model for short-range interactions, we can ask how well this model performs on specific important systems. Dispersion plays an important role in a range of biomolecular interactions, and one should hope a good model would describe such interactions accurately. Two instructive examples are water-water interactions and benzene stacking interactions. Both also happen to be instances where charge density overlap plays a role in their short-range interactions.

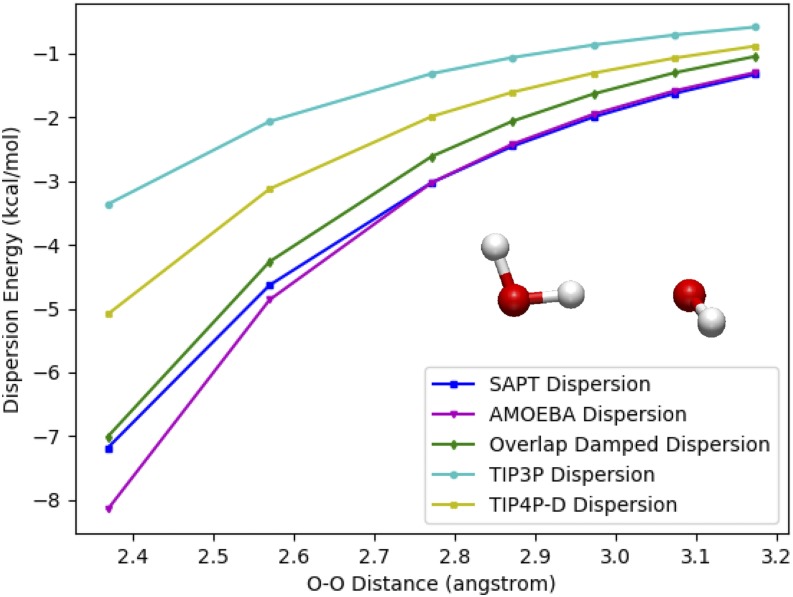
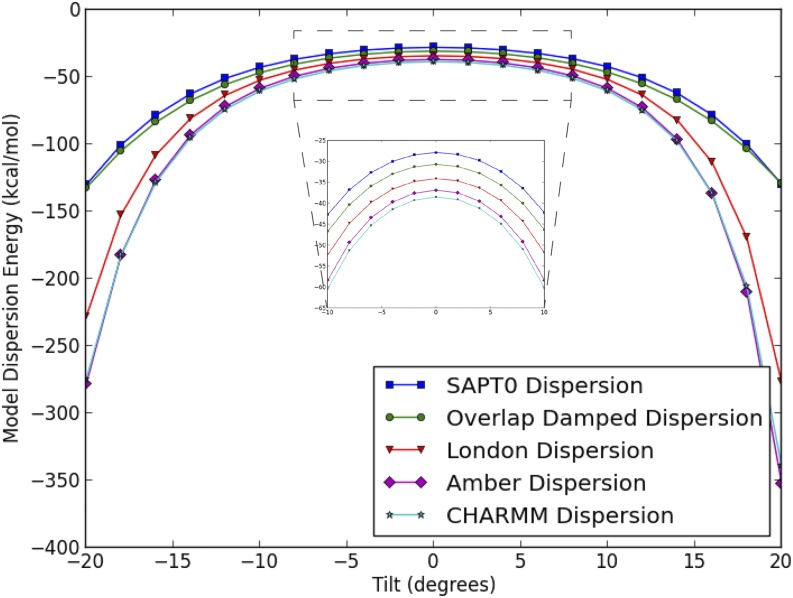
The balance between water-water and water-biomolecule interactions is known to be important to accurate simulations of biomolecules. Recently, a study by Piana and co-workers demonstrated that simulations with a few commonly used water models overpredict the compactness of disordered and partially disordered proteins.⁵² They suggest that this occurs because these typical water models underestimate water-water and water-protein dispersion interactions relative to ab initio dimer calculations. This conclusion may be overstated since for the TIP3P and SPCE models discussed, this underestimation is largely handled through the cancellation of errors within the rest of the force field. A goal of our work, however, is to reduce this reliance on such cancellation. The overlap damped dispersion model directly addresses this problem through an accurate prediction of the water dimer dispersion energy curve. As shown in Fig. 7, the damped model gives good overall agreement with the shape of the SAPT dispersion data.

FIG. 7.

Performance of various water dispersion models against SAPT2+ dispersion. Model dispersion energies are compared to SAPT2+ dispersion energies for a range of intermolecular distances of the water dimer. TIP3P⁵³ and TIP4P-D⁵² are undamped ∼1/r⁶ models, AMOEBA is the attractive, ∼1/r⁷, component of the buffered 14-7 potential with parameters from the water03 force field,¹⁹ and the overlap damped dispersion model is from this work.

Also shown in Fig. 7 is the quality of the fit of the AMOEBA water03¹⁹ model. Since this AMOEBA model is polarizable, one would expect the dispersion part of its van der Waals function should be close to the ab initio dispersion energy due to less reliance on the cancellation of errors. Indeed, near equilibrium, this model produces excellent agreement, but at short range, the dispersion energy becomes too negative. While the absolute energy error may not be large for these close points, one can see that the error in the slope is much greater. At an O–O distance of ∼2.6 Å, for example—well sampled in ambient water⁵⁴—one can see that the water03 dispersion force is slightly too attractive. Recent work has suggested that the cancellation of errors is responsible for the condensed phase behavior of AMOEBA water,^55,56 but as these compensatory components are removed for the next generation of the model, the error in the dispersion becomes more important to address directly. It is not novel to suggest that modeling the short and long-range dispersion interactions simultaneously requires a damping function. What is shown here, however, is that a simple, rationally constructed, and minimally parameterized model yields excellent agreement for this important interaction.

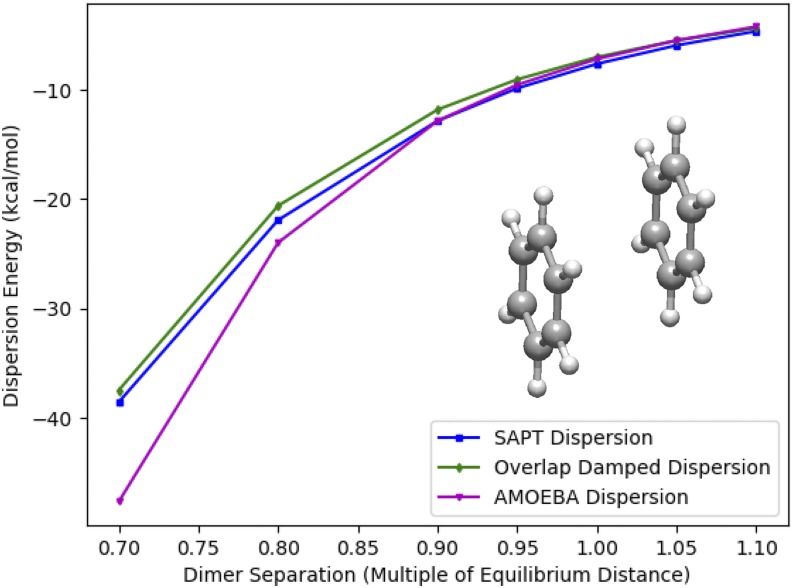
Another example interaction of importance in biomolecular modeling is the benzene “pi-stacking” interaction. In addition to being an important exemplar for the nucleic acid structure and drug binding, this interaction falls into the qualitative “dispersion-bound” category,⁵⁷ so accurately modeling it is imperative for a dispersion model. Figure 8 shows the performance of the overlap damped dispersion model against SAPT.

FIG. 8.

Benzene dimer dispersion. Model dispersion energies are compared to SAPT2+ dispersion energies for a range of intermolecular distance of the benzene dimer. The AMOEBA model functional form is the same as in Fig. 7, with parameters taken from the AMOEBA09 force field.

One can see that the agreement of the overlap damped dispersion model with the SAPT data is excellent across all benzene dimer separations. As was observed for the water dimer, the AMOEBA model produces good agreement near equilibrium, but characteristically deteriorates at short range. In particular, the divergence begins at ∼0.85 of the equilibrium separation or a ∼3.2 Å C–C distance. This distance is a close contact for liquid benzene at room temperature and 1 atm—it falls near the start of the radial distribution function.⁵⁸ As a model system, it is also close to the stacking distance between bases in B-DNA, ∼3.3 Å. Figure 8 shows that for small but relevant distances like this, the shape of SAPT dispersion is more closely matched by the overlap damped dispersion Model. Although less dramatic than with electrostatics, the deviation at a short range of the London dispersion model is due to the same phenomenon that drives the divergence in the electrostatics of the benzene dimer. Figure 8 shows us that the same treatment can be applied to fix the errors in both classical models.

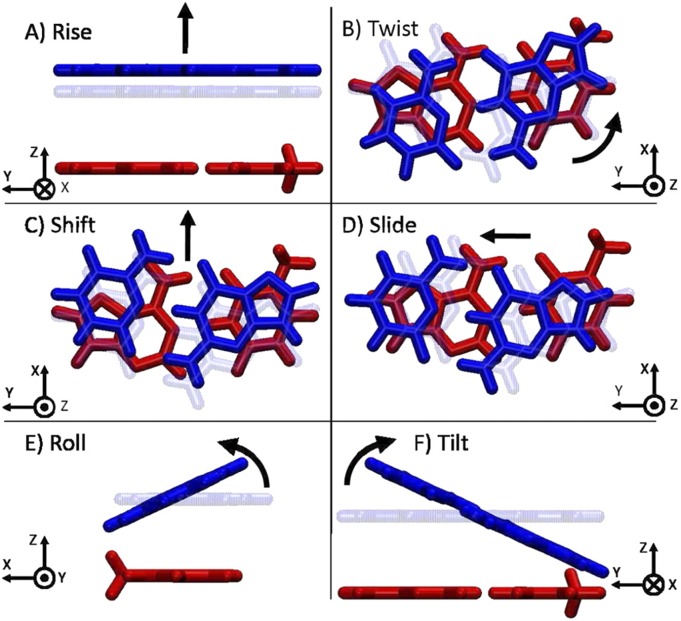
Finally, to check that the success at accurately fitting, the S101x7 dataset is not the result of overfitting, we employ a validation test on a system outside of the training set. For this purpose, we chose to test the dispersion component of nucleic acid base stacking interactions. In previously published work, Parker and Sherrill performed SAPT energy decomposition analysis calculations on a set of nucleic acid structures to evaluate the performance of current force fields. In order to assess how well a given model reproduces the energy components of base stacking interactions, Parker and Sherrill performed SAPT calculations at equilibrium and near equilibrium geometries of all ten possible two base-pair steps of DNA: AATT, ACGT, AGCT, ATAT, CATG, CGCG, GATG, GCGC, GGCC, and TATA. To generate trial geometries, Parker and Sherrill systematically varied the six geometrical degrees of freedom illustrated in Fig. 9 (shift, slide, rise, tilt, roll, and twist) for each base-pair step. See Ref. 49 for structure generation specifics and calculation details.

FIG. 9.

Illustration of the six degrees of freedom explored for nucleic acid structures. The example shown is for the AC:GT base step. Reprinted with permission from Parker and Sherrill, J. Chem. Theory Comput. 11, 4197–4204 (2015). Copyright 2015 American Chemical Society.

To see how our model measures up, we compare the published nucleic acid SAPT dispersion energies with the dispersion energies predicted by our overlap damped dispersion model using atom types, as defined in Table III. The results for this test set are shown in Fig. 10.

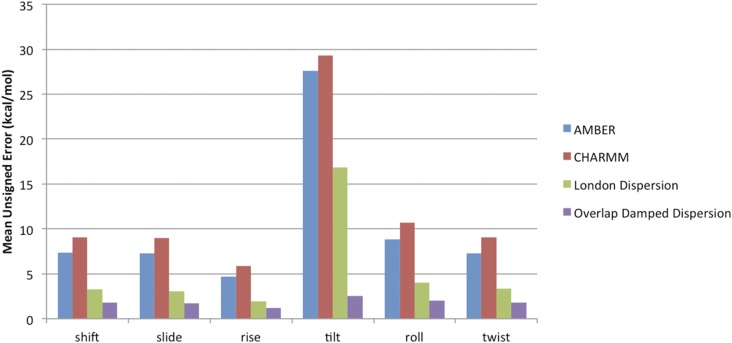
FIG. 10.

Mean unsigned error in dispersion energy for nucleic acid structures. Model error is relative to SAPT for each of the six structural parameters. The overlap damped dispersion model reduces the error in the dispersion across all six degrees of freedom. Amber and CHARMM results from Ref. 49.

There are two important features to point out in the figure. First, one will notice that the London dispersion model performs better than either the Amber or CHARMM nucleic acid dispersion models despite having an identical functional form. This, as noted by Parker and Sherrill, is primarily due to the cancellation of errors in the partial charge models. These models do not explicitly include the effects of charge penetration, so the dispersion function is called upon to absorb some of the errors in the electrostatics. What Parker and Sherrill find, however, is that while this cancellation of errors strategy produces total energies within 1 kcal/mol relative to dispersion-weighted CCSD(T^**) for structures near B-form DNA, the error in the total energy across the range of potential energy surface scans is closer to 2 kcal/mol with some errors over 10 kcal/mol even for attractive points on the surface. One can see from Fig. 10 that parameterizing a 1/r⁶ (London dispersion) model directly to SAPT reduces some of the need for the cancellation of error, but not all. The second and more important feature one observes is the agreement throughout the potential energy surface of the overlap damped dispersion model. In addition to relieving itself of the cancellation of errors burden, one can see that the damped model provides a minimum factor of two improvements in the mean unsigned error over the undamped London dispersion model for every degree of freedom. This has little to do with the behavior of the dispersion energy at equilibrium; the divergence occurs primarily for structures where the electron densities of the two base-pairs start to overlap.

As an instructive example, take the change in dispersion energy with respect to the tilt angle for the CATG base step shown in Fig. 11.

FIG. 11.

Dispersion energy of CATG interaction vs. tilt. The non-damped dispersion models uniformly overestimate the magnitude of the dispersion energy as the angle varies from equilibrium in either direction. The overlap damped dispersion model predicts the shape of the SAPT curve at both equilibrium and near-equilibrium geometries.

One can see that at equilibrium, both the London and overlap damped dispersion models predict the SAPT dispersion energy with good precision. However, as one changes the tilt angle in either direction, the dispersion energy of the undamped model diverges quickly from the SAPT while the overlap damped dispersion model follows the shape of the SAPT curve with fidelity. This trend holds across all six degrees of freedom and all ten base pair steps. Plots like Fig. 11 for each combination are available in the supplementary material. The divergence observed for non-damped models matters because it is not simply confined to high total energy areas of the DNA potential energy surface. In fact, Parker and Sherrill showed that for the stacked A-C pair (one half of the CATG base step) at a tilt angle of −15°, the total energy is −5 kcal/mol. This is only 0.5 kcal/mol above the minimum total energy of −5.5 kcal/mol. Figure 11 suggests that in order to accurately model this region of the potential energy surface without large cancellation of errors, a damped dispersion model is necessary.

V. DISPERSION PARTICLE MESH EWALD SUMMATION

Accuracy and efficiency are both important features of a molecular mechanics model. A good dispersion model must not only be accurate, but also fast to compute. While the accuracy of the overlap damped dispersion model has been solidly established in this paper, the exponentials required for its evaluation have the potential to slow potential energy calculations. To make the overlap damped dispersion model computationally efficient and tractable for use in biomolecular simulations, we have implemented the model with particle mesh Ewald (PME) summation in the Tinker molecular mechanics software package. In this section, we present a brief overview of the damped dispersion PME implementation and show how this implementation provides a substantial speed and accuracy improvement over the standard cutoff-based van der Waals implementation.

Ewald summation is classically considered to be primarily a solution to the pairwise long-range electrostatics problem. The Σ1/r electrostatic potential is conditionally convergent which makes direct computation of the electrostatic energy of a periodic system difficult. To circumvent this problem, Ewald methods split the sum into short-range and long-range parts, with short-range part being computed directly and the long-range via Fourier transformation. This separation not only makes periodic calculations possible, but also increases the speed with which the energy and gradient can be evaluated.

The same method can be applied to the dispersion energy calculation. Here we note that the following derivation is by no means original. In fact, Essman and co-workers proposed the possibility of using particle mesh Ewald summation for dispersion in their 1995 paper describing the method of smooth particle mesh Ewald summation.⁵⁹ We present here a brief summary simply to show that the inclusion of a damping term in this case does not change the ability to use the method.

The total dispersion energy, as given by Eq. (33) is

$$U_{dispersion}^{damp}=-\sum _{i\ne j}\frac{C_6^i{C}_6^j}{r_{ij}^6}{\left(f_{dispersion}^{damp}\right)}_{ij}^2.$$ (36)

This can be split into a short-range part, a long-range part, and a “self” term,

$$U_{total}^{dispersion}=U_{short-range}^{dispersion}+U_{long-range}^{dispersion}+U_{self}^{dispersion},$$ (37)

with

$$U_{short-range}^{dispersion}=\sum _{i\ne j}\frac{C_6^i{C}_6^j}{r_{ij}^6}{\left(f_{dispersion}^{damp}\right)}_{ij}^2\left(1+{\beta }^2{r}_{ij}^2+\frac{1}{2}{\beta }^4{r}_{ij}^4\right)e^{-{\beta }^2{r}_{ij}^2},$$ (38a)

$$U_{long-range}^{dispersion}=\frac{2{\pi }^{9/2}}{3V}\sum _{\mathbf{m}\ne 0}{\left|m\right|}^3\left[\frac{1}{2{\left(\pi \left|m\right|/\beta \right)}^3}\left(1-2{\left(\pi \left|m\right|/\beta \right)}^2\right)e^{\left(-{\left(\pi \left|m\right|/\beta \right)}^2+\sqrt{\pi }erfc\left(\pi \left|m\right|/\beta \right)\right)}\right]Ŝ\left(\mathbf{m}\right)Ŝ\left(-\mathbf{m}\right),$$ (38b)

$$U_{self}^{dispersion}=-\frac{{\beta }^6}{12}\sum _i{C}_i^2+\frac{{\beta }^3{\pi }^{3/2}}{6V}{\left(\sum _i{C}_i\right)}^2.$$ (38c)

Equations (38a) and (38b) are commonly known as the direct space sum and reciprocal space sum, respectively. The variable, β, is the parameter determining the Gaussian width, m is defined by the reciprocal lattice vectors, a, as m = m₁a₁^* + m₂a₂^* + m₃a₃^*_, and V is the volume of the unit cell. The structure factor, S, is defined for dispersion as

$$Ŝ=\sum _j{C}_j{e}^{i2\pi \left(\mathbf{m}\cdot {\mathbf{r}}_j\right)}.$$ (39)

The summation in Eq. (38b) is handled in the same manner as the reciprocal space sum for electrostatics. Tinker uses the FFTW (Fastest Fourier Transform in the West) package to perform the needed Fourier transforms.⁶⁰ To speed the calculation and because the dispersion energy decreases quickly with distance, Eq. (38a), the direct space sum, is truncated at a fixed distance.

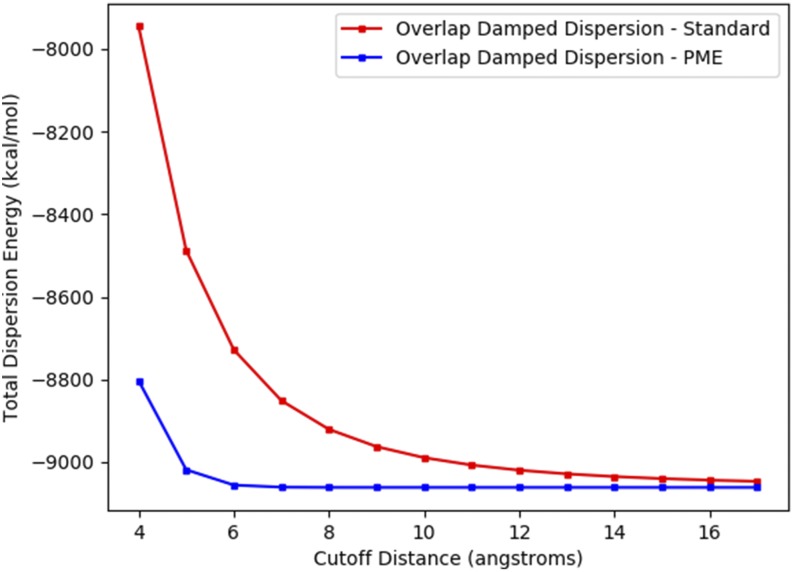
For simple dispersion PME, the choice of direct space cutoff matters very little; one simply chooses a cutoff that balances computational effort between direct space and reciprocal space. For overlap damped dispersion PME, however, some care must be taken with the choice. This is because Eqs. (38a)–(38c) as written do not strictly sum to Eq. (36). This imbalance is caused by the presence of the damping function in the direct space sum, without an equivalent component in the reciprocal space. In practice, however, this is easily overcome with a rational choice of cutoff distance. The function f_damp goes to unity very quickly with distance (much faster than 1/r⁶ goes to zero), so reasonable cutoff distances are easy to obtain. Figure 12 shows dispersion energy as a function of cutoff distance.

FIG. 12.

Cutoff distance convergence of the overlap damped dispersion model. The total dispersion energy of a 36 Å water box is shown for the standard and particle mesh Ewald (PME) implementations of the overlap damped dispersion model. The cutoff of the PME implementation refers to the cutoff of the real space summation. Computational details are enumerated in Sec. III.

One can see that for cutoffs longer than 6 Å, the energy of the PME implementation is constant due to the fact that f_damp is effectively unity for all atom pairs outside of this radius. For our model, we chose this cutoff of 6 Å to balance the direct and reciprocal space computational effort. Comparing the PME and non-PME curves in Fig. 12 illustrates an obvious advantage of using Ewald summation for dispersion interactions. While the non-PME curve converges to the asymptotic total energy very slowly with cutoff distance, the Ewald sum is converged within the 6 Å cutoff distance. The slow convergence of the non-Ewald sum is the reason many molecular mechanics models use 12–16 Å cutoffs or van der Waals correction terms for their dispersion interactions.

Because our model is not forced to use a longer cutoff distance, it can be faster to compute than standard dispersion models. As a point of reference, in the AMOEBA model, the van der Waals calculations currently comprise 10%-15% of the total calculation time. While this is certainly not the bottleneck for efficiency, it is important to keep this relative cost low. In Fig. 13, we compare energy evaluation times for our PME implementation of the model with the standard implementation for various cutoff distances.

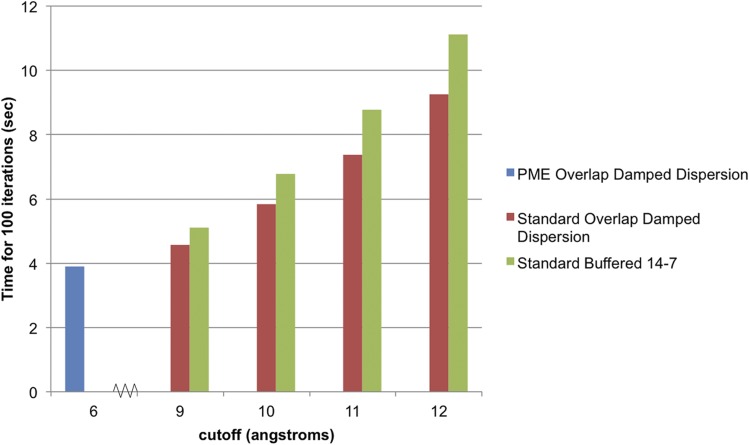
FIG. 13.

Computational effort for overlap damped dispersion. The time to complete 100 iterations of overlap damped dispersion and buffered 14-7 is plotted as a function of cutoff distance.

Figure 13 shows that for standard implementation cutoff distances of greater than 9 Å, the PME implementation of the overlap damped dispersion model provides a performance boost relative to the non-PME implementation. As a point of reference, Fig. 13 also shows the speed of the AMOEBA buffered 14-7 van der Waals functional form with its suggested cutoff distance of 12 Å. Even compared to this model, which has no required exponential evaluation, the overlap damped dispersion PME model provides a factor of 2.5 speed increase. The use of particle mesh Ewald summation minimizes the work needed in real space, thus enabling the use of our more complicated and accurate functional form without the loss of computational efficiency.

Finally, our model benefits from the utilization of simple combination rules. Using a multiplicative combination rule as indicated in Eq. (33) makes our DPME method exact. It is worth noting that many popular force fields, including all three mentioned in this paper (Amber, CHARMM, and AMOEBA), use additive combining rules for van der Waals parameters. Particle mesh Ewald methods can be used with additive combining rules in an approximate manner first proposed by Erik Lindahl and co-workers.^61,62 This method prevents what would otherwise be a discontinuity in the forces at the cutoff distance, but does introduce complexity when switching from direct to reciprocal space combining rules.¹⁵ The overlap damped dispersion PME model avoids this by explicitly parameterizing to a multiplicative combining rule. This implementation is certainly not unique or novel, but it is important to the future use of the overlap damped dispersion model in a complete force field because it shows that the benefit of a more physics-based short-range model can be realized at no increase in cost.

VI. DISCUSSION AND CONCLUSIONS

The universe of possible molecular mechanics models is immense. To discriminate between models and decide which models work best with each other, we must evaluate them based upon the goals they wish to achieve. The goal of our proposed model is use in biomolecular modeling, molecular dynamics simulation, and free energy calculations. To this end, it is important for the model to be accurate, transferable, and interpretable. Accuracy has obvious importance for describing the interactions of biological molecules with fidelity, but transferability and interpretability are no less important. In this last section, we summarize how the overlap damped dispersion model measures on each of these attributes.

The data in Table I show that when measured against symmetry adapted perturbation theory, damping is necessary to achieve 1 kcal/mol accuracy for the S101x7 data set. Interestingly, the overlap damped dispersion model is also shown to be more accurate than the attractive part of the slightly more complex buffered 14-7 potential. The root of this behavior seems to lie with the behavior of the dispersion energy at short range. Figure 6 shows that a damping function is necessary to fit both close-contact and large-separation dimer points. In most force fields, this inaccuracy at short range is handled through the cancellation of error. Relying on such cancellation, however, will not work as force fields become more accurate and, more importantly, is not guaranteed to function favorably across the wide variety of intermolecular interactions that occur in biomolecular applications.

The transferability of the overlap damped dispersion model is coupled to this idea of eliminating a reliance on the cancellation of errors. The most notable feature of the model, aside from its accuracy, is the fact that it has no additional adjustable parameters beyond the simple London dispersion model. The damping function, as presented in Sec. II, is entirely determined by the electrostatic model presented in Ref. 11 with no additional fitting or parameterization. This property of the model suggests two things. First, the overlap damped dispersion model is easily transferable to a range of chemical space because of the limited number of parameters. Evidence of this is shown in Figs. 10 and 11 where the S101-fitted parameters were used to predict the dispersion energy of nucleic acid base stacking interactions. Second, it hints at a physical reality behind the model. The fact that parameters generated through fitting to intermolecular electrostatic interactions, where density overlap is the determining factor in short-range interactions, work well for our dispersion model is a strong indicator that the same phenomenon is driving short-range dispersion.

This physical picture of short-range dispersion is what makes the overlap damped dispersion model interpretable. There are many damping functions that can be used to correct for the behavior of the dispersion energy at short range. Several of these damping functions can likely be parameterized to yield results against symmetry adapted perturbation theory that are as accurate as those presented here. What the current model offers over the alternatives is a physical interpretation. In this model, the dispersion interaction is the result of the electrostatic interaction between the instantaneous induced dipoles of two distinct charge distributions. This characteristic of the model is valuable for two reasons. First, it gives us some intuition about the nature of intermolecular interactions. Second, the interpretability of the model makes it easier to extend the model to new areas of chemical space. We make no claim that the 18 atom classes used in this paper will accurately describe all of the variety of chemistries in organic molecules. What is clear, however, is that the interpretation of the damping parameter as a measure of an atom’s charge distribution gives a clear path to determining new parameters where necessary. In this way, the overlap damped dispersion model is systematically improvable. As advanced molecular mechanics models evolve, this property will be important to their ongoing development. As models grow to explicitly take into account the short-range interactions between molecules, this dispersion model fits neatly into that framework.

Accurately modeling the short-range interactions between molecules is important to making trustworthy predictions on a range of biomolecular problems. Drug binding,⁶³ intrinsically disordered protein behavior,⁶⁴ and nucleic acid structure⁶⁵ are all areas where advanced force fields have been shown to be necessary for correct predictions. As models get more complex, the tendency is to accumulate additional parameters and with them empiricism. In the case of dispersion, this paper shows that a simple physical model can be employed that adds no new parameters while reducing the need to rely on the cancellation of errors. Moreover, combined with a dispersion particle mesh Ewald implementation, the evaluation of the necessary equations can be achieved as fast or faster than the standard implementation of simple non-damped models. This yields a simple physically interpretable model ready for the next generation of advanced molecular mechanics models. We are currently working on incorporating this model, along with the previously published charge penetration function, into a complete force field.

SUPPLEMENTARY MATERIAL

See supplementary material for plots showing the dispersion energy for ten different DNA base steps, including the energy as a function of rise, twist, shift, slide, roll, and tilt.

APPENDIX: HIGHER-ORDER DISPERSION TERMS

As indicated in the text, the full dispersion interaction between two real atoms also includes higher-order components that give rise to 1/r⁸, 1/r¹⁰, etc. terms. These terms come from instantaneous higher-order multipole interactions between atoms. Similar to the 1/r⁶ term, these can be derived from a simple Drude oscillator model of atomic polarizability. As the derivation of the origin of these terms is not readily available in the literature, we present here a derivation that continues the series started in the text.

1. Dipole-quadrupole dispersion

The derivation of the dipole-quadrupole dispersion energy starts from Eq. (5) in the text, where, instead of the dipole-dipole energy, the dipole-quadrupole interaction energy now enters into the Schrodinger equation,

$$\begin{array}{ccc}\hfill & \hfill & \frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_i^2}+\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_j^2}+\frac{2}{{\hslash }^2}\left(E-\frac{1}{2}k{z}_i^2-\frac{1}{2}k{z}_j^2\right.\hfill \\ \hfill & \hfill & \left.-U_{dipole-quadrupole}\right)\mathrm{\Psi }=0.\hfill \end{array}$$ (A1)

For a Drude oscillator dipole, interacting with a linear Drude oscillator quadrupole, the energy of the interaction is given by

$$U_{dipole-quadrupole}=\nabla \nabla \nabla U_{chg-chg}=-\frac{3\left({\mu }_i{\mathrm{\Theta }}_j+{\mu }_j{\mathrm{\Theta }}_i\right)}{r^4}.$$ (A2)

If we assume the magnitude of the dipole and quadrupole moments on i and j to be identical, combining Eqs. (A1) and (A2) yields

$$\begin{array}{ccc}\hfill \frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_i^2}+\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_j^2}+\frac{2}{{\hslash }^2}\left(E-\frac{1}{2}k{z}_i^2-\frac{1}{2}k{z}_j^2-\frac{6\mu \mathrm{\Theta }}{r^4}\right)\mathrm{\Psi }=0.& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ (A3)

We now follow a similar transformation of variables as in the text and define

$${\lambda }_1=\frac{z_i+z_j}{\sqrt{2}},{\lambda }_2=\frac{z_i-z_j}{\sqrt{2}}$$ (A4)

and rewrite Eq. (8) as

$$\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_i^2}+\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_j^2}+\frac{2}{{\hslash }^2}\left(E-\frac{1}{2}{k}_1{\lambda }_i^2-\frac{1}{2}{k}_2{\lambda }_j^2\right)\mathrm{\Psi }=0,$$ (A5)

where

$$k_1=k+\frac{6Q^2{z}_j}{r^4},k_2=k-\frac{6Q^2{z}_j}{r^4}.$$ (A6)

Equation (A6) is again a transformed version of the independent harmonic oscillator problem. It can be solved in the same manner giving

$$E\left(r\right)=\frac{1}{2}\hslash \left({\omega }_1+{\omega }_2\right),$$ (A7)

where

$$\begin{array}{ccc}\hfill {\omega }_1=\sqrt{\frac{k_1}{M}}={\omega }_0\sqrt{1-\frac{6Q{z}_j}{r^{4}k}},{\omega }_2=\sqrt{\frac{k_2}{M}}={\omega }_0\sqrt{1+\frac{6Q{z}_j}{r^{4}k}}.& \hfill & \hfill \\ \hfill & \hfill & \hfill \end{array}$$ (A8)

Applying the binomial expansion

$$\sqrt{1+x}=1+1/2x-1/8x+\cdots ,$$ (A9)

the total energy becomes

$$E\left(r\right)=\hslash {\omega }_0-\frac{36\hslash {\omega }_0}{8r^8{k}^2}+\cdots .$$ (A10)

We then subtract the energy of infinitely separated atoms. This gives the dipole-quadrupole term of the dispersion potential energy

$$E\left(r\right)=-\frac{36\hslash {\omega }_0}{8r^8{k}^2}+\cdots .$$ (A11)

It should be noted here that the spring constants, k, and frequencies, ω, are not the same as those for the dipole-dipole interaction. Therefore, just as with the dipole-dipole term, parameters are introduced to give the dipole-quadrupole dispersion model energy,

$$U^{dispersion}=-\frac{C_8^i{C}_8^j}{r^8}.$$ (A12)

2. Quadrupole-quadrupole dispersion

At the risk of repetition, the quadrupole-quadrupole derivation follows almost exactly the formulation above. The Schrodinger equation now reads

$$\begin{array}{ccc}\hfill & \hfill & \frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_i^2}+\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_j^2}+\frac{2}{{\hslash }^2}\left(E-\frac{1}{2}k{z}_i^2-\frac{1}{2}k{z}_j^2\right.\hfill \\ \hfill & \hfill & \left.-U_{dipole-quadrupole}\right)\mathrm{\Psi }=0.\hfill \end{array}$$ (A13)

In this case, we have two linear Drude oscillator quadrupoles, interacting with each other. The energy of the interaction is given by

$$U_{quadrupole-quadrupole}=\nabla \nabla \nabla \nabla U_{chg-chg}=-\frac{6{\mathrm{\Theta }}_i{\mathrm{\Theta }}_j}{r^5}.$$ (A14)

Combining Eqs. (A13) and (A14) yields

$$\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_i^2}+\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_j^2}+\frac{2}{{\hslash }^2}\left(E-\frac{1}{2}k{z}_i^2-\frac{1}{2}k{z}_j^2-\frac{6{\mathrm{\Theta }}_i{\mathrm{\Theta }}_j}{r^5}\right)\mathrm{\Psi }=0.$$ (A15)

The transformation of variables is identical to the dipole-quadrupole case

$${\lambda }_1=\frac{z_i+z_j}{\sqrt{2}},{\lambda }_2=\frac{z_i-z_j}{\sqrt{2}},$$ (A16)

which gives

$$\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_i^2}+\frac{1}{M}\frac{{\partial }^2\mathrm{\Psi }}{\partial z_j^2}+\frac{2}{{\hslash }^2}\left(E-\frac{1}{2}{k}_1{\lambda }_i^2-\frac{1}{2}{k}_2{\lambda }_j^2\right)\mathrm{\Psi }=0,$$ (A17)

where

$$k_1=k+\frac{6Q^2{z}_i{z}_j}{r^5},k_2=k-\frac{6Q^2{z}_i{z}_j}{r^5}.$$ (A18)

Equation (A17) again gives us the independent harmonic oscillator problem with the solution

$$E\left(r\right)=\frac{1}{2}\hslash \left({\omega }_1+{\omega }_2\right),$$ (A19)

where

$$\begin{array}{c}{\omega }_1=\sqrt{\frac{k_1}{M}}={\omega }_0\sqrt{1-\frac{6Q^2{z}_i{z}_j}{r^{5}k}},\hfill \\ {\omega }_2=\sqrt{\frac{k_2}{M}}={\omega }_0\sqrt{1+\frac{6Q^2{z}_i{z}_j}{r^{5}k}}.\hfill \end{array}$$ (A20)

Applying the binomial expansion as before, the total energy becomes

$$E\left(r\right)=\hslash {\omega }_0-\frac{36Q^4{z}_i^2{z}_j^2\hslash {\omega }_0}{8r^{10}{k}^2}+\cdots .$$ (A21)

Subtracting the energy of infinitely separated atoms gives the quadrupole-quadrupole term of the dispersion potential energy

$$E\left(r\right)=-\frac{36Q^4{z}_i^2{z}_j^2\hslash {\omega }_0}{8k^2{r}^{10}}+\cdots .$$ (A22)

Again, the spring constants, k, and frequencies, ω, are placeholders specific to this quadrupole-quadrupole interaction. To generalize, parameters are introduced to give

$$U_{\left(quadrupole-quadrupole\right)}^{dispersion}=-\frac{C_{10}^i{C}_{10}^j}{r^{10}},$$ (A23)

the quadrupole-quadrupole dispersion energy.

As is apparent from the above sequence of derivations, this pattern of even power dispersion coefficients continues indefinitely for as many higher-order multipole moments as one wishes to include. (We should note that at 1/r¹⁰ terms and higher, multiple multipole interactions start to be included in terms. The 1/r¹⁰ term, for example, involves a dipole-octopole component as well as quadrupole-quadrupole.) This pattern allows us to extrapolate to the full parameterized dispersion expansion

$$U_{ij}^{dispersion}=-\sum _{k\ge 6}^{even}\frac{C_k^i{C}_k^j}{r^k}.$$ (A24)