Hierarchy of transcriptomic specialization across human cortex captured by structural neuroimaging topography

Abstract

Hierarchy provides a unifying principle for the macroscale organization of anatomical and functional properties across primate cortex, yet microscale bases of specialization across human cortex are poorly understood. Anatomical hierarchy is conventionally informed by invasive tract-tracing measurements, creating a need for a principled proxy measure in humans. Moreover, cortex exhibits marked interareal variation in gene expression, yet organizing principles of cortical transcription remain unclear. We hypothesized that specialization of cortical microcircuitry involves hierarchical gradients of gene expression. We found that a noninvasive neuroimaging measure—MRI-derived T1w/T2w mapping—reliably indexes anatomical hierarchy, and captures the dominant pattern of transcriptional variation across human cortex. We found hierarchical gradients in expression profiles of genes related to microcircuit function, consistent with monkey microanatomy, and implicated in neuropsychiatric disorders. Our findings identify a hierarchical axis linking cortical transcription and anatomy, along which gradients of microscale properties may contribute to the macroscale specialization of cortical function.

Introduction

The neocortex of human and nonhuman primates exhibits interareal patterns of structural and functional variation. Cortical areas are distinguished by differences in their cellular composition, laminar differentiation, and long-range anatomical connectivity. Primate cortex is characterized by large-scale gradients of specialization in physiology and function, including in representational selectivity^1–3 and dynamics of intrinsic activity^4,5. Recent advances in large-scale high-throughput transcriptomics, which can produce genome-wide atlases of spatially distributed gene expression profiles, have also revealed a rich transcriptional architecture in humans characterized by spatially heterogeneous gene expression levels across brain areas^6–8. Interareal transcriptional diversity has been related to differences in cortical function, including the spatiotemporal structure of intrinsic network activity^7,9–11, and to spatially heterogeneous patterns of anatomical connectivity^11,12. Yet unifying principles for the macroscale organization of structural, functional, and transcriptional differences across human and nonhuman primate cortex are still unknown.

A parsimonious principle for the large-scale anatomical and functional organization of nonhuman primate cortex is the concept of cortical hierarchy^{2–4,13–16}. Anatomical hierarchy, defined as a globally self-consistent ordering of cortical areas according to characteristic laminar patterns of interareal projections, has been studied extensively in monkeys through histological tract-tracing methods^13–15. The ordering of cortical areas along the anatomical hierarchy, which situates early sensory areas toward the bottom and higher-order association areas toward the top of the hierarchical levels, has also been found to align with areas’ functional organization in sensory processing hierarchies^13,15. We hypothesized that the transcriptional architecture of human cortex is also hierarchically organized, such that the functional specialization of human cortical microcircuitry involves hierarchical gradients of gene expression levels. However, the highly invasive nature of the tract-tracing data acquisition procedures which are required to index hierarchy in nonhuman primates has thus far precluded analogous investigations of cortical organization in humans, thereby creating the need for noninvasive alternative measures.

To address these open questions, we analyzed transcriptional, anatomical, and neuroimaging data from humans and monkeys to study the hierarchical organization of cortical microcircuit specialization. We found that a structural neuroimaging measure, the MRI-derived T1w/T2w map¹⁷, provides a noninvasive proxy for anatomical hierarchy in primate cortex. To test for hierarchical gradients in gene expression, we then compared the spatial expression profiles of genes in the Allen Human Brain Atlas (AHBA) to the topography of the human T1w/T2w map. We found strong hierarchical gradients in expression profiles of genes related to synaptic physiology, cell-type specificity, and cortical cytoarchitecture, in line with monkey microanatomical measurements. Furthermore, we observed a remarkably close topographic correspondence between the T1w/T2w map and the dominant spatial pattern of gene expression variation across human cortex. Finally, we found that hierarchically patterned genes are preferentially associated with functional processes and brain disorders. Taken together, these findings suggest that the transcriptional and anatomical architectures of human cortex share a common principal axis of areal variation related to hierarchy, and that hierarchical gradients of microscale properties contribute to the macroscale specialization of cortical function.

Results

T1w/T2w maps noninvasively capture anatomical hierarchy

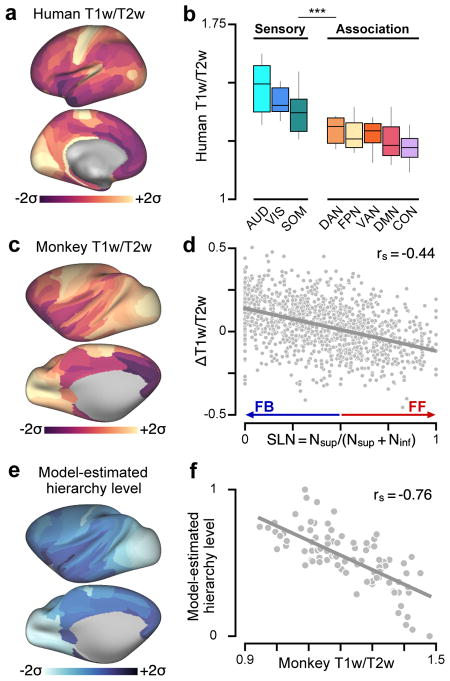
To enable the study of hierarchy in human cortex, we first sought to establish a neuroimaging measure that can serve as a noninvasive proxy for indexing anatomical hierarchy. One measure we examined was the cortical T1w/T2w map, a structural neuroimaging map defined by the contrast ratio of T1- to T2-weighted (T1w/T2w) magnetic resonance images. The cortical T1w/T2w map has been proposed as an in vivo measure that is sensitive to regional variation in gray-matter myelin content, based on its close correspondence with myelin stained sections in histological validation studies, and its recapitulation of known neuroanatomical borders between cyto- and myelo-architecturally delineated areas^17,18 (see Discussion). Motivated by the empirical observation that T1w/T2w map values are high in primary sensory cortex (visual, somatosensory, auditory) and low in association cortex, homologously in human and monkey (Fig. 1a–c, Supplementary Fig. 1), and stably across individuals, we hypothesized that the group-averaged cortical T1w/T2w map, through an inverse relationship with hierarchy, provides a noninvasive correlate for areas’ hierarchical positions.

Figure 1.

T1w/T2w neuroimaging maps noninvasively capture the hierarchical organization of primate cortex. (a) The parcellated group-averaged (N=339) human T1w/T2w map exhibits high values in primary sensory cortical areas relative to association areas. (b) Human T1w/T2w map values are significantly lower in functionally defined association networks than in sensory networks (P < 10⁻⁵; two-sided Wilcoxon signed-rank test on N=6608 paired differences) (Supplementary Fig. 1c, d). Box plots mark the median and inner quartile ranges for areas in each network, and whiskers indicate the 95% confidence interval. (c) The parcellated group-averaged (N=19) macaque monkey T1w/T2w map topography is similar to that of the human. (d) Interareal variation in the T1w/T2w map correlates with the laminar specificity of directed feedforward (FF) and feedback (FB) projections in monkey cortex, as quantified by the fraction of labeled supragranular layer neurons (SLN) in the source area. High and low SLN correspond to FF and FB projection motifs, respectively. SLN significantly correlates with pairwise difference (target minus source) in areal T1w/T2w map values across N=1243 directed projections (r_s = −0.44, P < 10⁻⁵; Spearman rank correlation). (e) Anatomical hierarchy levels across cortical areas are estimated by fitting a generalized linear model to predict projections’ SLNs as a function of pairwise hierarchical distance. (f) Model-estimated anatomical hierarchy levels are highly anti-correlated with T1w/T2w map values across N=89 areas of monkey cortex (r_s = −0.76, P < 10⁻⁵). T1w/T2w map values and model-estimated hierarchy levels in panels a, c, and e are standardized (i.e., z-scored) and shown in units of standard deviations (σ) from the mean.

We validated the T1w/T2w map as a proxy for hierarchy in monkey cortex by comparing T1w/T2w map values to model-estimated anatomical hierarchy levels, derived from conventional tract-tracing approaches that quantify long-range interareal projections and their laminar specificity¹⁵. These laminar connectivity data, which include only direct cortico-cortical projections, are used to specify a globally optimal hierarchical ordering of cortical areas, such that lower areas send feedforward projections to higher areas, and higher areas send feedback projections to lower areas^13–15,19 (Supplementary Fig. 2). Feedforward and feedback projections primarily originate from the supragranular and infragranular cortical layers, respectively^13,15. At the level of individual projections, we found that the difference in T1w/T2w map values between connected areas is correlated with the laminar feedforward/feedback structure of the connection (Fig. 1d), more strongly in high-T1w/T2w sensory areas than in low-T1w/T2w association areas (Supplementary Fig. 3). Global anatomical hierarchy levels were estimated by fitting a generalized linear model to pairwise laminar projection data^15,19 (see Methods). We found a strong negative correlation between model-estimated anatomical hierarchy levels and T1w/T2w map values (r_s = −0.76, P < 10⁻⁵; Spearman rank correlation) (Fig. 1e, f).

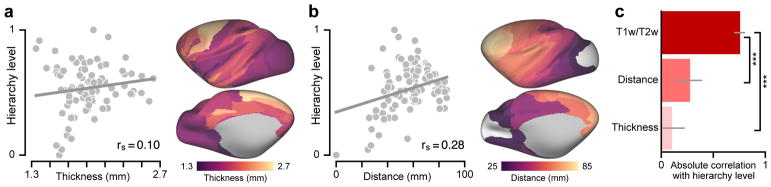
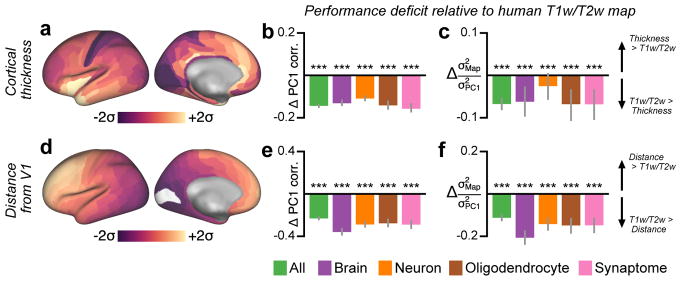
How well does the T1w/T2w map capture estimated anatomical hierarchy levels, relative to other putative proxy measures? We compared the performance of the T1w/T2w map against two alternative proxy candidates derived from structural MRI²⁰: the map of cortical thickness, as cortex is generally thicker in association cortex than sensory cortex; and the map of geodesic distance from primary visual cortex, which defines a posterior-anterior gradient. We found that the T1w/T2w map was more strongly correlated with model-estimated hierarchy than were either of the two other candidate proxy measures (Fig. 2). This finding, together with the observed inter-species homology¹⁸, supports the use of the T1w/T2w map as a noninvasive correlate of hierarchy across human cortex, for which lack of invasive tract-tracing data precludes a more direct characterization of anatomical hierarchy per conventional approaches.

Figure 2.

Model-estimated anatomical hierarchy in monkey cortex is better captured by the group-averaged T1w/T2w map than by two other candidate proxy measures derived from structural MRI. (a) Correlation between hierarchy and cortical thickness. (b) Correlation between hierarchy and geodesic distance from primary visual cortex (V1), which follows a rostro-caudal gradient. (c) Comparison of hierarchy correlation values for the T1w/T2w map, cortical thickness map, and map of geodesic distance from area V1. The T1w/T2w map is much more strongly correlated with model-estimated anatomical hierarchy than the other two maps (P < 10⁻⁵ for both maps). Grey lines mark the jackknife estimate of standard error. Statistical significance is calculated by a two-sided test of the difference between dependent correlations (*, P < 0.05; **, P < 10⁻²; ***, P < 10⁻³). Correlations and statistical significance values were computed across N=89 cortical areas.

Hierarchical gradients in cortical microcircuit specialization

We hypothesized that the large-scale organization of cortical microcircuit specialization—that is, areal variation in synaptic and cellular composition with functional relevance—may involve hierarchical gradients of gene expression levels across human cortex. To test this hypothesis, we examined areal patterns of cortical gene expression variation from the AHBA in relation to the T1w/T2w map. The AHBA is a transcriptional atlas that contains gene expression levels measured with DNA microarray probes and sampled from hundreds of neuroanatomical structures in the left hemisphere across six normal post-mortem human brains⁶. From these data, we calculated group-averaged gene expression profiles across 180 unilateral cortical areas using a multimodal parcellation from the Human Connectome Project²¹ (Fig. 3, see Methods). We then computed correlations of these expression profiles with the human T1w/T2w map. Because of the strong inverse relationship found between the T1w/T2w map and model-estimated hierarchy (Fig. 1), then by extension, expression levels of genes which negatively correlate with the T1w/T2w map tend to increase with progression to higher hierarchical levels—i.e., from sensory to association cortex—and thus exhibit a positive hierarchical gradient; conversely, genes with positive T1w/T2w map correlations (TMCs) exhibit decreasing expression levels along the hierarchical axis. To support the validity of our interpretations, we compared the TMCs of microcircuitry-related gene expression profiles in human cortex to TMCs with more direct anatomical measures in monkey cortex, with a focus on cytoarchitecture, inhibitory interneuron densities, and synaptic processes (Fig. 4).

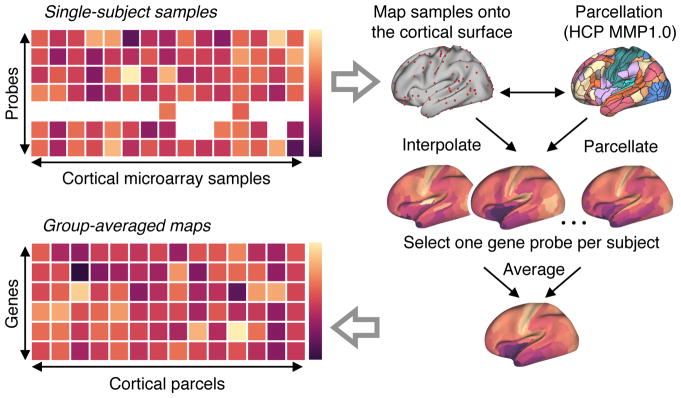
Figure 3.

Procedure for generating group-averaged parcellated maps of gene expression levels. All analyses of gene expression patterns used group-averaged parcellated expression maps derived from the Allen Human Brain Atlas (AHBA) (see Methods for details). The AHBA contains genes expression levels measured with DNA microarray probes and sampled from hundreds of neuroanatomical structures in the left hemisphere across six normal post-mortem human brains. First, cortical samples for each subject were mapped from volumetric space onto that subject’s native reconstructed two-dimensional cortical surface. Second, parcellated gene expression maps were constructed, for each subject, using the Human Connectome Project’s (HCP) Multi-Modal Parcellation (MMP1.0) of the left cortical surface into 180 contiguous areas. For genes profiled by multiple microarray probes, we selected a single representative probe for each subject. Finally, a group-level parcellated expression map for each unique gene was computed by averaging parcellated expression levels across subjects’ selected gene probes (see Methods).

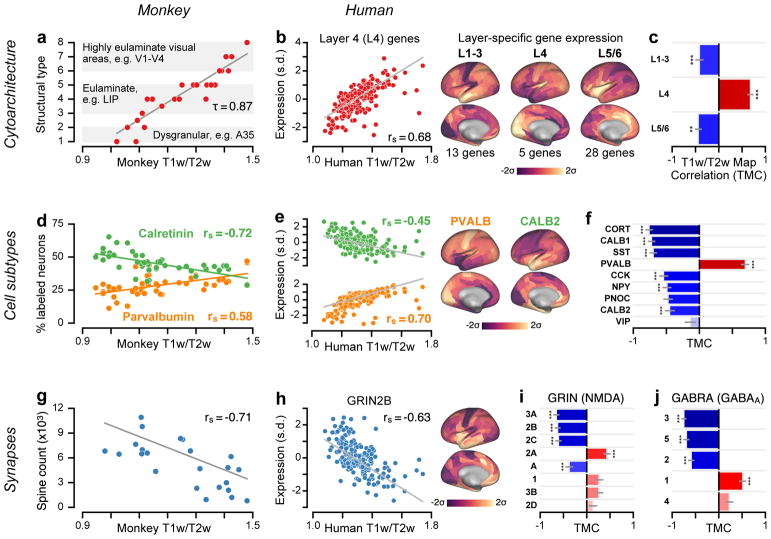
Figure 4.

Group-averaged T1w/T2w maps capture specialization of cortical microcircuitry in humans and nonhuman primates. (a) Cortical cytoarchitectural type is very strongly correlated with the macaque monkey T1w/T2w map across N=29 areas (τ = 0.87; P < 10⁻⁵; two-sided Kendall’s tau-b correlation) (r_s = 0.96; P < 10⁻⁵; Spearman rank correlation). (b) The average expression map of 5 genes preferentially expressed in human granular layer 4 (L4) is positively correlated with the human cortical T1w/T2w map (r_s = 0.68; P < 10⁻⁵; Spearman rank correlation), consistent with a more prominent granular L4 in sensory than association cortex. Expression is plotted in units of standard deviations (s.d.; σ) from the mean. (c) Average expression maps of laminar-specific genes show significant T1w/T2w map correlations (TMCs). L1–3: supragranular layers 1–3 (r_s = −0.42; P < 10⁻⁵); L5/6: infragranular layers 5 and 6 (r_s = −0.44; P = 2.49 * 10⁻³). (d) The T1w/T2w map captures areal variation in the relative proportions of calretinin- (r_s = −0.72; P < 10⁻⁵) and parvalbumin-expressing (r_s = 0.58; P = 1.7 * 10⁻⁵) inhibitory interneurons across N=47 areas of monkey cortex. (e) Genes coding for calretinin (CALB2; r_s = −0.45; P < 10⁻⁵) and parvalbumin (PVALB; r_s = 0.70; P < 10⁻⁵) exhibit homologous hierarchical gradients in human cortex. (f) TMCs of genes coding for markers of specific inhibitory interneuron cell types. (g) Basal-dendritic spine counts on pyramidal cells are significantly anti-correlated with the monkey T1w/T2w map across N=23 areas (r_s = −0.71; P = 1.6 * 10⁻⁴). (h) The gene coding for the NMDA receptor subunit NR2B (GRIN2B) exhibits a negative TMC (r_s = −0.63; P < 10⁻⁵). (i, j) TMCs of genes coding for distinct subunits of the excitatory NMDA receptor and inhibitory GABA_A receptor. For comparison with monkey measurements in panels a, d, and g, Spearman rank correlations with model-estimated hierarchy levels (instead of T1w/T2w map values) were −0.92 for cytoarchitectural type; 0.72 (−0.77) for relative calretinin (parvalbumin) expressing interneuron proportion; and 0.78 for spine count. Statistical significance in panels c, f, i, and j is calculated using a spatial autoregressive model to account for spatial autocorrelation, Bonferroni-corrected by the number of genes in each set (*, P < 0.05; **, P < 10⁻²; ***, P < 10⁻³), and grey lines mark the jackknife estimate of standard error (see Methods).

An established feature of microcircuit specialization that varies along the cortical hierarchy is the degree of laminar differentiation in local cytoarchitecture²²: primary sensory cortex is highly laminated and exhibits a thick and well-defined granular layer, whereas association cortex is characterized by decreasing laminar differentiation and a gradual loss of the granular layer with progression up hierarchical levels. In monkey cortex, we found that areas’ cytoarchitectural types²² correlate strongly with their T1w/T2w map values (Fig. 4a). In human cortex, we examined average expression profiles of genes reported to be preferentially expressed in specific cortical layers²³. Consistent with the cytoarchitectural trends observed in monkey cortex, we found a positive TMC for granular (L4) layer-specific genes, and negative TMCs for supra- (L1–3) and infra-granular (L5/6) layer-specific genes (Fig. 4b, c). These findings demonstrate that the noninvasive T1w/T2w map captures anatomical gradients related to cortical hierarchy in humans and nonhuman primates.

To gain further insight into microcircuit bases of hierarchical specialization, we examined the spatial distributions of markers for different inhibitory interneuron cell types. Inhibitory interneuron cell types fall into several biophysically distinct classes which differ in their synaptic connectivity patterns, morphology, electrophysiology, and functional roles^24,25. In monkey cortex, we found that immunohistochemically measured densities of parvalbumin- and calretinin-expressing interneurons exhibit positive and negative TMCs, respectively (Fig. 4d). Consistent with these trends, in human cortex we found corresponding negative and positive hierarchical gradients in the expression profiles for the genes which code for parvalbumin and calretinin (Fig. 4e). In general, we observed strong hierarchical gradients in transcriptional markers for a number of inhibitory interneuron cell types²⁴ (Fig. 4f), as well as for composite gene expression profiles associated with specific neuronal cell types derived from RNA sequencing in individual human neurons²⁶ (Supplementary Fig. 4). These findings suggest that hierarchical gradients in neuronal cell-type distributions may contribute to sensory–association specialization of cortical microcircuit function.

Gradients in the composition of synapses may endow cortical areas with diverse physiological properties required to perform the various computations which underlie specialized cognitive and behavioral functions. For instance, local increases in the strength of recurrent excitatory connectivity may endow cortical circuits in association cortex with extended temporal integration supporting cognitive computations^4,19,27. One putative microanatomical correlate for the strength of recurrent synaptic excitation in local cortical microcircuits is the number of excitatory synapses on pyramidal neurons, which can be quantified by counting the number of spines on pyramidal cell dendrites. In monkey cortex, we found a strong negative TMC for basal-dendritic spine counts on cortical pyramidal neurons²⁸ (Fig. 4g). This finding suggests a gradient of increasing local recurrent excitation strength along the cortical hierarchy in primates¹⁹.

Distinct subunits of synaptic receptor proteins that mediate neurotransmission are differentially expressed across neuronal cell types and produce physiologically diverse synaptic properties. In the AHBA dataset, we examined expression profiles of genes that code for various excitatory and inhibitory synaptic receptor subunits (Fig. 4h–j). The gene GRIN2B, which codes for a glutamatergic NMDA receptor subunit that mediates synaptic excitation preferentially in association cortex²⁹, exhibited a strong negative TMC. This result suggests increased recurrent excitatory strength in association cortical areas and is consistent with the spine count gradient observed in monkey. Gene sets coding for neuromodulatory synaptic receptor subunits also contain strong positive and negative TMCs (Supplementary Fig. 5). The positive and negative TMCs reported in Fig. 4i, j suggest that hierarchical gradients in local excitatory and inhibitory synaptic machinery contribute to the functional specialization of cortical microcircuitry^4,19.

T1w/T2w topography captures the dominant axis of transcriptional variation across human cortex

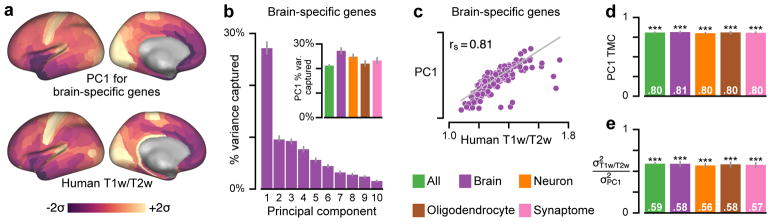
How well does the T1w/T2w map capture areal variation in the transcriptional architecture of human cortex in general? We performed principal component analysis (PCA) to identify the dominant areal patterns of gene expression variation (Fig. 5, Supplementary Fig. 6). To test for generality of effects, we analyzed categorical sets of genes which are preferentially expressed in human brain tissue, neurons, oligodendrocytes, and synaptic compartments^30,31. To assess statistical significance of effects, we developed a novel method for spatial autocorrelation-preserving permutation testing to generate random surrogate maps (Supplementary Fig. 7, see Methods). The first principal component (PC1) is defined as the spatial map that captures the greatest fraction of total gene expression variance across cortical areas (Fig. 5a). Across all five gene sets, PC1 captures a large fraction of gene expression variance (range: 21–27%, more than twice PC2) (Fig. 5b, Supplementary Fig. 6), revealing that cortical gene expression patterns are effectively low-dimensional.

Figure 5.

The group-averaged T1w/T2w map captures the dominant axis of gene expression variation across human cortex. (a) The first principal component (PC1), here for a set of brain-specific genes, is the areal map that linearly captures the maximum variation in gene expression. Both maps are standardized (i.e., z-scored) and shown in units of standard deviations (σ) from the mean. (b) PC1 captures a large fraction of total gene expression variance. Inset: Variance captured by PC1 for five categorical gene sets: all genes, and genes preferentially expressed in brain, neurons, oligodendrocytes, and synaptic processes (see Methods). (c) PC1 for the brain-specific gene set is highly correlated with the T1w/T2w map (r_s = 0.81; P < 10⁻⁵; Spearman rank correlation). (d) Across all sets, PC1 exhibits a highly similar areal topography to the T1w/T2w map (TMC range: 0.80–0.81; P < 10⁻⁵ for each). (e) Gene expression variance captured by the T1w/T2w map ( ${\sigma }_{T1w/T2w}^2$) relative to PC1 ( ${\sigma }_{PC1}^2$). Statistical significance in panels d and e is calculated through permutation testing with surrogate maps that preserve spatial autocorrelation structure (*, P < 0.05; **, P < 10⁻²; ***, P < 10⁻³), and grey lines in panels b, d, and e mark the bootstrap estimated 95% confidence interval (see Methods).

Remarkably, we found that T1w/T2w map topography is strongly correlated with PC1, i.e., the dominant spatial pattern of gene expression variation, across all tested gene sets (TMC range: 0.80–0.81; P < 10⁻⁵) (Fig. 5c, d). Like the T1w/T2w map, PC1 exhibits relatively high values in primary sensorimotor areas and low values in association areas (Supplementary Fig. 8), consistent with a prior report on a subset of the AHBA dataset⁶. We also quantified how much gene expression variance is captured by the T1w/T2w map (see Methods). We found that across all gene sets the T1w/T2w map captures more than half as much variance as PC1, which by construction is the spatial map that captures the maximum possible gene expression variation (Fig. 5e). We then compared performance of the T1w/T2w map against the two alternative candidate proxy maps, cortical thickness and geodesic distance from primary visual cortex (Fig. 6). Across all gene sets, the T1w/T2w map was more strongly correlated with PC1 and captured more gene expression variance than either alternative map. The close alignment between T1w/T2w map topography and spatial gene expression variation suggests that the dominant axis of transcriptional variation in human cortex relates to hierarchy. Furthermore, the robustness of our findings across gene sets demonstrates that this axis captures areal variation in general across a number of neurobiological processes.

Figure 6.

Principal component analysis (PCA) shows that the dominant mode of gene expression variation (PC1) is better captured by the group-averaged T1w/T2w map than by other candidate proxies. (a) Parcellated group-averaged (N=339) map of human cortical thickness. (b) The difference in correlation with PC1 between the T1w/T2w map and the cortical thickness map, i.e., (r_s(T1w/T2w, PC1) − r_s(Thickness, PC1)), across several categorical gene sets. Negative values indicate that the T1w/T2w map is more strongly correlated with PC1 than is the thickness map. (c) The difference in the fraction of gene expression variance captured, relative to the variance captured by PC1, between the T1w/T2w map and the cortical thickness map, i.e., $\left({\sigma }_{T1w/T2w}^2-{\sigma }_{\mathit{Thickness}}^2\right)/{\sigma }_{PC1}^2$, across several categorical gene sets. Negative values indicate that the T1w/T2w map captures more gene expression variance than does the thickness map. (d) Parcellated map of geodesic distance from primary visual cortical area V1. Maps in panels a and d are standardized (i.e., z-scored) and shown in units of standard deviations (σ) from the mean. (e) The difference in correlation with PC1 between the T1w/T2w map and the map of distance from area V1. (f) The difference in the fraction of gene expression variance captured, relative to the variance captured by PC1, between the T1w/T2w map and the map of distance from V1. Statistical significance in panels b and e is calculated by a two-sided test of the difference between dependent correlations (N=180), and in panels c and f, through permutation testing with surrogate maps that preserve spatial autocorrelation structure (*, P < 0.05; **, P < 10⁻²; ***, P < 10⁻³). Grey lines in panels b, c, e, and f mark the bootstrap estimated 95% confidence interval.

What effects may be driving the outliers which deviate from the otherwise strikingly strong correspondence between gene expression PC1 and the T1w/T2w map shown in Fig. 5c? We constructed a map of the absolute deviation (i.e., residual) of each cortical area from the best-fit line illustrated in Fig. 5c (Supplementary Fig. 9a), and noticed that the anomalously large residuals were preferentially located in areas of cortex with large gradients in local T1w/T2w map values (Supplementary Fig. 1a). Due to sparse cortical sampling in the AHBA (203 ± 27 samples per subject, 1220 total across six subjects), substantial spatial interpolation was required to produce our parcellated gene expression maps (Fig. 3). We therefore hypothesized that large discrepancies were due to relatively poor gene expression estimates in regions with large T1w/T2w gradients. To test this quantitatively, we computed for each area a measure of local T1w/T2w gradient and compared these values to the PC1 residuals. We indeed found a strong correlation between local T1w/T2w gradient and PC1 residual magnitude (r_p = 0.70, P < 10⁻⁵; Pearson correlation) (Supplementary Fig. 9b, c). Our prediction was further supported by a validation of our key results with an earlier group-averaged (N = 69) T1w/T2w map from the Conte69 dataset¹⁷. Results were highly consistent, and the Conte69 T1w/T2w map tended to yield stronger TMC values than did the HCP T1w/T2w map (Supplementary Fig. 10). Compared to the smoother Conte69 map, the HCP map contains more sharply separated T1w/T2w values among neighboring cortical parcels (autocorrelation space constant: 6.38 mm for Conte69 vs 6.16 mm for HCP), likely due to differences in surface registration²¹ and smoothing¹⁷. Together, these findings suggest that the remarkable relationships reported in this study, between cortical structure and transcription in humans, may be systematically underestimated, due to the limited spatial resolution in the AHBA dataset.

Stably expressed genes preferentially exhibit hierarchical gradients

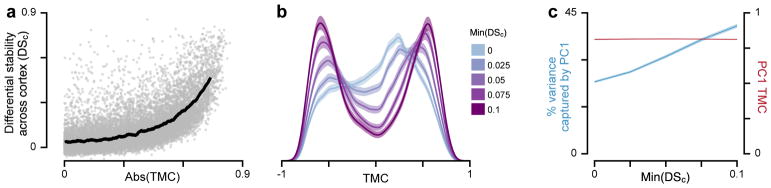
Genes that are especially vital to normal healthy cortical function may be more likely to have consistent spatial expression profiles across individual subjects. Hawrylycz and colleagues defined differential stability (DS) as the mean pairwise correlation between subjects’ individual gene expression profiles, which they found predicts association with key neurobiological functions when computed across all (i.e., cortical and subcortical) brain structures⁷. We found a strong nonlinear and positive relationship between DS computed across cortical areas (DS_c) and TMC magnitude (Fig. 7a). To gain additional insight into this relationship, we explored the impact of filtering genes through progressively higher DS_c thresholds on the TMC distribution. Exclusion of low-DS_c genes greatly alters the shape of the TMC distribution, collapsing the prominent peak centered near zero while progressively producing two roughly symmetric bimodal peaks at strong TMCs (Fig. 7b). Furthermore, exclusion of low-DS_c genes strongly increases the fraction of transcriptional variance captured by PC1 (Fig. 7c), rendering gene expression patterns more quasi-one-dimensional. Together, these findings suggest that high-DS_c genes—that is, genes whose spatial expression profiles in cortex are highly stable across individuals—preferentially exhibit strong positive and negative hierarchical gradients.

Figure 7.

Expression profiles of genes which exhibit strong hierarchical gradients tend to be relatively stable across individuals. (a) Differential stability across cortex (DS_C), defined as the mean pairwise Spearman rank correlation between subjects’ cortical gene expression maps, as a function of the magnitude of the T1w/T2w map correlation (TMC) for all 16088 genes (r_s = 0.66, P < 10⁻⁵; Spearman rank correlation). Each gray dot represents a single gene. The black line indicates the average value in a sliding window of size 600 points. (b) Filtering genes by a threshold on DS_C alters the shape of the TMC distribution. Increasing the DS_C threshold filters out genes whose cortical expression profiles are not relatively consistent across subjects. The trough which develops near TMC=0 suggests that high-DS_C genes preferentially exhibit strong hierarchical gradients. (c) Thresholding genes by DS_C substantially increases variance captured by the first principal component (PC1) of gene expression variation (blue), whereas it has little effect on PC1’s TMC (red). Shaded regions in panels b and c mark the bootstrap estimated 95% confidence interval. Number of genes which exceed each DS_C threshold: 0, 14509; 0.025, 12169; 0.05, 9494; 0.075, 7332; 0.1, 5853.

Hierarchically expressed genes are enriched for functional and disease annotations

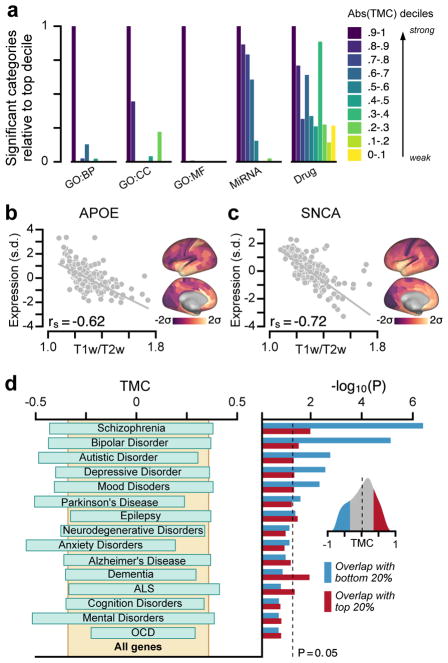
To examine the functional roles of genes with strong hierarchical gradients, we tested for their preferential enrichment in gene sets defined by functional and disease ontologies. We found that genes with stronger TMCs are enriched in more functional categories, relative to genes with weaker TMCs, for all functional gene ontologies tested^7,32: biological processes, cellular components, molecular functions, microRNA binding sites, and drug targets (Fig. 8a). These results suggest that diverse key cell-biological processes contribute to hierarchical differentiation of cortical microcircuitry. Finally, we examined whether hierarchical expression is a preferential property found in group-averaged profiles of genes associated with psychiatric and neurological disorders. For instance, we found that the genes APOE and SNCA, which are strongly linked to Alzheimer’s and Parkinson’s diseases, respectively³³, exhibit robust negative TMCs and are therefore more highly expressed in association cortex (Fig. 8b, c). For a systematic examination, we statistically quantified the enrichment of genes with strong hierarchical variation in disease-related gene sets⁷, obtained from the DisGeNet database³⁴. We found that genes with strongly negative TMCs were significantly over-represented across multiple disease-related gene sets (Fig. 8d). In particular, gene sets for schizophrenia, bipolar disorder, autistic disorders, and depressive disorders are significantly enriched with strongly negative TMC genes which are more highly expressed in association cortex. These findings suggest that brain disorders involve differential impacts to areas along the cortical hierarchy.

Figure 8.

Hierarchical variation relates to enrichment in neurobiological function and brain disorders. (a) Genes with strong TMCs are overrepresented in functional annotations across multiple gene ontologies (GOs). BP, biological process; CC, cellular component; MF, molecular function; MiRNA, microRNA binding sites; Drug, drug targets. (b, c) Two key risk genes for neurodegenerative disorders, APOE for Alzheimer’s disease and SNCA for Parkinson’s disease, exhibit strongly negative TMCs, with higher expression levels in association cortex relative to sensory cortex (APOE: r_s = −0.62, P < 10⁻⁵; SNCA: r_s = −0.72, P < 10⁻⁵; Spearman rank correlation). APOE is a leading risk gene for Alzheimer’s disease. The ε4 allele of APOE is the largest genetic risk factor for late-onset Alzheimer’s disease. SNCA (PARK1/PARK4) is a key risk gene for Parkinson’s disease. Duplication of SNCA is risk factor for familial Parkinson’s disease with dominant inheritance. SNCA codes for the alpha-synuclein protein which is the primary component of Lewy bodies, a biomarker of Parkinson’s disease. (d) Genes with strong negative TMCs are overrepresented in multiple gene sets associated with neuropsychiatric disorders. Left: 20–80% percentile range of TMCs for each disease gene set. Right: Enrichment is quantified by the hypergeometric test, which assesses the statistical significance of overlap between each gene set and the top (red) or bottom (blue) 20% TMC genes. Inset: Distribution of TMCs across all genes. Expression in panels b and c is plotted in units of standard deviations (s.d.; σ) from the mean for each map.

Discussion

Taken together, our findings show that multiple complementary measurement approaches reveal a robust hierarchical organization of microscale variation that may contribute to the macroscale specialization of primate cortical function. First, the MRI-derived T1w/T2w map provides a noninvasive neuroimaging proxy for anatomical hierarchy in the absence of axonal tract-tracing data. Second, the principal axis of transcriptional variation across human cortex aligns with cortical hierarchy as captured by the T1w/T2w map. Third, this hierarchical axis reflects a gradient of local microcircuit specialization involving synapses and cell types, with relevance to brain disease pathophysiology. Strong similarities between the patterns of anatomical, functional, and transcriptional variation suggest that hierarchical gradients of microcircuit properties play key roles in the functional specialization of large-scale networks across the human cortex. Moreover, the agreement between human transcriptional and monkey anatomical measures suggests conserved organizing principles in human and nonhuman primate cortex.

Specialization of cortical function may derive in part from the multiple features of microcircuitry identified here to exhibit hierarchical gradients. For instance, stronger recurrent excitation in association cortex can endow association circuits with longer timescales of intrinsic activity^19,35, as observed empirically^4,5, which subserve the prolonged integration of signals in these areas^3,16,27. Furthermore, computational modeling of cortical circuits identifies recurrent excitation strength as a key property governing functional specialization across areas for core cognitive computations such as working memory and decision making^27,35. Hierarchical gradients of inhibitory interneuron cell types can additionally shape regional specialization of dynamics and function, due to cell-type differences in physiology and synaptic connectivity^24,25. For example, parvalbumin-expressing inhibitory interneurons preferentially target the perisomatic areas of pyramidal neurons where they can gate pyramidal-neuron outputs. In contrast, calretinin-expressing inhibitory interneurons preferentially target distal dendrites of pyramidal neurons and other inhibitory interneurons, where they may play key computational roles in disinhibition-mediated gating of dendritic inputs³⁶. Cytoarchitectural differences between areas correlate with their pairwise laminar projection profiles^14,22, linking local microcircuit specialization of areas to their hierarchical long-range interactions.

Our study adds to a growing understanding of how transcriptional specialization shapes cortical function. Transcriptional diversity, particularly of genes which regulate synaptic function and ion channel activity, relates to the spatiotemporal organization of intrinsic activity in large-scale cortical networks^7,9–11, and transcriptional markers for synaptic, neuronal, and axonal structure relate to patterns of anatomical connectivity^11,12. Of note, Hawrylycz et al. (2015) found that genes most strongly predictive of functional connectivity patterns in cortex were shifted toward high DS_c, and that across all brain regions, high-DS genes were significantly enriched in gene sets related to functional ontologies and brain diseases, leading the authors to suggest these genes constitute a “canonical transcriptional blueprint” for the human brain⁷. We found that high-DS_c genes exhibit strong hierarchical gradients across human cortex (Fig. 7a), and that these strong-TMC genes exhibit similar functional and brain disease-related enrichments. These results suggest that hierarchically and stably expressed genes across the cortex contribute significantly to the transcriptional regulation of cortical function, and to its pathophysiological disruption in disease.

Our findings demonstrate that the T1w/T2w map generally captures an axis of hierarchical differentiation across cortex that reflects multiple features of interareal variation. The T1w/T2w map—an MR contrast map that removes shared imaging intensity biases and increases image contrast—is sensitive to gray-matter myelin content¹⁷, which may itself contribute to functional specialization in several ways¹⁸. However, both T1- and T2-weighted image intensities depend on multiple MRI parameters, each of which is sensitive to several other brain microstructural properties, including cell size and density, degree of dendritic arborization, iron, and water^37,38. Further in vivo characterization of microstructural variation can be provided by quantitative MRI techniques such as T1 mapping^39–42. Thus, the T1w/T2w map provides a readily acquired, noninvasive neuroimaging measure which is sensitive to areal variation in not one but several structural components of local cortical microarchitecture. We note that there are interesting deviations between the topographies of the T1w/T2w map and other hierarchical features. For instance, primary motor cortex and retrosplenial cortex exhibit high T1w/T2w map values yet differ from primary sensory areas in their laminar structure^17,18.

Multiple functionally defined hierarchies in human and nonhuman primate cortex have been proposed, none of which are mutually exclusive with the anatomical hierarchy informed by long-range laminar projection patterns. For instance, studies have found hierarchical differences across areas in the temporal selectivity of spontaneous dynamics and sensory processing^4,5, but it remains unclear how these differences relate to hierarchies of microcircuit specialization. In this study, we have identified multiple microanatomical and transcriptional properties of cortical microcircuitry which exhibit hierarchical gradients and may contribute to physiological and functional specialization. Importantly, cortical function has a complex multidimensional organization with multiple axes of areal variation^43,44, each of which can be represented by a scalar-valued map. Distinct information processing hierarchies can be defined for different sensory modalities, and within a modality, such as the dorsal and ventral processing streams in the primate visual system^13,15,45. Future studies can investigate how integration of multiple neuroimaging measures, for instance combining T1w/T2w imaging with diffusion weighted imaging, can reveal new multidimensional principles of cortical organization, both within and across functionally specialized networks.

Multiple lines of evidence point to a transcriptional basis for disease phenotypic variation, linking white matter dysconnectivity⁴⁶ and developmental changes in structural topology⁴⁷ to genes implicated in schizophrenia. Further characterization of the developmental trajectory of hierarchical transcriptional specialization^46,48,49, and structural brain tissue degeneration⁵⁰, may inform the progression of neurodevelopmental disorders. Strong hierarchical gradients in drug targets, such as receptor subunits, could enable preferential modulation of sensory or association cortical areas, at the group level, through targeted pharmacology. This may guide future rational design of drug treatments to target specific macroscale cortical circuits. Large-scale mapping of the cortical transcriptome at finer spatial resolution will further elucidate the microcircuit basis of hierarchical specialization with laminar²³ and cell-type^8,26 specificity.

Methods

Parcellated structural neuroimaging maps

The human T1w/T2w and cortical thickness maps in the surface-based CIFTI file format²¹ were obtained from the Human Connectome Project (HCP)⁵¹. To produce the T1w/T2w maps, high resolution T1- and T2-weighted images were first registered to a standard reference space using a state-of-the-art areal-feature-based technique^21,52, which precluded the need for spatial smoothing, and then corrected for bias-field intensity inhomogeneities, yielding dimensionless quantities defined with respect to a reference group-averaged map (for more details, see [17], [53], and [21]). Group-averaged (N=339) left-hemispheric T1w/T2w and thickness maps were parcellated into 180 areas using the HCP’s Multi-Modal Parcellation (MMP1.0)²¹. Parcellated maps were highly stable across individual subjects: the mean pairwise Spearman rank correlation between subjects’ individual maps was 0.94 (0.76) for the T1w/T2w (thickness) map. We note that the areal-feature-based surface registration technique is informed, in part, by alignment of subjects’ T1w/T2w maps⁵², which likely contributes to the discrepancy in stability observed between the two structural maps. Assignment of MMP1.0 parcels to functional networks (Fig. 1b, Supplementary Fig. 1d) was performed through community detection analysis⁵⁴ on time-series correlations in the HCP resting-state fMRI dataset. Six of 180 parcels were not assigned to one of the eight networks analyzed in this study.

For validation, key findings reported for human cortex were replicated using group-averaged (N=69) T1w/T2w maps from the publicly available Conte69 dataset¹⁷ (Supplementary Fig. 10). In contrast to the HCP maps, both individual and group-averaged T1w/T2w maps in the Conte69 dataset were smoothed using Gaussian filters weighted by geodesic distance to reduce high frequency spatial artifacts¹⁷.

The group-averaged (N=19) T1w/T2w and thickness maps for macaque monkey cortex were obtained from the publicly available BALSA database⁵⁵ (https://balsa.wustl.edu/study/show/W336) and were produced by adapting the HCP pre-processing pipelines to work with monkey MRI data (see [55] for more details). Monkey T1w/T2w map values for the left cortical hemisphere were parcellated into 91 areas using the M132 parcellation, which was used for the anatomical tract-tracing dataset⁵⁵.

To construct maps of geodesic distance from primary visual area V1 in human and monkey cortex, pairwise geodesic distance between two parcels i and j was calculated as the average of all pairwise surface-based distances between grayordinate vertices in parcel i and vertices in parcel j.

Anatomical hierarchy levels in monkey cortex

To assess whether macaque cortical T1w/T2w maps could reliably capture the laminar-specific interareal projection patterns conventionally used to define anatomical hierarchy, we fit a generalized linear model (GLM) to quantitative laminar projection data, yielding ordinal hierarchy values in 89 cortical areas, following the procedure of ref. [15]. Anatomical tract-tracing data, derived from retrograde tracers, was obtained from the publicly available Core-Nets database (http://core-nets.org). Retrograde tracer was injected into a target area i, and the number of tracer-labeled neurons in source area j were counted. The fraction of external labeled neurons, FLNe_ij, provides a quantitative measure of connection strength defined as the number of labeled neurons in the source area normalized by the total number of labeled neurons in all external cortical source areas for a given injection⁵⁶. Labeled neurons in source areas are classified by their location in either supragranular or infragranular layers. For a given projection, the proportion of supragranular labeled neurons, SLN_ij, is defined as the ratio of N_supra to N_supra + N_infra for neurons labeled in source area j. As feedforward and feedback connections preferentially originate in supragranular and infragranular layers, respectively^13–15, SLN is a quantitative measure of hierarchical distance between two cortical areas¹⁵: within this paradigm for laminar-specific projection motifs, a pure feedforward connection from source area j to target area i would originate entirely in the superficial layers, resulting in an SLN of 1. Conversely, a pure feedback projection originating entirely in deep infragranular layers would result in an SLN of 0. We note that two of the 91 areas in the M132 parcellation – SUBICULUM and PIRIFORM – were excluded from the model fitting procedure, as SLN for these two areas was undefined.

The GLM procedure for estimating hierarchy levels from SLN data is described in detail in ref. [15]. In brief, the hypothesis that SLN is a measure of hierarchical distance can be expressed as g(SLN_ij) = H_i − H_j, where H_i corresponds to the hierarchical level of area i, and g is an arbitrary and possibly nonlinear function linking SLN values on the unit interval (0, 1) to their corresponding hierarchical distance. We used a logit link function to map SLN values from the unit interval to the entire real number line following the procedure of ref. [19]. Fitting linear predictors (i.e. hierarchical levels) to logit-transformed SLN values constitutes a type of generalized linear model, with maximum likelihood estimation assuming a binomial family probability distribution for the supra- and infra-granular neuron counts. To assign more weight to stronger connections during model estimation of hierarchical levels, we also weight each pathway in the model by the negative logarithm of the FLNe value. We clip SLN values to lie in the interval (0.01, 0.99) so the logit-transformed SLN value is well-defined for all pathways used to fit the model. Furthermore, to reduce the impact of noise on model parameter estimation, we only included the N=1243 pathways which contained at least 10 projection neurons when fitting the GLM; we confirmed that results were generally robust to the choice of neuron count threshold.

Maximum likelihood estimation of model parameters was done in the R programming language using the glm function. The model-estimated hierarchy levels, invariant under linear transformations, were shifted and rescaled to span the unit interval [0,1]. To assess the statistical relationship between T1w/T2w map value and hierarchy level, we calculated the Spearman rank correlation between the 89 ordinal hierarchy values and their corresponding parcellated T1w/T2w map values (Fig. 1f). For visual clarity in Fig. 1e, f we remove the nonlinear logit transformation by displaying model-estimated hierarchy levels after applying the inverse-logit (i.e., logistic) transformation. This rescaling preserves the ordering of areas and therefore does not affect the reported Spearman rank correlations.

Macaque monkey anatomical data: cytoarchitectural types, inhibitory interneuron densities, and pyramidal neuron spine counts

To quantify the statistical relationship between T1w/T2w map value and categorical cytoarchitectural type (Fig. 4a), we compared T1w/T2w map values to structural classification values reported for 29 regions of primate visual cortex, obtained from ref. [22]. To characterize hierarchical distributions of cortical inhibitory interneuron cell types (Fig. 4d), we compiled, from multiple immunohistochemical studies, the relative densities of inhibitory interneurons which are immunoreactive (ir) to the calcium-binding proteins parvalbumin (PV) and calretinin (CR)^57–60. To characterize hierarchical variation in pyramidal neuron excitatory synaptic connectivity (Fig. 4g), we compiled, from multiple studies by Elston and colleagues^61–66, the number of spines of basal-dendritic trees of layer-3 pyramidal neurons.

For each of these three analyses, we produced a mapping between the 91 areas in the M132 atlas parcellation, which was used to calculate parcellated T1w/T2w map values in monkey cortex, to the architectonic areas reported in these collated studies (Supplementary Table 1). Where the anatomical mapping was not a one-to-one correspondence, we mapped the reported architectonic area onto the set of all M132 parcels with nonzero spatial overlap, and the corresponding T1w/T2w map value was calculated as the average across these M132 parcels.

Gene expression preprocessing

The Allen Human Brain Atlas (AHBA) is a publicly available transcriptional atlas containing gene expression data, measured with DNA microarrays, and sampled from hundreds of histologically validated neuroanatomical structures across six (five male and one female) normal post-mortem human brains⁶. After no significant interhemispheric transcriptional differences were observed in the first two bilaterally profiled brains⁶, the remaining four donor brains were profiled only in the left cortical hemisphere⁷. To construct parcellated group-averaged gene expression profiles, we therefore restricted all analyses to microarray data sampled from the left cortical hemisphere in each of the six brains. Microarray expression data and all accompanying metadata were downloaded from the AHBA (http://human.brain-map.org)^6,7. The raw microarray expression data for each of the six donors includes expression levels of 20,737 genes, profiled by 58,692 microarray probes. These data were preprocessed according to the following procedure:

1. Gene probes without a valid Entrez Gene ID were excluded.

2. Microarray samples exhibiting exceptionally low inter-areal similarity were excluded. We first computed the spatial correlation matrix of expression values between samples using the remaining 48,170 probes, then summed this matrix across all samples. Samples whose similarity measure was more than five standard deviations below the mean across all samples were excluded. At most, this step excluded three samples within a subject.

3. Samples whose annotations did not indicate that they originated in the left hemisphere of the cerebral cortex were excluded. To focus analysis on neocortex, we also excluded samples taken from cortical structures that are cytoarchitecturally similar to the hippocampus, including piriform cortex, the parahippocampal gyrus, and the hippocampal formation.

4. Samples whose measured expression level was not well above background, as provided in the AHBA dataset, were excluded⁷. Samples surviving this step i) belonged to a probe whose mean signal was significantly different from the corresponding background, and ii) had a background-subtracted signal which was at minimum 2.6 times greater than the standard deviation of the background.

5. The remaining cortical samples were mapped from volumetric space to the two-dimensional cortical surface by minimizing the pairwise Euclidean distance between stereotaxic MNI coordinates reported for each cortical sample, and coordinates of grayordinate vertices in each subject’s native cortical surface mesh (which was constructed using the procedure described in the following section below). Samples whose Euclidean distance to the nearest surface vertex was more than two standard deviations above the mean distance computed across all samples were excluded (excluding between 2 and 15 samples per subject). An average of 203 ± 27 samples per subject, yielding 1220 total samples across all six subjects, remained at this stage.

6. Expression levels for samples mapped onto the same surface vertex were averaged. Then expression levels within each remaining sample were z-scored across all gene probes.

7. Using cortical samples mapped onto subjects’ native surface meshes, expression profiles for each of the 180 unilateral parcels in the HCP’s MMP1.0 cortical parcellation²¹ were computed in one of the two following ways. (I) For parcels which had at least one sample mapped directly onto one of their constituent surface vertices, parcellated expression values were computed by averaging expression levels across all samples mapped directly onto the parcel. (II) For parcels which had no samples mapped onto any of their constituent vertices, we first created densely interpolated expression maps, in which each vertex in the native surface mesh was assigned the expression level associated with the most proximal surface vertex onto which a sample had been directly mapped, determined using surface-based geodesic distance along each subject’s cortical surface mesh (i.e., a Voronoi diagram approach); the average of expression levels across parcels’ constituent vertices was then computed to obtain parcellated expression values, effectively equivalent to performing a weighted average.

8. A coverage score was also assigned to each gene probe, defined as the fraction of 180 parcels that had at least one sample mapped directly onto one of its constituent surface vertices. Probes with coverage below 0.4 (i.e., probes for which fewer than 72 of the 180 parcels contained samples) were excluded from further analysis.

9. For each gene profiled by multiple gene probes, we selected and used the expression profile of a single representative probe. If two probes were available, we selected the probe with maximum gene expression variance across sampled cortical structures, in order to more reliably capture spatial patterns of areal heterogeneity. If three or more probes were available, we computed a correlation matrix of parcellated gene expression values across the available gene probes, summed the resultant matrix along one of its dimensions to obtain a quantitative similarity measure for each probe, relative to the other gene probes, and selected the probe with the highest similarity measure, as it is most highly representative among all available gene probes.

10. Each subject-level gene expression profile was z-scored before we computed group-level expression profiles, which were obtained by computing the mean across subjects which were assigned a probe for that gene. Group-level gene expression profiles were not computed if fewer than four subjects had an available gene probe. Finally, group-level expression profiles were z-scored across all 180 areas for each gene.

These steps yielded group-averaged expression values for 16,088 genes across 180 cortical areas, which were used for all reported analyses. The T1w/T2w map correlation (TMC) for each gene is reported in Supplementary Table 2. We also replicated all reported findings after mapping subjects’ gene expression samples to the HCP’s group-averaged surface mesh instead of subjects’ native surface meshes in step 5 above. However, we found that native surface-based expression sample mapping yielded slightly stronger TMCs and improved spatial registration in general (not shown).

Native surface mesh construction

Single-subject surface registration for each of the six subjects in the AHBA was performed following a procedure adapted from the HCP’s minimal preprocessing pipelines⁵³. Briefly, the T1w image was first rigidly aligned to the MNI coordinate axes to produce a native space volume, which was then nonlinearly registered to the standard MNI template using FSL’s FLIRT and FNIRT. The native space image was run through FreeSurfer’s recon-all pipeline, which performs automated segmentation of brain structures to reconstruct the white matter and pial surfaces. The FreeSurfer output surface was then converted to standard GIFTI format to produce each subject’s native surface mesh. Finally, subjects’ native surface meshes were registered to the standard HCP surface mesh.

Categorical gene sets

We conducted analyses on biologically and physiologically meaningful gene sets extracted from existing databases and neuroscientific literature, reported below (Supplementary Table 2):

1. Brain-specific. N=2413 genes with expression specific to human brain tissue, relative to other tissues, were obtained from supplementary data set 1 of ref. [67]. Following ref. [30], brain-specific genes were selected for which expression in brain tissue was four times higher than the median expression across all 27 different tissues.

2. Neuron- and oligodendrocyte-specific. Brain genes with expression specific to neurons (N=2530) or oligodendrocytes (N=1769), relative to other central nervous system (CNS) cell types, were obtained from supplementary data set S3b of ref. [68]. Following ref. [30], neuron-specific genes were selected for which log-expression in neurons of P7n cell type in the mouse was 0.5 greater than the median log-expression across 11 CNS cell types.

3. Synaptome. We aggregated four sets of synaptic genes (N=1886 in total) encoding proteins found in the presynaptic nerve terminal, presynaptic active zone, synaptic vesicles, and postsynaptic density, which were obtained from SynaptomeDB, an ontology-based database of genes in the human synaptome³¹.

4. Neuron subtype-specific. Gene sets representing distinct classes of neuronal subtypes were obtained from ref. [26], in which clustering and classification analyses yielded 16 distinct neuron subtypes, on the basis of differential gene expression measured by RNA sequencing from single neurons in human cortex. The fraction of positive values using exon-only derived transcripts per million (TPM) associated with each subtype-specific gene were obtained from supplementary table S5; within each neuronal subtype cluster, the TPM values for the cluster genes were normalized and used to create a weighted gene expression profile representative of each subtype’s spatial topography (Supplementary Fig. 4).

5. Layer-specific. Sets of laminar-specific genes localized to different layers of human neocortex were obtained from supplementary table S2 of ref. [23]. Genes were broadly grouped into sets representative of supragranular (L1–3), granular (L4), and infragranular (L5/6) layers.

Spatial autoregressive modeling

Significance values indicated by the number of stars reported on bar plots for T1w/T2w map correlations (TMCs) were corrected to account for spatial autocorrelation structure in parcellated T1w/T2w maps and gene expression maps. Because physical quantities like microstructural tissue composition and gene expression must vary smoothly and continuously in space, measurements recorded from proximal cortical areas tend to be more similar than measurements recorded from distal areas of cortex. This departure from the assumption of independent observations biases calculations of statistical significance. To model this spatial autocorrelation, we used a spatial lag model (SLM) commonly applied in the spatial econometrics literature⁶⁹, of the form y = ρWy + Xβ + v, where W is a user-defined weight matrix implicitly specifying the form of spatial structure in the data, and v is normally distributed.

To implement a spatial lag model in the python programming language, we used the maximum likelihood estimation routine defined in the Python Spatial Analysis Library (pysal)⁷⁰. We first determined the surface-based spatial separation between each pair of cortical parcels by computing the mean of the pairwise geodesic distances between each vertex in parcel i and each vertex in parcel j, from which we constructed a pairwise parcel distance matrix, D.

Similarity of gene expression profiles was well-approximated by an exponential decaying spatial autocorrelation function (Supplementary Fig. 7a, b), as was found in mouse cortex¹². We fit the correlation of gene expression profiles between two areas with the exponential function Corr(x_i, x_j) ~ exp(−D_ij/d₀), where x_i and x_j are vectors containing the parcellated gene expression values at parcels i and j, D_ij is the geodesic distance between the parcels, and d₀ is the characteristic spatial scale of autocorrelation. We empirically determined d₀ by first computing the pairwise gene co-expression matrix C_ij ≡ Corr(x_i, x_x). We then fit the free parameter d₀ using ordinary least squares (OLS) regression on the off-diagonal (upper-triangular) elements of the gene co-expression and parcel distance matrices, so as to minimize the sum-of-squared-residuals between empirical and model-estimated gene co-expression values over all pairs of cortical parcels, $S={\sum }_{i>j}{r}_{ij}^2={\sum }_{i>j}{\left[C_{ij}-exp(-D_{ij}/d_0)\right]}^2$. This empirical fit was performed on the gene co-expression matrix computing using the set of brain-specific genes. Using the OLS estimate of the spatial autocorrelation scale from the fit to the empirical gene expression data, we calculated the elements of the spatial weight matrix, W_ij = exp(−D_ij/d₀). Finally, we fit the SLM to parcellated gene expression profiles, using the maximum likelihood estimator routine ( pysal.spreg.ml_lag.ML_Lag) in pysal. P-values indicated by the number of stars in the bar plots of T1w/T2w map correlations (TMCs) correspond to p-values for model parameter β defined above.

Of note, spatial autoregressive model parameters do not have the same interpretation as they do in OLS regression. The parameter β reflects the direct (i.e. local) impact on the dependent variable y due to a unit change in the independent variable x. In addition, because of the underlying spatial structure, the direct impact of x_i on y_i results in an indirect effect of y_i on neighboring y_j. Therefore β cannot be interpreted as a corrected, global correlation coefficient, and we restrict our use of the SLM to correcting for the biasing effect of spatially autocorrelated samples on reported significance values.

Theil-Sen estimator

Grey trend lines in all figures were calculated using the Theil-Sen estimator – a nonparametric estimator of linear slope based on Kendall’s tau rank correlation – that is insensitive to the underlying distribution and robust to statistical outliers⁷¹. It is defined as the median of the set of slopes computed between all pairs of points.

Principal components analysis

We used principal component analysis (PCA) to identify the dominant modes of spatial variation in the transcriptional profiles of gene expression in the human cortex. For a set of N genes, each with group-averaged expression values for P cortical parcels, we constructed a gene expression matrix G with one row for each cortical parcel and one column for each unique gene (i.e. with dimensions P × N). The P × P spatial covariance matrix C was constructed by computing the covariance between vectors of gene expression values for each pair of cortical parcels: C_ij = Cov(G_i, G_j), where G_i is the i-th row in the matrix G, corresponding to the vector of N gene expression values for the i-th cortical parcel. Eigen-decomposition is performed on the spatial covariance matrix to obtain the matrix eigenvectors (i.e., the principal components, PCs) and their corresponding eigenvalues, which are proportional to the amount of variance captured by the corresponding PC. To enumerate each principal component, eigenvalues are ranked in descending order of absolute magnitude, with larger magnitudes indicating a greater proportion of the total variance captured by the associated PC (i.e., the associated mode of spatial covariation). PCA therefore allows for simultaneous identification of spatial patterns of covariation and quantification of the extent to which these spatial modes capture variance in cortical gene expression profiles.

To quantify the overlap of these spatial PCs with the cortical T1w/T2w map, we compute the Spearman rank correlation coefficient between each P-dimensional PC and the P-dimensional vector of T1w/T2w map values for each cortical parcel. We can quantify the amount of gene expression variance that is captured by any given spatial map, such as the T1w/T2w map (Fig. 5e, Supplementary Fig. 6f–j): from the spatial covariance matrix C, the variance captured along a unit-length vector a, here a demeaned and normalized map, is given by a^⊤Ca.

Differential stability

Differential stability (DS) is a correlation-based metric which quantifies the consistency of spatial gene expression patterns across individual brains. DS was originally defined in ref. [7] as “the tendency for a gene to exhibit reproducible differential expression relationships across brain structures.” To compute DS for a gene, we calculated the average pairwise Spearman rank correlation (r_s) across all subject-level gene expression profiles, for the (four to six) AHBA subjects with an available gene probe, for a maximum of 15 possible pairs (Supplementary Table 2). That is, for gene g whose expression profile across 180 cortical areas in brain i is the vector b_i(g), we define the DS in cortex (DS_c) by: ${\text{DS}}_{\mathrm{c}}(g)\equiv \frac{1}{15}{\sum }_{i=1}^6{\sum }_{j>i}{r}_s(b_i(g),b_j(g))$. We note that DS is therefore defined with respect to a specified set of brain structures, in this case 180 unilateral cortical areas. We note that any differences between cortical DS values shown in our Fig. 7a and those shown in Fig. 7b of ref. [7] are due to i) different cortical parcellations (containing 180 vs. 52 parcels, respectively); ii) different pre-processing procedures; and iii) different correlation coefficients (Spearman vs. Pearson, respectively).

Functional enrichment analyses

Functional enrichments were determined using the ToppGene (https://toppgene.cchmc.org/) web portal³², including gene ontology annotations (biological process, cellular component, and molecular function); microRNA targets (from all sources indicated on https://toppgene.cchmc.org/navigation/database.jsp); and drug annotations (from DrugBank, Comparative Toxicogenomics Database, including marker and therapeutic, and Broad Institute CMAP). Significant genes in each category were identified using the ToppFun utility. Disease annotations were determined using curated disease gene associations in the DisGeNet database³⁴ (http://www.disgenet.org/web/DisGeNET/menu/home). Hypergeometric testing was used to determine significant over-representation of brain-related disease genes in the top and bottom gene quintiles (20%, 3,218 genes) ranked by T1w/T2w map correlation, following ref. [7].

Statistical Methods

Multiple comparisons corrections

Significance values indicated by the number of stars reported on bar plots for T1w/T2w map correlations (TMCs) were Bonferroni-corrected for multiple comparisons. Specifically, statistical significance thresholds (*, P < 0.05; **, P < 10⁻²; ***, P < 10⁻³) were divided by the number of null hypotheses tested, i.e., by the number of constituent bars contained in each bar plot (Fig. 4, Supplementary Figs. 4, 5, and 10).

Surrogate data generation

To nonparametrically determine significance values in our PCA results, in Fig. 5 and Supplementary Fig. 6, we generated surrogate maps with a spatial autocorrelation structure matched to the empirical data (Supplementary Fig. 7c). Parameters characterizing the empirical spatial autocorrelation were determined numerically for the cortical T1w/T2w map, cortical thickness map, and the map of surface-based geodesic distance from area V1; in each case, we fit the data using a spatial lag model of the form y = ρWy, where y is a vector of first Box-Cox transformed and then mean-subtracted map values. The Box-Cox transformation was first applied to the maps so their values were approximately normally distributed. W is the row-normalized weight matrix with zero diagonal and off-diagonal elements proportional to $W_{ij}=z_i^{-1}exp(-D_{ij}/d_0)$, where D_ij is the surface-based geodesic distance between cortical areas i and j, and z_i ≡ Σ_jexp(−D_ij/d₀) is a row-wise normalization factor. Weights W_ij define the fraction of spatial influence on area i attributable to area j. Two free parameters ρ and d₀ are estimated by minimizing the residual sum-of-squares⁶⁹. Using best-fit parameter values ρ̂ and $\widehat{d_0}$, surrogate maps y_surr are generated according to ${\mathbf{y}}_{\text{surr}}={\left(\mathbb{I}-\widehat{\rho }\mathbf{W}[\widehat{d_0}]\right)}^{-1}\mathbf{u}$, where u ~ 𝒩(0,1). To match surrogate map values distributions to the distribution of values in the corresponding empirical map (e.g. the T1w/T2w map), rank-ordered surrogate map values were re-assigned the corresponding rank-ordered values in the empirical map. Note that this approach to surrogate data generation approximates a spatial autocorrelation-preserving permutation test of the empirical neuroimaging map.

Using these surrogate maps, we constructed null distributions for N = 10,000 statistics and report significance values as the proportion of samples in the null distributions whose absolute value is greater than or equal to the absolute value of the test statistic. To compute significance values reported in Fig. 6c, f, we first constructed null distributions of the statistic ${\sigma }_{\text{Map}}^2/{\sigma }_{\text{PC}1}^2$ using surrogate maps constructed for each neuroimaging map. For each neuroimaging map, we then computed distributions of the difference between the test statistic and each sample statistic in the null distribution. Finally, we used the non-parametric Wilcoxon signed-rank test on these difference distributions, one for the T1w/T2w map and one for either the cortical thickness or geodesic distance map, to test for statistically significant differences in the means of the distributions. The interpretation of our statistically significant results reported in Fig. 6c, f is that the T1w/T2w map tends to capture a more appreciable fraction of gene expression variance, relative to its surrogate maps, than do either of the other two candidate neuroimaging maps.

Jackknife estimate of standard error

To nonparametrically estimate the error on reported Spearman rank correlations between length-N vectors x and y, we used a leave-one-out jackknife replication procedure⁷². We generated N jackknife samples, denoted θ_−i, by removing the i-th element from vectors x and y, re-computing the rank correlation between the two new length-(N-1) vectors x_−i and y_−i, and repeating for i = 1 … N. Because the jackknife estimate consists of a linear operation (i.e., subtraction), we applied the Fisher z-transformation to the N jackknife sampled correlation coefficients. The jackknife estimate of standard error on the Fisher z-transformed jackknife samples, z(θ_−i), was then computed as $\widehat{SE}=\sqrt{\frac{N-1}{N}{\sum }_{i=1}^N{[z({\theta }_{-i})-\overline{z(\theta )}]}^2}$, where $\overline{z(\theta )}\equiv \frac{1}{N}{\sum }_{i=1}^{N}z({\theta }_{-i})$ is the mean of the N z-transformed jackknife samples. We then added (subtracted) $\widehat{SE}$ from the Fisher z-transformed sample statistic, z(r_s), before applying the inverse transformation to obtain the upper (lower) bound on each reported error bar, i.e., $z^{-1}\left(z(r_s)\pm \widehat{SE}\right)$. For all human analyses (i.e., for all correlations performed between principal components, neuroimaging maps, random surrogate maps, and gene expression profiles in Figs. 4–8, Supplementary Figs. 4–7, 9 and 10), correlations and their jackknife estimates were computed using N=180 cortical areas. For monkey analyses (i.e., Figs. 1, 2, 4, and Supplementary Fig. 3), we used the number of areas reported in figure legends. The interpretation of the jackknife estimate of standard error is the amount by which the correlation coefficient would change with the addition or removal of one area.

Bootstrap estimated confidence intervals

To nonparametrically estimate confidence intervals on reported statistics derived from PCA (i.e., Figs. 5–7, Supplementary Figs. 6 and 10) we performed a percentile bootstrap⁷³. We constructed bootstrap distributions for each sample statistic by repeatedly resampling with replacement from the sample data distribution – e.g., expression profiles of genes in each categorical gene set – and recomputing the test statistic on each of the resampled data sets. Specifically, we first performed PCA on the resampled data to obtain the first ten PCs and percent variance captured by each. The Procrustes rotation was used to align the bootstrap loading matrix to the sample loading matrix⁷⁴ – i.e., to establish the correspondence between bootstrap and sample PCs – then the bootstrap distributions of all test statistics derived from the PCA eigenspectrum were re-computed (e.g., PC1 TMCs and ${\sigma }_{\text{Map}}^2/{\sigma }_{\text{PC}1}^2$). We estimated confidence intervals on sample statistics using percentiles of bootstrap distributions – i.e., the 2.5% and 97.5% percentiles for the upper and lower bounds on the 95% confidence interval, respectively. All bootstrap distributions were computed using N=1,000 bootstrap samples. The bootstrap technique rests on the assumption that the sample distribution is a reasonable approximation of the “true” population distribution, which is unknown; thus, statistical inference on the resampled sample data is used to approximate statistical inference on the population.

No statistical methods were used to predetermine sample sizes, but our sample sizes are the same as those reported in previous publications [6,7,15]. Nonparametric tests that do not make assumptions about the form of the data distribution were used to compute statistical significance values. Spatial autocorrelation structure in the data violated the assumption that samples were independent, though we note that this is a feature which is frequently present in neuroimaging and transcriptional data, yet rarely addressed in the neuroscience literature. No data were excluded from our analyses unless otherwise noted. Data analyses were not performed blind to the conditions of the experiments. There were no allocated experimental groups or new data collected in this study.

Life sciences reporting summary

Further information on experimental design is available in the Life Sciences Reporting Summary.

Code availability

Custom analysis codes written in Python are available from the corresponding author upon reasonable request.

Data availability

All results derive from data that is publicly available from sources described above. Monkey neuroimaging maps were obtained from https://balsa.wustl.edu/study/show/W336. Monkey tract-tracing data were obtained from http://core-nets.org. Human gene expression data were obtained from http://human.brain-map.org. Annotated disease gene sets were obtained from http://www.disgenet.org/web/DisGeNET/menu/home. Monkey microanatomical data used in Fig. 4; correlations for each target area in Supplementary Fig. 3; TMC and DS_C values for all 16,088 genes; and constituent genes in the brain-, neuron-, oligodendrocyte-, synaptome-, and layer-specific sets are included in Supplementary Tables 1 and 2. Parcellated maps and connectivity matrices related to this study are available via the BALSA database (https://balsa.wustl.edu/).