Monitoring ¹⁵N Chemical Shifts During Protein Folding by Pressure-Jump NMR

Abstract

Pressure-jump hardware permits direct observation of protein NMR spectra during a cyclically repeated protein folding process. For a two-state folding protein, the change in resonance frequency will occur nearly instantaneously when the protein clears the transition state barrier, resulting in a mono-exponential change of the ensemble-averaged chemical shift. However, protein folding pathways can be more complex and contain meta-stable intermediates. With a pseudo-3D NMR experiment that utilizes stroboscopic observation, we measure the ensemble-averaged chemical shifts, including those of exchange-broadened intermediates, during the folding process. Such measurements for a pressure-sensitized mutant of ubiquitin show an on-pathway kinetic intermediate whose ¹⁵N chemical shifts differ most from the natively folded protein for strands β5, its preceding turn, and the two strands that pair with β5 in the native structure.

Graphical Abstract

Direct observation of protein folding by NMR initially was limited to slower folding or unfolding systems,^1–4 but more recent improvements in technology have significantly increased the accessible time resolution.^5–6 In such experiments, sample conditions are changed abruptly from denaturing to those favoring the native state. This may be accomplished by a sudden jump in pH or temperature, dilution of denaturant, release of a co-factor, or sudden drop in hydrostatic pressure. The latter mode of switching is often fully reversible and allows the protein to be probed under native buffer conditions. It requires that the volume of the protein in the unfolded state is substantially lower than in the folded state.^7–11 Analogous to pressure-jump fluorescence experiments,¹² the temporal change in the NMR spectrum following a step change in pressure contains kinetic information.^4,13

We recently developed a pressure-jump apparatus capable of reliably switching the hydrostatic pressure in an NMR sample cell between 1 bar and up to 2.8 kbar within a few milliseconds,¹⁴ and demonstrated it for ubiquitin, whose folding mechanism has been the subject of much experimental and computational work.^15–22 Although wild-type ubiquitin requires more than 5 kbar to unfold,²³ mutations that increase the volume difference between the folded and unfolded state reduce the pressure needed to unfold the protein.^24–25 Indeed, the V17A/V26A ubiquitin mutant (VA2-ubiquitin) lowered the mid-point of pressure-induced unfolding to 1.4 kbar, while retaining the native structure.^{14, 22}

At 2.5 kbar, 25 °C, the ¹⁵N-¹H heteronuclear single quantum correlation (HSQC) NMR spectrum of VA2-ubiquitin shows the protein is ca 94% unfolded, yielding narrow chemical shift dispersion and sharp resonances; the remaining 6% retains its natively folded spectrum. Immediately after dropping the pressure to 1 bar, the ¹⁵N shifts of the protein remain close to those of the pressure-denatured state, but also show evidence of exchange broadening (Figure S1).¹⁴

For a two-state folder, jumping from high pressure (denaturing) to 1 bar (native) conditions triggers a folding process that is manifested as a changing admixture of unfolded and folded proteins. For multi-state folders, intermediates will also become populated and can exhibit molten globule characteristics with correspondingly broad NMR resonances.^26–27 We demonstrate that the ensemble-averaged chemical shifts for such an admixture can be monitored stroboscopically^28,29 as a function of folding time, and permits determination of the folding intermediate chemical shifts.

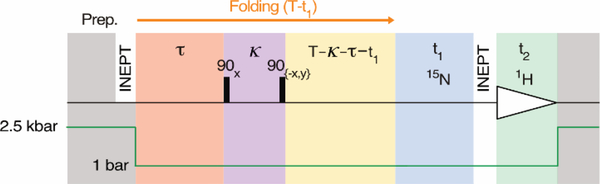
The NMR experiment (Figure 1) is a modification of the regular gradient-enhanced heteronuclear single quantum correlation (HSQC) pulse scheme³⁰ synchronized with the pressure jump, which includes a stroboscopic element to probe the resonance frequency during folding. During the preparation period (grey), ¹H magnetization is first transferred to in-phase ¹⁵N_z by means of a refocused INEPT element at high pressure, where the efficiency of such transfers is very high. This transfer is immediately followed by the opening of a hydraulic valve that drops the pressure in the sample cell to 1 bar, initiating the folding process. Following a duration τ (Figure 1, peach), the ¹⁵N chemical shift frequency is encoded “stroboscopically” by the 90_x-κ−90_-x pulse pair (purple) which modulates the ¹⁵N_z magnetization, and thereby the spectral intensity, M_x(τ), in the HSQC spectrum, by cos(ω_Nκ), where ω_N is the ¹⁵N angular offset frequency, averaged over duration κ and over all molecules that contribute to the final 2D HSQC spectrum (Figure 2A). Similarly, a 90_x-κ−90_y pulse pair is used to generate a second HSQC spectrum whose intensity, M_y(τ), is modulated by sin(ω_Nκ) (Figure 2B). The ratio of intensities observed in these two spectra therefore equals tan(ω_Nκ), thereby yielding <ω_N> at time τ, where the brackets denote the ensemble-averaged value. Linear weighting of contributions to <ω_N> from folded, unfolded or intermediate states of the protein requires that κ(Δω_N) « π, where Δω_N represents the angular chemical shift difference between them.

Figure 1.

Pressure-jump pseudo-3D NMR pulse scheme used for stroboscopic measurement of ¹⁵N chemical shifts during protein folding. For details, see Figure S2.

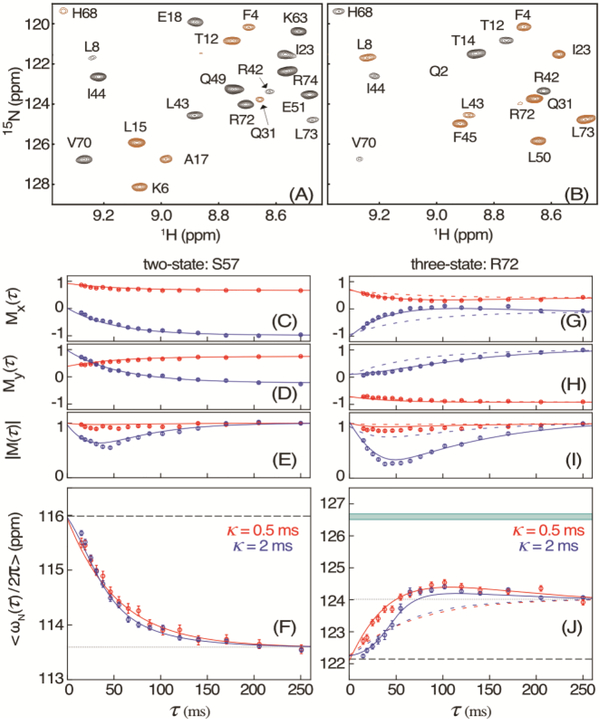
Figure 2.

Measurement of ¹⁵N chemical shifts during VA2-ubiquitin folding. (A, B) Small region of the HSQC spectrum, recorded with the scheme of Figure 1 for τ = 10 ms and κ = 2 ms, modulated by (A) cos(ω_Nκ) and (B) sin(ω_Nκ). Extension of the 50-ms t₁ time domain to 75 ms by the NUS reconstruction program SMILE³⁴ was used to slightly increase both resolution and sensitivity. Negative intensity is shown in brown. For full spectra, see Figure S3. (C) M_x(τ) and (D) M_y(τ) magnetization of residue S57 after evolution for κ = 0.5 ms (red) and κ = 2 ms (blue), and (E) the corresponding magnitude |M(τ)|, with these values normalized to |M(τ)| = 1 at τ = 248 ms. Solid colored lines correspond to the values predicted for a two-state folding model with ρ = 14.3 s⁻¹ and known chemical shifts¹⁴ of the unfolded (F, dashed line) and folded (F, dotted) states at 1 bar. (F) Apparent average chemical shift <ω_N/2π> at time τ after the pressure drop. (G-J) Analogous to (C-F) but for residue R72 with solid lines corresponding to a three-state model with k_u→i = 13.2 s⁻¹; k_u→f = 6.5 s⁻¹; and k_i→f = 12.0 s⁻¹, and colored dashed lines for the two-state model. The band at 126.6 ppm in (J) depicts the fitted ¹⁵N shift of the intermediate state. The full set of residues is shown in Figure S4. The error bars in (C-E) and (G-I) indicate the RMS noise in the M_x and M_y spectra, scaled by the normalization factor of |M|. Error bars in (F) and (J) indicate the uncertainty in the average chemical shift derived from the RMS noise in the M_x and M_y spectra

For a two-state folder at time t after the pressure is dropped to 1 bar, the probability that the angular resonance frequency of any given nucleus switches from unfolded ω_U to folded ω_F during a short interval dt equals ρe^-ρtdt, where ρ is the protein folding rate. Thus, at time τ a fraction e^−ρτ resonates with frequency ω_U and the remainder, (1 - e^−ρτ), with ω_F. During the κ interval, the corresponding magnetization vectors accumulate phases of ω_Uκ and ω_Fκ, respectively, of which the fractions cos(ω_Uκ) and cos(ω_Fκ) are returned to the +z axis by the subsequent 90_-x pulse, or sin(ω_Uκ) and sin(ω_Fκ) for the second experiment where a 90_y pulse terminates the stroboscopic observation. Only proteins that are natively folded at the start of the subsequent ¹⁵N evolution period contribute to the resonance intensity of the folded protein in the HSQC spectrum. While this requirement is met for all proteins in the (1 - e^−ρτ) folded fraction, only a fraction 1 - e^{−ρ(Τ−τ)} of the unfolded protein fraction (e^-ρτ) will switch to the folded state between its stroboscopic encoding and the start of ¹⁵N t₁ evolution. We also must account for the small fraction, A, of the protein that does not unfold at 2.5 kbar (A≈6%).

In the limit where ρκ « 1, the amplitude of the observed, folded protein magnetization is then given by

$${\mathrm{M}}_{\mathrm{x}}(\tau )\approx \left(1-A\right)[1-{\mathrm{e}}^{-\mathrm{\rho }(\mathrm{T}-\tau )}]{\mathrm{e}}^{-\mathrm{\rho }\tau }\cos ({\mathrm{\omega }}_{\mathrm{U}}\mathrm{\kappa })+[A+\left(1-A\right)(1-{\mathrm{e}}^{-}{}^{\mathrm{\rho }\tau })]\cos ({\mathrm{\omega }}_{\mathrm{F}}\mathrm{\kappa })$$ (1)

and an analogous expression for M_y(τ) in which sin substitutes for cos. Depending on the values of ω_Uκ, the amplitude of the HSQC signal can be positive or negative (Figure 2A, B; Figure S3).

The weighted average frequency is given by

$$<\mathrm{\omega }(\tau )>={\mathrm{\kappa }}^{-1}{\tan }^{-1}\left[{\mathrm{M}}_{\mathrm{y}}(\tau )/{\mathrm{M}}_{\mathrm{x}}(\tau )\right]$$ (2)

up to the addition of an integer multiple of 2π/κ, analogous to aliasing in traditional Fourier sampling. For a two-state folder with small chemical shift difference (ω_U-ω_F) and ρT » 1, <ω(τ)> simply becomes the population-weighted average frequency, decaying exponentially from [(1-A)ω_U + Aω_F] to ω_F when τ is incremented from 0 to T (Figure 2F). When κ « π(Δω_N)⁻¹ is not satisfied, the signal magnitude exhibits a minimum in |M(τ)| = √[M_x(τ)² + M_y(τ)²] where

$${\tau }_{\min }={\mathrm{\rho }}^{-1}\ln \left[2\left(1-A\right)\right],$$ (3)

with fractional amplitude cos[(ω_U −ω_F)τ_min/2] relative to |M(Τ)|. Note that ω_U at 1 bar can be measured at high precision from a separate pressure-jump HSQC spectrum (Figure S1),¹⁴ and ω_F is known from the folded protein HSQC spectrum. Therefore, for the 2-state folding model, M_x(τ), M_y(τ), |M(τ)|, and <ω(τ)> can be calculated for any value of κ (Figures 2 and S4), and then be compared to experimental data to test validity of the model. The use of large κ values subsequently becomes advantageous, as the minimum of |M(τ)| becomes deeper, and its position better defined. As seen from eq 3, for a 2-state folder, the position of the minimum should be the same for all residues.

Experiments were carried out at 600 MHz ¹H frequency, for a 0.3 mM ¹⁵N labeled VA2ubiquitin sample, pH 6.4, using a Bruker Instruments cryogenic probehead with a z-axis pulsed field gradient accessory. A 2.7-mm ID zirconia sample cell (Daedalus Inc.) was used, rated to withstand pressures of up to 3 kbar.³¹ Two data sets were collected, using κ = 0.5 ms and κ = 2 ms. For κ = 0.5 ms, <ω(τ)> can be determined uniquely from the ratio of M_x(τ) and M_y(τ) over a bandwidth of 2 kHz, which suffices to cover the entire range of backbone amide ¹⁵N chemical shifts in VA2-ubiquitin. The precision, ε, at which <ω(τ)>= θ /κ can be determined from M_y(τ) / M_x(τ) is limited by the uncertainty in θ, which is determined by the root-mean-square noise, N, in these spectra:

$$\mathrm{\epsilon }(\mathrm{\tau })=\{N/|\mathrm{M}(\tau )\left|\right\}/\mathrm{\kappa }$$ (4)

In practice, we obtain |M(τ)| / N ratios of ca 40:1 when using 2 scans per free induction decay (FID). This corresponds to an uncertainty of ε(τ) ≈ 50 rad/s, or 0.13 ppm for κ = 0.5 ms. As seen from eq (4), longer κ durations reduce the uncertainty in <ω(τ)>; however, (ω_U - ω_F)κ « π may no longer be satisfied, causing a loss in |M(τ)| when τ approaches τ_min, which may offset the gain from the larger denominator.

We have previously shown that VA2-ubiquitin folds with comparable efficiency via two parallel pathways: one with a single barrier, and one with two barriers, giving rise to a meta-stable, short-lived intermediate that was identified through an upfield shifted resonance of L50-C^δ2H₃.¹⁴ However, in the above analysis of M(τ), three-state folding will be indistinguishable from two-state if the resonance frequency of the intermediate ω_I equals that of the folded state ω_F, as applies for example for S57 (Figure 2; Figure S4). By contrast, many other residues deviate strongly from simple two-state behavior. For example, <ω(τ)> of R72 initially increases from its unfolded value of 122 ppm to downfield of 124 ppm, before returning to its folded value of 123.9 ppm (Figure 2J). The latter behavior points to a chemical shift value of the intermediate that is downfield of 124 ppm. Considering the folding process is dominated by the sum of two- and three-state pathways, fitting the predicted <ω(τ)> to the data (SI, text) yields the chemical shifts, ω_I, of the intermediate in the three-state pathway (Figure 3B; Table S1).

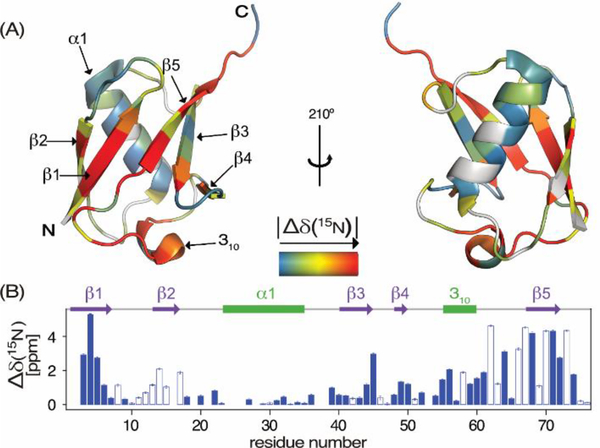
Figure 3.

¹⁵N chemical shift differences, |Δδ(¹⁵N)| = |δ^I – δ^F|, between the meta-stable intermediate and natively folded VA2-ubiquitin. (A) Color coded on a backbone ribbon structure. Residues for which Δδ(¹⁵N) could not be determined are shown in grey. (B) Δδ(¹⁵N) as a function of residue number, with negative values depicted as open bars.

Evaluation of ω_F and ω_I shows that the largest differences between them are located in strands β5, the loop preceding β5, strand β1, and the last few residues of β3 (Figure 3). Remarkably, deviations from 2-state folding extend to at least residue R74, indicating that this residue must be structured in the intermediate state, even while in the native protein it is significantly disordered. Remaining residuals in the 3-state fits (Figure 2J; Figure S4) could point to low fractional population of additional intermediates, but also could result from small non-idealities in the pressure profile, or from the change in temperature following the adiabatic expansion associated with the pressure drop.

We have shown that it is possible to determine ¹⁵N chemical shifts of short-lived protein folding intermediates. We anticipate that the method can be readily extended to the measurement of ¹³C′ and ¹³C^α frequencies, provided the folding process is not more complex than three-state. These chemical shifts then will provide an alternate pathway to studying the structure of such intermediates, analogous to the probing of chemical shifts of invisible structural states by relaxation dispersion NMR.^32–33