The effects of varying class distribution on learner behavior for medicare fraud detection with imbalanced big data

Abstract

Healthcare in the United States is a critical aspect of most people’s lives, particularly for the aging demographic. This rising elderly population continues to demand more cost-effective healthcare programs. Medicare is a vital program serving the needs of the elderly in the United States. The growing number of Medicare beneficiaries, along with the enormous volume of money in the healthcare industry, increases the appeal for, and risk of, fraud. In this paper, we focus on the detection of Medicare Part B provider fraud which involves fraudulent activities, such as patient abuse or neglect and billing for services not rendered, perpetrated by providers and other entities who have been excluded from participating in Federal healthcare programs. We discuss Part B data processing and describe a unique process for mapping fraud labels with known fraudulent providers. The labeled big dataset is highly imbalanced with a very limited number of fraud instances. In order to combat this class imbalance, we generate seven class distributions and assess the behavior and fraud detection performance of six different machine learning methods. Our results show that RF100 using a 90:10 class distribution is the best learner with a 0.87302 AUC. Moreover, learner behavior with the 50:50 balanced class distribution is similar to more imbalanced distributions which keep more of the original data. Based on the performance and significance testing results, we posit that retaining more of the majority class information leads to better Medicare Part B fraud detection performance over the balanced datasets across the majority of learners.

Introduction

The healthcare industry in the United State (U.S.) faces fundamental challenges, with the availability and affordability of medical care, today and into the future. As the overall population increases, the need for quality healthcare becomes more and more vital to society contributing to the general health and well-being of all U.S. citizens. In particular, the growth of the U.S. elderly population [1] places additional strain on medical systems and insurance programs. The number of elderly citizens, ages 65 years or older, went up 28% from 2004 to 2015, versus an increase of just 6.5% for people under the age of 65 [2]. This increase is further compounded by skyrocketing U.S. healthcare spending which rose by 5.8%, totaling over $3.2 trillion, in 2015 [3]. These statistics adversely affect all U.S. healthcare programs but are of particular interest to the Medicare program. Medicare is a subsidized U.S. government program providing insurance to over 54.3 million beneficiaries over the age of 65 or younger individuals with specific medical conditions and disabilities [4]. Note that due to the federal and subsidized nature of the program, Medicare is not a functioning health insurance market in the same way as private insurance companies.

In order to improve the current state of healthcare, private and government programs are leveraging digital information, such as electronic health records (EHR), and embracing the use of big data [5, 6]. The quantity of the information in the healthcare industry today continues to grow with the adoption of EHRs and electronic insurance claims records [7], making big data fairly ubiquitous for data modeling and analytics in the healthcare industry [6]. Given the continued growth and use of big data, employing advanced data analytics and machine learning can be used to help improve U.S. healthcare through the use of healthcare-related big datasets [8]. There are currently efforts to reduce Fraud, Waste, and Abuse (FWA) in healthcare [9], but these efforts, in general, are not doing enough to reduce financial losses [10]. The Federal Bureau of Investigations (FBI) estimates that fraud accounts for 3–10% of all medical costs [11], or $19 billion to $65 billion in potential losses due to FWA. With Medicare alone accounting for 20% of U.S. healthcare spending [3], recovering even a fraction of losses due to FWA can lead to significant benefits for the Medicare program and its beneficiaries. The Centers for Medicare and Medicaid Services (CMS) has stated [12] that “those intent on abusing Federal health care programs can cost taxpayers billions of dollars while putting beneficiaries’ health and welfare at risk. The impact of these losses and risks magnifies as Medicare continues to serve a growing number of people.” Medicare fraud is traditionally detected by auditors, or investigators, who manually check thousands of claims for specific patterns indicating possibly suspicious, and possibly fraudulent, behaviors [13]. To improve the fraud detection process, big data and machine learning can be used to predict, or classify, possibly fraudulent events or providers, which could substantially lessen the workload for a fraud investigator [14–16]. To help facilitate novel methods of detecting fraud, the CMS has recently released Medicare data, for the 2012 to 2015 Calendar Years, to the public [17]. Medicare has two primary payment systems: fee-for-service and Medicare Advantage. We use the former as Medicare Advantage is obtained through a private company contracted with Medicare [18]. The interested reader can find more information on Medicare and Medicare fraud in [19, 20].

We address the issues presented herein by demonstrating methods to effectively detect Medicare fraud. We use the Medicare Provider Utilization and Payment Data: Physician and Other Supplier data, also known as Medicare Part B, from CMS which includes information on services provided to Medicare beneficiaries by physicians and other healthcare professionals within the U.S. and its commonwealths. The Medicare data is from calendar years 2012 to 2015, with 2015 being released in June 2017. The original combined Medicare dataset, with over 37 million instances, is considered big data for which we use to build different learners. In order to validate that the learners actually detect fraud, we incorporate fraud labels. The Medicare data does not include labels for fraud, so we use information in the Office of Inspector General’s (OIG) List of Excluded Individuals/Entities (LEIE) database [21].

In our paper, we detail a novel approach for processing the Part B data and integrating fraud labels, from the LEIE database, with the Medicare data, per provider [22]. This involves aggregating the Medicare data to the provider-level, to mirror what is currently available in the LEIE database, and appropriately labeling each instance as fraud or non-fraud. We also discuss a unique method of handling mismatched date formats to reduce incorrect fraud labeling. Known fraudulent providers are much less common than non-fraudulent providers leading to an imbalance in the number of fraud class labels, or class distributions. This class imbalance is problematic for machine learning approaches due to such a small number of fraud instances (minority or positive class) versus non-fraud instances (majority or negative class), leaving a learner with very few discriminatory patterns to assess fraudulent providers. This is akin to looking for the proverbial needle in a haystack and fairly common when using big data sources [23]. We mitigate the adverse effects of class imbalance on learners by using data sampling, specifically random undersampling, to create seven class distributions. The learners are trained on each class distribution and evaluated using 5-fold cross-validation with 10 repeats. With the Medicare Part B data and LEIE fraud labels, we validate six learners using the Area Under the Receiver Operating Characteristic (ROC) Curve (AUC) to gauge fraud detection performance. Lastly, we discuss interpreting learner fraud predictions to provide insights into how predictions are made and future research into possible real-world applications.

Overall, Random Forest produced the highest AUC of 0.87302 for the 90:10 class distribution, with Naive Bayes being the worst performing learner. The trend across class distributions shows that most learners have decreasing performance as the classes become more imbalanced with less minority class representation, with the exception of C4.5 decision tree. With that, Logistic Regression, C4.5, and Naive Bayes show relatively stable performance across all class distributions, both balanced and imbalanced. Our results indicate that varying class distributions, due to the highly-imbalanced nature of the data, provides good Medicare fraud detection performance. Moreover, the information provided by the non-fraud instances changes learner performance and produces varying results based on the particular learner used with most learners benefiting from the increased majority class representation. Even so, Random Forest is significantly better than all other learners for all but the most imbalanced class distribution. The main contributions of this paper are:

• Detailing Medicare Part B big data processing with a unique approach to mapping fraud labels

• Discussing fraud detection performance, focusing on learner behavior across different class distributions with limited fraud labels

To the best of our knowledge, there are no other studies that detail, to this extent, Medicare Part B data processing and the mapping of fraud labels, using this big dataset to investigate learner behavior and performance with varying class distributions for Medicare fraud detection.

The remainder of the paper is organized as follows. Section 2 discusses works related to the current research, focusing class imbalance and Medicare-related fraud. In Sect. 3, we detail the Medicare dataset and LEIE database and discuss our design of experiment which includes class imbalance, learners, performance metric, and hypothesis testing. In Sect. 4, the results of our research are discussed. Finally, Sect. 5 summarizes our conclusions and ideas for future work.

Related works

Several studies incorporate the Medicare provider and utilization data from CMS to assess potential fraudulent activities. These works detect fraud in various ways by using descriptive statistics, data mining techniques, or supervised or unsupervised machine learning classification methods [24]. Because our research is on fraud detection using Medicare data, we focus our discussion on works using only this dataset for identifying potential fraud.

A study by Feldman et al. [25] discusses correlations between a physician’s schooling, or educational background, and the how they practice medicine. The authors use 2012 Medicare data to compare physician’s medical school charges, procedures, and payments. From this, they identify possible practice anomalies. A geographical analysis is presented with the national distribution of school procedure payments and charges to compare against specific physician information. The authors then attempt to determine potential misuse of the Medicare system, and, potentially, mark certain physicians as being fraudulent early in their careers which can be seen as a preventative step. One study [26] uses 2012 Medicare data with exclusion labels. The authors are interested in who the perpetrators are and what happens after they get caught. They use descriptive statistics and make recommendations, such as the use predictive models to detect Medicare claims fraud. Another work by Ko et al. [27] look at variability between physicians to detect possible misuse or inefficiencies in provider utilization. They focus their work on Urologists from the 2012 Medicare dataset using the utilization and payment information to determine any estimated savings from standardized service utilization data. The authors found a strong correlation between the number of patient visits with Medicare reimbursements. They found that there could be a potential $125 million in savings in provider utilization, which is about 9% of total expenditures within Urology.

Rather than using only descriptive statistics and correlations, other works employ unsupervised machine learning approaches to detect possible Medicare fraud. Sadiq et al. [28] propose a framework called the Patient Rule Induction Method. This uses bump hunting to determine the peak anomalies in the data by spotting spaces of higher modes and masses. From the 2014 Medicare data, the authors use their framework to find anomalous events which could be indicative of fraud or misuse, better characterizing the data’s feature space to uncover events leading to monetary losses. In a previous work [29], we build a multivariate regression model, for each provide type or specialty such as Cardiology. From this model, the studentized residuals are generated and used as inputs into a Bayesian probability model. The idea is to characterize possible outliers in the Medicare data and then produce the probability of each instance being an outlier, which could indicate the likelihood of fraud. We provided some preliminary comparisons between other outlier detection methods, like Local Outlier Factor, and our method performed favorably. Using the 2013 Medicare dataset, we flag possible fraud by using a regression model to establish a baseline for expected payments [30]. We use this baseline and compare the actual payments with any deviations beyond a defined threshold, which are seen as outliers, marked as possible fraud.

Even with the aforementioned works, the number of studies using the publicly available CMS Medicare data is minimal. In particular, classifying Medicare fraud using supervised machine learning approaches and integrating known fraudulent provider labels are limited. These remaining works incorporate labels to detect fraud using supervised methods.

Though not using fraud labels, our research group conducted an exploratory study to classify a physician’s provider type, or specialty [31]. We specifically look at whether the predicted specialty differs from the actual specialty, as seen in the Medicare data. Thus, if we can predict a physician’s specialty accurately (based on F-score), then we could potentially find anomalous physician behaviors and flag these as potential fraud for further investigation. For instance, if a Dermatologist is accurately classified as a Cardiologist, then this could indicate that this particular physician is acting in fraudulent or wasteful ways. We build a Multinomial Naive Bayes classifier using the 2013 Florida-only Medicare data and the F-score to assess classification performance. We show that 67% of the eighteen known fraudulent physicians were found to be fraudulent.

In order to better assess fraud detection capabilities, several studies employ the LEIE database to generate fraud labels. Chandola et al. [32] present a preliminary study using Medicare claims data with enrollment data to detect fraud employing techniques such as social network analysis, text mining, and temporal analysis. Specifically, the authors build a logistic regression model, using features derived from temporal analysis, to classify fraudulent providers. The labels come from the Texas Office of Inspector General’s exclusion database which is similar to the LEIE database. In their study, the discussion on mapping of labels to the Medicare data is unclear. To validate and improve upon a previous study [31], our research group conducted experiments using the 2013 and 2014 Florida-only Medicare data and the LEIE database for fraud labels [33]. In order to improve upon the Multinomial Naive Bayes learner, we propose and test three improvement methods: feature selection and sampling, removal of low scoring specialties, and grouping similar specialties. Additionally, to mitigate some of the adverse effects of class imbalance, we generate new datasets using random undersampling and Synthetic Minority Over-sampling Technique (SMOTE) each with only a single class distribution. Again, F-score is used to measure detection performance. We found that our improvement methods are dependent on the specialties with some specialties showing good improvement with certain methods and others indicating mixed results.

A study by Branting et al. [34] uses the 2012 to 2014 Medicare data, to include Part D, and LEIE exclusion labels for fraud detection. They generate a graph of providers, prescriptions, and procedures. A J48 decision tree, implemented in Weka, was built with 11 graph-derived features using 10-fold cross-validation. To address class imbalance, the authors kept 12,000 excluded providers and randomly selected 12,000 non-excluded providers, using only a 50:50 class distribution. The authors used 12,153 excluded providers for the fraud labels from the LEIE database. They use NPI matching and an identity-matching algorithm to incorporate exclusion labels with the Medicare data. Nevertheless, it is not apparent as to whether the authors made any adjustments for waivers, exclusion start dates, or the length of the exclusion period. The specific exclusion rules used are also missing. These details are necessary to reduce redundant exclusion labels and determining accurate fraud detection performance results. Thus, due to this lack of discussion on the mapping of exclusion labels, the results of their study cannot be reproduced or compared with our current research.

We differ from the related works in several key ways. We provide a detailed account of Part B data processing and the mapping and generation of fraud labels using the LEIE database. With regards to detecting Medicare fraud, our study is focused on the behavior of each learner using different class distributions. We look at how sensitive each learner is to varying distributions and how well they detect fraudulent providers. Furthermore, our study is a more complete and comprehensive study using six different learners, over seven class distributions. There are a very limited number of Medicare fraud detection studies that provide sufficient details on data processing making it difficult to reproduce experiments and directly compare fraud detection performance. We know of no other related papers that incorporate all of these elements into such a representative study on Medicare Part B fraud detection.

Methodology

In this section, we present our design of experiment. We describe the data and the data processing steps and fraud label mapping. Additionally, we discuss class imbalance, the learners, and the experiment including cross-validation, the performance metric, and hypothesis testing.

Data

Our research considers Medicare provider claims information and known excluded providers for fraud detection. There are two different sources of data used to generate the final dataset. The main dataset is the publicly available 2012 to 2015 Medicare Provider Utilization and Payment Data: Physician and Other Supplier data [35]. The other dataset is the LEIE database [21] used to generate class labels. The former provides the bulk of the information, whereas the latter is only used to match excluded providers. In this section we discuss the Medicare and LEIE datasets, as well as the data processing and mapping of LEIE fraud labels.

Medicare Part B

This dataset describes Medicare provider claims information, for the entire U.S. and its commonwealths, where each instance in the data shows the claims for a provider and procedure performed for a given year. Note that because the claims information is recorded by CMS after claims payments are made [36], we assume the data has been cleansed and is correct. The Medicare data includes provider information, average payments and charges, procedure codes, the number of procedures performed, and medical specialty (also known as provider type). Each provider, or physician, is denoted by his or her unique National Provider Identifier (NPI) [37]. The Medicare data is aggregated to, or grouped by, the following: (1) NPI of the performing provider, (2) Healthcare Common Procedure Coding System (HCPCS) code [38] for the procedure or service performed, and (3) the place of service which is either a facility or non-facility, such as a hospital or office, respectively. More specifically, each provider is associated with an HCPCS code (i.e. a specific service performed), for each place of service, thus the Medicare Part B data can be considered to provide procedure-level information.

In combining the 2012 to 2015 calendar year for Medicare Part B, we filter the data for non-prescription instances only. The prescription data are those HCPCS codes that are for specific services listed on the Medicare Part B Drug Average Sales Price file [17] and are not actual medical procedures. Moreover, keeping the prescription data affects the line_srvc_cnt feature which, instead of being the number of procedures performed, reflects the weight or volume of the drug. We filter for providers who participate in the Medicare program. Additionally, we only include features found in all four years. For example, the standardized payment variables are excluded because they only appear in the 2014 and 2015 Medicare data. Similarly, the standard deviation variables were excluded, because they are only in 2012 and 2013. Lastly, we retain providers with valid NPI numbers removing any instances with values of “0000000000” or instances missing both NPI and HCPCS values. The combined unaltered Medicare Part B dataset has 37,255,346 instances and 30 features. Table 1 lists the eight original Medicare features used in our study, to include a new ‘exclusion’ feature made up of the mapped LEIE fraud labels, and the feature type: numerical or categorical. NPI is the only feature not used to train learners, but rather for aggregation and identification. The remaining selected features include all available numerical values, such as payments, as well as certain categorical information like gender and specialty, which are all readily usable by most machine learning algorithms. It is important to note that these algorithms provide a principled way of including predictors and covariates that matter to the predictive outcome via feature selection or regularization. Each learner incorporates either automatic feature selection, regularization, or simply uses all the features to include predictors and possible covariates, for training. Given these machine learning-based techniques, it is not necessary to manually account for different features, but rather include them and allow the algorithm to incorporate a data-driven approach in using the information from the features towards a prediction. With that said, the remaining 22 features, which consist of mostly demographic information (such as address) and as such are non-trivial to use with most machine learning methods, will be considered, along with other feature selection techniques and regularization configurations, in future work.

Table 1.

Description of Medicare features

Feature	Description	Type
npi	Unique provider identification number	Categorical
provider_type	Medical provider’s specialty (or practice)	Categorical
nppes_provider_gender	Provider’s gender	Categorical
line_srvc_cnt	Number of procedures/services the provider performed	Numerical
bene_unique_cnt	Number of distinct Medicare beneficiaries receiving the service	Numerical
bene_day_srvc_cnt	Number of distinct Medicare beneficiary/per day services performed	Numerical
average_submitted_chrg_amt	Average of the charges that the provider submitted for the service	Numerical
average_medicare_payment_amt	Average payment made to a provider per claim for the service performed	Numerical
exclusion	Fraud labels from the LEIE database	Categorical

LEIE

The OIG, in accordance with Sections 1128 and 1156 of the Social Security Act, can exclude individuals and entities from federally funded healthcare programs for a designated period [21]. Excluded providers are forbidden from participating in programs, such as Medicare, for a minimum exclusion period. The LEIE is aggregated to the provider-level, thus does not have information regarding specific procedures related to fraudulent activities. Understanding the grouping, as with the Part B data, is important for data integration and/or class label generation. Even though the LEIE database contains excluded providers to be used as fraud labels, it is not all-inclusive where 38% of providers with fraud convictions continue to practice medicine and 21% were not suspended from medical practice despite their convictions [26]. We incorporate these excluded providers from the LEIE database [21] as labels to indicate fraud. There are different categories of exclusions, based on severity of the offense, described by various rule numbers. We do not use all exclusions, but rather filter the excluded providers by selected rules indicating more severe convictions and/or revocations. These rules are shown in Table 2.

Table 2.

LEIE exclusion rules

Rule number	Description	Min. period
1128(a)(1)	Conviction of program-related crimes	5 years
1128(a)(2)	Conviction for patient abuse or neglect	5 years
1128(a)(3)	Felony conviction due to healthcare fraud	5 years
1128(b)(4)	License revocation or suspension	5 years
1128(c)(3)(g)(i)	Conviction of 2 mandatory offenses	10 years
1128(c)(3)(g)(ii)	Conviction on 3 or more mandatory offenses	Indefinite

Data processing and fraud labeling

As mentioned, the Medicare data is considered a procedure-level dataset, whereas the LEIE database only contains provider-level information with no reference to location or procedure performed. For our study, in order to obtain exact matches, we use only NPI to match fraud labels to the Medicare data. Future work may incorporate other approaches, such as fuzzy string matching, to possibly increase the number of fraud labels. In integrating fraud labels with the Medicare data, we only consider providers on the exclusion list as fraudulent and those not on the list as non-fraudulent providers. Additionally, the Medicare dataset is annual, whereas the LEIE database has a specific date (month/day/year) for when the exclusion starts and the length of the exclusion period. For example, if a provider is convicted for patient abuse or neglect (rule number 1128(a)(2)) beginning 1/1/2008, then, based on a minimum exclusion period of 5 years, this provider would have an exclusion period from 1/1/2008 to 1/1/2013.

Because the Medicare dataset is at the procedure-level (NPI and HCPCS) but the LEIE database is at the provider- or NPI-level, we elect to aggregate the Medicare data to the provider-level for a one-to-one mapping of fraud labels from the LEIE database. Note that there is currently no known data source for fraud labels by provider and procedure procedure performed. The process for aggregating the Medicare data to the provider-level involved grouping the data by specialty (provider type), provider (NPI), gender, and Medicare year, aggregating over procedure (HCPCS) and place of service. To avoid too much information loss due to this aggregation, we derive additional numeric features, from the original five numeric features, to include the mean, sum, median, standard deviation, minimum, and maximum. It is important to note that all features are complete, except for standard deviation which contains NA indicating missing or not available values. The reason for this is the grouping creates individual, unique claims (i.e. instances) for any given year. The sample standard deviation of this single instance is NA, whereas the population standard deviation is 0 showing no claim variability. Given that there is a legitimate claim, we assume nothing is missing and replace standard deviation NA values with 0 to show that this single claim, in fact, has no claim-to-claim variability. In addition to the aforementioned numerical features, we include the specialty and gender categorical features. To build each learner with a mixture of numerical and categorical features, we transform the categorical by using one-hot encoding. This method uses the categorical values to generate dummy features with binary values indicating the presence of this variable. A value of one is assigned if a value is present otherwise zero, versus all other dummy features. This translates each of the original categorical values into distinct binary features. Note the original gender feature contains missing values which are represented by a value of 0 for both male and female. Table 3 summarizes the original Medicare data, the NPI-level aggregated data, and the NPI-level aggregated data with the one-hot encoded categorical features.

Table 3.

Summary of Medicare datasets

Dataset	Instances	Features
Original	37,255,346	30
NPI-level	3,692,555	35
NPI-level (one-hot encoded)	3,692,555	126

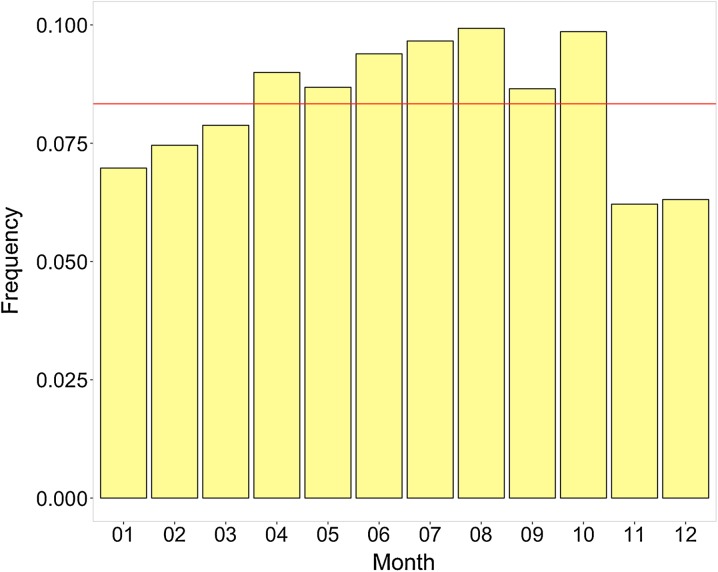
From the LEIE database, we first create the range of each exclusion period by adding the minimum length of the exclusion to the exclusion start date to get the exclusion end date. We then compare the month and year of the exclusion end date with any waiver or reinstatement dates. The smallest month and year is then assigned as the new exclusion end date. For example, if the exclusion end date is 2/12/2015 and there is a waiver date of 1/1/2013, then the new exclusion end date is changed to the earlier date of 1/1/2013. This accounts for providers that may still be in the exclusion period but received a waiver or reinstatement to use Medicare, thus no longer considered fraudulent on or after this waiver or reinstatement date. In order to avoid too few or too many fraud labels, we round the new exclusion end date to the nearest years based on the month. So, if the month is greater than 6 then the exclusion end year is increased to the following year, otherwise the current year is used. In this way, partial years are addressed with the assumption that if an exclusion end date occurs during the latter part of a year, the majority of that year can be assumed as fraud. Otherwise, very little of the year is before the exclusion end date, then we assume the provider claims in that year are not fraudulent. Figure 1 shows the distribution of exclusion end date frequency by month over all Medicare Part B years. The frequencies are generally uniform, i.e. March is similar to September. Therefore, a simple half-year rounding scheme is leveraged to better represent the fraud labels in a given year based on the monthly distribution. Again, this is because the Medicare Part B dataset only includes years, whereas the LEIE has the full date. The exclusion end dates are key to generating the fraud label mapping in the Medicare Part B data.

Fig. 1.

Monthly frequency of exclusion end dates

The updated LEIE database is then joined with the Medicare Part B data based on NPI. A flag is created, initialized to false, to hold the fraud labels (where fraud is set to true). We then mark any provider as fraudulent if there claims year is prior to the exclusion end year. For example, if a provider’s exclusion start year is 2008, with a 5-year period, then the exclusion end date is 2013 which overlaps with the available Medicare years, thus 2012 and 2013 are labeled as fraud for that provider in those years. Note that providers can only be labeled as fraudulent if they are in the LEIE database and the exclusion period is within the 2012, 2013, 2014, and 2015 Medicare years, because these are the only years of Part B data currently available. By using a threshold where anything less than the exclusion end date is flagged as fraud, we can detect behaviors leading up to the fraud, as well as so-called improper payments made by excluded providers. Detecting the latter behavior is valid and can be considered as fraud per the False Claims Act (FCA) [39]. The final Part B dataset includes all known excluded providers marked via the exclusion class feature. There are 3,691,146 non-fraud and 1,409 fraud labels. This data is considered highly imbalanced with only 0.04% of instances being labeled as fraud.

Class imbalance

Since our Medicare dataset is severely imbalanced, we employ data sampling to mitigate the adverse effects of class imbalance [40]. The issue with class imbalance is that a learner tends to focus on the majority class (non-fraud), since the number of minority class (fraud) instances is so small thus do not offer sufficient discriminatory value. Data sampling is an effective means of improving learner performance on imbalance datasets by changing the class distributions in the training data [41]. Oversampling and undersampling are two general techniques for applying random data sampling for class imbalance. Oversampling balances classes by adding instances to the minority class via sampling with replacement. Undersampling reduces the size of the majority class by sampling without replacement. Another popular method for oversampling is Synthetic Minority Oversampling TEchnique (SMOTE) [42]. This approach generates artificial data using sampling with replacement and k-nearest neighbors to increase the size of the minority class. Any method to reduce the deleterious effects of class imbalance has both strengths and weaknesses. For undersampling, the primary weakness is the loss of potentially useful information in discarding instances from the majority class. Oversampling increases the overall size of the dataset, which can be a problem for a learner when using big data. With such a severely imbalanced dataset, oversampling creates too many duplicate instances of the minority class given the pool instances in this class is so small. Additionally, because oversampling can duplicate minority class instances, overfitting can be caused [43]. SMOTE suffers from an increase in data size, but, since this method uses artificial data and not exact instances, it is not as prone to overfitting.

In our study, we use random undersampling (RUS) because it retains all of the fraud labels, it affords good performance (especially with big data), and has relatively few weaknesses [44, 45]. We generate seven different class distribution (majority:minority) which include: 99.9:0.1, 99:1, 95:5, 90:10, 75:25, 65:35, and 50:50. The selected distributions, or ratios, were chosen because they provide a reasonable representation of the majority class and reduce loss of information relative to the minority class. Retaining only 1% of the minority class is close to the minority class percentage of 0.4% in the original NPI-level Medicare Part B dataset, and substantially reduces the size of the dataset and decreases the time needed to build each learner. Moreover, the class distributions vary levels of imbalance to a balanced 50:50 distribution, so we can better gauge learner performance using severely imbalanced and balanced data. It is not necessarily advantageous to use a fully balanced class distribution for severely imbalanced data, because it entails throwing away a large proportion of the original dataset population. Because we elected to use RUS, we repeat the data sampling 10 times, per distribution, in order to reduce the overall information loss by reducing the size of the majority class. Each repeat randomly samples a different set of instances to remove from the majority class, thus selecting more majority class instances across the repetitions. Table 4 details the number of instances for each of the training datasets for the class distributions. This indicates that as the percentage of fraud instances increases, the representation of the non-fraud instances decreases relative to the full dataset.

Table 4.

Class distribution sample size

Technique	Fraud		Non-fraud
	%	#	%	#	Total
RUS	0.1	1,409	99.9	301,591	1,409,000
RUS	1	1,409	99	139,491	140,900
RUS	5	1,409	95	26,771	28,180
RUS	10	1,409	90	12,681	14,090
RUS	25	1,409	75	4,227	5,636
RUS	35	1,409	65	2,617	4,026
RUS	50	1,409	50	1,409	2,818

Learners

We use six different learners to assess fraud detection behavior across class distributions from severely imbalanced to balanced. Each learner is built and validated using the Weka machine learning software [24]. The default configurations and parameters are used with changes made when preliminary analysis indicated increased learner performance. Any additional learner optimization is left as future work. In this section, we briefly describe each learner and note any configuration changes herein.

The Naive Bayes (NB) learner [46] determines the probability that an instance belongs to a particular class using Bayes’ theorem. NB makes an assumption that all features, and thus conditional probabilities, are independent from one another in deciding on the predicted class label. Logistic Regression (LR) uses a sigmoidal, or logistic, function to generate values from [0,1] that can be interpreted as class probabilities. LR is similar to linear regression but uses a different hypothesis class to predict class membership [47]. In Weka, we use the default LR setting for the ‘ridge’ parameter which is the penalized maximum likelihood estimation with a quadratic penalty function (also known as L2 regularization). K-nearest neighbors (KNN), also called instance-based learning or case-based reasoning, uses distance-based comparisons among instances [48]. The distance measure is critical for KNN performance, with Euclidean distance being the typical choice. The ‘distanceWeighting’ parameter was set to ‘Weight by 1/distance’ and the number of neighbors was set to 5 (called 5NN herein).

Support vector machine (SVM) learner [49] creates a hyperplane to divide instances into two distinct groups, with the assumption that the classes are linearly separable. Support vectors are chosen to divide the instances in two groups by maximizing the distance between the classes. SVM uses regularization to avoid overfitting via the complexity parameter ‘c’. The Weka implementation of SVM incorporates sequential minimal optimization (SMO) for training SVM models. We set the complexity parameter ‘c’ to 5.0 and the ‘buildLogisticModels’ parameter to true. The C4.5 Decision Tree algorithm [50] uses a divide-and-conquer approach to split the data at each node based on the feature with the most information. The features at each node are automatically selected by minimizing entropy and maximizing information gain. Entropy can be seen as the measure of impurity or uncertainty of attributes, and information gain is a means to find the most informative attribute. The most important features are near the root node, with classification results found at the leaf nodes. In our experiments, we use ‘Laplace Smoothing’ and ‘no pruning’ which can lead to improved results on imbalanced data [51].

Our last learner is random forest (RF). This is an ensemble approach building multiple unpruned decision trees representing the forest. The classification results are calculated by combining the results of the individual trees, typically using majority voting [52, 53]. RF generates random datasets via sampling with replacement to build each tree. The feature at each node is automatically selected to be the most discriminating feature based on entropy and information gain. Furthermore, RF incorporates feature subspace selection to randomly assign i features for each decision tree. Due to the ensemble nature of and randomness in RF, this method is not likely to overfit the data. We build each RF learner with 100 trees only (denoted as RF100), with preliminary analysis showing no significant difference between 100 and 500 trees.

Performance metric

The highly imbalanced nature of the Medicare dataset can make the selection of a meaningful performance metric challenging. To mitigate this issue in imbalanced data, we use AUC [54] to evaluate learner fraud detection performance which has been shown to be an effective metric for class imbalance [55, 56]. The AUC, which indicates learner performance for binary classification, is calculated as the area under the receiver operating characteristic (ROC) curve. The ROC curve is used to characterize the trade-off between true positive (TP) rate, also known as recall or sensitivity, ($\frac{\mathit{TP}}{TP+FN}$) and false positive (FP) rate ($\frac{\mathit{FP}}{FP+TN}$), where FN and TN are the numbers of false negatives and true negatives, respectively. The ROC curve depicts a learner’s performance across all decision thresholds. The AUC is a single value that ranges from 0 to 1, where a perfect classifier results in an AUC of 1 and a value of 0.5 or less is equivalent to random guessing.

Cross validation

To evaluate learner performance, we incorporate k-fold cross-validation. The training data is divided into k-folds. A learner is trained on $k-1$ folds and tested on the remaining fold, with this process repeated k times. This ensures all data is used in training and validation. To prevent folds with little to no minority class instances, we use stratified cross-validation [24] which tries to ensure that each class is approximately equally represented across each fold. Specifically, we use 5-fold cross-validation repeated 10 times. The average of the 5-fold cross-validation scores, across all 10 repeats, is used for the final learner performance results. The use of repeats helps to reduce bias due to bad random draws when creating the folds.

Significance testing

In order to provide additional rigor around our AUC performance results, we use hypothesis testing to show the statistical significance of the Medicare fraud detection results. Both ANalysis Of VAriance (ANOVA) [57] and post hoc analysis via Tukey’s Honestly Significant Different (HSD) test [58] are used in our study. ANOVA is a statistical test determining whether the means of several groups (or factors) are equal. Tukey’s HSD test determines factor means that are significantly different from each other. This test compares all possible pairs of means using a method similar to a t-test, where statistically significant differences are grouped by assigning different letter combinations (e.g. group a is significantly different than group b).

Results and discussion

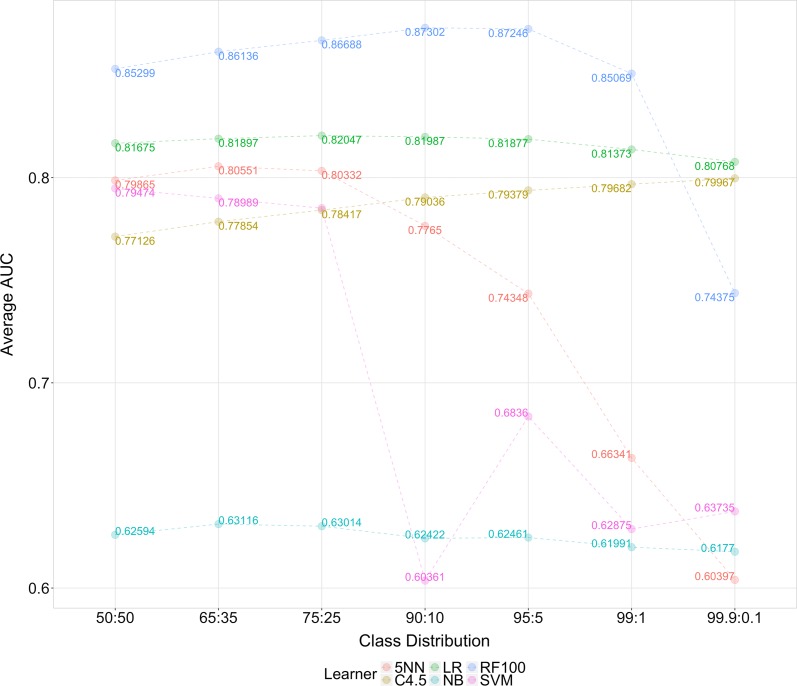
In this section, we present the results of our study focusing on fraud detection performance across the varying levels of class imbalance. In particular, we ascertain the best performing learner for detecting Medicare fraud and discuss the behavior of each learner over the class distribution. Table 5 shows the AUC results by learner and class distribution, with the highest scores in boldface for each class distribution. RF100 has the highest average AUC scores for all class distributions except for the most imbalanced ratio, with the highest overall AUC of 0.87302 at the 90:10 distribution. LR has the next highest performance results, with the best score for the 99:0.1 imbalanced class distribution. NB has the worst overall fraud detection performance, consistently poor for all distributions. The ensemble nature of RF100 with the randomness introduced in the dataset and automatic feature selection makes it robust to noise and overfitting which may contribute to its good overall fraud detection performance using the Medicare Part B data. Furthermore, regularization in LR and automatic feature selection in C4.5 (second and third best overall results, respectively) could also contribute to their relatively good detection performance over the other learners that do not perform any feature selections or modifications.

Table 5.

Learner AUC results by class distribution

Class distribution	5NN	C4.5	LR	NB	RF100	SVM
99.9:0.1	0.60397	0.79967	0.80768	0.61770	0.74375	0.63735
99:1	0.66341	0.79682	0.81373	0.61991	0.85069	0.62875
95:5	0.74348	0.79379	0.81877	0.62461	0.87246	0.68360
90:10	0.77650	0.79036	0.81987	0.62422	0.87302	0.60361
75:25	0.80332	0.78417	0.82047	0.63014	0.86688	0.78512
65:35	0.80551	0.77854	0.81897	0.63116	0.86136	0.78989
50:50	0.79865	0.77126	0.81675	0.62594	0.85299	0.79474

Figure 2 depicts the AUC trends for each learner for each class distribution, from imbalanced to balanced. Recall that with RUS, the number of minority class instances is equal that of the full dataset for all class distributions with modifications made to the majority class only. Thus, for these learners, the trend indicates datasets with a higher number of majority class (non-fraud) instances, while retaining a good minority class representation, produce similar or better AUC results. In other words, the balanced 50:50 class distribution exhibits performance similar to that of the more imbalanced distributions, such as 90:10, 95:5, and 99:1. Even so, AUC results for RF100, 5NN, and SVM decrease significantly as the training datasets becoming more imbalanced. Both 5NN and SVM perform quite poorly below the 75:25 class ratio indicating an inability to effectively discriminate non-fraud and fraud instances requiring more balanced datasets. For SVM, since only a limited number of fraud instances are represented in the entire dataset, there are more possible options for the separating hyperplane thus more likely to classify new instances into the non-fraud class. The 5NN learner’s poor performance could be due to overfitting the training data or the poor detection of global patterns in the dataset, as this method focuses on the nearest neighbors. Both of these learners, given more class imbalance, will tend to predict the most represented class.

Fig. 2.

AUC trends by Learner

Interestingly, for LR, C4.5, and NB, learner performance does not exhibit the same AUC variability across the different class distributions. This means that these learners perform similarly with either more balanced or imbalanced distributions. For instance, the 50:50 class distribution AUC is similar to the 99:0.01 class distribution. The C4.5 decision tree learner performs slightly better as the level of class imbalance increases. Additionally, LR and C4.5 outperform RF100 below the 99:1 class distribution, with LR being the most consistent learner across class distributions. For these learners with less variability in performance across class distributions, the fraud instances, from our previously discussed labeling process, provide adequate feature discrimination allowing these learners to detect the minority class patterns. These learners are less sensitive to changes in class distribution, especially with increasing class imbalance, showing similar fraud detection performance.

Table 6 shows the ANOVA test results with two factors: Learner and Class Distribution. The results indicate that each factor, and their interactions, are significant at a 5% significance level. In order to evaluate group differences, a Tukey’s HSD test is performed. Table 7 summarizes the significance of learner performance across all class distributions. RF100 is significantly better than all other learners followed by LR and C4.5. Table 8 shows the Tukey’s HSD results for each class distribution across all learners. The 75:25, 65:35, and 50:50 distributions are significantly better across all learners. This seems to indicate that more balanced datasets give improved fraud detection performance. And given that the 50:50 distribution is only slightly worse than some of the more imbalanced class distribution for each learner (with the exception of C4.5), we would expect it to be among the better class distributions. This is further skewed by the poor performance of 5NN and SVM below the 75:25 class distribution. With these patterns in mind, these post hoc test results do not necessarily imply that the 50:50 is the best distribution for detecting fraudulent activities.

Table 6.

ANOVA test results

	Df	Sum Sq	Mean Sq	F value	Pr(<F)
Learner	5	2.3033	0.4607	4139.6	< 2e−16
Class distribution	6	0.3248	0.0541	486.4	< 2e−16
Learner:class distribution	30	0.6127	0.0204	183.5	< 2e−16
Residuals	378	0.0421	0.0001

Table 7.

Tukey’s HSD learner results

Learner	Group	AUC	SD	r	Min	Max
RF100	a	0.84588	0.04299	70	0.73184	0.87809
LR	b	0.81661	0.00509	70	0.80421	0.82449
C4.5	c	0.78780	0.01027	70	0.76329	0.80438
5NN	d	0.74212	0.07374	70	0.59613	0.81067
SVM	e	0.70329	0.08011	70	0.57333	0.80285
NB	f	0.62481	0.01900	70	0.58679	0.68260

Table 8.

Tukey’s HSD class distribution results

Class distribution	Group	AUC	SD	r	Min	Max
75:25	a	0.78168	0.07449	60	0.60310	0.87122
65:35	a	0.78091	0.07299	60	0.59701	0.86816
50:50	a	0.77672	0.07286	60	0.58937	0.86045
95:05	b	0.75612	0.08495	60	0.59932	0.87809
90:10	c	0.74793	0.10114	60	0.57333	0.87705
99:01	d	0.72888	0.09519	60	0.58679	0.86023
99.9:0.1	e	0.70169	0.08627	60	0.59108	0.81047

Because half of the learners showed little variability in AUC across the class distributions, we assess the significance of varying the class distributions per learner. So, unlike the results in Table 8 which are across all learners, we now focus on each learner and their detection behavior for the different class distributions. Table 9 shows that the 75:25, 65:35, and 50:50 are all statistically similar for 5NN, LR, NB, and SVM, thus the high performance across all learners. The best RF100 class distributions, 99:10 and 99:5, are also higher performers along with LR which both provide significantly better fraud detection performance over the other learners and class distributions. Therefore, with the good performance of RF100, and to some extent LR, with more imbalanced datasets, we recommend using the 90:10 class distribution for Medicare Part B fraud detection. The use of this more imbalanced dataset ensures less loss of information, relative to the original dataset, by retaining more of the majority class instances unlike the balanced 50:50 class distribution.

Table 9.

Tukey’s HSD by learner results

Learner	Class distribution	AUC	Group	Learner	Class distribution	AUC	Group
RF100	90:10	0.87302	a	C4.5	99.9:0.1	0.79967	a
	95:5	0.87246	ab		99:1	0.79682	ab
	75:25	0.86688	bc		95:5	0.79379	bc
	65:35	0.86136	c		90:10	0.79036	c
	50:50	0.85299	d		75:25	0.78417	d
	99:1	0.85069	d		65:35	0.77854	e
	99.9:0.1	0.74375	e		50:50	0.77126	f
5NN	65:35	0.80551	a	LR	75:25	0.82047	a
	75:25	0.80332	ab		90:10	0.81987	a
	50:50	0.79865	b		65:35	0.81897	a
	90:10	0.77650	c		95:5	0.81877	a
	95:5	0.74348	d		50:50	0.81675	ab
	99:1	0.66341	e		99:1	0.81373	b
	99.9:0.1	0.60397	f		99.9:0.1	0.80768	c
NB	65:35	0.63116	a	SVM	50:50	0.79474	a
	75:25	0.63014	a		65:35	0.78989	a
	50:50	0.62594	a		75:25	0.78512	a
	95:5	0.62461	a		95:5	0.68360	b
	90:10	0.62422	a		99.9:0.1	0.63735	c
	99:1	0.61991	a		99:1	0.62875	c
	99.9:0.1	0.61770	a		90:10	0.60361	d

To be effectively incorporated into a real-word fraud detection scenario, a learner should be able to detect actual fraud cases (as demonstrated herein using AUC) and provide insight into how predictions are being made. Different learners provide differing levels of global and local interpretations for extrapolating meaning from their predictions. The former allows a learner to describe a prediction across all instances, whereas the latter explains predictions for a local region (i.e. a single instance). For example, LR and C4.5 decision tree allows for both global and local interpretations, with the coefficients of LR describing feature contributions towards each prediction and a decision tree’s paths outlining the features used when making predictions. This type of learner interpretability can provide important information for investigators in further examining possible fraudulent cases. As mentioned, we recommend the RF learner due to the accuracy, based on the AUC metric, of detecting Medicare Part B fraud. But, unfortunately, because RF is an ensemble of trees and thus not easily interpretable, directly explaining RF from a global perspective is not possible (unlike a single decision tree or logistic regression learner). Feature importance, however, can be derived from a trained learner and represent a measure of the impact a feature has on the overall prediction. Unlike the regression coefficients, the important features from a RF learner do not indicate how a feature may impact the results but simply importance related to other features. It is, however, possible to explore the path traversed for a particular instance and its associated prediction [59, 60] to indicate both the importance of certain features and how they may affect predictions (providing limited global interpretations). This is not a perfect solution, as this interpretation is not truly local or global, but does provide more meaningful information on fraud-related predictions. Even so, we have demonstrated that the models that can be interpreted both globally and locally (e.g. C4.5 and LR) have significantly worse fraud detection performance than the top performing RF learner. Future research will include performing additional experiments to assess feature importance and provide estimates for local and global interpretability.

Conclusion

The problem of healthcare fraud is of critical concern to all U.S. citizens. The monetary losses due to fraud are estimated in the billions of dollars, which negatively impact the U.S. government and beneficiaries. In particular, due to the increase in the elderly population, programs such as Medicare are becoming increasingly important and susceptible to fraud. Given the importance of Medicare, combating fraud is an essential part in providing quality healthcare for the elderly. In this study, we focus on detecting fraudulent provider claims in the Medicare Part B big dataset. We provide a detailed discussion on data processing and the mapping of fraud labels using excluded providers from the LEIE database. In particular, we discuss the differences in Part B and LEIE data aggregation and a method to more accurately map fraud labels. In addition, the disparities in dates between the datasets are reviewed with a unique method to reduce under- or over-labeling fraudulent instances. From this processed and labeled big data, we generate seven different class distributions to help mitigate the issue of class imbalance, due to the limited number of known fraudulent providers. For each of these distributions, we assess six different learners. Overall, RF100 with the 90:10 class distribution is the best learner with a 0.873 AUC. Furthermore, we show that the 50:50 balanced class distribution does not lead to the best performance, for any learner, and is similar to that of more imbalanced class distributions. The better performing methods, like RF100 and LR, perform better with some imbalance indicating that a better representation of the majority (non-fraud) class can increase performance. We show statistically significant differences between all the learners, as well as differences in class distributions for each learner which further supports the recommendation to use RF100. Lastly, we discuss interpreting learner fraud predictions and show there are possible implementations that provide additional insights into fraud predictions that could be used for further investigations into possible fraudulent providers. Future work includes adding other Medicare-related data sources, such as Medicare Part D, using more data sampling methods for class imbalance, and testing other feature selection and engineering approaches. Furthermore, if possible, the recommended RF learner should be compared to other Medicare fraud detection methods found in the related literature [61].